Towards a Transferable Antecedent Rainfall—Susceptibility Threshold Approach for Landsliding
Abstract
1. Introduction
2. Study Area and Data
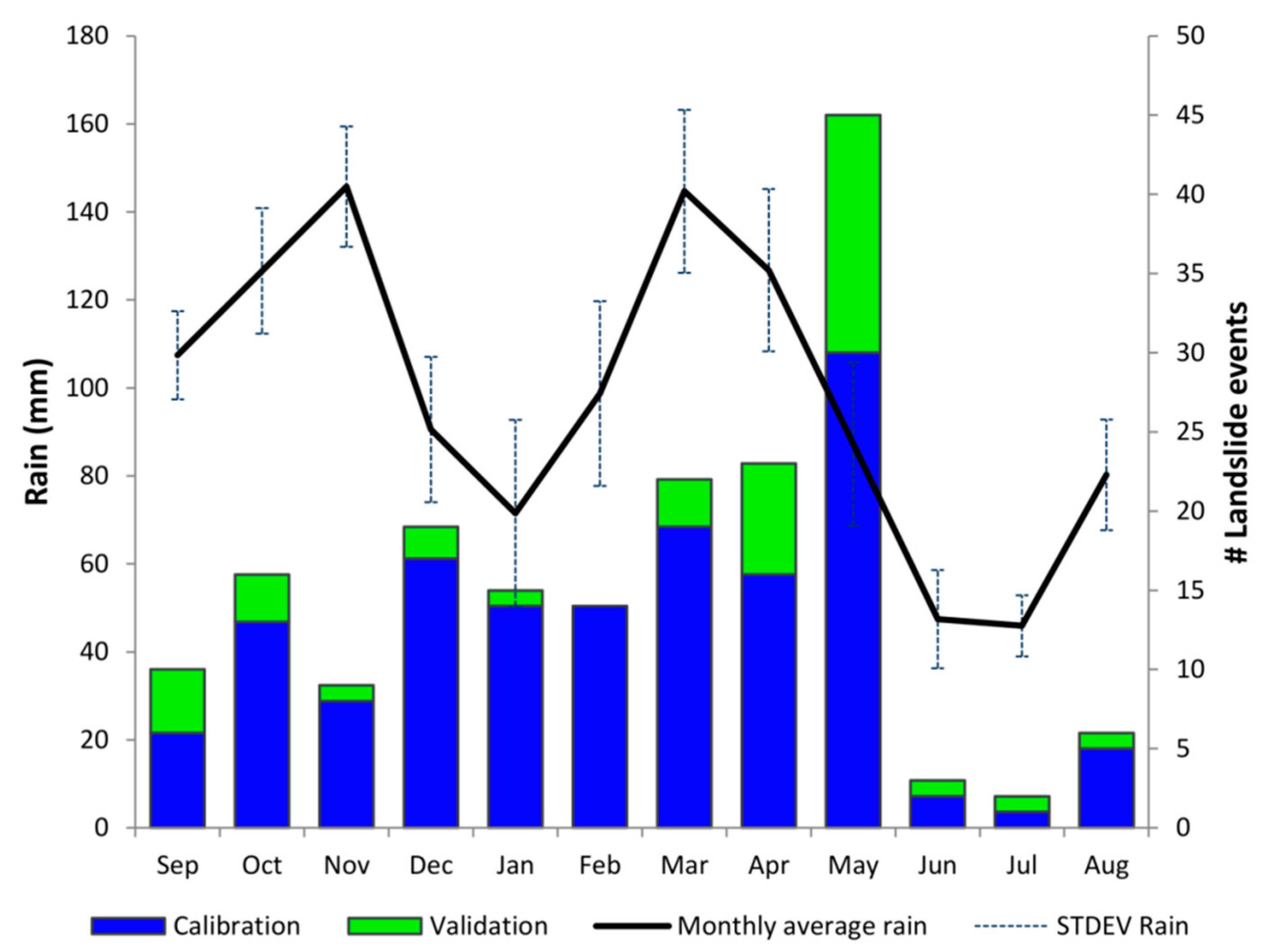
2.1. Underreported Landslide Events in the WEAR
2.2. Satellite-Based Rainfall
2.3. Susceptibility Models
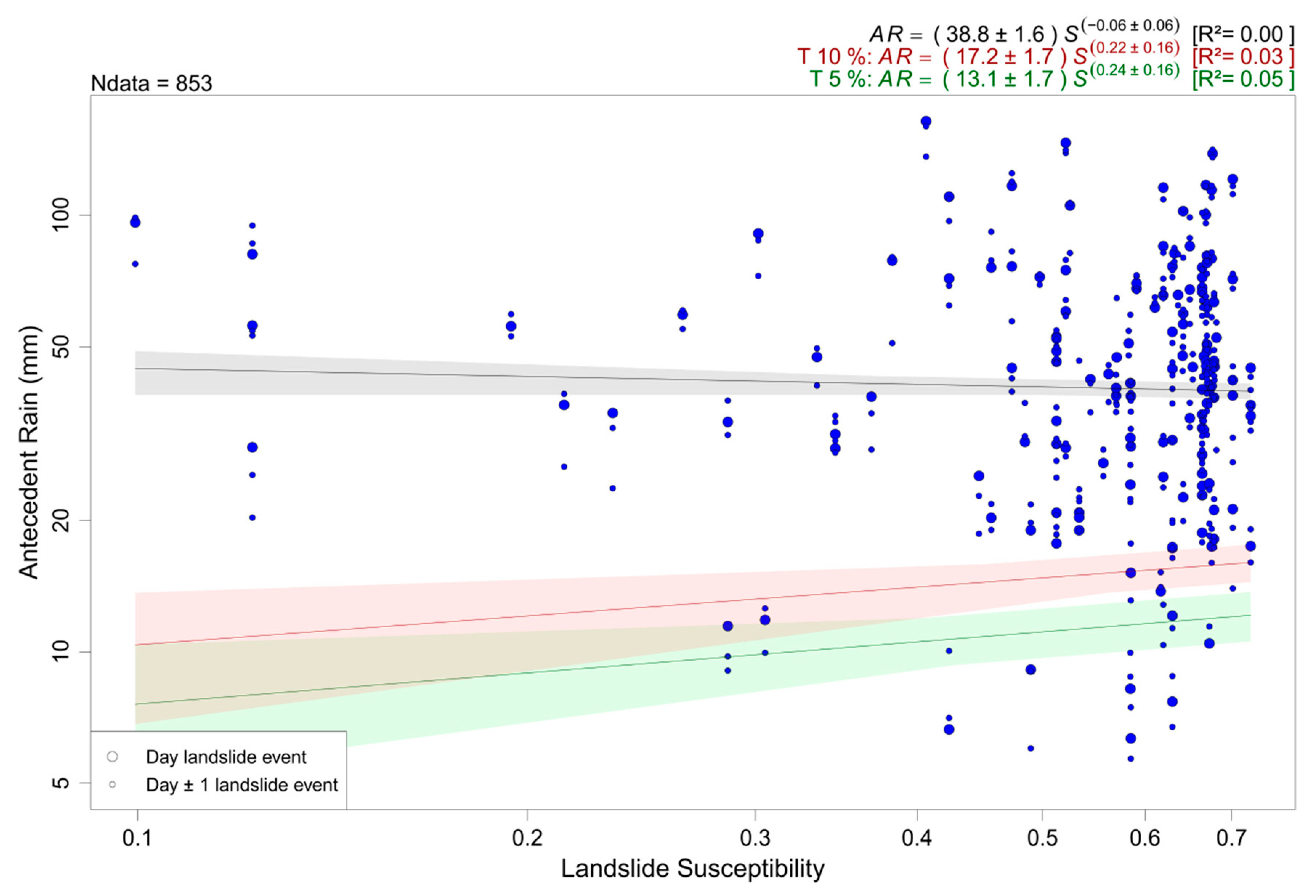
3. Problem Statement
4. Improving the Data Distribution over the S Range of the Data Used for Threshold Calculation
4.1. Rationale
- Data preparation.
- A.1.
- AR values associated with each day of a reported landslide plus the days prior and after these dates are extracted from the AR time series of the corresponding pixels calculated according to Equation (1) and the parameterization adopted in [35], i.e., a = b = 1.2, n = 42 days, for which the index is relevant for landslide types ranging from shallow to deep-seated landslides [35,63]. Data with AR < 5 mm are discarded from the data set as unlikely to have been triggered by rainfall [35]. The size of the provisional data set Q is then q ≤ 3p, where p is the number of landslide events in the raw calibration set.
- A.2.
- The data are weighted to account for the event date uncertainty: w = 24/36 for the day a landslide was reported, w = 6/36 for the days prior and after the landslide was reported. This weighting is implemented by expanding the data set as described in [35]. The expanded set is noted R.
- Threshold calibration.
- B.1.
- The number tC of data to be selected per S class is determined aswhere TPE refers to the desired threshold probability of exceedance, r is the number of data in R, and 10 is the number of log(S) classes.
- B.2.
- The data of R are grouped by S class. For each S class, data with the lowest AR values are selected until they amount to tC. The set of selected data points over all S classes is referred to as T and contains a number of data t ≤ (2 × TPE × r).
- B.3.
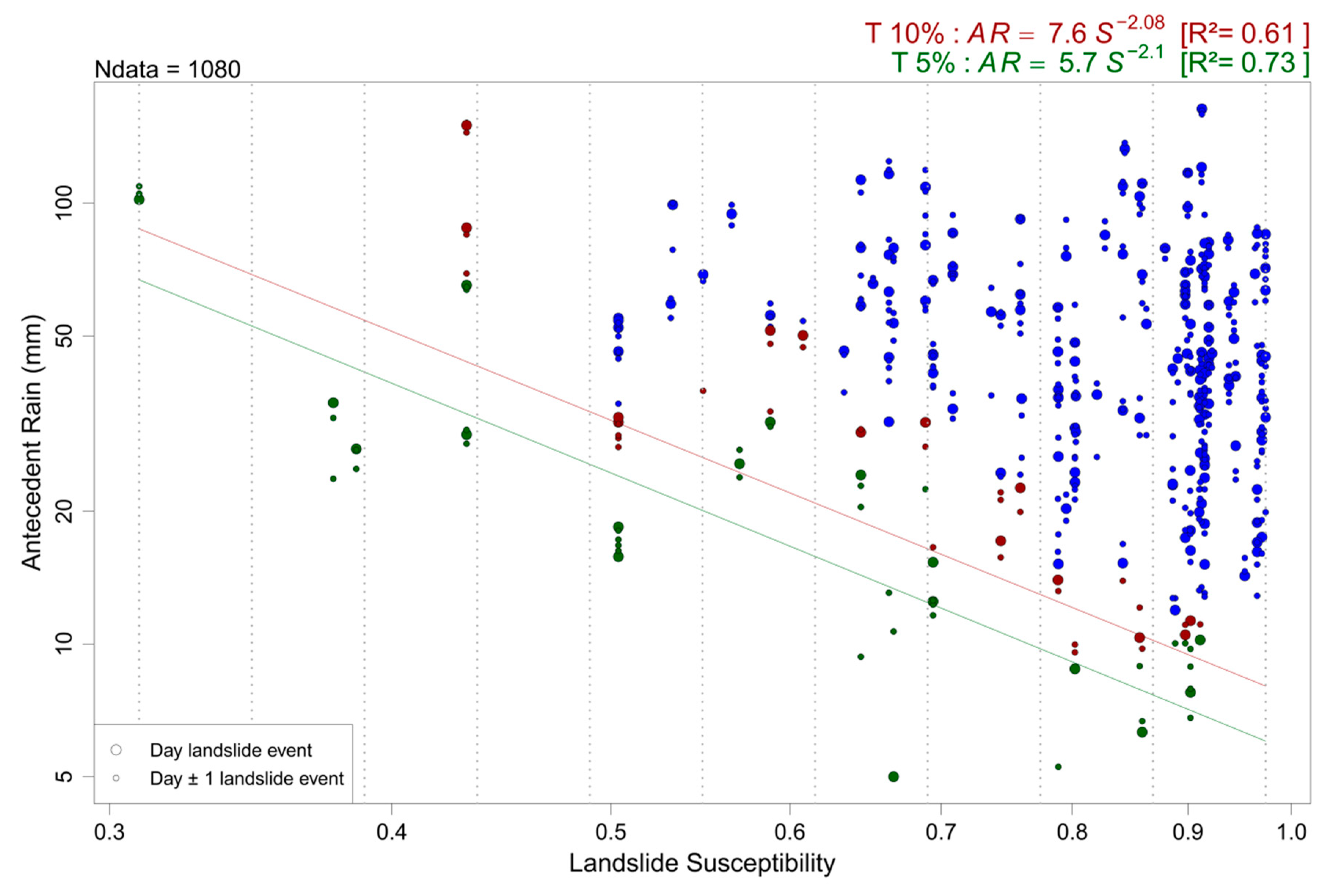
- Thresholds are then calculated through linear least-square regressions using the log-transformed AR and S data from T and the bootstrap technique as in [35] to obtain threshold relations in the form of Equation (2).
- Threshold evaluation
- Threshold quality is evaluated through the correspondence between the obtained false negative rate (FNR, actual ratio of data in R below the calculated threshold) and the nominal TPE. Differences may result from t significantly smaller than (2 × TPE × r), large outliers in T, and possibly also from bootstrap issues (see Section 5).
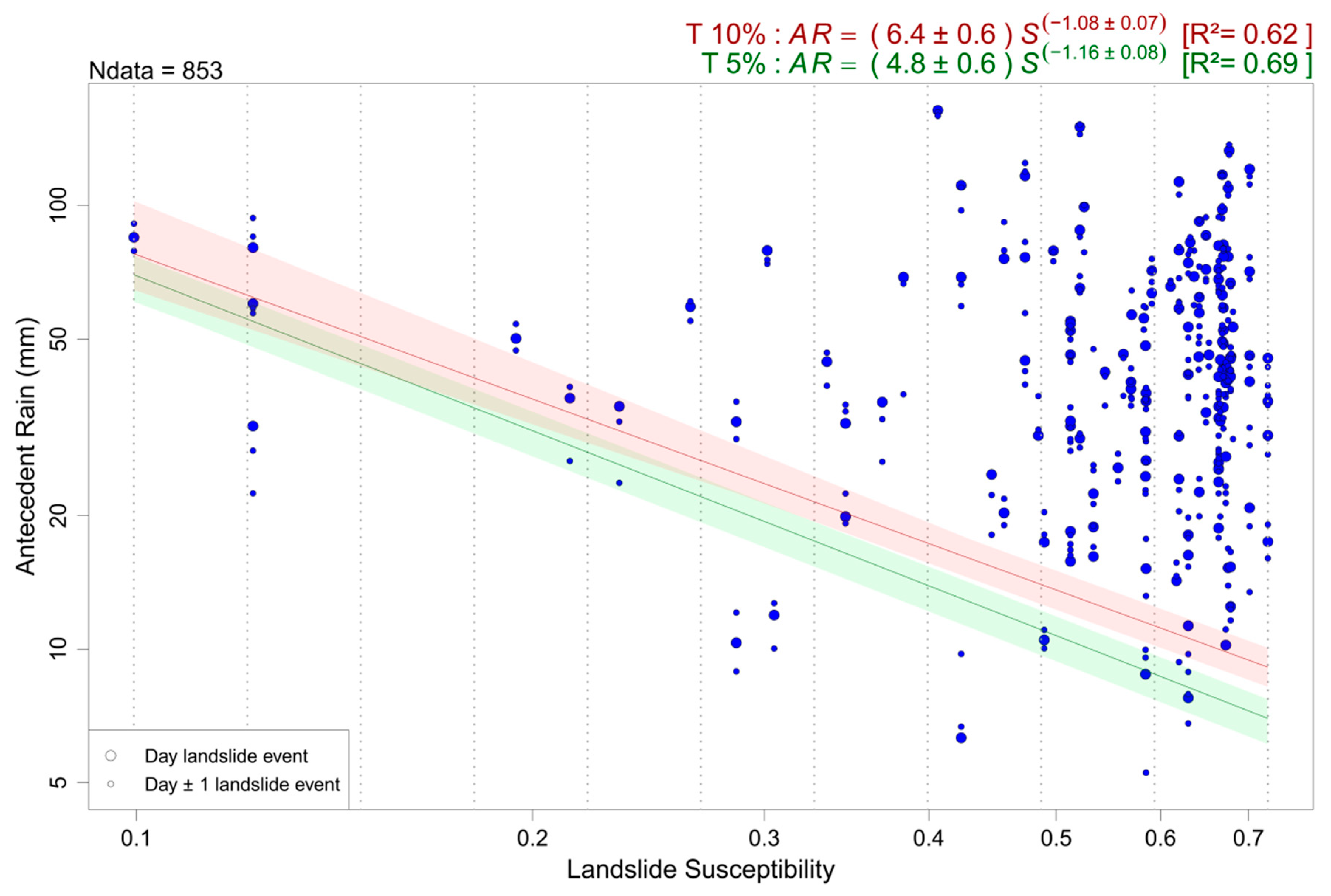
4.2. Increased Efficiency of the Method
5. Bootstrapping Called into Question
6. Robustness of the Modified AR-S Threshold Method
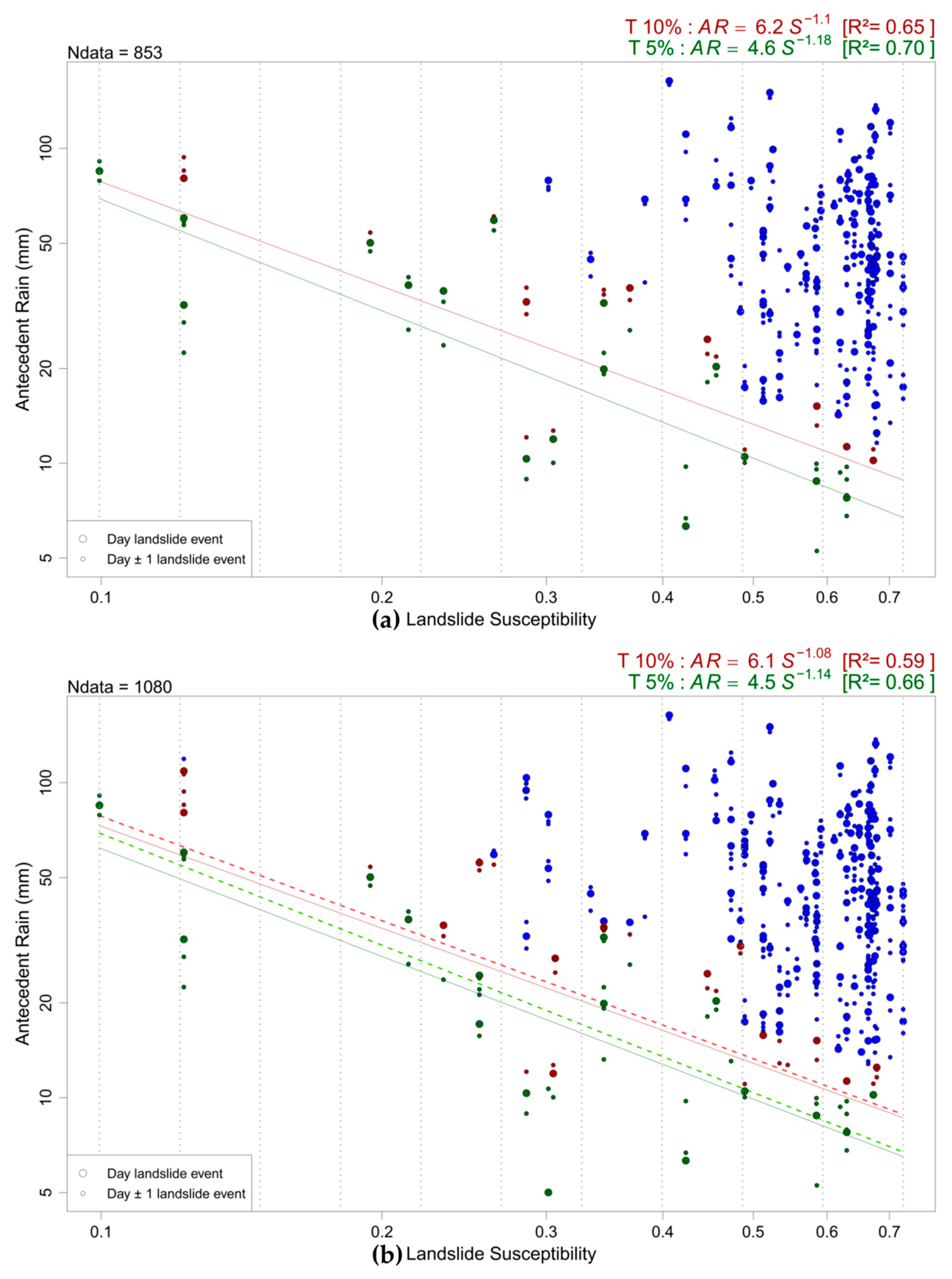
6.1. First Test: Sensitivity to New Data on Landslide Occurrence
6.2. Second Test: Robustness to Different S Data Sets
7. Relevance to Landslide Hazard and Early Warning Studies
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Froude, M.J.; Petley, D.N. Global fatal landslides 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Haque, U.; da Silva, P.F.; Devoli, G.; Pilz, J.; Zhao, B.; Khaloua, A.; Wilopo, W.; Andersen, P.; Lu, P.; Lee, J.; et al. The human cost of global warming: Deadly landslides and their triggers (1995–2014). Sci. Total Environ. 2019, 682, 673–684. [Google Scholar] [CrossRef] [PubMed]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Intrieri, E.; Carlà, T.; Gigli, G. Forecasting the time of failure of landslides at slope-scale: A literature review. Earth Sci. Rev. 2019, 193, 333–349. [Google Scholar] [CrossRef]
- Piciullo, L.; Calvello, M.; Cepeda, J.M. Territorial early warning systems for rainfall-induced landslides. Earth Sci. Rev. 2018, 179, 228–247. [Google Scholar] [CrossRef]
- Giannecchini, R.; Galanti, Y.; D’Amato Avanzi, G. Critical rainfall thresholds for triggering shallow landslides in the Serchio River Valley (Tuscany, Italy). Nat. Hazards Earth Syst. Sci. 2012, 12, 829–842. [Google Scholar] [CrossRef]
- Giannecchini, R. Relationship between rainfall and shallow landslides in the southern Apuan Alps (Italy). Nat. Hazards Earth Syst. Sci. 2006, 6, 357–364. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Luciani, S.; Vennari, C.; Guzzetti, F. Lithological and seasonal control on rainfall thresholds for the possible initiation of landslides in central Italy. Geomorphology 2012, 139–140, 79–90. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Bittelli, M.; Valentino, R.; Salvatorelli, F.; Rossi Pisa, P. Monitoring soil-water and displacement conditions leading to landslide occurrence in partially saturated clays. Geomorphology 2012, 173–174, 161–173. [Google Scholar] [CrossRef]
- Bogaard, T.A.; Greco, R. Landslide hydrology: From hydrology to pore pressure. Wiley Interdiscip. Rev. Water 2016, 3, 439–459. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G. The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Bierman, P.R.; Montgomery, D. Key Concepts in Geomorphology; W. H. Freeman and Company Publishers: New York, NY, USA, 2013; ISBN 9781429238601. [Google Scholar]
- McGlynn, A.L.; McDonnel, J.J.; Brammer, D.D.; Mcglynn, B.L.; Mcdonnel, J.J.; Brammer, D.D. A Review of the Evolving Perceptual Model of Hillslope Flowpaths at the Maimai Catchment, New Zealand. J. Hydrol. 2002, 257, 1–26. [Google Scholar] [CrossRef]
- Haitjema, H.M.; Mitchell-Bruker, S. Are water tables a subdued replica of the topography? Groundwater 2005, 43, 781–786. [Google Scholar] [CrossRef]
- Thompson, S.E.; Harman, C.J.; Heine, P.; Katul, G.G. Vegetation-infiltration relationships across climatic and soil type gradients. J. Geophys. Res. Biogeosci. 2010, 115, 1–12. [Google Scholar] [CrossRef]
- Wilson, G.V.; Luxmoore, R.J. Infiltration, Macroporosity, and Mesoporosity Distributions on Two Forested Watersheds. Soil Sci. Soc. Am. J. 1988, 52, 329–335. [Google Scholar] [CrossRef]
- Johnson, K.A.; Sitar, N. Hydrologic conditions leading to debris-flow initiation. Can. Geotech. J. 1990, 27, 789–801. [Google Scholar] [CrossRef]
- Rahardjo, H.; Leong, E.C.; Rezaur, R.B. Effect of antecedent rainfall on pore-water pressure distribution characteristics in residual soil slopes under. Hydrol. Process. 2008, 22, 506–5023. [Google Scholar] [CrossRef]
- Wilson, R.C.; Wieczorek, G. Rainfall thresholds for the initiation of debris flows at La Honda, California. Environ. Eng. Geosci. 1995, 1, 11–27. [Google Scholar] [CrossRef]
- Watakabe, T.; Matsushi, Y. Lithological controls on hydrological processes that trigger shallow landslides: Observations from granite and hornfels hillslopes in Hiroshima, Japan. Catena 2019, 180, 55–68. [Google Scholar] [CrossRef]
- Xue, J.; Gavin, K. Effect of rainfall intensity on infiltration into partly saturated slopes. Geotech. Geol. Eng. 2008, 26, 199–209. [Google Scholar] [CrossRef]
- Iverson, M.R. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Thomas, M.A.; Mirus, B.B.; Collins, B.D. Identifying Physics-Based Thresholds for Rainfall-Induced Landsliding. Geophys. Res. Lett. 2018, 45, 9651–9661. [Google Scholar] [CrossRef]
- Kim, D.; Im, S.; Lee, S.H.; Hong, Y.; Cha, K.S. Predicting the rainfall-triggered landslides in a forested mountain region using TRIGRS model. J. Mt. Sci. 2010, 7, 83–91. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A.; Greco, R.; Bogaard, T.A. Influence of uncertain identification of triggering rainfall on the assessment of landslide early warning thresholds. Nat. Hazards Earth Syst. Sci. 2018, 18, 633–646. [Google Scholar] [CrossRef]
- Monsieurs, E.; Jacobs, L.; Michellier, C.; Basimike Tchangaboba, J.; Ganza, G.B.; Kervyn, F.; Maki Mateso, J.C.; Mugaruka Bibentyo, T.; Kalikone Buzera, C.; Nahimana, L.; et al. Landslide inventory for hazard assessment in a data-poor context: A regional-scale approach in a tropical African environment. Landslides 2018, 15, 2195–2209. [Google Scholar] [CrossRef]
- Taylor, F.E.; Malamud, B.D.; Freeborough, K.; Demeritt, D. Enriching Great Britain’s National Landslide Database by searching newspaper archives. Geomorphology 2015, 249, 52–68. [Google Scholar] [CrossRef]
- Kirschbaum, D.B.; Stanley, T.; Zhou, Y. Spatial and temporal analysis of a global landslide catalog. Geomorphology 2015, 249, 4–15. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Melillo, M.; Peruccacci, S.; Ciabatta, L.; Brocca, L. How far are we from the use of satellite rainfall products in landslide forecasting? Remote Sens. Environ. 2018, 210, 65–75. [Google Scholar] [CrossRef]
- Monsieurs, E.; Kirschbaum, D.B.; Tan, J.; Maki Mateso, J.C.; Jacobs, L.; Plisnier, P.D.; Thiery, W.; Umutoni, A.; Musoni, D.; Bibentyo, T.M.; et al. Evaluating TMPA Rainfall over the Sparsely Gauged East African Rift. J. Hydrometeorol. 2018, 19, 1507–1528. [Google Scholar] [CrossRef]
- Bogaard, T.; Greco, R. Invited perspectives: Hydrological perspectives on precipitation intensity-duration thresholds for landslide initiation: Proposing hydro-meteorological thresholds. Nat. Hazards Earth Syst. Sci. 2018, 18, 31–39. [Google Scholar] [CrossRef]
- Monsieurs, E.; Dewitte, O.; Demoulin, A. A susceptibility-based rainfall threshold approach for landslide occurrence. Nat. Hazards Earth Syst. Sci. 2019, 19, 775–789. [Google Scholar] [CrossRef]
- Kirschbaum, D.B.; Adler, R.; Hong, Y.; Kumar, S.; Peters-Lidard, C.; Lerner-Lam, A. Advances in landslide nowcasting: Evaluation of a global and regional modeling approach. Environ. Earth Sci. 2012, 66, 1683–1696. [Google Scholar] [CrossRef]
- Berti, M.; Martina, M.L.V.; Franceschini, S.; Pignone, S.; Simoni, A.; Pizziolo, M. Probabilistic rainfall thresholds for landslide occurrence using a Bayesian approach. J. Geophys. Res. Earth Surf. 2012, 117, 1–20. [Google Scholar] [CrossRef]
- Postance, B.; Hillier, J.; Dijkstra, T.; Dixon, N. Comparing threshold definition techniques for rainfall-induced landslides: A national assessment using radar rainfall. Earth Surf. Process. Landf. 2018, 43, 553–560. [Google Scholar] [CrossRef]
- Mirus, B.; Morphew, M.; Smith, J. Developing Hydro-Meteorological Thresholds for Shallow Landslide Initiation and Early Warning. Water 2018, 10, 1274. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Lucian, S.; Valigi, D.; Guzzetti, F. Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 447–458. [Google Scholar] [CrossRef]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Roccati, A.; Guzzetti, F. A tool for the automatic calculation of rainfall thresholds for landslide occurrence. Environ. Model. Softw. 2018, 105, 230–243. [Google Scholar] [CrossRef]
- Gariano, S.L.; Brunetti, M.T.; Iovine, G.; Melillo, M.; Peruccacci, S.; Terranova, O.; Vennari, C.; Guzzetti, F. Calibration and validation of rainfall thresholds for shallow landslide forecasting in Sicily, southern Italy. Geomorphology 2015, 228, 653–665. [Google Scholar] [CrossRef]
- Marra, F.; Destro, E.; Nikolopoulos, E.I.; Zoccatelli, D.; Creutin, J.D.; Guzzetti, F.; Borga, M. Impact of uncertainty in rainfall estimation on the identification of rainfall thresholds for debris flow occurrence. Geomorphology. 2017, 21, 4525–4532. [Google Scholar] [CrossRef]
- Nobile, A.; Dille, A.; Monsieurs, E.; Basimike, J.; Bibentyo, T.M.; d’Oreye, N.; Kervyn, F.; Dewitte, O. Multi-temporal DInSAR to characterise landslide ground deformations in a tropical urban environment: Focus on Bukavu (DR Congo). Remote Sens. 2018, 10, 626. [Google Scholar] [CrossRef]
- Broeckx, J.; Vanmaercke, M.; Duchateau, R.; Poesen, J. A data-based landslide susceptibility map of Africa. Earth Sci. Rev. 2018, 185, 102–121. [Google Scholar] [CrossRef]
- Stanley, T.; Kirschbaum, D.B. A heuristic approach to global landslide susceptibility mapping. Nat. Hazards 2017, 87, 145–164. [Google Scholar] [CrossRef]
- Jacobs, L.; Dewitte, O.; Poesen, J.; Sekajugo, J.; Nobile, A.; Rossi, M.; Thiery, W.; Kervyn, M. Field-based landslide susceptibility assessment in a data-scarce environment: The populated areas of the Rwenzori Mountains. Nat. Hazards Earth Syst. Sci. 2018, 18, 105–124. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Depicker, A.J.S.P.; Jacobs, L.; Delvaux, D.; Havenith, H.B.; Maki Mateso, J.C.; Govers, G.; Dewitte, O. The added value of a regional landslide susceptibility assessment: The western branch of the East African Rift. Geomorphology 2019, in press. [Google Scholar]
- Dille, A.; Kervyn, F.; Mugaruka Bibentyo, T.; Delvaux, D.; Bamulezi Ganza, G.; Mawe Ilombe, G.; Buzera Kalikone, C.; Safari Makito, E.; Moeyersons, J.; Monsieurs, E.; et al. Causes and triggers of deep-seated hillslope instability in the tropics—Insights from a 60-year record of Ikoma landslide (DR Congo). Geomorphology 2019. [Google Scholar] [CrossRef]
- Moeyersons, J.; Tréfois, P.; Lavreau, J.; Alimasi, D.; Badriyo, I.; Mitima, B.; Mundala, M.; Munganga, D.O.; Nahimana, L. A geomorphological assessment of landslide origin at Bukavu, Democratic Republic of the Congo. Eng. Geol. 2004, 72, 73–87. [Google Scholar] [CrossRef]
- Delvaux, D.; Mulumba, J.L.; Sebagenzi, M.N.S.; Bondo, S.F.; Kervyn, F.; Havenith, H.B. Seismic hazard assessment of the Kivu rift segment based on a new seismotectonic zonation model (western branch, East African Rift system). J. Afr. Earth Sci. 2017, 134, 831–855. [Google Scholar] [CrossRef]
- Maki Mateso, J.C.; Dewitte, O. Towards an inventory of landslide processes and the elements at risk on the Rift flanks west of Lake Kivu (DRC). Geo-Eco-Trop 2014, 38, 137–154. [Google Scholar]
- Jacobs, L.; Dewitte, O.; Poesen, J.; Maes, J.; Mertens, K.; Sekajugo, J.; Kervyn, M. Landslide characteristics and spatial distribution in the Rwenzori Mountains, Uganda. J. Afr. Earth Sci. 2017, 134, 917–930. [Google Scholar] [CrossRef]
- Monsieurs, E.; Kirschbaum, D.B.; Thiery, W.; van Lipzig, N.; Kervyn, M.; Demoulin, A.; Jacobs, L.; Kervyn, F.; Dewitte, O. Constraints on Landslide-Climate Research Imposed by the Reality of Fieldwork in Central Africa. In Proceedings of the 3rd North American Symposium on Landslides: Landslides: Putting Experience, Knowledge, and Emerging Technologies into Practice, Roanoke, VA, USA, 4–8 June 2017; pp. 158–168. [Google Scholar]
- Camberlin, P.; Barraud, G.; Bigot, S.; Dewitte, O.; Makanzu Imwangana, F.; Maki Mateso, J.; Martiny, N.; Monsieurs, E.; Moron, V.; Pellarin, T.; et al. Evaluation of remotely sensed rainfall products over Central Africa. Q. J. R. Meteorol. Soc. 2019, 145, 2115–2138. [Google Scholar] [CrossRef]
- USGS. Shuttle Radar Topography Mission, Global Land Cover Facility; University of Maryland: College Park, MD, USA, 2006. [Google Scholar]
- Giardini, D.; Grunthal, G.; Shedlock, K.M.; Zhang, P. The GSHAP Global Seismic Hazard Map. Ann. Geophys. 1999, 42, 1225–1228. [Google Scholar] [CrossRef]
- Hartmann, J.; Moosdorf, N. The new global lithological map database GLiM: A representation of rock properties at the Earth surface. Geochem. Geophys. Geosystems 2012, 13, 1–37. [Google Scholar] [CrossRef]
- Smets, B.; Delvaux, D.; Ross, K.A.; Poppe, S.; Kervyn, M.; d’Oreye, N.; Kervyn, F. The role of inherited crustal structures and magmatism in the development of rift segments: Insights from the Kivu basin, western branch of the East African Rift. Tectonophysics 2016, 683, 62–76. [Google Scholar] [CrossRef]
- European Space Agency (ESA). Climate Change Initiative—Land Cover Project 2017. 20 m Resolution; European Space Agency: Paris, France, 2016. [Google Scholar]
- Maidment, R.I.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.; Nkonde, E.; Senkunda, S.; et al. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Sci. Data 2017, 4, 170082. [Google Scholar] [CrossRef]
- Sidle, R.C.; Bogaard, T.A. Dynamic earth system and ecological controls of rainfall-initiated landslides. Earth Sci. Rev. 2016, 159, 275–291. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Lee, S.R.; Kim, Y.T. A shallow slide prediction model combining rainfall threshold warnings and shallow slide susceptibility in Busan, Korea. Landslides 2019, 16, 647–659. [Google Scholar] [CrossRef]
- Segoni, S.; Lagomarsino, D.; Fanti, R.; Moretti, S.; Casagli, N. Integration of rainfall thresholds and susceptibility maps in the Emilia Romagna (Italy) regional-scale landslide warning system. Landslides 2015, 12, 773–785. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997; ISBN 0521573912. [Google Scholar]
- Koley, B.; Nath, A.; Saraswati, S.; Bandyopadhyay, K.; Ray, B.C. Assessment of Rainfall Thresholds for Rain-Induced Landslide Activity in North Sikkim Road Corridor in Sikkim Himalaya, India. J. Geogr. Environ. Earth Sci. Int. 2019, 19, 1–14. [Google Scholar] [CrossRef]
- Valenzuela, P.; Zêzere, J.L.; Domínguez-Cuesta, M.J.; Mora García, M.A. Empirical rainfall thresholds for the triggering of landslides in Asturias (NW Spain). Landslides 2019. [Google Scholar] [CrossRef]
- Bell, F.G.; Maud, R.R. Landslides associated with the colluvial soils overlaying the Natal group in the greater Durban region of Natal, South Africa. Environ. Geol. 2000, 39, 1029–1038. [Google Scholar] [CrossRef]
- Rossi, M.; Luciani, S.; Valigi, D.; Kirschbaum, D.B.; Brunetti, M.T.; Peruccacci, S.; Guzzetti, F. Statistical approaches for the definition of landslide rainfall thresholds and their uncertainty using rain gauge and satellite data. Geomorphology 2017, 285, 16–27. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Dorigo, W.A.; Parinussa, R.M.; De Jeu, R.A.M.; Wagner, W.; McCabe, M.F.; Evans, J.P.; Van Dijk, A.I.J.M. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sens. Environ. 2012, 123, 280–297. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Scipal, K.; Parinussa, R.M.; Liu, Y.Y.; Wagner, W.; De Jeu, R.A.M.; Naeimi, V. Error characterisation of global active and passive microwave soil moisture datasets. Hydrol. Earth Syst. Sci. 2010, 14, 2605–2616. [Google Scholar] [CrossRef]
- Liu, Y.; Weerts, A.H.; Clark, M.; Hendricks Franssen, H.J.; Kumar, S.; Moradkhani, H.; Seo, D.J.; Schwanenberg, D.; Smith, P.; Van Dijk, A.I.J.M.; et al. Advancing data assimilation in operational hydrologic forecasting: Progresses, challenges, and emerging opportunities. Hydrol. Earth Syst. Sci. 2012, 16, 3863–3887. [Google Scholar] [CrossRef]
- Crosta, G. Regionalization of rainfall thresholds: An aid to landslide hazard evaluation. Environ. Geol. 1998, 35, 131–145. [Google Scholar] [CrossRef]
- Michellier, C.; Pigeon, P.; Kervyn, F.; Wolff, E. Contextualizing vulnerability assessment: A support to geo-risk management in central Africa. Nat. Hazards 2016, 82, 27–42. [Google Scholar] [CrossRef]
- López-Carr, D.; Pricope, N.G.; Aukema, J.E.; Jankowska, M.M.; Funk, C.; Husak, G.; Michaelsen, J. A spatial analysis of population dynamics and climate change in Africa: Potential vulnerability hot spots emerge where precipitation declines and demographic pressures coincide. Popul. Environ. 2014, 35, 323–339. [Google Scholar] [CrossRef]


| Threshold | with Bootstrap | without Bootstrap |
|---|---|---|
| 5% threshold, S = 0.10 | 69.4 | 69.6 |
| 5% threshold, S = 0.72 | 7.0 | 6.8 |
| 10% threshold, S = 0.10 | 76.9 | 78.1 |
| 10% threshold, S = 0.72 | 9.1 | 8.9 |
| Threshold | Continental S Data | Regional S Data |
|---|---|---|
| 5% threshold, min S | 66.7 | 62.1 |
| 5% threshold, max S | 6.1 | 6.5 |
| 10% threshold, min S | 86.9 | 73.3 |
| 10% threshold, max S | 8.1 | 8.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monsieurs, E.; Dewitte, O.; Depicker, A.; Demoulin, A. Towards a Transferable Antecedent Rainfall—Susceptibility Threshold Approach for Landsliding. Water 2019, 11, 2202. https://doi.org/10.3390/w11112202
Monsieurs E, Dewitte O, Depicker A, Demoulin A. Towards a Transferable Antecedent Rainfall—Susceptibility Threshold Approach for Landsliding. Water. 2019; 11(11):2202. https://doi.org/10.3390/w11112202
Chicago/Turabian StyleMonsieurs, Elise, Olivier Dewitte, Arthur Depicker, and Alain Demoulin. 2019. "Towards a Transferable Antecedent Rainfall—Susceptibility Threshold Approach for Landsliding" Water 11, no. 11: 2202. https://doi.org/10.3390/w11112202
APA StyleMonsieurs, E., Dewitte, O., Depicker, A., & Demoulin, A. (2019). Towards a Transferable Antecedent Rainfall—Susceptibility Threshold Approach for Landsliding. Water, 11(11), 2202. https://doi.org/10.3390/w11112202





