Abstract
Idukki is a South Indian district in the state of Kerala, which is highly susceptible to landslides. This hilly area which is a hub of a wide variety of flora and fauna, has been suffering from slope stability issues due to heavy rainfall. A well-established landslide early warning system for the region is the need of the hour, considering the recent landslide disasters in 2018 and 2019. This study is an attempt to define a regional scale rainfall threshold for landslide occurrence in Idukki district, as the first step of establishing a landslide early warning system. Using the rainfall and landslide database from 2010 to 2018, an intensity-duration threshold was derived as I = 0.9D−0.16 for the Idukki district. The effect of antecedent rainfall conditions in triggering landslide events was explored in detail using cumulative rainfalls of 3 days, 10 days, 20 days, 30 days, and 40 days prior to failure. As the number of days prior to landslide increases, the distribution of landslide events shifts towards antecedent rainfall conditions. The biasness increased from 72.12% to 99.56% when the number of days was increased from 3 to 40. The derived equations can be used along with a rainfall forecasting system for landslide early warning in the study region.
1. Introduction
The state of Kerala (India) experienced the worst disaster in its history in 2018. The disaster affected around 5.4 million people and 433 lives were lost [1]. Several landslides, particularly debris flows, were associated with the event. Among the 14 districts in the state, 13 are part of the Western Ghats and are susceptible to landslide hazards. The scarps of the Western Ghats, which are the steepest parts, are more susceptible to landslides due to heavy rainfall. Attempts have been made by researchers to study the triggering factors of landslides in the Himalayas [2,3,4,5,6,7,8] and the Western Ghats [9,10]. However, on a regional scale, establishing rainfall thresholds for the occurrence of landslides in the Western Ghats has not yet been attempted. This paper is an endeavor to define a regional threshold for the Idukki district (Kerala) which is a severe landslide prone zone in the Western Ghats.
A rainfall threshold can be defined using process-based or empirical methods. The process-based approach considers physical and hydrological parameters which can initiate a landslide event. This requires highly sophisticated inputs, as the spatial and temporal distribution of these parameters can only be analyzed through detailed site-specific studies [11]. Owing to the limitations of defining process-based thresholds, this study defines the rainfall conditions that when surpassed, are likely to initiate landslide events in the Idukki district in the Western Ghats. This is an empirical approach which primarily focuses on the occurrence of rainfall and landslide events. Empirical thresholds can be divided into three categories: (1) thresholds which use rainfall data for specific events, (2) thresholds which consider rainfall conditions prior to failure, and (3) others which include hydrological thresholds [12]. In the current research, thresholds in the first two categories are derived for Idukki using historical rainfall and landslide information. A rainfall event is defined by three parameters, viz., rainfall event, rainfall intensity, and rainfall duration. cumulated rainfall is the the total amount rainfall from the beginning of the rainfall event to the occurrence of failure [13]; the term duration indicates the duration of the rainfall event considered or precipitation period [14]; rainfall intensity is the amount of precipitation in a given time, i.e., the rate of precipitation over the period considered [15]. Thus the term rainfall intensity gives an idea about the average rate of rainfall during an event, not the peak intensities. Another important factor which defines the applicability of the threshold is the area considered for the study. Based on the area, thresholds are classified into local, regional, and global. The stability of the slopes depends upon the hydro-meteo-geological parameters of the region and the conditions for the triggering of landslides differ from place to place. Global thresholds give a universal minimum, below which chances of landslide occurrence is nil, without considering any physical factors. Regional thresholds deal with areas of a few to some thousands of square kilometers where climatic, physiographic, and meteorological features are similar. Local thresholds can be applied to single or a small group of landslides in regions of sizes up to the range of hundreds of square kilometers. Regional and local thresholds perform well for the area they were developed for, but they cannot be exported to other areas easily [16]. These thresholds can be used in regional/local warning systems for providing an alert level to the government and public in general.
Empirical thresholds can be classified again based on the rainfall parameters used as intensity-duration (ID) thresholds, total rainfall event-duration (ED) thresholds, and total rainfall event-intensity (EI) thresholds [12]. A general, well-accepted agreement which determines the selection of rainfall parameters is that shallow/rapid landslides are initiated by rainfalls of high intensity and short duration [16] and deep-seated landslides occur when it rains continuously over a long time [17]. This research focuses on the initiation of shallow landslides which cause maximum casualties during the monsoon time in the region and hence thresholds based on intensity-duration plane and antecedent rainfall are defined for Idukki. The objective is to start the preliminary steps towards an effective regional scale warning system for the Idukki district.
2. Study Area
In the state of Kerala, Idukki was the worst-hit district during 2018 disaster, with 143 major landslides in the state government records [1]. As shown in the slope map of Idukki, the geography of the area consists of slopes as steep as 80° (Figure 1) and the elevation ranges up to 2692 m (Figure 3). A significant share of the population of the district had houses in these unstable slopes, which were destroyed in the 2018 landslides irrespective of the building typology [1]. 97% of the major roads in the districts cut through the rugged mountains and hills, which are often blocked due to landslides in the monsoons [18]. Sprawling across an area of 4358 km2, Idukki supplies 66% of the electric power requirements of Kerala [19]. This district with more than half of the area covered by forests is the second largest one in terms of area in the state.
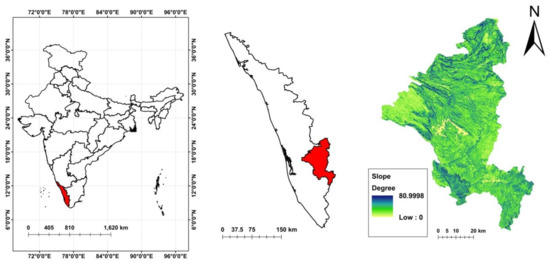
Figure 1.
Location and slope map of the Idukki district.
The Western Ghats can be divided into two segments, north and south, separated by the Gap of Palghat. Deep-seated landslides are reported in the northern segment and the eastern flank while the southern segment mostly experiences shallow landslides [20]. Idukki belongs to the southern part, where regolith thickness ranges from 0.25–5 m [21] and is prone to shallow landslides [1]. Geomorphic classification of the terrain divides the area into four, viz., rugged hills, ridges and valleys, fringe slope, and plateau [22]. Scarps of the Western Ghats consist of frictional soil with less cohesion, thus being stable in dry conditions and losing their strength when the moisture content increases. Plateu regions have a thick layer of top soil, rich in clay content due to their morphology and tropical climate [23]. Geologically, rocks of Wayanad, Charnockite, Khondalite, and Migmatite groups contribute the formation of a part of South Indian Precambrian metamorphic shield [22]. The primary weathering process is hydrolysis in the area, which is due to the high precipitation [24].
2.1. Triggering Factors
The scarps of the Western Ghats experience an annual rainfall as high as 5000 mm as a result of the southwest monsoon, northeast monsoon, and premonsoon showers [25]. The Western flank of the Western Ghats experiences landslides during the southwest monsoon and the eastern side is affected mainly during the northeast monsoon [20]. Large amounts of high-intensity rainfalls increase the pore water pressure within the soil mass, which eventually decreases the shear strength of the soil. This is considered as the primary triggering factor of landslides in the Indian Himalayas [2,4,26] and the Western Ghats [27]. The fissures in bedrock siphons the excess rainwater to unstable zones in the slopes during the monsoon [28]. Photographs of some landslides which happened during the 2018 monsoon are shown in Figure 2. The population of this region increased rapidly after the 19th century, as the people from the midlands started migrating into the hilly region [29]. The industrially backward district was in a quest for better infrastructure due to an increase in population. As an effect, the land use has changed significantly in a short span of time, which favoured the occurrence of landslides in the region. Large scale hill-toe modifications have been done in the district in recent decades for the purpose of infrastructure development, due to which the hill slopes have become steep, without any lateral support. The terraced slopes, modified for monoculture plantations with no sufficient drainage provisions, aggravated the scenario. Due to the drain blockages, water from the intense rainfall accumulates in the top soil layers, leading to landslides.

Figure 2.
Damages that happened due to landslides in the Idukki district in 2018. (a) Debris slide at Anachal. (b) Debris flow at Kallimai. (c) Subsidence at Kallarkutty approach road. (d) Earth slide at Cheruthoni [22].
In a detailed landslide inventory of Kerala until 2010, prepared by the Geological Survey of India (GSI), 64 major cases were reported in the Idukki district [30]. The landslide typologies vary from creep and subsidence to debris flows and avalanches. Along the major road corridors of the district, earth/debris slides have become common during monsoon period [18]. The sharp turnings and vertical cuts along the roads are highly susceptible to cut-slope failures. Incessant rainfall and the subsequent pore pressure increase adversely affects the steep slopes and results in landslides. To conclude, from the case studies conducted by GSI, a major share of the events in Idukki are of debris flow type triggered by heavy rainfall and are influenced by factors like slope, land use, overburden thickness, and disposition of streams etc. [18,23,31,32].
2.2. Database for Analysis
Building a chronology of landslides based on the historical records is the first stage of any landslide hazard study [33]. A landslide database for the research has been developed taking inputs from the Geological Survey of India [22], newspapers, state government reports [1,34], and from interactions with the people of the area. The dates of initiation of landslides were collected with a weekly accuracy, and the locations were collected with a spatial accuracy of nearest mentioned site from the reports. The database consists of the spatial (Figure 3) and temporal distribution of landslides and the typology.
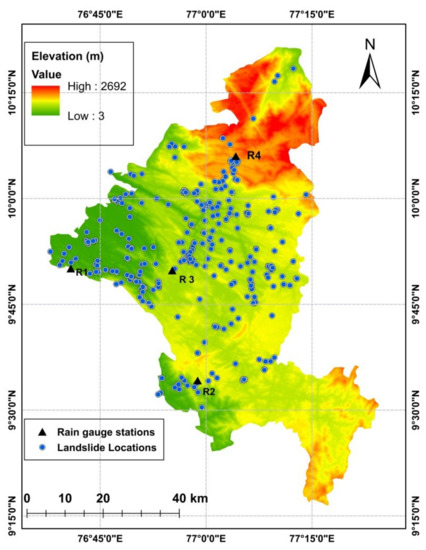
Figure 3.
Digital Elevation Model [35] of the Idukki district along with the spatial distribution of landslide locations and rain gauge stations (2010–2018).
The rainfall data of daily resolution from the year 2010 was collected from four rain gauge stations in the Idukki district, maintained by the India Meteorological Department (IMD) [36], for the analysis. The locations of rain gauge stations are given in Table 1. The monthly distribution of effective rainfall in the Idukki district from 2010 to 2018 is shown in the box plot shown in Figure 4.

Table 1.
Location of rain gauge stations.
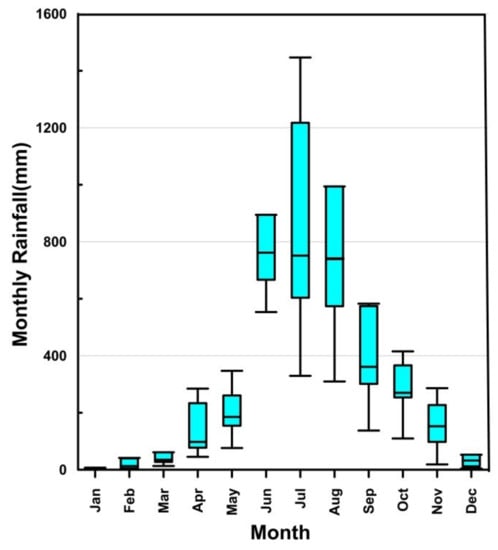
Figure 4.
Box and whisker plot with monthly distributions of rainfall in the Idukki district (2010–2018). The bottom and top lines indicate minimum and maximum values respectively and the line inside the box represents the median.
The distribution of rainfall is not uniform throughout the district. In a long term rainfall analysis conducted by GSI, it was found that the average annual rainfall varies from less than 1000 mm in the northeast parts of Anamudi peak to around 5000 mm near Peermedu [18]. The four rain gauges from which we collected data are located at Thodupuzha, Peermedu, Idukki, and Munnar (Figure 3). The variation of annual rainfall from the four rain gauges and the district average is plotted in Figure 5. The differences in rainfall conditions will lead to over-estimation or under-estimation of the intensity and duration values if we consider the average rainfall. Hence the rainfall event associated with each landslide was found out based on the spatial distribution of the four rain gauges [37].
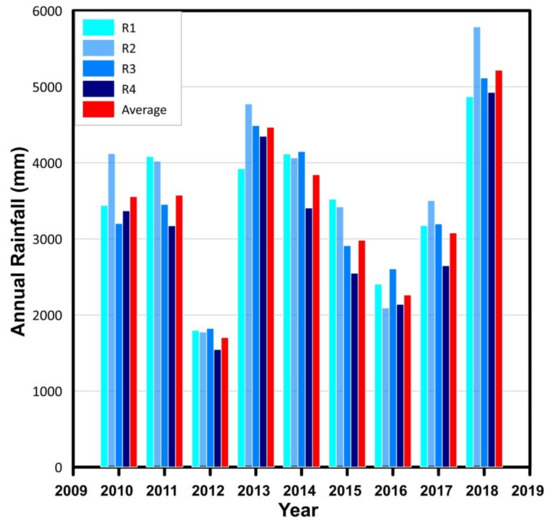
Figure 5.
Variation of annual rainfall measured in four rain gauges during the study period.
Identifying a reference rain gauge is a challenging task as explained by many practitioners [14,38], especially when the number of available rain gauges is limited. One of the most common practices is to choose the rain gauge based on its proximity to the landslide location. Hence in this study, the district was divided into four Thiessen polygons, based on the location of rain gauges (Figure 6). P1 Polygon is occupied by a flat and plain territory, P2 is located in the eastern hilly sector of the study area, P3 represents the central hilly sector, and P4 contains the flanks of the mountain and the hills immediately at the foot of the mountainside, thus separating this area with peculiar physiographic characteristics from the other three. As a consequence, splitting up the area in four sectors by means of Thiessen polygons is better than operating considering the entire area as a whole.
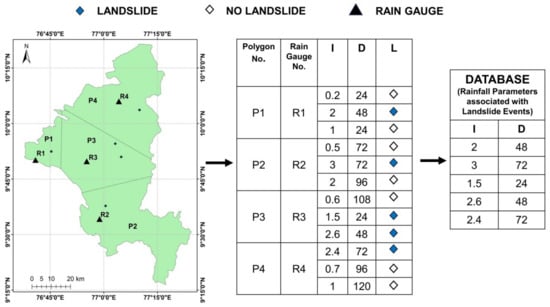
Figure 6.
Conceptual sketch showing development of dataset: P1, P2, P3, and P4 represent the four Polygons and R1, R2, R3, and R4 are the reference rain gauges in each polygon. D = Duration of rainfall (hours); I = Intensity of rainfall (mmh−1); L = Occurrence of landslide (Modified after [37]).
Each polygon defines a space, which is closest to the rain gauge in it (reference gauge). Each point inside a polygon is closer to the reference gauge, than the other three rain gauges. The division of polygons and the selection of reference gauge is constrained by spatial distribution only. Each polygon is assumed to be an area of similar rainfall conditions with a reference rain gauge.
The method of developing a dataset is illustrated in Figure 6 [37] using a sample dataset, i.e, the values (I,D) and the locations of landslides are not from the actual dataset, but are arbitrarily chosen for demonstrating the methodology. For all landslide events that happened in Thiessen polygon P1, the readings from R1 are considered. The procedure was same for all landslide events.
The readings corresponding to landslide events, recorded by individual reference rain gauges, were then merged to a single database. The exact number of triggered landslides and sites were not available from the reports and therefore multiple landslides on the same date within the same polygon are considered as a single landslide event. A threshold defines the possibility of occurrence of a minimum of one landslide event in the region. Thus, a total of 225 landslide events are considered in the present analysis, which happened during the time period of 2010–2018.
3. Analysis of Thresholds
The key for the development of any empirical threshold is the definition of rainfall and landslide events and the parameters related to it [39]. The necessity of developing rainfall thresholds and early warning systems for the Idukki district has been emphasized in some of the specific site studies conducted by the GSI [23]. Considering the increased number of casualties which occurred in the study area in the recent past, rainfall thresholds using intensity-duration relationships and antecedent rainfall conditions have been developed in the current research.
3.1. Intensity-Duration Thresholds
A total of 225 landslide events were recorded during the study period (2010–18), which were triggered by rainfall. The hourly intensities of all the rainfall events associated with the occurrence of landslides were calculated and plotted against the duration of events in hours in a logarithmic scale. The distribution of the events is fitted with the power-law distribution using an equation in the form
where
- I is Intensity of rainfall in mmh−1,
- D is Duration of rainfall event in hours,
- and α and β are empirical parameters,
- which is in the form of a straight line y = mx + c.
Use of this power-law equation has two fundamental assumptions. The first one is that with increase in the rainfall intensities, there is a nonlinear increase in the probability of occurrence of landslides. Below the threshold value, the likelihood of initiation of landslide is low, and above the threshold, the probability of occurrence of landslides increases nonlinearly. The second assumption is that the initiation of slides decreases as the duration of rainfall increases [2]. The term ‘β’ in Equation (1) defines this rate at which the critical intensity declines with the rise in duration. The frequentist approach of defining intensity-duration thresholds is used in this study. Empirical rainfall conditions which triggered landslides were first log-transformed and fitted using Equation (2), which is equivalent to the power-law in Equation (1). Using the Frequentist method, a best fit line for the distribution was obtained as I = 2.54D−0.16 (Figure 7) with a coefficient of determination (R2) of 0.04. The scattering of data results in a lower value of R2 and hence the uncertainty associated with the fitted line is evaluated with a confidence interval of 95%. Considering the uncertainties, Equation (1) gets modified to
I = (α ± Δα) D(β ± Δβ)
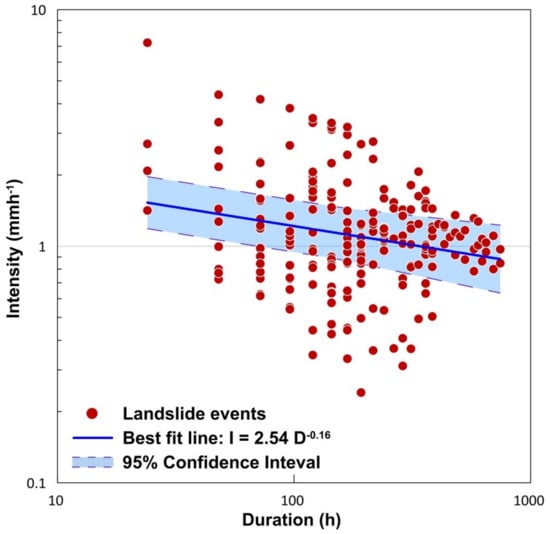
Figure 7.
Rainfall Intensity vs. Duration (ID) plot on logarithmic scale for the Idukki district fitted using power-law.
The equation of the best fit line was obtained as I = 2.54D−0.16, with a confidence interval of I = (2.54 ± 0.65)D(−0.16 ± 0.05).
The approach is based on least square regression and the data is fitted using a power-law. The difference between the value on the best fit line log (If) and logarithm of event intensity log (I) for each event is calculated. This difference is termed as ‘δI’. Kernel density estimation is used to determine the probability density function of the distribution of ‘δI’ and the result was fitted using a Gaussian function of the following form [40,41]:
where a and b are real constants and c is nonzero.
a,b,c, ϵ, R, and thresholds corresponding to various exceedance probabilities can be defined for the region. For a normally distributed random variable, a = b = μ and c2 = σ2 where μ and σ are the mean and standard deviation of the distribution, respectively. Hence the equation becomes
This equation is used to fit the distribution of ‘δI’, to determine the rainfall threshold as shown in Figure 8.
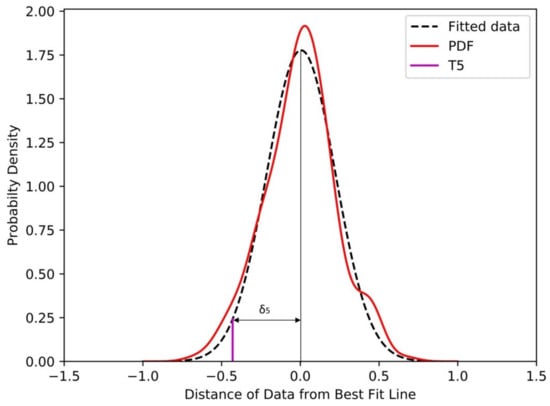
Figure 8.
Probability density function of the distribution of δI, fitted using a Gaussian distribution.
The data follows a distribution similar to the standard Gaussian distribution. Hence based on standard Gaussian distribution, a T5 line was plotted as in Figure 8, with an exceedance probability of 5%. The distance ‘δ5’ indicates the deviation of threshold line from the best fit line. This deviation was used to establish the intercept of the threshold line (Figure 9).
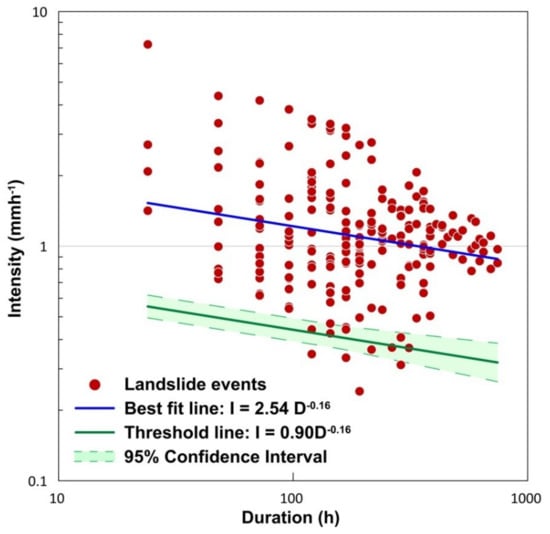
Figure 9.
Intensity-duration threshold for the Idukki district on logarithmic scale.
From the threshold line, it can be inferred that for the minimum duration (24 hours), a continuous rainfall of 0.54 mmh−1 can trigger landslides. The maximum duration of a rainfall event observed during the study period was 31 days. The obtained results predict that an intensity of 0.3 mmh−1 over a period of 31 days can trigger landslides in the region. The confidence interval was obtained as I = (0.9 ± 0.1)D(−0.16 ± 0.05). The maximum number of events occurred at a duration of 7 days for which the minimum intensity to initiate a landslide event was found to be 0.4 mmh−1. The lesser value of thresholds for short duration events emphasizes the need for considering antecedent rainfall conditions for defining thresholds. Hence thresholds based on antecedent rainfall conditions are also defined for the area.
3.2. Thresholds Based on Antecedent Rainfall
Intensity-duration thresholds consider only the immediate preceding rainfall event as a triggering factor of landslides. Landslides may occur as result of moisture content variation due to continuous precipitation also, which is difficult to monitor precisely. Thus a simple way is to study the effect of antecedent rainfall and define a threshold based on antecedent rainfall before the landslide event. Studies have been conducted across the globe, considering different antecedent periods ranging from 3 days to 120 days [2,4,42].
The data of 225 landslides over a period of nine years has been used for the analysis. Daily rainfall records at failure are compared with the antecedent rainfall of 3, 10, 20, 30, and 40 days before failure. The graph is plotted with antecedent rainfall (mm) and daily rainfall (mm) in x and y axes respectively. The diagonal line of the plot determines the scattering bias of the data (Figure 10).
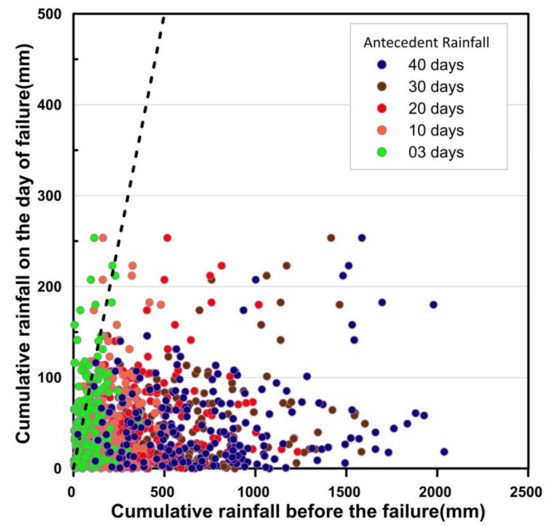
Figure 10.
Plot of daily rainfall vs. antecedent rainfall (3, 10, 20, 30, and 40 days).
A significant share of landslide events is biased towards the antecedent rainfall in all cases. Hence a threshold is defined for all individual time durations of antecedent rainfall considered in the study as shown in Figure 11a–e. In the first case, three days’ antecedent rainfall was considered, 28% of the total events considered are shifted towards daily rainfall, and the remaining 163 landslides are biased towards three days’ antecedent rainfall. For other cases, the biasness ratio to daily rainfall and antecedent rainfall was found to be 11:214 for 10 days’, 6:219 for 20 days’, 3:222 for 30 days’, and 1:224 for 40 days’ antecedent rainfall prior to the slide event. It is evident from the analysis that the biasness towards antecedent rainfall, which was 72% in case of 3 days’ antecedent rainfall increased to 99.56% when the antecedent rainfall of 40 days was considered as shown in Figure 11f. The study can be refined if the temporal resolution of the rainfall data available is improved.
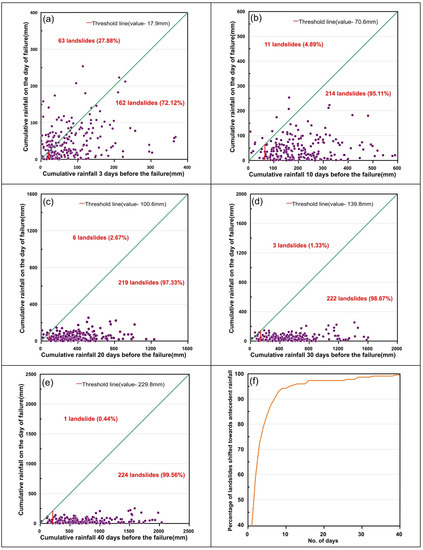
Figure 11.
Plot between daily rainfall and antecedent rainfall before failure for (a) 3 days, (b) 10 days, (c) 20 days, (d) 30 days, (e) 40 days, and (f) Biasness towards antecedent rainfall.
4. Discussions
The rainfall thresholds defined in this study establish a minimum cut off below which chances of occurrence of rainfall is very low. Above these thresholds, the probability of occurrence increases exponentially, but still the chance of false alarms cannot be neglected. Even though rainfall is the major triggering factor, other physical factors also influence the stability of slopes. For a powerful Landslide Early Warning System to work effectively, parameters like soil moisture and soil movement/tilt etc. should be incorporated along with the rainfall thresholds. An integrated system with multiple sensors and rain gauges can be installed in the region for this purpose. Similar researches have been carried out for the Darjeeling Himalayas [5] using Micro Electrical Mechanical System (MEMS) tilt sensors. A network of such sensors can effectively transfer the data to the authorities in real time which can be used as an effective warning system. The frequency of available rainfall data is the key factor which determines the accuracy of thresholds. In the current scenario, the temporal resolution of rainfall data available for the region is one day, and for an area of 4358 km2 only five rain gauge stations (as of 2019) are available. By establishing a network of sensors across the district, the spatial and temporal resolution of rainfall measurements can also be improved.
Several rainfall thresholds have been developed and periodically updated [43] for forecasting landslide events across the globe. Choosing the best method for establishing rainfall thresholds for a particular region requires detailed analysis and a quantitative comparison using statistical attributes [44]. Simple empirical models can also be modified conceptually by incorporating physical or hydrological parameters to improve the prediction power [45,46]. Further studies must be conducted for the area using existing models which are being practiced in different parts of the world [11,47,48,49,50] and the best suited rainfall threshold should be integrated with a sensor network and rainfall forecasting system. This research is a humble step towards achieving the goal of establishing an effective Landslide Early Warning System, which can minimize the casualties due to landslide hazards in the Idukki district.
5. Conclusions
This study is an effort to establish thresholds in intensity-duration plane based on antecedent rainfall data for the Idukki district in Kerala State at a regional scale. This is the first of its kind for the region and can be improved on with the availability of short term rainfall data.
The analysis was conducted using a database of 9 years from 2010 to 2018, which included 225 landslide events occurring at different parts of the district, and the principal observations can be summarized as:
- For short duration rainfall events (24 hours), a continuous rainfall intensity of 0.54 mmh−1 can trigger landslides. For the maximum observed duration of 31 days, a rainfall intensity as less as 0.3 mmh−1 can also trigger landslides. The values of thresholds are too low for a regional scale threshold, and the reason can be the biasness of occurrence of landslides to the antecedent rainfall conditions, other than the immediate preceding event.
- From the analysis of antecedent rainfall conditions, it can be stated that for the Idukki district, an antecedent rainfall of 70.6 mm over a period of 10 days and 229.8 mm over a period of 40 days can trigger a landslide event. Around 99.56% of the events are biased towards the antecedent rainfall conditions when duration of 40 days is considered.
- It is evident from the results that the occurrence of landslide events are more influenced by antecedent rainfall conditions rather than the amount of rainfall on the day of occurrence.
- It is expected that this first attempt will encourage more research for the study area, which is profoundly suffering from the increased number of landslide events in the recent hazards and this will become the first step towards establishing a regional scale warning system for the Idukki district.
Author Contributions
Data curation, M.T.A. and D.P.; Formal analysis, M.T.A. and D.P.; Supervision, N.S.; Writing—original draft, M.T.A.; Writing—review & editing, N.S.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to Geological Survey of India Kerala State Unit, Kerala State Disaster Management Authority (KSDMA) and District Soil Conservation Office, Idukki for the support they have offered for the research. The authors are also grateful to all the three reviewers for their constructive suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kerala Post Disaster Needs Assessment Floods and Landslides—August 2018; Government of Kerala: Thiruvananthapuram, India, 2018; pp. 1–440.
- Kanungo, D.P.; Sharma, S. Rainfall thresholds for prediction of shallow landslides around Chamoli-Joshimath region, Garhwal Himalayas, India. Landslides 2014, 11, 629–638. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, D.N. Estimation of rainfall thresholds for landslide occurrences in Kalimpong, India. Innov. Infrastruct. Solut. 2018, 3, 24. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, N. Rainfall Thresholds for the prediction of Landslides using Empirical Methods in Kalimpong, Darjeeling, India. In Proceedings of the JTC1 Workshop on Advances in Landslide Understanding, Barcelona, Spain, 24–26 May 2017. [Google Scholar]
- Dikshit, A.; Satyam, N. Probabilistic rainfall thresholds in Chibo, India: Estimation and validation using monitoring system. J. Mt. Sci. 2019, 16, 870–883. [Google Scholar] [CrossRef]
- Dikshit, A.; Sarkar, R.; Satyam, N. Probabilistic approach toward Darjeeling Himalayas landslides—A case study. Cogent Eng. 2018, 5, 1–11. [Google Scholar] [CrossRef]
- Soja, R.; Starkel, L. Extreme rainfalls in Eastern Himalaya and southern slope of Meghalaya Plateau and their geomorphologic impacts. Geomorphology 2007, 84, 170–180. [Google Scholar] [CrossRef]
- Prokop, P.; Walanus, A. Impact of the Darjeeling–Bhutan Himalayan front on rainfall hazard pattern. Nat. Hazards 2017, 89, 387–404. [Google Scholar] [CrossRef]
- Kuriakose, S.L. Effect of Vegetation on Debris Flow Initiation: Conceptualisation and Parametrisation of a Dynamic Model for Debris Flow Initiation in Tikovil River Basin, Kerala, India, using PC Raster; International Institute of Geo-Information Science and Earth Observation and Indian Institute of Remote Sensing: Enschede, The Netherlands; Uttarakhand, India, 2006. [Google Scholar]
- Kuriakose, S.L.; Luna, B.Q.; Portugues, S.B.; Van Westen, C.J. Modelling the runout of a debris flow of the Western Ghats, Kerala, India. Assembly 2009, 11, 4276. [Google Scholar]
- Martelloni, G.; Segoni, S.; Fanti, R.; Catani, F. Rainfall thresholds for the forecasting of landslide occurrence at regional scale. Landslides 2012, 9, 485–495. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Innes, J.L. Debris flows. Prog. Phys. Geogr. 1983, 7, 469–501. [Google Scholar] [CrossRef]
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Geogr. Ann. Ser. Phys. Geogr. 1980, 62, 23–27. [Google Scholar]
- Crosta, G. Regionalization of rainfall thresholds: An aid to landslide hazard evaluation. Environ. Geol. 1998, 35, 131–145. [Google Scholar] [CrossRef]
- Bonnard, C.; Noverraz, F. Influence of climate change on large landslides: Assessment of long term movements and trends. In Proceedings of the International Conference on Landslides Causes Impact and Countermeasures, Davos, Switzerland, 17–21 June 2001; pp. 121–138. [Google Scholar]
- Sajeev, R.; Praveen, K.R. Landslide Susceptibility Mapping on Macroscale along the Major Road Corridors in Idukki District, Kerala; Geological Survey of India: Thiruvananthapuram, India, 2014. [Google Scholar]
- Idukki District Webpage. Available online: https://idukki.nic.in/ (accessed on 23 August 2019).
- Kuriakose, S.L. Physically-Based Dynamic Modelling of the Effect of Land Use Changes on Shallow Landslide Initiation in the Western Ghats of Kerala, India. Ph.D. Thesis, University of Utrecht, Enschede, The Netherlands, 2010. [Google Scholar]
- Sreekumar, S. Techniques for slope stability analysis: Site specific studies from Idukki district, Kerala. J. Geol. Soc. India 2009, 73, 813–820. [Google Scholar] [CrossRef]
- Sulal, N.L.; Archana, K.G. Note On Post Disaster Studies For Landslides Occurred in June 2018 At Idukki District, Kerala; Geological Survey of India: Thiruvananthapuram, India, 2019.
- Sajeev, R.; Sajinkumar, K.S. Detailed Site Specific Landslide Study at Govt. College, Munnar, Idukki District, Kerala; Geological Survey of India: Thiruvananthapuram, India, 2013.
- Deepthy, R.; Balakrishnan, S. Climatic control on clay mineral formation: Evidence from weathering profiles developed. J. Earth Syst. Sci. 2005, 114, 545–556. [Google Scholar] [CrossRef]
- Kuriakose, S.L.; Sankar, G.; Muraleedharan, C. History of landslide susceptibility and a chorology of landslide-prone areas in the Western Ghats of Kerala, India. Environ. Geol. 2009, 57, 1553–1568. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, D.N.; Towhata, I. Early warning system using tilt sensors in Chibo, Kalimpong, Darjeeling Himalayas, India. Nat. Hazards 2018, 94, 727–741. [Google Scholar] [CrossRef]
- Jaiswal, P.; van Westen, C.J. Estimating temporal probability for landslide initiation along transportation routes based on rainfall thresholds. Geomorphology 2009, 112, 96–105. [Google Scholar] [CrossRef]
- Muraleedharan, M.P. Landslides in Kerala—A Drenched State Phenomena in Regolith; Center for Earth Sciences: Thiruvananthapuram, India, 1995. [Google Scholar]
- Jha, C.S.; Dutt, C.B.S.; Bawa, K.S. Deforestation and land use changes in Western Ghats, India. Curr. Sci. 2000, 79, 231–238. [Google Scholar]
- Muraleedharan, C.; Sajinkumar, K.S. Landslide Inventory of Kerala; Geological Survey of India: Thiruvananthapuram, India, 2010.
- Muraleedharan, C.; Praveen, M.N. Detailed Site Specific Study Of Landslide Initiation At Kuttikanam, Peermade Taluk, Idukki District, Kerala; Geological Survey of India: Thiruvananthapuram, India, 2011.
- Muraleedharan, C. Landslide Hazard Zonation on Meso-Scale for Munnar, Devikulam Taluk, Idukki District, Kerala; Geological Survey of India: Thiruvananthapuram, India, 2010.
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Ardizzone, F.; Galli, M. The impact of landslides in the Umbria region, central Italy. Nat. Hazards Earth Syst. Sci. 2003, 3, 469–486. [Google Scholar] [CrossRef]
- Details of Landslip Damages in Agricultural Lands of Different Panchayats of Idukki District during the Monsoon 2018; District Soil Conservation Office: Idukki, India, 2018.
- CartoDEM. Available online: https://bhuvan-app3.nrsc.gov.in/data/download/index.php (accessed on 20 August 2019).
- India Meteorological Department (IMD). Available online: http://dsp.imdpune.gov.in/ (accessed on 23 July 2019).
- Berti, M.; Martina, M.L.V.; Franceschini, S.; Pignone, S.; Simoni, A.; Pizziolo, M. Probabilistic rainfall thresholds for landslide occurrence using a Bayesian approach. J. Geophys. Res. Earth Surf. 2012, 117, 1–20. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Nasrollahi, N.; Li, J.; Imam, B.; Sorooshian, S. Geometrical characterization of precipitation patterns. J. Hydrometeorol. 2011, 12, 274–285. [Google Scholar] [CrossRef]
- Segoni, S.; Rossi, G.; Rosi, A.; Catani, F. Landslides triggered by rainfall: A semi-automated procedure to define consistent intensity-duration thresholds. Comput. Geosci. 2014, 63, 123–131. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Luciani, S.; Valigi, D.; Guzzetti, F. Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 447–458. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; School of Mathematics University of Bath: Bath, UK, 1986. [Google Scholar]
- Pasuto, A.; Silvano, S. Rainfall as a trigger of shallow mass movements. A case study in the Dolomites, Italy. Environ. Geol. 1998, 35, 184–189. [Google Scholar] [CrossRef]
- Rosi, A.; Lagomarsino, D.; Rossi, G.; Segoni, S.; Battistini, A.; Casagli, N. Updating ews rainfall thresholds for the triggering of landslides. Nat. Hazards 2015, 78, 297–308. [Google Scholar] [CrossRef]
- Lagomarsino, D.; Segoni, S.; Rosi, A.; Rossi, G.; Battistini, A.; Catani, F.; Casagli, N. Quantitative comparison between two different methodologies to define rainfall thresholds for landslide forecasting. Nat. Hazards Earth Syst. Sci. 2015, 15, 2413–2423. [Google Scholar] [CrossRef]
- Segoni, S.; Rosi, A.; Lagomarsino, D.; Fanti, R.; Casagli, N. Brief communication: Using averaged soil moisture estimates to improve the performances of a regional-scale landslide early warning system. Nat. Hazards Earth Syst. Sci. 2018, 18, 807–812. [Google Scholar] [CrossRef]
- Segoni, S.; Rosi, A.; Fanti, R.; Gallucci, A.; Monni, A.; Casagli, N. A regional-scale landslide warning system based on 20 years of operational experience. Water 2018, 10, 1297. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. An Algorithm for the objective reconstruction of rainfall events responsible for landslides. Landslide 2015, 12, 311–320. [Google Scholar] [CrossRef]
- Capparelli, G.; Tiranti, D. Application of the MoniFLaIR early warning system for rainfall-induced landslides in Piedmont region (Italy). Landslides 2010, 7, 401–410. [Google Scholar] [CrossRef]
- Lagomarsino, D.; Segoni, S.; Fanti, R.; Catani, F. Updating and tuning a regional-scale landslide early warning system. Landslides 2013, 10, 91–97. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).