Feasibility of the Use of Variable Speed Drives in Center Pivot Systems Installed in Plots with Variable Topography
Abstract
1. Introduction
2. Material and Methods
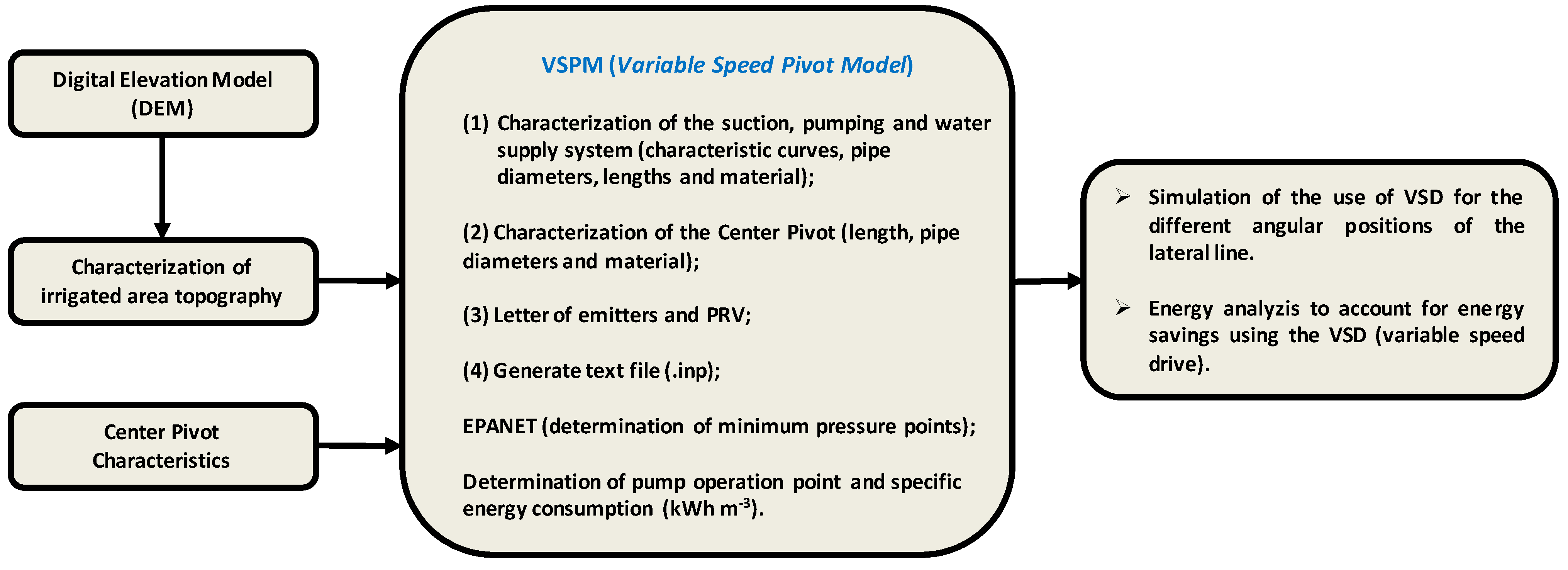
2.1. Proposed Procedure
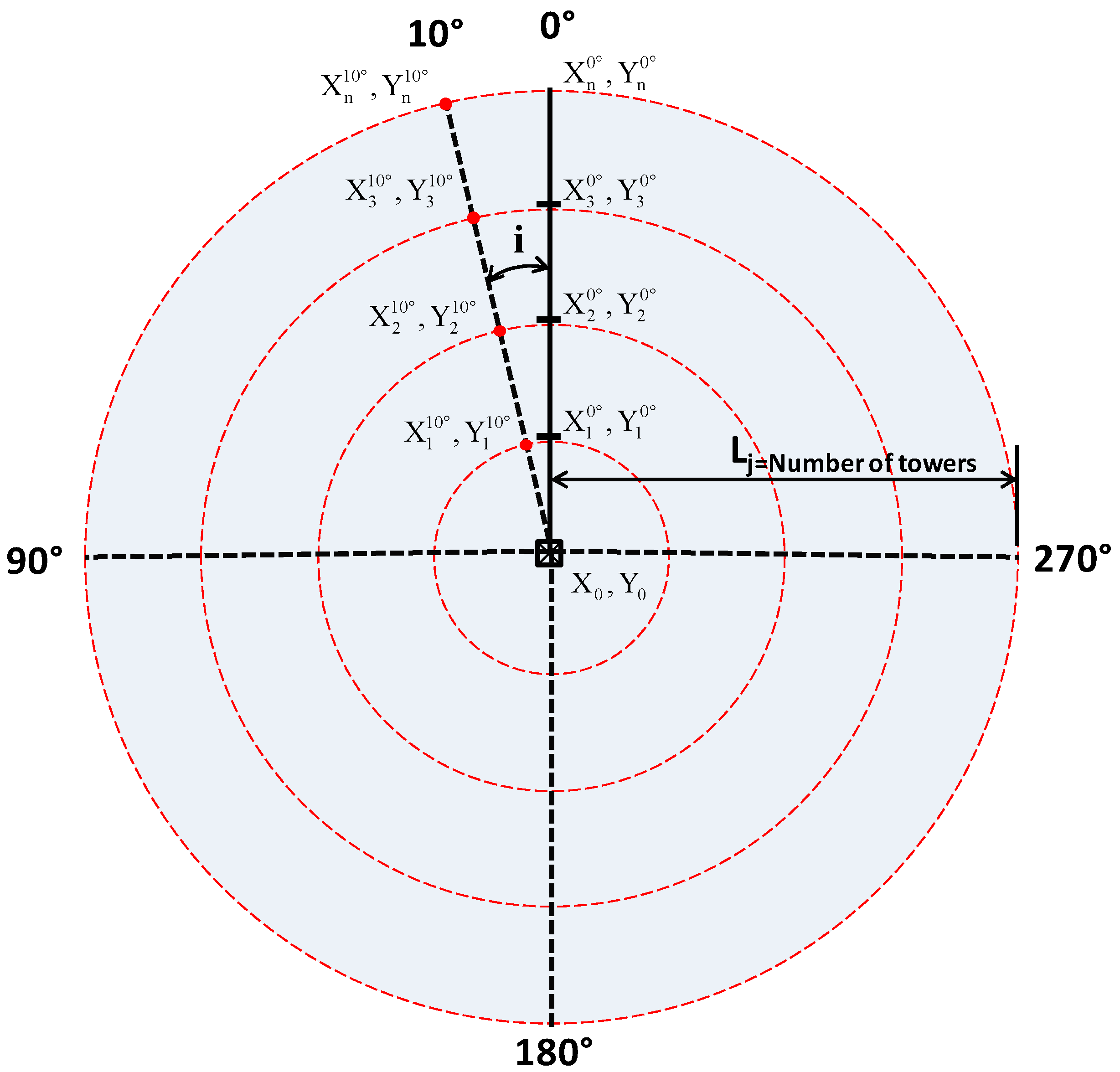
2.2. Topography of the Irrigated Area
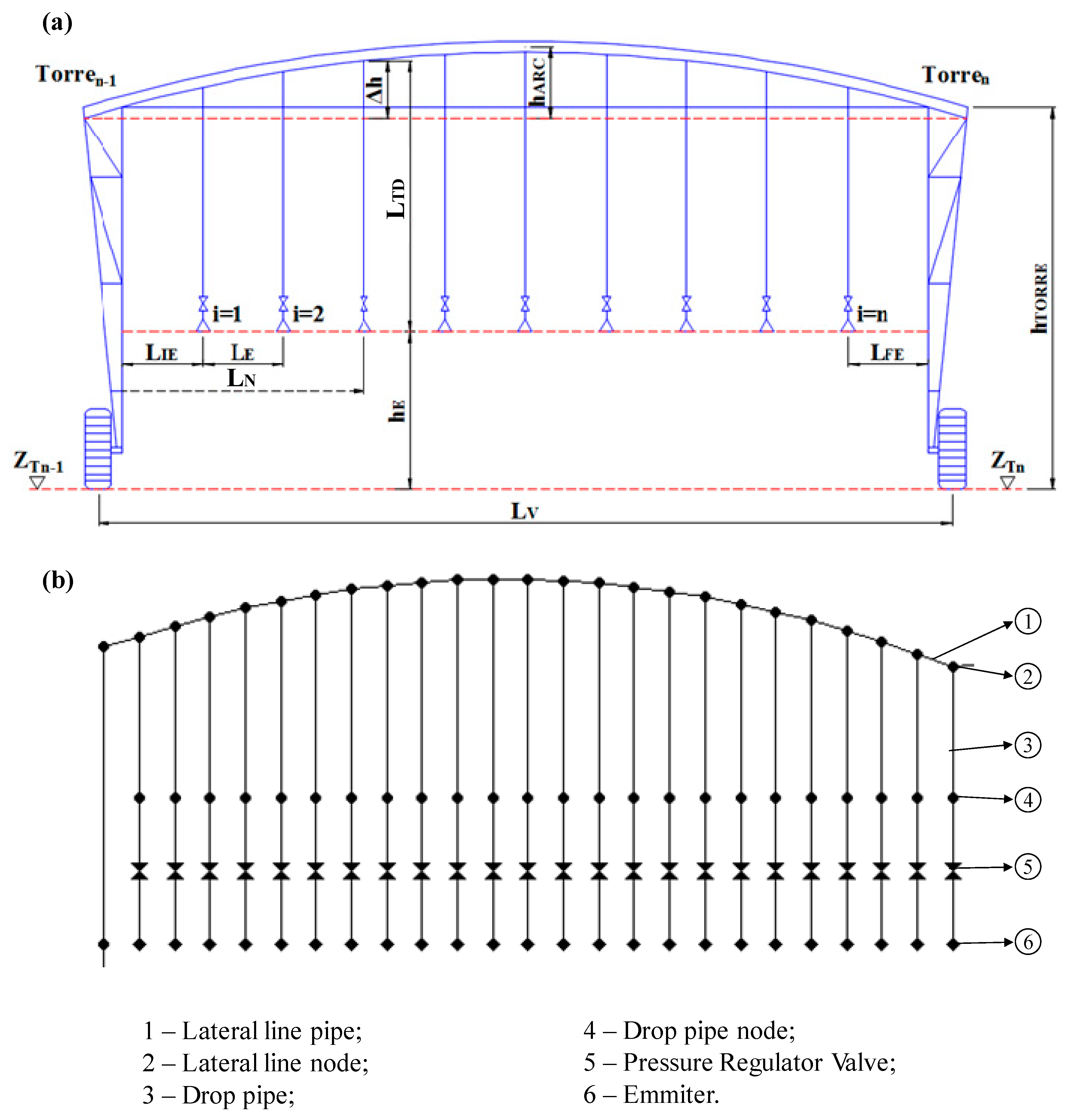
2.3. Hydraulic Model Description
2.3.1. Flow Rate of the Emitters
2.3.2. Determination of Elevations and Lengths
2.4. Calculation of the Pumping Operation Point and Energy Consumption
Hydraulic Model
2.5. Determination of Specific Energy Consumption (CEE)
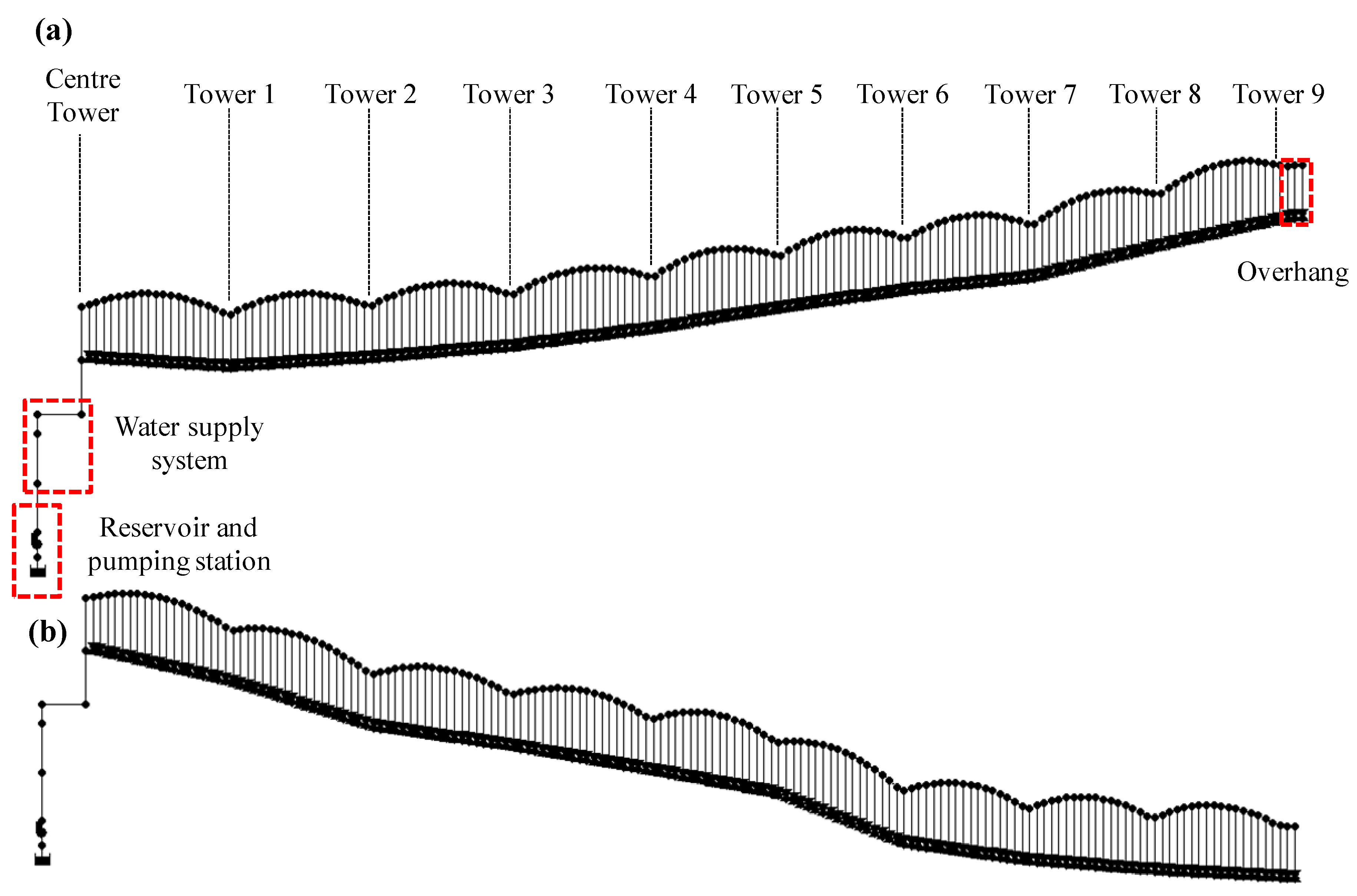
2.6. Case Study
3. Results and Discussion
3.1. Hydraulic Model
3.2. Operating Point
3.3. Pressure Distribution Along the Lateral Line
3.4. Energy Analysis
3.5. Economic Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Ac | cross-sectional area of cable (mm2) |
| Cc | electrical conductivity of copper (m Ω−1 mm−2) |
| CEEf | specific energy consumption, considering the pumping station with fixed speed (kWh m−3) |
| specific energy consumption using the VSD, for each angular position i (kWh m−3) | |
| ()av | average of the specific energy consumption in the different angular positions (kWh m−3) |
| CHW | roughness coefficient of the pipe material of the Hazen-Williams equation |
| cosϕ | power factor |
| D | pipe diameter of the lateral line |
| DEM | Digital Elevation Model |
| EC | Energy Consumption (kWh) |
| ER | Energy Reduction (%) |
| GIWR | gross irrigation water requirement (mm) |
| harc | maximum height of the lateral line arc (m) |
| hE | height of the emitter relative to the ground (m) |
| hf | head loss (m) |
| Hi | pressure head that the pump must provide for each angular position i (m) |
| Hmin(i) | minimum pressure along the lateral line for each angular position i (m) |
| Hp | pressure head at the fixed pumping speed (m) |
| Hprv | nominal pressure of the PRV (m) |
| PRV pressure, including the minimum regulator requirement (m) | |
| hT | height of moving towers (m) |
| i | angular position of the lateral line (0°, 10°, …, 350°) |
| j | number of moving towers |
| ke | emitter discharge coefficient (m2.5 s−1) |
| L | equivalent length of lateral line (m) |
| Lb | gross irrigation depth (mm day−1) |
| Lc | cable length (m) |
| LDP | total length of the drop pipe (m) |
| LE | spacing between emitters (m) |
| LFE | distance between the last emitter and next tower of the span (m) |
| LIE | spacing between the tower and the first emitter (m) |
| Lj | distance from the centre tower to the index tower j (m) |
| LN | distance of the node referring to the water outlet in relation to the previous tower (m) |
| LS | length of span (m) |
| N | water outlet in the span |
| NO | number of water outlets in the span |
| PH | hydraulic power (kW) |
| PNOA | Spanish National Program of aerial photogrammetry |
| PAbs(i) | absorbed power (kW) |
| PNom | nominal power (kW) |
| PRV | Pressure Regulator Valve |
| Q | total flow rate of the irrigation system |
| qx | flow of the outlet with order number x (m3 h−1) |
| Rinst | radius of installation of the emitter, relative to the centre tower (m) |
| RT | radius of rotation of the tower relative to the centre tower (m) |
| ST | slope between towers n e n −1 |
| Tg | rotation time (h) |
| To | operating time of irrigation system (h) |
| U | nominal voltage (V) |
| VSD | Variable Speed Drive |
| VSPM | Variable Speed Pivot Model |
| , | geographical coordinates of the moving towers j (m) |
| Zn=x | elevation of the node x (m) |
| ZTn | tower elevation posterior to node n (m) |
| ZTn-1 | tower elevation previous to node n (m) |
| α | ratio between the speed of the variable speed drive and the maximum speed as a fixed speed drive |
| β | exponent of the pressure |
| γ | water specific weight (N m−3) |
| Δh | length of the drop pipe between the lateral line and the tower (m) |
| ηc | cable efficiency |
| ηm | motor efficiency |
| ηp | pump efficiency |
| ηt | total efficiency of the pumping station |
| ηv | VSD efficiency |
References
- Alexandratos, N.; Bruinsma, J. World Agriculture Towards 2030/2050: The 2012 Revision; ESA Work. Pap. No. 12–03; FAO: Rome, Italy, 2012; p. 153. [Google Scholar]
- Pereira, L.S. Water, Agriculture and Food: Challenges and Issues. Water Resour. Manag. 2017, 31, 2985–2999. [Google Scholar] [CrossRef]
- World Business Council for Sustainable Development. Water, Food and Energy Nexus Challenges; World Business Council for Sustainable Development: Geneve, Switzlerand, 2014. [Google Scholar]
- Tarjuelo, J.M.; Rodriguez-diaz, J.A.; Abadía, R.; Camacho, E.; Rocamora, C.; Moreno, M.A. Efficient water and energy use in irrigation modernization: Lessons from Spanish case studies. Agric. Water Manag. 2015, 162, 67–77. [Google Scholar] [CrossRef]
- AQUASTAT Database. FAO’s Global Water Information System: Area Equipped for Irrigation; FAO: Rome, Italy, 2014. [Google Scholar]
- Frizzone, J.A.; Rezende, R.; Camargo, A.P.; Colombo, A. Irrigação por Aspersão: Sistema Pivô Central, 1st ed.; Editora UEM: Maringá, PR, Brazil, 2018. [Google Scholar]
- Keller, J.; Bliesner, R.D. Sprinkle and Trickle Irrigation; Van Nostrand Reinholh: New York, NY, USA, 1990. [Google Scholar]
- Folegatti, M.V.; Pessoa, P.C.S.; Paz, V.P.S. Avaliação do desempenho de um Pivô Central de Grande Porte e Baixa Pressão. Sci. Agric. 1998, 55, 119–127. [Google Scholar] [CrossRef]
- Gilley, J.R.; Watts, D.G. Possible Energy Savings in Irrigation. J. Irrig. Drain. Div. 1977, 103, 445–457. [Google Scholar]
- Moreno, M.A.; Planells, P.; Córcoles, J.I.; Tarjuelo, J.M.; Carrión, P.A. Development of a new methodology to obtain the characteristic pump curves that minimize the total cost at pumping stations. Biosyst. Eng. 2008, 102, 95–105. [Google Scholar] [CrossRef]
- Moreno, M.A.; Medina, D.; Ortega, J.F.; Tarjuelo, J.M. Optimal design of center pivot systems with water supplied from wells. Agric. Water Manag. 2012, 107, 112–121. [Google Scholar] [CrossRef]
- Barbosa, B.D.S.; Colombo, A.; de Souza, J.G.N.; da Baptista, V.B.; de Araújo, A.C.S. Energy Efficiency of a Center Pivot Irrigation System. Eng. Agrícola 2018, 38, 284–292. [Google Scholar] [CrossRef]
- King, B.A.; Wall, R.W. Distributed Instrumentation for Optimum Control of Variable Speed Eletric Pumping Plants with Center Pivots. Appl. Eng. Agric. 2000, 16, 45–50. [Google Scholar] [CrossRef]
- Kranz, W.L.; Irmak, S.; Martin, D.L.; Yonts, C.D. Flow Control Devices for Center Pivot Irrigation Systems. Univ. Neb. Linc. Ext. Inst. Agric. Nat. Resour. 2007, 888, 1–3. [Google Scholar]
- Alandi, P.P.; Pérez, P.C.; Álvarez, J.F.O.; Moreno, M.Á.; Tarjuelo, J.M. Pumping Selection and Regulation for Water-Distribution Networks. J. Irrig. Drain. Eng. 2005, 131, 273–281. [Google Scholar] [CrossRef]
- Khadra, R.; Moreno, M.A.; Awada, H.; Lamaddalena, N. Energy and Hydraulic Performance-Based Management of Large-Scale Pressurized Irrigation Systems. Water Resour. Manag. 2016, 30, 3493–3506. [Google Scholar] [CrossRef]
- Fernández García, I.; Moreno, M.A.; Rodríguez Díaz, J.A. Optimum pumping station management for irrigation networks sectoring: Case of Bembezar MI (Spain). Agric. Water Manag. 2014, 144, 150–158. [Google Scholar] [CrossRef]
- Hanson, B.R.; Weigand, C.; Orloff, S. Variable-frequency drives for electric irrigation pumping plants save energy. Calif. Agric. 1996, 50, 36–39. [Google Scholar] [CrossRef]
- Lamaddalena, N.; Khila, S. Energy saving with variable speed pumps in on-demand irrigation systems. Irrig. Sci. 2012, 30, 157–166. [Google Scholar] [CrossRef]
- Brar, D.; Kranz, W.L.; Lo, T.; Irmak, S.; Martin, D.L. Energy Conservation Using Variable-Frequency Drives for Center-Pivot Irrigation: Standard Systems. Trans. ASABE 2017, 60, 95–106. [Google Scholar] [CrossRef]
- Scaloppi, E.J.; Allen, R.G. Hydraulics of Center Pivot Laterals. J. Irrig. Drain. Eng. 1993, 119, 554–567. [Google Scholar] [CrossRef]
- Moreno, M.A.; Córcoles, J.I.; Tarjuelo, J.M.; Ortega, J.F. Energy efficiency of pressurised irrigation networks managed on-demand and under a rotation schedule. Biosyst. Eng. 2010, 107, 349–363. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2: User Manual; National Risk Management Research Laboratory Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2000.
- Valiantzas, J.D.; Dercas, N. Hydraulic Analysis of Multidiameter Center-Pivot Sprinkler Laterals. J. Irrig. Drain. Eng. 2005, 131, 137–146. [Google Scholar] [CrossRef]
- Bernier, M.A.; Bourret, B. Pumping energy and variable frequency drives. ASHRAE J. 1999, 41, 37–40. [Google Scholar]
- Alazba, A.A.; Asce, M.; Mattar, M.A.; Elnesr, M.N.; Amin, M.T. Field Assessment of Friction Head Loss and Friction Correction Factor Equations. J. Irrig. Drain. Eng. 2012, 138, 166–176. [Google Scholar] [CrossRef]
- Córcoles, J.; Gonzalez Perea, R.; Izquiel, A.; Moreno, M. Decision Support System Tool to Reduce the Energy Consumption of Water Abstraction from Aquifers for Irrigation. Water 2019, 11, 323. [Google Scholar] [CrossRef]
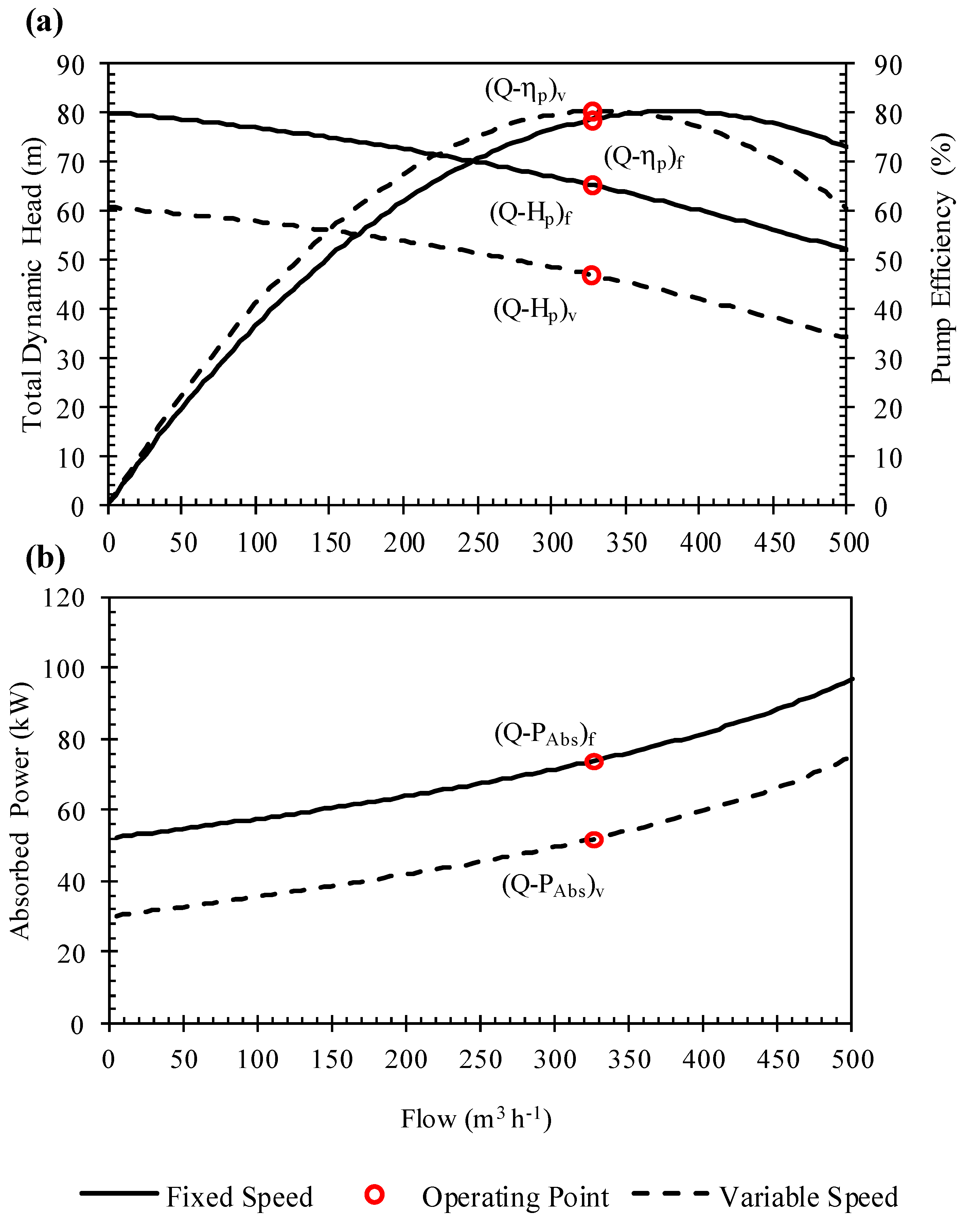
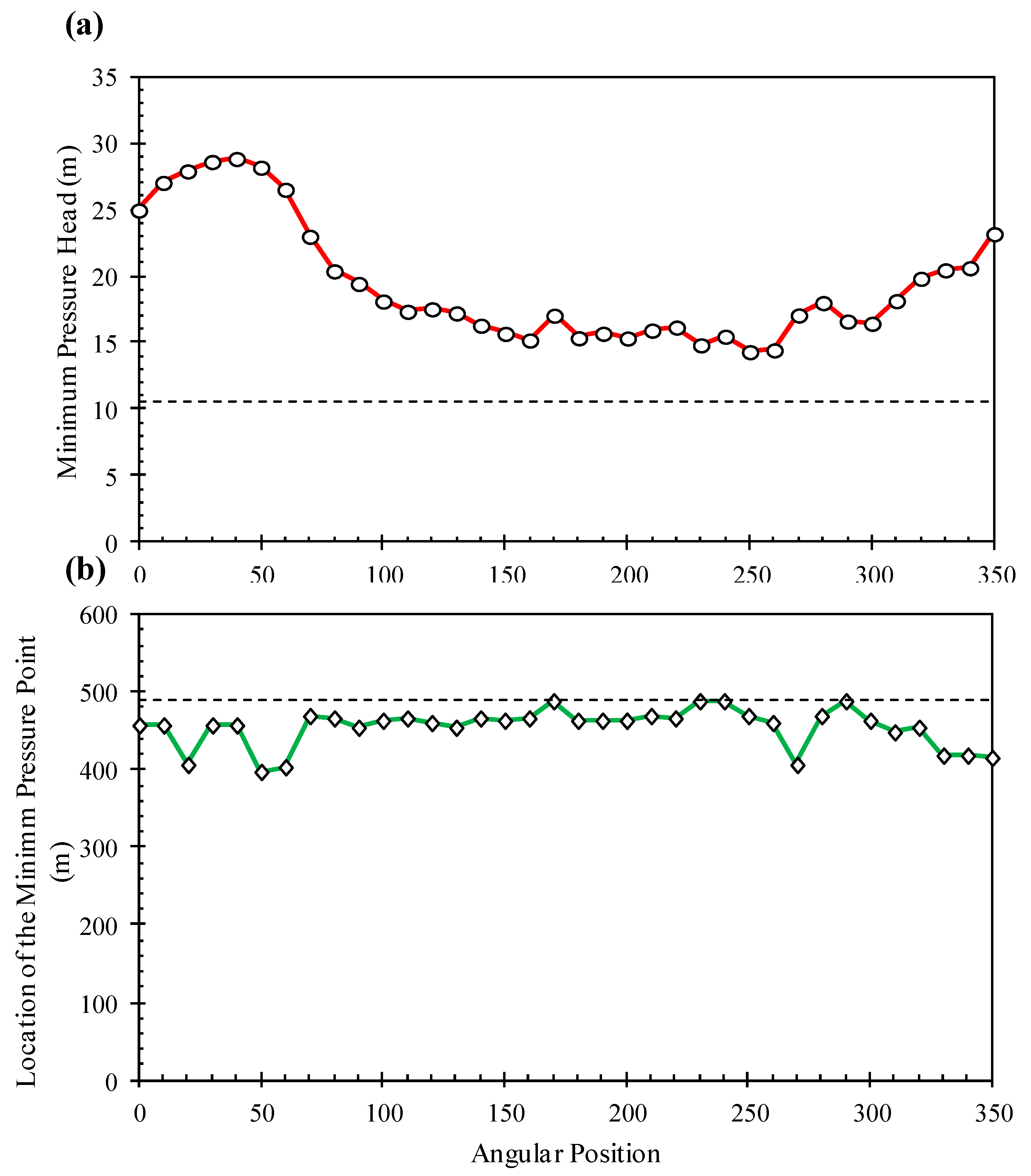
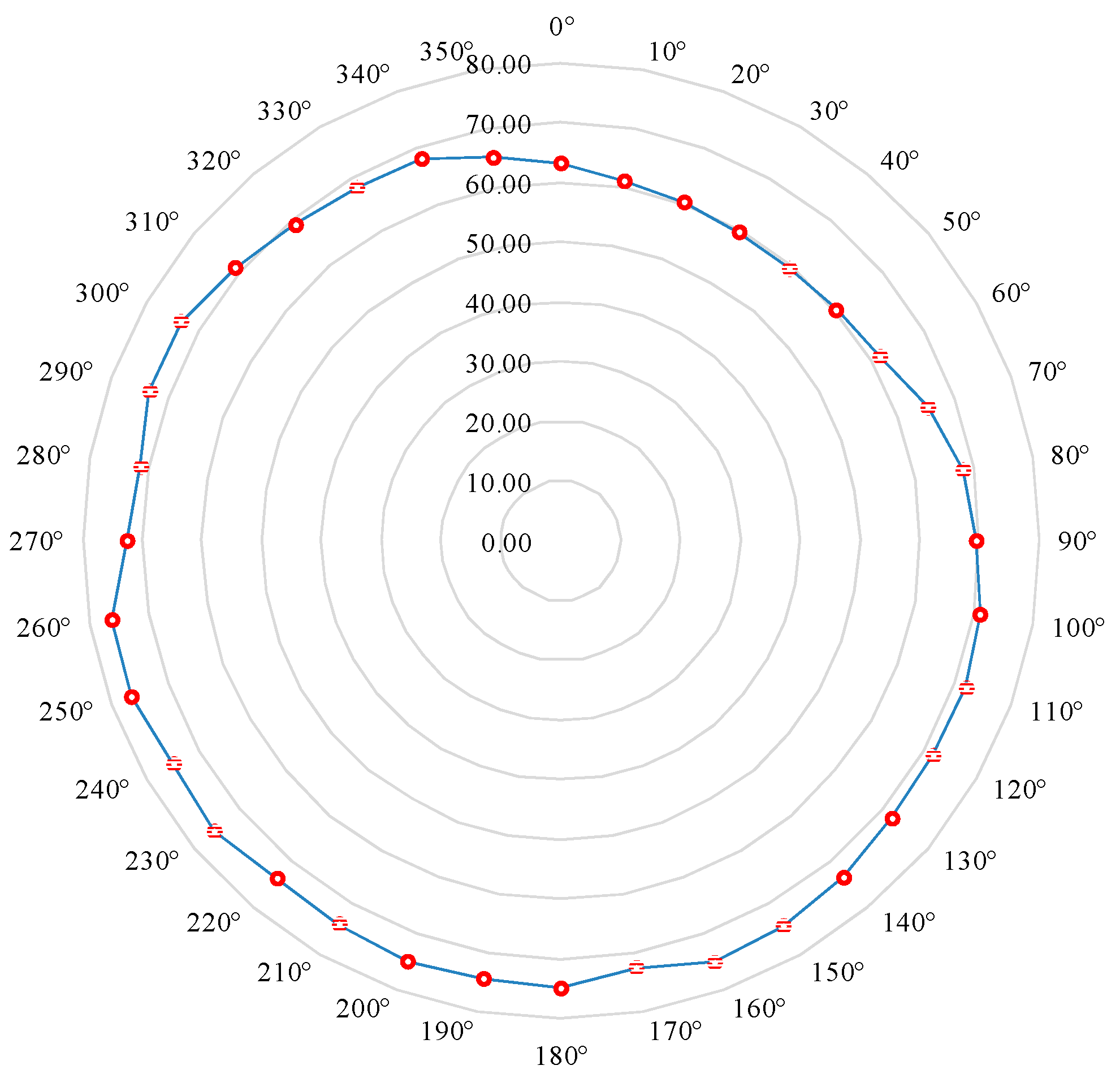
| Angular Position | Q (m3 h−1) | Hi (m) | PH (kW) | n | α | ηp (%) | ηm (%) | ηv (%) | ηc (%) | ηt 1 (%) | CEE (kWh m−3) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fixed | 326.61 | 65.23 | 58.04 | 1750 | 1.00 | 78.54 | 94.13 | 98.60 | 72.90 | 0.244* | |
| 0° | 326.61 | 50.72 | 45.12 | 1574 | 0.90 | 80.08 | 93.86 | 96.75 | 98.65 | 71.74 | 0.193 |
| 10° | 326.61 | 48.64 | 43.27 | 1547 | 0.88 | 80.20 | 93.77 | 96.21 | 98.66 | 71.38 | 0.186 |
| 20° | 326.61 | 47.77 | 42.50 | 1535 | 0.88 | 80.23 | 93.73 | 95.95 | 98.66 | 71.19 | 0.183 |
| 30° | 326.61 | 47.07 | 41.88 | 1526 | 0.87 | 80.26 | 93.69 | 95.71 | 98.66 | 71.01 | 0.181 |
| 40° | 326.61 | 46.84 | 41.67 | 1523 | 0.87 | 80.26 | 93.68 | 95.63 | 98.67 | 70.94 | 0.180 |
| 50° | 326.61 | 47.49 | 42.25 | 1531 | 0.88 | 80.24 | 93.71 | 95.86 | 98.66 | 71.12 | 0.182 |
| 60° | 326.61 | 49.16 | 43.74 | 1553 | 0.89 | 80.17 | 93.79 | 96.36 | 98.66 | 71.48 | 0.187 |
| 70° | 326.61 | 52.69 | 46.88 | 1599 | 0.91 | 79.93 | 93.93 | 97.13 | 98.64 | 71.93 | 0.200 |
| 80° | 326.61 | 55.29 | 49.20 | 1631 | 0.93 | 79.70 | 94.00 | 97.43 | 98.63 | 72.00 | 0.209 |
| 90° | 326.61 | 56.24 | 50.04 | 1643 | 0.94 | 79.61 | 94.02 | 97.48 | 98.63 | 71.96 | 0.213 |
| 100° | 326.61 | 57.57 | 51.22 | 1659 | 0.95 | 79.47 | 94.04 | 97.51 | 98.63 | 71.88 | 0.218 |
| 110° | 326.61 | 58.33 | 51.90 | 1669 | 0.95 | 79.39 | 94.05 | 97.50 | 98.62 | 71.80 | 0.221 |
| 120° | 326.61 | 58.15 | 51.73 | 1666 | 0.95 | 79.41 | 94.05 | 97.50 | 98.62 | 71.82 | 0.221 |
| 130° | 326.61 | 58.45 | 52.01 | 1670 | 0.95 | 79.38 | 94.06 | 97.50 | 98.62 | 71.79 | 0.222 |
| 140° | 326.61 | 59.38 | 52.83 | 1681 | 0.96 | 79.27 | 94.07 | 97.45 | 98.62 | 71.67 | 0.226 |
| 150° | 326.61 | 60.00 | 53.38 | 1689 | 0.96 | 79.20 | 94.08 | 97.41 | 98.62 | 71.58 | 0.228 |
| 160° | 326.61 | 60.49 | 53.82 | 1695 | 0.97 | 79.14 | 94.09 | 97.37 | 98.62 | 71.49 | 0.230 |
| 170° | 326.61 | 58.63 | 52.16 | 1672 | 0.96 | 79.36 | 94.06 | 97.49 | 98.62 | 71.77 | 0.223 |
| 180° | 326.61 | 60.33 | 53.67 | 1693 | 0.97 | 79.16 | 94.08 | 97.38 | 98.62 | 71.52 | 0.230 |
| 190° | 326.61 | 59.99 | 53.37 | 1688 | 0.96 | 79.20 | 94.08 | 97.41 | 98.62 | 71.58 | 0.228 |
| 200° | 326.61 | 60.35 | 53.69 | 1693 | 0.97 | 79.16 | 94.08 | 97.38 | 98.62 | 71.52 | 0.230 |
| 210° | 326.61 | 59.75 | 53.16 | 1686 | 0.96 | 79.23 | 94.08 | 97.43 | 98.62 | 71.61 | 0.227 |
| 220° | 326.61 | 59.52 | 52.96 | 1683 | 0.96 | 79.25 | 94.07 | 97.44 | 98.62 | 71.65 | 0.226 |
| 230° | 326.61 | 60.86 | 54.15 | 1699 | 0.97 | 79.10 | 94.09 | 97.33 | 98.62 | 71.43 | 0.232 |
| 240° | 326.61 | 60.21 | 53.57 | 1691 | 0.97 | 79.17 | 94.08 | 97.39 | 98.62 | 71.54 | 0.229 |
| 250° | 326.61 | 61.37 | 54.60 | 1705 | 0.97 | 79.03 | 94.10 | 97.27 | 98.61 | 71.33 | 0.234 |
| 260° | 326.61 | 61.24 | 54.48 | 1703 | 0.97 | 79.05 | 94.09 | 97.28 | 98.61 | 71.36 | 0.234 |
| 270° | 326.61 | 58.61 | 52.15 | 1672 | 0.96 | 79.36 | 94.06 | 97.49 | 98.62 | 71.77 | 0.222 |
| 280° | 326.61 | 57.68 | 51.32 | 1661 | 0.95 | 79.46 | 94.04 | 97.51 | 98.63 | 71.87 | 0.219 |
| 290° | 326.61 | 59.07 | 52.56 | 1677 | 0.96 | 79.31 | 94.07 | 97.47 | 98.62 | 71.71 | 0.224 |
| 300° | 326.61 | 59.24 | 52.70 | 1679 | 0.96 | 79.29 | 94.07 | 97.46 | 98.62 | 71.69 | 0.225 |
| 310° | 326.61 | 57.53 | 51.19 | 1659 | 0.95 | 79.48 | 94.04 | 97.51 | 98.63 | 71.88 | 0.218 |
| 320° | 326.61 | 55.85 | 49.69 | 1638 | 0.94 | 79.65 | 94.01 | 97.47 | 98.63 | 71.98 | 0.211 |
| 330° | 326.61 | 55.22 | 49.13 | 1630 | 0.93 | 79.71 | 93.99 | 97.42 | 98.63 | 72.00 | 0.209 |
| 340° | 326.61 | 55.05 | 48.98 | 1628 | 0.93 | 79.73 | 93.99 | 97.41 | 98.63 | 72.00 | 0.208 |
| 350° | 326.61 | 52.50 | 46.71 | 1596 | 0.91 | 79.95 | 93.92 | 97.10 | 98.64 | 71.92 | 0.199 |
| Crop | Maize | |
|---|---|---|
| GIWR (gross irrigation water requirement) | mm | 627.00 |
| Flow rate | m3 h−1 | 326.61 |
| Operation time | h | 1440.00 |
| ECf | kWh | 114739.03 |
| ECv | kWh | 100632.47 |
| Average cost | € kW h−1 | 0.20 |
| Cf | € | 22947.96 |
| Cv | € | 20126.49 |
| Energy Savings | € year−1 | 2821.47 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buono da Silva Baptista, V.; Córcoles, J.I.; Colombo, A.; Moreno, M.Á. Feasibility of the Use of Variable Speed Drives in Center Pivot Systems Installed in Plots with Variable Topography. Water 2019, 11, 2192. https://doi.org/10.3390/w11102192
Buono da Silva Baptista V, Córcoles JI, Colombo A, Moreno MÁ. Feasibility of the Use of Variable Speed Drives in Center Pivot Systems Installed in Plots with Variable Topography. Water. 2019; 11(10):2192. https://doi.org/10.3390/w11102192
Chicago/Turabian StyleBuono da Silva Baptista, Victor, Juan Ignacio Córcoles, Alberto Colombo, and Miguel Ángel Moreno. 2019. "Feasibility of the Use of Variable Speed Drives in Center Pivot Systems Installed in Plots with Variable Topography" Water 11, no. 10: 2192. https://doi.org/10.3390/w11102192
APA StyleBuono da Silva Baptista, V., Córcoles, J. I., Colombo, A., & Moreno, M. Á. (2019). Feasibility of the Use of Variable Speed Drives in Center Pivot Systems Installed in Plots with Variable Topography. Water, 11(10), 2192. https://doi.org/10.3390/w11102192








