Effects of Submerged Vegetation Density on Turbulent Flow Characteristics in an Open Channel
Abstract
1. Introduction
2. Experimental Setup and Measurement
3. Results
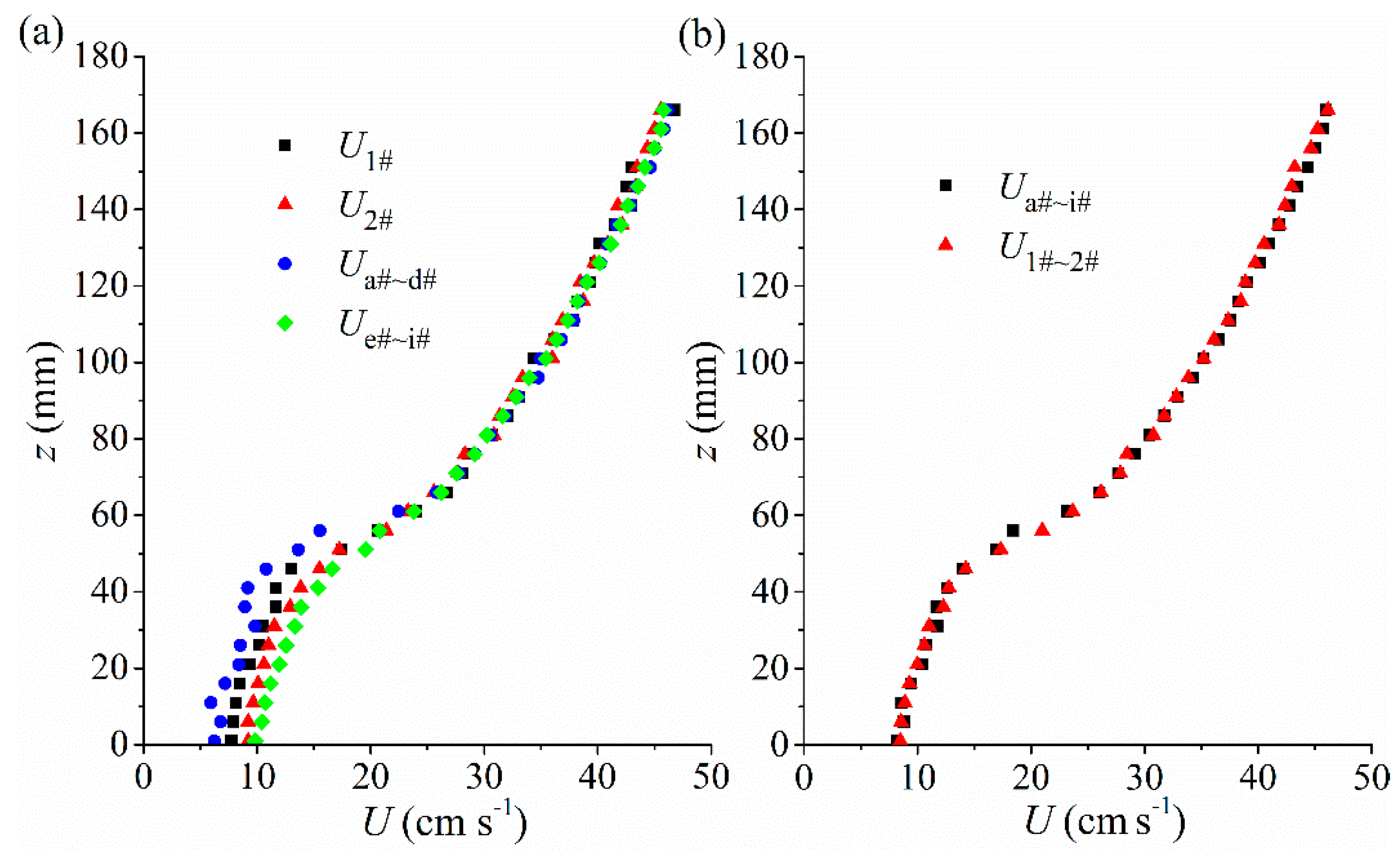
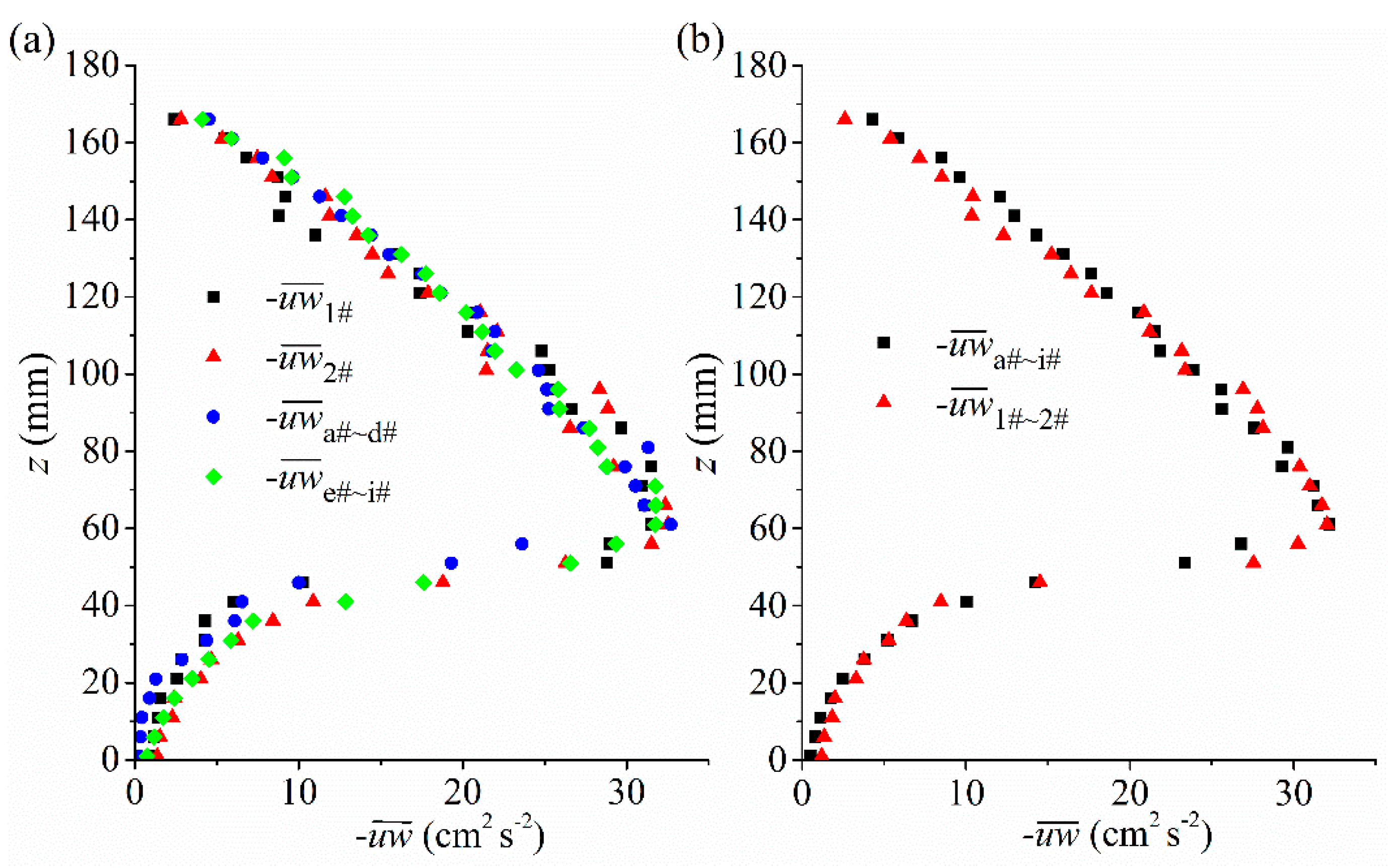
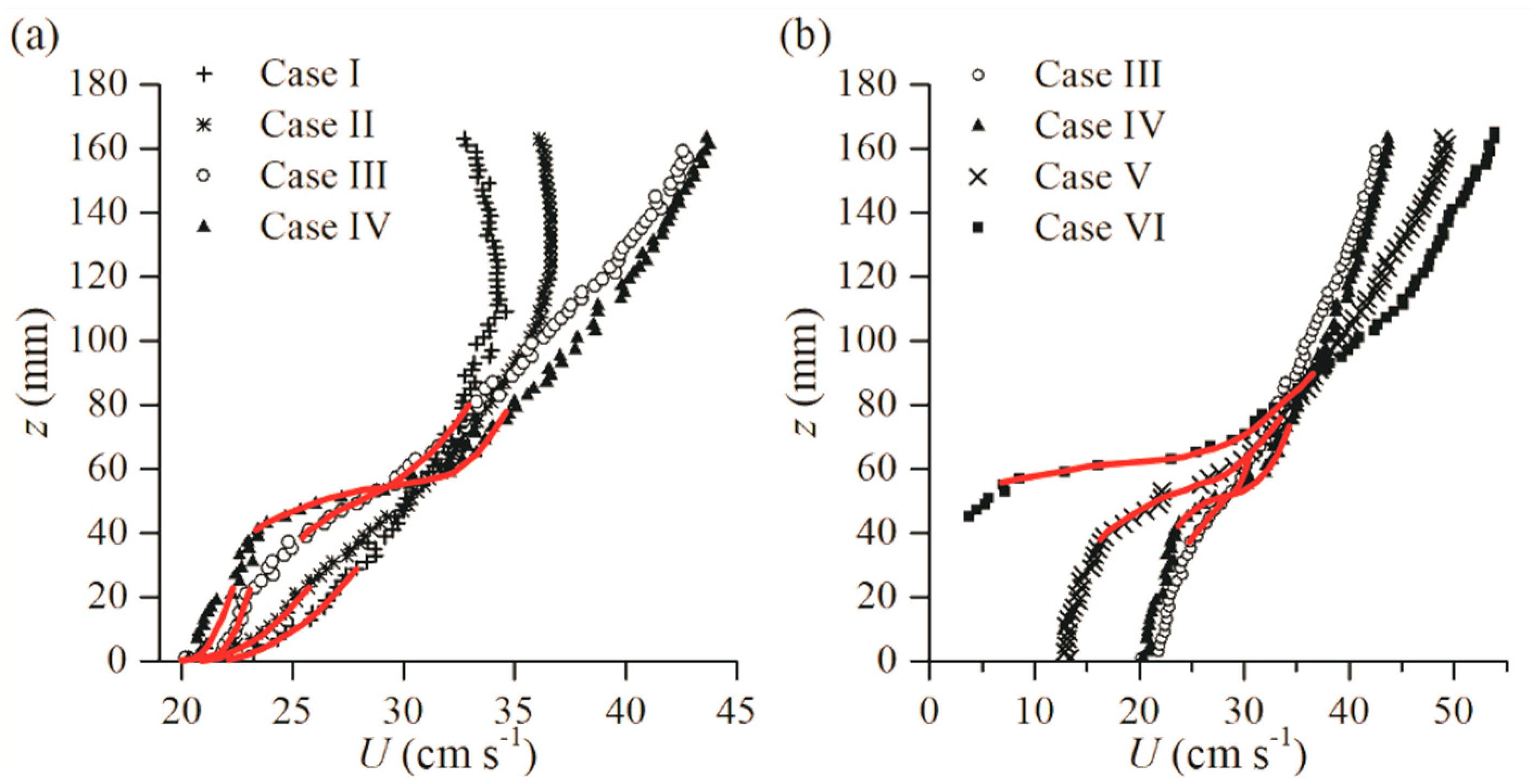
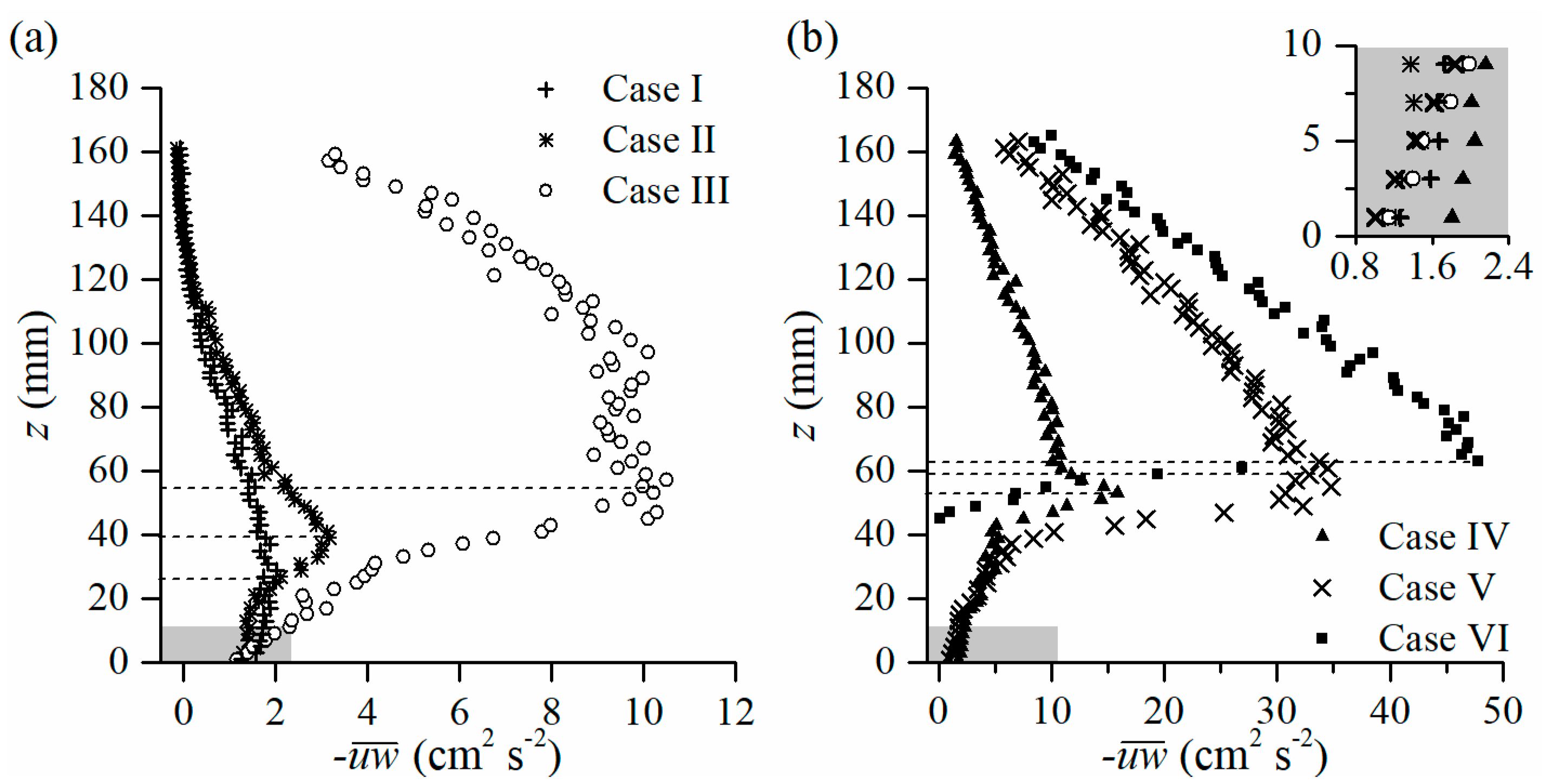
3.1. Spatial Variation of the Velocity and Reynolds Stress Profiles
3.2. Turbulent Statistics
3.2.1. Velocity
3.2.2. Shear Stress
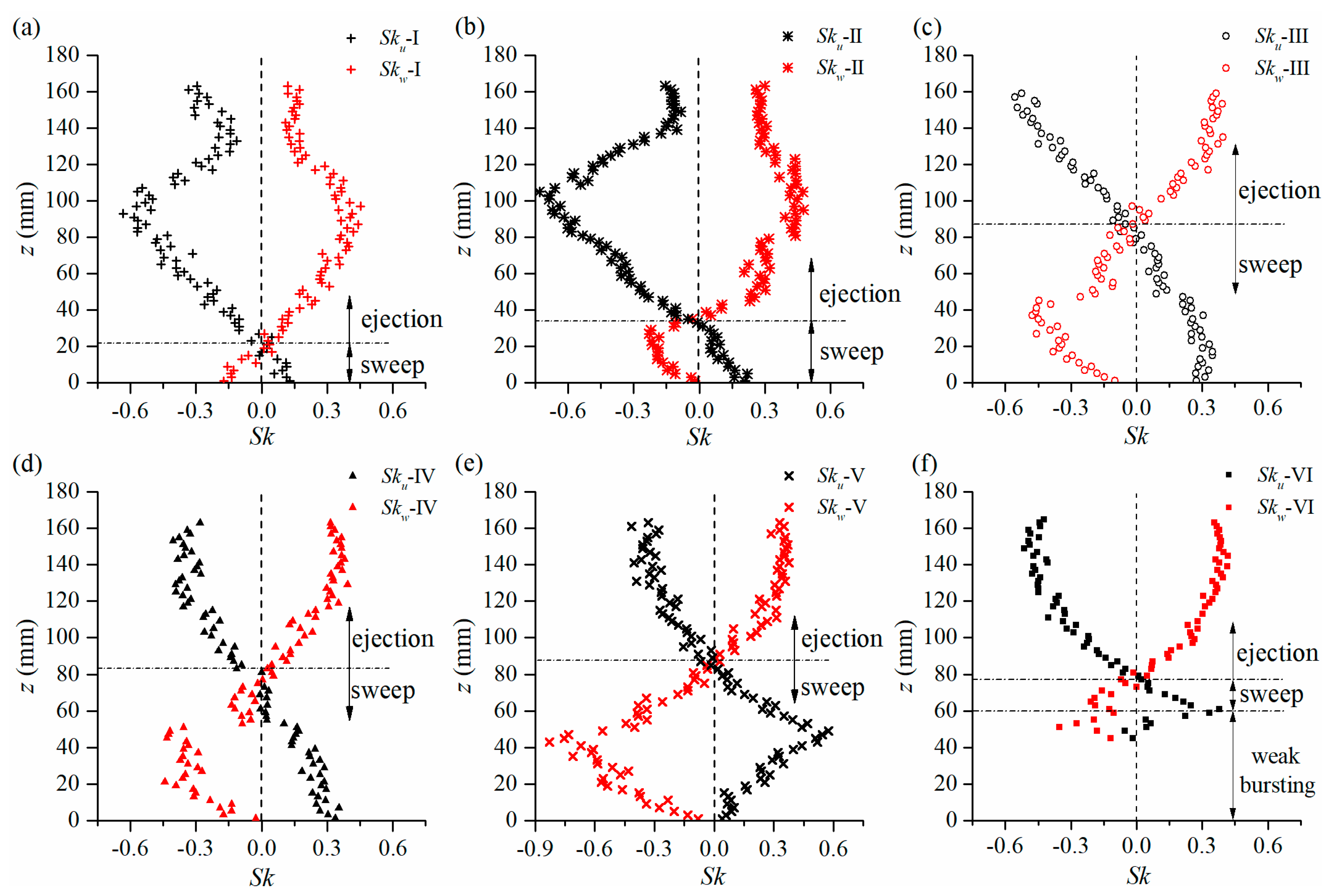
3.2.3. Skewness Coefficients
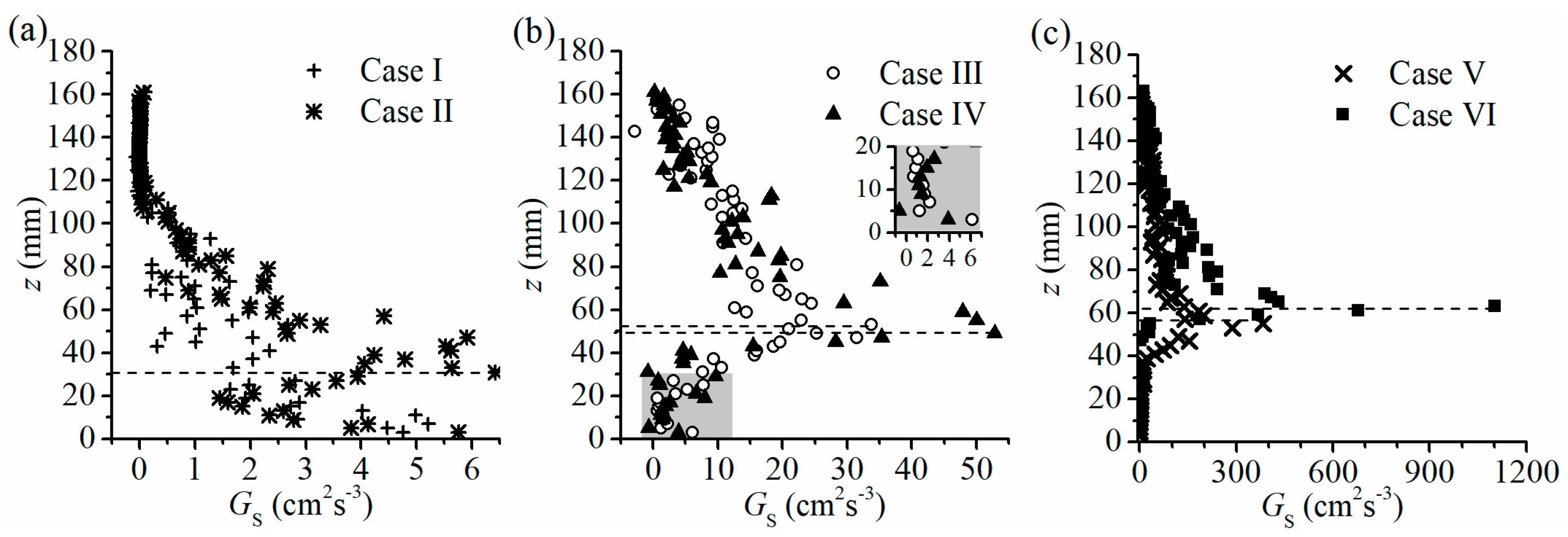
3.3. Turbulence Kinetic Energy Generation Rate
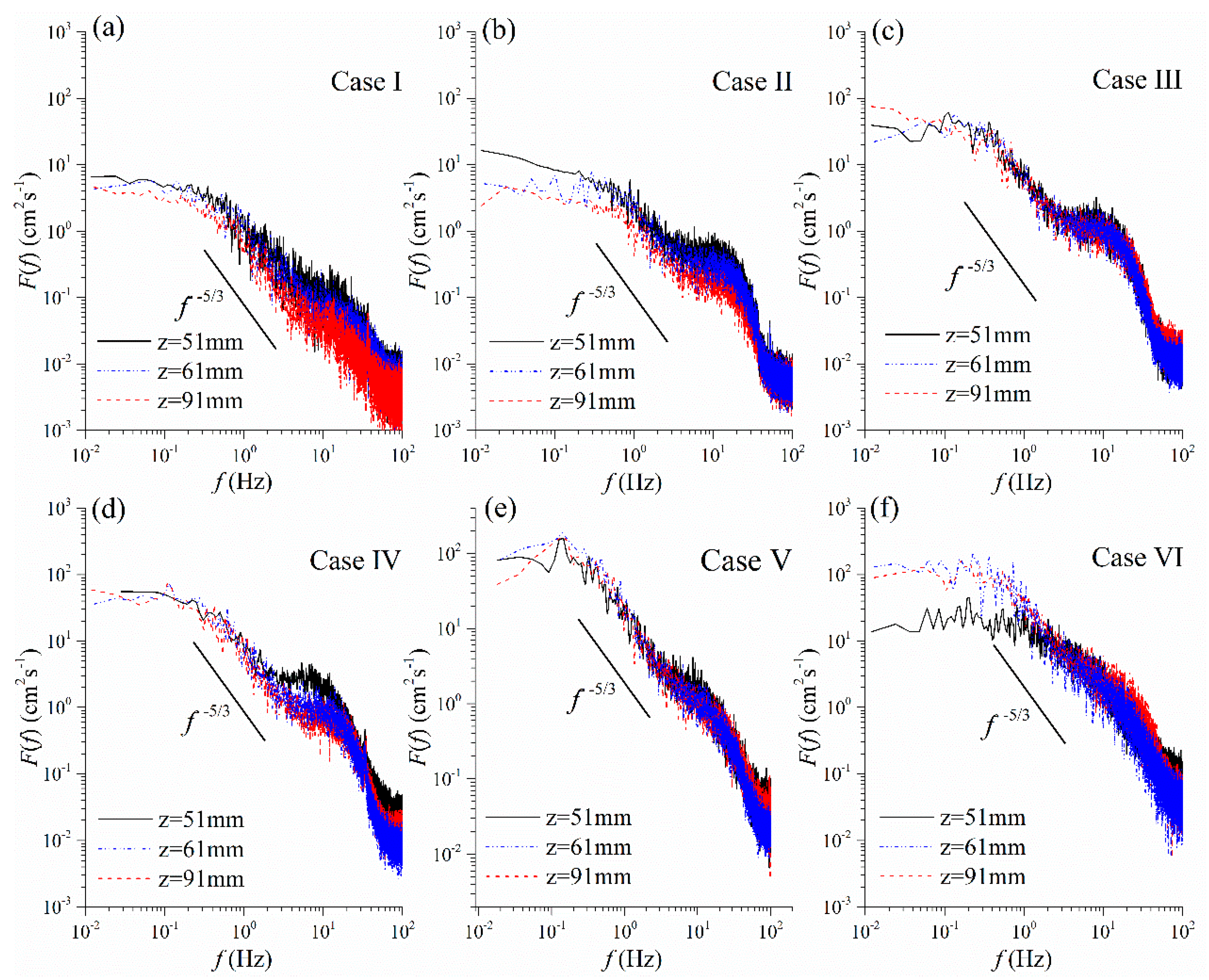
3.4. Turbulence Spectra
3.5. Distribution Law of the Velocity Profiles
4. Discussion
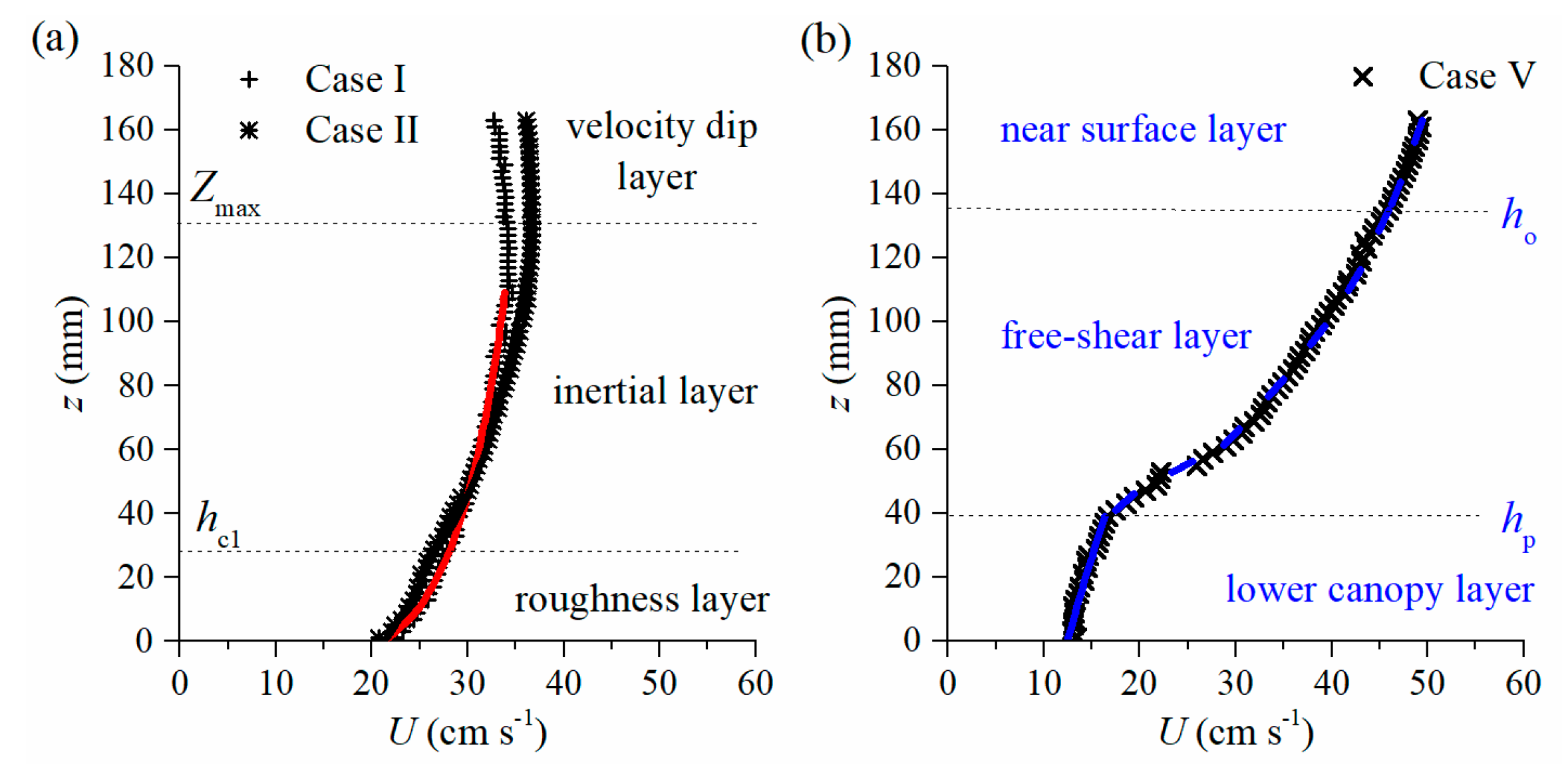
4.1. Horizontal Heterogeneity in the Flow Field
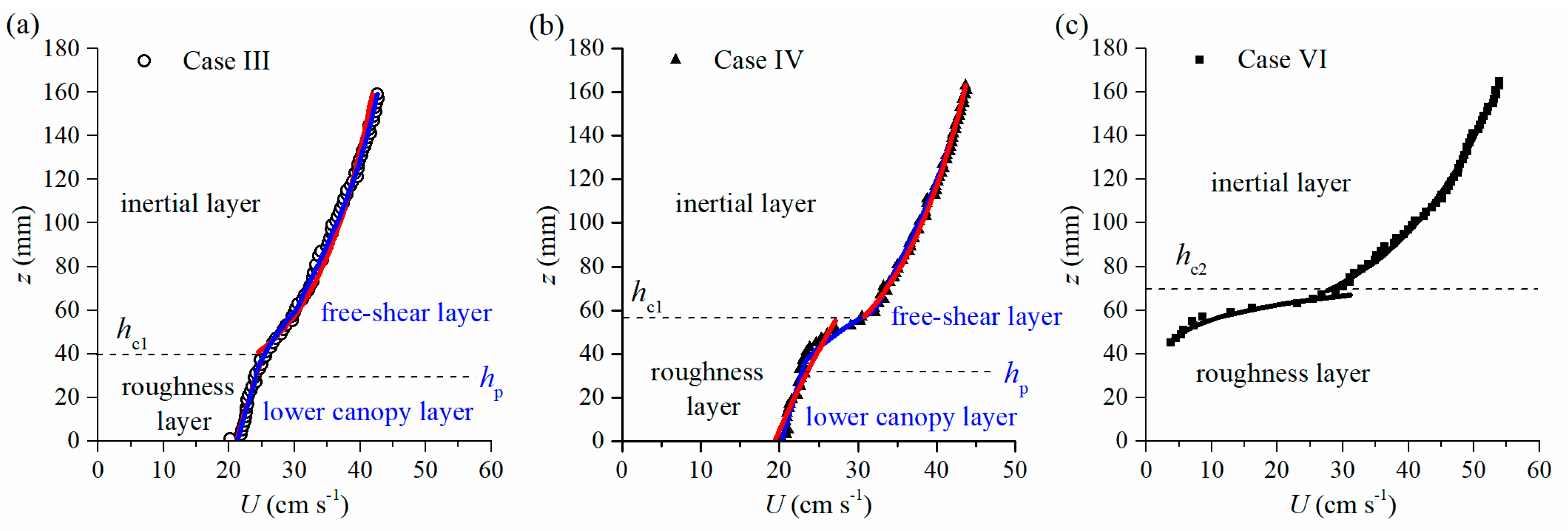
4.2. Flow at 0.04 < λ < 0.1
4.3. The Secondary Boundary-Shear Flow
5. Conclusions
- It is sufficiently accurate to represent overall flow characteristic by an average of velocities measured at Locations 1# & 2#;
- For a modest value of 0.04 < λ < 0.1, characteristics of profiles for turbulent statistics are similar to both the bed-shear flow one and the free-shear flow one. U profile could be described to comply with either the free-shear flow or the bed-shear flow features;
- The secondary boundary-shear flow occurs in Case VI with λ = 1.44. U profile could be described to comply with the bed- shear flow feature, and the boundary between the roughness layer and the inertial layer locates above the canopy;
- The change of turbulent flow type induced by an increase of λ would intensify the turbulence with large maximum value of GS. The point where turbulence is vertically fiercest moves upwards gradually with λ;
- The ISRs of spectral curves range from 0.4 to 4 Hz at different heights except within canopy in the secondary boundary-shear flow. For spectral curves of the low-frequency eddies, there are some slight humps at 0.04 < λ < 0.1, and the curves fluctuate intensely while λ > λNB.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huai, W.X.; Li, C.G. Longitudinal dispersion in open channel flow with suspended canopies. Water Sci. Technol. 2016, 74, 722–728. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.H.; Bai, F.P.; Huai, W.X.; An, R.D.; Wang, H.Y. Modelling open-channel flow with rigid vegetation based on two-dimensional shallow water equations using the lattice Boltzmann method. Ecol. Eng. 2017, 106, 75–81. [Google Scholar] [CrossRef]
- Li, D.; Yang, Z.H.; Sun, Z.H.; Huai, W.X.; Liu, J.H. Theoretical model of suspended sediment concentration in a flow with submerged vegetation. Water 2018, 10, 1656. [Google Scholar] [CrossRef]
- Yilmazer, D.; Ozan, A.Y.; Cihan, K. Flow characteristics in the wake region of a finite-length vegetation patch in a partly vegetated channel. Water 2018, 10, 459. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- Yan, J.; Dai, K.; Tang, H.W.; Cheng, N.S.; Chen, Y. Advances in research on turbulence structure in vegetated open channel flows. Adv. Water Sci. 2014, 18, 456–461. [Google Scholar]
- Cheng, N.S.; Nguyen, H.T.; Tan, S.K.; Shao, S.D. Scaling of Velocity profiles for depth-limited open channel flows over simulated rigid vegetation. J. Hydraul. Eng. 2012, 138, 673–683. [Google Scholar] [CrossRef]
- Wang, X.K.; Shao, X.J.; Li, D.X. Fundamental River Mechanics; Water & Power Press: Beijing, China, 2002. [Google Scholar]
- Nezu, I.; Sanjou, M. Turbulence structure and coherent motion in vegetated canopy open- channel flows. J. Hydro-Environ. Res. 2008, 2, 62–90. [Google Scholar] [CrossRef]
- Caroppi, G.; Gualtieri, P.; Fontana, N.; Giugni, M. Vegetated channel flows: Turbulence anisotropy at flow- rigid canopy interface. Geosciences 2018, 8, 259. [Google Scholar] [CrossRef]
- Wang, H.; Tang, H.W.; Zhao, H.Q.; Zhao, X.Y.; Lv, S.Q. Incipient motion of sediment in presence of submerged flexible vegetation. Water Sci. Eng. 2015, 8, 63–67. [Google Scholar] [CrossRef]
- Lv, S.Q.; Guo, M.J.; Yuan, L.W. Effects of submerged flexible vegetation on bed load movement in open channel. Yangtze River 2016, 47, 67–71. [Google Scholar]
- Yan, J. Experimental Study on Flow Resistance and Turbulence Characteristics of Open Channel Flows with Vegetation. Ph.D. Thesis, Hohai University, Nanjing, China, 2008. [Google Scholar]
- Nezu, I.; Nakagawa, H.; Tominaga, A. Secondary currents in a straight channel flow and the relation to its aspect ratio. Turbul. Shear Flows 1985, 4, 246–260. [Google Scholar]
- Ghisalberti, M.; Nepf, H.M. Mixing layers and coherent structures in vegetated aquatic flows. J. Geophysical Res. 2002, 107. [Google Scholar] [CrossRef]
- Belcher, S.; Jerram, N.; Hunt, J. Adjustment of a turbulent boundary layer to a canopy of roughness elements. J. Fluid Mech. 2003, 488, 369–398. [Google Scholar] [CrossRef]
- Katul, G.G.; Poggi, D.; Ridolfi, L. A flow resistance model for assessing the impact of vegetation on flood routing mechanics. Water Resour. Res. 2011, 47, W08533. [Google Scholar] [CrossRef]
- Ei-Hakim, O.; Salama, M.M. Velocity distribution inside and above branched flexible roughness. J. Irrig. Drain. Eng. 1992, 118, 914–927. [Google Scholar] [CrossRef]
- Wilson, J.D. A second-order closure model for flow through vegetation. Bound. Layer Meteorol. 1988, 42, 371–392. [Google Scholar] [CrossRef]
- Nikora, V.; Koll, K.; Mclean, S.; Dittrich, A.; Aberle, J. Zero-plane displacement for rough-bed open-channel flows. In Proceedings of the River Flow 2002, Louvain-la-Neuve, Belgium, 4–6 September 2002. [Google Scholar]
- Baptist, M.J.; Babovic, V.; Uthurburu, J.R.; Keijzer, M.; Uittenbogaard, R.E.; Mynett, A.; Verwey, A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Liu, D.; Diplas, P.; Hodges, C.C.; Fairbanks, J.D. Hydrodynamics of flow through double layer rigid vegetation. Geomorphology 2010, 116, 286–296. [Google Scholar] [CrossRef]
- Huai, W.X.; Zeng, Y.H.; Xu, Z.G.; Yang, Z.H. Three-layer model for vertical velocity distribution in open channel flow with submerged rigid vegetation. Adv. Water Resour. 2009, 32, 487–492. [Google Scholar] [CrossRef]
- Tang, H.W.; Tian, Z.J.; Yan, J.; Yuan, S.Y. Determining drag coefficients and their application in modelling of turbulent flow with submerged vegetation. Adv. Water Resour. 2014, 69, 134–145. [Google Scholar] [CrossRef]
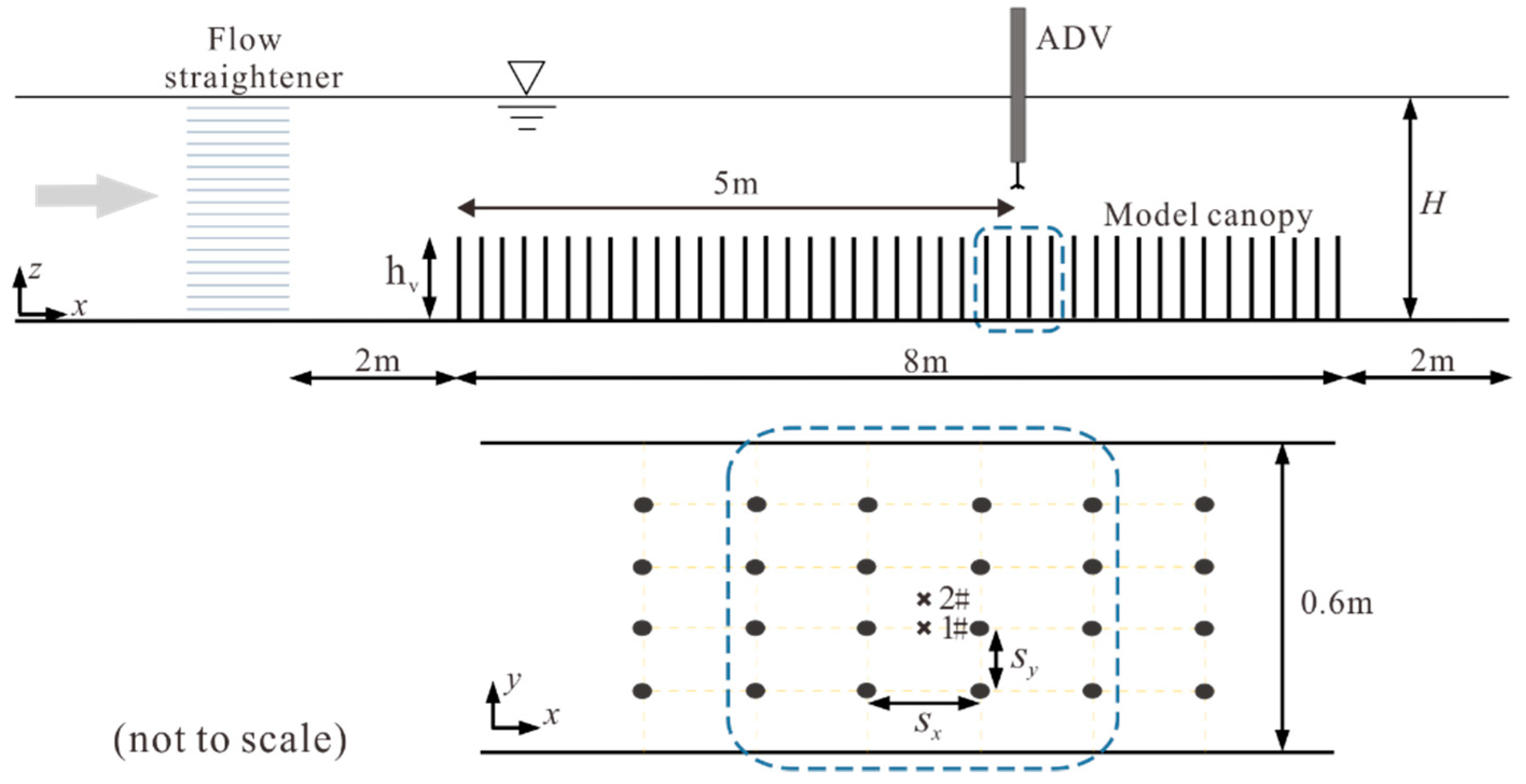
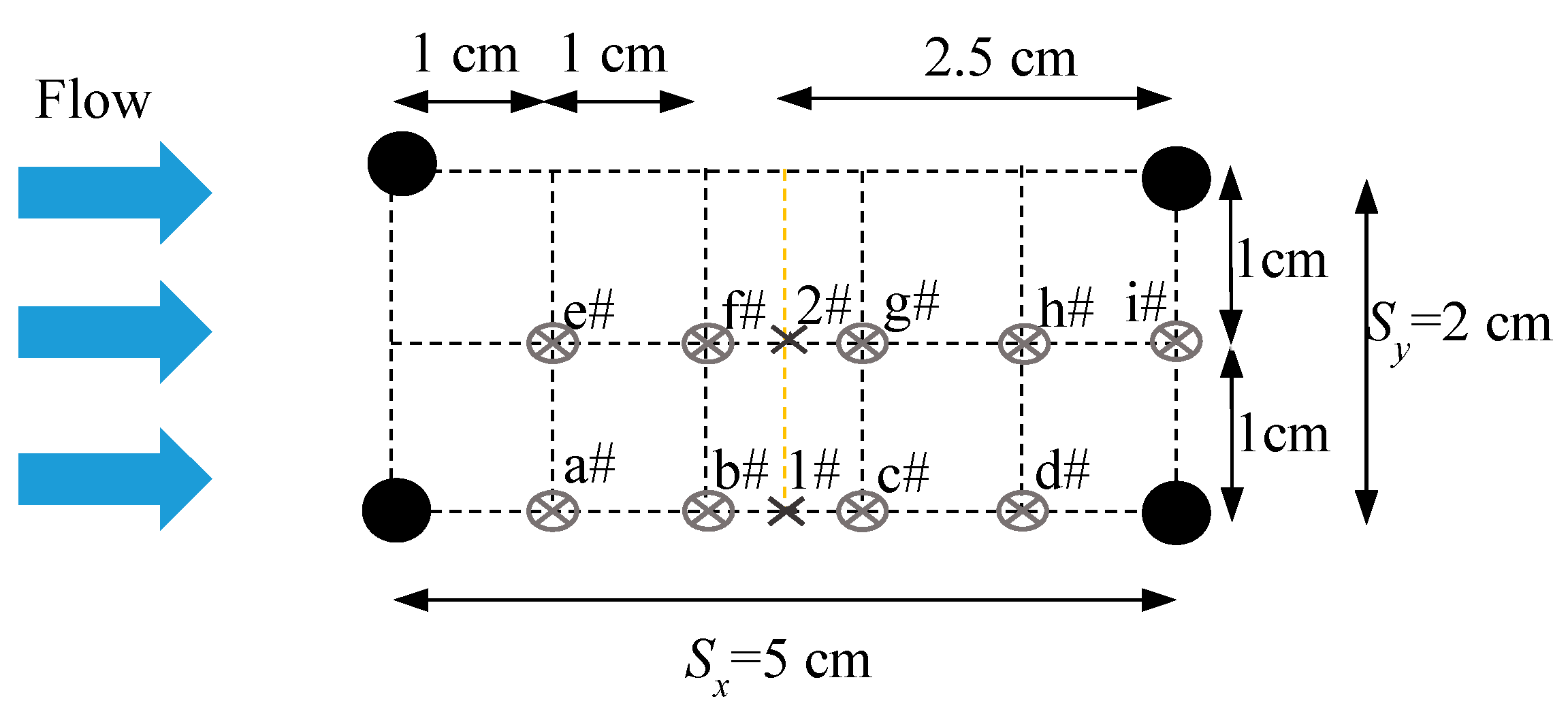
| Case | λ | Sx (cm) | Sy (cm) | H (cm) | Sub | Q (L/s) | Um (cm/s) |
|---|---|---|---|---|---|---|---|
| I | 0 | 0 | 0 | 18 | — | 32.44 | 30.04 |
| II | 0.0056 | 40 | 16 | 18 | 3 | 32.34 | 29.94 |
| III | 0.045 | 10 | 8 | 18 | 3 | 32.43 | 30.03 |
| IV | 0.09 | 5 | 8 | 18 | 3 | 32.35 | 29.95 |
| V | 0.36 | 5 | 2 | 18 | 3 | 32.4 | 30 |
| VI | 1.44 | 2.5 | 1 | 18 | 3 | 32.48 | 30.07 |
| Case I | Case II | Case III | Case IV | Case V | Case VI | |
|---|---|---|---|---|---|---|
| 0 < z< 10 mm | 2.99 | 3.462 | 2.407 | 2.03 | −0.068 | — |
| 55 ≤ z ≤ 65 mm | 1.126 | 1.38 | 2.025 | 3.077 | 4.978 | 19.764 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Yan, J.; Yuan, S.; Liu, J.; Zheng, J. Effects of Submerged Vegetation Density on Turbulent Flow Characteristics in an Open Channel. Water 2019, 11, 2154. https://doi.org/10.3390/w11102154
Zhao H, Yan J, Yuan S, Liu J, Zheng J. Effects of Submerged Vegetation Density on Turbulent Flow Characteristics in an Open Channel. Water. 2019; 11(10):2154. https://doi.org/10.3390/w11102154
Chicago/Turabian StyleZhao, Hanqing, Jing Yan, Saiyu Yuan, Jiefu Liu, and Jinyu Zheng. 2019. "Effects of Submerged Vegetation Density on Turbulent Flow Characteristics in an Open Channel" Water 11, no. 10: 2154. https://doi.org/10.3390/w11102154
APA StyleZhao, H., Yan, J., Yuan, S., Liu, J., & Zheng, J. (2019). Effects of Submerged Vegetation Density on Turbulent Flow Characteristics in an Open Channel. Water, 11(10), 2154. https://doi.org/10.3390/w11102154






