Rainfall Thresholds for Prediction of Landslides in Idukki, India: An Empirical Approach
Abstract
1. Introduction
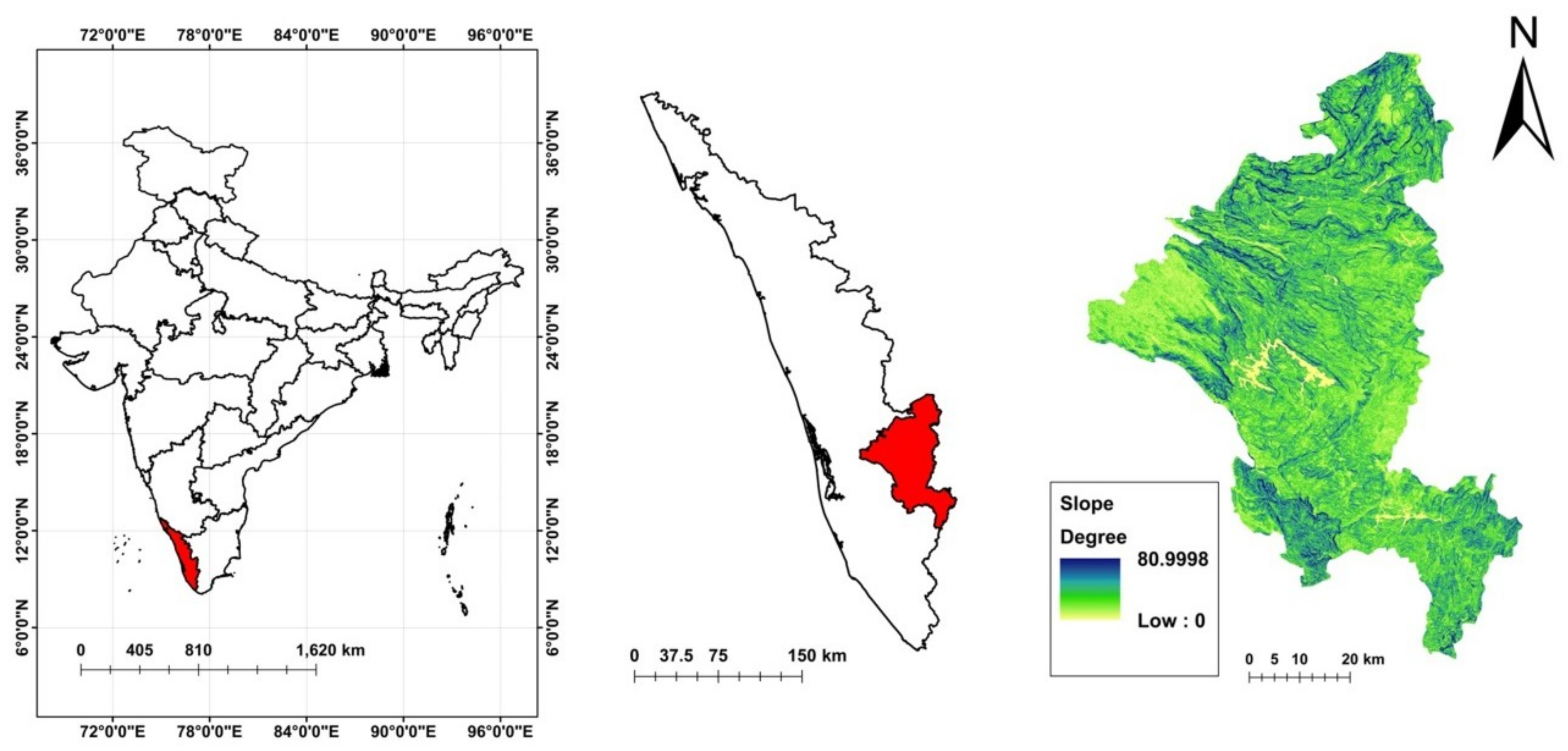
2. Study Area
2.1. Triggering Factors
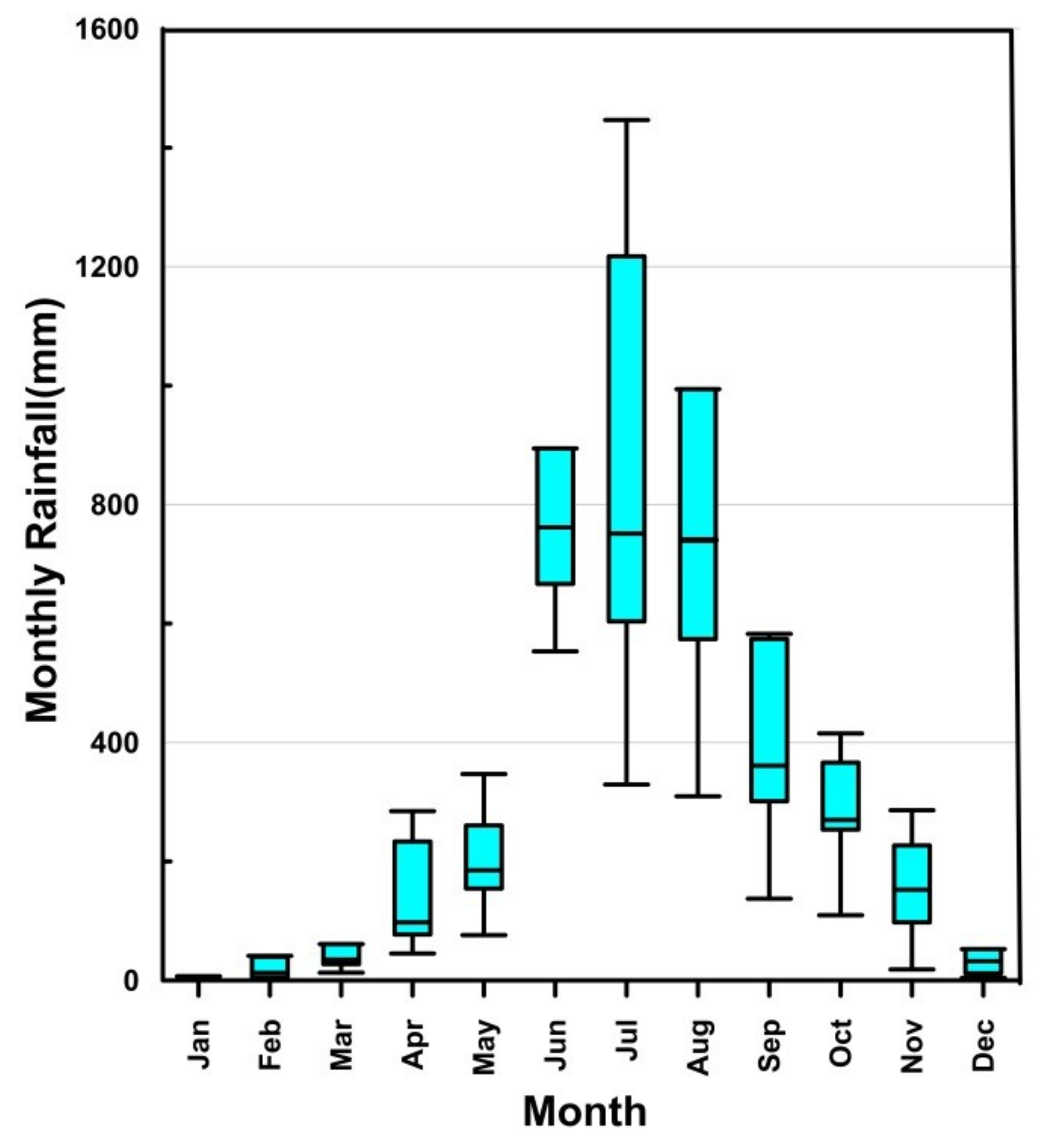
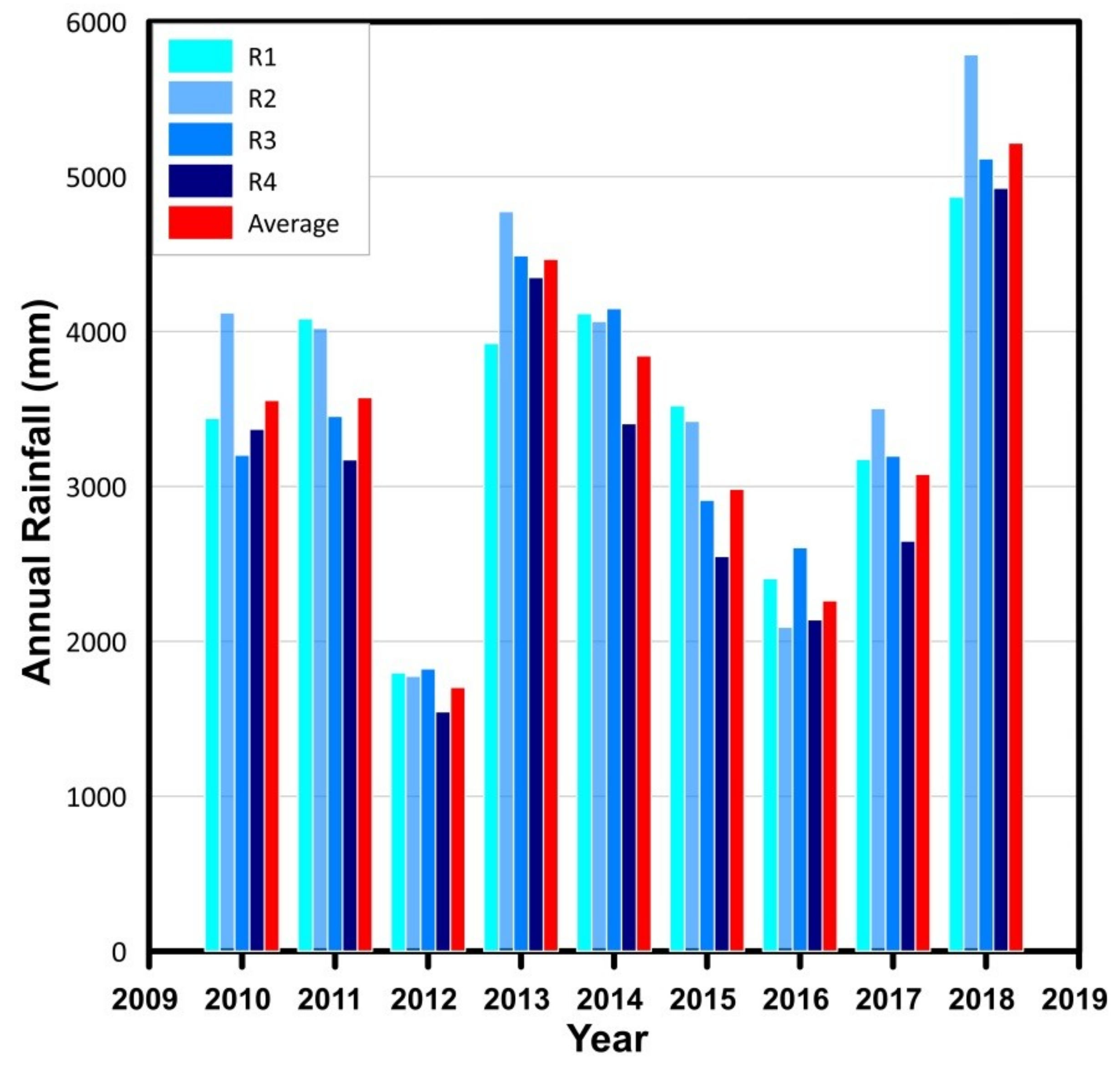
2.2. Database for Analysis
3. Analysis of Thresholds
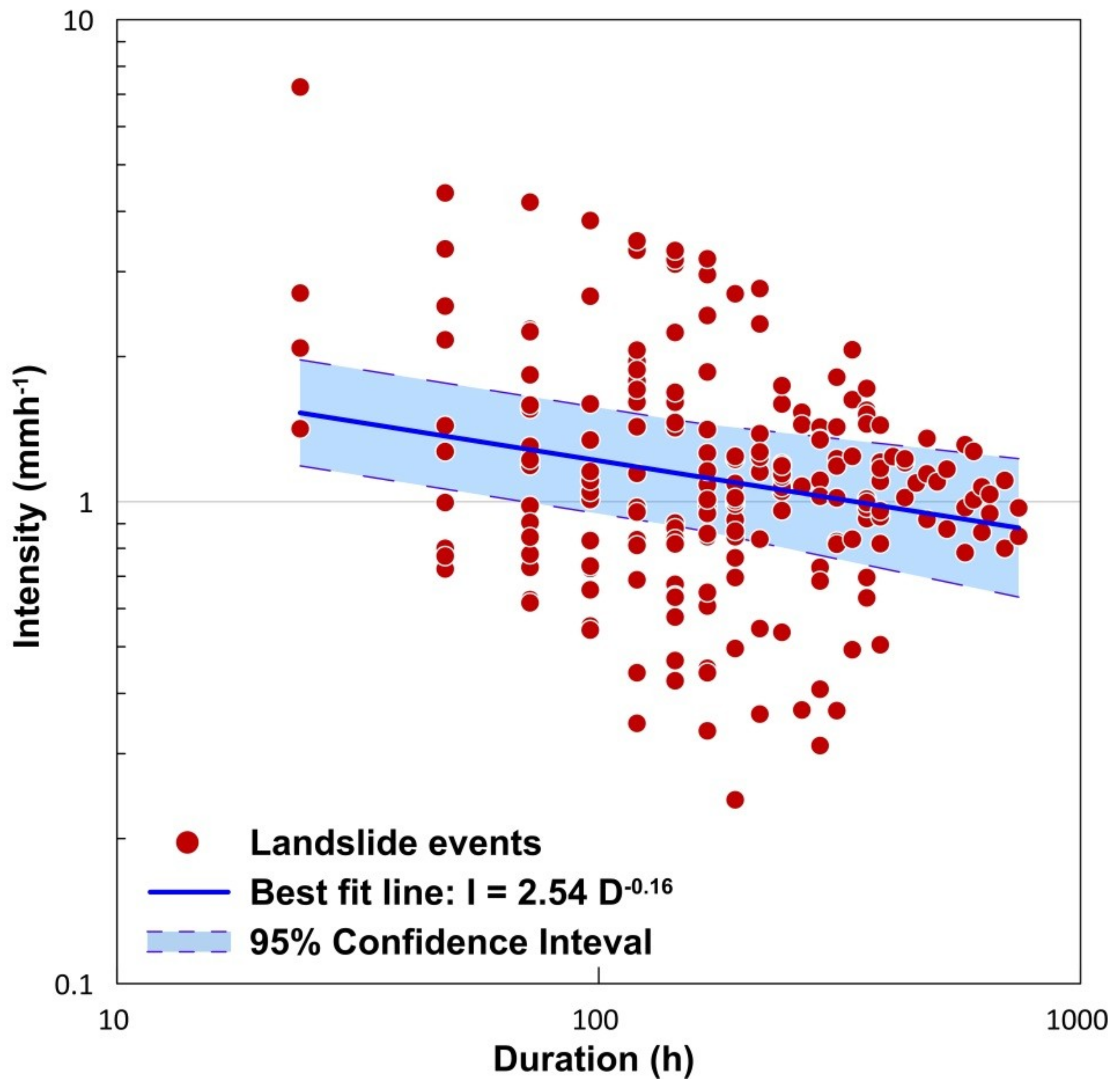
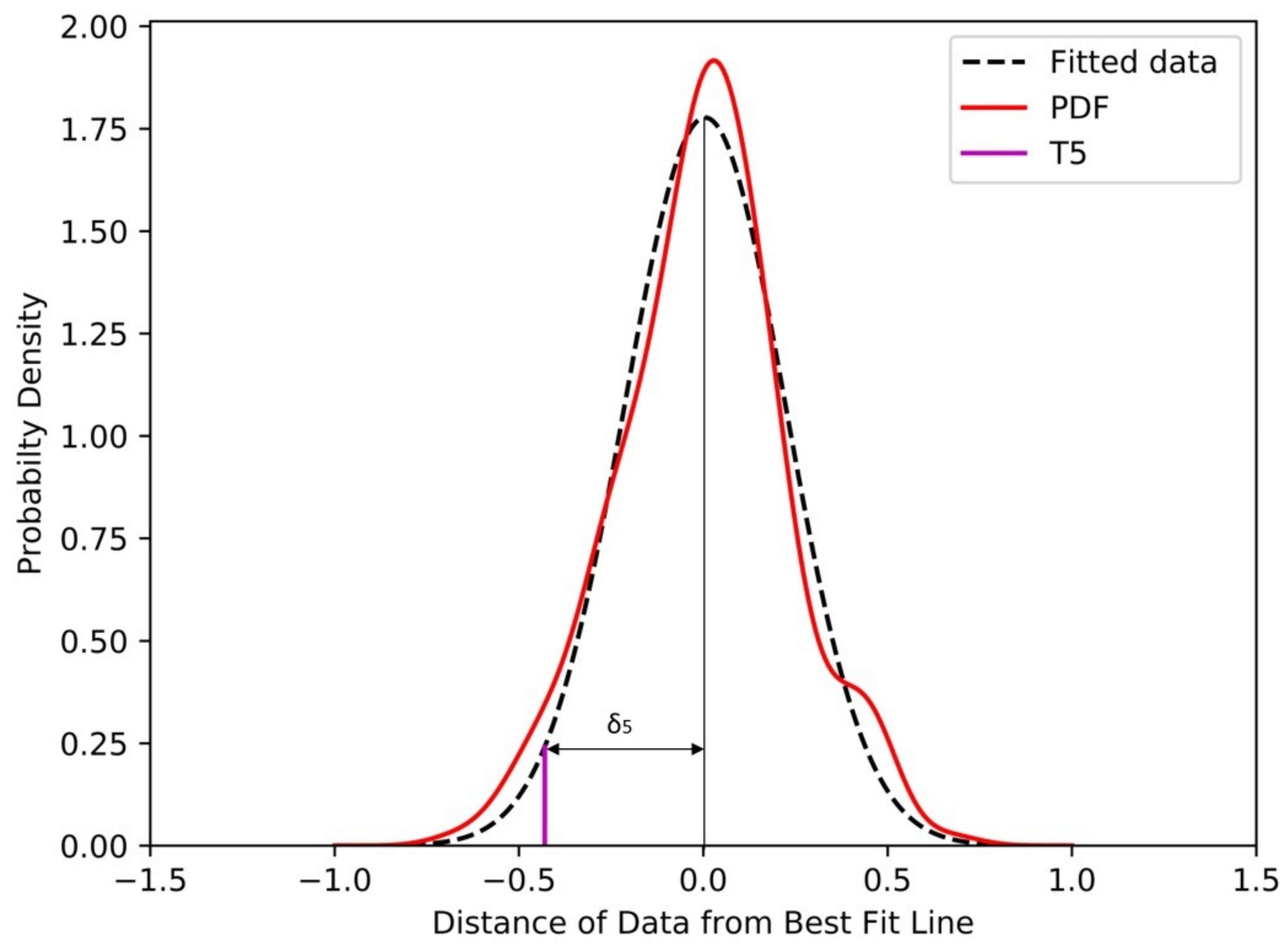
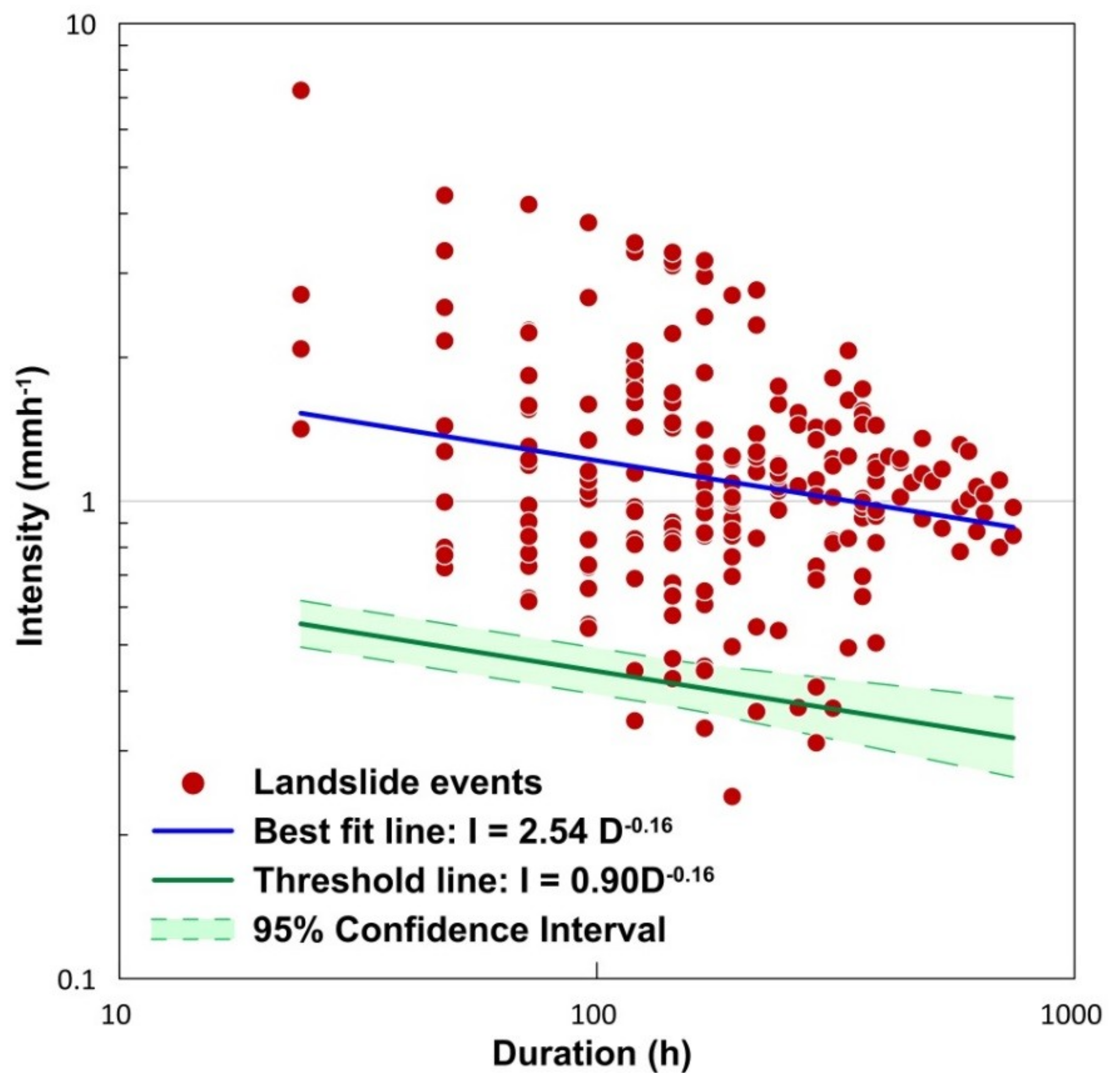
3.1. Intensity-Duration Thresholds
- I is Intensity of rainfall in mmh−1,
- D is Duration of rainfall event in hours,
- and α and β are empirical parameters,
- which is in the form of a straight line y = mx + c.
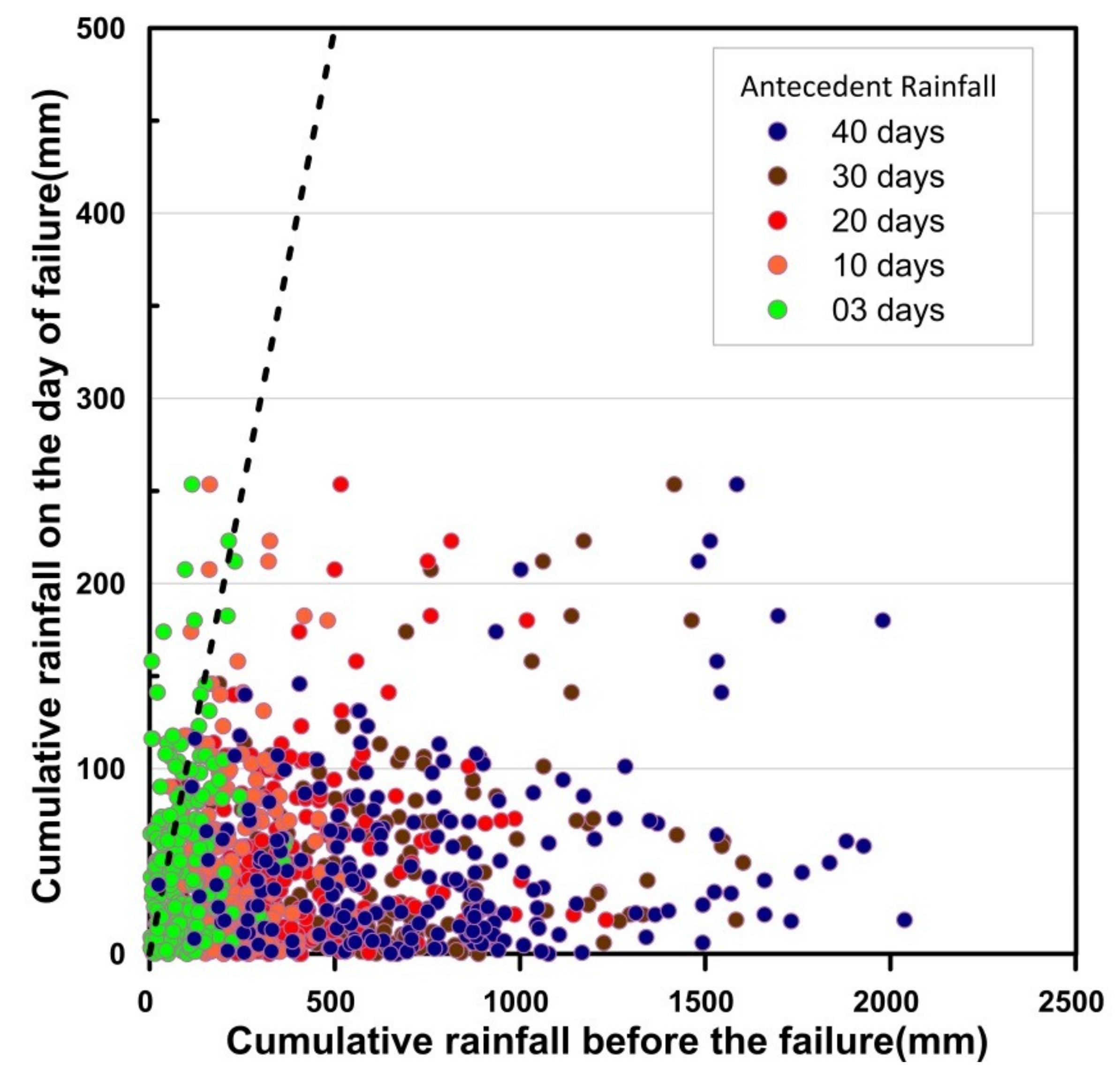
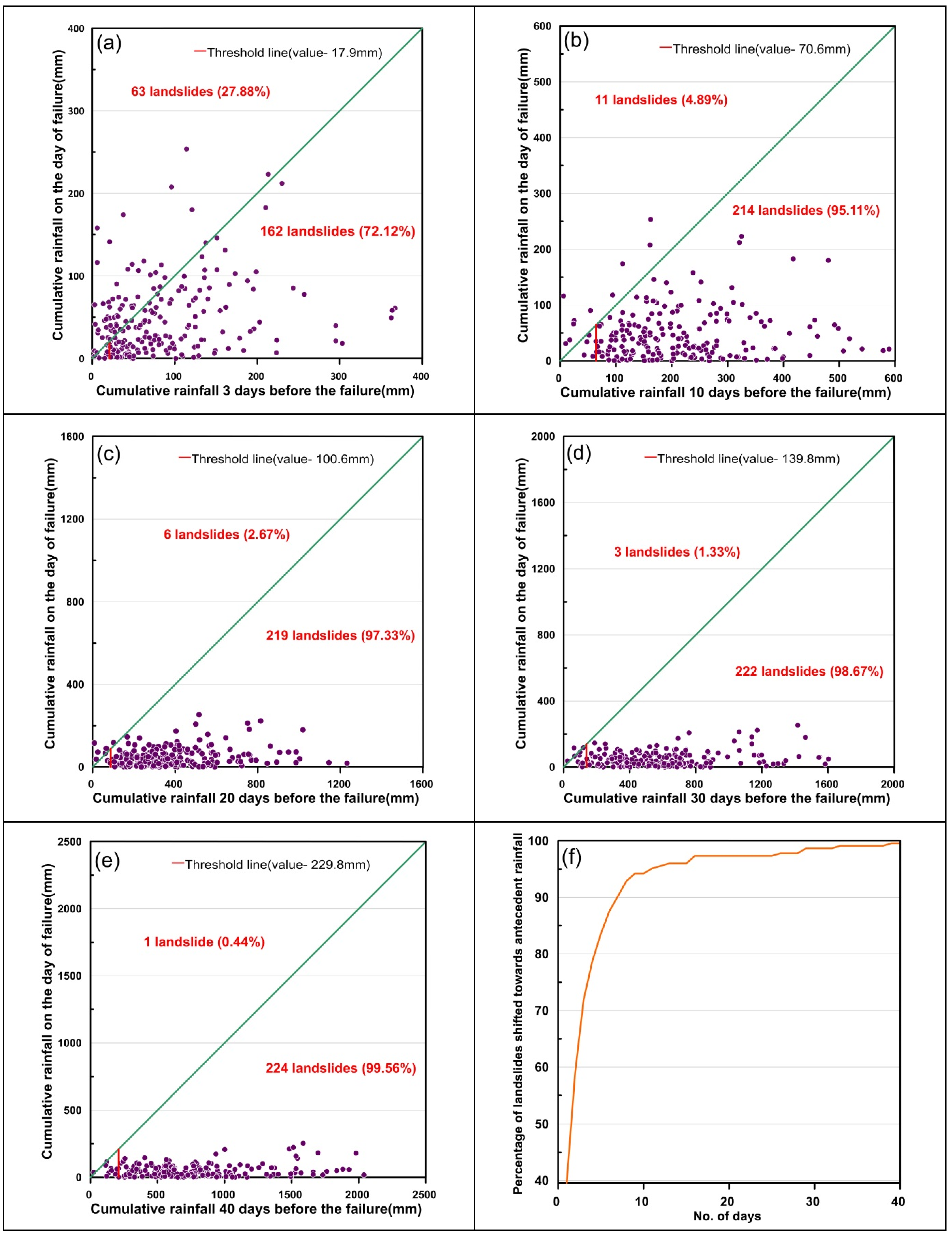
3.2. Thresholds Based on Antecedent Rainfall
4. Discussions
5. Conclusions
- For short duration rainfall events (24 hours), a continuous rainfall intensity of 0.54 mmh−1 can trigger landslides. For the maximum observed duration of 31 days, a rainfall intensity as less as 0.3 mmh−1 can also trigger landslides. The values of thresholds are too low for a regional scale threshold, and the reason can be the biasness of occurrence of landslides to the antecedent rainfall conditions, other than the immediate preceding event.
- From the analysis of antecedent rainfall conditions, it can be stated that for the Idukki district, an antecedent rainfall of 70.6 mm over a period of 10 days and 229.8 mm over a period of 40 days can trigger a landslide event. Around 99.56% of the events are biased towards the antecedent rainfall conditions when duration of 40 days is considered.
- It is evident from the results that the occurrence of landslide events are more influenced by antecedent rainfall conditions rather than the amount of rainfall on the day of occurrence.
- It is expected that this first attempt will encourage more research for the study area, which is profoundly suffering from the increased number of landslide events in the recent hazards and this will become the first step towards establishing a regional scale warning system for the Idukki district.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kerala Post Disaster Needs Assessment Floods and Landslides—August 2018; Government of Kerala: Thiruvananthapuram, India, 2018; pp. 1–440.
- Kanungo, D.P.; Sharma, S. Rainfall thresholds for prediction of shallow landslides around Chamoli-Joshimath region, Garhwal Himalayas, India. Landslides 2014, 11, 629–638. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, D.N. Estimation of rainfall thresholds for landslide occurrences in Kalimpong, India. Innov. Infrastruct. Solut. 2018, 3, 24. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, N. Rainfall Thresholds for the prediction of Landslides using Empirical Methods in Kalimpong, Darjeeling, India. In Proceedings of the JTC1 Workshop on Advances in Landslide Understanding, Barcelona, Spain, 24–26 May 2017. [Google Scholar]
- Dikshit, A.; Satyam, N. Probabilistic rainfall thresholds in Chibo, India: Estimation and validation using monitoring system. J. Mt. Sci. 2019, 16, 870–883. [Google Scholar] [CrossRef]
- Dikshit, A.; Sarkar, R.; Satyam, N. Probabilistic approach toward Darjeeling Himalayas landslides—A case study. Cogent Eng. 2018, 5, 1–11. [Google Scholar] [CrossRef]
- Soja, R.; Starkel, L. Extreme rainfalls in Eastern Himalaya and southern slope of Meghalaya Plateau and their geomorphologic impacts. Geomorphology 2007, 84, 170–180. [Google Scholar] [CrossRef]
- Prokop, P.; Walanus, A. Impact of the Darjeeling–Bhutan Himalayan front on rainfall hazard pattern. Nat. Hazards 2017, 89, 387–404. [Google Scholar] [CrossRef]
- Kuriakose, S.L. Effect of Vegetation on Debris Flow Initiation: Conceptualisation and Parametrisation of a Dynamic Model for Debris Flow Initiation in Tikovil River Basin, Kerala, India, using PC Raster; International Institute of Geo-Information Science and Earth Observation and Indian Institute of Remote Sensing: Enschede, The Netherlands; Uttarakhand, India, 2006. [Google Scholar]
- Kuriakose, S.L.; Luna, B.Q.; Portugues, S.B.; Van Westen, C.J. Modelling the runout of a debris flow of the Western Ghats, Kerala, India. Assembly 2009, 11, 4276. [Google Scholar]
- Martelloni, G.; Segoni, S.; Fanti, R.; Catani, F. Rainfall thresholds for the forecasting of landslide occurrence at regional scale. Landslides 2012, 9, 485–495. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Innes, J.L. Debris flows. Prog. Phys. Geogr. 1983, 7, 469–501. [Google Scholar] [CrossRef]
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Geogr. Ann. Ser. Phys. Geogr. 1980, 62, 23–27. [Google Scholar]
- Crosta, G. Regionalization of rainfall thresholds: An aid to landslide hazard evaluation. Environ. Geol. 1998, 35, 131–145. [Google Scholar] [CrossRef]
- Bonnard, C.; Noverraz, F. Influence of climate change on large landslides: Assessment of long term movements and trends. In Proceedings of the International Conference on Landslides Causes Impact and Countermeasures, Davos, Switzerland, 17–21 June 2001; pp. 121–138. [Google Scholar]
- Sajeev, R.; Praveen, K.R. Landslide Susceptibility Mapping on Macroscale along the Major Road Corridors in Idukki District, Kerala; Geological Survey of India: Thiruvananthapuram, India, 2014. [Google Scholar]
- Idukki District Webpage. Available online: https://idukki.nic.in/ (accessed on 23 August 2019).
- Kuriakose, S.L. Physically-Based Dynamic Modelling of the Effect of Land Use Changes on Shallow Landslide Initiation in the Western Ghats of Kerala, India. Ph.D. Thesis, University of Utrecht, Enschede, The Netherlands, 2010. [Google Scholar]
- Sreekumar, S. Techniques for slope stability analysis: Site specific studies from Idukki district, Kerala. J. Geol. Soc. India 2009, 73, 813–820. [Google Scholar] [CrossRef]
- Sulal, N.L.; Archana, K.G. Note On Post Disaster Studies For Landslides Occurred in June 2018 At Idukki District, Kerala; Geological Survey of India: Thiruvananthapuram, India, 2019.
- Sajeev, R.; Sajinkumar, K.S. Detailed Site Specific Landslide Study at Govt. College, Munnar, Idukki District, Kerala; Geological Survey of India: Thiruvananthapuram, India, 2013.
- Deepthy, R.; Balakrishnan, S. Climatic control on clay mineral formation: Evidence from weathering profiles developed. J. Earth Syst. Sci. 2005, 114, 545–556. [Google Scholar] [CrossRef]
- Kuriakose, S.L.; Sankar, G.; Muraleedharan, C. History of landslide susceptibility and a chorology of landslide-prone areas in the Western Ghats of Kerala, India. Environ. Geol. 2009, 57, 1553–1568. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, D.N.; Towhata, I. Early warning system using tilt sensors in Chibo, Kalimpong, Darjeeling Himalayas, India. Nat. Hazards 2018, 94, 727–741. [Google Scholar] [CrossRef]
- Jaiswal, P.; van Westen, C.J. Estimating temporal probability for landslide initiation along transportation routes based on rainfall thresholds. Geomorphology 2009, 112, 96–105. [Google Scholar] [CrossRef]
- Muraleedharan, M.P. Landslides in Kerala—A Drenched State Phenomena in Regolith; Center for Earth Sciences: Thiruvananthapuram, India, 1995. [Google Scholar]
- Jha, C.S.; Dutt, C.B.S.; Bawa, K.S. Deforestation and land use changes in Western Ghats, India. Curr. Sci. 2000, 79, 231–238. [Google Scholar]
- Muraleedharan, C.; Sajinkumar, K.S. Landslide Inventory of Kerala; Geological Survey of India: Thiruvananthapuram, India, 2010.
- Muraleedharan, C.; Praveen, M.N. Detailed Site Specific Study Of Landslide Initiation At Kuttikanam, Peermade Taluk, Idukki District, Kerala; Geological Survey of India: Thiruvananthapuram, India, 2011.
- Muraleedharan, C. Landslide Hazard Zonation on Meso-Scale for Munnar, Devikulam Taluk, Idukki District, Kerala; Geological Survey of India: Thiruvananthapuram, India, 2010.
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Ardizzone, F.; Galli, M. The impact of landslides in the Umbria region, central Italy. Nat. Hazards Earth Syst. Sci. 2003, 3, 469–486. [Google Scholar] [CrossRef]
- Details of Landslip Damages in Agricultural Lands of Different Panchayats of Idukki District during the Monsoon 2018; District Soil Conservation Office: Idukki, India, 2018.
- CartoDEM. Available online: https://bhuvan-app3.nrsc.gov.in/data/download/index.php (accessed on 20 August 2019).
- India Meteorological Department (IMD). Available online: http://dsp.imdpune.gov.in/ (accessed on 23 July 2019).
- Berti, M.; Martina, M.L.V.; Franceschini, S.; Pignone, S.; Simoni, A.; Pizziolo, M. Probabilistic rainfall thresholds for landslide occurrence using a Bayesian approach. J. Geophys. Res. Earth Surf. 2012, 117, 1–20. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Nasrollahi, N.; Li, J.; Imam, B.; Sorooshian, S. Geometrical characterization of precipitation patterns. J. Hydrometeorol. 2011, 12, 274–285. [Google Scholar] [CrossRef]
- Segoni, S.; Rossi, G.; Rosi, A.; Catani, F. Landslides triggered by rainfall: A semi-automated procedure to define consistent intensity-duration thresholds. Comput. Geosci. 2014, 63, 123–131. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Luciani, S.; Valigi, D.; Guzzetti, F. Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 447–458. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; School of Mathematics University of Bath: Bath, UK, 1986. [Google Scholar]
- Pasuto, A.; Silvano, S. Rainfall as a trigger of shallow mass movements. A case study in the Dolomites, Italy. Environ. Geol. 1998, 35, 184–189. [Google Scholar] [CrossRef]
- Rosi, A.; Lagomarsino, D.; Rossi, G.; Segoni, S.; Battistini, A.; Casagli, N. Updating ews rainfall thresholds for the triggering of landslides. Nat. Hazards 2015, 78, 297–308. [Google Scholar] [CrossRef]
- Lagomarsino, D.; Segoni, S.; Rosi, A.; Rossi, G.; Battistini, A.; Catani, F.; Casagli, N. Quantitative comparison between two different methodologies to define rainfall thresholds for landslide forecasting. Nat. Hazards Earth Syst. Sci. 2015, 15, 2413–2423. [Google Scholar] [CrossRef]
- Segoni, S.; Rosi, A.; Lagomarsino, D.; Fanti, R.; Casagli, N. Brief communication: Using averaged soil moisture estimates to improve the performances of a regional-scale landslide early warning system. Nat. Hazards Earth Syst. Sci. 2018, 18, 807–812. [Google Scholar] [CrossRef]
- Segoni, S.; Rosi, A.; Fanti, R.; Gallucci, A.; Monni, A.; Casagli, N. A regional-scale landslide warning system based on 20 years of operational experience. Water 2018, 10, 1297. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. An Algorithm for the objective reconstruction of rainfall events responsible for landslides. Landslide 2015, 12, 311–320. [Google Scholar] [CrossRef]
- Capparelli, G.; Tiranti, D. Application of the MoniFLaIR early warning system for rainfall-induced landslides in Piedmont region (Italy). Landslides 2010, 7, 401–410. [Google Scholar] [CrossRef]
- Lagomarsino, D.; Segoni, S.; Fanti, R.; Catani, F. Updating and tuning a regional-scale landslide early warning system. Landslides 2013, 10, 91–97. [Google Scholar] [CrossRef]

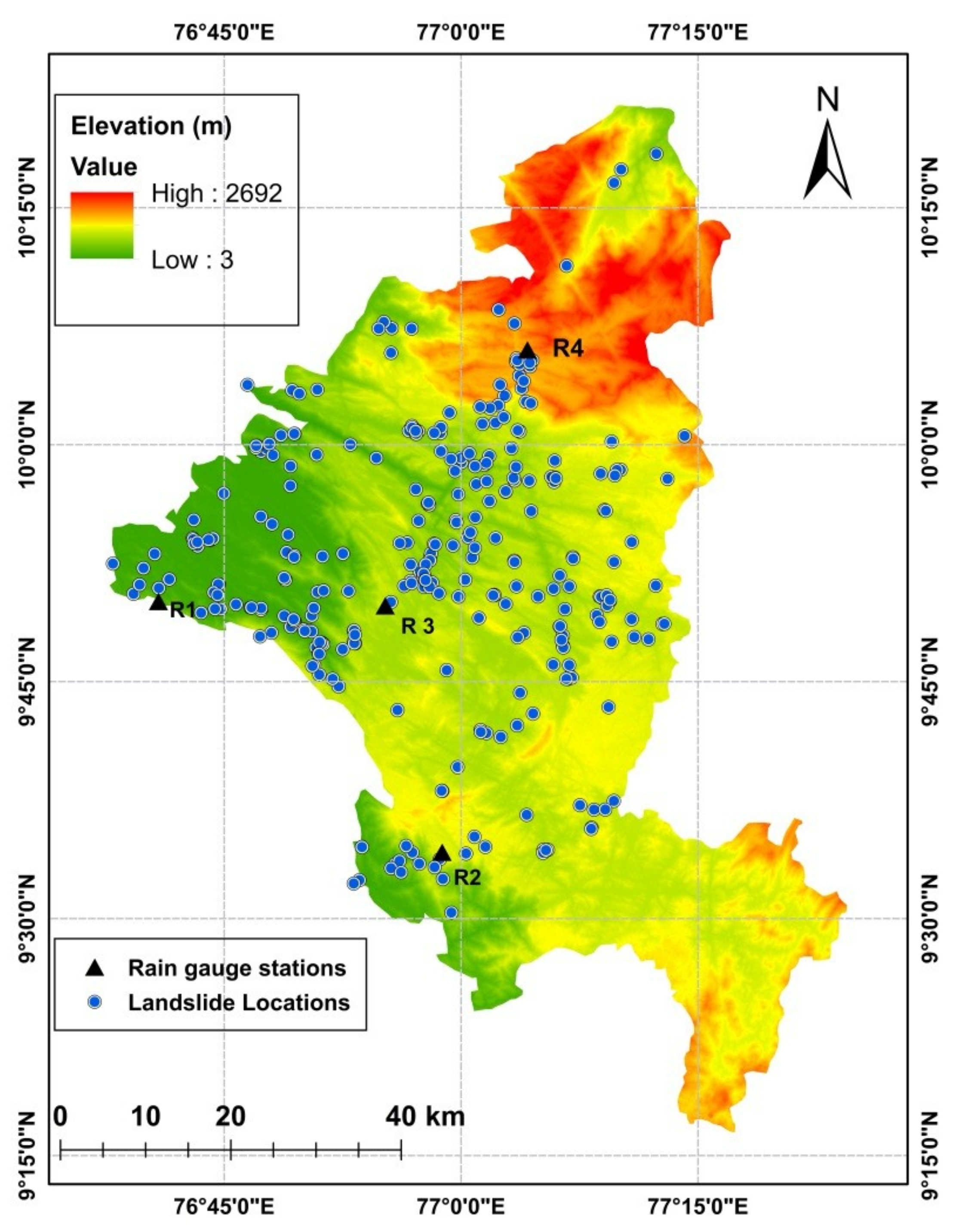
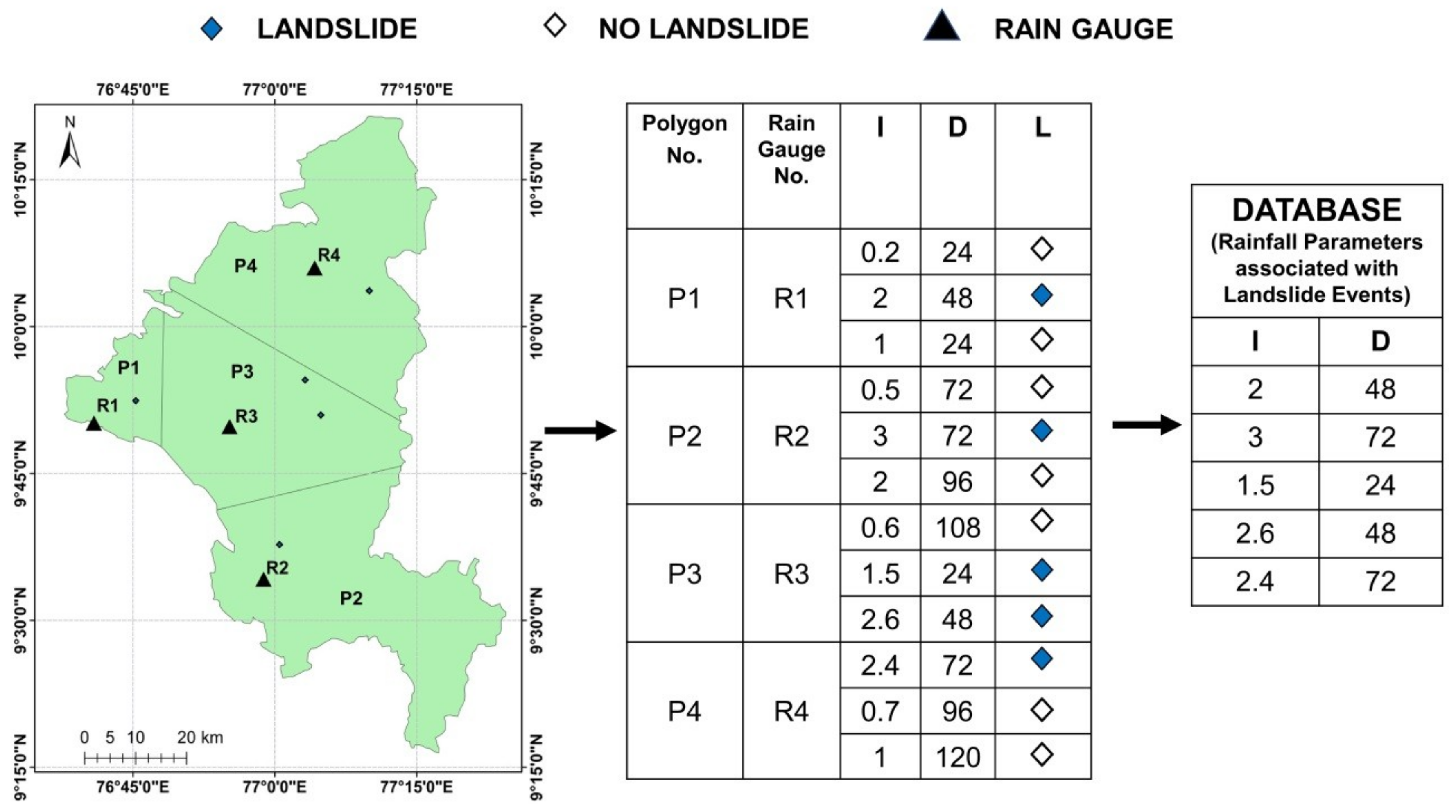
| Rain Gauge Number | Place | Location |
|---|---|---|
| R1 | Thodupuzha | 9.83° N, 76.67° E |
| R2 | Peermedu | 9.57° N, 76.98° E |
| R3 | Idukki | 9.83° N, 76.92° E |
| R4 | Munnar | 10.10° N, 77.07° E |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abraham, M.T.; Pothuraju, D.; Satyam, N. Rainfall Thresholds for Prediction of Landslides in Idukki, India: An Empirical Approach. Water 2019, 11, 2113. https://doi.org/10.3390/w11102113
Abraham MT, Pothuraju D, Satyam N. Rainfall Thresholds for Prediction of Landslides in Idukki, India: An Empirical Approach. Water. 2019; 11(10):2113. https://doi.org/10.3390/w11102113
Chicago/Turabian StyleAbraham, Minu Treesa, Deekshith Pothuraju, and Neelima Satyam. 2019. "Rainfall Thresholds for Prediction of Landslides in Idukki, India: An Empirical Approach" Water 11, no. 10: 2113. https://doi.org/10.3390/w11102113
APA StyleAbraham, M. T., Pothuraju, D., & Satyam, N. (2019). Rainfall Thresholds for Prediction of Landslides in Idukki, India: An Empirical Approach. Water, 11(10), 2113. https://doi.org/10.3390/w11102113





