Design Equation for Stirring Fluid by a Stream Pump in a Circulating Tank
Abstract
1. Introduction
2. Theoretical Considerations
2.1. General Concept of the Proposed Mathematical Model
2.2. Assumptions and Simplifications
2.3. Determination of the Induced Power
2.4. Determination of the Dissipation Power
2.5. Proposed Design Equation
3. Experimental Verification
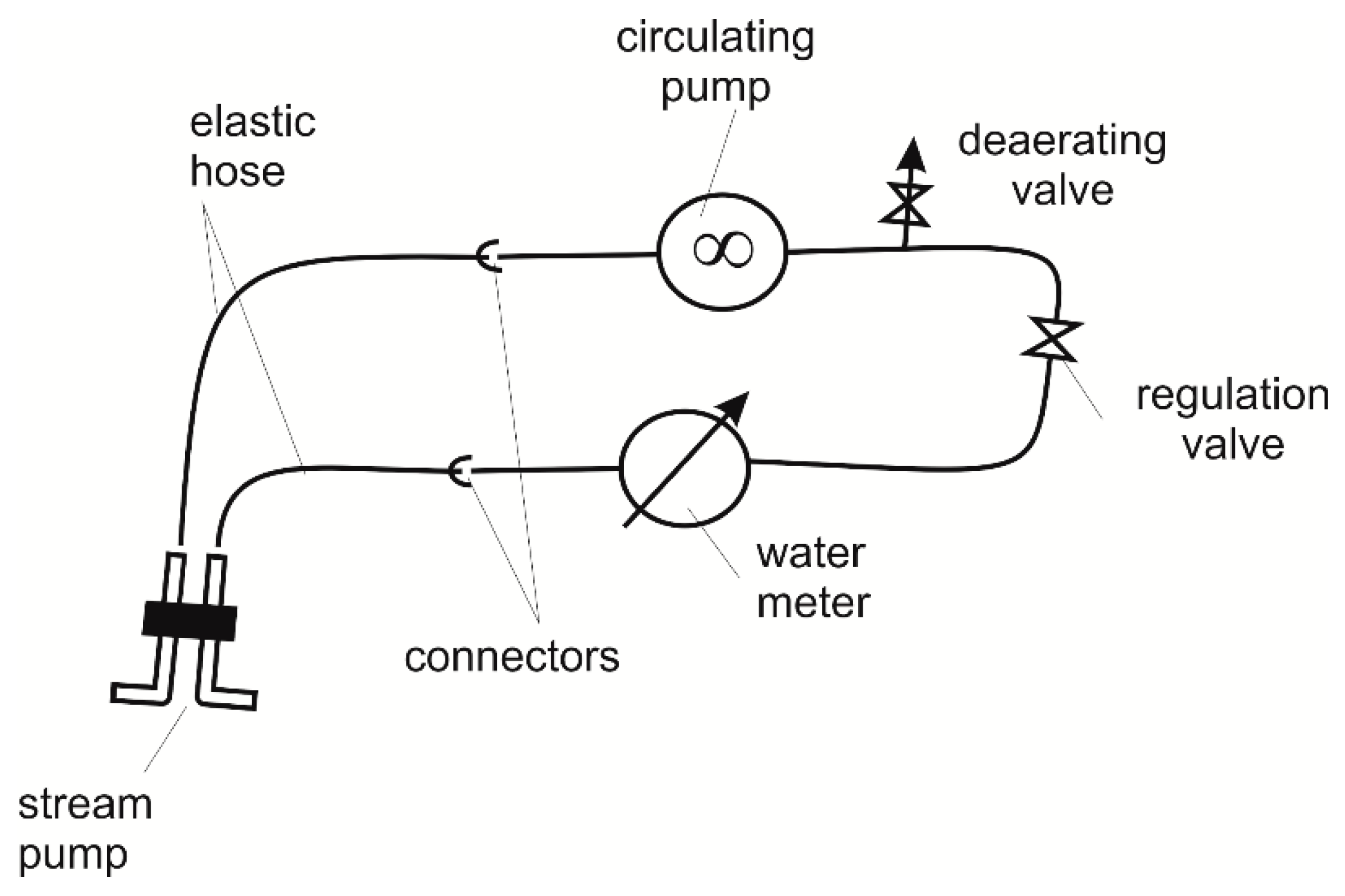
3.1. Laboratory Stand
3.2. Measurement Results
QS = 1.05 × 10−4 m3/s — QR = 2.58 × 10−3 m3/s;
QS = 1.17 × 10−4 m3/s — QR = 2.91 × 10−3 m3/s;
dSB = 0.012m: QS = 6.4 × 10−5 m3/s — QR = 1.64 × 10−3 m3/s;
QS = 8.6 × 10−5 m3/s — QR = 2.30 × 10−3 m3/s;
QS = 9.6 × 10−5 m3/s — QR = 2.68 × 10−3 m3/s,
3.3. Verification of the Proposed Equation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shah, M. Course Material Process Engineering: Agitation Mixing. Available online: http://www.dduanchor.org/site/wp-content/uploads/2014/11/Process-Engineering-Agitation-Mixing.pdf (accessed on 13 August 2019).
- Demirel, E.; Aral, M.M. Unified Analysis of Multi-Chamber Contact Tanks and Mixing Efficiency Based on Vorticity Field. Part I: Hydrodynamic Analysis. Water 2016, 8, 495. [Google Scholar] [CrossRef]
- Maruyama, T.; Ban, Y.; Mizushina, T. Jet mixing of fluids in tanks. J. Chem. Eng. Jpn. 1982, 15, 342–348. [Google Scholar] [CrossRef]
- Matej, K.; Pawliczka, I.; Sawicki, J.M.; Wielgat, P.; Zima, P. Whirling System of Water Exchange in Breeding Pools. Arch. Hydro-Eng. Environ. Mech. 2016, 63, 253–263. [Google Scholar] [CrossRef]
- Higgins, H.W. Water Jet Air Pump Theory and Performance; Pennsylvania State University: State College, PA, USA, 1964. [Google Scholar]
- Wilman, J.T. Jet Pumps; European Atomic Energy Community—EURATOM Reactor Centrum Nederland—RCN: Brussels, Belgium, 1966. [Google Scholar]
- Zima, P.; Makinia, J.; Swinarski, M.; Czerwionka, K. Effects of different hydraulic models on predicting longitudinal profiles of reactive pollutants in activated sludge reactors. Water Sci. Technol. J. Int. Assoc. Water Pollut. Res. 2008, 58, 555–561. [Google Scholar] [CrossRef] [PubMed]
- Zima, P.; Makinia, J.; Swinarski, M.; Czerwionka, K. Combining computational fluid dynamics with a biokinetic model for predicting ammonia and phosphate behavior in aeration tanks. Water Environ. Res. Res. Publ. Water Environ. Fed. 2009, 81, 2353–2362. [Google Scholar] [CrossRef] [PubMed]
- Sawicki, J.M. Aerated Grit Chambers Hydraulic Design Equation. J. Environ. Eng. 2004, 130, 1050–1058. [Google Scholar] [CrossRef][Green Version]
- Sawicki, J.M.; Pawłowska, A. Energy balance for air lift pumps. Arch. Hydro-Eng. Environ. Mech. 1999, 46, 63–72. [Google Scholar]
- Gronowska-Szneler, M.A.; Sawicki, J.M. Simple design criteria and efficiency of hydrodynamic vortex separators. Water Sci. Technol. J. Int. Assoc. Water Pollut. Res. 2014, 70, 457–463. [Google Scholar] [CrossRef] [PubMed]
- Mielczarek, S.; Sawicki, J.M. Dimensioning of vortex storm overflows. Water Sci. Technol. J. Int. Assoc. Water Pollut. Res. 2018, 78, 259–265. [Google Scholar] [CrossRef] [PubMed]
- Artichowicz, W.; Sawicki, J.M. Determination of Mechanical Energy Loss in Steady Flow by Means of Dissipation Power. Arch. Hydro-Eng. Environ. Mech. 2017, 64, 73–85. [Google Scholar] [CrossRef]
- Slattery, J.C. Advanced Transport Phenomena; Cambridge University Press: Cambridge, UK, 1999; ISBN 978-1-316-58390-6. [Google Scholar]
- Luo, C. Distribution of Velocities and Velocity Gradients in Mixing and Flocculation Vessels: Comparison between LDV Data and CFD Predictions. Ph. D. Thesis, New Jersey Institute of Technology, Newark, NJ, USA, 1997. [Google Scholar]
- Kasat, G.R.; Pandit, A.B. Mixing Time Studies in Multiple Impeller Agitated Reactors. Can. J. Chem. Eng. 2004, 82, 892–903. [Google Scholar] [CrossRef]
- Dickley, S.D. Minimize Blending Time. Available online: https://www.chemicalprocessing.com/articles/2009/120/ (accessed on 12 August 2019).
- Abramovich, G.N.; Schindel, L. The Theory of Turbulent Jets; MIT-Press: Cambridge, UK, 2003; ISBN 978-0-262-01008-5. [Google Scholar]
- Qiao, Q.S.; Choi, K.W.; Chan, S.N.; Lee Joseph, H.W. Internal Hydraulics of a Chlorine Jet Diffuser. J. Hydraul. Eng. 2017, 143, 06017022. [Google Scholar] [CrossRef]
- Das, B.S.; Khatua, K.K. Flow Resistance in a Compound Channel with Diverging and Converging Floodplains. J. Hydraul. Eng. 2018, 144, 04018051. [Google Scholar] [CrossRef]
- Idelchik, I.E.; Ginevskiĭ, A.S. Handbook of Hydraulic Resistance, 4th ed.; rev. and augmented.; Begell House: Redding, CT, USA, 2007; ISBN 978-1-56700-251-5. [Google Scholar]
- SonTek/YSI, Inc. ADVField/Hydra Acoustic Doppler Velocimeter (Field) Technical Documentation; SonTec: San Diego, CA, USA, 2001. [Google Scholar]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sawicki, J.; Wielgat, P.; Zima, P. Design Equation for Stirring Fluid by a Stream Pump in a Circulating Tank. Water 2019, 11, 2114. https://doi.org/10.3390/w11102114
Sawicki J, Wielgat P, Zima P. Design Equation for Stirring Fluid by a Stream Pump in a Circulating Tank. Water. 2019; 11(10):2114. https://doi.org/10.3390/w11102114
Chicago/Turabian StyleSawicki, Jerzy, Paweł Wielgat, and Piotr Zima. 2019. "Design Equation for Stirring Fluid by a Stream Pump in a Circulating Tank" Water 11, no. 10: 2114. https://doi.org/10.3390/w11102114
APA StyleSawicki, J., Wielgat, P., & Zima, P. (2019). Design Equation for Stirring Fluid by a Stream Pump in a Circulating Tank. Water, 11(10), 2114. https://doi.org/10.3390/w11102114





