Non-Intrusive Underwater Measurement of Local Scour Around a Bridge Pier
Abstract
1. Introduction
2. Experimental Set-Up and Procedure
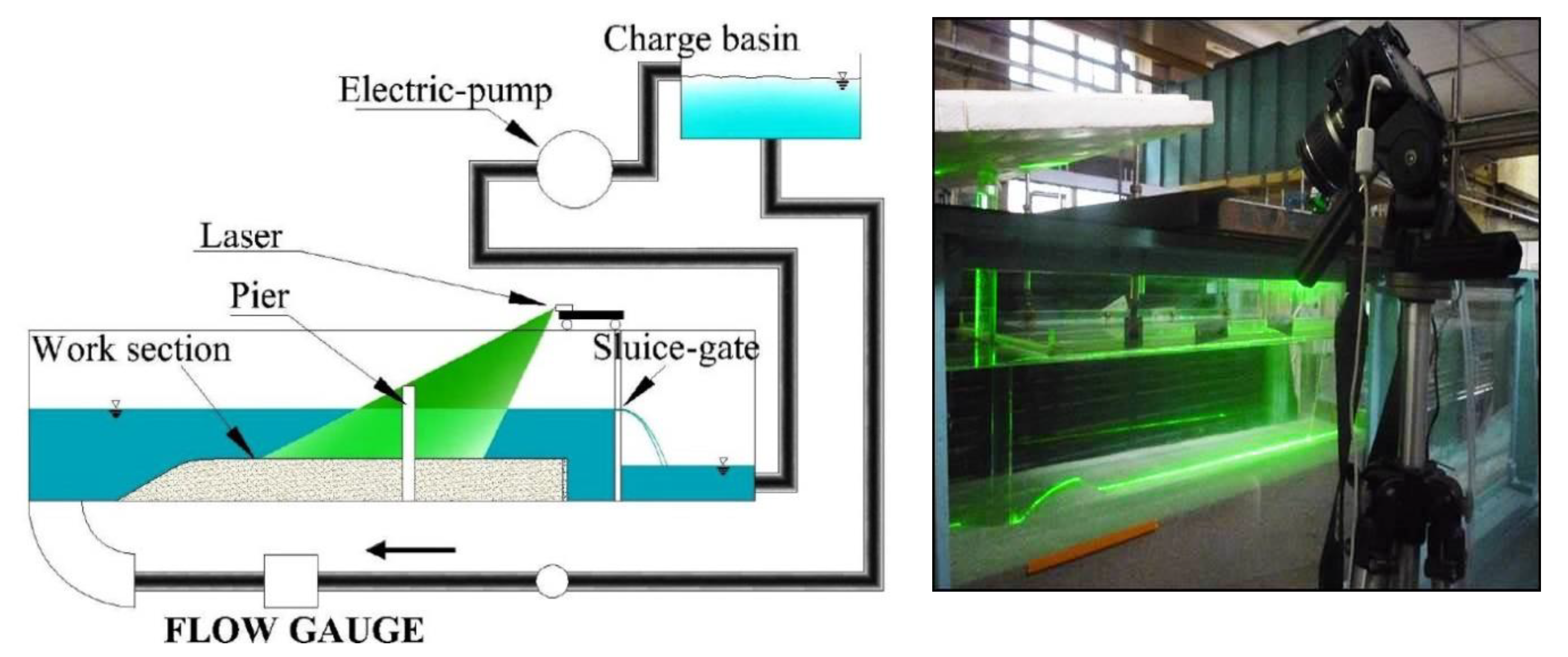
2.1. Experimental Design and Flume
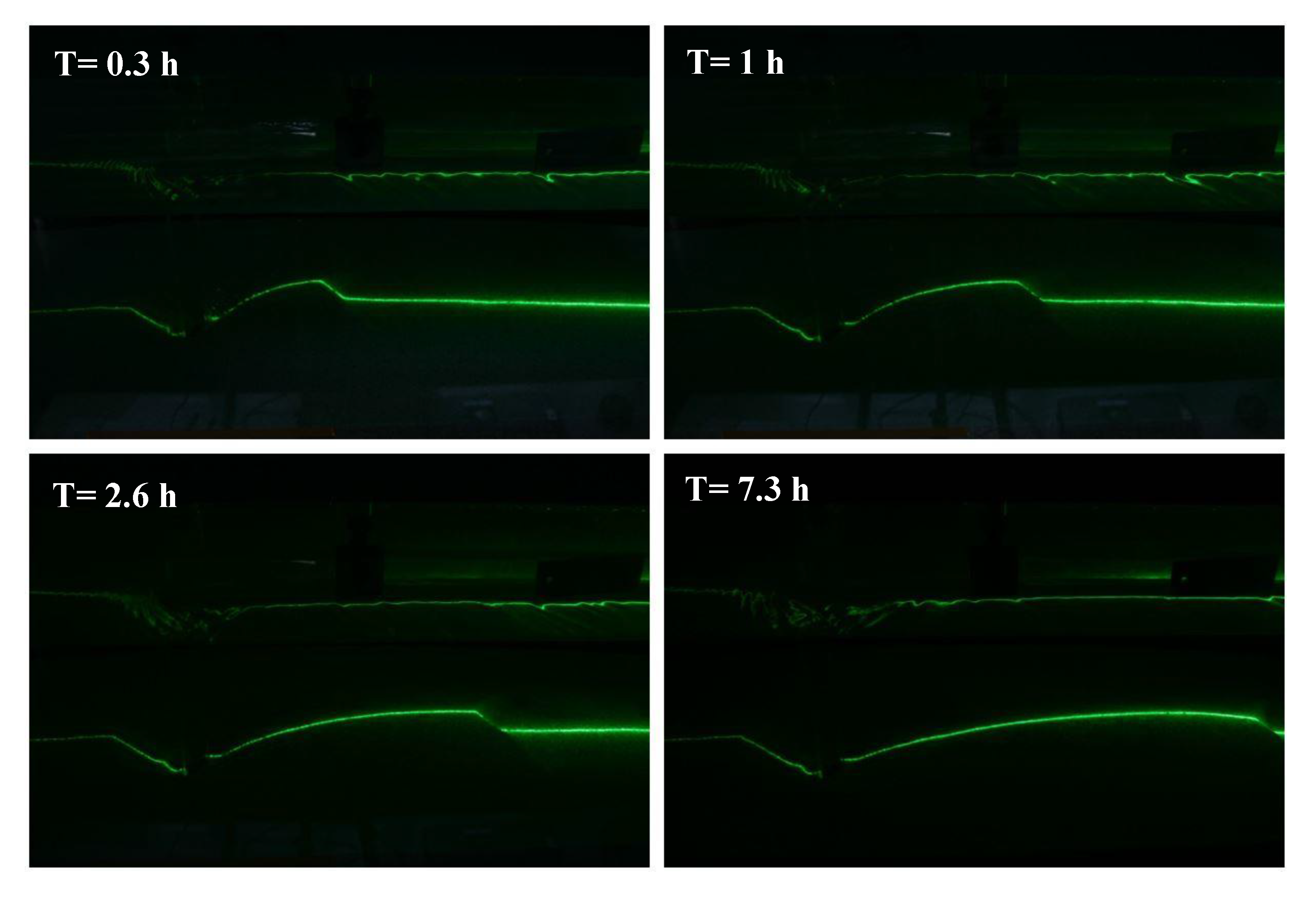
2.2. Measuring System
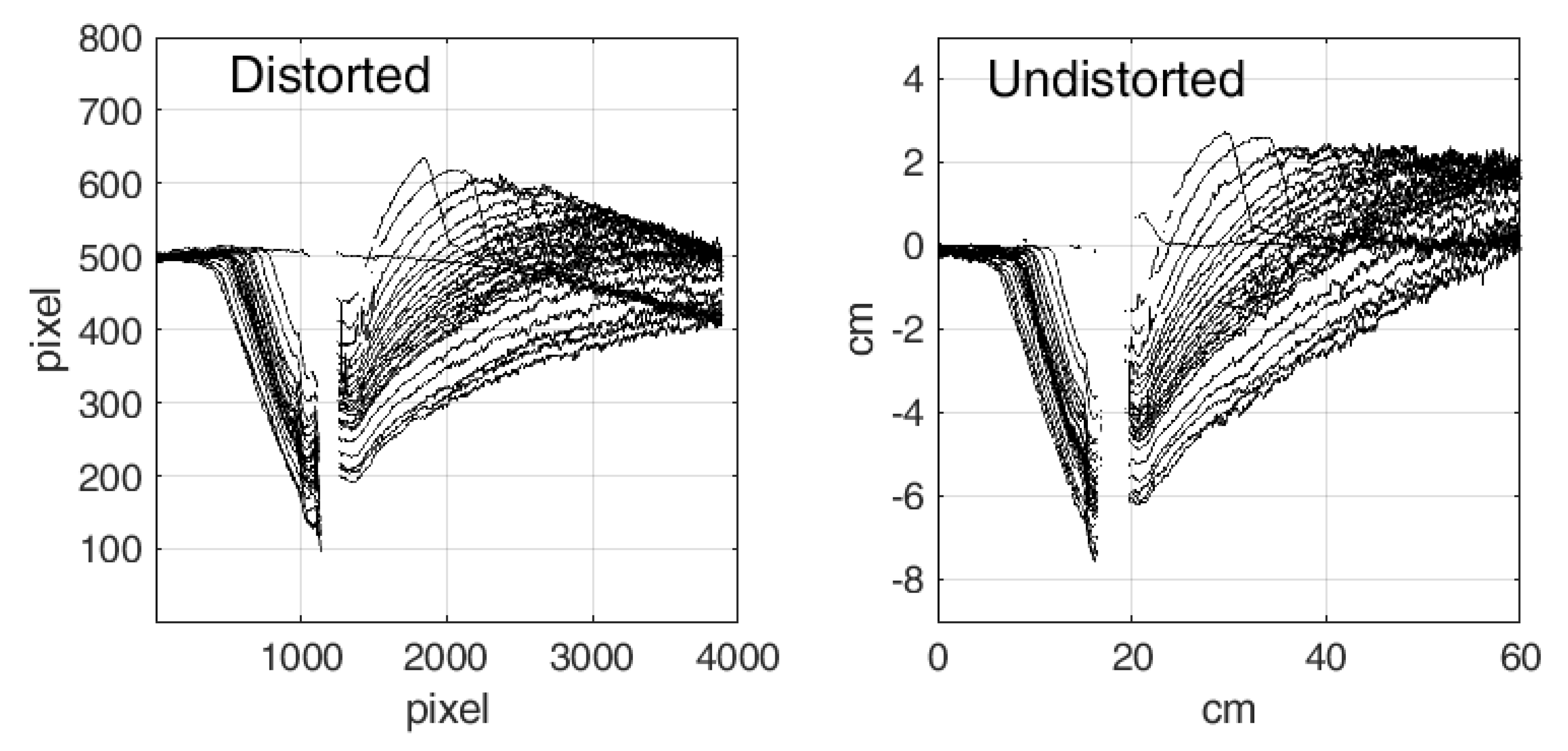
2.3. Calibration and Image Processing
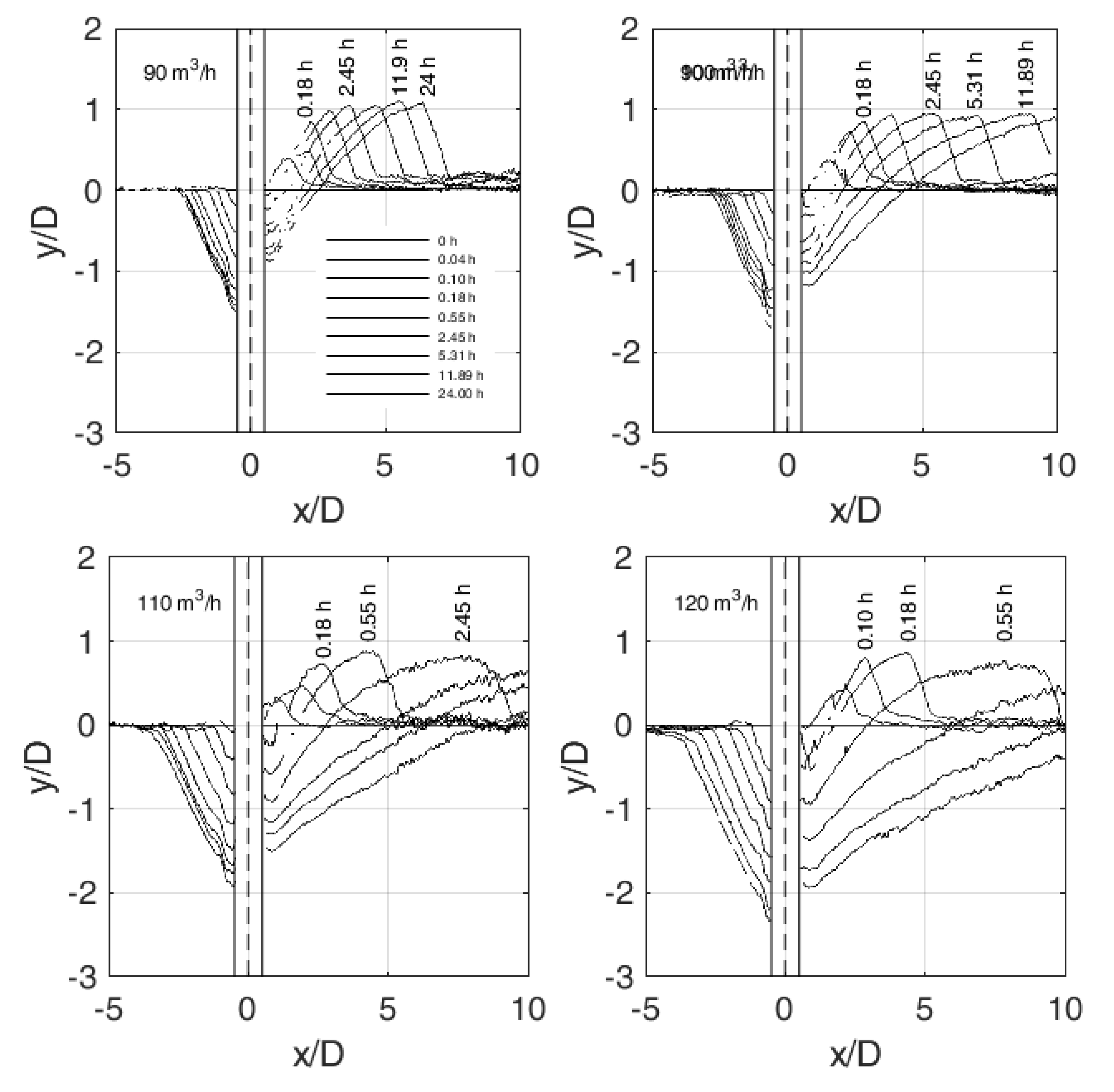
3. Results and Discussion
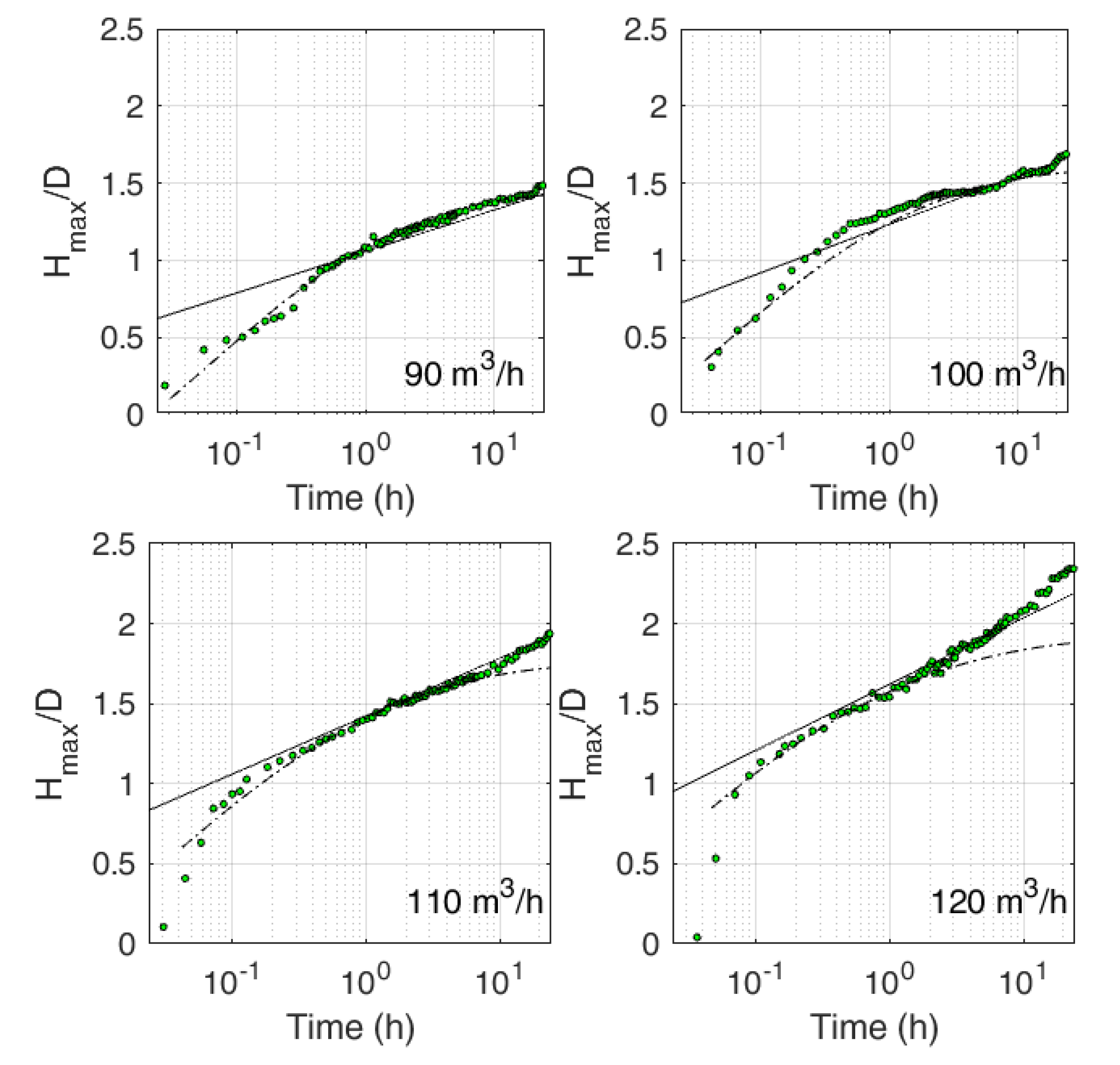
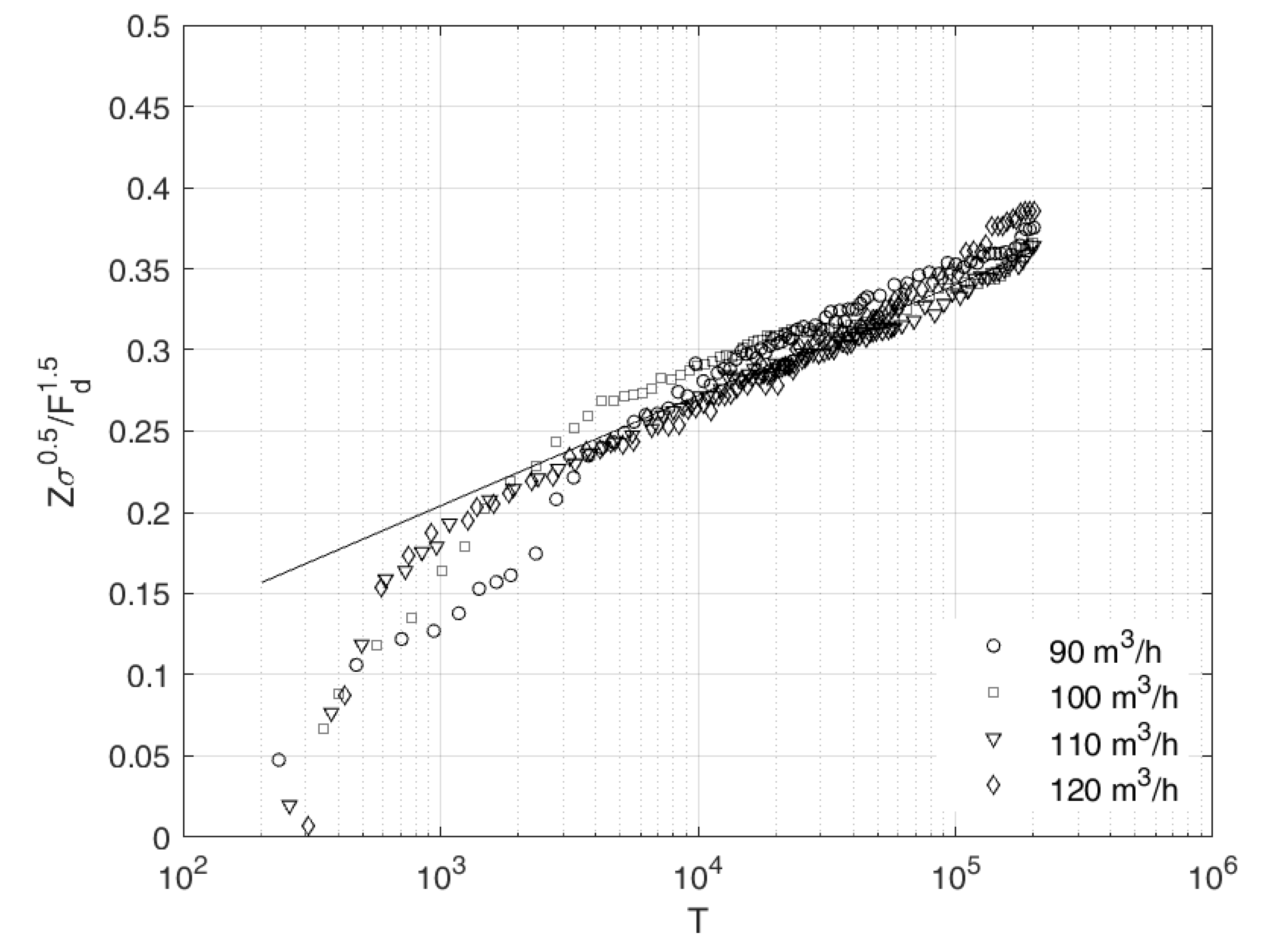
3.1. Existing Equations for Temporal Scour Depth
3.2. Comparison with Existing Equations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wardhana, K.; Hadipriono, F.C. Analysis of Recent Bridge Failures in the United States. J. Perform. Constr. Facil. 2003, 17, 144–150. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y.-M. Time Scale for Local Scour at Bridge Piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Johnson, P.A.; Dock, D.A. Probabilistic Bridge Scour Estimates. J. Hydraul. Eng. 1998, 124, 750–754. [Google Scholar] [CrossRef]
- Tubaldi, E.; Macorini, L.; Izzuddin, B.A.; Manes, C.; Laio, F. A framework for probabilistic assessment of clear-water scour around bridge piers. Struct. Saf. 2017, 69, 11–22. [Google Scholar] [CrossRef]
- Lagasse, P.F. Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction; Transportation Research Board: Washington, DC, USA, 2013; ISBN 978-0-309-28356-4. [Google Scholar]
- Wang, C.; Yu, X.; Liang, F. A review of bridge scour: Mechanism, estimation, monitoring and countermeasures. Nat. Hazards 2017, 87, 1881–1906. [Google Scholar] [CrossRef]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publication: Highlands Ranch, CO, USA, 2000; ISBN 978-1-887201-18-6. [Google Scholar]
- Dargahi, B. Controlling Mechanism of Local Scouring. J. Hydraul. Eng. 1990, 116, 1197–1214. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kang, S.; Sotiropoulos, F. Experimental and computational investigation of local scour around bridge piers. Adv. Water Resour. 2012, 37, 73–85. [Google Scholar] [CrossRef]
- Manes, C.; Brocchini, M. Local scour around structures and the phenomenology of turbulence. J. Fluid Mech. 2015, 779, 309–324. [Google Scholar] [CrossRef]
- Melville, B.W. Live-bed Scour at Bridge Piers. J. Hydraul. Eng. 1984, 110, 1234–1247. [Google Scholar] [CrossRef]
- Toth, E.; Brandimarte, L. Prediction of local scour depth at bridge piers under clear-water and live-bed conditions: Comparison of literature formulae and artificial neural networks. J. Hydroinform. 2011, 13, 812–824. [Google Scholar] [CrossRef]
- Ettmer, B.; Orth, F.; Link, O. Live-Bed Scour at Bridge Piers in a Lightweight Polystyrene Bed. J. Hydraul. Eng. 2015, 141, 04015017. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hager, W.H.; Oliveto, G. Generalized Approach for Clear-Water Scour at Bridge Foundation Elements. J. Hydraul. Eng. 2007, 133, 1229–1240. [Google Scholar] [CrossRef]
- Lança, R.M.; Fael, C.S.; Maia, R.J.; Pêgo, J.P.; Cardoso, A.H. Clear-Water Scour at Comparatively Large Cylindrical Piers. J. Hydraul. Eng. 2013, 139, 1117–1125. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal Evolution of Clear-Water Pier and Abutment Scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Garde, R.C.J.; Ranga, R.K.G. Temporal Variation of Scour around Circular Bridge Piers. J. Hydraul. Eng. 1992, 118, 1091–1106. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Further Results to Time-Dependent Local Scour at Bridge Elements. J. Hydraul. Eng. 2005, 131, 97–105. [Google Scholar] [CrossRef]
- Pandey, M.; Sharma, P.K.; Ahmad, Z.; Singh, U.K. Evaluation of existing equations for temporal scour depth around circular bridge piers. Environ. Fluid Mech. 2017, 17, 981–995. [Google Scholar] [CrossRef]
- Mia, M.F.; Nago, H. Design Method of Time-Dependent Local Scour at Circular Bridge Pier. J. Hydraul. Eng. 2003, 129, 420–427. [Google Scholar] [CrossRef]
- Sheppard, D.M.; Odeh, M.; Glasser, T. Large Scale Clear-Water Local Pier Scour Experiments. J. Hydraul. Eng. 2004, 130, 957–963. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Morphological Evolution of Dune-Like Bed Forms Generated by Bridge Scour. J. Hydraul. Eng. 2014, 140, 06014009. [Google Scholar] [CrossRef]
- Chavan, R.; Kumar, B. Prediction of scour depth and dune morphology around circular bridge piers in seepage affected alluvial channels. Environ. Fluid Mech. 2018, 18, 923–945. [Google Scholar] [CrossRef]
- Pagliara, S.; Carnacina, I. Scour and dune morphology in presence of large wood debris accumulation at bridge pier. In River Flow 2010: Proceedings of the Fifth International Conference on Fluvial Hydraulics, Braunschweig, Germany, 8–10 June 2010; Bundesanstalt für Wasserbau: Karlsruhe, Germany, 2010. [Google Scholar]
- Pagliara, S.; Carnacina, I. Influence of Wood Debris Accumulation on Bridge Pier Scour. J. Hydraul. Eng. 2011, 137, 254–261. [Google Scholar] [CrossRef]
- Pagliara, S.; Carnacina, I. Influence of large woody debris on sediment scour at bridge piers. Int. J. Sediment Res. 2011, 26, 121–136. [Google Scholar] [CrossRef]
- Carnacina, I.; Pagliara, S.; Leonardi, N. Bridge pier scour under pressure flow conditions. River Res. Appl. 2019, 35, 844–854. [Google Scholar] [CrossRef]
- Hill, D.F.; Younkin, B.D. PIV measurements of flow in and around scour holes. Exp. Fluids 2006, 41, 295–307. [Google Scholar] [CrossRef]
- Zhang, H.; Nakagawa, H.; Kawaike, K.; Baba, Y. Experiment and simulation of turbulent flow in local scour around a spur dyke. Int. J. Sediment Res. 2009, 24, 33–45. [Google Scholar] [CrossRef]
- Lu, S.-Y.; Lu, J.-Y.; Shih, D.-S. Temporal and Spatial Flow Variations over a Movable Scour Hole Downstream of a Grade-Control Structure with a PIV System. Water 2018, 10, 1002. [Google Scholar] [CrossRef]
- Sambrook, S.G.H.; Nicholas, A.P. Effect on flow structure of sand deposition on a gravel bed: Results from a two-dimensional flume experiment: Effect on Flow Structure of Sand Deposit. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Bottacin-Busolin, A.; Tait, S.J.; Marion, A.; Chegini, A.; Tregnaghi, M. Probabilistic description of grain resistance from simultaneous flow field and grain motion measurements: Characterizing Grain Resistance. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- González, E.P.; Marqués, J.F.; Díaz-Pache, F.S.-T.; Agudo, J.P.; Gómez, L.C. Experimental validation of a sediment transport two-dimensional depth-averaged numerical model using PIV and 3D Scanning technologies. J. Hydraul. Res. 2008, 46, 489–503. [Google Scholar] [CrossRef]
- Chang, W.-Y.; Lai, J.-S.; Yen, C.-L. Evolution of Scour Depth at Circular Bridge Piers. J. Hydraul. Eng. 2004, 130, 905–913. [Google Scholar] [CrossRef]
- Thorne, P.D.; Hanes, D.M. A review of acoustic measurement of small-scale sediment processes. Cont. Shelf Res. 2002, 22, 603–632. [Google Scholar] [CrossRef]
- Branß, T.; Núñez-González, F.; Dittrich, A.; Aberle, J. A flume study to investigate the contribution of main-channel bedforms on levee formation. E3S Web. Conf. 2018, 40, 02018. [Google Scholar] [CrossRef]
- Dahal, P.; Peng, D.; Yang, Y.L.; Sharif, H. RSS Based Bridge Scour Measurement Using Underwater Acoustic Sensor Networks. Commun. Netw. 2013, 5, 641–648. [Google Scholar] [CrossRef][Green Version]
- Lanzoni, S. Experiments on bar formation in a straight flume: 1. Uniform sediment. Water Resour. Res. 2000, 36, 3337–3349. [Google Scholar] [CrossRef]
- Ballio, F.; Radice, A. A non-touch sensor for local scour measurements. J. Hydraul. Res. 2003, 41, 105–108. [Google Scholar] [CrossRef]
- Lam, N.; Nathanson, M.; Lundgren, N.; Rehnström, R.; Lyon, S.W. A Cost-Effective Laser Scanning Method for Mapping Stream Channel Geometry and Roughness. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 1211–1220. [Google Scholar] [CrossRef]
- Marion, A.; Tait, S.J.; McEwan, I.K. Analysis of small-scale gravel bed topography during armoring. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Visconti, F.; Stefanon, L.; Camporeale, C.; Susin, F.; Ridolfi, L.; Lanzoni, S. Bed evolution measurement with flowing water in morphodynamics experiments: Bed Evolution Measurement with Flowing Water. Earth Surf. Process. Landf. 2012, 37, 818–827. [Google Scholar] [CrossRef]
- Bouratsis, P.; Diplas, P.; Dancey, C.L.; Apsilidis, N. High-resolution 3-D monitoring of evolving sediment beds. Water Resour. Res. 2013, 49, 977–992. [Google Scholar] [CrossRef]
- Müller, G.; Mach, R.; Kauppert, K. Mapping of bridge pier scour with projection moiré. J. Hydraul. Res. 2001, 39, 531–537. [Google Scholar] [CrossRef]
- Chourasiya, S.; Mohapatra, P.K.; Tripathi, S. Non-intrusive underwater measurement of mobile bottom surface. Adv. Water Resour. 2017, 104, 76–88. [Google Scholar] [CrossRef]
- Wei, M.; Cheng, N.-S.; Chiew, Y.-M.; Yang, F. Vortex Evolution within Propeller Induced Scour Hole around a Vertical Quay Wall. Water 2019, 11, 1538. [Google Scholar] [CrossRef]
- Brown, D.C. Decentering Distortion of Lenses. Photogramm. Eng. 1966, 24, 555–566. [Google Scholar]
- Lauchlan, C.S.; Melville, B.W. Riprap Protection at Bridge Piers. J. Hydraul. Eng. 2001, 127, 412–418. [Google Scholar] [CrossRef]
- Choi, S.-U.; Choi, B. Prediction of time-dependent local scour around bridge piers: Time-dependent local scour around bridge piers. Water Environ. J. 2016, 30, 14–21. [Google Scholar] [CrossRef]
- Yilmaz, M.; Yanmaz, A.M.; Koken, M. Clear-water scour evolution at dual bridge piers. Can. J. Civ. Eng. 2017, 44, 298–307. [Google Scholar] [CrossRef]
- Rouse, H. Criteria for Similarity in the Transportation of Sediment. Univ. Iowa Stud. Eng. 1940, 20, 33–49. [Google Scholar]
- Hager, W.H. Forum Article: Plunge Pool Scour: Early History and Hydraulics. J. Hydraul. Eng. 1998, 124, 1185–1187. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poggi, D.; Kudryavtseva, N.O. Non-Intrusive Underwater Measurement of Local Scour Around a Bridge Pier. Water 2019, 11, 2063. https://doi.org/10.3390/w11102063
Poggi D, Kudryavtseva NO. Non-Intrusive Underwater Measurement of Local Scour Around a Bridge Pier. Water. 2019; 11(10):2063. https://doi.org/10.3390/w11102063
Chicago/Turabian StylePoggi, Davide, and Natalia O. Kudryavtseva. 2019. "Non-Intrusive Underwater Measurement of Local Scour Around a Bridge Pier" Water 11, no. 10: 2063. https://doi.org/10.3390/w11102063
APA StylePoggi, D., & Kudryavtseva, N. O. (2019). Non-Intrusive Underwater Measurement of Local Scour Around a Bridge Pier. Water, 11(10), 2063. https://doi.org/10.3390/w11102063




