Abstract
Recently, climate change has increased the frequency of extreme weather events. In South Korea, extreme droughts are frequent and cause serious damage. To identify the risk of extreme drought, we need to calculate the hydrologic risk using probabilistic analysis methods. In particular, future hydrologic risk of extreme drought should be compared to that of the control period. Therefore, this study quantitatively assessed the future hydrologic risk of extreme drought in South Korea according to climate change scenarios based on the representative concentration pathway (RCP) 8.5. A threshold level method was applied to observation-based rainfall data and climate change scenario-based future rainfall data to identify drought events and extract drought characteristics. A bivariate frequency analysis was then performed to estimate the return period considering both duration and severity. The estimated return periods were used to calculate and compare hydrologic risks between the control period and the future. Results indicate that the average duration of drought events for the future was similar with that for the control period, however, the average severity increased in most future scenarios. In addition, there was decreased risk of maximum drought events in the Yeongsan River basin in the future, while there was increased risk in the Nakdong River basin. The median of risk of extreme drought in the future was calculated to be larger than that of the maximum drought in the control period.
1. Introduction
Climate change induces changes of rainfall pattern as the consequence of global warming. Contrary to climate variability, climate change is characterized by a slow-varying oscillation in the climate system and can modify the possibility of extreme events by changing hydrological cycles [1]. According to the precipitation outlook based on climate change scenarios [2,3,4], climate change is likely to produce very different patterns of flood and drought around the world [1]. Compared with other natural disasters, the spatial extent of drought is usually much larger and the duration is greater [5]. In addition, the frequency of extreme droughts will increase and the damage caused by extreme droughts will be severe. Therefore, drought should be quantitatively analyzed to mitigate damage. Due to the multi-sided characteristics and the non-structural impacts of drought, it is difficult to quantify drought damage [6].
For quantitative drought analysis, drought should be defined and characterized. Various drought indices related to agricultural, soil moisture and streamflow data are used to quantify the climate dryness anomalies. For example, Standardized Precipitation Index (SPI) and Palmer Hydrological Drought Index (PHSI) have been used in practice to quantitatively analyze the characteristics of meteorological and hydrological droughts [7,8]. A threshold level method is another frequently applied tool for defining a drought event and has practical advantages—(i) no a-priori knowledge of probability distributions is required and (ii) it simply and directly produces drought characteristics such as duration and severity [9,10]. Mirakbari et al. [11] and Yu et al. [12] defined drought events using a certain threshold level of hydro-meteorological variables and analyzed the probabilistic return period through hydrological drought frequency analysis.
To estimate the risk of extreme drought, the drought frequency analysis is usually performed first. In this study, the drought frequency analysis was conducted using drought characteristics calculated by the threshold level method. Because droughts are characterized by highly correlated random variables, such as duration, intensity and peak, their joint and conditional distributions, as well as their marginal distributions, need to be analyzed to understand multivariate behaviors. Using joint and conditional distributions, the limitations of the univariate frequency analysis could be overcome and the multivariate behavior of droughts could be understood more thoroughly [13]. Both drought duration and severity could be determined easily and simultaneously through bivariate frequency analysis. Since drought duration and severity may be represented by different marginal distributions, copulas can be used to construct the joint distribution function of drought characteristics [14]. For example, Yoo et al. [15] generated synthetic monthly rainfall using the copula-GARCH rainfall generation model, after investigating performance of various copula functions. Janga and Ganguli [5] presented a copula-based multivariate probabilistic approach to analyze the severity–duration–frequency (S-D-F) relationship of drought events in western Rajasthan, India.
Since the hydrologic risk of drought is defined as the probability that a given level of dryness is exceeded in any year, results of bivariate frequency analysis can be used to analyze the risk for certain drought events. Ganguli and Janga [16] presented a risk assessment of hydrologic extreme droughts using copula-based distribution functions in the Saurashtra and Kutch regions of Gujarat, India. Recently, Yoo et al. [17] compared and analyzed drought risks based on the SPI and the Standardized Precipitation Evapotranspiration Index (SPEI) using future climate change scenario data. Kim et al. [18] performed temporal and spatial analyses on extreme drought events on the Korean peninsula to estimate hydrologic risk and evaluate future droughts using future climate change scenario data. Yu et al. [19] conducted a bivariate frequency analysis using copula functions to determine critical severity according to the non-exceedance probability and calculated the hydrologic risk for extreme drought events.
Although numerous studies have focused on drought risk analysis using observed data, more studies about hydrologic risk are needed to quantitatively analyze future extreme droughts. It also needs to compare and analyze the risk of extreme drought for future periods in South Korea under various climate change scenarios. Therefore, this study estimates the hydrologic risk for extreme drought in South Korea and investigates the changes of the drought risk in future.
2. Study area and Data
In this study, drought characteristics were analyzed for 109 medium-sized watersheds in South Korea, as shown in Figure 1. The drought characteristics of medium-sized watersheds directly contribute to regional drought management according to the governmental natural disaster response system.
Figure 1.
Map of the study area.
Observed daily precipitation data (January 1983–December 2014) were obtained from the Korea Meteorological Administration (KMA) and climate change scenario-based daily precipitation data (January 2015–December 2099) were obtained from the Asia-Pacific Economic Cooperation Climate Center (APCC). The observed data were analyzed for a control period and the climate change scenario-based data were analyzed for the future period based on the Representative Concentration Pathway (RCP) 8.5 scenario. Although there are four RCP scenarios such as 2.6, 4.5, 6.0 and 8.5 according to greenhouse gas emissions, the RCP 8.5 represents increases in emissions based on the current trend, without a greenhouse gas reduction policy [20]. The RCP 8.5 scenario is more appropriate for extreme drought analysis than other RCP scenarios, because it realizes the extreme circumstances. 19 Global Climate Models (GCMs) were selected to provide future precipitation data, as shown in in Table 1.

Table 1.
Dataset of global climate models used in this study.
Direct use of GCMs in regional-scale hydrologic analysis is constrained, because the atmospheric dynamics at scales greater than 2 degrees of longitude and latitude yields unrealistic hydrologic outcomes [21]. Dynamic and statistical methods are used to downscale the output from GCMs to regional-scale. The dynamic method is a physical process to enhance the spatial resolution of GCMs climate output through regional climate models (RCMs) [22]; however, it results in biases in precipitation simulations from RCMs due to limited understanding of regional climate processes [1]. The climate change scenario-based data used in this study were provided by the APCC after correcting the bias of GCMs using statistical relationships between observed historical climate data and GCM-based climate variables [22]. In addition, the KMA certifies and releases climate change scenario-based data after validating and examining their soundness and applicability.
3. Methodology
3.1. Threshold Level Method
The most widely used method to define drought is the threshold level method (TLM). The TLM is based on run theory and has two main advantages—(i) no a priori knowledge of probability distributions is required and (ii) it directly produces drought characteristics if the threshold is set according to drought-impacted sectors [9]. Because the TLM is convenient for identifying drought events, it is efficient for applying hydro-meteorological time series compared to other drought identification methods using a drought index like SPI and PDSI [23]. Wada et al. [24] applied the TLM to quantify the impact of human water consumption on intensity and frequency of hydrological drought worldwide over the period 1960–2010. Yoo et al. [25] employed the 3-month and 12-month moving averages as the threshold level and analyzed drought characteristics. Due to the simplicity and efficiency for defining drought, the TLM was used in this study to analyze the drought risk effectively. According to the TLM, the period during which rainfall is less than the predefined threshold is regarded as the drought duration and the accumulated sum of rainfall deficit volume during the duration is defined as the drought severity [26,27]. The period from the beginning of any drought event to the beginning of the next drought event is called interarrival time. Figure 2 illustrates the details of defining drought characteristics by applying the monthly threshold level.
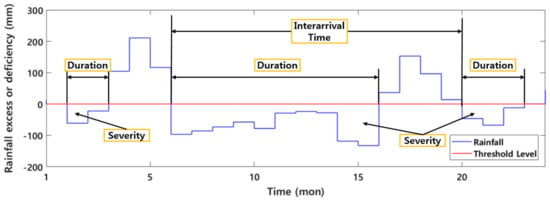
Figure 2.
Definition of drought characteristics using a threshold level.
There are many ways to determine the threshold level. Because the characteristics of drought vary according to threshold level, an appropriate threshold level should be chosen [12]. In this study, the threshold level was determined as percentiles of precipitation based on the empirical cumulative distribution function (ECDF). The threshold level commonly ranges between the 70th and 95th percentiles depending on regional characteristics when applying the TLM to precipitation [28,29]. The threshold may be constant or a variable over a year. If the threshold is derived from the ECDF, it implies that the whole precipitation record (or a predefined period) is used in the derivation of the threshold [30]. This leads to increased accuracy of the rainfall deficit investigation during months with low and high precipitation [31].
3.2. Bivariate Frequency Analysis
To quantify the hydrologic risk of drought, it is necessary to estimate the return period through drought frequency analysis. Drought frequency analysis is divided into univariate and bivariate frequency analysis. Since drought is usually represented by its duration and severity, univariate frequency analysis using a single drought property may not reveal significant relationships among the drought properties [10,32]. Therefore, both duration and severity should be considered together in bivariate frequency analysis to reveal the multivariate characteristics of drought [32]. There are several kinds of bivariate drought frequency analysis—(i) parametric methods, (ii) nonparametric methods and (iii) copula function methods. Parametric methods fit an assumed theoretical probability distribution for drought properties, whereas nonparametric methods do not require any assumptions about probability distribution [26]. Lately, copula function methods have been widely applied in hydrology and water resources engineering [33,34,35,36,37,38,39,40] because they have an advantage of reflecting the dependency structure between two variables and combining their probability distributions [41,42,43,44]. The copula function for calculating the joint probability distribution of drought duration (D) and severity (S) is shown in Equation (1).
where is the bivariate distribution function of two correlated random variables D and S. and are marginal CDFs of D and S, respectively. C represents a copula function.
Copula functions are classified into four categories—Archimedean, elliptical, extreme value and Plackett. The Archimedean copula can be constructed easily, includes a large variety of copula functions and can be applied whether the correlations amongst hydrologic variables are positive or negative [19,45,46]. Therefore, the Archimedean copula functions are more applicable to drought frequency analysis compared to the others. Table 2 shows the Archimedean copula functions.

Table 2.
Equations of Archimedean copula functions.
The return period of an event can be calculated as the inverse of the exceedance probability of the event. The univariate frequency analysis needs only marginal probability of interest variable [47], while bivariate frequency analysis considers two distinctive joint probabilities—(i) AND probability that two variables are exceed specific values, (ii) OR probability that one of two variables is exceeded specific values. In design of a water resources system, it is appropriate to consider the AND probability for a safe design [48]. The joint return period of drought is available for the AND probability, as given by Equation (2).
where E(L) is the expected drought interarrival time.
There are many ways to assess the risk of drought—it is commonly divided into drought risk in the field of natural disasters and drought risk in the fields of hydrology and water resources engineering. Drought risk in the natural disaster field is defined as the scale of potential damage caused by a disaster for a specific period in a particular region and is calculated as the product of hazard and vulnerability. Drought risk in the fields of hydrology and water resources engineering is represented by the hydrologic risk (R) of failure which is the probability of occurrence when the magnitude of the design return period (TDS) is exceeded within the expected life (n) of the structure [49], as given by Equation (3).
The hydrologic risk for each drought event can be estimated through the bivariate return period calculated by Equation (2).
4. Results
4.1. Definition of a Drought Event
In this study, to extract drought characteristics from precipitation time series, the TLM was applied. The threshold level was set based on the percentile of the empirical cumulative distribution function obtained by ordering precipitation data. The threshold level was determined as the closest percentile, within the 70–95th percentiles, which generated as many drought events as using the SPI. After applying the determined threshold to the observed and climate change scenario-based precipitation, drought events were extracted and the duration and severity of drought events were calculated. For the efficiency of analysis, the characteristics of drought events in 109 watersheds are summarized in Table 3, in which average duration and severity are shown for five large river basins.

Table 3.
Characteristics of drought events.
Table 3 demonstrates that HadGEM2-ES produced the lowest average duration and the differences between average durations from the observed and the future scenario were small. CESM1-BGC produced the lowest average severity and the averages of future severity were larger than those of control period for all large basins. It was expected that there will be many droughts in the future with similar duration but greater severity than in the control period. These findings suggest that extreme droughts occur in the future, consistent with results of previous studies.
4.2. Drought Risk Analysis Using Bivariate Frequency Analysis
Various distributions such as exponential, normal, gamma, lognormal, Poisson, Weibull, generalized extreme value and generalized pareto were employed as possible distributions for duration and severity. After estimating distribution parameters using the maximum likelihood method, the optimal probabilistic distributions were individually determined for 109 medium-sized watershed based on χ2 goodness-of-fit test. Among the Archimedean copula functions such as Clayton, Frank and Gumbel, a suitable copula function was selected for observed data in individual watershed and applied to the future climate change scenario data to perform the bivariate frequency analysis. Consequently, the largest value of the bivariate return periods was chosen as the maximum drought event for a watershed and dataset. The characteristics of maximum drought events are shown in Figure 3 and Figure 4. Table 4 summaries the characteristics of maximum drought event.
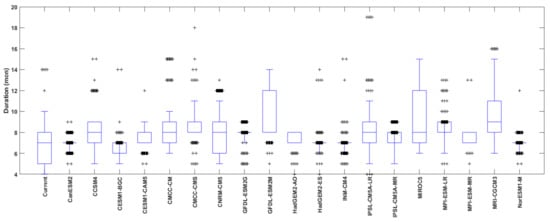
Figure 3.
Duration of maximum droughts for each dataset.
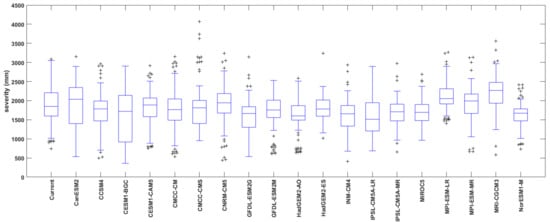
Figure 4.
Severity of maximum droughts for each dataset.

Table 4.
Characteristics of maximum drought events.
Comparison of duration and severity of maximum drought events for each dataset indicated that the median duration of maximum drought in the control period was 7 months. The median severity of maximum drought in the control period was 1849 mm. These medians are the criteria for future risk analysis. In this study, the risk analysis was conducted in two ways using the results of bivariate frequency analysis. We calculated hydrologic risks for the maximum drought events of the control period and then estimated hydrologic risks of extreme droughts in the future period, which are the drought events that are larger than the maximum drought in the control period. The design return periods of a large dam are set to 100–200 years in South Korea. Therefore, in this study, the expected life (n in Equation (3)) of hydrologic risk was set to 100 years. The hydrologic risks of maximum drought events calculated for 109 watersheds are shown in Figure 5.
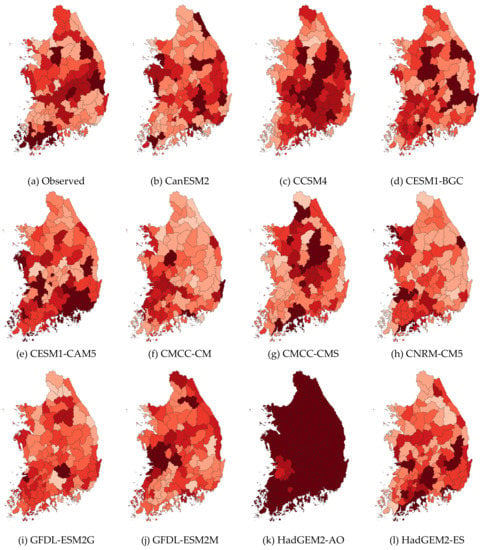
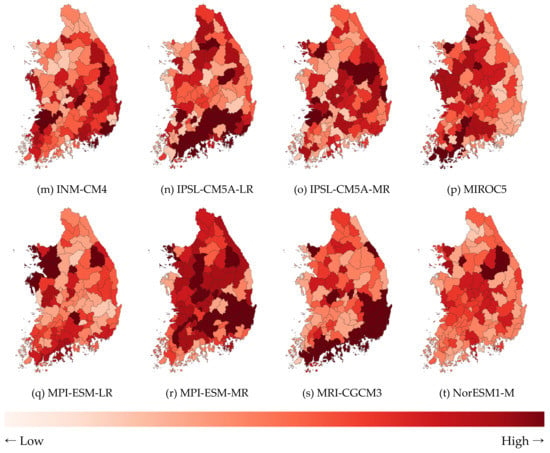
Figure 5.
Hydrologic risk of maximum drought events for each dataset.
In the control period, the highest risk was in the downstream area of the Yeongsan River and the upstream area of the Nakdong River and the lowest risk was in the downstream area of the Nakdong River. However, the results of the future period indicated that the Yeongsan River basin was greatly decreased and the Nakdong River basin was rather dangerous in both upstream and downstream areas. Future drought events exceeding the maximum drought of the control period were defined as extreme droughts and were analyzed using the hydrologic risk. The results for future extreme droughts are shown in Figure 6. The red line represents the median risk for the maximum drought of the control period.
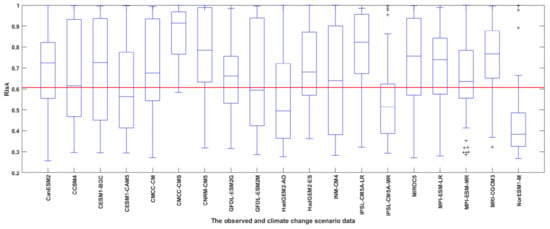
Figure 6.
Hydrologic risk of extreme drought for each dataset.
The median risk of the maximum drought of the control period was 0.61, which was lower than most of the future scenario data. CMCC-CMS of the future scenario data had the highest value of 0.91 compared to the control period and NorESM1-M had the lowest value of 0.38. Table 5 demonstrates the average risk for extreme drought by watershed.

Table 5.
Average hydrologic risk of extreme drought event in each basin.
These results show that CMCC-CMS had the highest risk compared to other GCMs, while NorESM1-M had the lowest risk. In addition, the risks of the Han River, Nakdong River and Seomjin River basins were expected to increase, while the risks of the Geum River and Yeongsan River basins were expected to be similar to those in the control period. Those results are similar to those of Park et al. [50] and the Nakdong, Seomjin and Han River basins are expected to experience more severe drought in the future.
5. Conclusions
In this study, we conducted a bivariate frequency analysis for 109 medium-sized watershed of South Korea using the observed data and 19 RCP 8.5-based synthetic data and then assessed the hydrologic risk of drought for control and future periods. The main conclusions are as follows; (1) The average drought duration of control period and the average drought duration of future period were similar. However, the average drought in the future was higher according to climate change. Consequently, it was expected that extreme droughts would occur in the future. (2) Considering hydrologic risk of drought, the Yeongsan River basin and the upstream area of the Nakdong River basin were dangerous in the control period. In the future, the hydrologic risk of the Yeongsan River basin decreased but that of the Nakdong River basin increased in the downstream region. (3) The hydrologic risks of extreme drought, which was more severe than the maximum drought in the control period, were up to 1.5 times higher than those of the control period. The Han River, Nakdong River and Seomjin River basins predicted high risk of severe drought.
This study demonstrated that drought would be more severe and dangerous in the future in South Korea. Current design standards do not consider the change of extreme drought risk in the future. Therefore, design standards for water resources systems should be established to cope with future extreme droughts considering the climate change. The results of this study can be useful in establishing risk-based quantitative design standards of water resource systems for drought mitigation. Consequently, the design standards of the water resource system can be changed considering the risk of drought and the government can give priority to the area with high risk when preparing the drought measures.
Author Contributions
J.E.K.: Writing-original draft; J.Y.: Investigation and validation; G.H.C.: Writing-review & editing; T.-W.K.: Conceptualization and project administration
Funding
This work was supported by Korea Environment Industry & Technology Institute (KEITI) through Advanced Water Management Research Program, funded by Korea Ministry of Environment (Grant. 83070).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, J.H.; Kwon, H.H.; Jang, H.W.; Kim, T.W. Future changes in drought characteristics under extreme climate change over South Korea. Adv. Meteorol. 2016, 2016, 1–19. [Google Scholar] [CrossRef]
- Kwon, H.-H.; Khalil, A.F.; Siegfried, T. Analysis of extreme summer rainfall using climate teleconnections and typhoon characteristics in South Korea. J. Am. Water Resour. Assoc. 2008, 44, 436–448. [Google Scholar] [CrossRef]
- Kwon, H.-H.; Brown, C.; Lall, U. Climate informed flood frequency analysis and prediction in Montana using hierarchical Bayesian modeling. Geophys. Res. Lett. 2008, 35, 05404. [Google Scholar] [CrossRef]
- Kwon, H.-H.; Sivakumar, B.; Moon, Y.-I.; Kim, B.-S. Assessment of change in design flood frequency under climate change using a multivariate downscaling model and a precipitation runoff model. Stoch. Environ. Res. Risk Assess. 2011, 25, 567–581. [Google Scholar] [CrossRef]
- Janga, R.M.; Ganguli, P. Application of copulas for derivation of drought severity-duration-frequency curves. Hydrol. Process. 2012, 26, 1672–1685. [Google Scholar] [CrossRef]
- Obasi, G.O.P. WMO’s role in the international decade for natural disaster reduction. Bull. Am. Meteorol. Soc. 1994, 75, 1655–1662. [Google Scholar] [CrossRef]
- Lee, J.H.; Park, S.Y.; Kim, J.S.; Sur, C.; Chen, J. Extreme drought hotspot analysis for adaptation to a changing climate: Assessment of applicability to the five major river basins of the Korean Peninsula. Int. J. Climatol. 2018, 38, 4025–4032. [Google Scholar] [CrossRef]
- Waseem, M.; Ajmal, M.; Kim, T.W. Development of a new composite drought index for multivariate drought assessment. J. Hydrol. 2015, 527, 30–37. [Google Scholar] [CrossRef]
- Van Huijgevoort, M.H.J.; Hazenberg, P.; van Lanen, H.A.J.; Uijlenhoet, R. A generic method for hydrological drought identification across different climate regions. Hydrol. Earth Syst. Sci. 2012, 16, 2437–2451. [Google Scholar] [CrossRef]
- Shiau, J.T.; Shen, H.W. Recurrence analysis of hydrologic droughts of differing severity. J. Water Resour. Plan. Manag. 2001, 127, 30–40. [Google Scholar] [CrossRef]
- Mirakbari, M.; Ganji, A.; Fallah, S.R. Regional bivariate frequency analysis of meteorological droughts. J. Hydrol. Eng. 2010, 15, 985–1000. [Google Scholar] [CrossRef]
- Yu, J.S.; Shin, J.Y.; Kwon, M.S.; Kim, T.W. Bivariate drought frequency analysis to evaluate water supply capacity of multi-purpose dams. J. Korean Soc. Civ. Eng. 2017, 37, 231–238. [Google Scholar] [CrossRef]
- Kim, T.-W.; Valdés, J.B.; Yoo, C.S. Nonparametric approach for estimating return periods of droughts in arid regions. J. Hydrol. Eng. 2003, 8, 237–246. [Google Scholar] [CrossRef]
- Mirabbasi, R.; Fakheri-Fard, A.; Dinpashoh, Y. Bivariate drought frequency analysis using the copula method. Theor. Appl. Climatol. 2012, 108, 191–206. [Google Scholar] [CrossRef]
- Yoo, J.; Kim, D.; Kim, H.; Kim, T.W. Application of copula functions to construct confidence intervals of bivariate drought frequency curve. J. Hydrol. Environ. Res. 2016, 11, 113–122. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Risk assessment of droughts in Gujarat using bivariate copulas. Water Resour. Manag. 2012, 26, 3301–3327. [Google Scholar] [CrossRef]
- Yoo, J.Y.; Kwon, H.H.; Lee, J.H.; Kim, T.W. Influence of evapotranspiration of future drought risk using bivariate drought frequency curves. KSCE J. Civ. Eng. 2016, 20, 2059–2069. [Google Scholar] [CrossRef]
- Kim, N.S.; Kim, J.S.; Jang, H.W.; Lee, J.H. Hydrologic risk analysis based on extreme drought over the Korean peninsula under climate change. J. Korea Soc. Hazard Mitig. 2015, 15, 45–52. [Google Scholar] [CrossRef]
- Yu, J.S.; Yoo, J.Y.; Lee, J.H.; Kim, T.W. Estimation of drought risk through the bivariate drought frequency analysis using copula functions. J. Korea Water Resour. Assoc. 2016, 49, 217–225. [Google Scholar] [CrossRef]
- Park, M.W.; Lee, O.J.; Park, Y.K.; Kim, S.D. Future drought projection In Korea under AR5 RCP climate change scenarios. J. Korea Soc. Hazard Mitig. 2015, 15, 423–433. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Bae, D.H.; Jung, I.W.; Lettenmaier, D.P. Hydrologic uncertainties in climate change from IPCC AR4 GCM simulations of the Chungju basin, Korea. J. Hydrol. 2011, 401, 90–105. [Google Scholar] [CrossRef]
- Kwak, J.W.; Lee, S.D.; Kim, Y.S.; Kim, J.S. Return period estimation of droughts using drought variables from standardized precipitation index. J. Korea Water Resour. Assoc. 2013, 46, 795–805. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.H.; Wanders, N.; Bierkens, M.F.P. Human water consumption intensifies hydrological drought worldwide. Environ. Res. Lett. 2013, 8, 034036. [Google Scholar] [CrossRef]
- Yoo, J.Y.; Kim, T.W.; Kim, S.D. Drought frequency analysis using cluster analysis and bivariate probability distribution. J. Korea Water Resour. Assoc. 2010, 30, 599–606. [Google Scholar] [CrossRef]
- Yoo, J.Y.; Kwon, H.H.; Kim, T.W.; Ahn, J.H. Drought frequency analysis using cluster analysis and bivariate probability distribution. J. Hydrol. 2012, 14, 102–111. [Google Scholar] [CrossRef]
- Sung, J.H.; Chung, E.S. Proposal and application of water deficit-duration-frequency curve using threshold level method. J. Korea Water Resour. Assoc. 2014, 47, 997–1005. [Google Scholar] [CrossRef]
- Carrão, H.; Singleton, A.; Naumann, G.; Barbosa, P.; Vogt, J. An optimized system for the classification of meteorological drought intensity with applications in frequency analysis. J. Appl. Meteor. Climatol. 2014, 53, 1943–1960. [Google Scholar] [CrossRef]
- Van Loon, A.F. Hydrological drought explained. Wiley Interdiscip. Rev. Water 2015. [Google Scholar] [CrossRef]
- Hisdal, H.; Tallaksen, T. Drought Event Definition; Technical Report; ARIDE Technical Report NO. 6; University of Oslo: Oslo, Norway, 2000. [Google Scholar]
- Karimi, M.; Shahedi, K. Hydrological drought analysis of Karkheh River basin in Iran using variable threshold level method. Curr. World Environ. J. 2013, 8, 419–428. [Google Scholar] [CrossRef]
- Kim, T.-W.; Valdés, J.B.; Yoo, C.S. Nonparametric approach for bivariate drought characterization using Palmer drought index. J. Hydrol. Eng. 2006, 11, 134–143. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G. A generalized pareto intensity-duration model of storm rainfall exploiting 2-copulas. J. Geophys. Res. 2003, 108, 4067. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Canossi, M.; Petaccia, A.; Rosso, R. Bivariate statistical approach to check adequacy of dam spillway. J. Hydrol. Eng. 2005, 10, 50–57. [Google Scholar] [CrossRef]
- Favre, A.C.; Adlouni, S.E.; Perreault, L.; Thiemonge, N.; Bobbe, B. Multivariate hydrological frequency using copulas. Water Resour. Res. 2004, 40, 1–12. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Analytical calculation of storm volume statistics with pareto-like intensity-duration marginals. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resour. Res. 2004, 40, 1–17. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Statistical characterization of temporal structure of storms. Adv. Water Resour. 2006, 29, 827–842. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. On the use of copulas in hydrology: Theory and practice. J. Hydrol. Eng. 2007, 12, 369–380. [Google Scholar] [CrossRef]
- Wong, G. A comparison between the Gumbel-Hougaard and distorted Frank copulas for drought frequency analysis. Int. J. Hydrol. Sci. Technol. 2013, 3, 77–91. [Google Scholar] [CrossRef]
- Wong, G.; Lambert, M.F.; Leonard, M.; Metcalfe, A.V. Drought analysis using trivariate copulas conditional on climate states. J. Hydrol. Eng. 2010, 15, 129–141. [Google Scholar] [CrossRef]
- Lee, T.; Salas, J.D. Copula-based stochastic simulation of hydrological data applied to Nile River flows. Hydrol. Res. 2011, 42, 318–330. [Google Scholar] [CrossRef]
- Yoo, J.Y.; Yu, J.S.; Kwon, H.H.; Kim, T.W. Determination of drought events considering the possibility of relieving drought and estimation of design drought severity. J. Korea Water Resour. Assoc. 2016, 49, 275–282. [Google Scholar] [CrossRef]
- Shiau, J.-T.; Wang, H.-Y.; Tsai, C.-T. Bivariate frequency analysis of flood using copulas. J. Am. Water Resour. Assoc. 2006, 42, 1549–1564. [Google Scholar] [CrossRef]
- Nelson, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 1999. [Google Scholar]
- Zhang, L.; Singh, V.P. Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Chen, L.; Sinngh, V.P.; Guo, S.; Mishra, A.K.; Guo, J. Drought analysis using copulas. J. Hydrol. Eng. 2013, 18, 797–808. [Google Scholar] [CrossRef]
- Kwon, Y.-M.; Kim, T.-W. Derived I-D-F curve in Seoul using bivariate precipitation frequency analysis. J. Korean Soc. Civ. Eng. 2009, 29, 155–162. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988; p. 572. [Google Scholar]
- Park, B.S.; Lee, J.H.; Kim, C.J.; Jang, H.W. Projection of future drought of Korea based on probabilistic approach using multi-model and multi climate change scenarios. J. Korean Soc. Civ. Eng. 2013, 33, 1871–1885. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).