Next Article in Journal
Hydrologic Risk Assessment of Future Extreme Drought in South Korea Using Bivariate Frequency Analysis
Next Article in Special Issue
Numerical Study of Remote Sensed Dredging Impacts on the Suspended Sediment Transport in China’s Largest Freshwater Lake
Previous Article in Journal
Characterisation of the Water Renewal in a Macro-Tidal Marina Using Several Transport Timescales
Previous Article in Special Issue
Secondary Flow Effects on Deposition of Cohesive Sediment in a Meandering Reach of Yangtze River
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 11
Issue 10
10.3390/w11102051
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Validation of a Novel, Shear Reynolds Number Based Bed Load Transport Calculation Method for Mixed Sediments against Field Measurements

by
Gergely T. Török
1,2,*,
János Józsa
1,2 and
Sándor Baranya
2
1
MTA-BME Water Management Research Group; Hungarian Academy of Science, Budapest University of Technology and Economics, Műegyetem rakpart 3, H-1111 Budapest, Hungary
2
Department of Hydraulic and Water Resources Engineering, Faculty of Civil Engineering, Budapest University of Technology and Economics, Műegyetem rakpart 3, H-1111 Budapest, Hungary
*
Author to whom correspondence should be addressed.
Water 2019, 11(10), 2051; https://doi.org/10.3390/w11102051
Submission received: 30 July 2019 / Revised: 25 September 2019 / Accepted: 27 September 2019 / Published: 30 September 2019
(This article belongs to the Special Issue The Application of Hydraulic and Sediment Transport Models in Fluvial Geomorphology)
Browse Figures
Versions Notes

Abstract

:
In this study, the field measurement-based validation of a novel sediment transport calculation method is presented. River sections with complex bed topography and inhomogeneous bed material composition highlight the need for an improved sediment transport calculation method. The complexity of the morphodynamic features (spatially and temporally varied bed material) can result in the simultaneous appearance of the gravel and finer sand dominated sediment transport (e.g., parallel bed armoring and siltation) at different regions within a shorter river reach. For the improvement purpose of sediment transport calculation in such complex river beds, a novel sediment transport method was elaborated. The base concept of it was the combined use of two already existing empirical sediment transport models. The method was already validated against laboratory measurements. The major goal of this study was the verification of the novel method with a real river case study. The combining of the two sediment transport models was based on the implementation of a recently presented classification method of the locally dominant sediment transport nature (gravel or sand transport dominates). The results were compared with measured bed change maps. The verification clearly referred to the meaningful improvement in the sediment transport calculation by the novel manner in the case of spatially varying bed content.

1. Introduction

Sediment transport modeling is a recently still developing topic of morphodynamic investigations. Although researchers elaborate an increasingly accurate description of the sediment motion, there is still no one generally accurately applicable sediment transport model. The selection of the applied appropriate sediment transport method for a given case with even unique morphodynamic features (such as grain size, homogeneity of the bed content, bed slope, bed shear stress, hydraulic flow regime, the measure of armoring, etc.) must be preceded by a careful preliminary examination. There are, however, a large amount of empirically derived bed load transport formulas [1,2,3,4,5,6,7,8,9,10]. A comprehensive collection of the most widely applied formulas can be found in the Sedimentation Engineering Handbook [11]. The collection contains the most relevant sediment transport models, such as the ones from Meyer-Peter and Müller [1], from Einstein [2], Ashida and Michiue [4], Parker, Klingeman and McLean [5], surface-based relation of Parker [6], two-fraction relation of Wilcock and Kenworthy [7], surface-based relation of Wilcock and Crowe [8], relation of Wu et al. [9] and of Powell et al. [10]. The summary provides a short description of the hydraulic and sediment conditions of the experiments for which the given bed load formulas are developed (such as grain size, homogeneity of the bed material, bed slope, range of the bed shear stress and the measure of armoring). Although the applicability limits of the formulas are usually not defined in an exact way, they can be indirectly concluded based on the conditions of the benchmark experiments.
Török et al. [12] elaborated on a novel calculation method, which does not represent a new sediment transport model. The method says that by the combined and parallel application of the present models the applicability range can be increased. The laboratory measurements based validation evinced that the novel method can result in significantly more accurate sediment transport calculation [12]. However, the novel method was not yet verified with field measurements based comparative investigation.

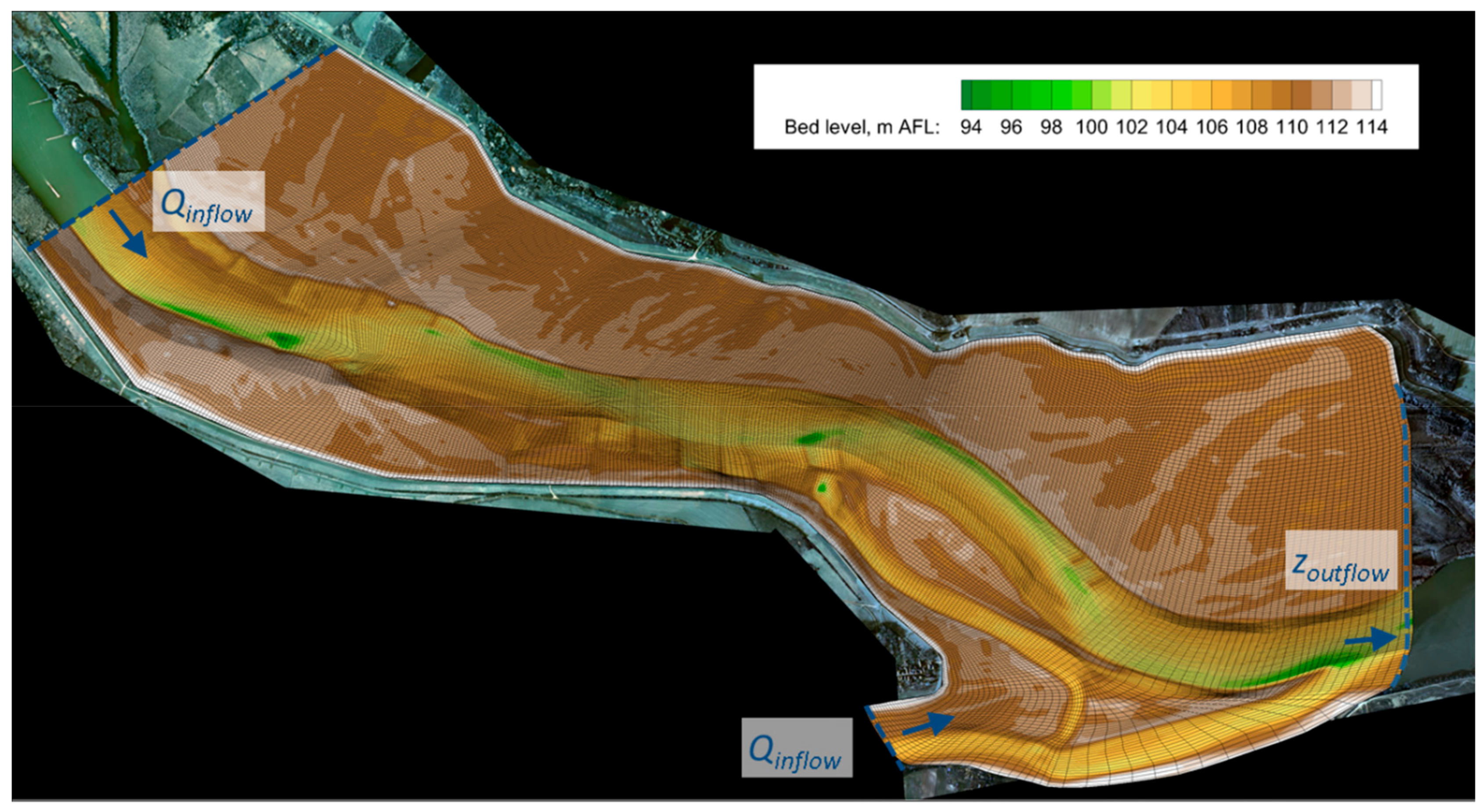
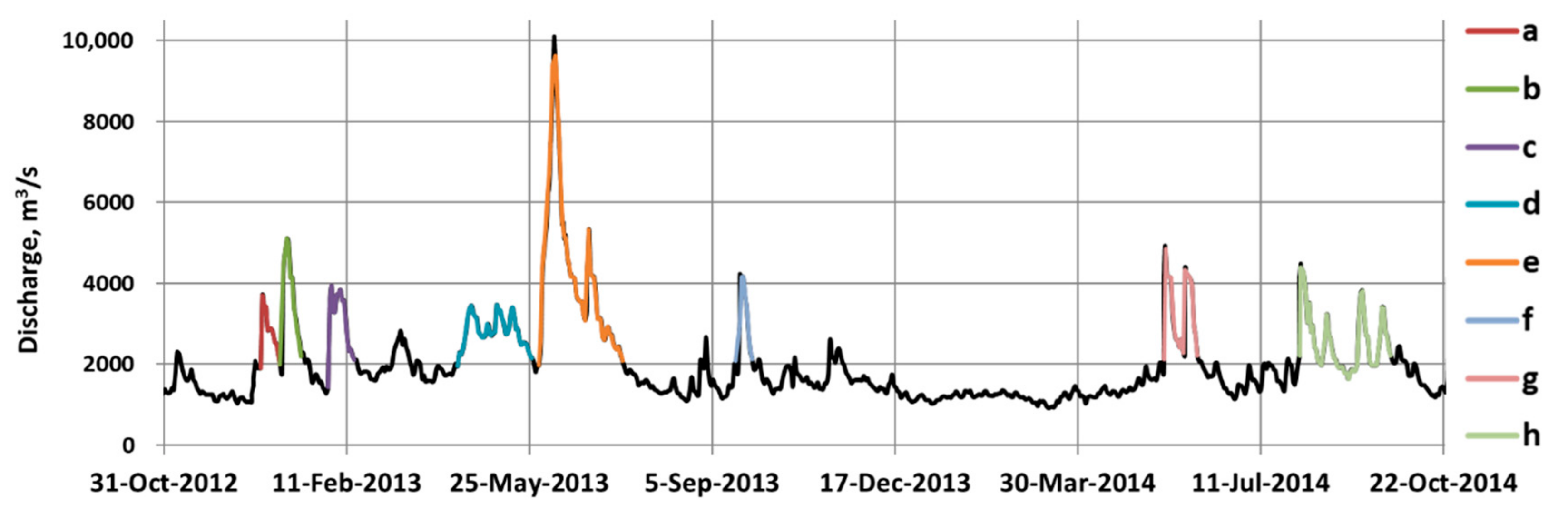
2. Case Study

A problematic reach of the upper Hungarian Danube reach (river km (rkm) 1796–rkm 1794, Figure 1) has undergone major morphological changes during the last decades. Many studies presented in the literature [13,14,15,16,17,18,19] that because of installations of many river regulation measures (e.g., groin fields, ripraps and hydropower plant at rkm 1819) in the last decades, intensive gravel formations [19], important bed level incision [20] and bed armoring processes [16,19] could be detectable, mainly in the main channel [21]. In contrast, the bed content is much finer in the groin fields, causing siltation and erosion of the finer sediments during flood waves [19,22].
The river reach can be characterized by the following parameters: the channel bed width at mean water-stage ranges between 150 m and 350 m [19] with the average water surface gradient of 0.0002–0.00025. As Figure 1 shows, the river section is regulated by conventional structures, such as groins and the banks are protected against erosion by ripraps. Also, sidearms, islands, gravel bars, confluence zone can be observed, which refer to the complex topography of the river section. Bed material samples were taken from the main stream, groin fields and gravel bars. Some of the grain size distributions can be seen in Figure 1 right. The figures refer to very diverse spatial bed contents (0.32 mm < d50 < 70.5 mm, where d50 is the median grain size). Such a wide dispersion of the bed content is a unique feature of the Danube River (~rkm 1600–rkm 1800); at the Lower Austrian Danube, (~rkm 1885, 90 km upstream), the Danube flows through a gravel bed, where d50 is 21.1 mm without any finer fractions [24]. In turn, the middle Hungarian Danube (~200 km downstream) has a typical sandy bed with d50 < 0.05 mm [25]. The complexity of the topography and bed content suggest spatially and temporally varied sediment transport nature [22]. That is in some places the gravel, elsewhere the sand transport dominates [26]. This kind of individual complexity was presented e.g., by the field measurements of Török and Baranya [19], or in [27,28].
Based on field measurements, the researchers could make approximate estimates regarding the ongoing local- and reach-scale morphodynamic processes. For instance, the essential bed changes in the last decades caused important water management related problems and also difficulties in navigation, which could be detected with the field measurements [19,20,27,28,29]. However, the studies emphasize that additional studies are required for even more reliable morphodynamic investigation. Computational modeling offers an alternative for analyzing and predicting the recent and expected processes [30,31]. That is, the numerical modeling based investigation could be an important complementary manner with meaningful added value.
For this reason, the reliable calculation of the morphological changes is a major interest to researchers and the application of a 3D computational fluid dynamics (CFD) sediment transport model became justified. However, the choice of the applied sediment transport model was not obvious. Many formulas can be found in the literature (e.g., [1,2,3,4,32]). Most of them are developed focusing on a given morphodynamic process (e.g., Wilcock and Crowe model: bed armoring [8]; van Rijn model: sand erosion and deposition [33] etc.). However, in the case of the examined river section, spatially and temporally varied sediment transport nature occurs. That is, none of the existing sediment transport formula are expected to operate reliably for both the sand and coarse bed material, within a given river reach.

3. Materials and Methods

3.1. Introducing the Combining Sediment Transport Calculation Method

A novel combined approach [12] of the van Rijn and the Wilcock and Crowe bed load sediment transport formulas were applied because of the complex and spatially varied bed material and dominant sediment transport nature. From now, the Wilcock and Crowe formula will be indicated with W&C, while the van Rijn will be with vR. A brief summary of these models can be read in the Appendix A. The combined manner was already presented and validated against laboratory measurements [12]. In that study, laboratory experiments were used, which were carried out in an 11 m long, 1 m wide straight flume with non-uniform bed material. A groin was installed 5 m far from the outlet, which caused scouring, bed armoring and sand aggradation processes in the channel [34].
Török and Baranya [22,26] pointed out a novel decision criterion, which is a suitable method for indicating whether the sand or rather the sand transport dominates locally. The herein presented combining method was based on this statement. Namely, if the shear Reynolds number (Re*) is below 300, the sand transport is prevalent. Otherwise, if the Re* occurs above 400 the gravel transport dominates. Based on these, the combined calculation method said that the local bed load sediment transport rate was calculated as the following ( q b i , W & C is the sediment transport rate calculated by W&C and q b i , v R is the rate by vR):
q b i = q b i , W & C   i f   R e * > 400 q b i , v R   i f   R e * ≤ 300 e l s e f · q b i , W & C   + 1 − f · q b i , v R ,
where
f = 1 100 R e * − 300 .
These models do not contain any variable to calibrate, the constants (e.g., the constant von Karman, or the lift coefficient) and base equations (e.g., the original Shields curve [35] was used in the van Rijn model) were defined as they are published and recommended in the original papers [8,33].
In addition to the bed load transport estimation, the suspended sediment transport was calculated in each computational grid according to the suspended vR formula [36]. Thus, the bed load was calculated according to Equations (1) and (2), while the suspended load was estimated by the van Rijn equation.

3.2. Applied 3D Flow Model

The numerical model used in this study [37,38] solved the 3D Reynolds-averaged Navier–Stokes (RANS) equations with the k-ε turbulence closure (see e.g., [39]) by using a finite-volume method and the (semi-implicit method for pressure linked equations) SIMPLE algorithm [40,41] on a 3D non-orthogonal grid. At the boundaries, where the fluid flow cannot be considered as a free turbulence zone, the wall law was applied for the velocity profile calculation [42]. The momentum equations were in the complete form, describing the hydrodynamic effects in all directions. The roughening impact of the vegetation in the flood plain area was described as an energy loss term in the Navier–Stokes equations [43], and could be specified for each cell. Using this option, the effect of the vegetation was taken into account as a drag-effect.
In order to eliminate the boundary effect, the computational grid was longer in both upstream (rkm 1801) and downstream (rkm 1793.5) direction than the investigated ~ rkm 1795 and rkm 1799 river reach. The applied grid can be seen in Figure 2.
The study side was discretized with 355 cells in the streamwise direction and 150 cells in the lateral direction, respectively, resulting in the streamwise direction in an average resolution of 18 m and transversely 5 m in the main channel, while 13 m in the floodplain area. Vertically 11 layers were defined, at every ten percent of the depth, resulting in a maximum of 585,750 computational cells. The resolution of the grid was set based on previous 3D model studies [37,44,45,46,47,48] and Section 3.2.2 demonstrates its applicability.
The bed material was discretized by five fractions, which were: d 1 = 0.3125 mm, d 2 = 1.25 mm, d 3 = 5.7 mm, d 4 = 16.2 mm and d 5 = 56.57 mm. The ripraps and groins were characterized by d = 300 mm. According to field measurement based considerations, the active layer thickness was set to 0.5 m.

3.2.1. Parameterization

For instance, Parker mentioned [11] that the bed material of most river reaches is less complex and the grain sizes happen in a narrow range. In turn, in rare cases—e.g., the herein studied river section—the occurring grain sizes cover a significantly wider range (silt–gravel), resulting in a very complex spatial distribution. The bed material cannot be supposed as spatially uniform because of this (as many studies do at most river sections [44,46]), which makes the allocation of the bed material a less obvious method. According to Baranya [49], a relation can be stated between the calculated local bed shear stress value by 3D flow model at the mean-water stage and the local d50. Thus, applying the fitted function, a transitional and continuous d50 map can be estimated based on the calculated bed shear stress distributions. This method was used based on 33 bed material samples [19,26]. The standard deviation of the calculated d50 to the measured d50 was 3.2 mm.
As the boundary conditions for the RANS equations, at the inflow boundaries the water discharge, at the outflow boundary, the water level was set. The discharge time series (Figure 3) and the water levels of the Danube were defined based on the measured time series. Additionally, the flow discharge time series of the Mosoni-Danube was set based on a 1D numerical Danube model [50].
An essential part of the model setup is the correct set of the inflow sediment rate. For this purpose, the flow discharge dependence of the suspended load [51] and the bed load [19] functions were used.
The riverbed topography of the main river channel was available from 2012 and 2014. The initial bed geometry was set according to the map from 2012. The calculated bed change map could be prepared for this two-year-long period, which included the historical flood wave from 2013 (Figure 3). This bed change map was used as a benchmark for the validation purpose (Figure 4).
Four regions in the river reach were highlighted by green rectangles and an ellipse, marked by A, B, C and D. In these places, the following bedforms and morphodynamic processes were detected by field measurements [16,19]. At region A and D, the blue spots refer to a pronounced scouring downstream of the groins. In region B a groin field could be found. Here, local bed changes took place, both scouring processes (blue spots) and sediment depositions (brown spots). The ellipse (C) and the brown spot in region D show the places where gravel bars were located. As these phenomena basically determine the reach-scale morphodynamic processes, a key question is whether the novel sediment transport calculation manner introduced a more reliable estimation of them.
The numerical simulation of the 2 years, 722 days long period demands very large computational capacity. According to the preliminary estimation calculations, the simulation of one model variant for such a long time period would take around half a year. Therefore, to reduce the duration of the simulation, only the periods that exceeded the bed-forming flow discharge (Q > 2100 m3/s) [19,24] were simulated. It meant that the inflow boundary condition was set to a continuous flow discharge series, including the highlighted periods in Figure 3a–h, respectively and omitting the intermediate periods. In this range, 66% of the annual bed load amount passed [23]. In turn, it is emphasized that the ignored 34% of the annual bed load yield was still significant. That is, the numerical model neglects the simulation of bed changes that take place during the lower water regime. However, many studies (including papers regarding the investigated river reach) display that the major bed changes such as scouring, bar formations and flushing of the groin fields are expected rather during floods [16,19,24,52]. That is, the mean and lower water stages are less important in the view of bed changes. Based on the above, the bed changes caused by the eight flood waves (Figure 3a–h, a total of 211 days) approach well the real two years changes. Hence, the calculated bed changes were comparable to the measured.

3.2.2. 3D Flow Model Validation

The herein applied 3D CFD model was already adapted and validated for the investigated Hungarian reach of River Danube, which was published in previous research works, e.g., [45,46,53,54]. Those studies have already demonstrated the reliable application of the 3D flow model. Regardless of these, the flow model validation was elaborated for the peak of the historical flood wave in 2013. The cross-sectional acoustic Doppler current profiler (ADCP) flow measurements by the North-Transdanubian Water Directorate regarding the peak stage of the flood wave were used as benchmark flow values. Figure 5 shows the measured (left) and the calculated (right) cross-sectional velocity distributions, from exactly the same points. However, as the ADCP instrument is not able to measure at the direct water - and bed surfaces, the measured cross-sections are smaller slices, respectively. Furthermore, regarding the comparison it is important to mention that the moving boat ADCP measurements record the momentary flow conditions, which include the effect of turbulence, resulting in velocity pulsation in 0.1 m/s order of magnitude [25,53,55]. In turn, the RANS model calculates the time-averaged velocity values.
Comparing the measured and calculated cross-sections, the following remarks can be stated. The velocity values were in the same ranges (0–3 m/s). The highest velocities (yellow and red spots) were calculated at the same place as the cross-sections than in the real case, which underlined the reliable estimation of the main stream. The locations of the lower velocities (blue and light green spots) were calculated as trustworthy also. That is the calculated flow pattern could be realized reliable at the groin fields (e.g., at the right-bank sides of cross-section III, IV and V, Figure 5) and gravel bars also (e.g., at the right-bank sides of cross-section VII). Finally, the root-mean-square deviation (RMSD) between the measured and calculated velocities could be calculated for all the seven cross-sections. These values can be seen in Table 1.
Considering the maximum cross-sectional horizontal velocities (Table 1, third row), the RMSD values displayed that the deviation of the flow calculation was below ~12% of the maximum values. The only two sections, where the inaccuracy happens ~15% were cross-sections V and VI. In these cross-sections, the higher deviation suggested that the numerical model estimated a narrower main stream as the measurements display. Around these cross-sections, the varying geometry increasec the transverse flow structure. However, a known limitation of the time-averaged RANS modeling was just this phenomenon, which is the underestimation of the secondary flow strength [56,57,58]. Next to this section, the flow model could be considered as validated for higher flood waves too, taking into account the available measurement data. For a more comprehensive validation, fixed boat ADCP measurements would have been expedient, which could be used to obtain time-averaged velocity values and also to estimate local bed shear stresses. The model validation for the 100-year flood wave should be evaluated in this light.

4. Results

4.1. Comparison of the Calculation Methods

In order to confirm the better operation of the novel Re* dependent combined method, the bed change calculation by the van Rijn, Wilcock and Crowe and the combined method were compared.
The simulations were performed only for the d and e flood waves because of the significant computational time (see Figure 3d,e). The initial model setup (the flow field, water levels and the bed material) was given for each run from the results of the model runs for the first three flood waves by the Re* dependent combined method. The flood wave d was a relatively low (peak is around 3460 m3/s), but durable (~2 months long) flood wave, while the e was the historical one with a peak higher than 10,000 m3/s. Thus, the comparative analysis presented the operational characteristics of the sediment transport models for both the durable lower and also for the extreme water regimes. As a benchmark, the measured bed change map indicated the extent of the possible bed changes. However, the measured and calculated maps could not be compared directly, because the measured belonged to the whole two-year-long period (Figure 3).
The calculated bed change maps for the flood wave d (Figure 3) are presented in Figure 6, Figure 7 and Figure 8.
As the results show, the vR model estimated unrealistic changes both spatially and in magnitude. The unrealistically huge bed changes suggest that the vR model did not seem to be an appropriate model for the given Danube reach, particularly not for bed change calculation in the main channel.
The W&C sediment transport model estimated a more stable bed surface than the vR (Figure 7). In this particular case, the bed surface seemed so resistant that the mean flow field was too weak to cause any significant bed changes. The motion of the very fine, basically suspended inlet load was calculated by the W&C model as bed load. Therefore, that part of the inlet sediments settled progressively along the channel. However, because of the quite low suspended load [51], the bed level rise caused by sedimentation was negligible (<0.005 m).
Figure 8 shows the bed changes calculated by the combined method. The red lines illustrate the borderline which separated the areas where the vR or the W&C model was activated in the initial moment of the model run. Accordingly, it can be seen that the vR formula was invoked at the near-bank areas, at the groin fields and also at a smaller part of the Vének lower gravel bar. At these regions, more significant (~0.05 m) sedimentation was estimated. That is, at these less hydraulically rough parts of the river bed, the deposition of both the finer bed load and suspended load were expected, which areas can be detected by the Re* [22]. In turn, in the navigation channel, no considerable bed change happened. According to the suspended form of the vR formula, the finer suspended load passes over the calculation domain, while the bed surface remains still, calculated by the W&C formula. This assumption is consistent with the conclusions of the field measurements [19]; the main channel seems to be armored enough to be resistant at the mean water regime.
The other flood wave, for which the comparative analysis of the three calculation methods (vR: Figure 9, W&C: Figure 10 and combined: Figure 11) was established was the historical flood wave from 2013 (Figure 3). Regarding this hydrological case, the vR model estimated also an unrealistic bed change map (Figure 9.). This was mainly true for the main channel. There, the motion of the coarser grains was probably overestimated, resulting in huge erosions and depositions. In turn, at the near-bank regions, at gravel bars and at the groin fields, the changes seemed to be partly in the expectable order of magnitude. However, it is clearly visible that the vR formula is not an appropriate choice for the morphological change calculation of such a complex river reach.
The W&C model calculated more realistic bed changes (Figure 10), especially in the main channel. However, the measurements at the lower gravel bar and also at the whole main channel showed significant (Δz > ±0.2 m) changes. Based on these, the W&C formula likely overestimated the stability of the channel. A remarkable bed level increase can be pointed out, which moderated towards the downstream direction. These bed level changes could be explained by the settling of the inlet finer load, which could not be taken into account as suspended load. The publication of Török et al. [59] pointed out that in the case of mixed bed content, the Shields diagram predicts lower critical bed shear stress for the bed load of the finer, sand particles, than the reference shear stress of the W&C model. Accordingly, the W&C model estimates respectively higher stability for the sand particles, than the Shields diagram and thus the vR model. This leads to such kind of deposition pattern in the main stream which is unrealistic compared to the measured bed changes map [19].
The combined method predicts (Figure 11) more significant bed changes, compared to the one resulted by the W&C model. The red borderline suggested that as at the flood wave d, the combined method calculated the sediment transport by the vR formula in the near-bank regions. During the flood wave e, the remarkable erosion at the groin field B meant that the groin field got flushed and the earlier deposited finer sands got eroded. Also, notable changes took place at the vicinity of the gravel bar at region D. Here, the widening of the downstream sides of the gravel bar can be seen, in accordance with the measured bed change map in Figure 4. Around the groin pair at the left bank, on the opposite side of the gravel bar, the blue spots refer to erosion. This process was probably the result of a similar, flushing process like the one which happened at the upstream groin field. In turn, in the main and navigation channel, no considerable bed change happened. According to the suspended form of the vR formula, the finer suspended load passed over the calculation domain, while the bed surface remained still, calculated by the W&C formula. The conclusions of the field measurements [19] referred also to the resistant main channel.
The results indicate that the interactions between the sediment transport at different channel sections (groin fields, gravel bars and main channel) could not be estimated by the vR or W&C formulas. However, the expedient combination of them gives an opportunity to deal with the interaction-mechanism between the local- and reach-scale processes.
Analyzing the calculated bed changes in the marked boxes, the following assumptions can be stated. In this part, the results of the vR model were skipped because of the unrealistic bed change calculations. At region A, the real bed level deepening (Figure 4) could not be reproduced by any method. In region B, only the combining method was able to predict significant depositions and erosions. Accordingly, the depositions probably took place during the lower water regime, while the bed level incision occurred during the flood waves. Thus, the measured bed level changes during the two years were formed most likely indeed during the whole two-year-long period. In region C, all two model results suggested that the gravel bar was in a stable state. Besides region A, the bed level increase in the main channel between region C and D (Figure 4) could not be pointed out by any sediment transport formula. Finally, in region D the model results showed that the widening of the gravel bar and also the erosion at the vicinity of the groin pair occurred rather during the higher flood wave than during the slighter flood waves, or mean water regime.

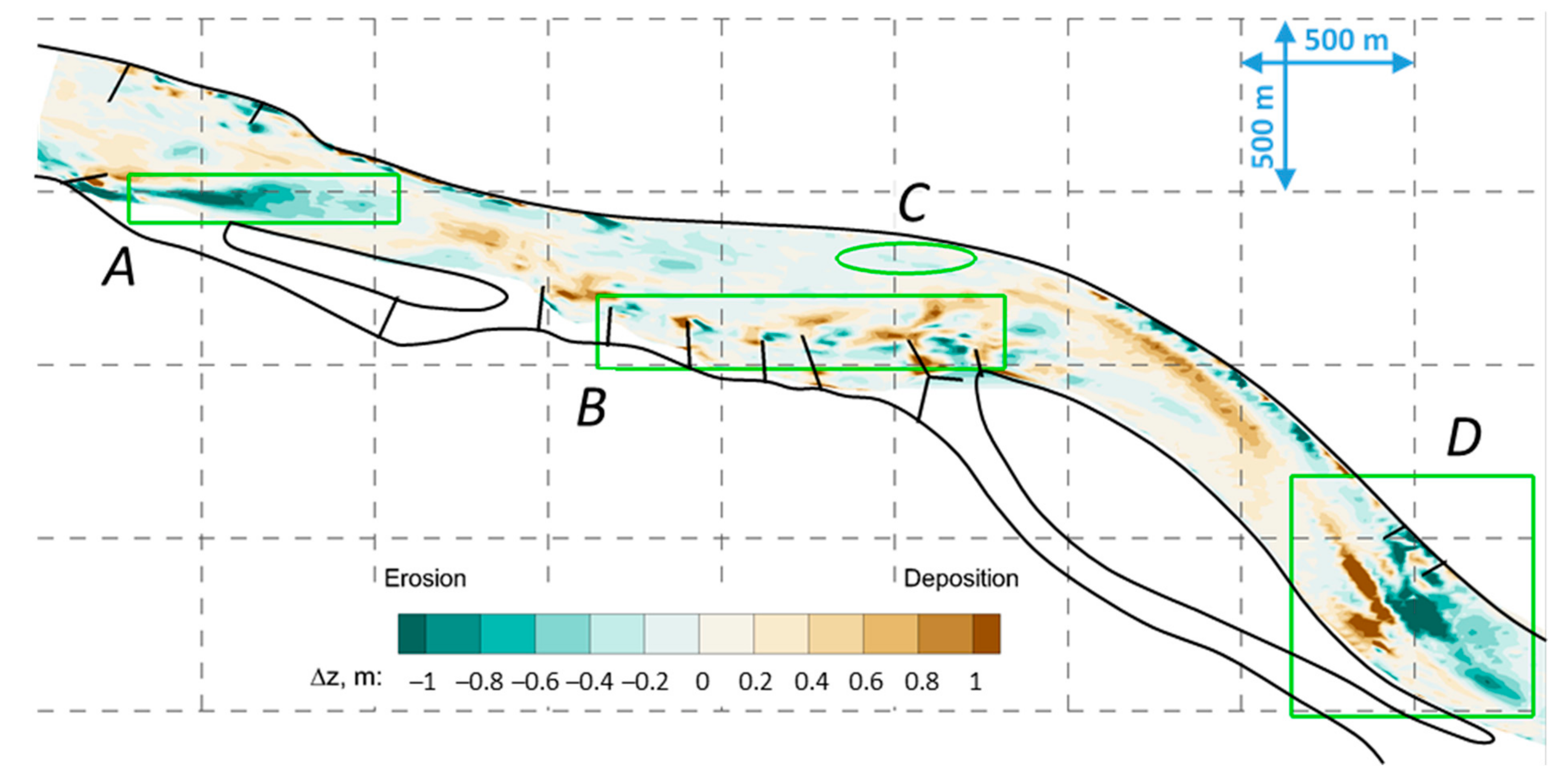
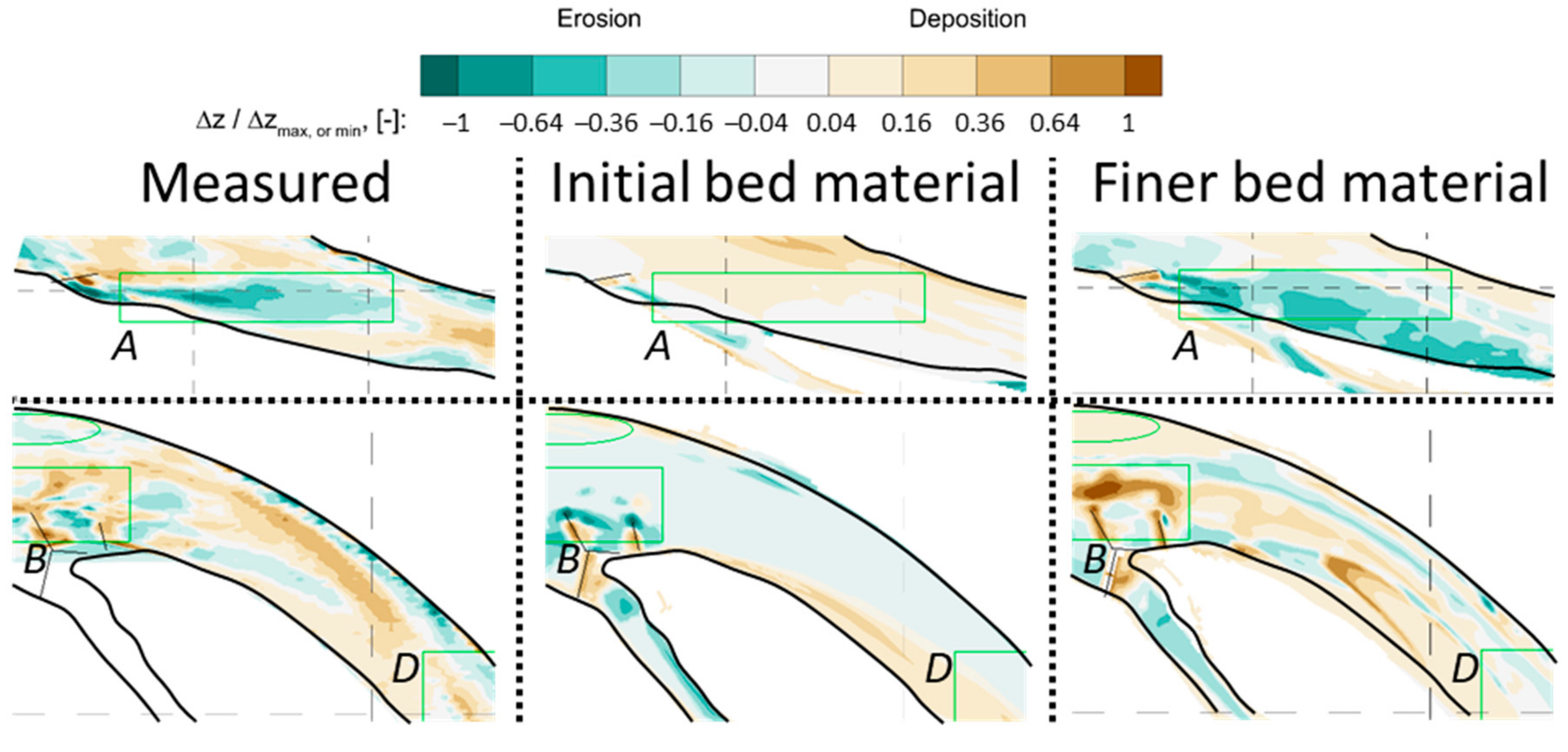
4.2. Measured Data-Based Verification of the Combined Method

A quantitative assessment of the tested sediment transport formulas was performed based on the results of the comparative analysis. First, in accordance with the conclusions of the field measurement based investigation, it was assumed that the measured erosion and deposition took place mainly during higher water regimes in region D, when the flow discharge was higher than the bed forming discharge [19,23]. Thus, the measured and calculated data could be considered as indirectly comparable in this region. Therefore, from the measured bed level change maps, the total volume of the erosion and deposition could be calculated. Furthermore, counting the number of days of the higher water levels, the average daily rate of the volume of both the erosion and deposition could be estimated. Likewise, based on the calculated bed change maps and knowing the duration of the historical flood wave, the daily average volume changes of the deposition and erosion could be estimated.
Table 2 shows data about these volumes. The table presents the ratio of the calculated volume to the measured, regarding the deposition and erosion separately, for each sediment transport formula. A value of 1 would indicate a perfect match to the measured volume change. Table 2 shows that the vR model was the one which overestimates most both the deposition and erosion volumes. The W&C model calculated the deposition rate more accurately, but still indicated more than the measured. This was partly explained by the lack of the suspended sediment calculation. In turn, the W&C model estimated negligible low erosion. In total, the more reliable results were provided by the combined method. With this, the erosions at the near-bank parts were calculated more accurately by the vR model, resulting in sediment feed for region D. Thus, because of the capturing of the coming sediments, the widening of the deposition could be better represented. As the Re* dependent criterion activated the vR formula at the groin pair, the bed level incision at its vicinity was also estimated better.
Even though the measured and calculated bed changes could not be compared directly, the nature, the magnitudes and the locations of the remarkable bed changes suggested the greater aptitude of the combined method.
As it was discussed in Section 3.2.1, the calculated bed changes were elaborated only for the higher flow discharges (>2100 m3/s, Figure 3), so the results could not be compared with the measured changes directly. Therefore, to achieve a notionally common scale, the bed change values were normalized. That is both the measured and calculated bed changes got divided by the highest bed level decrease or increase the value of the main channel:
Δ z n o r m = i f   Δ z > 0 →   Δ z Δ z m a x e l s e →   Δ z Δ z m i n .
Thus, the occurring values develop between −1 and 1, where 1 indicates the maximum deposition height along the river reach, while −1 belongs to the biggest erosion ( Δ z m a x ,   m e a s = 1.5   m , Δ z m i n ,   m e a s = 1.8   m ; Δ z m a x ,   c a l c = 0.5   m , Δ z m i n ,   m e a s = 0.25   m ). The measured bed changes of both the erosions and depositions were consequently higher than the calculated. That is, the numerical model underestimated the magnitudes of the bed changes. This could be partly explained by the ignoring of the third part of the annual bed load in the numerical model estimation.
By the comparison of the measured (Figure 12) and calculated normalized bed changes (Figure 13) the following remarks can be stated. The modeled bed changes did not represent the remarkable erosion at region A. It is noted that this difference also meant a sediment supply loss for the downstream in the model calculation. Since the model did not manifest any bed level decrease, the bed material was probably finer here than it was set in the model. At region B, the measured scours appeared in the calculated results (blue spots). However, not as concentric scours, but rather as lengthwise formations. The numerical model represented depositions close to the measured magnitude at region B also. However, their location iwa not accurate; the brown spots occur between the groins, instead of in the front of the groins, like in Figure 12.
At the gravel bar in region C, negligible bed changes were measured. Likewise, the numerical model predicted a stable bed surface. Finally, the combined method pointed out the growing of the lower part of the Vének lower gravel bar (region D, Figure 13). The measured bed changes indicated two, separable depositions. These double depositions were also represented by the model results. Like the measured changes, the model also calculated scouring in front of the left bank groin pair. However, the extension of it was considerably lower than the scale of the measured deepening. In turn, the lengthwise deposition between the groins (between regions C and D) was also indicated in both measured and calculated maps. However, the calculated deposition occurred in a significantly lower range and formed at the right bank side and not in the main stream. Also, an important match was that neither the measured nor the calculated values suggested any essential large-scale bed changes in the main channel.
A significant difference between the measured and calculated bed changes happened in region A. Here, the effect of the potential error in the initial bed material was further examined. An investigation was performed, which was based on the assumption that the initial bed material was set inaccurately around region A. The bed material samples around d50 ≈ 0.01 m. Considering the grain-size distributions [19], a still realistic, but considerably finer bed material was presupposed. Therefore, the model was set up by 30% lower d50, which was d50 ≈ 0.007 m. With this only one difference, the model was run for the historical flood wave. Figure 14 presents the bed changes at region A, and at the downstream of it.
The right side of Figure 14 shows the bed changes in the case of finer bed material. It can be seen that the 30% decrease of the d50 resulted in major erosion at region A. Considering the measured changes in the left figure it is obvious that the decreasing of the d50 led to a better match to the real bed changes. The lower row of Figure 14 represents the bed changes at the downstream. Here, important deposition formations could be measured (left Figure 14) in front of the right bank groin pair (region B) and also in the main stream, between the two gravel bars (between region B and D). These changes could not be represented by the original model setup (middle Figure 14). In turn, in the case of finer bed material (right Figure 14), the model predicted important depositions in these regions. The extension of the deposition in front of the groin pair (region B) was very similar to the measured. Also, the lengthwise extension of the deposition downstream (between regions B and D), in the main stream were also reproduced. However, the location of it was not correct. It seems that the model underestimated the crosswise sediment transport, which is a known limitation of the Reynolds averaged description of the flow field [56,57,58,60]. Concluding, the herein presented investigation suggested that the bed material at region A was finer than the predicted d50 allocation for the original model setup. With this assumption, the deposition nature at the downstream has become also detectable.

5. Discussion

There are existing proven models in the literature that work reliably for given morphodynamic cases (e.g., the van Rijn model for hydraulic smooth regimes, which mainly occurs in clear sand bed; or the Wilcock and Crowe model for hydraulic rougher regimes, which develops in coarser bed surfaces). However, there are river reaches, within which hydraulic smoother and rougher zones can form, resulting in a completely different type of sediment transport, such as bed armoring and silt aggradation parallelly. For such cases, Török et al. developed a novel sediment transport calculation method and validated it against laboratory measurements.
In this study, its validation against field measurements was introduced. The results showed that the combined application of the Wilcock and Crowe and the van Rijn models could significantly increase the precision of numerical bed change calculations. The results showed that the combined method calculated both erosion and deposition the most reliably. It estimated the volume of the scouring by order of magnitude more precisely than the other two models. Additionally, the results also evinced that the location, extension and shape of the bed formations (e.g., scours, deposition, bar evolvement) could be calculated more reliably by the novel combined approach. These results were consistent with the laboratory measurements based on validation of the calculation method.
The sediment transport interaction between the sand and gravel dominated parts of a river reach played an essential role in the bed changes. For instance, the flushing of the silt dominated groin fields can feed the downstream gravel bars, leading to the growth of the bars. The application of the combined approach really makes sense, within river reaches, where such well-separated morphodynamic situations prevail (e.g., sand aggradation in groin fields; bed armoring in the main stream). In such cases, the local-scale morphodynamic processes are calculated by the proven models, while the interaction between them leads to a more accurate reach-scale calculation. The comparison of the numerical simulations to the measured data presented that such reach-scale interactions can be taken into account by the novel combining method.

6. Conclusions

The validation against both laboratory and field measurements suggests that not necessarily the development of completely new models can lead to the evolution of the sediment transport calculation. This study highlights that the optimally combined use of sediment transport models can be a promising alternative in the sediment transport calculation. In this context, it is important to state that regardless of whether a sediment transport model is applied in combination or simply, the determination of its applicability limits by any morphodynamic variables in a well-defined way is vital. In this study, a shear Reynolds number based description was applied which allowed for the authors an easily described combination criteria. However, the essence of the combining theory does not insist on any variable for the applicability limit description. However, the herein presented example highlights the need for such a kind of description method and also the potential of the parallel use of any sediment transport models.

Author Contributions

Conceptualization, methodology, software, validation, writing—original draft preparation, visualization, G.T.T., resources, data curation, G.T.T. and S.B.; formal analysis, writing—review and editing, S.B.; supervision, project administration, funding acquisition, S.B. and J.J.

Funding

This research received no external funding.

Acknowledgments

This research was supported by MTA TKI (Office for Research Groupsof the Hungarian Academy of Sciences). Support of grant BME FIKP-VÍZ by EMMI (Ministry of Human Capacities) is also kindly acknowledged. The authors acknowledge the funding of the OTKA (Hungarian Scientific Research Fund) FK 128429 grant. The research was partly supported by the ÚNKP-19-4 New National Excellence Program of the Ministry for Innovation and Technology. The last author acknowledges the funding from the János Bolyai fellowship of the Hungarian Academy of Sciences.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Appendix A.1. Wilcock and Crowe Bed Load Transport Formula

The well-known surface-based bed load formula of W&C [8] was developed for mixed gravel/sand sediments. The gravel ranged in size from 2.0 to 64 mm, the sand from 0.5 to 2.0 mm. They conducted laboratory experiments in a tilting laboratory flume, in which both the water and the sediments were recirculated. Five different sediment mixtures were investigated, varying the sand content of the sediment mixtures from 6.2% up to 34.3% [60]. The mixture grain-size distribution used in the experiments of Török et al. [34] and of Wilcock et al. [60] shows a good match. In case of the experiments of Wilcock et al. [60], dm grain size of the initial bed materials was in the range of 4.1–10.5 mm, whereas dm was 8.7 mm the measurements of Török et al. [34]. The W&C formula is therefore expected to be capable of describing the gravel/sand bed load transport processes in our experiments. In the case of such non-uniform bed material, the interaction between (hiding and exposure) the particles of different sizes plays an essential role in the stability of the sediments and can result in bed armoring. The W&C formula is reported to be capable of predicting the transient conditions of bed armoring or scouring processes. The preliminary numerical simulations of Török et al. [46] also supported this statement.
The transport formula uses the collapse similarity hypothesis, which estimates the fractional sediment transport rate (wi*) as the function of the ratio of the shear stress (τ) and the reference shear stress (τri). The reference shear stress τri is the value of τ at which wi* is equal to a small but already perceptible value wi* = 0.002. That is the reference shear stress has a similar physical meaning to the critical shear stress (τc), which indicates the initiation of motion of particles. The dimensionless transport rate is obtained according to the following equation:
W i * = 0.002 θ 7.5 i f   θ < 1.35 14 1 − 0.894 θ 0.5 4.5 i f   θ ≥ 1.35 ,
where
θ = τ / τ r i .
The volumetric transport rate per unit width qbi can be expressed from the following formula:
W i * = s − 1 g q b i F i u * 3 ,
where Fs is the proportion of sand in surface size distribution.
For the estimating of τri, the W&C model suggests that the stability of the sediment particles depends on the sand content. Thus τri can be calculated by the following steps:
τ r m * = 0.021 + 0.015 e − 20 F S ,
where τ*rm is the dimensionless reference shear stress for the mean size of the bed surface. The reference shear stress for the mean size can be obtained from the particle Froude number equation:
τ r m * = τ r m g ρ S − ρ W d .
Then, the last step is the estimation of the reference shear stress for the particle sizes separately:
τ r i τ r m = D i D s m b ,
where
b = 0.67 1 + e 1.5 − D i D s m .

Appendix A.2. Van Rijn Bed Load Transport Formula

The development of the vR formula is based on laboratory and field measurements. Van Rijn presented a mathematical method for the computation of bed load transport rate. The formula is basically the numerical solution of the equations of motions for a solitary particle. The mathematical model was calibrated based only on the experiments of Fernandez Luque [61,62], where the motions of uniform particles (d = 0.18 mm) under steady flow (u* = 0.04 m/s) were monitored.
The lifting term of the equation of motion for a particle is derived as [63]:
F L s h e a r = α L ρ ν 0.5 D 2 v r ∂ u ∂ z 0.5 ,
where FL is the lift force, αL is the lift coefficient, ν is the kinematic viscosity coefficient, ρ is the density of the fluid, vr is the relative particle velocity and ∂ u / ∂ z is the velocity gradient. The mathematical method uses the turbulent wall law Equation (A9) for calculation of the vertical flow velocity distribution:
U z = u * κ l n z z 0 ,
where U(z) is the horizontal velocity as the function of the z, z is the level above the bed, u* is the bed shear velocity, κ is constant von Karman (κ = 0.41), and z0 is the zero-velocity level above the bed.
The volumetric bed load transport rate is defined as:
q b s − 1 g 0.5 D 50 1.5 = 0.053 T 2.1 D * 0.3 ,
where qb is the bed load transport per unit width, D50 is the particle size, s is the specific density, g is the acceleration of gravity, T is the transport stage parameter, can be represented as:
T = u * ′ 2 − u * , c r 2 u * , c r 2 ,
where u*,cr is the critical bed shear velocity according to Shields [35], u * ′ = g 0.5 / C ′ u ¯ is the bed shear velocity related to grains, where C´ is the Chézy-coefficient related to grains and u ¯ is the mean flow velocity.
In the Equation (A10), D* is the particle parameter defined as:
D * = D 50 s − 1 g ν 2 1 / 3
Finally, the vR formula was verified based on 56 field measurements and 524 flume data. The bed load formula is recommended to use for particles in the range of 200–2000 μm (i.e., below 2 mm). As such the formula is not expected to reliably calculate the motion of gravels and the interaction between particles of different sizes and to describe such a process, like bed armoring. However, the model can presumably describe the transport of finer grains.

References

  1. Meyer-Peter, E.; Müller, R. Formulas for Bed-Load Transport. In Proceedings of the IAHSR 2nd Meeting, Stockholm, Sweden, 7–9 June 1948. [Google Scholar]
  2. Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; United States Department of Agriculture, Economic Research Service: Washington, DC, USA, 1950. [Google Scholar]
  3. Egiazaroff, I.V. Calculation of Nonuniform Sediment Concentrations. J. Hydraul. Div. 1965, 91, 225–247. [Google Scholar]
  4. Ashida, K.; Michiue, M. Study on hydraulic resistance and bedload transport rate in alluvial streams. Trans. Jpn. Soc. Civ. Eng. 1972, 206, 59–69. [Google Scholar] [CrossRef]
  5. Parker, G.; Klingeman, P.; McLean, D. Bedload and size distribution in natural paved gravel bed streams. J. Hydraul. Eng. 1982, 108, 544–571. [Google Scholar]
  6. Parker, G. Surface-based bedload transport relation for gravel rivers. J. Hydraul. Res. 1990, 28, 417–436. [Google Scholar] [CrossRef]
  7. Wilcock, P.R.; Kenworthy, S.T. A two-fraction model for the transport of sand/gravel mixtures. Water Resour. Res. 2002, 38, 12-1–12-12. [Google Scholar] [CrossRef]
  8. Wilcock, P.R.; Crowe, J.C. Surface-based transport model for mixed-size sediment. J. Hydraul. Eng. ASCE 2003, 129, 120–128. [Google Scholar] [CrossRef]
  9. Wu, W.; Wang, S.S.Y.; Jia, Y. Nonuniform sediment transport in alluvial rivers. J. Hydraul. Res. 2000, 38, 427–434. [Google Scholar] [CrossRef]
  10. Powell, D.M.; Reid, I.; Laronne, J.B. Evolution of bed load grain size distribution with increasing flow strength and the effect of flow duration on the caliber of bed load sediment yield in ephemeral gravel bed rivers. Water Resour. Res. 2001, 37, 1463–1474. [Google Scholar] [CrossRef]
  11. Parker, G. Transport of Gravel and Sediment Mixtures. In Sedimentation Engineering; Garcia, M., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 165–251. ISBN 978-0-7844-0814-8. [Google Scholar]
  12. Török, G.T.; Baranya, S.; Rüther, N. 3D CFD Modeling of Local Scouring, Bed Armoring and Sediment Deposition. Water 2017, 9, 56. [Google Scholar] [CrossRef]
  13. Rákóczi, L.; Sass, J. A Felső-Duna és a Szigetközi mellékágak mederalakulása a dunacsúni duzzasztómű üzembe helyezése után (Changes of the channel of the Hungarian Upper Danube and of the side river arms of the Szigetköz upon putting the Dunacsúny I. river barrage into operati. Vízügyi Közlemények 1995, 77, 46–75. [Google Scholar]
  14. Hankó, Z. Gondolatok a Duna Szap és Szob közötti szakaszának fejlesztéséről (Considerations related to the development of the Danube reach between Szap and Szob). Vízügyi Közlemények 2000, 82, 285–299. [Google Scholar]
  15. Holubová, K.; Capeková, Z.; Szolgay, J. Impact of hydropower schemes at bedload regime and channel morphology of the Danube River. In Proceedings of the River Flow 2004: Second International Conference on Fluvial Hydraulics, Napoli, Italy, 23–25 June 2004; CRC Press: Napoli, Italy, 2004; pp. 135–142. [Google Scholar]
  16. Baranya, S.; Józsa, J.; Török, G.T.; Ficsor, J.; Mohácsiné Simon, G.; Habersack, H.; Haimann, M.; Riegler, A.; Liedermann, M.; Hengl, M. A Duna hordalékvizsgálatai a SEDDON osztrák-magyar együttműködési projekt keretében (Introduction of the joint Austro-Hungarian sediment research under the SEDDON ERFE-project). Hidrológiai Közlöny 2015, 95, 41–46. [Google Scholar]
  17. Hankó, Z.; Starosolszky, Ö.; Bakonyi, P. Megvalósíthatósági tanulmány a Duna környezetének és hajózhatóságának fejlesztésére (Danube Environmental and navigation Project, Feasibility Study). Vízügyi Közlemények 1996, 78, 291–315. [Google Scholar]
  18. Goda, L. A Duna gázlói Pozsony-Mohács között (Shallows of the River Danube between Pozsony, Bratislava and Mohács. Vízügyi Közlemények 1995, 77, 71–102. [Google Scholar]
  19. Török, G.T.; Baranya, S. Morphological Investigation of a Critical Reach of the Upper Hungarian Danube. Period. Polytech. Civ. Eng. 2017, 61, 752–761. [Google Scholar] [CrossRef]
  20. Holubová, K.; Comaj, M.; Lukac, M.; Mravcová, K.; Capeková, Z.; Antalová, M. Final Report in DuRe Flood Project—Danube Floodplain Rehabilitation to Improve Flood Protection and Enhance the Ecological Values of the River in the Stretch between Sap and Szob; Danube Transnational Programme: Bratislava, Slovakia, 2015. [Google Scholar]
  21. Varga-Lehofer, D.T. A Felső-Magyarországi Duna Morfológiai Változásainak Elemzése (Investigation of the Morphological Changes of the Hungarian Upper Danube). Bachelor’s Thesis, Budapest Univerity of Technology and Economics, Budapest, Hungary, 2014. [Google Scholar]
  22. Török, G.T.; Józsa, J.; Baranya, S. A Shear Reynolds Number-Based Classification Method of the Nonuniform Bed Load Transport. Water 2019, 11, 73. [Google Scholar] [CrossRef]
  23. Török, G.T. Methodological Improvement of Morphodynamic Investigation Tools for Rivers with Non-Uniform Bed Material. Ph.D. Thesis, Budapest Univerity of Technology and Economics, Budapest, Hungary, 2018. [Google Scholar]
  24. Liedermann, M.; Gmeiner, P.; Kreisler, A.; Tritthart, M.; Habersack, H. Insights into bedload transport processes of a large regulated gravel-bed river. Earth Surf. Process. Landf. 2018, 43, 514–523. [Google Scholar] [CrossRef]
  25. Baranya, S. Three-Dimensional Analysis of River Hydrodynamics and Morphology. Ph.D. Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2009. [Google Scholar]
  26. Török, G.T.; Baranya, S. A shear Reynolds number based sediment transport classification method for complex river beds. In Proceedings of the 8th International Symphosium on Environmental Hydraulics, Notre Dame, IN, USA, 4–7 June 2018. [Google Scholar]
  27. Rákóczi, L. A Duna Szap-Gönyű Közötti Szakaszának Hajózási Viszonyait Javító Beavatkozások Vizsgálata (Investigation of Interventions for Navigation Improvment at the Danube Channel between Szap and Szob); Technical Report; Budapest University of Technology and Economics: Budapest, Hungary, 2004. [Google Scholar]
  28. Baranya, S.; Goda, L.; Józsa, J.; Rákóczi, L. Complex hydro- and sediment dynamics survey of two critical reaches on the Hungarian part of river Danube. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Bled, Slovenia, 2–4 June 2008; Volume 4. [Google Scholar]
  29. Habersack, H.; Haimann, M.; Baranya, S.; Józsa, J.; Riegler, A.; Sindelar, C.; Liedermann, M.; Ficsor, J.; Simon, G.M.; Hengl, M. Gemeinsame österreichisch-ungarische Sedimentforschung im Rahmen des EFRE-Projektes SEDDON. Österreichische Wasser Und Abfallwirtschaft 2014, 66, 340–347. [Google Scholar] [CrossRef]
  30. Wu, K.; Yeh, K.-C.; Lai, Y.G. A Combined Field and Numerical Modeling Study to Assess the Longitudinal Channel Slope Evolution in a Mixed Alluvial and Soft Bedrock Stream. Water 2019, 11, 735. [Google Scholar] [CrossRef]
  31. Sattar, A.M.A.; Bonakdari, H.; Gharabaghi, B.; Radecki-Pawlik, A. Hydraulic Modeling and Evaluation Equations for the Incipient Motion of Sandbags for Levee Breach Closure Operations. Water 2019, 11, 279. [Google Scholar] [CrossRef]
  32. Bogárdi, J. A Hordalékmozgás Elmélete; Vilmos, I., Ed.; Akadémiai Kiadó: Budapest, Hungary, 1955. [Google Scholar]
  33. Van Rijn, L.C. Sediment Transport, Part I: Bed Load Transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef] [Green Version]
  34. Török, G.T.; Baranya, S.; Rüther, N.; Spiller, S. Laboratory analysis of armor layer development in a local scour around a groin. In Proceedings of the International Conference on Fluvial Hydraulics, RIVER FLOW 2014, Lausanne, Switzerland, 7–10 July 2014; Taylor and Francis Group: Lausanne, Switzerland, 2014; pp. 1455–1462. [Google Scholar]
  35. Shields, A. Application of Similarity Principles and Turbulence Research to Bed-Load Movement. Mitt. Preuss. Versuchsanst. Wasserbau Schiffbau 1936, 26, 47. [Google Scholar]
  36. van Rijn, L.C. Mathematical modelling of morphological processes in the case of suspended sediment transport. Ph.D. Thesis, Civil Engineering and Geoscience, TU Delft, Delft, The Netherlands, 1987. [Google Scholar]
  37. Reidar, B.; Olsen, N. A Three-Dimensional Numerical Model for Simulation of Sediment Movements in Water Intakes with Moving Option; Trondheim, Norway. 2018. Available online: http://folk.ntnu.no/nilsol/ssiim/manual5.pdf (accessed on 30 September 2019).
  38. Olsen, N.R.B. Numerical Modelling and Hydraulics; Online Manuscript. 2012. Available online: http://folk.ntnu.no/nilsol/tvm4155/flures6.pdf (accessed on 30 September 2019).
  39. Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; ISBN 9780521598866. [Google Scholar]
  40. Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Minkowycz, M.J., Sparrow, E.m., Eds.; McGraw-Hill Book Company: New York, NY, USA, 1980; ISBN 0-07-048740-5. [Google Scholar]
  41. Glock, K.; Tritthart, M.; Habersack, H.; Hauer, C. Comparison of Hydrodynamics Simulated by 1D, 2D and 3D Models Focusing on Bed Shear Stresses. Water 2019, 11, 226. [Google Scholar] [CrossRef]
  42. Schlichting, H. Boundary-Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
  43. Fischer-Antze, T.; Stoesser, T.; Bates, P.; Olsen, N.R.B. 3D numerical modelling of open-channel flow with submerged vegetation 3D numerical modelling of open-channel flow with submerged vegetation Modélisation numérique 3D d’un écoulement en canal avec vegetation submergée. J. Hydraul. Res. 2013, 39, 303–310. [Google Scholar] [CrossRef]
  44. Fischer-Antze, T.; Reidar, B.; Olsen, N.; Gutknecht, D. Three-dimensional CFD modeling of morphological bed changes in the Danube River. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
  45. Baranya, S.; Józsa, J. Numerical and laboratory investigation of the hydrodynamic complexity of a river confluence. Period. Polytech. Civ. Eng. 2007, 51, 3–8. [Google Scholar] [CrossRef]
  46. Török, G.T.; Baranya, S.; Rüther, N. Three-dimensional numerical modeling of non-uniform sediment transport and bed armoring process. In Proceedings of the 18th Congress of the Asia & Pacific Division of the International Association for Hydro-Environment Engineering and Research 2012, Jeju, Korea, 19–23 August 2012. [Google Scholar]
  47. Bihs, H.; Olsen, N.R.B. Numerical Modeling of Abutment Scour with the Focus on the Incipient Motion on Sloping Beds. J. Hydraul. Eng. 2011, 137, 1287–1292. [Google Scholar] [CrossRef]
  48. Rüther, N.; Olsen, N.R.B. Modelling free-forming meander evolution in a laboratory channel using three-dimensional computational fluid dynamics. Geomorphology 2007, 89, 308–319. [Google Scholar] [CrossRef]
  49. Baranya, S. River Bed Material Mapping to Support Habitat Assesment in Large Rivers. In Proceedings of the 12th International Symposium on Ecohydraulics, Tokyo, Japan, 19–24 August 2018. [Google Scholar]
  50. Krámer, T.; Szilágyi, J.; Józsa, J. Mértékadó árvízszintek: Országos felülvizsgálat után (High Water Levels in Hungary: after the reconsideration). Mérnök Újság 2015, 1–2, 22–25. [Google Scholar]
  51. Ficsor, J. Lebegtetett Hordalék Vizsgálata a Felsö-Magyarorszaági Duna-Szakaszon (Study of Suspended Sediment Transport on the Upper Hungarian Reach of the Danube River). Master’s Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2016. [Google Scholar]
  52. Luo, P.; Mu, D.; Xue, H.; Ngo-duc, T.; Dang-dinh, K.; Takara, K.; Nover, D.; Schladow, G. Flood inundation assessment for the Hanoi Central Area, Vietnam under historical and extreme rainfall conditions. Sci. Rep. 2018, 8, 12623. [Google Scholar] [CrossRef]
  53. Baranya, S.; Józsa, J. Flow analysis in River Danube by field measurement and 3D CFD turbulence modelling. Period. Polytech. Civ. Eng. 2006, 50, 57–68. [Google Scholar]
  54. Török, G.T. Vegyes szemcseösszetételű folyómedrek numerikus vizsgálata (Numerical investigation of non-uniform river bed). Hidrológiai Tájékoztató 2013, 22–24. Available online: http://www.hidrologia.hu/mht/letoltes/hidrologiai_tajekoztato_2013.pdf (accessed on 30 September 2019).
  55. Guerrero, M.; Lamberti, A. Flow Field and Morphology Mapping Using ADCP and Multibeam Techniques: Flow Field and Morphology Mapping Using ADCP and Multibeam Techniques: Survey in the Po River. J. Hydraul. Eng. 2011, 137, 1576–1587. [Google Scholar] [CrossRef]
  56. Koken, M.; Constantinescu, G. An investigation of the flow and scour mechanisms around isolated spur dikes in a shallow open channel: 1. Conditions corresponding to the initiation of the erosion and deposition process. Water Resour. Res. 2008, 44, 1–19. [Google Scholar] [CrossRef]
  57. Catalano, P.; Wang, M.; Iaccarino, G.; Moin, P. Numerical simulation of the flow around a circular cylinder at high Reynolds numbers. Int. J. Heat Fluid Flow 2003, 24, 463–469. [Google Scholar] [CrossRef]
  58. Roulund, R.; Sumer, B.M.; Fredsøe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
  59. Török, G.T.; Baranya, S.; Rüther, N. Validation of a combined sediment transport modelling approach for the morphodynamic simulation of the upper Hungarian Danube River. In Proceedings of the 19th EGU General Assembly, Vienna, Austria, 8–13 April 2018; Volume 19, p. 15749. [Google Scholar]
  60. Baranya, S.; Olsen, N.R.B.; Stoesser, T.; Sturm, T. Three-dimensional rans modeling of flow around circular piers using nested grids. Eng. Appl. Comput. Fluid Mech. 2012, 6, 648–662. [Google Scholar] [CrossRef]
  61. Wilcock, P.R.; Kenworthy, S.T.; Crowe, J.C. Experimental Study of the Transport of Mixed Sand and Gravel. Water Resour. Res. 2001, 37, 3349–3358. [Google Scholar] [CrossRef]
  62. Fernandez Luque, R. Erosion and Transport of Bed-load Sediment. Bachelor’s Thesis, Delft Technical University, Delft, The Netherland, 1974. [Google Scholar]
  63. Fernandez Luque, R.; van Beek, R. Erosion and Transport of Bed-load Sediment. J. Hydraul. Res. 1976, 14, 127–144. [Google Scholar] [CrossRef]
Water 11 02051 g001 550
Figure 1. The sketch of the investigated Danube study reach (left) and grain size distributions taken from the investigated reach (right). The characteristic water discharges are mean flow Qm = 2000 m3/s, range of bankfull discharge Qbf = 4300–4500 m3/s, 2, 10 and 100-year flood event Q2 = 5950 m3/s, Q10 = 7950 m3/s and Q100 = 10,400 m3/s [23].
Figure 1. The sketch of the investigated Danube study reach (left) and grain size distributions taken from the investigated reach (right). The characteristic water discharges are mean flow Qm = 2000 m3/s, range of bankfull discharge Qbf = 4300–4500 m3/s, 2, 10 and 100-year flood event Q2 = 5950 m3/s, Q10 = 7950 m3/s and Q100 = 10,400 m3/s [23].
Water 11 02051 g001
Water 11 02051 g002 550
Figure 2. The computational grid of the investigated Danube study reach.
Figure 2. The computational grid of the investigated Danube study reach.
Water 11 02051 g002
Water 11 02051 g003 550
Figure 3. Discharge time series at rkm 1801 for the period October 2012–October 2014. The different colored periods marked with letters a–h display the flood waves (including the 100-year historical flood wave from 2013, e) which exceed the bed-forming flow discharge (Q > 2100 m3/s).
Figure 3. Discharge time series at rkm 1801 for the period October 2012–October 2014. The different colored periods marked with letters a–h display the flood waves (including the 100-year historical flood wave from 2013, e) which exceed the bed-forming flow discharge (Q > 2100 m3/s).
Water 11 02051 g003
Water 11 02051 g004 550
Figure 4. Measured bed changes for the period October 2012–October 2014.
Figure 4. Measured bed changes for the period October 2012–October 2014.
Water 11 02051 g004
Water 11 02051 g005 550
Figure 5. Measured and calculated cross-sectional horizontal velocity distributions.
Figure 5. Measured and calculated cross-sectional horizontal velocity distributions.
Water 11 02051 g005
Water 11 02051 g006 550
Figure 6. Calculated bed changes by the van Rijn (vR) formula for a 2.5 month-long period (Figure 3).
Figure 6. Calculated bed changes by the van Rijn (vR) formula for a 2.5 month-long period (Figure 3).
Water 11 02051 g006
Water 11 02051 g007 550
Figure 7. Calculated bed changes by the Wilcock and Crowe (W&C) formula for a 2.5 month-long period (Figure 3).
Figure 7. Calculated bed changes by the Wilcock and Crowe (W&C) formula for a 2.5 month-long period (Figure 3).
Water 11 02051 g007
Water 11 02051 g008 550
Figure 8. Calculated bed changes by the combined method for a 2.5 month-long period (Figure 3).
Figure 8. Calculated bed changes by the combined method for a 2.5 month-long period (Figure 3).
Water 11 02051 g008
Water 11 02051 g009 550
Figure 9. Calculated bed changes by the vR formula for the historical flood wave (Figure 3).
Figure 9. Calculated bed changes by the vR formula for the historical flood wave (Figure 3).
Water 11 02051 g009
Water 11 02051 g010 550
Figure 10. Calculated bed changes by the W&C formula for the historical flood wave (Figure 3).
Figure 10. Calculated bed changes by the W&C formula for the historical flood wave (Figure 3).
Water 11 02051 g010
Water 11 02051 g011 550
Figure 11. Calculated bed changes by the combined method for the historical flood wave (Figure 3).
Figure 11. Calculated bed changes by the combined method for the historical flood wave (Figure 3).
Water 11 02051 g011
Water 11 02051 g012 550
Figure 12. Normalized bed changes of the measured values (Figure 4) regarding the whole period October 2012–October 2014.
Figure 12. Normalized bed changes of the measured values (Figure 4) regarding the whole period October 2012–October 2014.
Water 11 02051 g012
Water 11 02051 g013 550
Figure 13. Normalized bed changes of the calculated values. The calculation was elaborated for the eight flood waves in the period October 2012–October 2014 (Figure 3).
Figure 13. Normalized bed changes of the calculated values. The calculation was elaborated for the eight flood waves in the period October 2012–October 2014 (Figure 3).
Water 11 02051 g013
Water 11 02051 g014 550
Figure 14. Calculated bed changes by the combining method for the historical flood wave. The model in the middle figure was set up with the initial, while in the right figure with finer bed material.
Figure 14. Calculated bed changes by the combining method for the historical flood wave. The model in the middle figure was set up with the initial, while in the right figure with finer bed material.
Water 11 02051 g014
Table
Table 1. The root-mean-square deviation (RMSD) between the measured and calculated velocities, the maximum cross-sectional horizontal velocity and the percentage deviation of them for the seven cross-sections.
Table 1. The root-mean-square deviation (RMSD) between the measured and calculated velocities, the maximum cross-sectional horizontal velocity and the percentage deviation of them for the seven cross-sections.
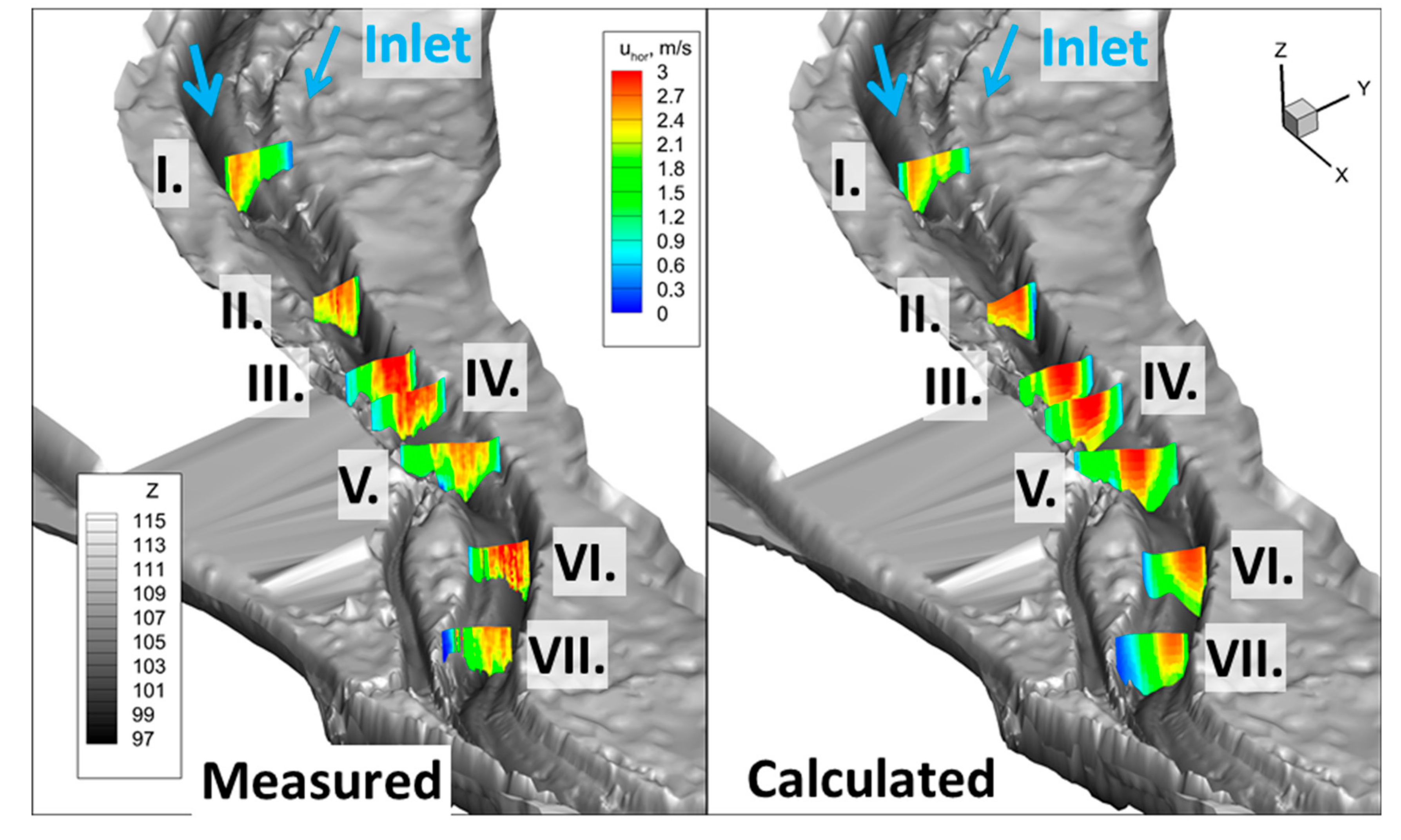
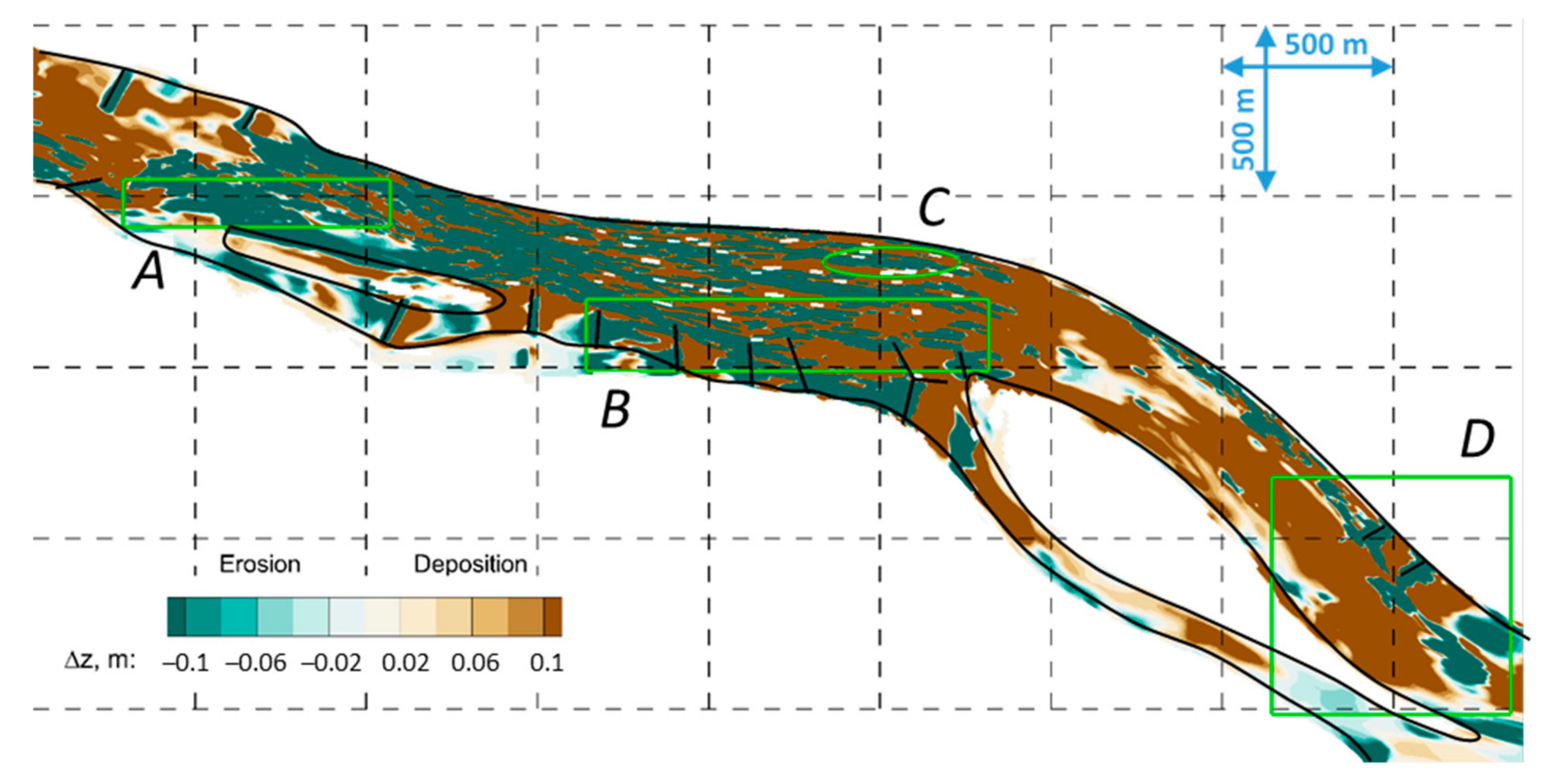
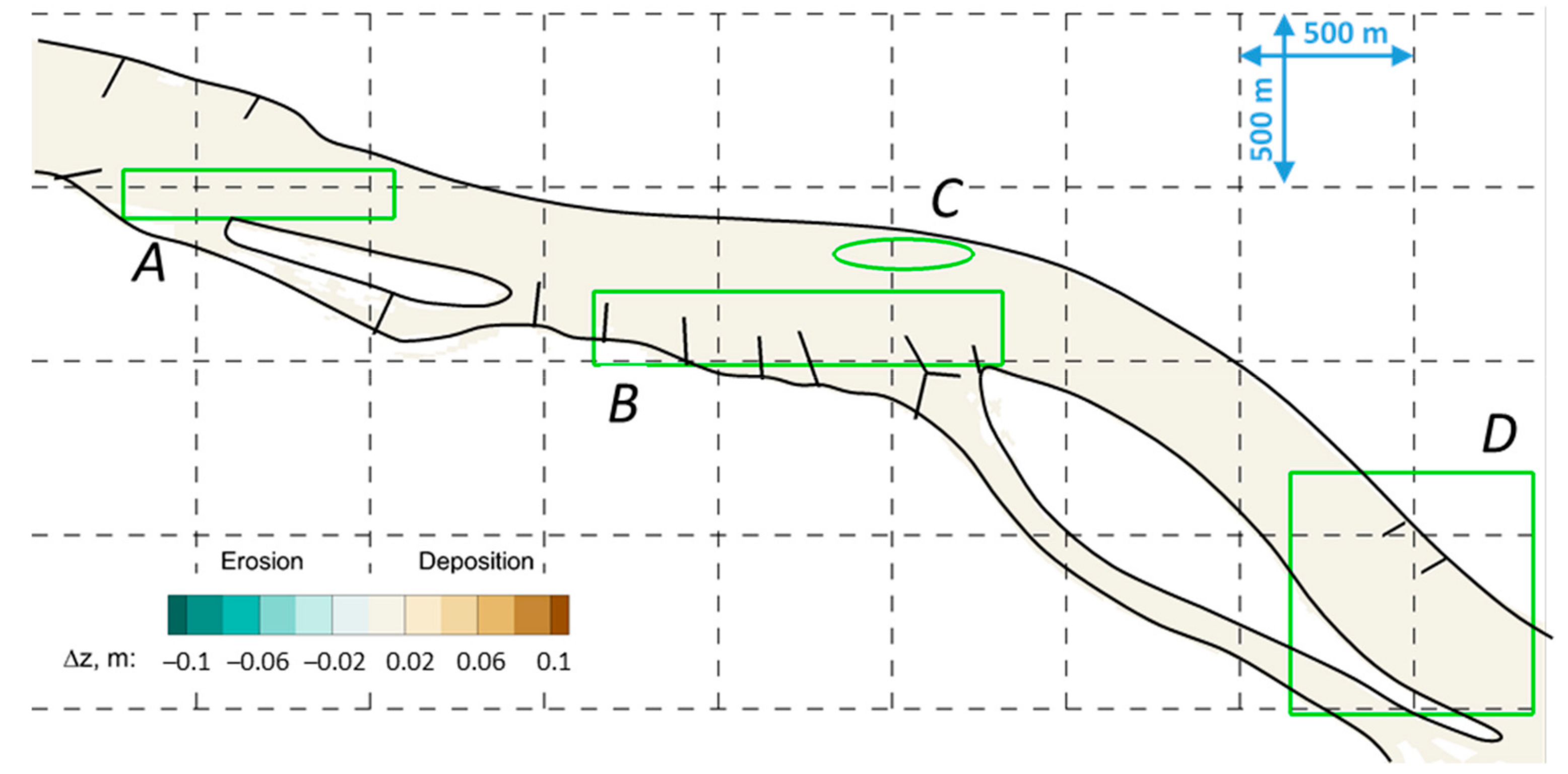
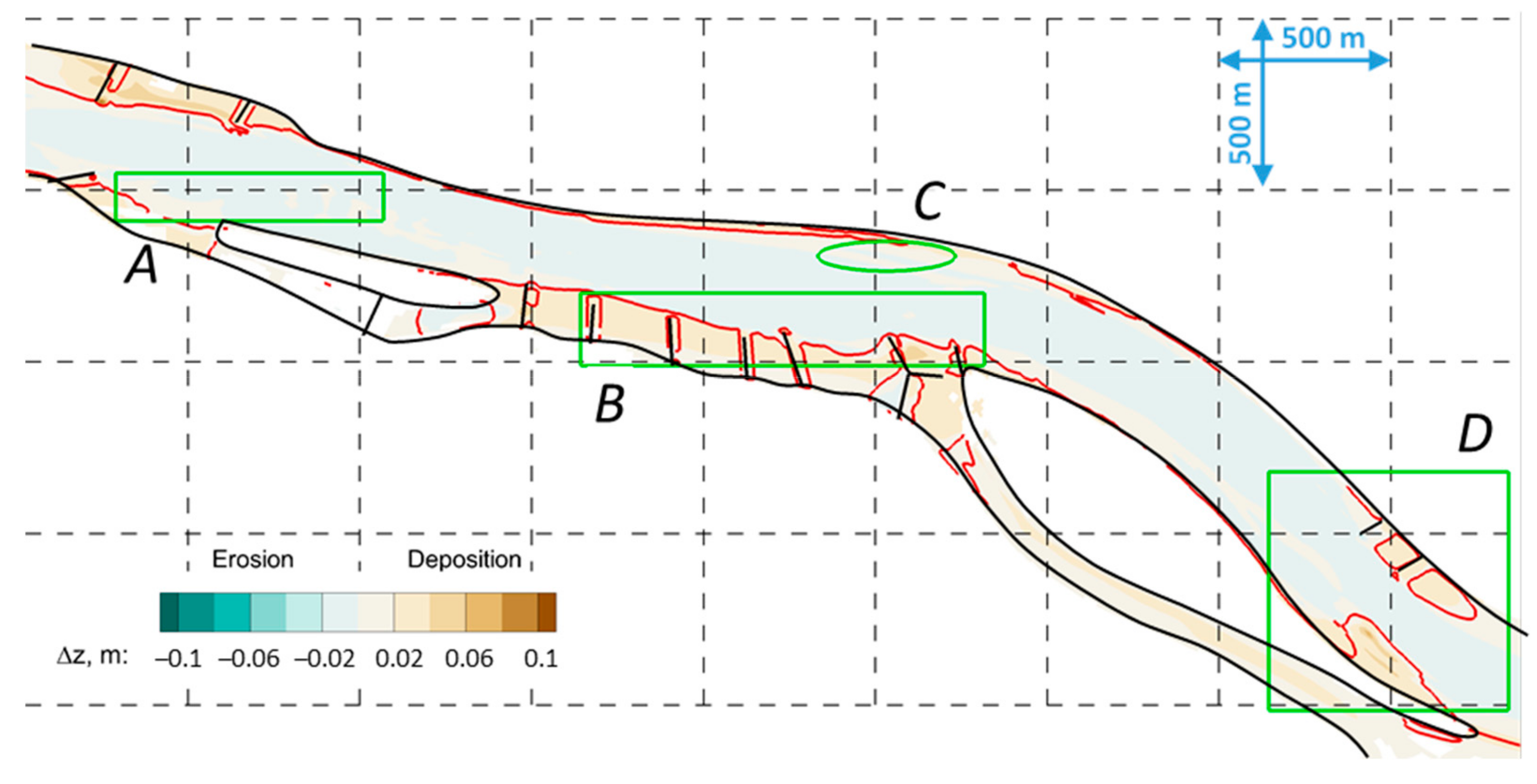
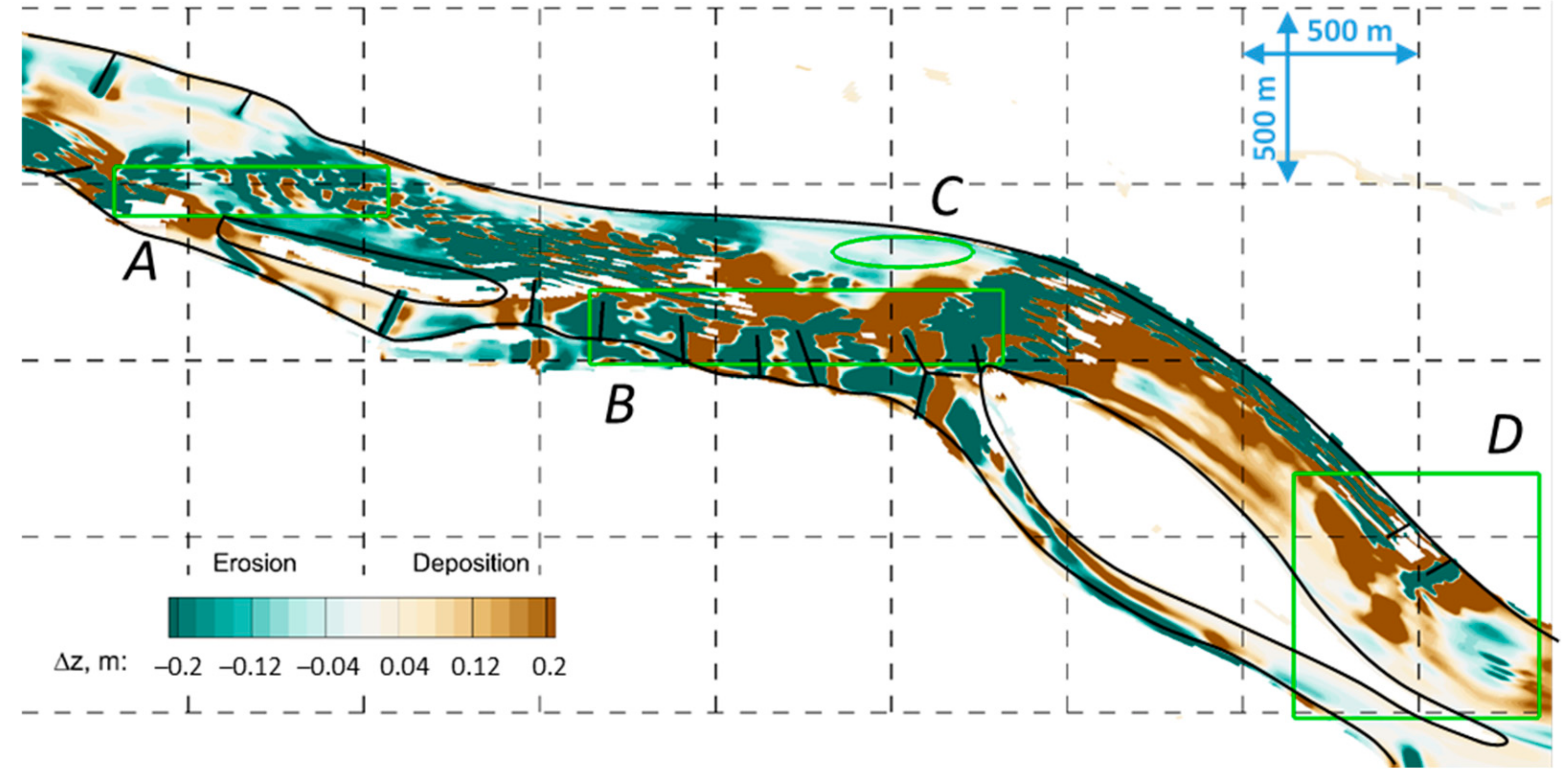
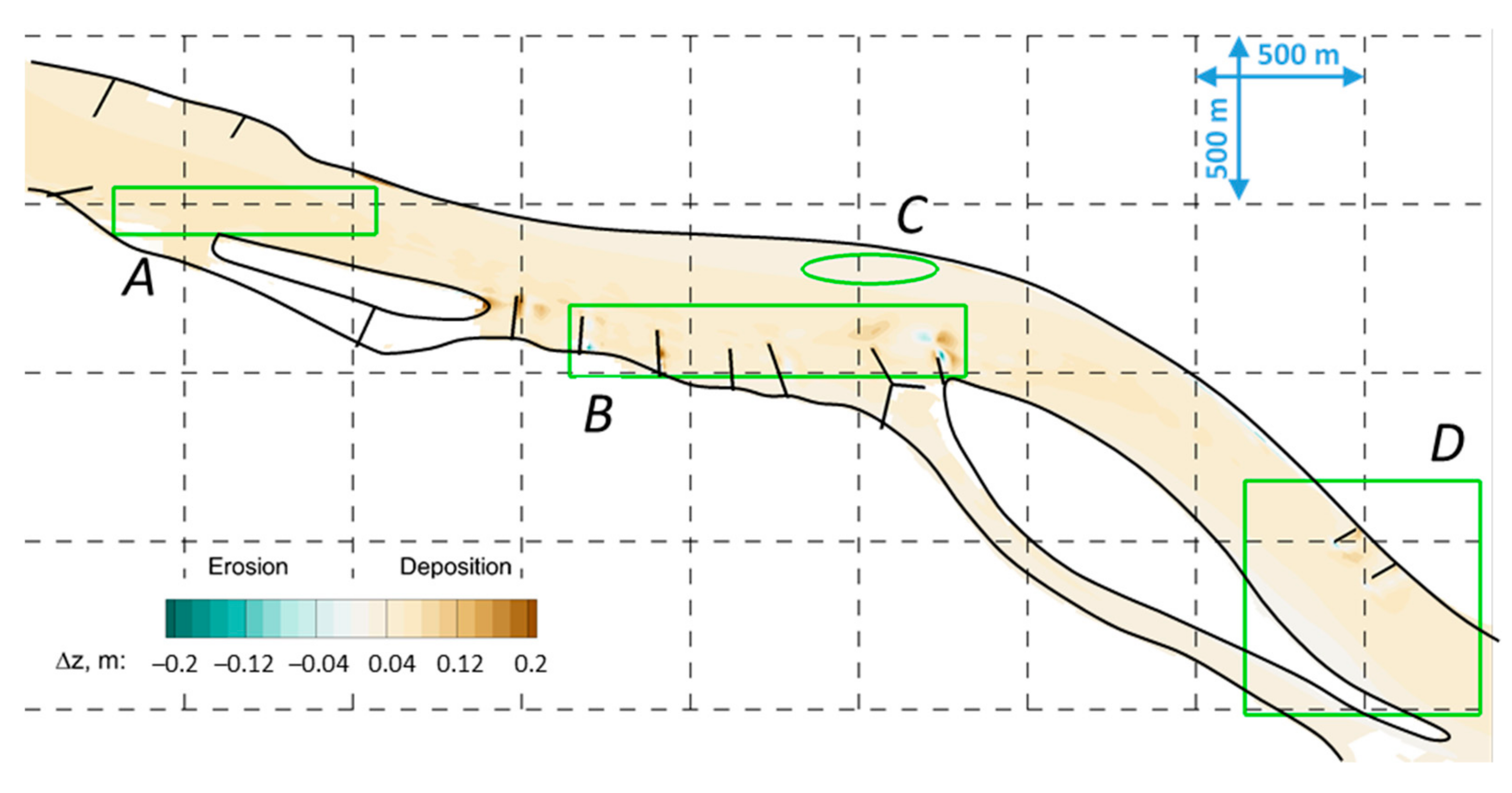
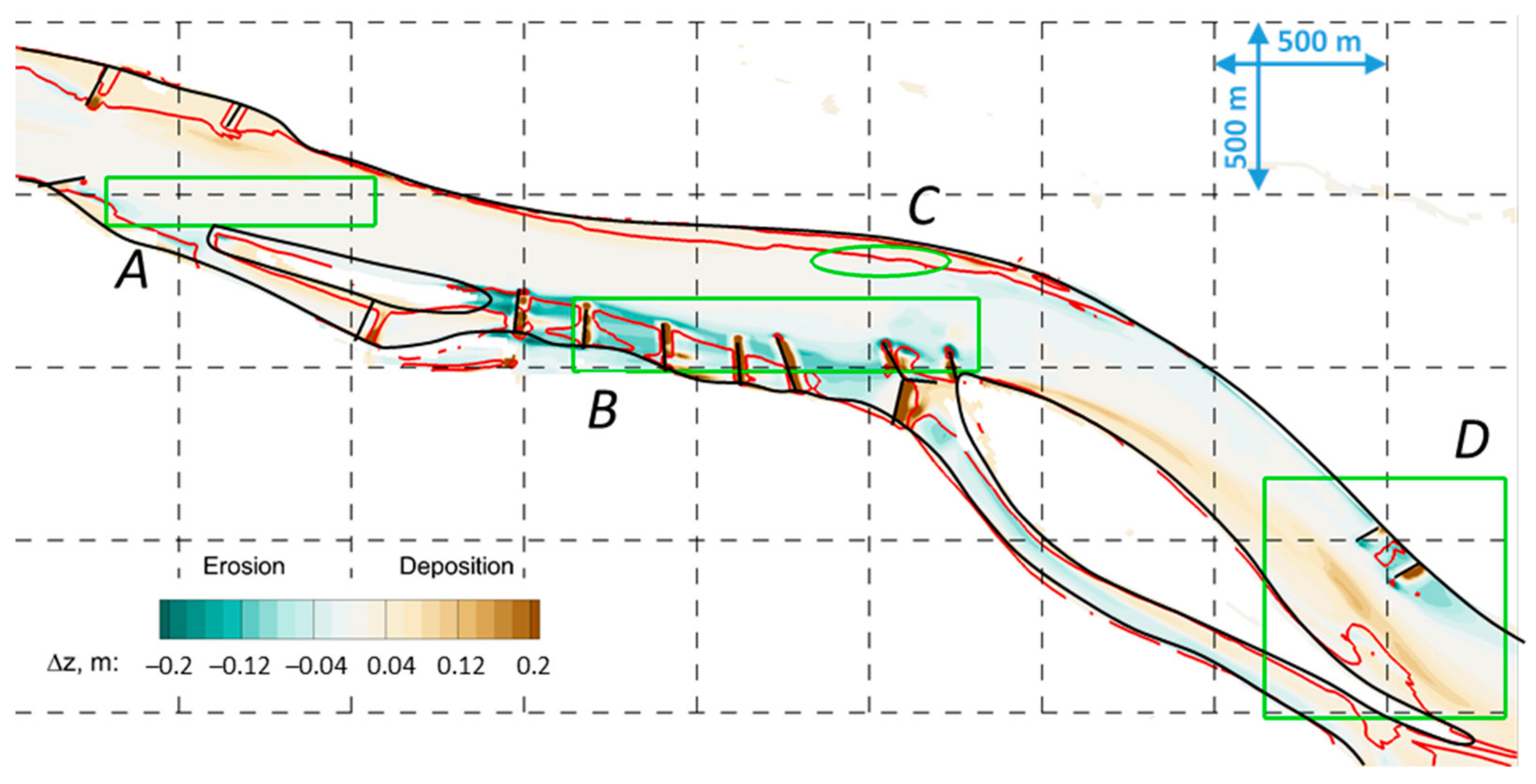
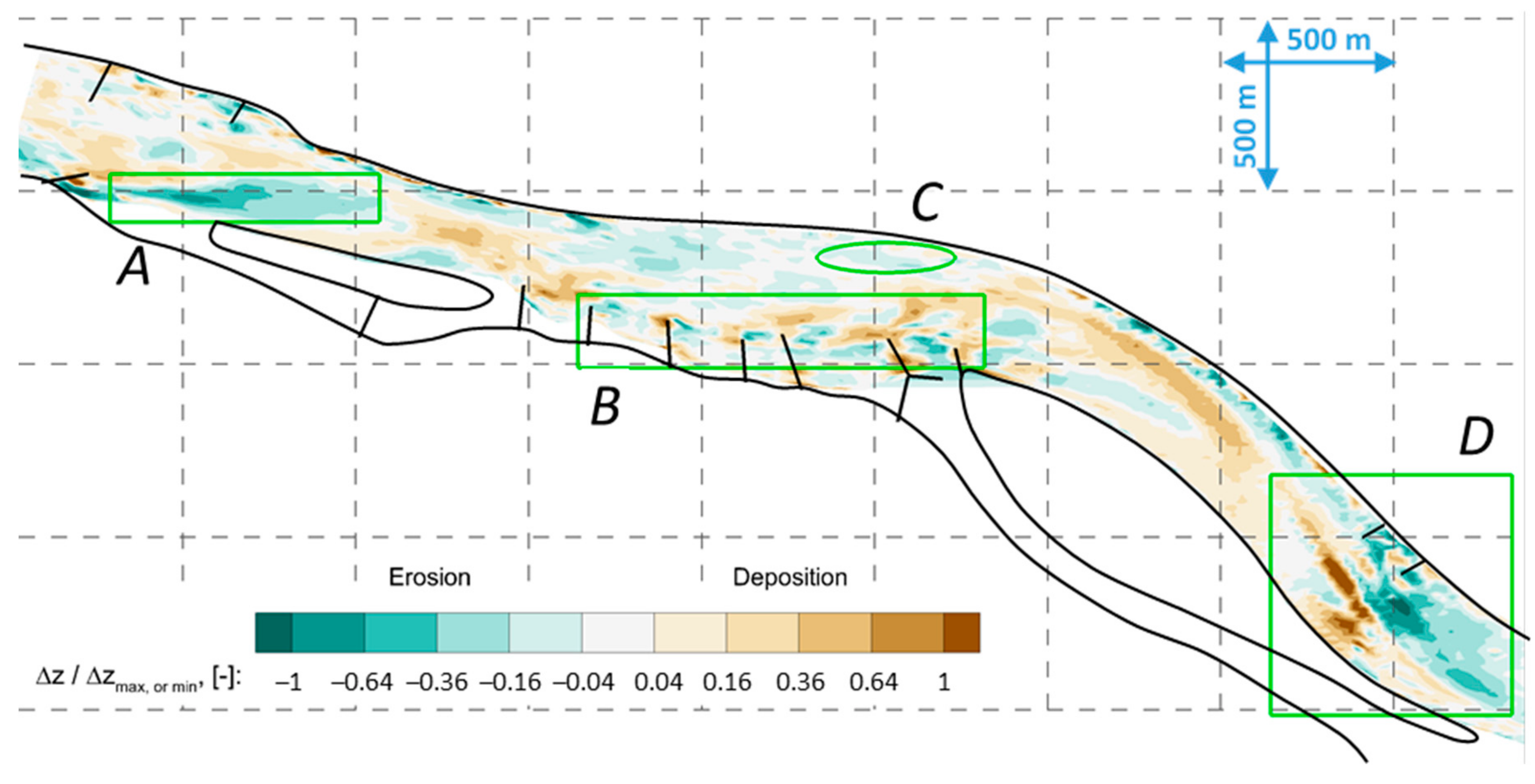
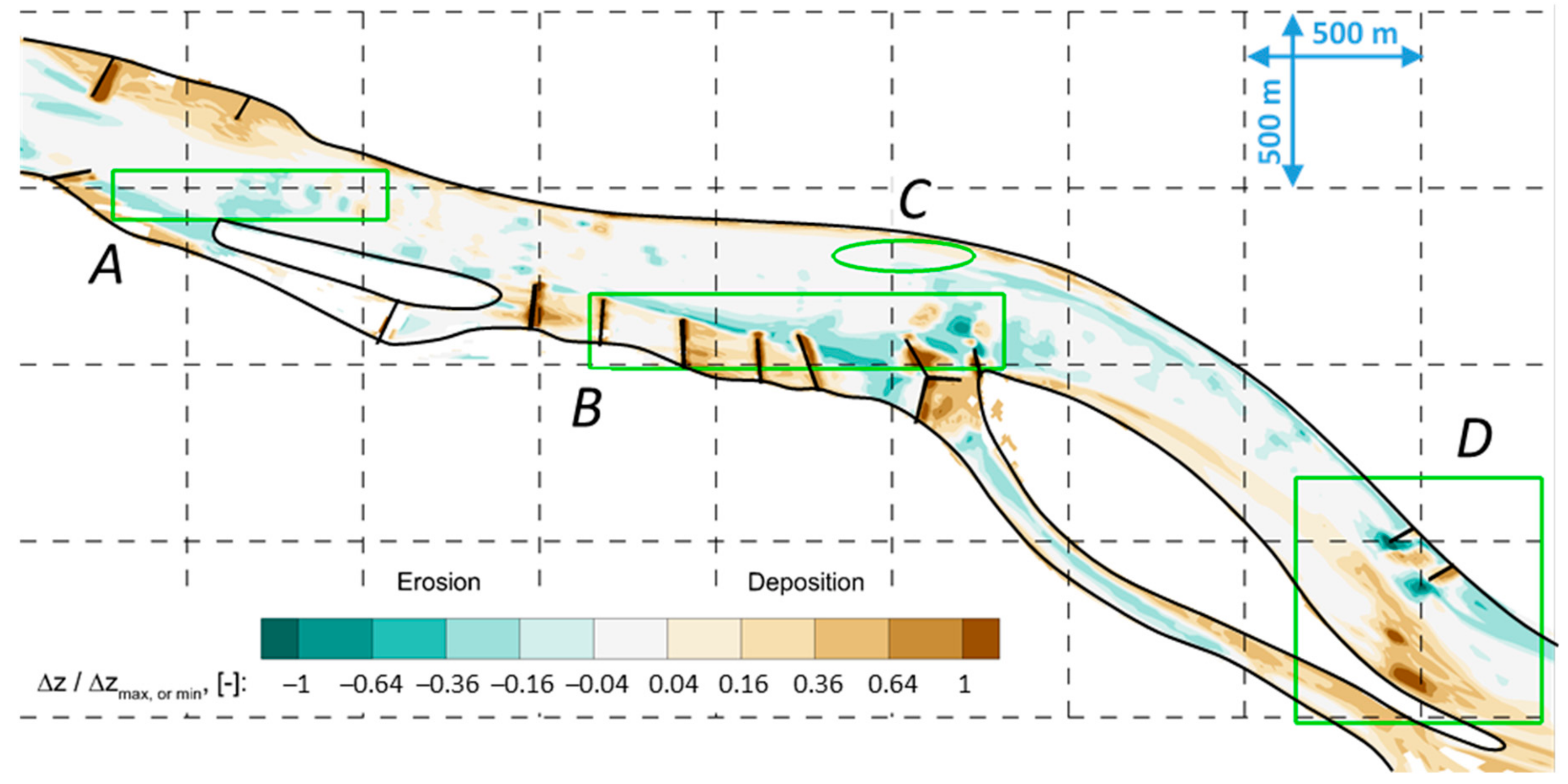
Cross-SectionI.II.III.IV.V.VI.VII.
RMSD, m/s0.350.190.170.190.470.420.27
Max vhor, m/s2.732.843.013.143.132.882.62
Average dif., %12.76.75.76.214.914.610.4
Table
Table 2. The average daily volume changes for calculated (∆Vc) and measured (∆Vm) volume ratio values ∆Vc/∆Vm for region D. A value of 1 would indicate the perfect match.
Table 2. The average daily volume changes for calculated (∆Vc) and measured (∆Vm) volume ratio values ∆Vc/∆Vm for region D. A value of 1 would indicate the perfect match.
Sediment Transport Model
van RijnWilcock and CroweRe* Based Combined
The rate of the calculated to measured volumesDeposition48.74.93.5
Erosion7.200.7

Share and Cite

MDPI and ACS Style

Török, G.T.; Józsa, J.; Baranya, S. Validation of a Novel, Shear Reynolds Number Based Bed Load Transport Calculation Method for Mixed Sediments against Field Measurements. Water 2019, 11, 2051. https://doi.org/10.3390/w11102051

AMA Style

Török GT, Józsa J, Baranya S. Validation of a Novel, Shear Reynolds Number Based Bed Load Transport Calculation Method for Mixed Sediments against Field Measurements. Water. 2019; 11(10):2051. https://doi.org/10.3390/w11102051

Chicago/Turabian Style

Török, Gergely T., János Józsa, and Sándor Baranya. 2019. "Validation of a Novel, Shear Reynolds Number Based Bed Load Transport Calculation Method for Mixed Sediments against Field Measurements" Water 11, no. 10: 2051. https://doi.org/10.3390/w11102051

APA Style

Török, G. T., Józsa, J., & Baranya, S. (2019). Validation of a Novel, Shear Reynolds Number Based Bed Load Transport Calculation Method for Mixed Sediments against Field Measurements. Water, 11(10), 2051. https://doi.org/10.3390/w11102051

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop