On the Use of Parametric Wind Models for Wind Wave Modeling under Tropical Cyclones
Abstract
1. Introduction
2. Methods and Data
2.1. Wind and Wave Data
2.2. Parametric Wind Fields
2.3. Wave Model
3. Results and Discussion
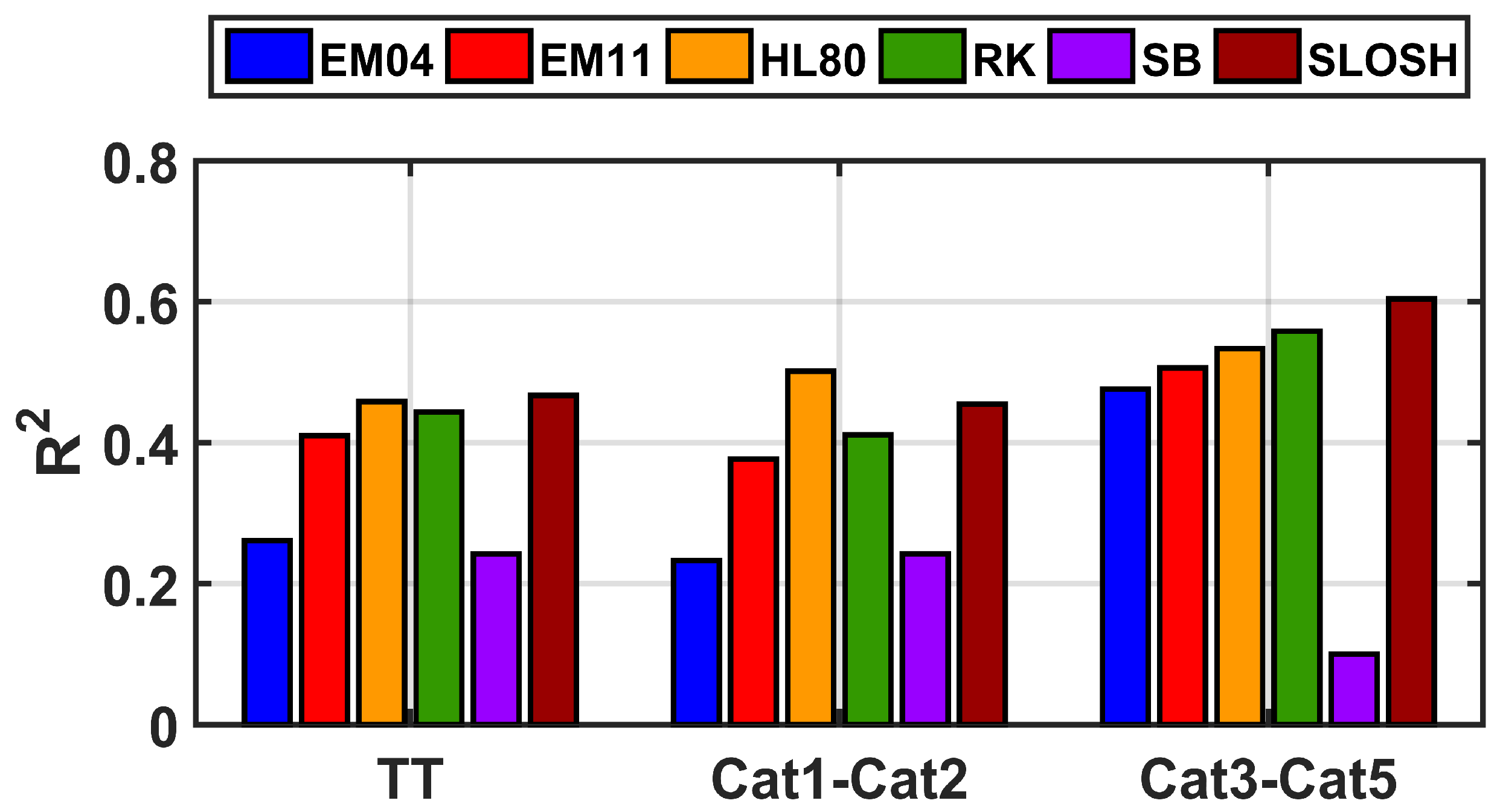
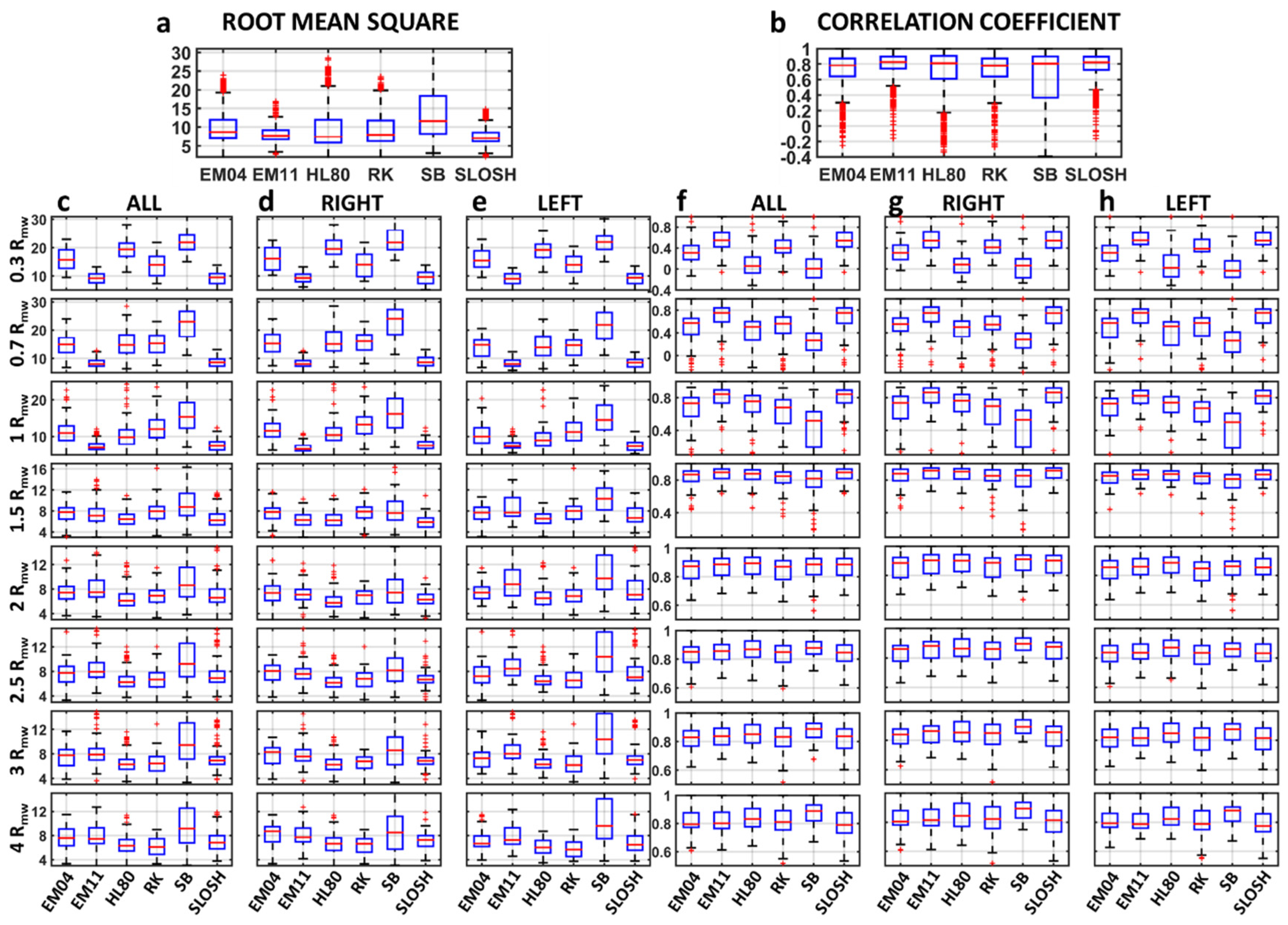
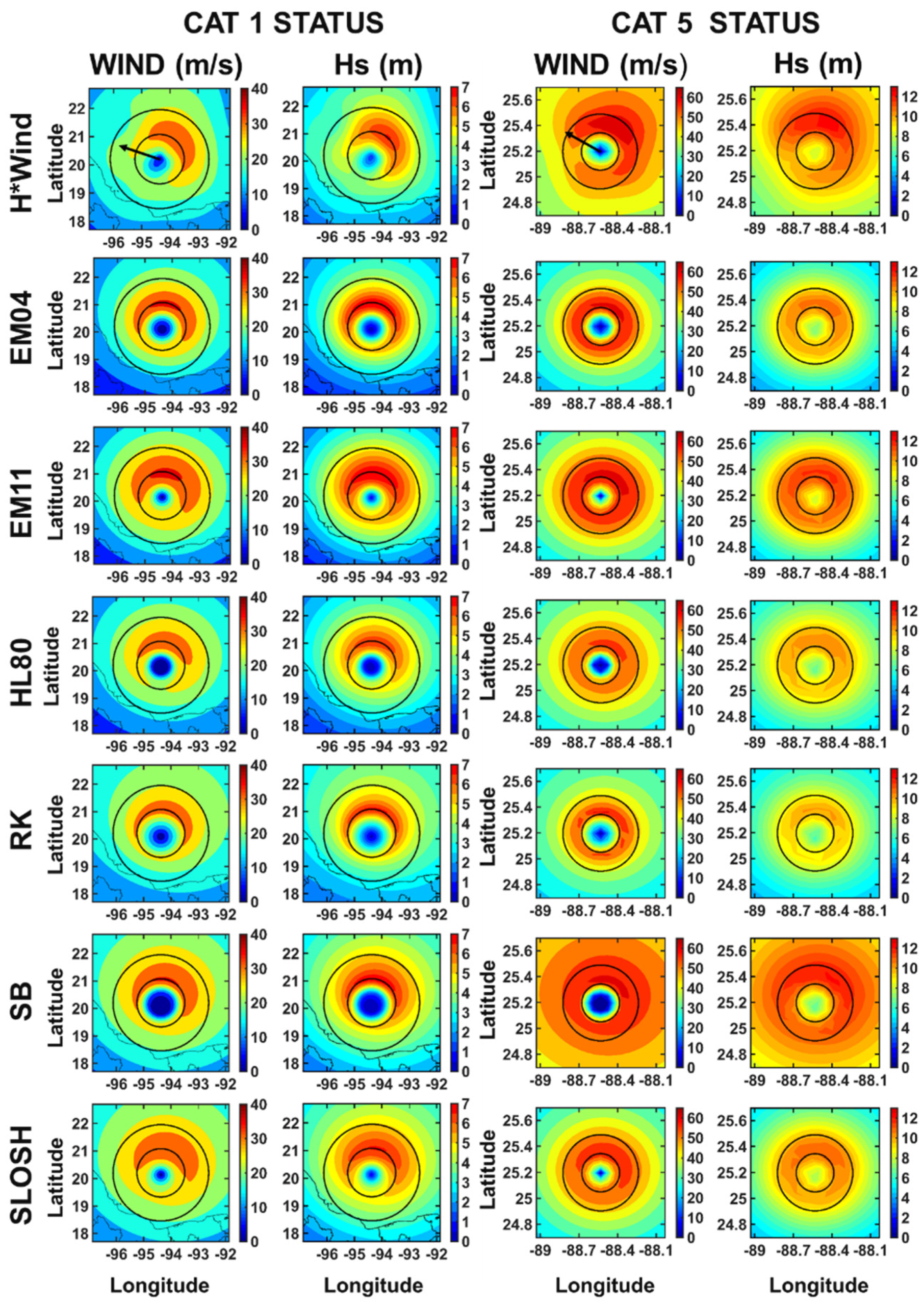
3.1. Wind Assessment
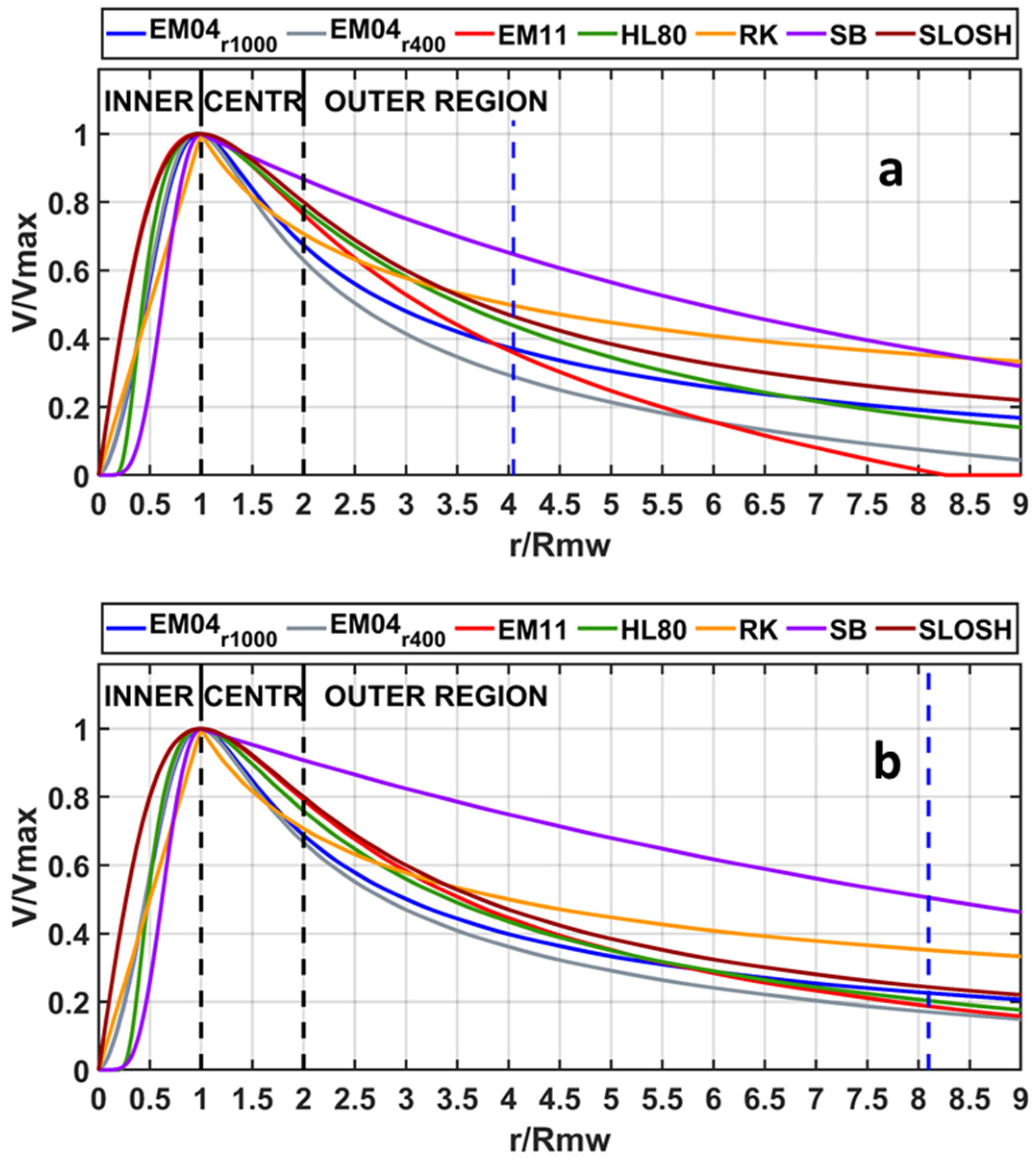
- Generally, the HL80 and SB models overestimate the size of TC eye.
- The EM11 and SLOSH models show the most accurate fit for the inner area of the wind speed profile during major category events.
- The SB model overestimates the winds in central and outer regions of the profile for high categories, showing good agreement only for some periods during cat3 or minor categories when the wind profile decays slowly with radius in outer areas.
- For less intense events (cat1 and cat2), the EM04, HL80, and RK models show the best fit with H*Wind radial profiles, with a better representation of the central region in comparison to the outer region.
- In general, no model accurately represents the outer region (beyond 2–3 Rmw), where generally the wind profiles decay too fast.
Temporal and Spatial Distribution Assessment
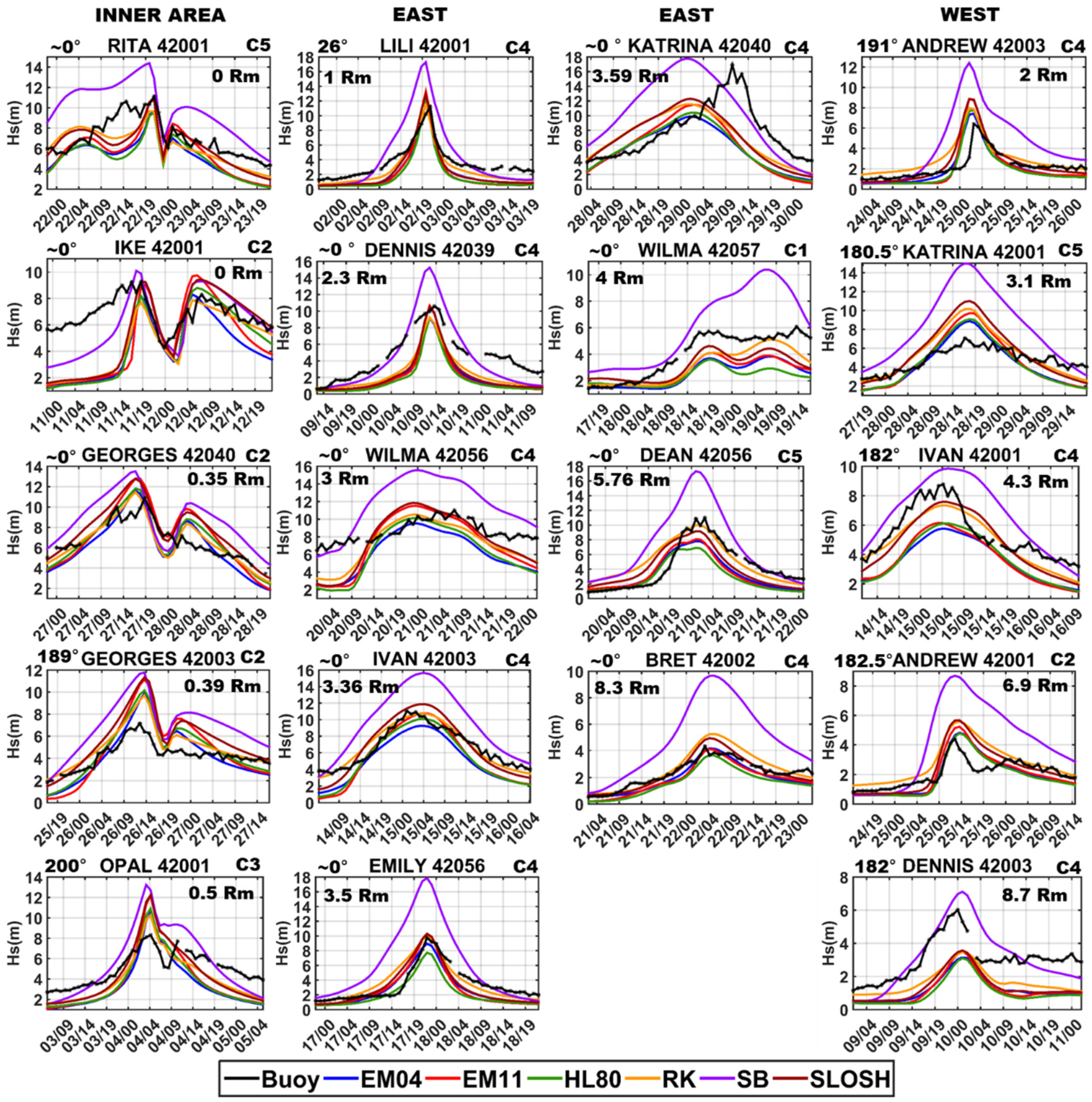
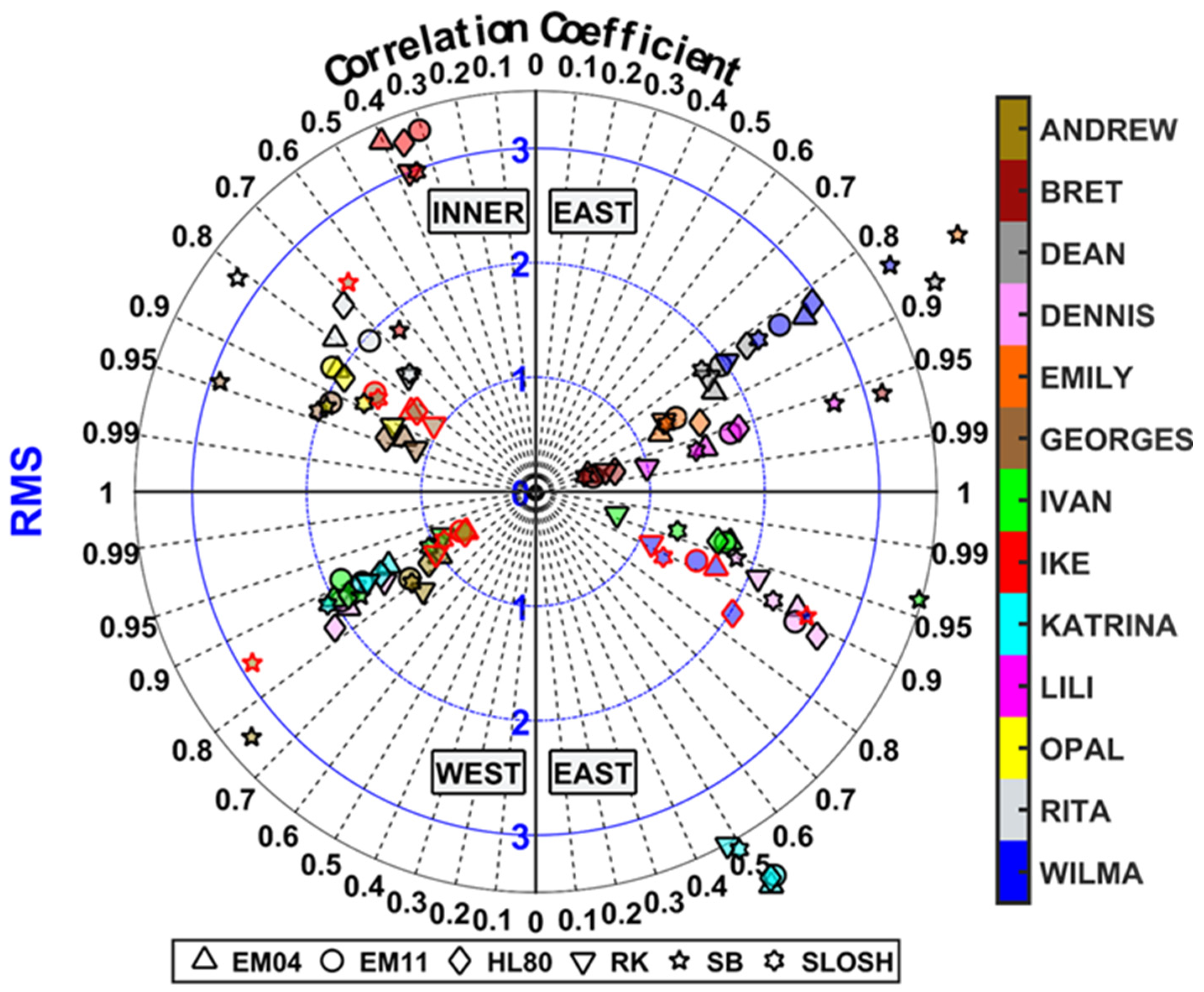
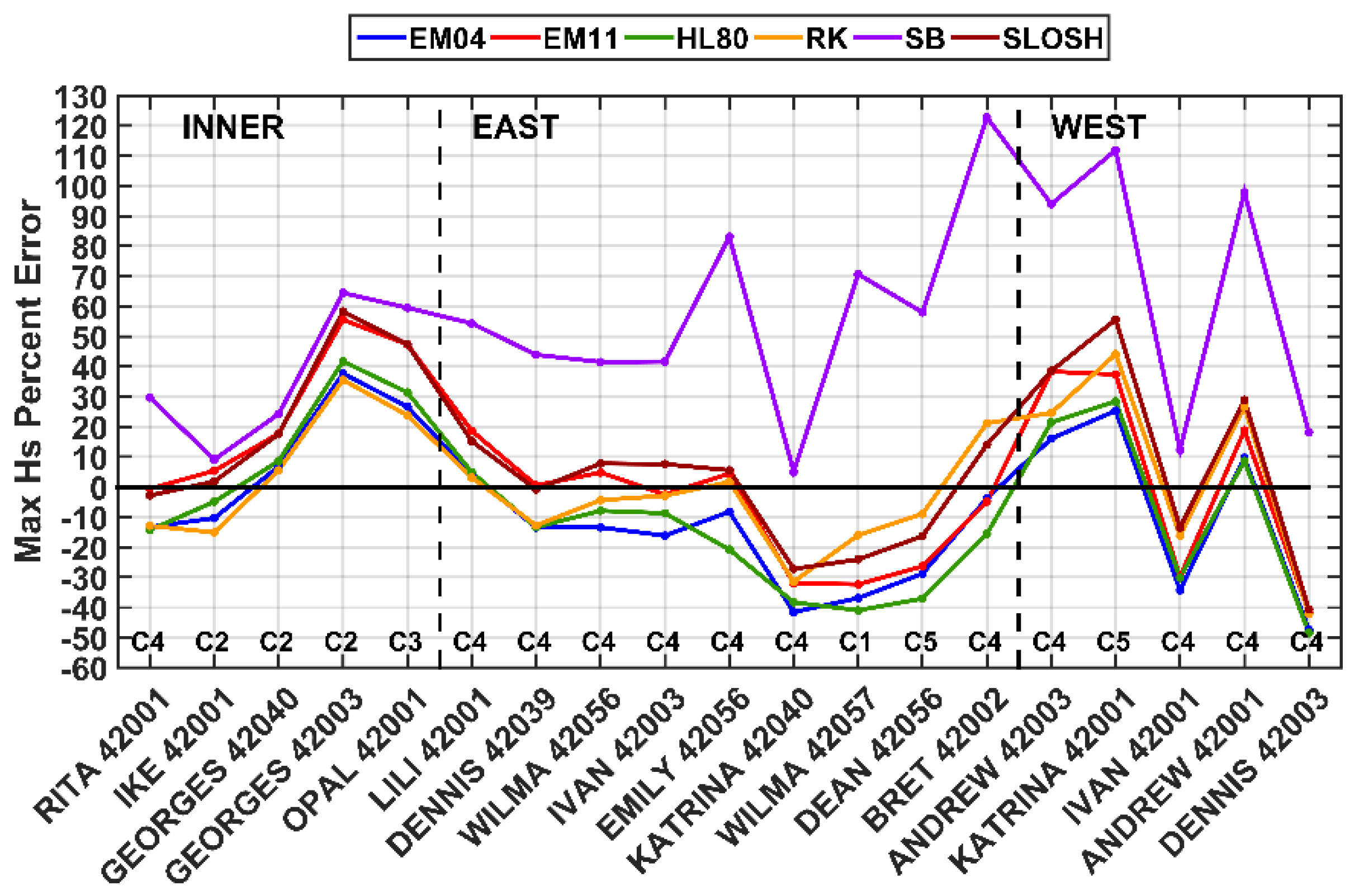
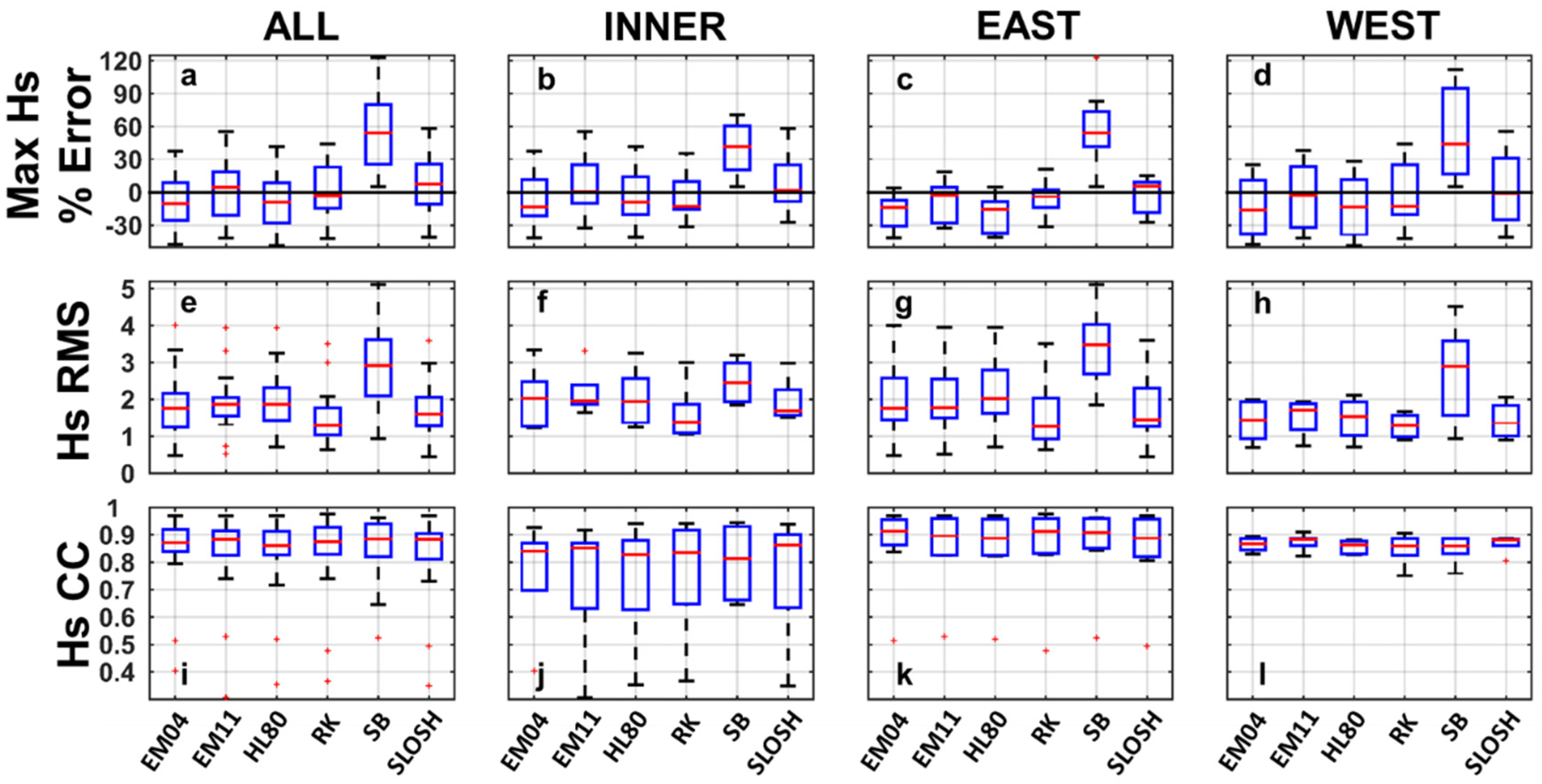
3.2. Wave Assessment
3.2.1. Spatial Distribution Assessment
3.2.2. Wave Time-Series Assessment
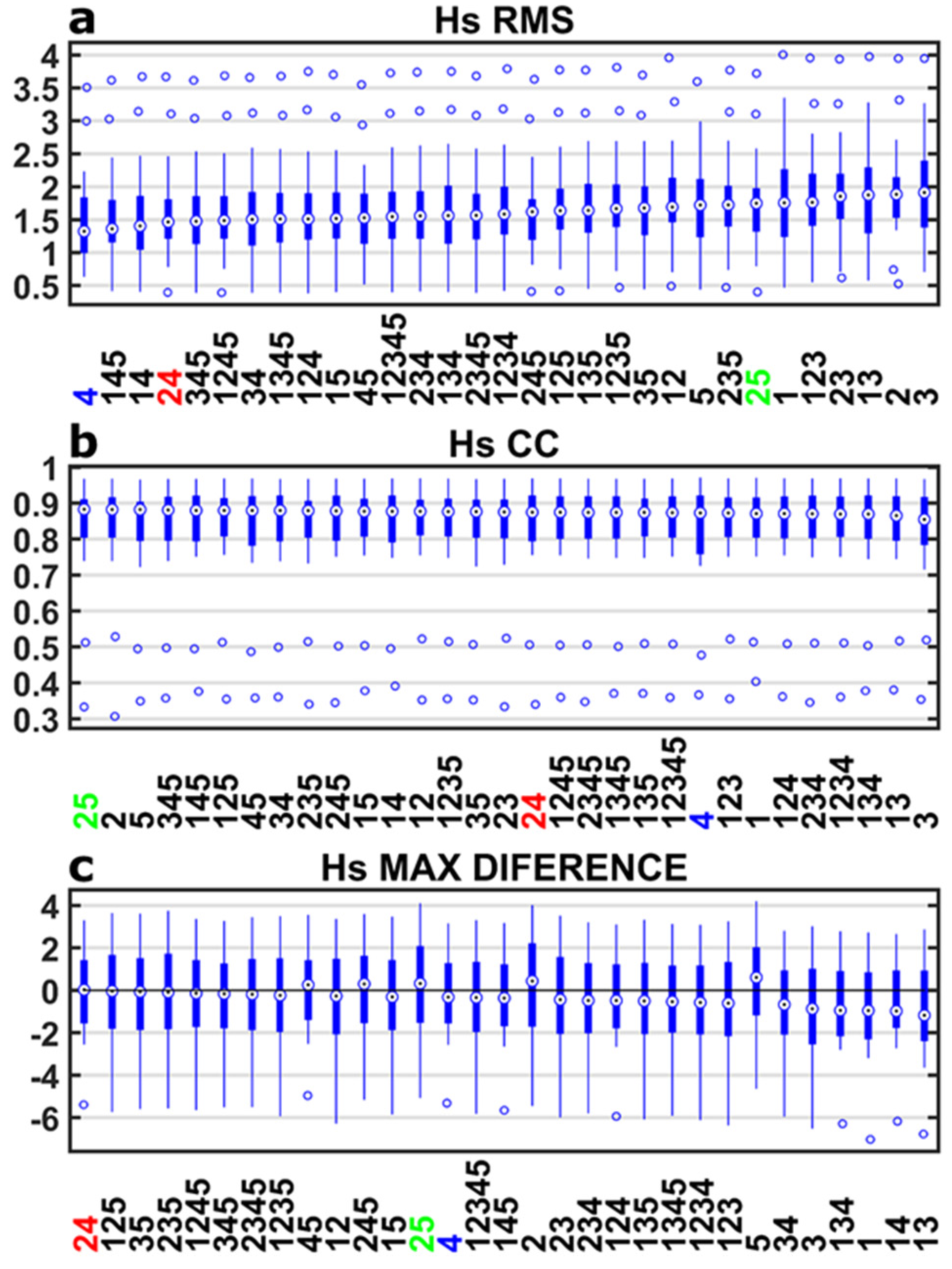
3.2.3. Time Series Permutations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stewart, S.R. Hurricane Ivan: 2–24 September 2004; National Hurricane Center: Miami, FL, USA, 2004; Volume 3.
- Panchang, V.G.; Li, D. Large waves in the Gulf of Mexico caused by Hurricane Ivan. Bull. Am. Meteorol. Soc. 2006, 87, 481–489. [Google Scholar] [CrossRef]
- Wang, D.P.; Oey, L.Y. Hindcast of waves and currents in hurricane Katrina. Bull. Am. Meteorol. Soc. 2008, 89, 487–495. [Google Scholar] [CrossRef]
- Cruz, A.M.; Krausmann, E. Damage to offshore oil and gas facilities following hurricanes Katrina and Rita: An overview. J. Loss Prev. Process Ind. 2008, 21, 620–626. [Google Scholar] [CrossRef]
- American Petroleum Institute. Interim Guidance on Hurricane Conditions in the Gulf of Mexico; American Petroleum Institute: Washington, DC, USA, 2007. [Google Scholar]
- Caires, S.; Sterl, A.; Bidlot, J.R.; Graham, N.; Swail, V. Intercomparison of different wind-wave reanalyses. J. Clim. 2004, 17, 1893–1913. [Google Scholar] [CrossRef]
- Hemer, M.A.; Wang, X.L.; Church, J.A.; Swail, V.R. Coordinating global ocean wave climate projections. Bull. Am. Meteorol. Soc. 2010, 91, 451–454. [Google Scholar] [CrossRef]
- Jeong, C.K.; Panchang, V.; Demirbilek, Z. Parametric Adjustments to the Rankine Vortex Wind Model for Gulf of Mexico Hurricanes. J. Offshore Mech. Arct. Eng. 2012, 134, 041102. [Google Scholar] [CrossRef]
- Rotunno, R.; Chen, Y.; Wang, W.; Davis, C.; Dudhia, J.; Holland, G.J. Large-eddy simulation of an idealized tropical cyclone. Bull. Am. Meteorol. Soc. 2009, 90, 1783–1788. [Google Scholar] [CrossRef]
- Hodges, K.; Cobb, A.; Vidale, P.L. How well are tropical cyclones represented in reanalysis datasets? J. Clim. 2017, 30, 5243–5264. [Google Scholar] [CrossRef]
- Appendini, C.M.; Torres-Freyermuth, A.; Oropeza, F.; Salles, P.; López, J.; Mendoza, E.T. Wave modeling performance in the Gulf of Mexico and Western Caribbean: Wind reanalyses assessment. Appl. Ocean Res. 2013, 39, 20–30. [Google Scholar] [CrossRef]
- Wang, X.L.; Swail, V.R. Trends of Atlantic wave extremes as simulated in a 40-yr wave hindcast using kinematically reanalyzed wind fields. J. Clim. 2002, 15, 1020–1035. [Google Scholar] [CrossRef]
- Knutson, T.R.; Sirutis, J.J.; Garner, S.T.; Held, I.M.; Tuleya, R.E. Simulation of the Recent Multidecadal Increase of Atlantic Hurricane Activity Using an 18-km-Grid Regional Model. Bull. Am. Meteorol. Soc. 2007, 88, 1549–1565. [Google Scholar] [CrossRef]
- Emanuel, K.; Sundararajan, R.; Williams, J. Hurricanes and global warming: Results from downscaling IPCC AR4 simulations. Bull. Am. Meteorol. Soc. 2008, 89, 347–367. [Google Scholar] [CrossRef]
- Powell, M.D.; Houston, S.H.; Amat, L.R.; Morisseau-Leroy, N. The HRD real-time hurricane wind analysis system. J. Wind Eng. Ind. Aerodyn. 1998, 77, 53–64. [Google Scholar] [CrossRef]
- Powell, M.D.; Murillo, S.; Dodge, P.; Uhlhorn, E.; Gamache, J.; Cardone, V.; Cox, A.; Otero, S.; Carrasco, N.; Annane, B.; et al. Reconstruction of Hurricane Katrina’s wind fields for storm surge and wave hindcasting. Ocean Eng. 2010, 37, 26–36. [Google Scholar] [CrossRef]
- Rankine, W.J.M. A Manual of Applied Physics; Charles Griff and Co.: London, UK, 1882. [Google Scholar]
- Depperman, C.E. Notes on the origin and structure of Phillipine typhoons. Bull. Am. Meteorol. Soc. 1947, 28, 399–404. [Google Scholar] [CrossRef]
- Schloemer, R.W. Analysis and Synthesis of Hurricane Wind Patterns over Lake Okeechobee, Florida; Hydrometeorological Reports No. 31; Department of Commerce: Washington, DC, USA, 1954; p. 49.
- Myers, V.A. Maximum hurricane winds. Bull. Am. Meteorol. Soc. 1957, 38, 227–228. [Google Scholar]
- Holland, G. An analytic model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Willoughby, H.E.; Rahn, M.E. Parametric Representation of the Primary Hurricane Vortex. Part I: Observations and Evaluation of the Holland (1980) Model. Mon. Weather Rev. 2004, 132, 3033–3048. [Google Scholar] [CrossRef]
- Holland, G.J.; Belanger, J.I.; Fritz, A. A Revised Model for Radial Profiles of Hurricane Winds. Mon. Weather Rev. 2010, 138, 4393–4401. [Google Scholar] [CrossRef]
- Vickery, P.J.; Wadhera, D. Statistical models of Holland pressure profile parameter and radius to maximum winds of hurricanes from flight-level pressure and H* wind data. J. Appl. Meteorol. Climatol. 2008, 47, 2497–2517. [Google Scholar] [CrossRef]
- Thompson, E.F.; Cardone, V.J. Practical Modeling of Hurricane Surface Wind Fields. J. Waterw. Port Coast. Ocean Eng. 1996, 122, 195–205. [Google Scholar] [CrossRef]
- Vickery, P.J.; Skerlj, P.F.; Steckley, A.C.; Twisdale, L.A. Hurricane wind field model for use in hurricane simulations. J. Struct. Eng. 2000, 126, 1203–1221. [Google Scholar] [CrossRef]
- Emanuel, K. Tropical cyclone energetics and structure. In Atmospheric Turbulence and Mesoscale Meteorology; Fedorovich, E., Rotunno, R., Stevens, B., Eds.; Cambridge University Press: Cambridge, UK, 2004; pp. 165–192. [Google Scholar]
- Hu, K.; Chen, Q.; Kimball, S.K. Consistency in hurricane surface wind forecasting: an improved parametric model. Nat. Hazards 2011, 61, 1029–1050. [Google Scholar] [CrossRef]
- Wood, V.T.; White, L.W.; Willoughby, H.E.; Jorgensen, D.P. A New Parametric Tropical Cyclone Tangential Wind Profile Model. Mon. Weather Rev. 2013, 141, 1884–1909. [Google Scholar] [CrossRef]
- Chavas, D.R.; Lin, N.; Emanuel, K. A model for the complete radial structure of the tropical cyclone wind field. Part I: Comparison with observed structure. J. Atmos. Sci. 2015, 3647–3662. [Google Scholar] [CrossRef]
- Phadke, A.C.; Martino, C.D.; Cheung, K.F.; Houston, S.H. Modeling of tropical cyclone winds and waves for emergency management. Ocean Eng. 2003, 30, 553–578. [Google Scholar] [CrossRef]
- Tolman, H.L.; Alves, J.-H.G.M. Numerical modeling of wind waves generated by tropical cyclones using moving grids. Ocean Model. 2005, 9, 305–323. [Google Scholar] [CrossRef]
- Peng, M.; Xie, L.; Pietrafesa, L.J. Tropical cyclone induced asymmetry of sea level surge and fall and its presentation in a storm surge model with parametric wind fields. Ocean Model. 2006, 14, 81–101. [Google Scholar] [CrossRef]
- Lin, N.; Smith, J.A.; Villarini, G.; Marchok, T.P.; Baeck, M.L. Modeling Extreme Rainfall, Winds, and Surge from Hurricane Isabel (2003). Weather Forecast. 2010, 25, 1342–1361. [Google Scholar] [CrossRef]
- Lin, N.; Chavas, D. On hurricane parametric wind and applications in storm surge modeling. J. Geophys. Res. 2012, 117, D09120. [Google Scholar] [CrossRef]
- Meza-Padilla, R.; Appendini, C.M.; Pedrozo-Acuña, A. Hurricane-induced waves and storm surge modeling for the Mexican coast. Ocean Dyn. 2015, 65, 1199–1211. [Google Scholar] [CrossRef]
- Kim, S.Y.; Yasuda, T.; Mase, H. Wave set-up in the storm surge along open coasts during Typhoon Anita. Coast. Eng. 2010, 57, 631–642. [Google Scholar] [CrossRef]
- Lin, N.; Emanuel, K.A.; Smith, J.A.; Vanmarcke, E. Risk assessment of hurricane storm surge for New York City. J. Geophys. Res. 2010, 115, D18121. [Google Scholar] [CrossRef]
- Lin, N.; Lane, P.; Emanuel, K.A.; Sullivan, R.M.; Donnelly, J.P. Heightened hurricane surge risk in northwest Florida revealed from climatological-hydrodynamic modeling and paleorecord reconstruction. J. Geophys. Res. Atmos. 2014, 119, 8606–8623. [Google Scholar] [CrossRef]
- Rey, W.; Mendoza, T.E.; Salles, P.; Zhang, K.; Teng, Y.; Miguel, A.; Franklin, G.L. Hurricane Flood Risk Assessment for the Yucatan and Campeche State Coastal Area. Nat. Hazards 2019, 96, 1041–1065. [Google Scholar] [CrossRef]
- Mattocks, C.; Forbes, C. A real-time, event-triggered storm surge forecasting system for the state of North Carolina. Ocean Model. 2008, 25, 95–119. [Google Scholar] [CrossRef]
- Appendini, C.M.; Rosengaus, M.; Meza-Padilla, R.; Camacho-Magaña, V. Operational hazard assessment of waves and storm surges from tropical cyclones in Mexico. Bull. Am. Meteorol. Soc. 2017, 98, 503–515. [Google Scholar] [CrossRef]
- Appendini, C.M.; Torres-Freyermuth, A.; Salles, P.; López-González, J.; Mendoza, E.T. Wave climate and trends for the Gulf of Mexico: A 30-yr wave hindcast. J. Clim. 2014, 27, 1619–1632. [Google Scholar] [CrossRef]
- Vickery, P.J.; Wadhera, D.; Galsworthy, J.; Peterka, J.A.; Irwin, P.A.; Griffis, L.A. Ultimate Wind Load Design Gust Wind Speeds in the United States for Use in ASCE-7. J. Struct. Eng. 2009, 136, 613–625. [Google Scholar] [CrossRef]
- Appendini, C.M.; Pedrozo-Acuña, A.; Meza-Padilla, R.; Torres-Freyermuth, A.; Cerezo-Mota, R.; López-González, J.; Ruiz-Salcines, P. On the Role of Climate Change on Wind Waves Generated by Tropical Cyclones in the Gulf of Mexico. Coast. Eng. J. 2017, 59, 32. [Google Scholar] [CrossRef]
- Panchang, V.; Kwon Jeong, C.; Demirbilek, Z. Analyses of Extreme Wave Heights in the Gulf of Mexico for Offshore Engineering Applications. J. Offshore Mech. Arct. Eng. 2013, 135, 031104. [Google Scholar] [CrossRef]
- Krien, Y.; Arnaud, G.; Cécé, R.; Khan, J.; Madani, A.B.; Bernard, D.; Islam, A.K.M.S.; Durand, F.; Testut, L.; Palany, P.; et al. Can We Improve Parametric CyclonicWind Fields Using Recent Satellite Remote Sensing Data? Remote Sens. 2018, 10, 1963. [Google Scholar] [CrossRef]
- Landsea, C.W.; Franklin, J.L. Atlantic Hurricane Database Uncertainty and Presentation of a New Database Format. Mon. Weather Rev. 2013, 141, 3576–3592. [Google Scholar] [CrossRef]
- Silva, R.; Govare, G.; Salles, P.; Bautista, G.; Diaz, G. Oceanographic Vulnerability to Hurricanes on the Mexican Coast. Costal Eng. Conf. 2002, 1, 39–51. [Google Scholar]
- Knaff, J.A.; Sampson, C.R.; DeMaria, M.; Marchok, T.P.; Gross, J.M.; McAdie, C.J. Statistical Tropical Cyclone Wind Radii Prediction Using Climatology and Persistence. Weather Forecast. 2007, 22, 781–791. [Google Scholar] [CrossRef]
- Takagi, H.; Wu, W. Maximum wind radius estimated by the 50 kt radius: Improvement of storm surge forecasting over the western North Pacific. Nat. Hazards Earth Syst. Sci. 2016, 16, 705–717. [Google Scholar] [CrossRef]
- Jarvinen, B.R.; Neumann, C.J.; Davis, M.A.S. A Tropical Cyclone Data Tape for The North Atlantic Basin, 1886–1983: Contents, Limitations, and Uses; NOAA Technical Memorandum NWS NHC 22, NOAA/Tropical Prediction Center; National Oceanic and Atmospheric Administration: Miami, FL, USA, 1984.
- Dinapoli, S.M.; Bourassa, M.A.; Powell, M.D. Uncertainty and Intercalibration Analysis of H*Wind. J. Atmos. Ocean. Technol. 2012, 29, 822–833. [Google Scholar] [CrossRef]
- Mears, C.A.; Smith, D.K.; Wentz, F.J. Comparison of Special Sensor Microwave Imager and buoy-measured wind speeds from 1987 to 1997. J. Geophys. Res. 2001, 106, 11719. [Google Scholar] [CrossRef]
- Riehl, H. Some relationships between wind and thermal structure of steady state hurricanes. J. Atmos. Sci. 1963, 20, 276–287. [Google Scholar] [CrossRef]
- Emanuel, K.A. An Air-Sea Interaction Theory for Tropical Cyclones. Part I: Steady-State Maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Cao, Y.; Fovell, R.G.; Corbosiero, K.L. Tropical cyclone track and structure sensitivity to initialization in idealized simulations: A preliminary study. Terr. Atmos. Ocean. Sci. 2011, 22, 559–578. [Google Scholar] [CrossRef]
- Mallen, K.J.; Montgomery, M.T.; Wang, B. Reexamining the Near-Core Radial Structure of the Tropical Cyclone Primary Circulation: Implications for Vortex Resiliency. J. Atmos. Sci. 2005, 62, 408–425. [Google Scholar] [CrossRef]
- Levinson, D.H.; Vickery, P.J.; Resio, D.T. A review of the climatological characteristics of landfalling Gulf hurricanes for wind, wave, and surge hazard estimation. Ocean Eng. 2010, 37, 13–25. [Google Scholar] [CrossRef]
- Young, I.; Sobey, R. The Numerical Prediction of Tropical Cyclone Wind-Waves; Department of Civil & Systems Engineering, James Cook University of North Queensland: Townsville, Australia, 1981. [Google Scholar]
- Jelesnianski, C.P.C. Numerical computations o f storm surges without bottom stress. Mon. Weather Rev. 1966, 94, 379–394. [Google Scholar] [CrossRef]
- Houston, S.H.; Powell, M.D. Observed and Modeled Wind and Water-Level Response from Tropical Storm Marco (1990). Weather Forecast. 1994, 9, 427–439. [Google Scholar] [CrossRef][Green Version]
- Houston, S.H.; Shaffer, W.A.; Powell, M.D.; Chen, J. Comparisons of HRD and SLOSH Surface Wind Fields in Hurricanes: Implications for Storm Surge Modeling. Weather Forecast. 1999, 14, 671–686. [Google Scholar] [CrossRef]
- Emanuel, K.; Ravela, S.; Vivant, E.; Risi, C. A statistical deterministic approach to hurricane risk assessment. Bull. Am. Meteorol. Soc. 2006, 87, 299–314. [Google Scholar] [CrossRef]
- Chavas, D.R.; Emanuel, K.A. A QuikSCAT climatology of tropical cyclone size. Geophys. Res. Lett. 2010, 37, 10–13. [Google Scholar] [CrossRef]
- Emanuel, K.; Ravela, S. Synthetic Storm Simulation for Wind Risk Assessment. In Storm Surge Barriers to Protect New York City Against The Deluge; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 15–36. ISBN 978-0-7844-1252-7. [Google Scholar]
- Emanuel, K.; Rotunno, R. Self-Stratification of Tropical Cyclone Outflow. Part I: Implications for Storm Structure. J. Atmos. Sci. 2011, 68, 2236–2249. [Google Scholar] [CrossRef]
- Chan, J.C.L.L. the Physics of Tropical Cyclone Motion. Annu. Rev. Fluid Mech. 2005, 37, 99–128. [Google Scholar] [CrossRef]
- Lin, N.; Emanuel, K.; Oppenheimer, M.; Vanmarcke, E. Physically based assessment of hurricane surge threat under climate change. Nat. Clim. Chang. 2012, 2, 462–467. [Google Scholar] [CrossRef]
- Powell, M.D.; Houston, S.H. Hurricane Andrew’s Landfall in South Florida. Part II: Surface Wind Fields and Potential Real-Time Applications. Weather Forecast. 1996, 11, 329–349. [Google Scholar] [CrossRef]
- Dunion, J.P.; Landsea, C.W.; Houston, S.H.; Powell, M.D. A Reanalysis of the Surface Winds for Hurricane Donna of 1960. Mon. Weather Rev. 2003, 131, 1992–2011. [Google Scholar] [CrossRef]
- Vickery, P.J.; Wadhera, D.; Powell, M.D.; Chen, Y. A Hurricane Boundary Layer and Wind Field Model for Use in Engineering Applications. J. Appl. Meteorol. Climatol. 2009, 48, 381–405. [Google Scholar] [CrossRef]
- Kepert, J.D. Slab-and height-resolving models of the tropical cyclone boundary layer. Part I: Comparing the simulations. Q. J. R. Meteorol. Soc. 2010, 136, 1686–1699. [Google Scholar] [CrossRef]
- Bretschneider, C.L. A Non-Dimensional Stationary Hurricane Wave Model. In Proceedings of the Offshore Technology Conference; Offshore Technology Conference, Houston, TX, USA, 1–3 May 1972. [Google Scholar]
- Vickery, P.J.; Masters, F.J.; Powell, M.D.; Wadhera, D. Hurricane hazard modeling: The past, present, and future. J. Wind Eng. Ind. Aerodyn. 2009, 97, 392–405. [Google Scholar] [CrossRef]
- Harper, B.; Holland, G. An updated parametric model of the tropical cyclone. In Proceedings of the 23rd Conference Hurricanes and Tropical Meteorology, Dallas, TX, USA, 10–15 January 1999; pp. 10–15. [Google Scholar]
- Powell, M.D. Evaluations of Diagnostic Marine Boundary-Layer Models Applied to Hurricanes. Mon. Weather Rev. 1980, 108, 757–766. [Google Scholar] [CrossRef]
- Powell, M.D. An analytic model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1987, 115, 75–89. [Google Scholar] [CrossRef]
- Powell, M.D.; Black, P.G. The relationship of hurricane reconnaissance flight-level wind measurements to winds measured by NOAA’s oceanic platforms. J. Wind Eng. Ind. Aerodyn. 1990, 36 Pt 1, 381–392. [Google Scholar] [CrossRef]
- Georgicu, P.N.; Davenport, A.G.; Vickery, B.J. Design windspeeds in regions dominated by tropical cyclones. J. Wind Eng. Ind. Aerodyn. 1983, 13, 139–152. [Google Scholar] [CrossRef]
- Batts, M.E.; Cordes, M.R.; Russell, L.R.; Shaveri, J.R.; Simiu, E. Hurricane Wind Speeds in the United States; U.S. Department of Commerce: Washington, DC, USA; National Bureau of Standards: Gaithersburg, MD, USA, 1984.
- Willoughby, H.E.; Clos, J.A.; Shoreibah, M.G.; Willoughby, H.E.; Clos, J.A.; Shoreibah, M.G. Concentric Eye Walls, Secondary Wind Maxima, and The Evolution of the Hurricane vortex. J. Atmos. Sci. 1982, 39, 395–411. [Google Scholar] [CrossRef]
- Sørensen, O.R.; Kofoed-Hansen, H.; Rugbjerg, M.; Sørensen, L.S. A third-generation spectral wave model using an unstructured finite volume technique. In Proceedings of the 29th International Conference on Coastal Engineering, Lisbon, Portugal, 19–24 September 2004; pp. 894–906. [Google Scholar]
- Ruiz-Salcines, P. Campos de Viento Para HIndcast de Oleaje: Reanálisis, Paramétricos y Fusión; Universidad de Cantabria: Santander, Cantabria, 2013. [Google Scholar]
- Tolman, H.L. Alleviating the Garden Sprinkler Effect in wind wave models. Ocean Model. 2002, 4, 269–289. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; NOAA Technical Memorandum NESDIS NGDC-24; National Geophysical Data Center: Boulder, CO, USA; Marine Geology and Geophysics Division: Boulder, CO, USA, 2009; p. 19.
- DeMaria, M. The Effect of Vertical Shear on Tropical Cyclone Intensity change. J. Atmos. Sci. 1996, 53, 2076–2087. [Google Scholar] [CrossRef]
- Wang, Y.; Holland, G.J. Tropical cyclone motion and evolution in vertical shear. J. Atmos. Sci. 1996, 53, 3313–3332. [Google Scholar] [CrossRef]
- Bender, M.A. The Effect of Relative Flow on the Asymmetric Structure in the Interior of Hurricanes. J. Atmos. Sci. 1997, 54, 703–724. [Google Scholar] [CrossRef]
- Frank, W.M.; Ritchie, E.A. Effects of Vertical Wind Shear on the Intensity and Structure of Numerically Simulated Hurricanes. Mon. Weather Rev. 2001, 129, 2249–2269. [Google Scholar] [CrossRef]
- Shay, L.K.; Goni, G.J.; Black, P.G. Effects of a Warm Oceanic Feature on Hurricane Opal. Mon. Weather Rev. 2000, 128, 1366–1383. [Google Scholar] [CrossRef]
- Powell, M.D.; Houston, S.H. Surface wind fields of 1995 Hurricanes Erin, Opal, Luis, Marilyn, and Roxanne at landfall. Mon. Weather Rev. 1998, 126, 1259–1273. [Google Scholar] [CrossRef]
- Houze, R.A.; Chen, S.S.; Smull, B.F.; Lee, W.C.; Bell, M.M. Hurricane intensity and eyewall replacement. Science 2007, 315, 1235–1239. [Google Scholar] [CrossRef]
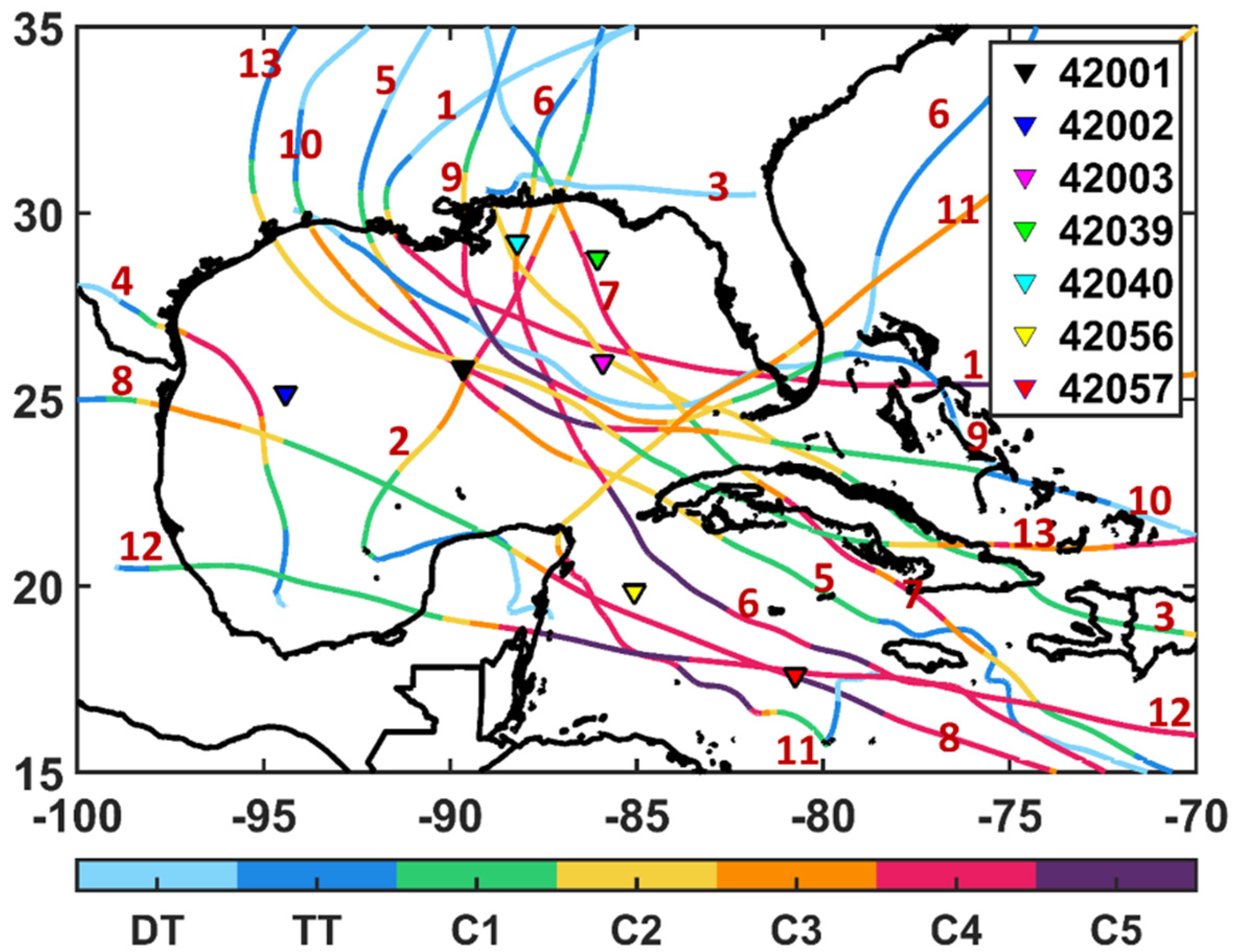
| NDBC BUOYS | |||||
|---|---|---|---|---|---|
| Buoy ID | Longitude (°) | Latitude (°) | Depth (m) | Anemometer Height (m) | Period |
| 42001 | −89.658 | 25.888 | 3246 | 10 | 1975–2017 |
| 42002 | −93.666 | 25.79 | 3566.16 | 10 | 1973–2017 |
| 42003 | −85.612 | 26.044 | 3282.7 | 5 | 1976–2017 |
| 42039 | −86.008 | 28.791 | 307 | 5 | 1995–2017 |
| 42040 | −88.205 | 29.205 | 274.3 | 10 | 1995–2017 |
| 42056 | −85.059 | 19.874 | 4446 | 5 | 2005–2017 |
| 42057 | −81.501 | 16.834 | 293 | 5 | 2005–2017 |
| MODEL | EM04 | EM11 | HL80 | RK | SB | SLOSH |
|---|---|---|---|---|---|---|
| SWRF | 0.8 | 0.85 | 0.775 | 0.85 | 0.85 | 0.8 |
| r/Rmw | EM04r1000 | EM04r400 | EM11 | HL80 | RK | SB | SLOSH | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C5 | C1 | C5 | C1 | C5 | C1 | C5 | C1 | C5 | C1 | C5 | C1 | C5 | |
| 1.5 | 16.0 | 15.2 | 18.8 | 16.5 | 9.4 | 8.1 | 9.3 | 10.3 | 21.6 | 21.6 | 6.9 | 4.7 | 7.7 | 7.7 |
| 2 | 32.6 | 31.2 | 37.0 | 33.3 | 23.6 | 20.9 | 21.9 | 24.0 | 34.0 | 34.0 | 13.3 | 9.2 | 20.0 | 20.0 |
| 2.5 | 43.9 | 42.2 | 49.6 | 44.8 | 36.4 | 32.3 | 32.9 | 35.2 | 42.3 | 42.3 | 19.3 | 13.5 | 31.0 | 31.0 |
| 3 | 52.0 | 49.9 | 58.6 | 53.0 | 47.1 | 41.7 | 41.9 | 44.0 | 48.3 | 48.3 | 24.8 | 17.5 | 40.0 | 40.0 |
| 3.5 | 58.0 | 55.7 | 65.4 | 59.1 | 56.0 | 49.3 | 49.4 | 50.9 | 52.8 | 52.8 | 30.0 | 21.4 | 47.2 | 47.2 |
| 4 | 62.6 | 60.1 | 70.7 | 63.9 | 63.4 | 55.4 | 55.6 | 56.5 | 56.5 | 56.5 | 34.8 | 25.1 | 52.9 | 52.9 |
| 5 | 69.5 | 66.6 | 78.6 | 70.9 | 75.2 | 64.8 | 65.5 | 65.0 | 61.9 | 61.9 | 43.5 | 32.0 | 61.5 | 61.5 |
| 6 | 74.3 | 71.2 | 84.4 | 75.9 | 84.4 | 71.6 | 72.8 | 71.1 | 65.9 | 65.9 | 51.0 | 38.2 | 67.6 | 67.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Salcines, P.; Salles, P.; Robles-Díaz, L.; Díaz-Hernández, G.; Torres-Freyermuth, A.; Appendini, C.M. On the Use of Parametric Wind Models for Wind Wave Modeling under Tropical Cyclones. Water 2019, 11, 2044. https://doi.org/10.3390/w11102044
Ruiz-Salcines P, Salles P, Robles-Díaz L, Díaz-Hernández G, Torres-Freyermuth A, Appendini CM. On the Use of Parametric Wind Models for Wind Wave Modeling under Tropical Cyclones. Water. 2019; 11(10):2044. https://doi.org/10.3390/w11102044
Chicago/Turabian StyleRuiz-Salcines, Pablo, Paulo Salles, Lucia Robles-Díaz, Gabriel Díaz-Hernández, Alec Torres-Freyermuth, and Christian M. Appendini. 2019. "On the Use of Parametric Wind Models for Wind Wave Modeling under Tropical Cyclones" Water 11, no. 10: 2044. https://doi.org/10.3390/w11102044
APA StyleRuiz-Salcines, P., Salles, P., Robles-Díaz, L., Díaz-Hernández, G., Torres-Freyermuth, A., & Appendini, C. M. (2019). On the Use of Parametric Wind Models for Wind Wave Modeling under Tropical Cyclones. Water, 11(10), 2044. https://doi.org/10.3390/w11102044








