Laboratory Experimental Investigation on the Hydrodynamic Responses of an Extra-Large Electrical Platform in Wave and Storm Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Model Similarity
2.2. Mechanical Test of the Experimental Material
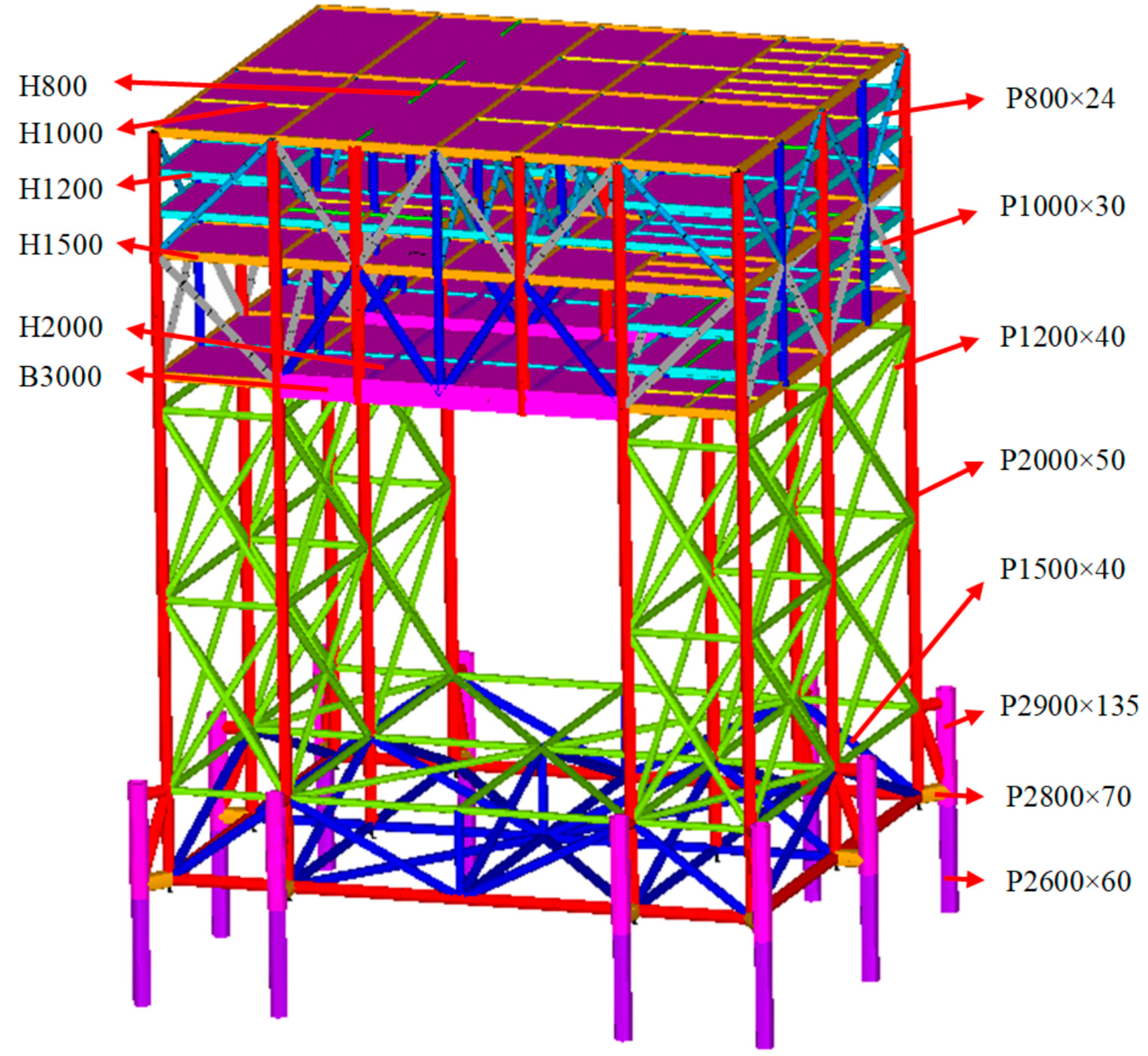
2.3. Experimental Model Design
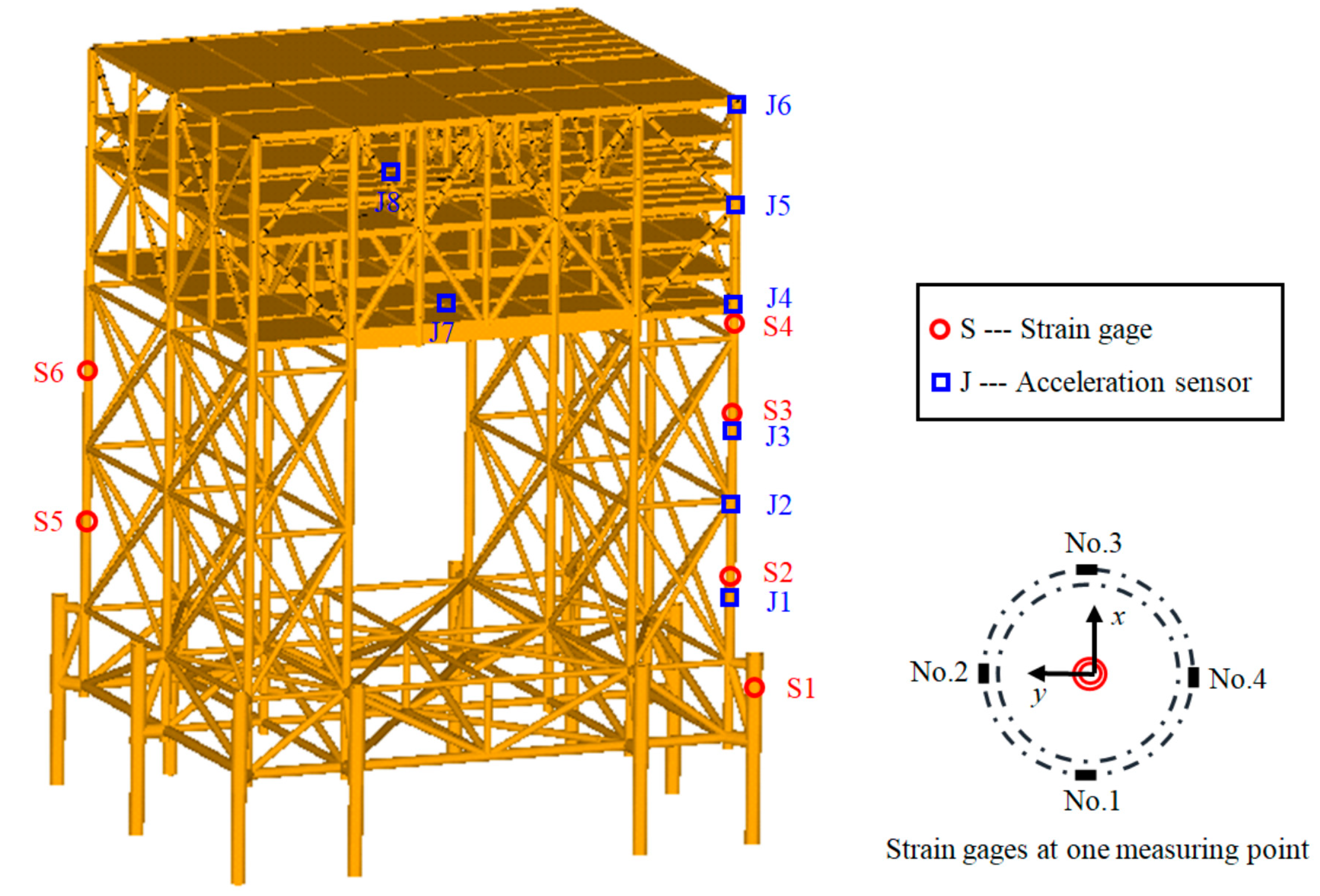
2.4. Experimental Set-Up
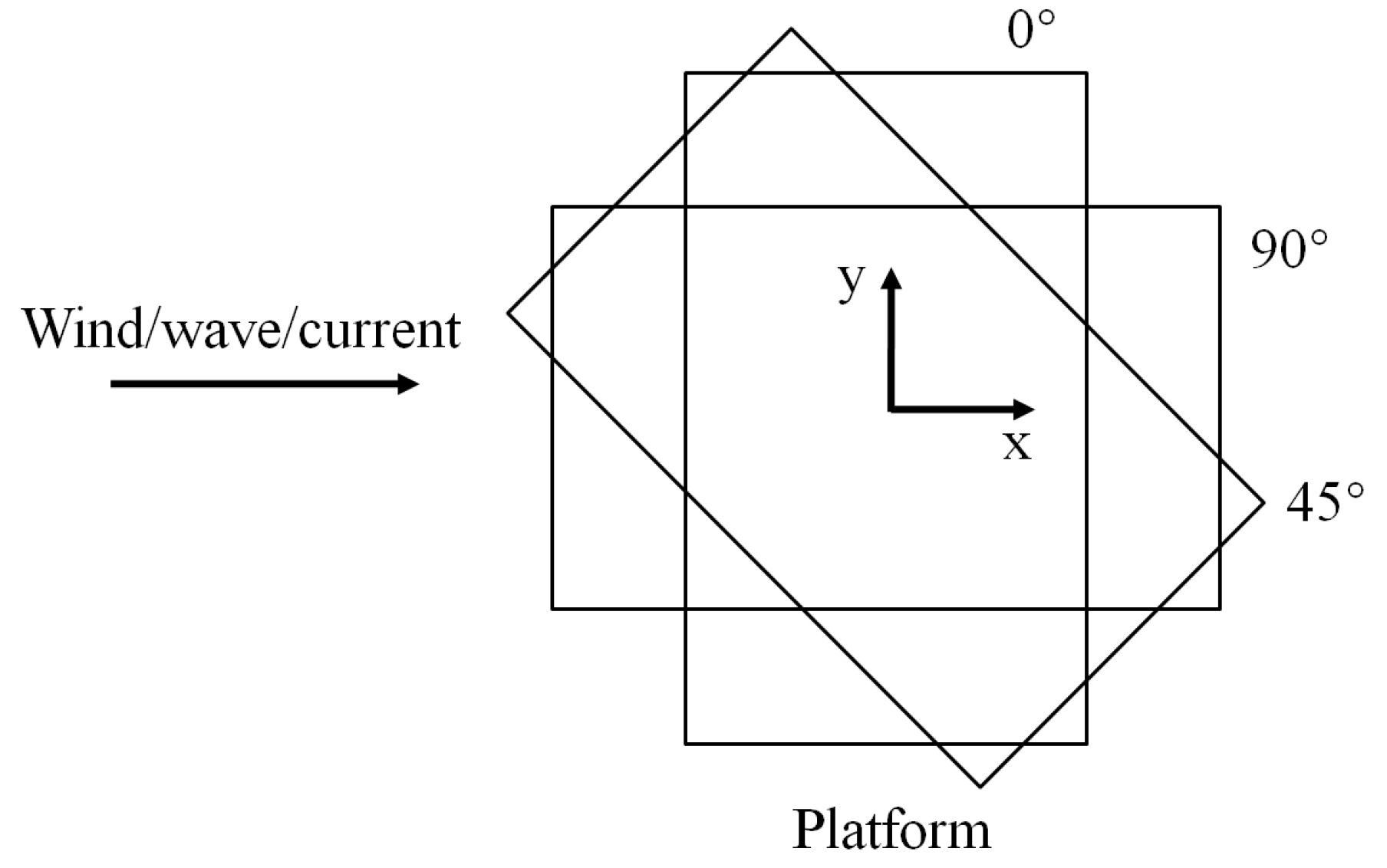
2.5. Experimental Conditions
3. Results
3.1. Strain Response of Electrical Platform
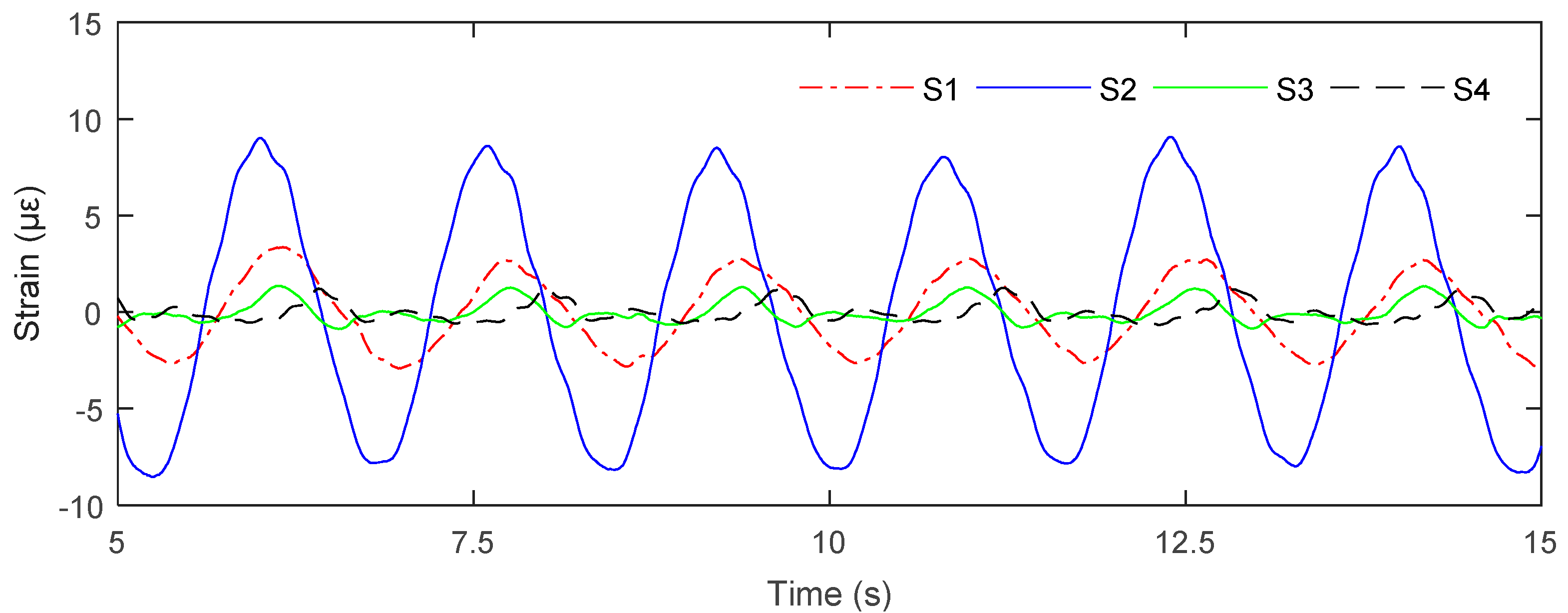
3.1.1. The Electrical Platform in Regular Waves
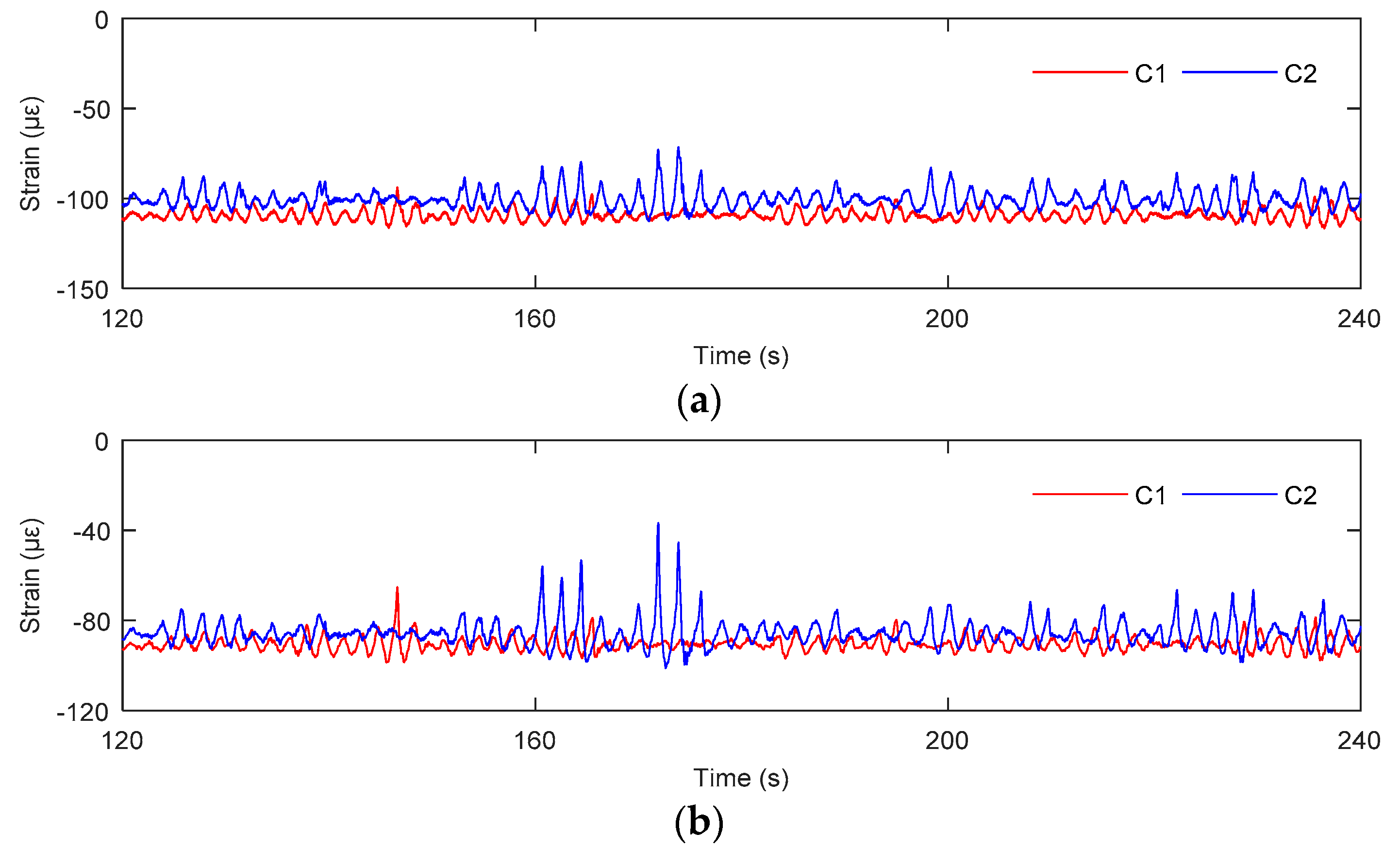
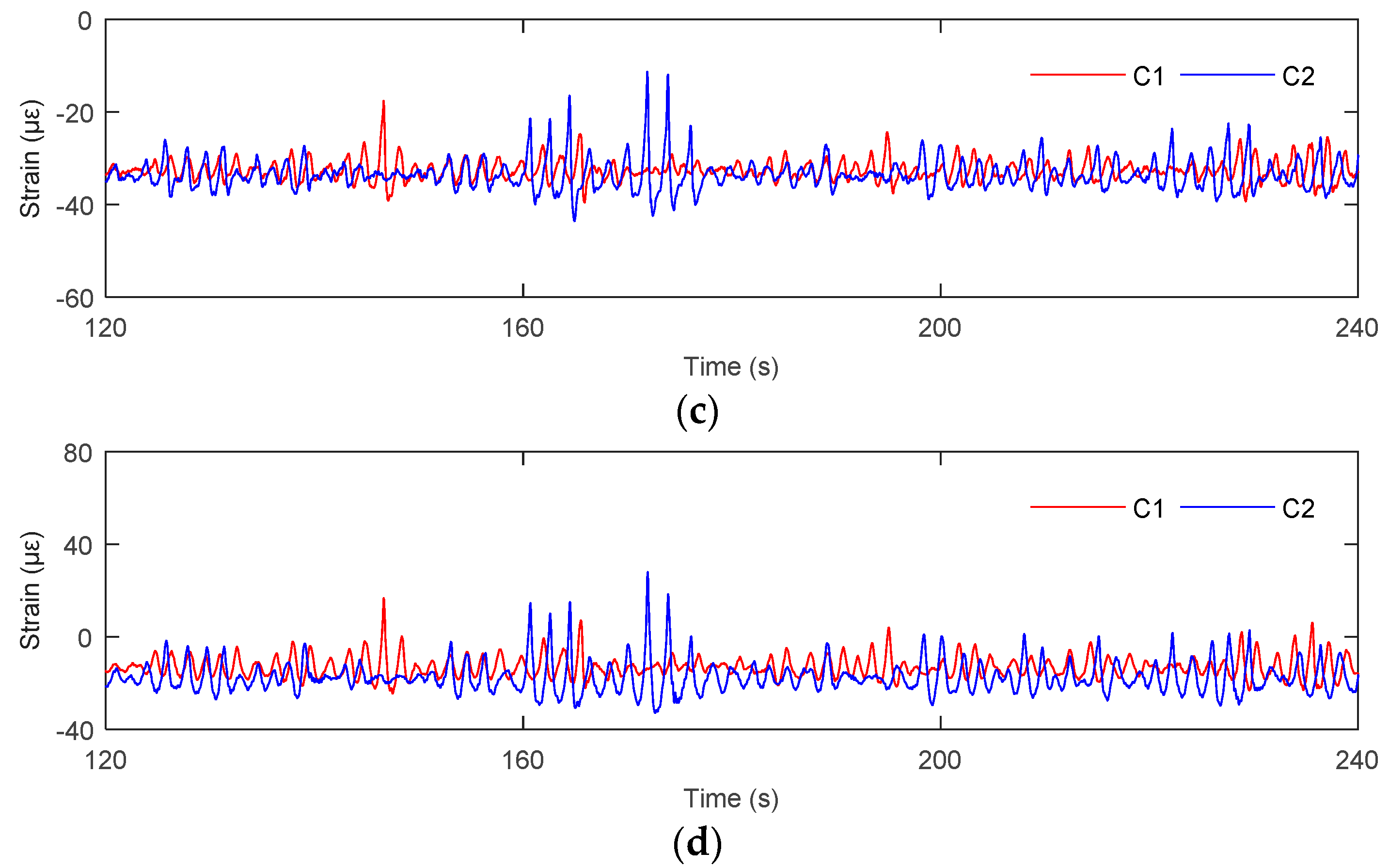
3.1.2. The Electrical Platform in Storm Condition
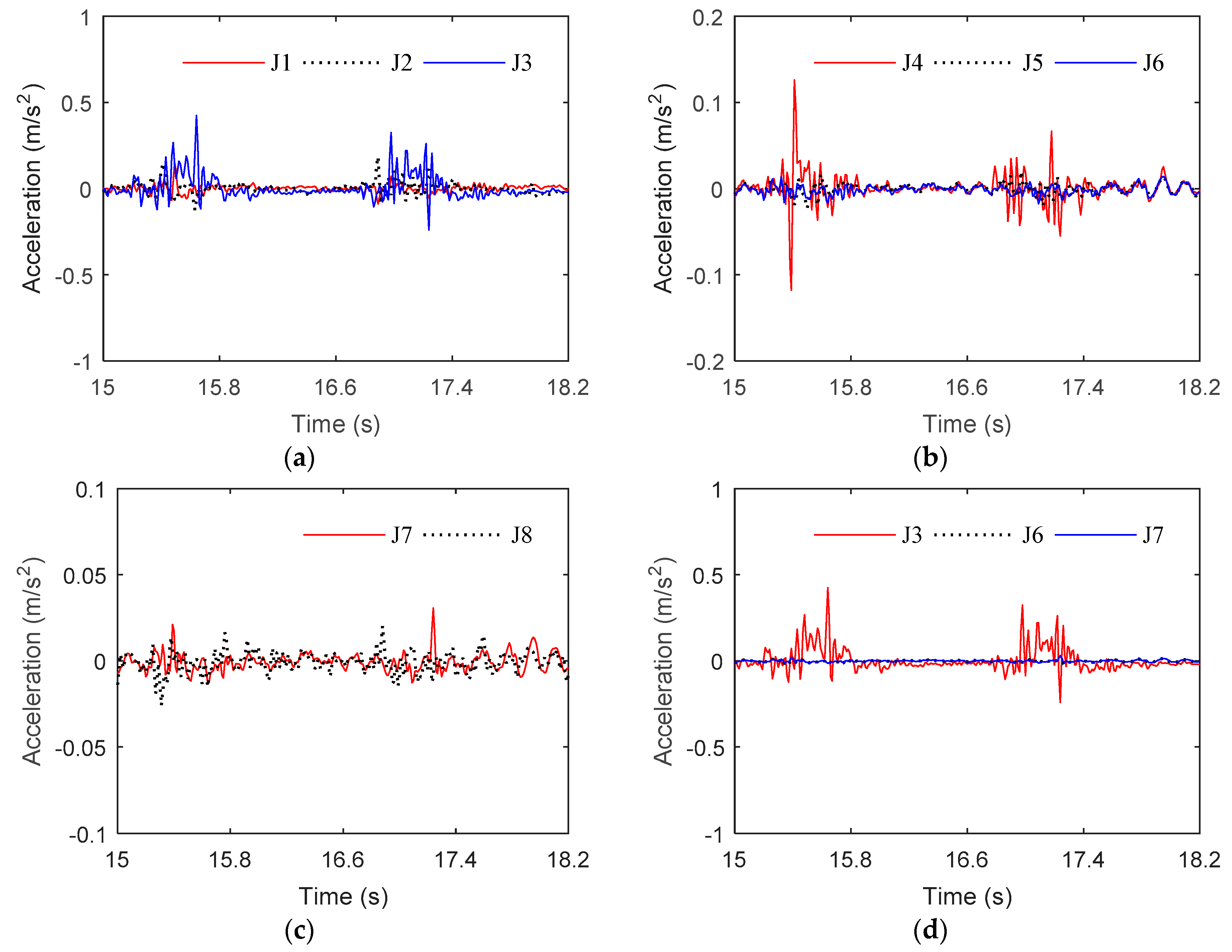
3.2. Acceleration Response of Electrical Platform
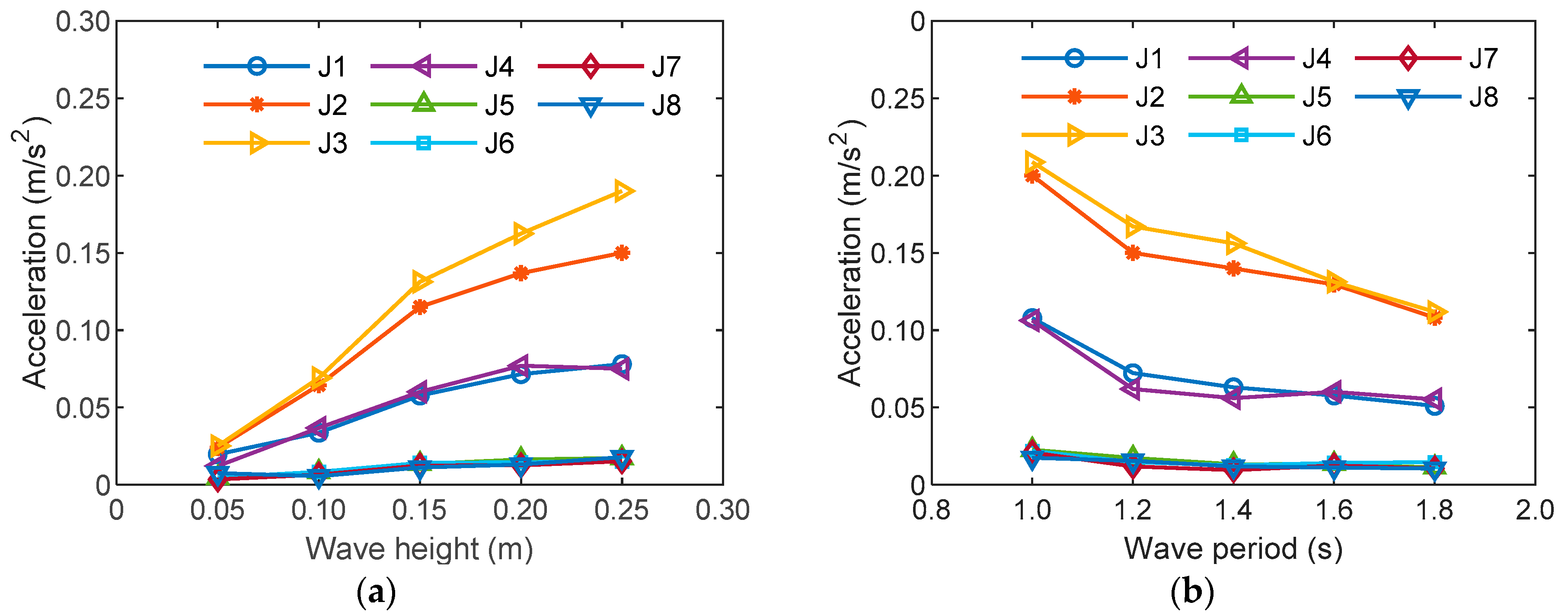
3.2.1. The Electrical Platform in Regular Waves
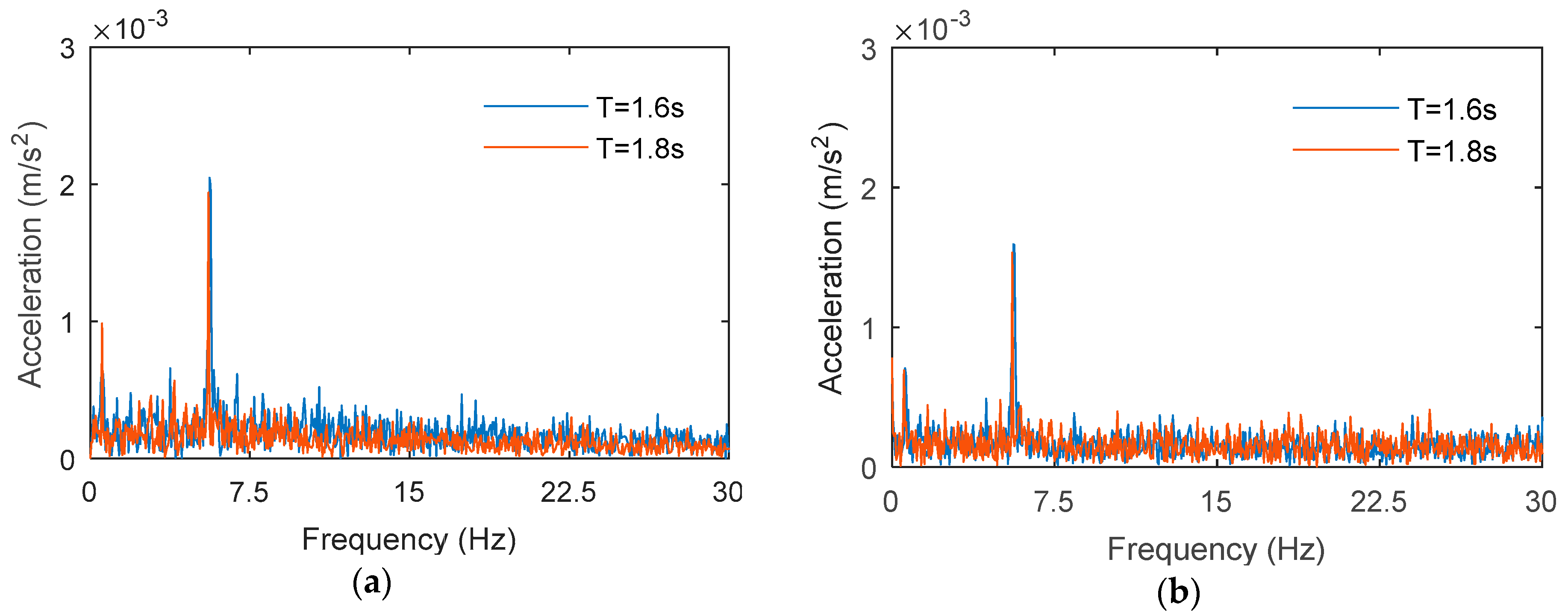
3.2.2. The Electrical Platform in Storm Condition
4. Discussion
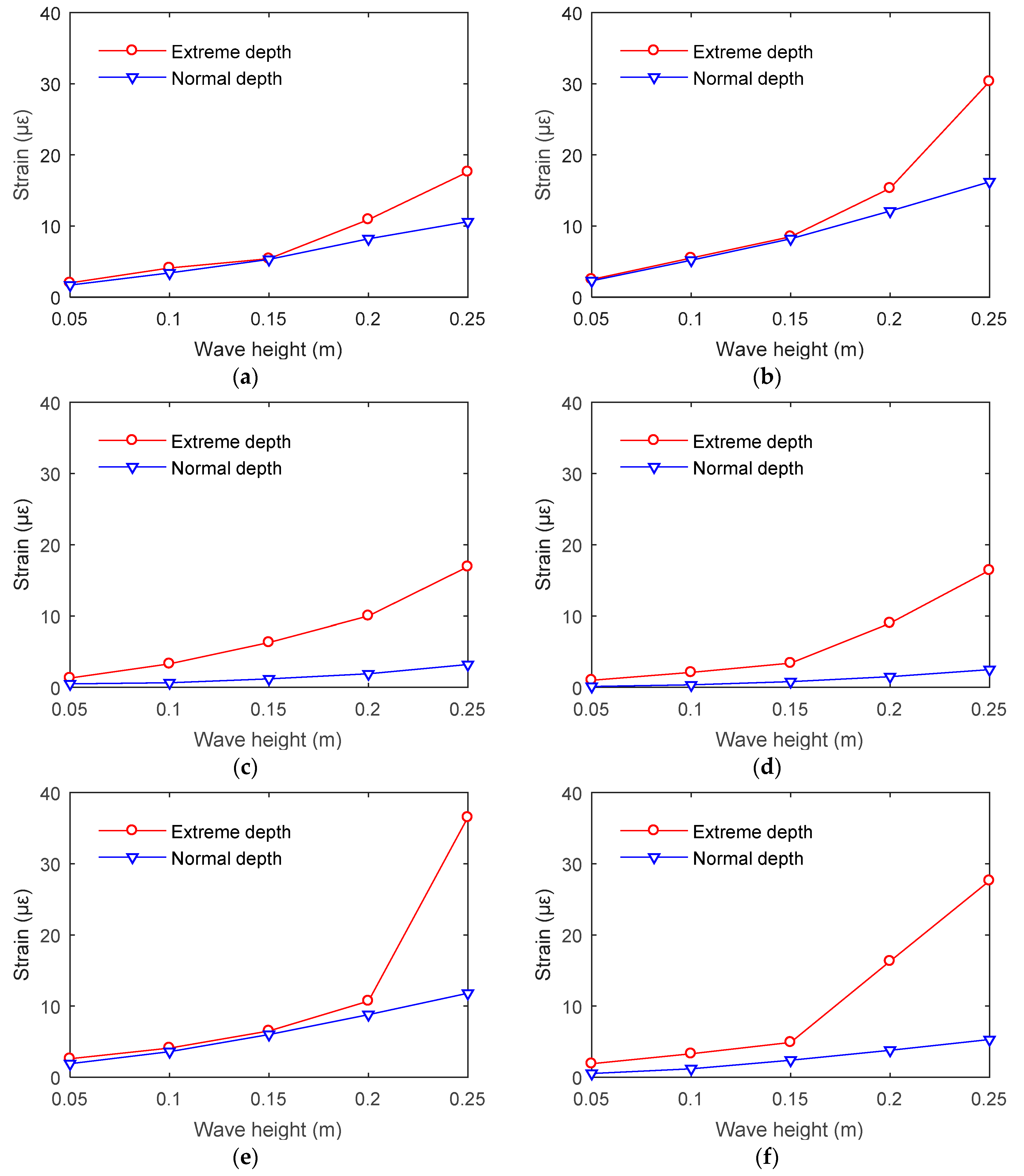
4.1. Effect of Water Depth on Strain Response
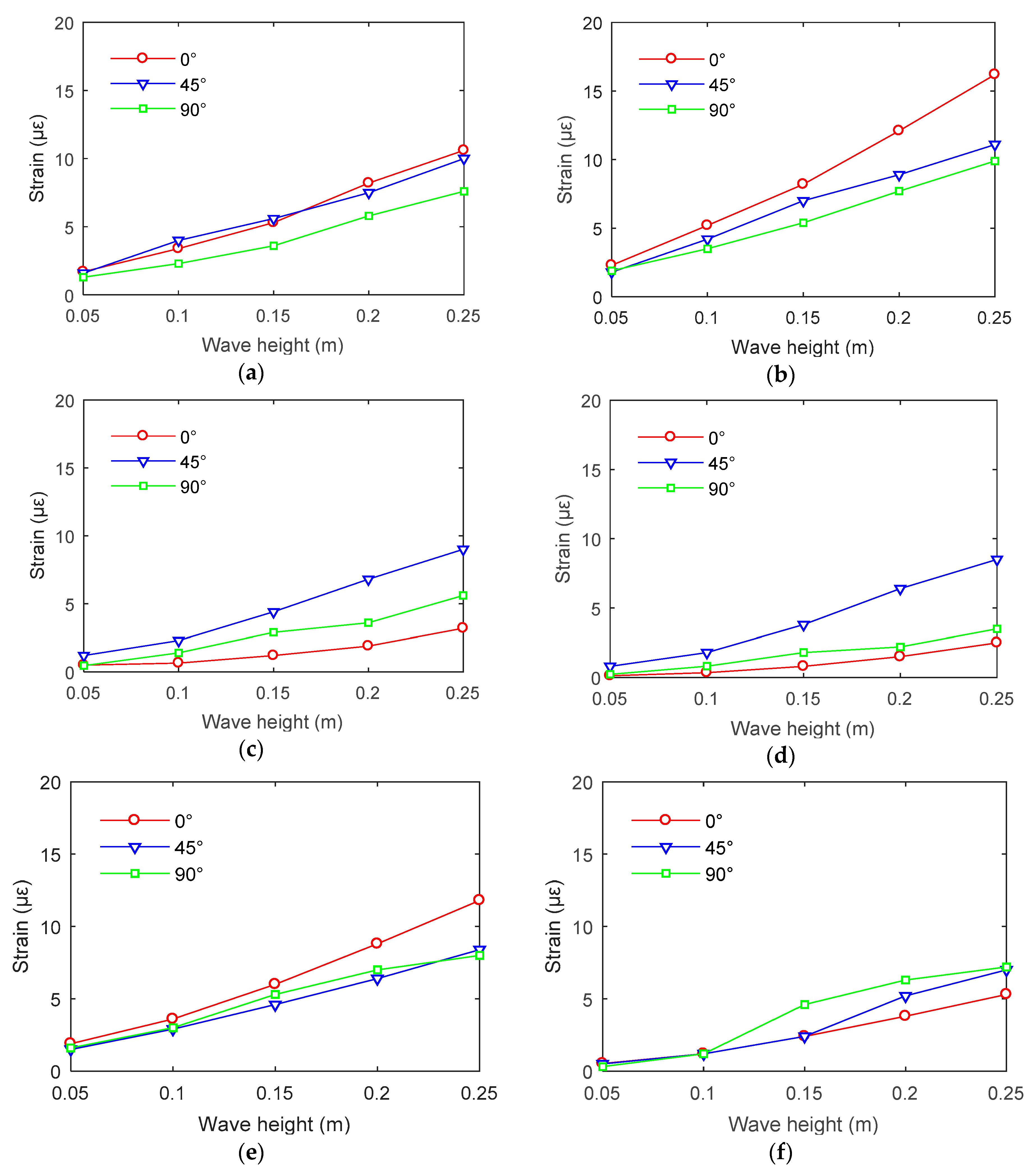
4.2. Effect of Attack Angle on Strain Response
4.3. Effect of Environmental Loads on Strain Response
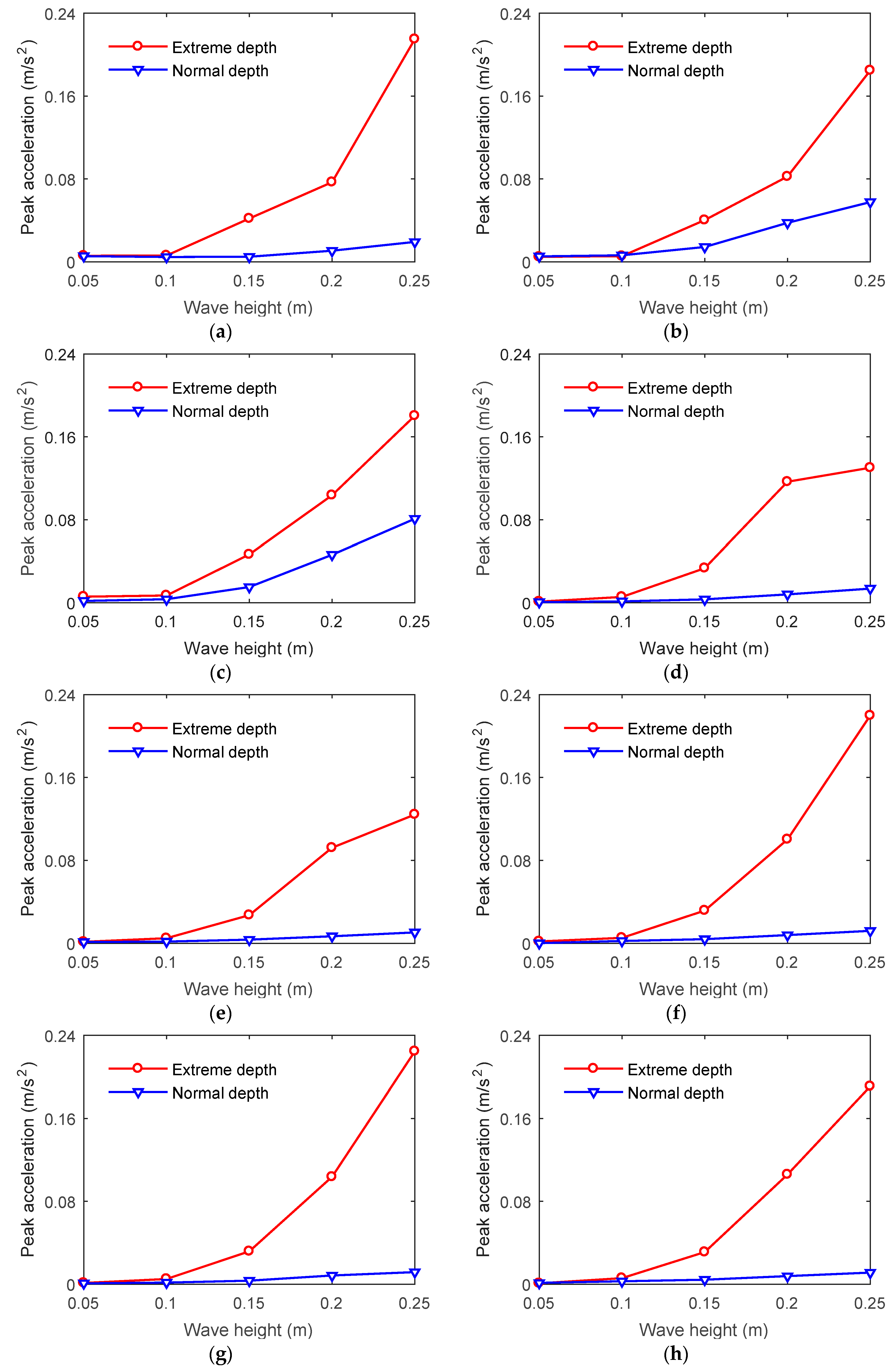
4.4. Effect of Water Depth on Acceleration Response
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Elshafey, A.A.; Haddara, M.R.; Marzouk, H. Dynamic response of offshore jacket structures under random loads. Mar. Struct. 2009, 22, 504–521. [Google Scholar] [CrossRef]
- Dong, W.; Moan, T.; Gao, Z. Long-term fatigue analysis of multi-planar tubular joints for jacket-type offshore wind turbine in time domain. Eng. Struct. 2011, 33, 2002–2014. [Google Scholar] [CrossRef]
- Park, M.S.; Koo, W.; Kawano, K. Numerical analysis of the dynamic response of an offshore platform with a pile-soil foundation system subjected to random waves and currents. J. Waterw. Port Coast. Ocean Eng. 2012, 138, 275–285. [Google Scholar] [CrossRef]
- Taylor, P.H.; Santo, H.; Choo, Y.S. Current blockage: Reduced Morison forces on space frame structures with high hydrodynamic area, and in regular waves and current. Ocean Eng. 2013, 57, 11–24. [Google Scholar] [CrossRef]
- Santo, H.; Taylor, P.H.; Day, A.H.; Nixon, E.; Choo, Y.S. Current blockage and extreme forces on a jacket model in focused wave groups with current. J. Fluid. Struct. 2018, 78, 24–35. [Google Scholar] [CrossRef]
- Santo, H.; Taylor, P.H.; Day, A.H.; Nixon, E.; Choo, Y.S. Blockage and relative velocity Morison forces on a dynamically-responding jacket in large waves and current. J. Fluids Struct. 2018, 81, 161–178. [Google Scholar] [CrossRef]
- Saha, N.; Gao, Z.; Moan, T.; Naess, A. Short-term extreme response analysis of a jacket supporting an offshore wind turbine. Wind Energy 2014, 17, 87–104. [Google Scholar] [CrossRef]
- Raheem, A.; Shehata, E. Study on nonlinear response of steel fixed offshore platform under environmental loads. Arabian J. Sci. Eng. 2014, 39, 6017–6030. [Google Scholar] [CrossRef]
- Zadeh, S.M.G.; Baghdar, R.S.; Olia, S.V.K. Finite element numerical method for nonlinear interaction response analysis of offshore jacket affected by environment marine forces. Open J. Mar. Sci. 2015, 5, 422–442. [Google Scholar] [CrossRef]
- Devaney, L.C. Breaking Wave Loads and Stress Analysis of Jacket Structures Supporting Offshore Wind Turbines; University of Manchester: Manchester, UK, 2012. [Google Scholar]
- Dezvareh, R.; Bargi, K.; Mousavi, S.A. Control of wind/wave-induced vibrations of jacket-type offshore wind turbines through tuned liquid column gas dampers. Struct. Infrast. Eng. 2016, 12, 312–326. [Google Scholar] [CrossRef]
- Wang, W.H.; Gao, Z.; Moan, T.; Li, X. Model Test and Numerical Analysis of a Multi-Pile Offshore Wind Turbine under Seismic, Wind, Wave and Current Loads. J. Offshore Mech. Arct. Eng. 2016, 139, 031901. [Google Scholar] [CrossRef]
- Wei, K.; Myers, A.T.; Arwade, S.R. Dynamic effects in the response of offshore wind turbines supported by jackets under wave loading. Eng. Struct. 2017, 142, 36–45. [Google Scholar] [CrossRef]
- Gho, W.M.; Yang, Y. Ultimate strength of completely overlapped joint for fixed offshore wind turbine jacket substructures. J. Mar. Sci. Appl. 2019, 18, 99–113. [Google Scholar] [CrossRef]
- Liu, F.; Li, X.; Tian, Z.; Zhang, J.; Wang, B. Transient response estimation of an offshore wind turbine support system. Energies 2019, 12, 891. [Google Scholar] [CrossRef]
- Lin, G.; Zhu, T.; Lin, B. Dynamic model test similarity criterion. J. Dalian Univ. Technol. 2000, 40, 1–8. (In Chinese) [Google Scholar]
- Chakrabarti, S. Handbook of Offshore Engineering; Elsevier Press: Amsterdam, The Netherlands, 2005. [Google Scholar]
- API. Recommended Practice for Planning, Designing, and Constructing Fixed Offshore Platforms-Working Stress Design, 22nd, ed.; American Petroleum Institute Recommended Practice 2A-WSD: Washington, DC, USA, 2007. [Google Scholar]
- Gaeta, M.G.; Bonaldo, D.; Samaras, A.G.; Carniel, S.; Archetti, R. Coupled wave-2D hydrodynamics modeling at the Reno river mouth (Italy) under climate change scenarios. Water 2018, 10, 1380. [Google Scholar] [CrossRef]
- Hu, X.; Yang, F.; Song, L.; Wang, H. An unstructured-grid based morphodynamic model for sandbar simulation in the Modaomen Estuary, China. Water 2018, 10, 611. [Google Scholar] [CrossRef]
- Petti, M.; Bosa, S.; Pascolo, S. Lagoon sediment dynamics: A coupled model to study a medium-term silting of tidal channels. Water 2018, 10, 569. [Google Scholar] [CrossRef]
- He, Z.; Hu, P.; Zhao, L.; Wu, G.; Pähtz, T. Modeling of breaching due to overtopping flow and waves based on coupled flow and sediment transport. Water 2015, 7, 4283–4304. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Bi, C.W.; Zhao, S.X.; Dong, G.H.; Yu, H.F. Experimental analysis on dynamic responses of an electrical platform for an offshore wind farm under earthquake load. J. Mar. Sci. Eng. 2019, 7, 279. [Google Scholar] [CrossRef]







| Parameter | Similarity | Similar Scale |
|---|---|---|
| Length | λ | 60 |
| Area | λA | 1120.7 |
| Volume | λ·λA | 67,241 |
| Density | λρ = 1 | 1 |
| Mass | λρ·λ·λA | 67,241 |
| Speed | λ0.5 | 7.746 |
| Acceleration | λg = 1 | 1 |
| Time | λ0.5 | 7.746 |
| Frequency | λ−0.5 | 0.129 |
| Force | λ3 | 603 |
| Moment | λ4 | 604 |
| Moment of area | λA·λr2 | 4.59e6 |
| Moment of mass | λ·λA·λr2 | 2.76e8 |
| Stress | λ4·λD·λA−1·λr−2 | 176.3 |
| Member Type | Model Number | Sectional Dimension (mm) | Section for Model |
|---|---|---|---|
| Box beam | B3000 | 59.1 × 23 | Rectangular section (Height × Width) |
| I-beam | H2000 | 45.5 × 8.6 | |
| H1500 | 34.2 × 6.8 | ||
| H1200 | 27.6 × 6.4 | ||
| H1000 | 22.8 × 5.1 | ||
| H800 | 18.1 × 3.8 | ||
| Pipe | P2000 × 50 | 32 × 3 | Pipe (Outside diameter × Thickness) |
| P1500 × 40 | 25 × 2 | ||
| P1000 × 30 | 22 | Solid bar (Diameter) | |
| P800 × 24 | 18 |
| Member Type | Model Number | Sectional Dimension (mm) | Section for Model |
|---|---|---|---|
| Pipe | P2000 × 50 | 32 × 3 | Pipe (Outside diameter × Thickness) |
| P1500 × 40 | 25 × 2 | ||
| P1200 × 40 | 20 × 2 | ||
| P2800 × 70 | 45 × 5 | ||
| P2600 × 60 | 45 × 3 | ||
| P2900 × 135 | 50 × 5 |
| Test Number | Wave Height (m) | Wave Period (s) |
|---|---|---|
| A1 | 0.05 (3) 1 | 1.6 (12.4) |
| A2 | 0.10 (6) | 1.6 (12.4) |
| A3 | 0.15 (9) | 1.0, 1.2, 1.4, 1.6, 1.8 (7.7, 9.3, 10.8, 12.4, 13.9) |
| A4 | 0.20 (12) | 1.6 (12.4) |
| A5 | 0.25 (15) | 1.6 (12.4) |
| Test Number | Significant Wave Height (m) | Significant Wave Period (s) |
|---|---|---|
| B1 | 0.15 (9) | 1.6 (12.4) |
| B2 | 0.20 (12) | 1.8 (13.9) |
| Test Number | Wind Speed (m/s) | Current Speed (m/s) | Irregular Wave |
|---|---|---|---|
| C1 | 4.6 (36) | 0.226 (1.75) | Hs = 0.15 m Tp = 1.6 s |
| C2 | 6.6 (51.5) | 0.258 (2) | Hs = 0.20 m Tp = 1.8 s |
| Wave Condition | Measuring Point | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| H0.05_T1.6 | 1.7 | 2.3 | 0.5 | 0.13 | 1.9 | 0.53 |
| H0.10_T1.6 | 3.4 | 5.2 | 0.65 | 0.35 | 3.6 | 1.2 |
| H0.15_T1.0 | 1.8 | 5.1 | 1.2 | 0.8 | 3.7 | 2.8 |
| H0.15_T1.2 | 2.1 | 6.5 | 0.9 | 0.5 | 3.7 | 3.3 |
| H0.15_T1.4 | 3.9 | 7.7 | 1.1 | 0.6 | 4.9 | 3 |
| H0.15_T1.6 | 5.3 | 8.2 | 1.2 | 0.81 | 6 | 2.4 |
| H0.15_T1.8 | 6.4 | 9.2 | 1.7 | 1.3 | 6.7 | 2.2 |
| H0.20_T1.6 | 8.2 | 12.1 | 1.9 | 1.5 | 8.8 | 3.8 |
| H0.25_T1.6 | 10.6 | 16.2 | 3.2 | 2.5 | 11.8 | 5.3 |
| Wave Condition | Measuring Point | |||||||
|---|---|---|---|---|---|---|---|---|
| J1 | J2 | J3 | J4 | J5 | J6 | J7 | J8 | |
| H0.05_T1.6 | 0.0197 | 0.024 | 0.0251 | 0.0121 | 0.0044 | 0.0047 | 0.0035 | 0.0075 |
| H0.10_T1.6 | 0.0336 | 0.0644 | 0.0691 | 0.0368 | 0.0082 | 0.0083 | 0.0065 | 0.0055 |
| H0.15_T1.0 | 0.1078 | 0.2110 | 0.2087 | 0.1063 | 0.0226 | 0.0219 | 0.0208 | 0.0174 |
| H0.15_T1.2 | 0.0722 | 0.1510 | 0.167 | 0.0619 | 0.0173 | 0.0146 | 0.0119 | 0.0155 |
| H0.15_T1.4 | 0.0630 | 0.1420 | 0.1561 | 0.056 | 0.0132 | 0.0126 | 0.0095 | 0.0118 |
| H0.15_T1.6 | 0.0577 | 0.1296 | 0.1313 | 0.0601 | 0.0134 | 0.0141 | 0.0124 | 0.0111 |
| H0.15_T1.8 | 0.0510 | 0.1081 | 0.1118 | 0.0552 | 0.0112 | 0.0146 | 0.0106 | 0.0104 |
| H0.20_T1.6 | 0.0715 | 0.1369 | 0.1624 | 0.077 | 0.0163 | 0.0146 | 0.0126 | 0.0131 |
| H0.25_T1.6 | 0.078 | 0.1505 | 0.1901 | 0.075 | 0.0173 | 0.0149 | 0.0152 | 0.0178 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.-L.; Bi, C.-W.; Wu, G.-Y.; Zhao, S.-X.; Dong, G.-H. Laboratory Experimental Investigation on the Hydrodynamic Responses of an Extra-Large Electrical Platform in Wave and Storm Conditions. Water 2019, 11, 2042. https://doi.org/10.3390/w11102042
Zhang D-L, Bi C-W, Wu G-Y, Zhao S-X, Dong G-H. Laboratory Experimental Investigation on the Hydrodynamic Responses of an Extra-Large Electrical Platform in Wave and Storm Conditions. Water. 2019; 11(10):2042. https://doi.org/10.3390/w11102042
Chicago/Turabian StyleZhang, Dong-Liang, Chun-Wei Bi, Guan-Ye Wu, Sheng-Xiao Zhao, and Guo-Hai Dong. 2019. "Laboratory Experimental Investigation on the Hydrodynamic Responses of an Extra-Large Electrical Platform in Wave and Storm Conditions" Water 11, no. 10: 2042. https://doi.org/10.3390/w11102042
APA StyleZhang, D.-L., Bi, C.-W., Wu, G.-Y., Zhao, S.-X., & Dong, G.-H. (2019). Laboratory Experimental Investigation on the Hydrodynamic Responses of an Extra-Large Electrical Platform in Wave and Storm Conditions. Water, 11(10), 2042. https://doi.org/10.3390/w11102042




