Analysis of the Interconnections between Classic Vortex Models of Coherent Structures Based on DNS Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Closed Channel Flow: DNS
2.2. Detection of Streaky Structures
2.2.1. Detection Function
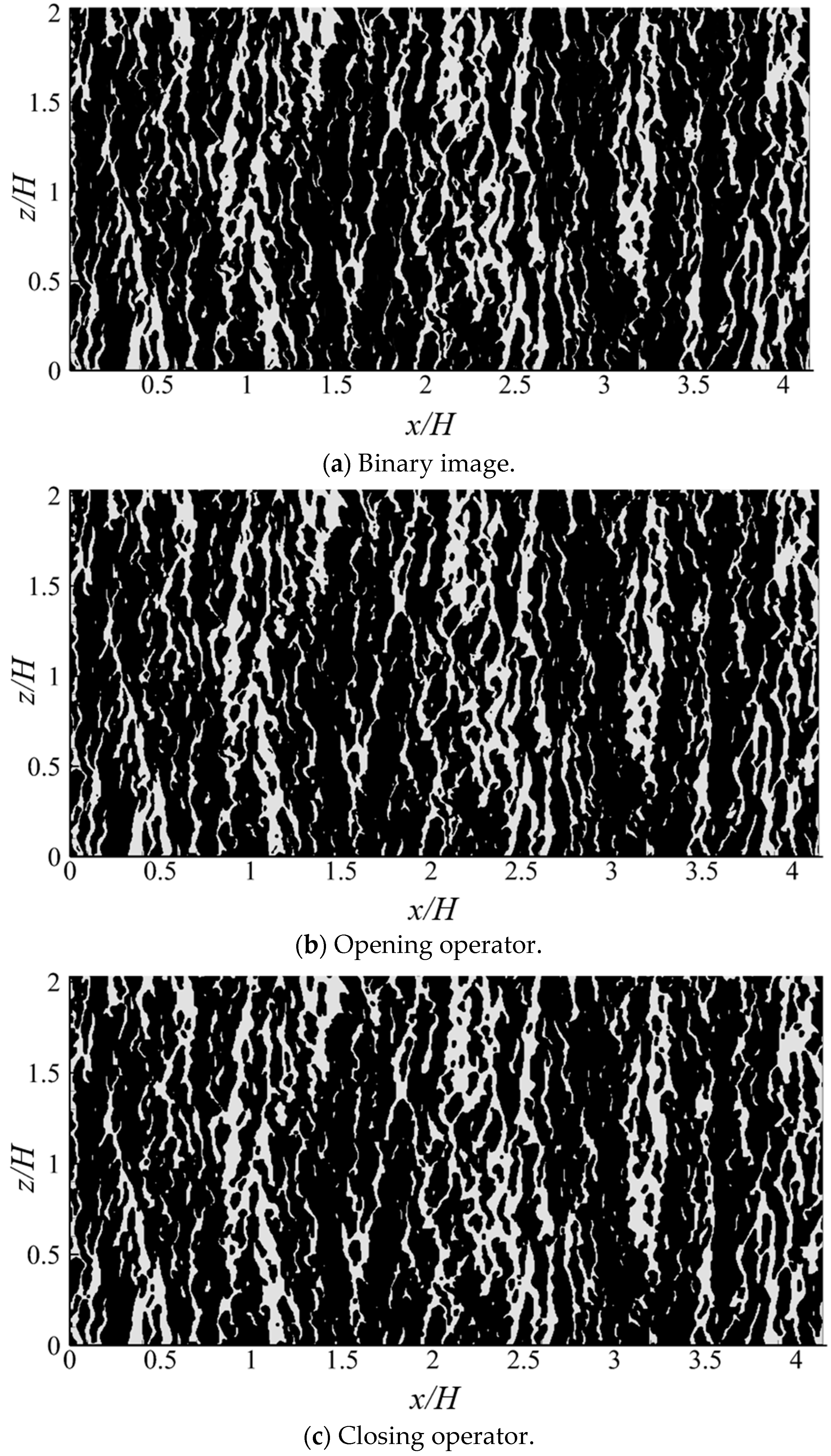
2.2.2. Image Processing
2.2.3. Model of Streaky Structures
3. Results
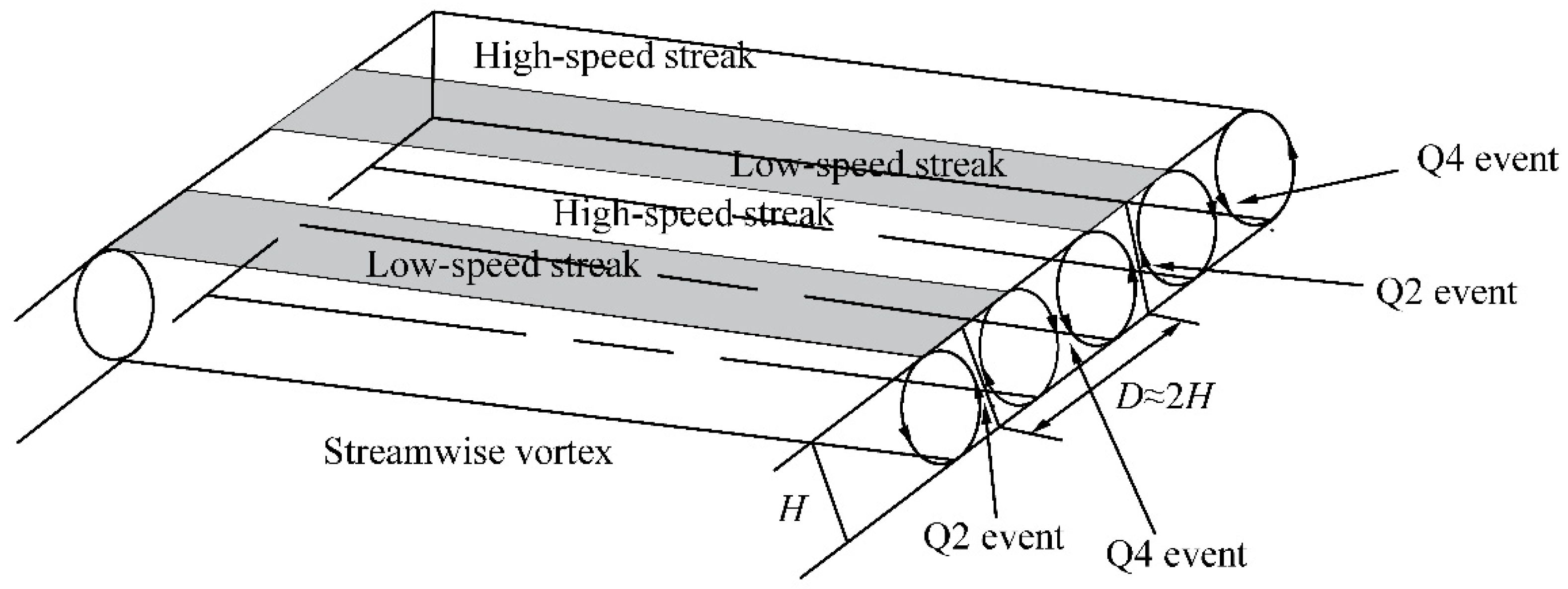
3.1. Streamwise Vortex Model
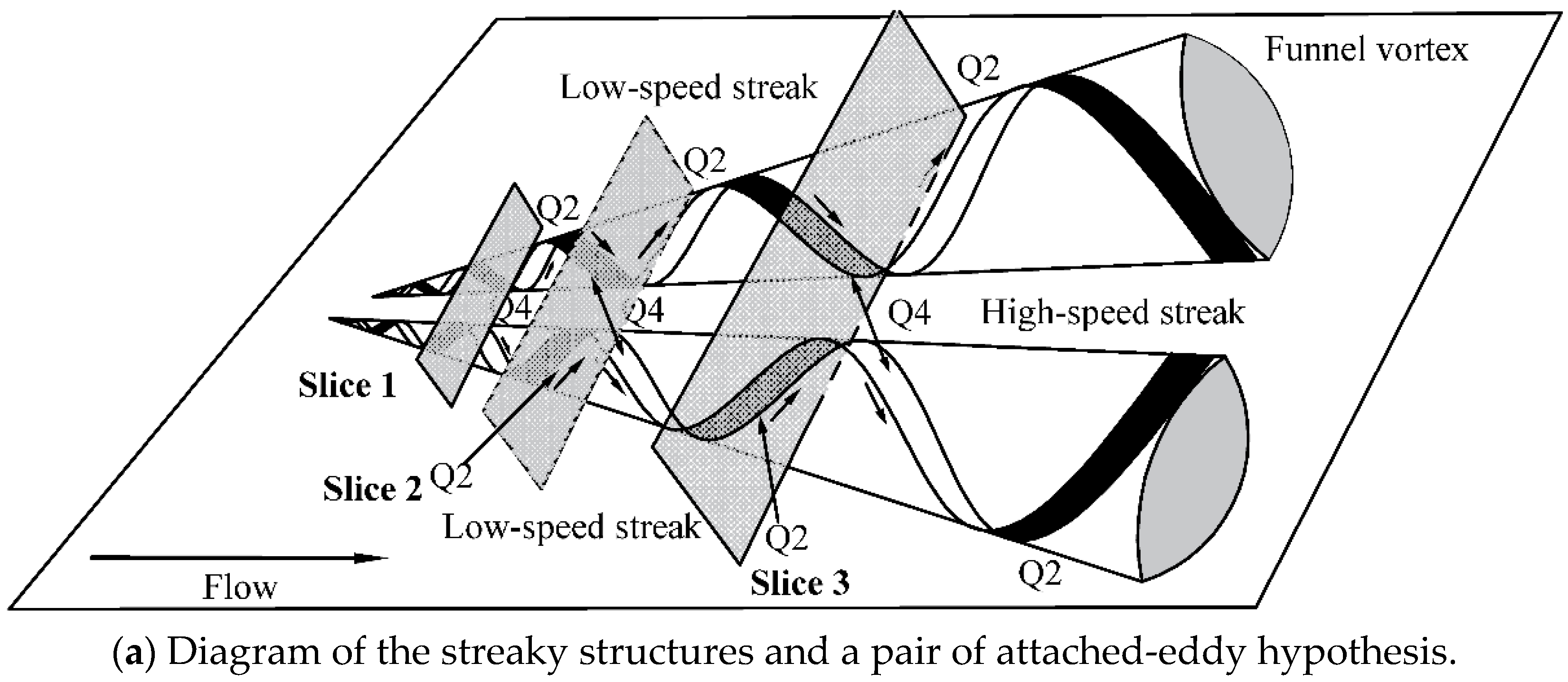
3.2. Attached Eddy Vortex Model
3.3. Hairpin Vortex Model
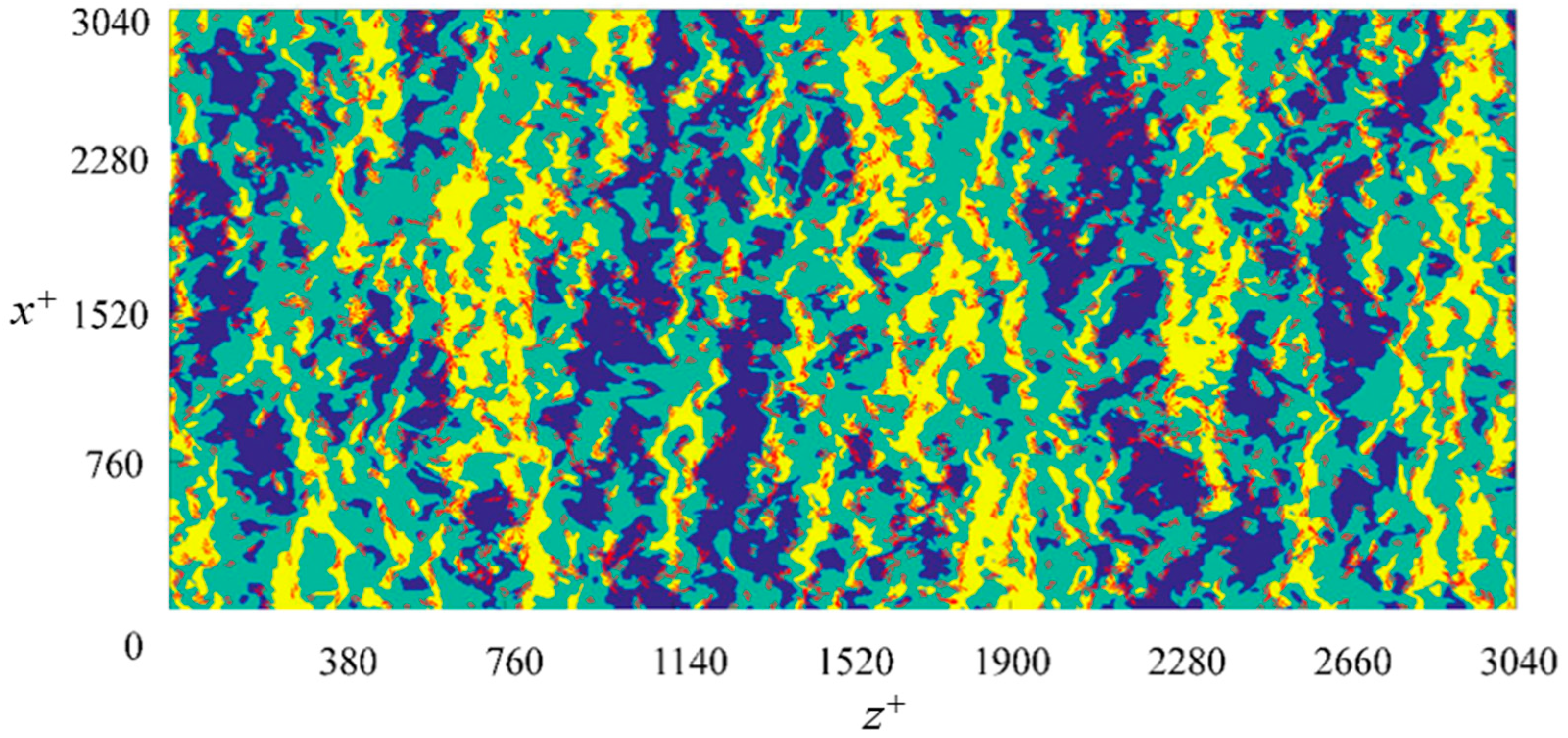
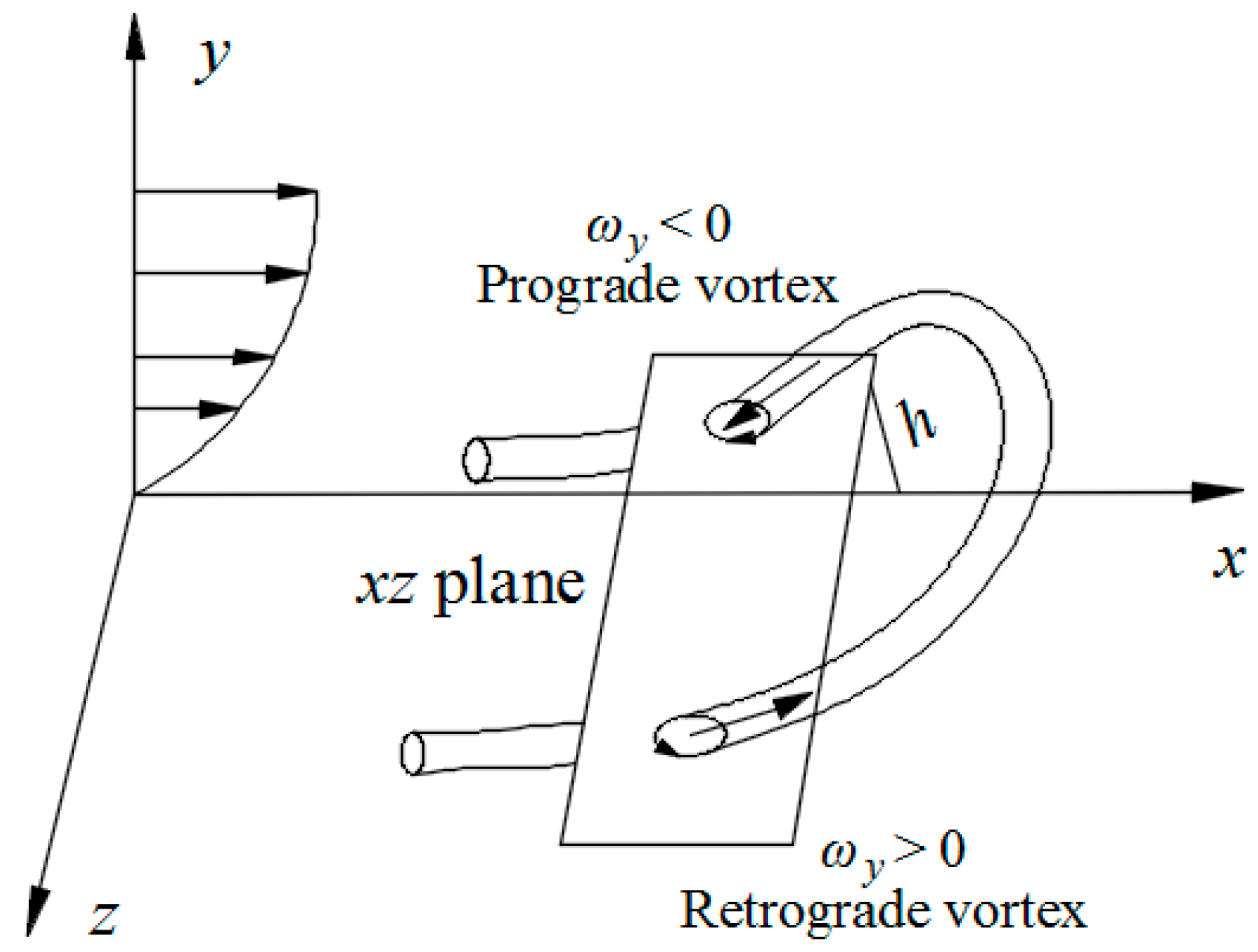
3.3.1. Vortex Extraction in the X–Z Plane
3.3.2. Vortex Density
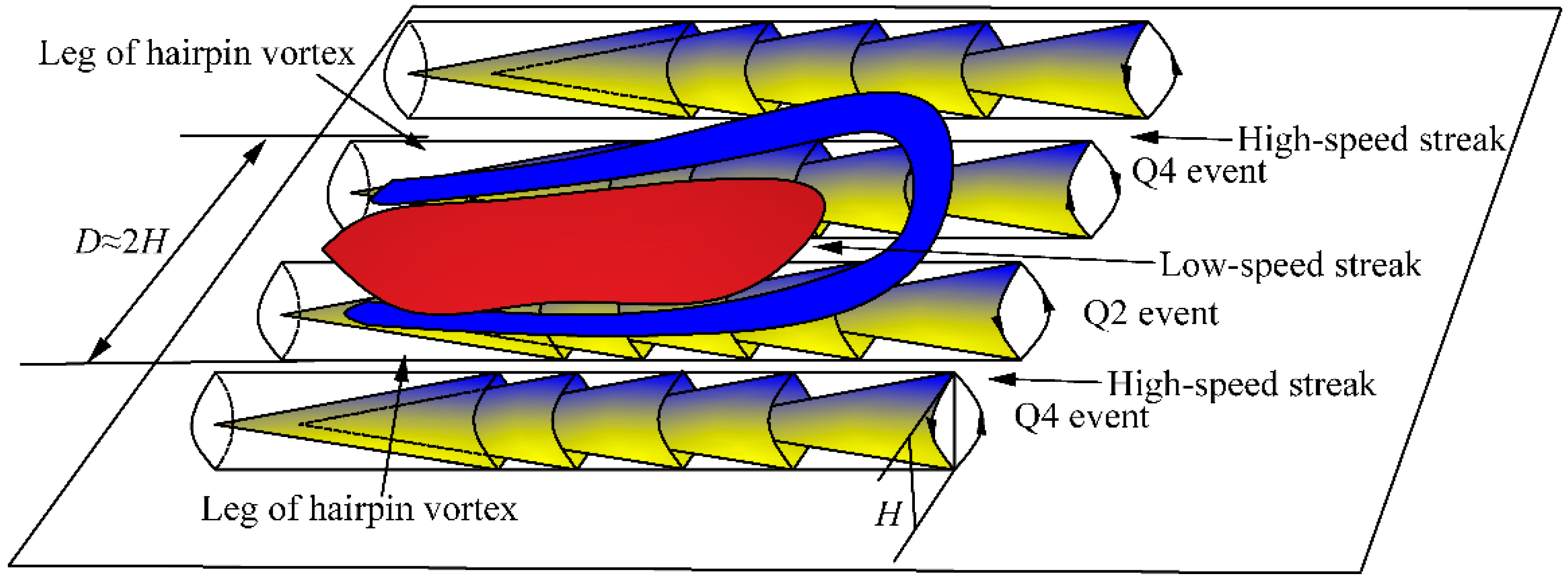
3.3.3. Location of Vortices and Streaks
3.3.4. Vortex Density in Different Streaks
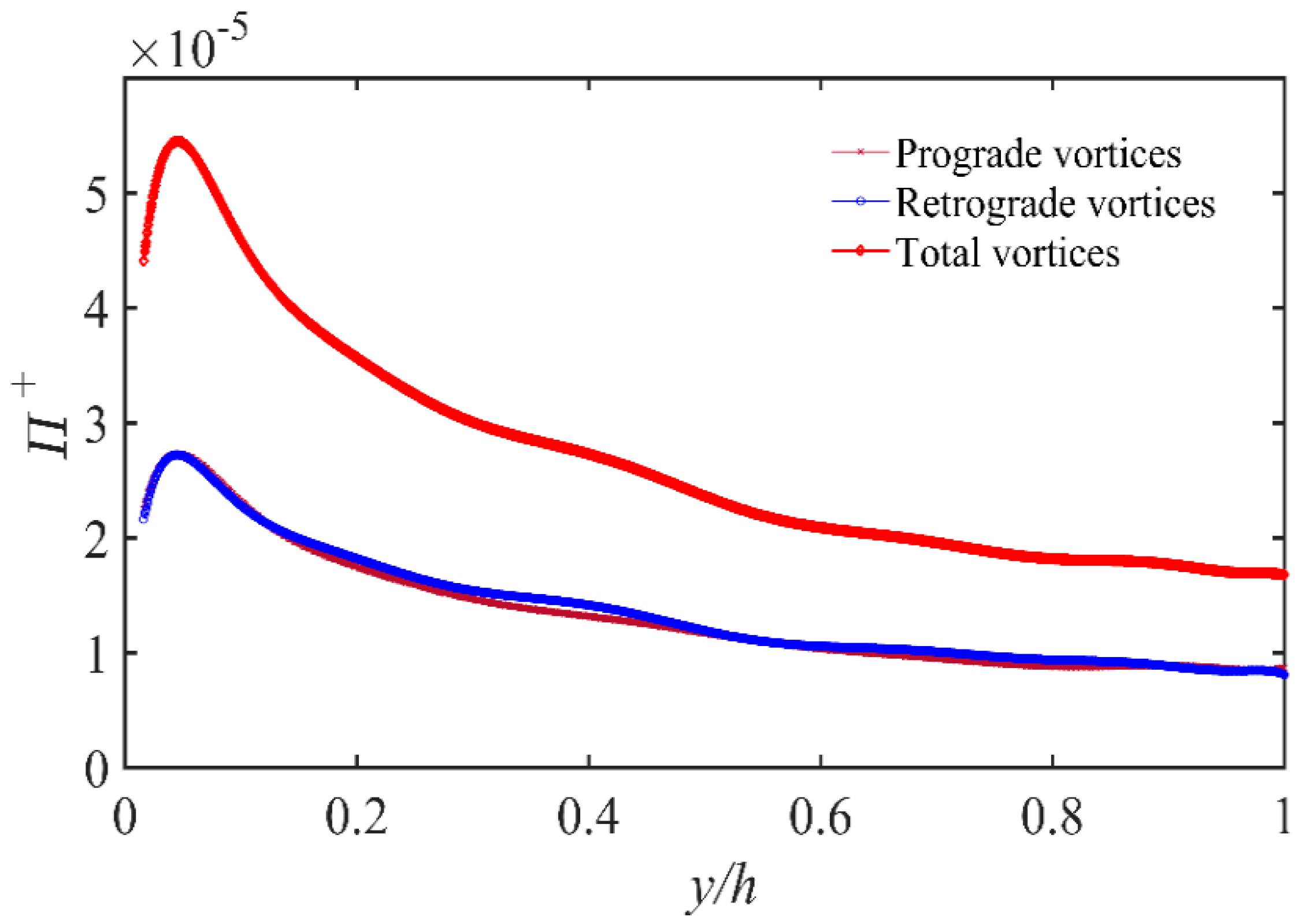
3.3.5. Calculation of Vortex Density
4. Discussion and Conclusions
4.1. Discussion
4.2. Conclusions
- (1)
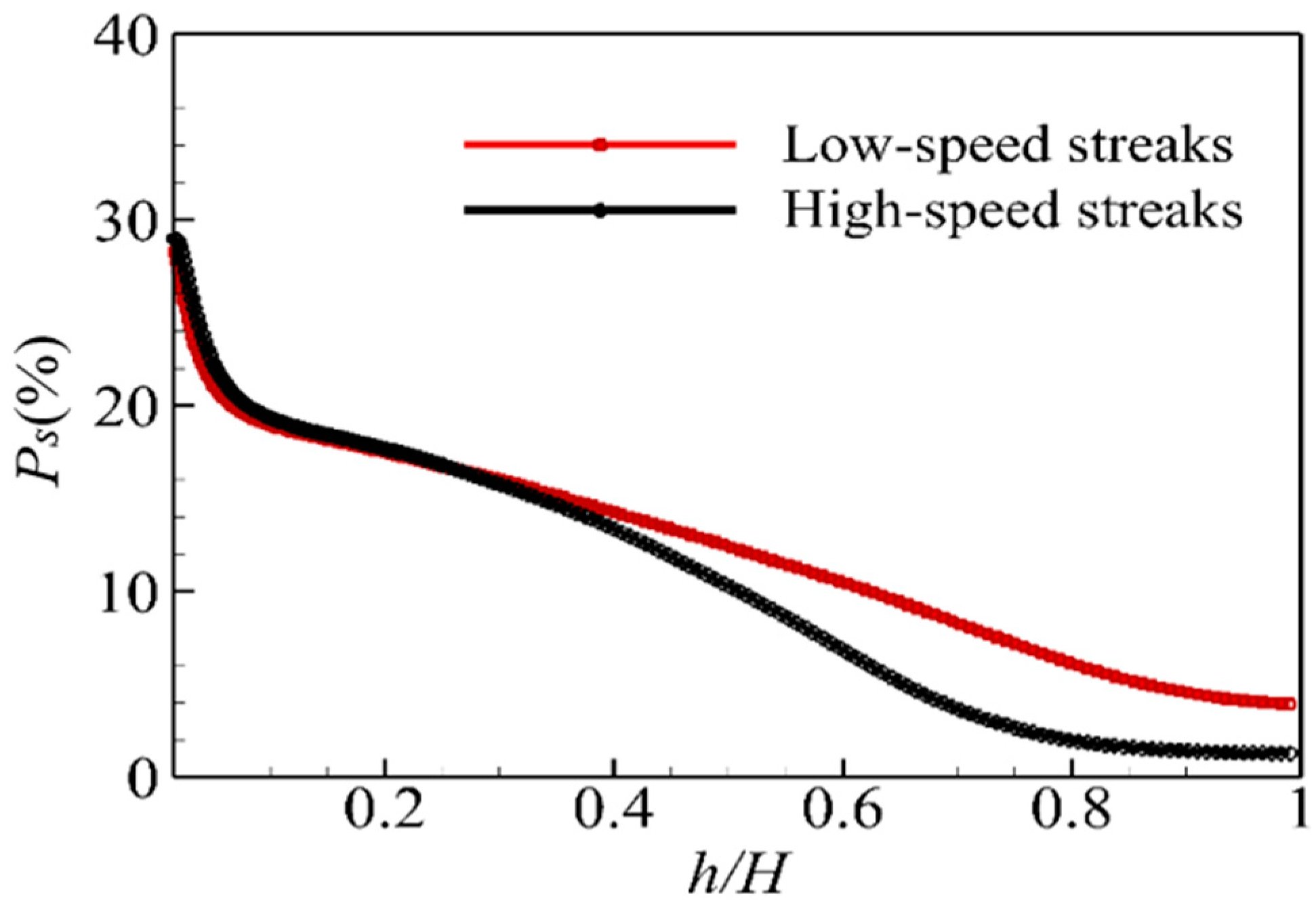
- The average width of streaks and the average distance between adjacent streaks that we observed are consistent with the results of previous studies, which indicates the suitability of our method of identifying and calculating both low- and high-speed streaky structures.
- (2)
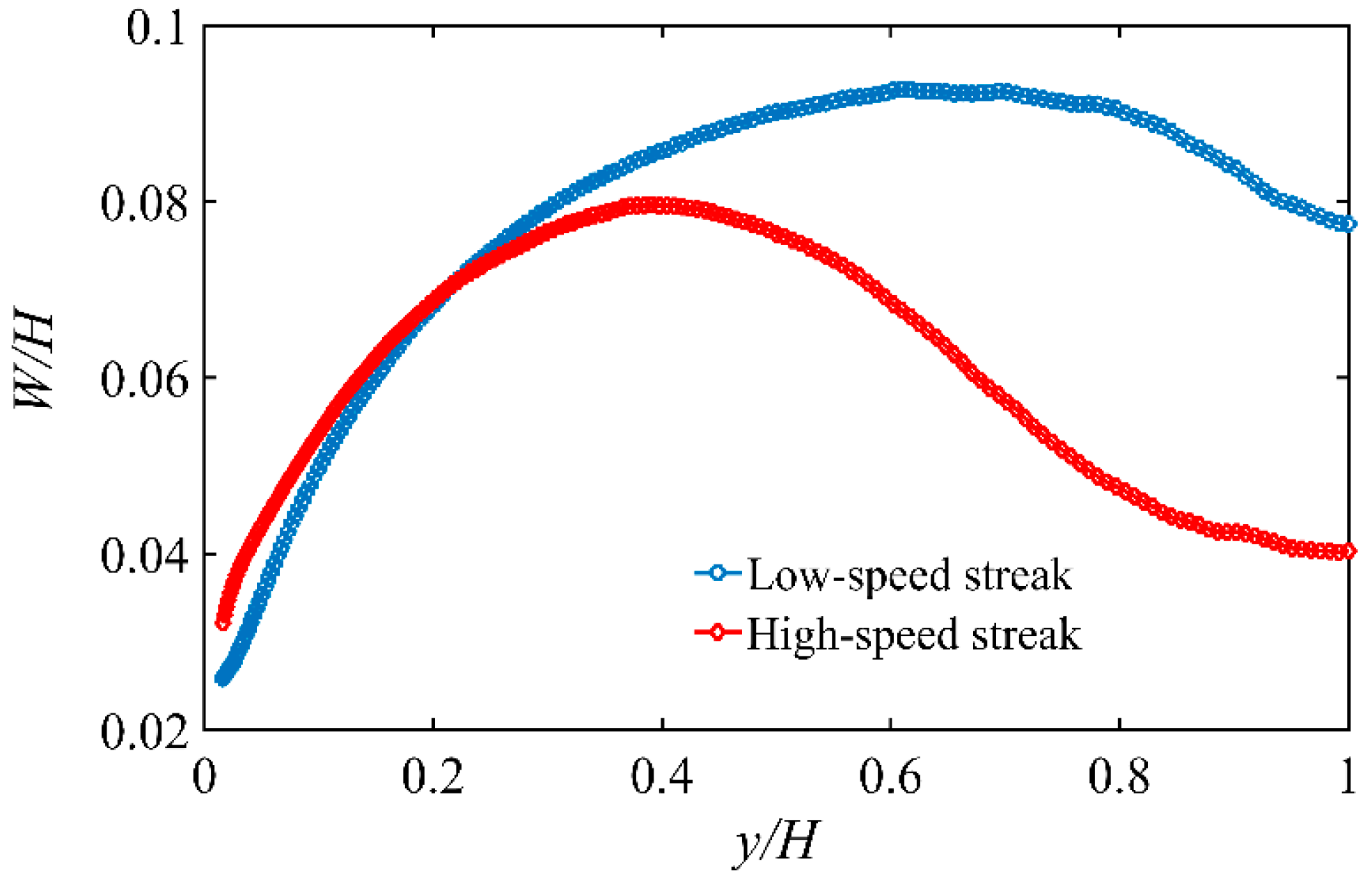
- The development of streaks from the inner turbulent region to the outer region is a continuous process. The length of streaky structures increases linearly with the water depth, and it is approximately twice the water depth. This result also shows the suitability of both the streamwise vortex and the funnel vortex models.
- (3)
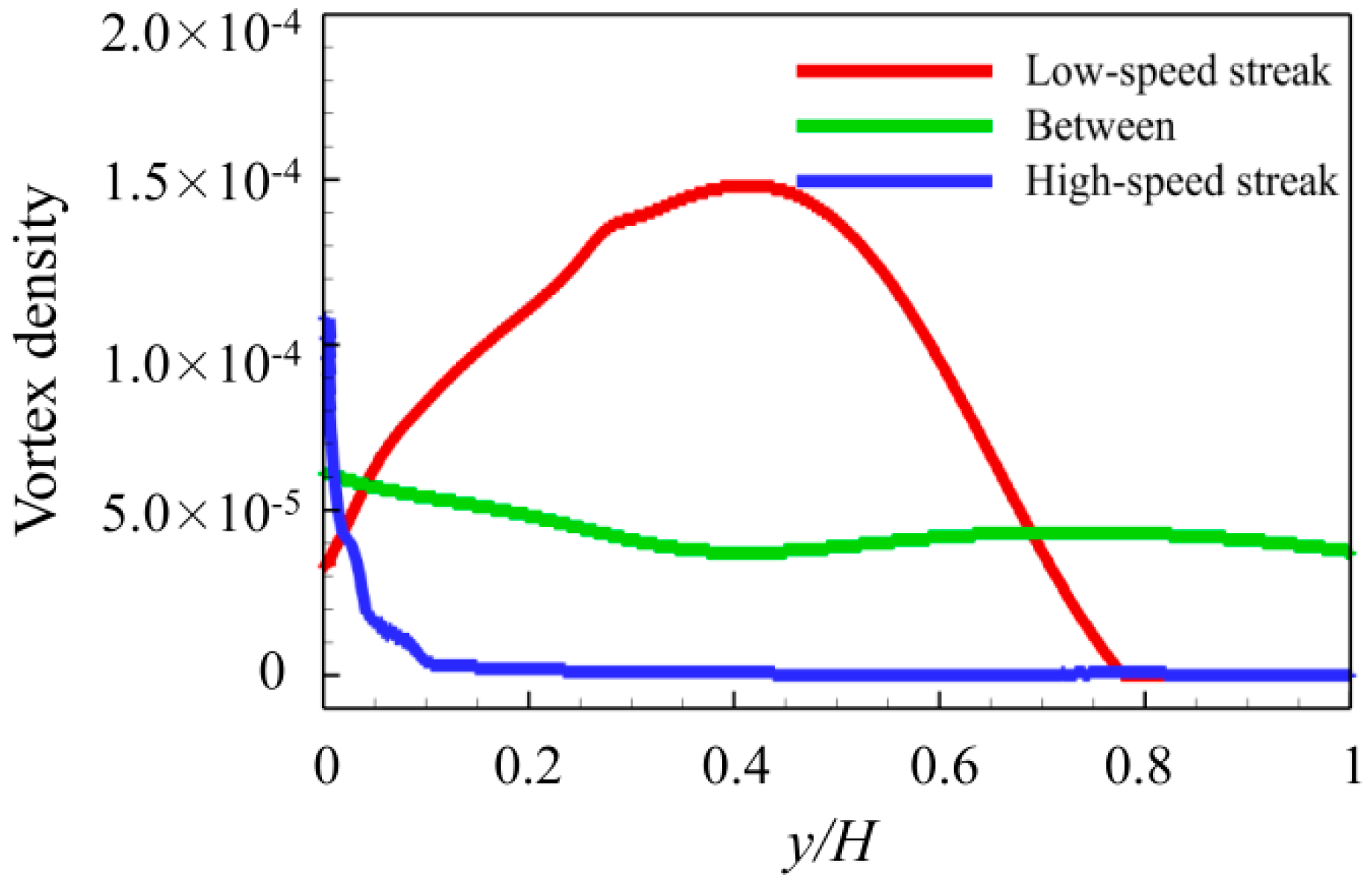
- The spanwise vortex density in the x–z plane is greatest within low-speed streaks, intermediate in the in-between region, and least in the high-speed streaks. We infer that the legs of the hairpin vortices envelop the low-speed streaky structures to move in the streamwise direction and conclude that the hairpin vortex model provides a suitable representation.
- (4)
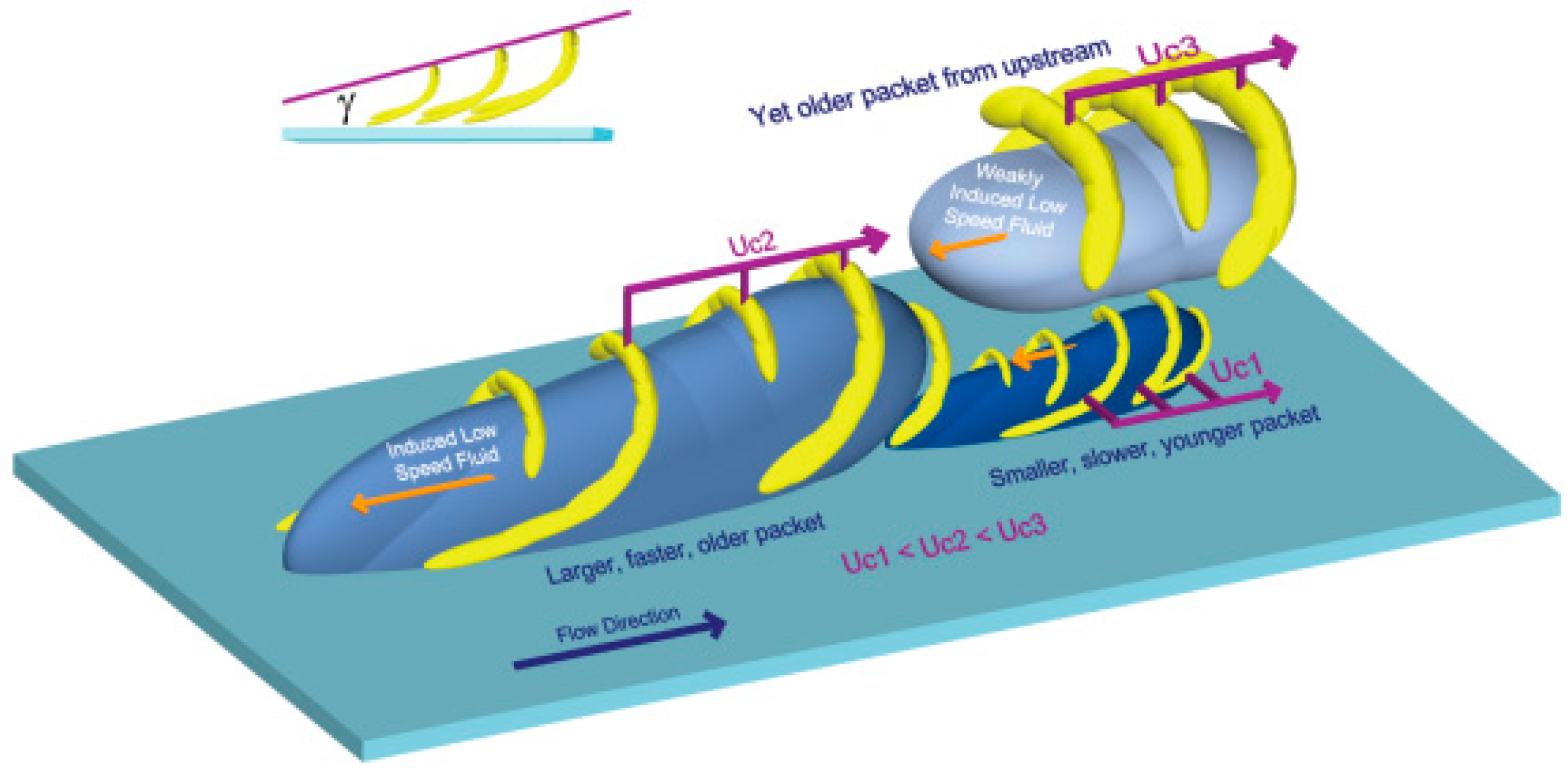
- The theoretical model of the locations in the x–z plane of streamwise vortices, attached-eddy vortices and hairpin vortices established the possibility of the coexistence of three vortex structures; this recognition increases our understanding of the mechanics of coherent structures in turbulent flows.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Parameter Description Unit | |
| As | Total area of low- or high-speed streaky structures |
| At | Total area of the flow field (2048 × 1536) |
| Ct(y+) | Streak threshold at y+ |
| d(r) | Dimensionless spanwise distance at each y+ |
| D | Nondimensional spanwise distance |
| Detection function value of average vortex velocity | |
| Fd | Dimensionless value of detection function |
| m | Total number of rows of the flow field |
| Nx | Grid numbers in the x direction |
| Ny | Grid numbers in the y direction |
| Nz | Grid numbers in the x direction |
| Nvortex | Number of spanwise vortices at position y+ |
| Ps | Area percentages of low- and high-speed streaky structures |
| u | Instantaneous velocity in the x direction m/s |
| u* | Friction velocity m/s |
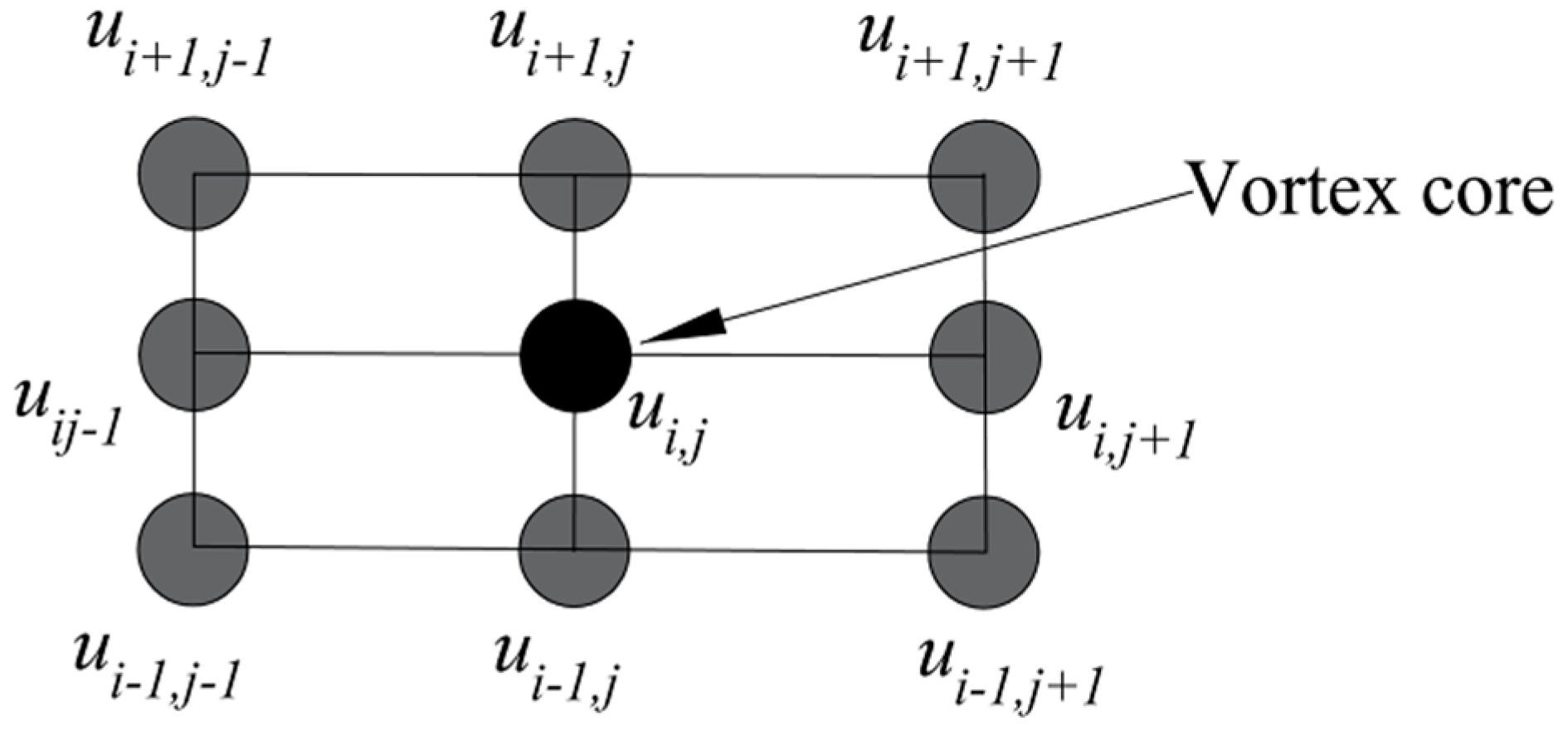
| uij | Velocity at the position of vortex core |
| ū | Average velocity of spanwise vortices in the x–z plane m/s |
| ū′ | Fluctuating velocity m/s |
| u′ | Streamwise velocity fluctuation m/s |
| v | Instantaneous velocity in the y direction m/s |
| w | Instantaneous velocity in the z direction m/s |
| W | Average nondimensional width |
| x | Streamwise direction |
| Δx | Grid resolution in the x directions |
| y* | Inner scale |
| y | Vertical direction |
| Δyc | Wall-normal grid spacing at the channel left |
| z | Spanwise direction |
| Δz | Grid resolution in the z directions |
| (m, n) | Grid position in the x–z plane |
| ustd(y+) | Standard deviation of the streamwise velocity at y+ |
| λci | Two-dimensional swirling-strength 1/s |
| Λci | Dimensionless swirling strength |
| ωz | Fluctuating spanwise vorticity 1/s |
| Local root mean square of Λci at the wall-normal position y | |
| Ωci | Normalized swirling strength |
| Π+ | Vortex population density |
| υ | Kinematic viscosity cm2/s |
References
- Zhong, Q.; Chen, Q.G.; Wang, H.; Li, D.X.; Wang, X.K. Statistical analysis of turbulent super-streamwise vortices based on observations of streaky structures near the free surface in the smooth open channel flow. Water Resour. Res. 2016, 52, 3563–3578. [Google Scholar] [CrossRef]
- Kline, S.J.; Reynolds, W.C.; Schraub, F.A.; Runstadler, P.W. The structure of turbulent boundary layers. J. Fluid Mech. 1967, 30, 741–773. [Google Scholar] [CrossRef]
- Kähler, C.J. Investigation of the spatio-temporal flow structure in the buffer region of a turbulent boundary layer by means of multiplane stereo PIV. Exp. Fluids 2004, 36, 114–130. [Google Scholar] [CrossRef]
- Carlier, J.; Stanislas, M. Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 2005, 535, 143–188. [Google Scholar] [CrossRef]
- Lagraa, B.; Labraga, L.; Mazouz, A. Characterization of low-speed streaks in the near-wall region of a turbulent boundary layer. Eur. J. Mech. B Fluids 2004, 23, 587–599. [Google Scholar] [CrossRef]
- Lin, J.; Laval, J.; Foucaut, J.; Stanislas, M. Quantitative characterization of coherent structures in the buffer layer of near-wall turbulence. Exp. Fluids 2008, 45, 999–1013. [Google Scholar] [CrossRef]
- Nakagawa, H.; Nezu, I. Structure of space-time correlations of bursting phenomena in an open-channel flow. J. Fluid Mech. 1981, 104, 1–43. [Google Scholar] [CrossRef]
- Shvidchenko, A.B.; Pender, G. Macroturbulent structure of open-channel flow over gravel beds. Water Resour. Res. 2001, 37, 709–719. [Google Scholar] [CrossRef]
- Roy, A.G.; Buffin-Belanger, T.; Lamarre, H.; Kirkbride, A.D. Size, shape and dynamics of large-scale turbulent flow structures in a gravel-bed river. J. Fluid Mech. 2004, 500, 1–27. [Google Scholar] [CrossRef]
- Wang, H.; Zhong, Q.; Wang, X.K.; Li, D.X. Quantitative characterization of streaky structures in open-channel flows. J. Hydraul. Eng. 2017, 143, 04017040. [Google Scholar] [CrossRef]
- Sukhodolov, A.N.; Nikora, V.I.; Katolikov, V.M. Flow dynamics in alluvial channels: The legacy of Kirill V. Grishanin. J. Hydraul. Res. 2011, 49, 285–292. [Google Scholar] [CrossRef]
- Fox, J.F.; Patrick, A. Large-scale eddies measured with large scale particle image velocimetry. Flow Meas. Instrum. 2008, 19, 283–291. [Google Scholar] [CrossRef]
- Panton, R.L. Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 2001, 37, 341–383. [Google Scholar] [CrossRef]
- Gulliver, J.S.; Halverson, M.J. Measurements of large streamwise vortices in an open-channel flow. Water Resour. Res. 1987, 23, 115–123. [Google Scholar] [CrossRef]
- Imamoto, H.; Ishigaki, T. Visualization of longitudinal eddies in an open channel flow. In Proceedings of the Fourth International Symposium on Flow Visualization IV, Paris, France, 26–29 August 1986; pp. 323–337. [Google Scholar]
- Rashidi, M.; Banerjee, S. Turbulence structure in free-surface channel flows. Phys. Fluids 1988, 31, 2491–2503. [Google Scholar] [CrossRef]
- Townsend, A.A. Equilibrium layers and wall turbulence. J. Fluid Mech. 1961, 11, 97–120. [Google Scholar] [CrossRef]
- Adrian, R.J.; Marusic, I. Coherent structures in flow over hydraulic engineering surfaces. J. Hydraul. Res. 2012, 50, 451–464. [Google Scholar] [CrossRef]
- Nezu, I.; Rodi, W. Open-channel flow measurements with a laser Doppler anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H.; Jirka, G.H. Turbulence in open-channel flows. J. Hydraul. Eng. 1994, 120, 1235–1237. [Google Scholar] [CrossRef]
- Del Alamo, J.C.; Jiménez, J.; Zandonade, P.; Moser, R.D. Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 2004, 500, 135–144. [Google Scholar] [CrossRef]
- Herpin, S.; Stanislas, M.; Soria, J. The organization of near- wall turbulence: A comparison between boundary layer SPIV data and channel flow DNS data. J. Turbul. 2010, 11, 1–30. [Google Scholar] [CrossRef]
- Kaftori, D.; Hetsroni, G.; Banerjee, S. Particle behavior in the turbulent boundary layer. I. Motion, deposition, and entrainment. Phys. Fluids 1995, 7, 1095–1106. [Google Scholar] [CrossRef]
- Adrian, R.J. Hairpin vortex organization in wall turbulence. Phys. Fluids 2007, 19, 041301. [Google Scholar] [CrossRef]
- Zhou, J.; Adrian, R.J.; Balachandar, S.S.; Kendall, T.M. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Wu, Y.; Christensen, K.T. Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 2006, 568, 55–76. [Google Scholar] [CrossRef]
- Chen, H.; Adrian, R.J.; Zhong, Q.; Wang, X.K. Analytic solutions for three dimensional swirling strength in compressible and incompressible flows. Phys. Fluids 2014, 26, 81701. [Google Scholar] [CrossRef]
- Zhong, Q.; Li, D.X.; Chen, Q.G.; Wang, X.K. Coherent structures and their interactions in smooth open channel flows. Environ. Fluid Mech. 2015, 15, 653–672. [Google Scholar] [CrossRef]
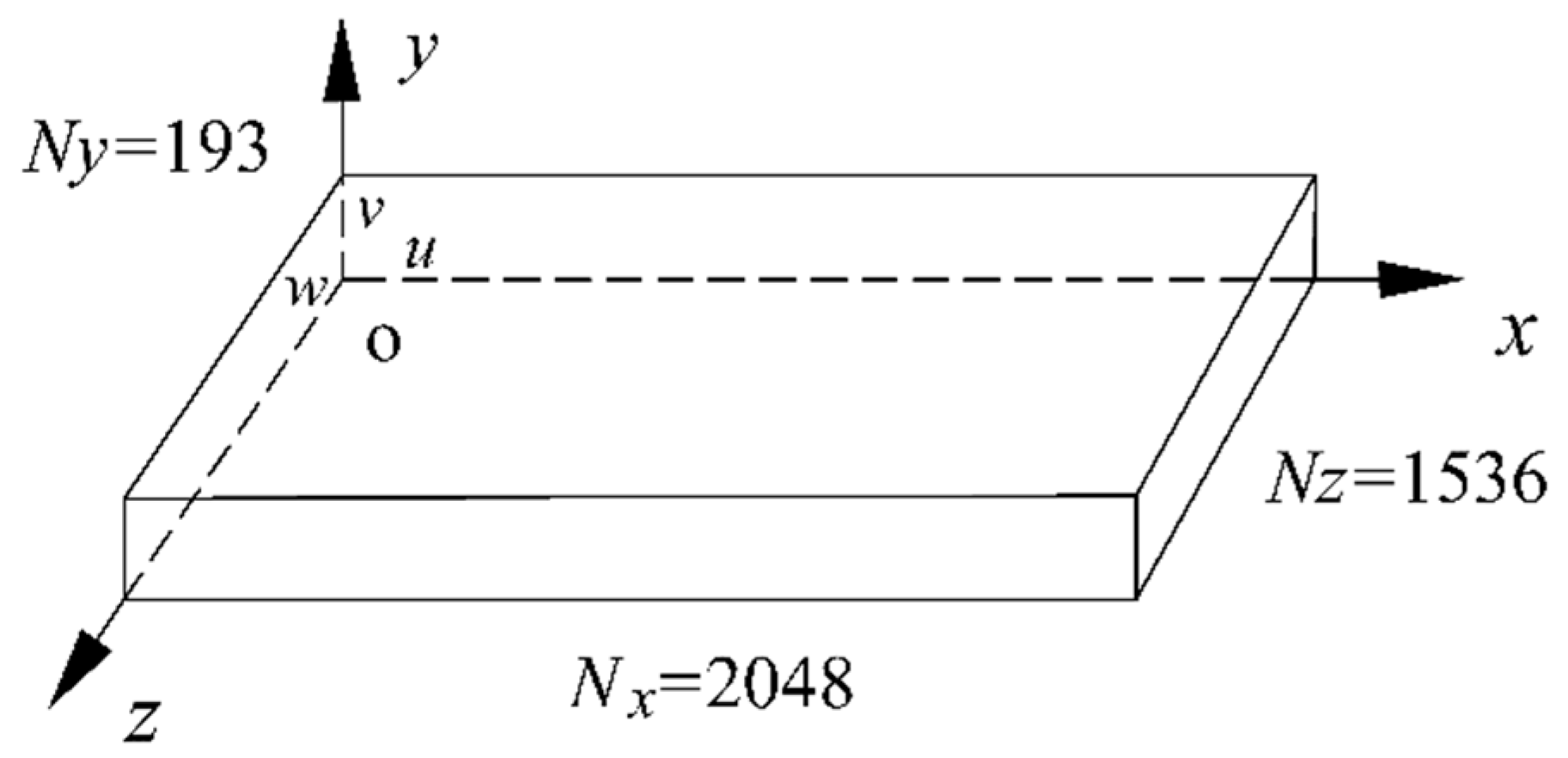




| Parameter | Lx/H | Lz/H | Ly/H | Δx+ | Δz+ | Δyc+ | Nx | Nz | Ny |
|---|---|---|---|---|---|---|---|---|---|
| Original | 8π | 3π | 2 | 7.6 | 3.8 | 7.6 | 3072 | 2304 | 385 |
| Present study | 16π/3 | 2π | 1 | 7.6 | 3.8 | 7.6 | 2048 | 1536 | 193 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Peng, G.; Chen, M.; Fan, J. Analysis of the Interconnections between Classic Vortex Models of Coherent Structures Based on DNS Data. Water 2019, 11, 2005. https://doi.org/10.3390/w11102005
Wang H, Peng G, Chen M, Fan J. Analysis of the Interconnections between Classic Vortex Models of Coherent Structures Based on DNS Data. Water. 2019; 11(10):2005. https://doi.org/10.3390/w11102005
Chicago/Turabian StyleWang, Hao, Guoping Peng, Ming Chen, and Jieling Fan. 2019. "Analysis of the Interconnections between Classic Vortex Models of Coherent Structures Based on DNS Data" Water 11, no. 10: 2005. https://doi.org/10.3390/w11102005
APA StyleWang, H., Peng, G., Chen, M., & Fan, J. (2019). Analysis of the Interconnections between Classic Vortex Models of Coherent Structures Based on DNS Data. Water, 11(10), 2005. https://doi.org/10.3390/w11102005




