A Numerical Simulator for Modeling the Coupling Processes of Subsurface Fluid Flow and Reactive Transport Processes in Fractured Carbonate Rocks
Abstract
:1. Introduction
2. The Mathematical Models
2.1. The Stokes–Brinkman Model
2.2. The Reactive-Transport Model
2.3. The Rock Property Models
3. Numerical Solution Strategies
- (1)
- Firstly, the Stokes–Brinkman equation (Equation (1)) and the continuity equation (Equation (2)) are solved by a staggered grid finite difference method for velocities and pressure.
- (2)
- Secondly, the velocities at grid-cell centers are calculated by averaging the velocities of grid faces obtained from the solution of the Stokes–Brinkman equation.
- (3)
- Thirdly, based on the calculated velocities at cell centers, the concentrations of primary species are determined by solving the reactive-transport equations using an implicit control-volume upwinding finite difference scheme.
- (4)
- The last step is then to update the rock porosities and absolute permeabilities based on the concentrations of primary species.
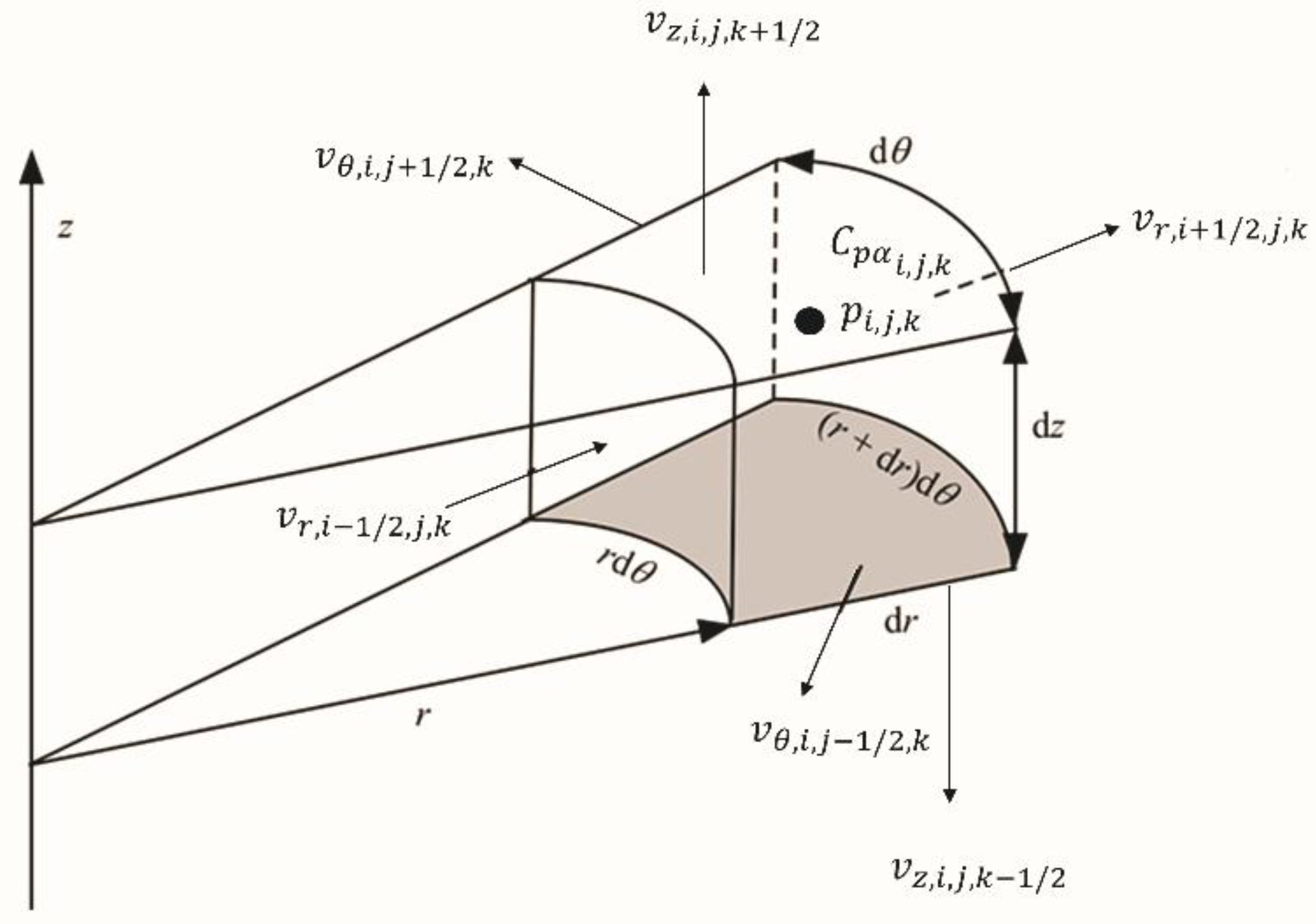
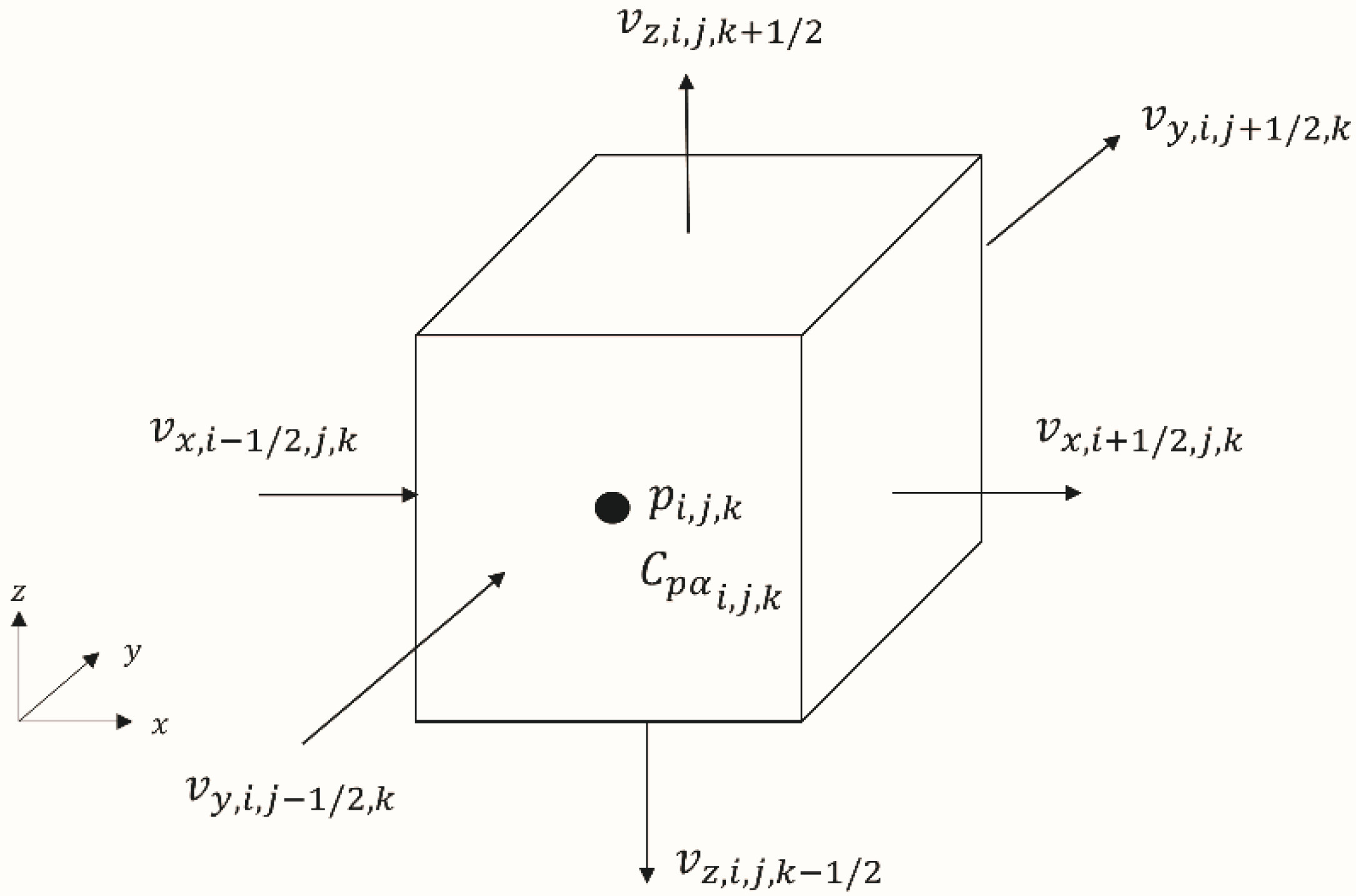
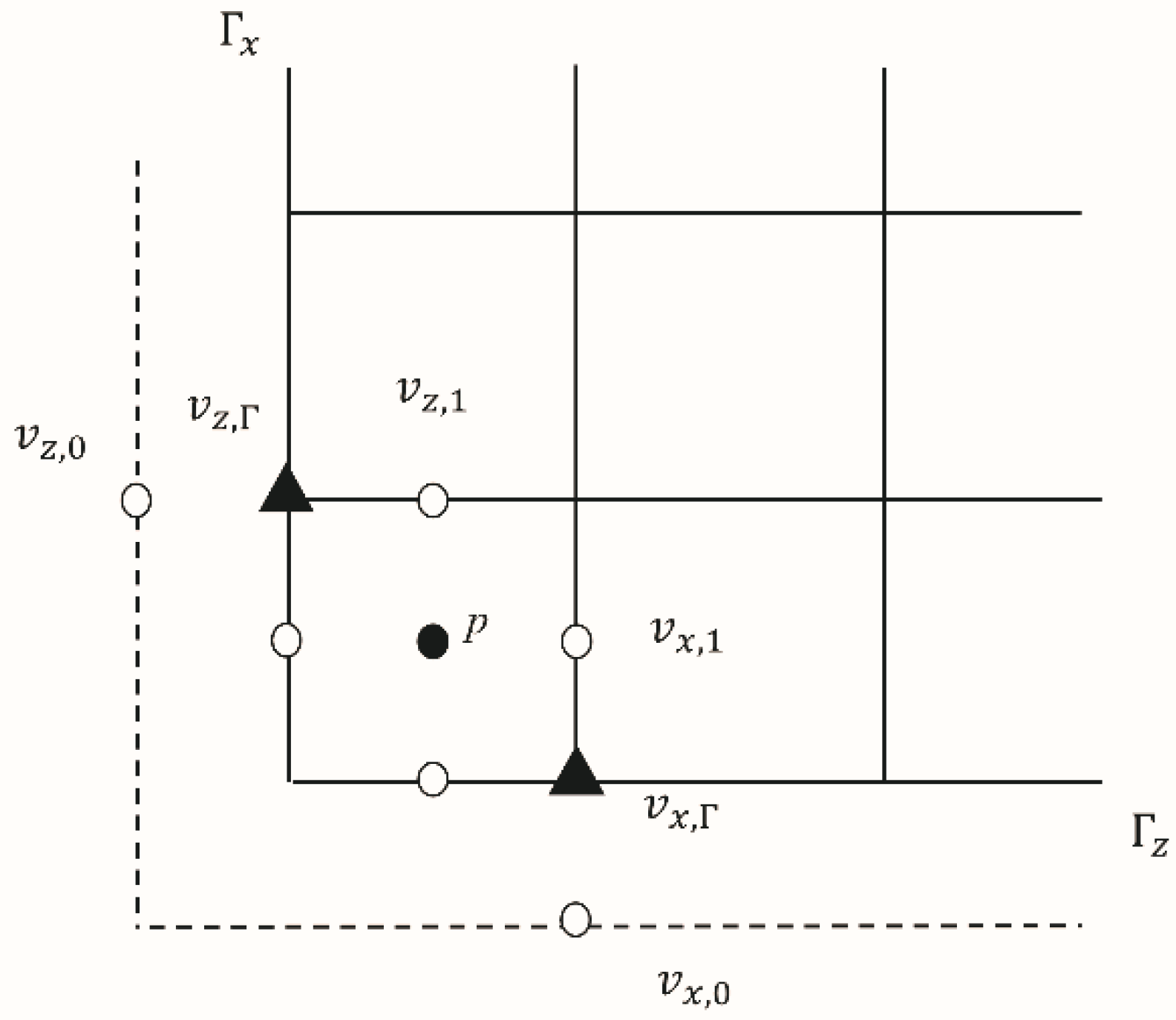
3.1. Numerical Solution of the Stokes–Brinkman Model
3.2. Numerical Solution of the Reactive Transport Model
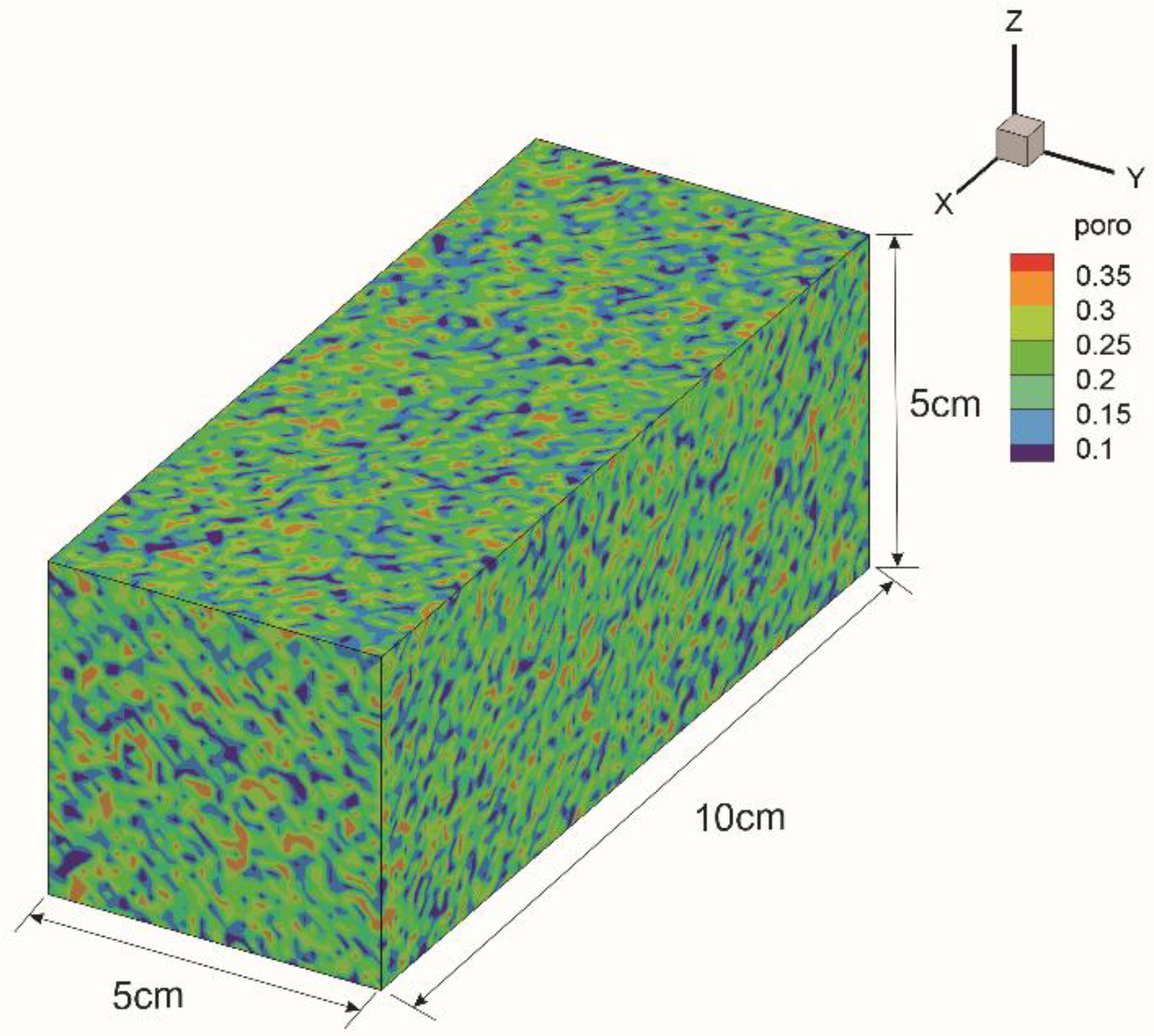
4. Numerical Experiments
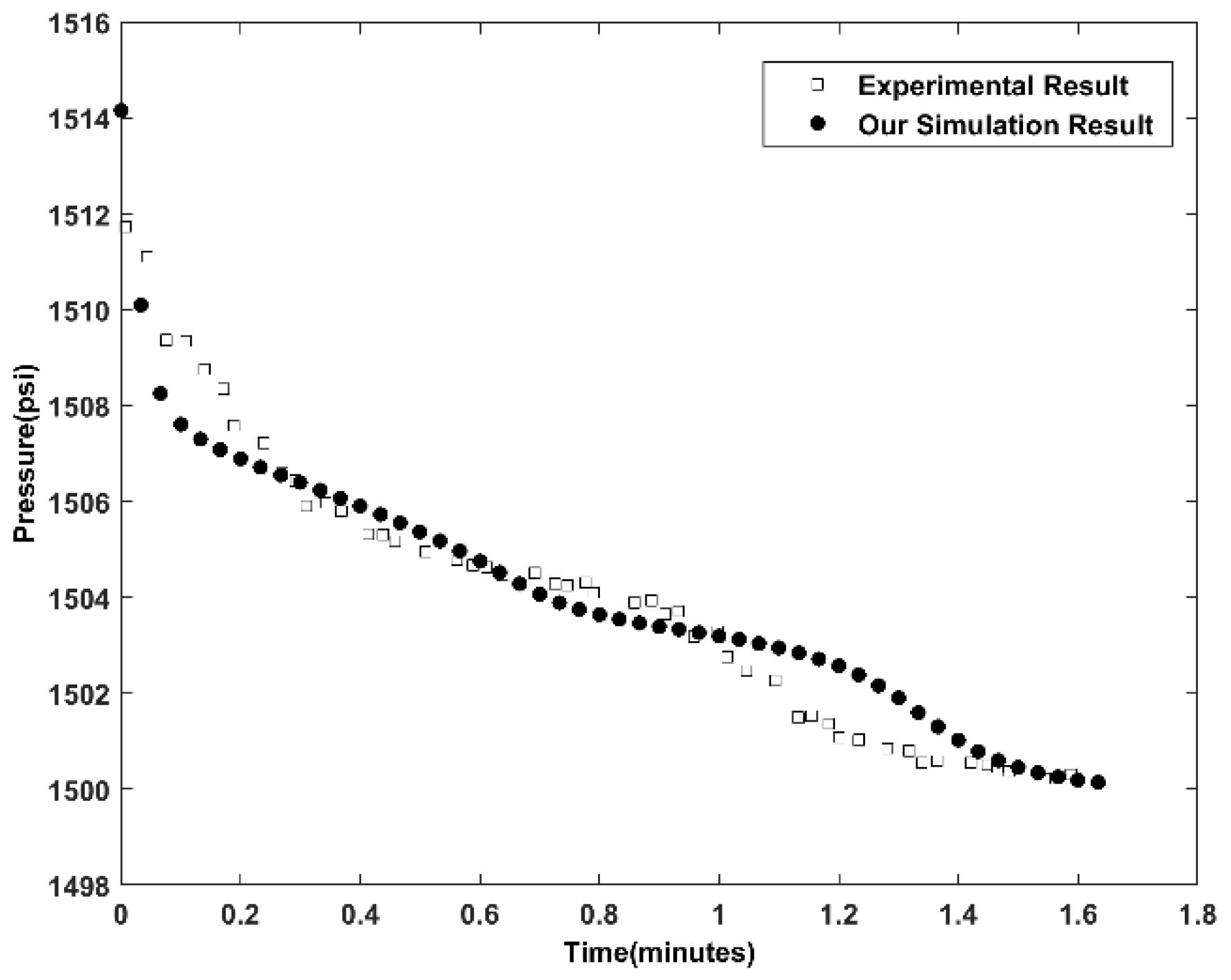
4.1. Model Validation
4.2. Numerical Studies
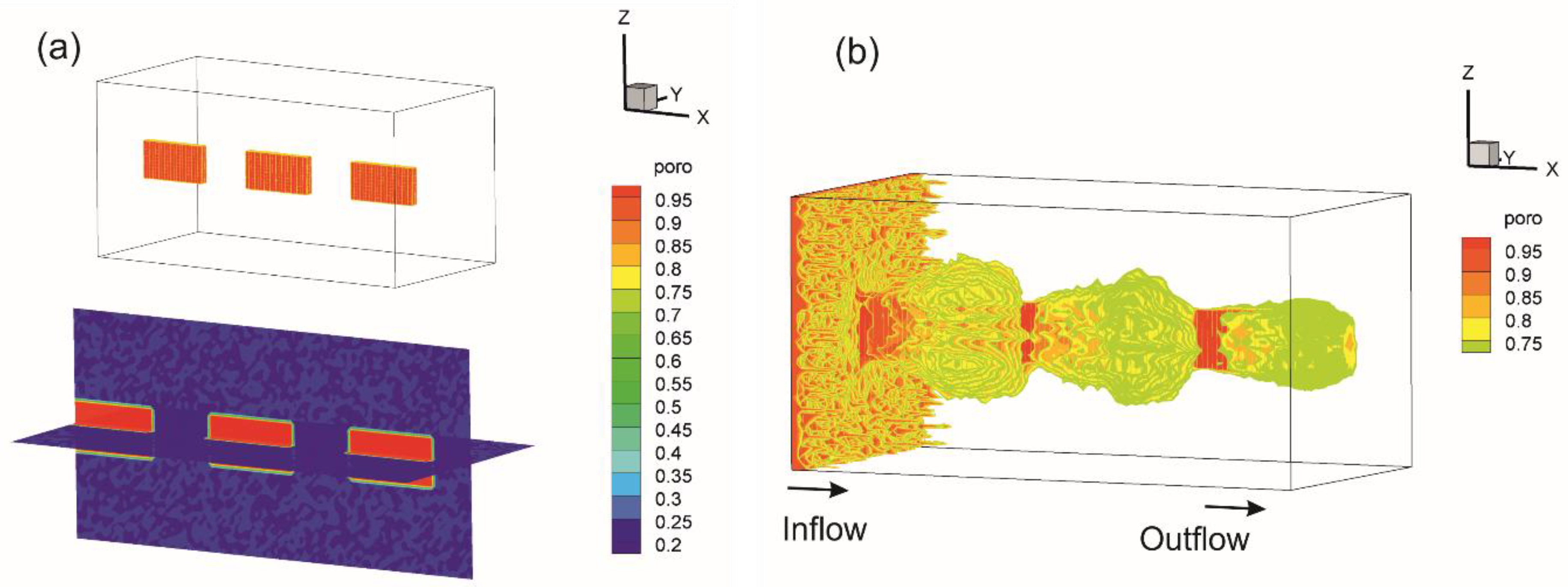
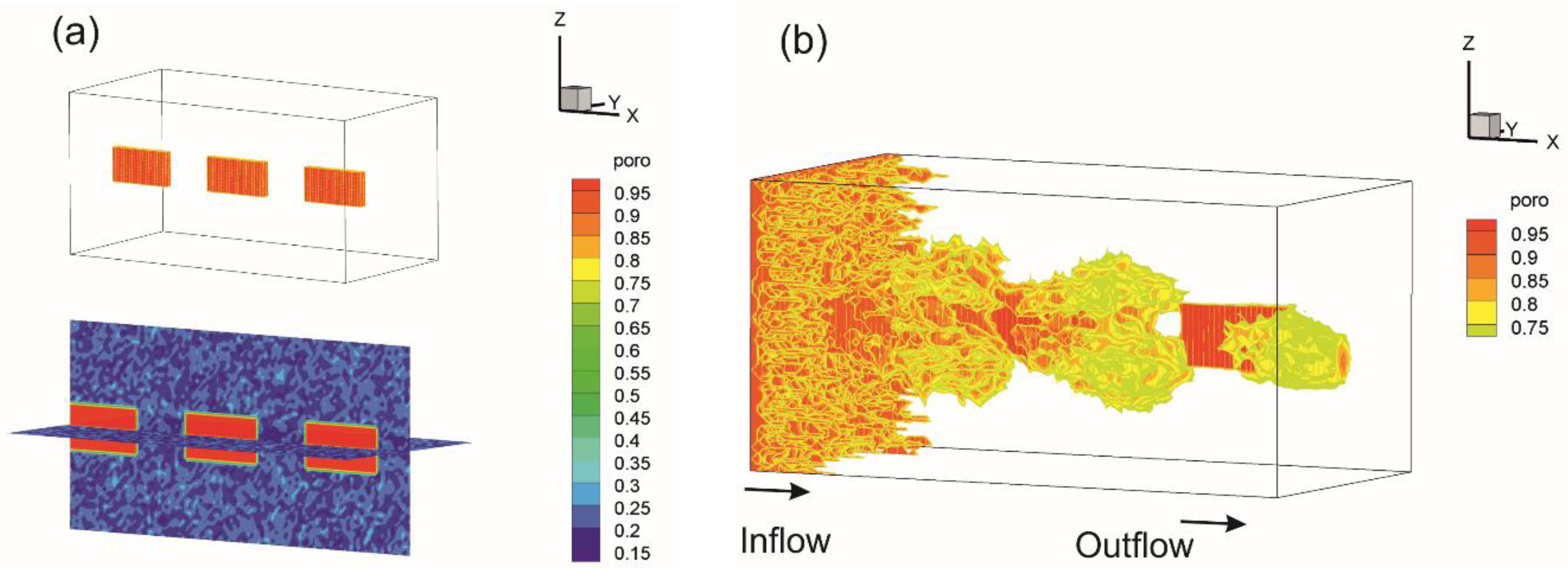
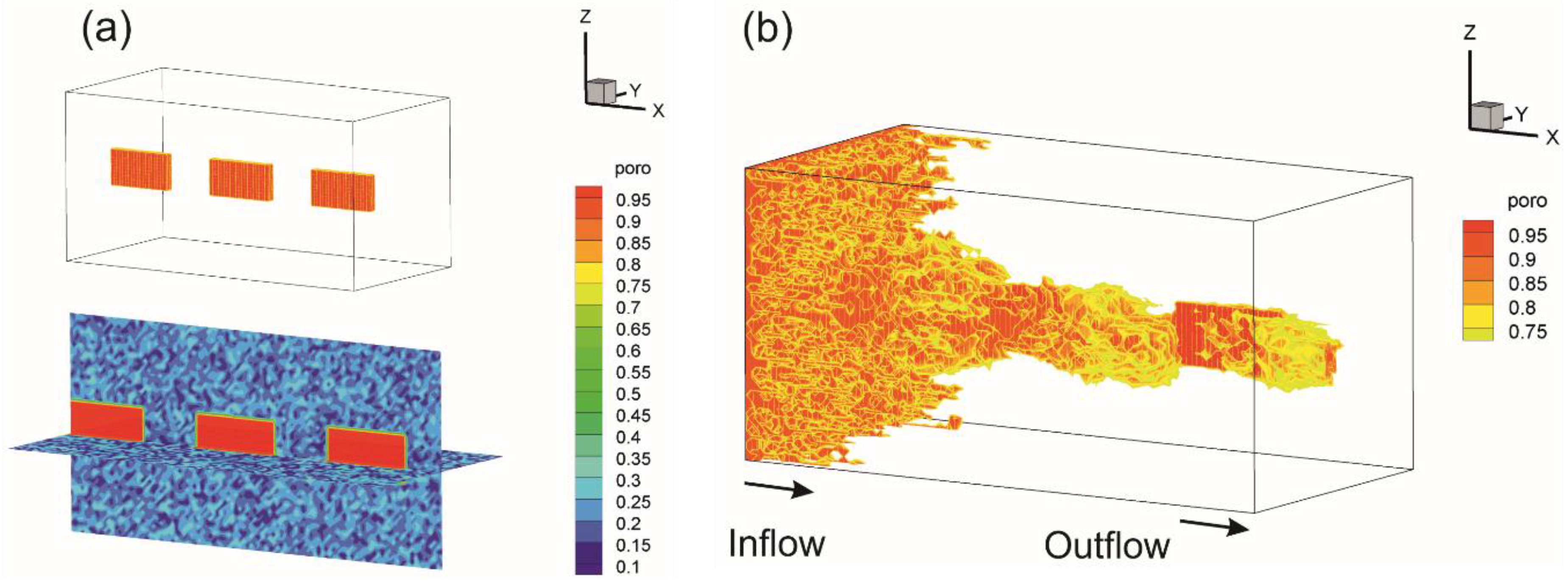
4.2.1. The Effect of Heterogeneity
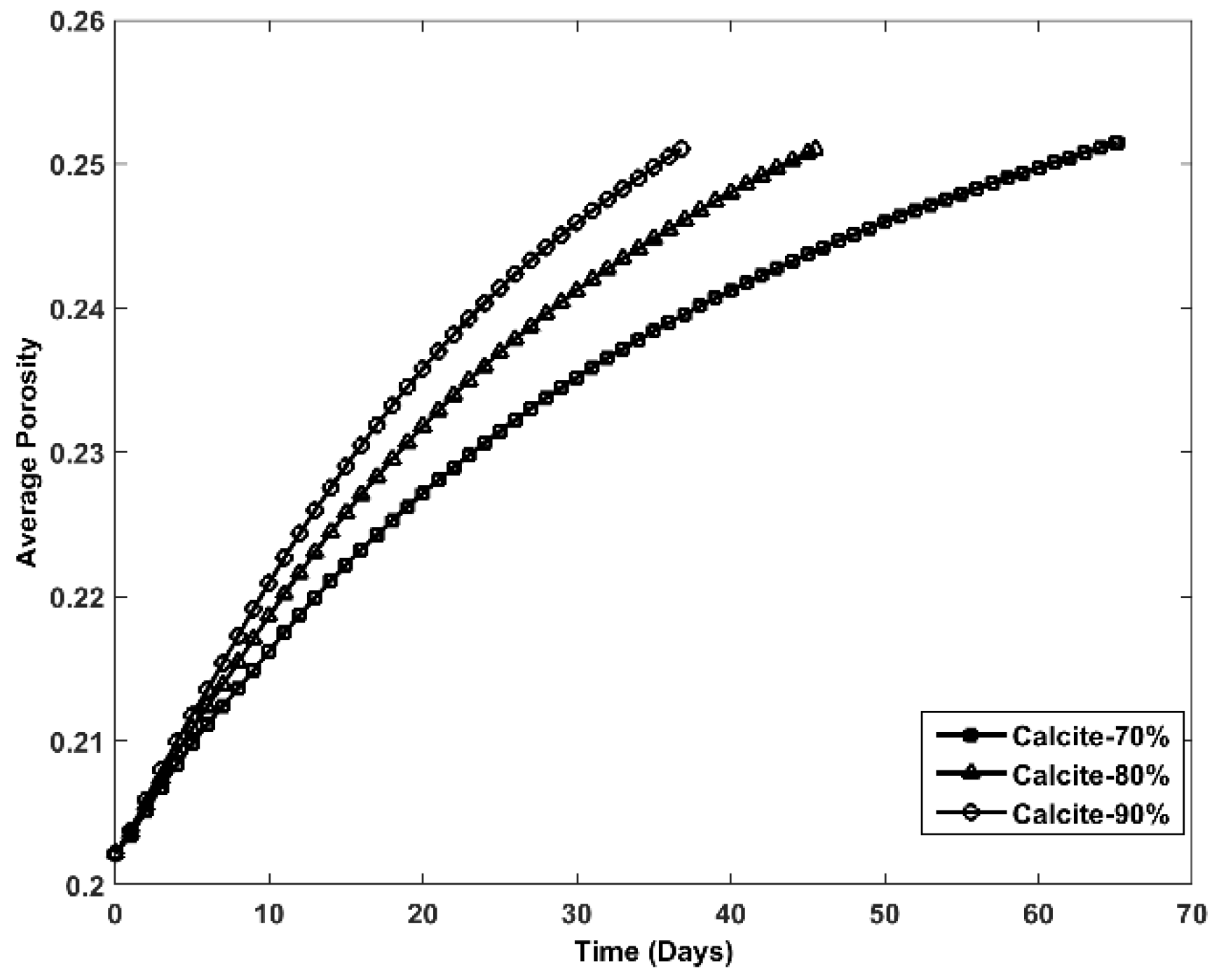
4.2.2. The Effect of the Mineral Volume Fraction
5. Conclusions
- Firstly, the proposed numerical model is applied for 3D linear core flooding in a multi-mineral system, which consists of calcite, quartz, and clay. Sensitivity studies clearly show the effects of heterogeneity of porous media and mineral volume fractions on the rock properties and dissolution patterns. The numerical results demonstrate that the magnitude of heterogeneity has a significant impact on the structure of the dominant wormholes: Without heterogeneity, the dissolution front propagates uniformly. The higher initial calcite content has a significant impact on porosity and fracture evolution via an increase in the reactive surface area and the subsequent augmentation of the chemical reaction rate.
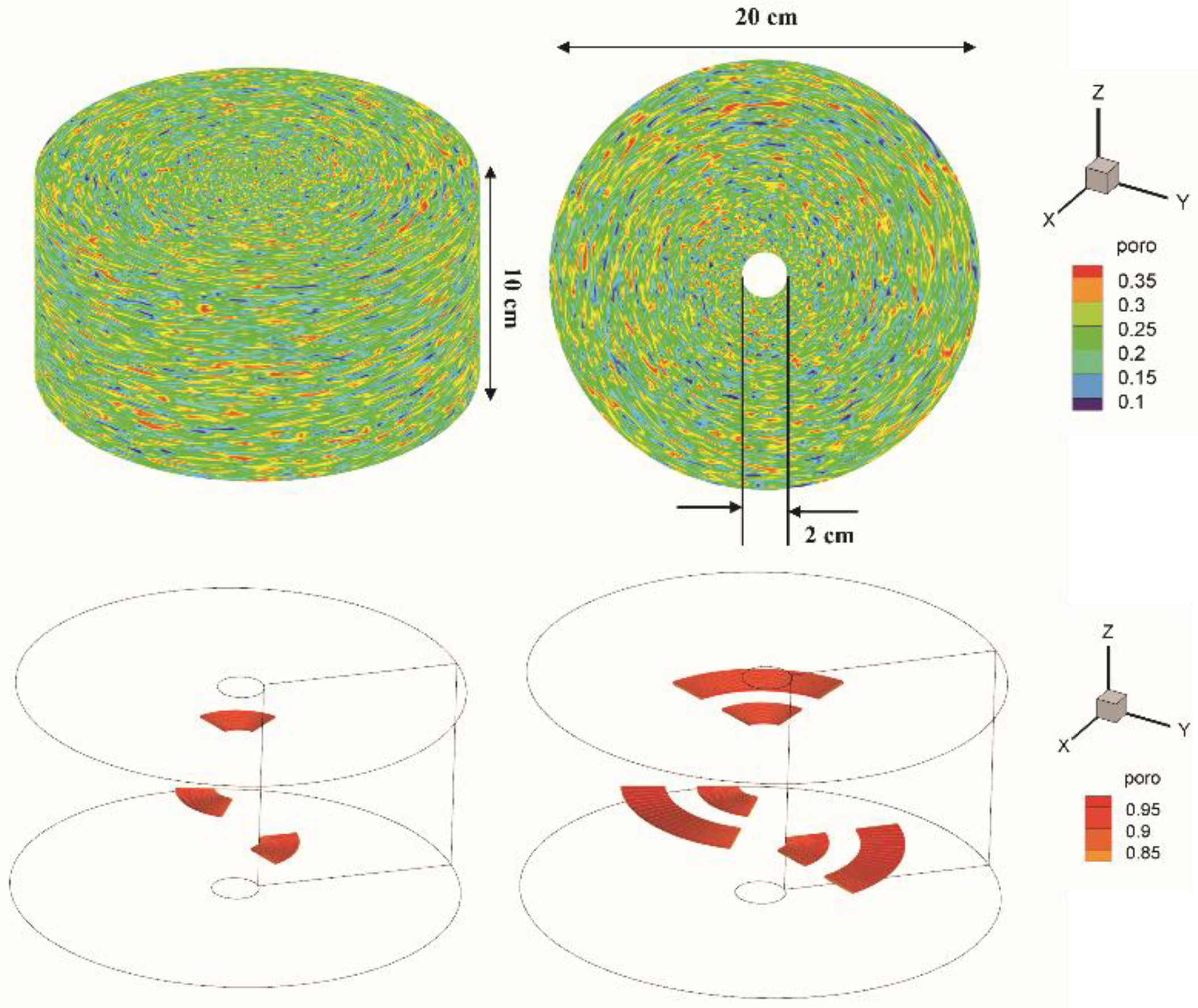
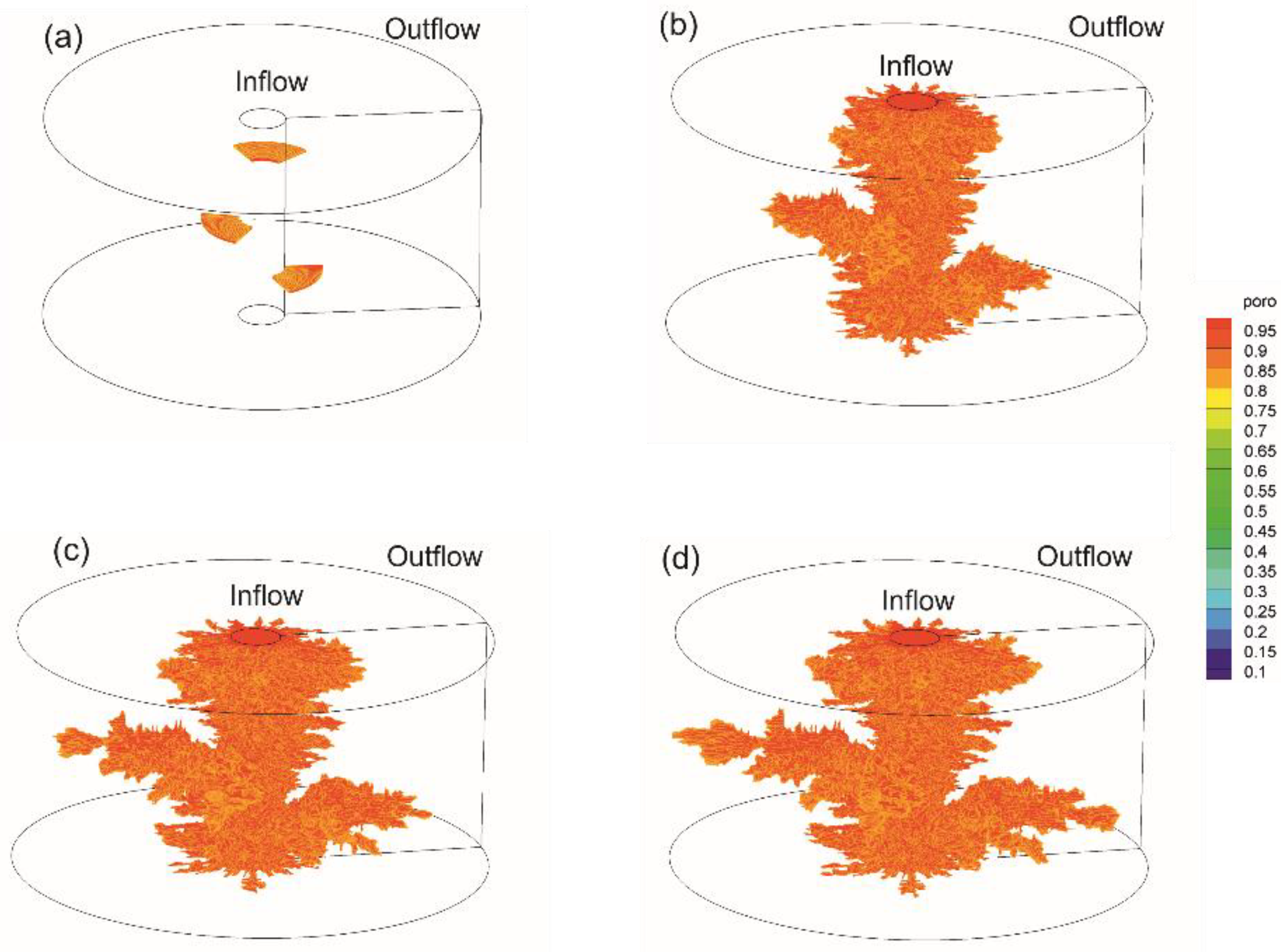
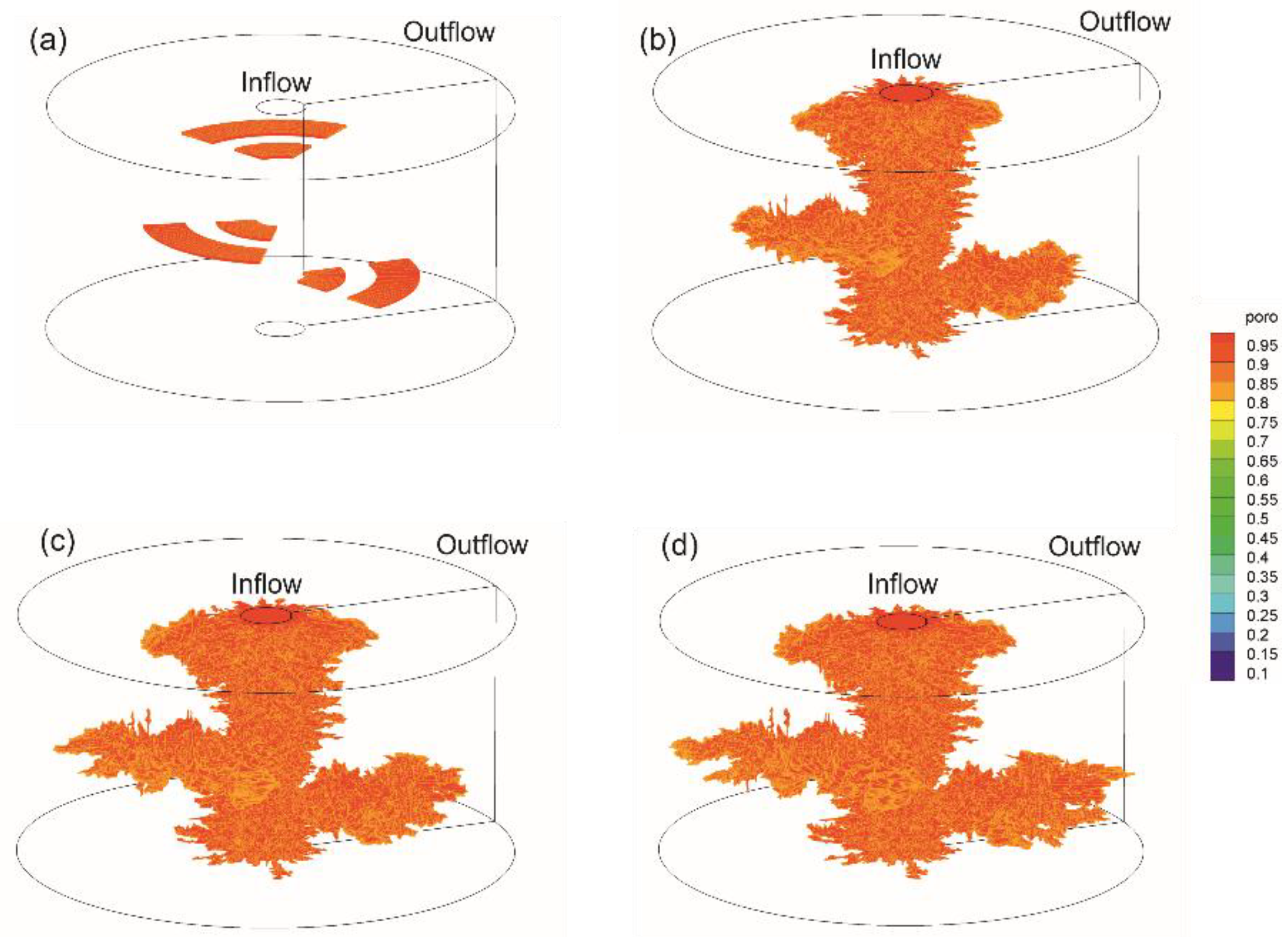
- In the second case study, the proposed numerical model is applied for 3D radial core flooding in a single calcite system. Several disconnected fractures are randomly distributed inside of porous media. During the flooding process, the fractures propagate radially within the porous media and eventually form the conductive channels, wormholes. Therefore, the proposed numerical model can be applied to simulate the matrix acidizing process in fractured carbonate formations at exact downhole environments.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Wolery, T.J.; Jackson, K.J.; Bourcier, W.L.; Bruton, C.J.; Viani, B.E.; Knauss, K.G.; Delany, J.M. Current Status of the EQ3/6 Software Package for Geochemical Modeling. Chem. Model. Aqueous Syst. II 1990, 416, 104–116. [Google Scholar]
- Smith, D.; Giraud, M.; Kemp, C.; McBee, M.; Taitano, J.; Winfield, M.; Protwood, J.; Everett, D. The successful evolution of anton irish conformance efforts. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. SPE 103044. [Google Scholar]
- Metz, B.; Davidson, O.; de Coninck, H.C.; Loos, M.; Meyer, L. IPCC Special Report on Carbon Dioxide Capture and Storage; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2005. [Google Scholar]
- Harvey, OR.; Cantrell, KJ.; Qafoku, NP.; Brown, C. Geochemical Implications of CO2 Leakage Associated with Geologic Storage: A Review; Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2012. [Google Scholar]
- McLeod, H.O. Matrix Acidizing. J. Pet. Technol. 1984, 36, 2055–2069. [Google Scholar] [CrossRef]
- Hung, K.M.; Hill, A.D.; Sepehrnoori, K. A Mechanistic Model of Wormhole Growth in Carbonate Matrix Acidizing and Acid Fracturing. J. Pet. Technol. 1989, 41, 59–66. [Google Scholar] [CrossRef]
- Assayag, N.; Matter, J.; Ader, M.; Goldberg, D.; Agrinier, P. Water–rock interactions during a CO2 injection field-test: Implications on host rock dissolution and alteration effects. Chem. Geol. 2009, 265, 227–235. [Google Scholar] [CrossRef]
- Gaus, I.; Azaroual, M.; Czernichowski-Lauriol, I. Preliminary Modelling of the Geochemical Impact of CO2-Injection on the Cap Rock at Sleipner; Rep. BRGM/RP-52081-FR; 2002. [Google Scholar]
- Jun, Y.S.; Giammar, D.E.; Werth, C.J. Impacts of geochemical reactions on geologic carbon sequestration. Environ. Sci. Technol. 2013, 47, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Lions, J.; Devau, N.; De Lary, L.; Dupraz, S.; Parmentier, M.; Gombert, P.; Dictor, M.C. Potential impacts of leakage from CO2 geological storage on geochemical processes controlling fresh groundwater quality: A review. Int. J. Greenh. Gas Control 2014, 22, 165–175. [Google Scholar] [CrossRef]
- Kharaka, Y.K.; Thordsen, J.J.; Hovorka, S.D.; Seay Nance, H.; Cole, D.R.; Phelps, T.J.; Knauss, K.G. Potential environmental issues of CO2 storage in deep saline aquifers: Geochemical results from the Frio-I Brine Pilot test, Texas, USA. Appl. Geochem. 2009, 24, 1106–1112. [Google Scholar] [CrossRef]
- Dong, C.; Zhu, D.; Hill, A.D. Modeling of the acidizing process in naturally fractured carbonates. SPE J. 2002, 7, 400–408. [Google Scholar] [CrossRef]
- Golfier, F.; Bazin, B.; Zarcone, C.; Lernormand, R.; Lasseux, D.; Quintard, M. Acidizing Carbonate Reservoirs: Numerical Modelling of Wormhole Propagation and Comparison to Experiments. In Proceedings of the SPE European Formation Damage Conference, The Hague, The Netherlands, 20–22 May 2001; pp. 1–11. [Google Scholar]
- Huang, T.; Zhu, D.; Hill, A.D. Prediction of Wormhole Population Density in Carbonate Matrix Acidizing. In Proceedings of the SPE European Formation Damage Conference, The Hague, The Netherlands, 31 May–1 June 1999. [Google Scholar]
- McDuff, D.; Shuchart, C.E.; Jackson, S.; Postl, D.; Brown, J.S. Understanding Wormholes in Carbonates: Unprecedented Experimental Scale and 3-D Visualization. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010; pp. 78–81. [Google Scholar]
- Daccord, G.; Lenormand, R.; Liétard, O. Chemical dissolution of a porous medium by a reactive fluid-I. Model for the “wormholing” phenomenon. Chem. Eng. Sci. 1993, 48, 169–178. [Google Scholar] [CrossRef]
- Daccord, G.; Liétard, O.; Lenormand, R. Chemical dissolution of a porous medium by a reactive fluid-II. Convection vs reaction, behavior diagram. Chem. Eng. Sci. 1993, 48, 179–186. [Google Scholar] [CrossRef]
- Fredd, C.N.; Fogler, H.S. Influence of transport and reaction on wormhole formation in porous media. AIChE J. 1998, 44, 1933–1949. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Steefel, C.I.; Yang, L. Scale dependence of mineral dissolution rates within single pores and fractures. Geochim. Cosmochim. Acta 2008, 72, 360–377. [Google Scholar] [CrossRef]
- Li, L.; Steefel, C.I.; Kowalsky, M.B.; Englert, A.; Hubbard, S.S. Effects of physical and geochemical heterogeneities on mineral transformation and biomass accumulation during biostimulation experiments at Rifle, Colorado. J. Contam. Hydrol. 2010, 112, 45–63. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Gawande, N.; Kowalsky, M.B.; Steefel, C.I.; Hubbard, S.S. Physicochemical heterogeneity controls on uranium bioreduction rates at the field scale. Environ. Sci. Technol. 2011, 45, 9959–9966. [Google Scholar] [CrossRef] [PubMed]
- Steefel, C.I.; DePaolo, D.J.; Lichtner, P.C. Reactive transport modeling: An essential tool and a new research approach for the Earth sciences. Earth Planet. Sci. Lett. 2005, 240, 539–558. [Google Scholar] [CrossRef]
- Steefel, C.I.; Lasaga, A.C. A Coupled Model for Transport of Multiple Chemical-Species and Kinetic Precipitation Dissolution Reactions with Application to Reactive Flow in Single-Phase Hydrothermal Systems. Am. J. Sci. 1994, 294, 529–592. [Google Scholar] [CrossRef]
- Lasaga, A.C. Kinetic Theory in the Earth Sciences; Princeton University Press: Princeton, NJ, USA, 1998; ISBN 0691037485. [Google Scholar]
- Lichtner, P.C. The quasi-stationary state approximation to coupled mass transport and fluid-rock interaction in a porous medium. Geochim. Cosmochim. Acta 1988, 52, 143–165. [Google Scholar] [CrossRef]
- Steefel, C.I. CrunchFlow Software for Modeling Multicomponent Reactive Flow and Transport. User’s Manual; Earth Science Division. Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2009. [Google Scholar]
- Molins, S. Reactive Interfaces in Direct Numerical Simulation of Pore-Scale Processes. Rev. Mineral. Geochem. 2015, 80, 461–481. [Google Scholar] [CrossRef] [Green Version]
- Kang, Q.; Lichtner, P.C.; Zhang, D. Lattice Boltzmann pore-scale model for multicomponent reactive transport in porous media. J. Geophys. Res. 2006, 111, 1–12. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Carey, B.; Tao, W.-Q. International Journal of Heat and Mass Transfer Pore-scale study of diffusion—Reaction processes involving dissolution and precipitation using the lattice Boltzmann method. Int. J. Heat Mass Transf. 2014, 75, 483–496. [Google Scholar] [CrossRef]
- Panga, M.K.R.; Ziauddin, M.; Balakotaiah, V. Two-scale continuum model for simulation of wormholes in carbonate acidization. AIChE J. 2005, 51, 3231–3248. [Google Scholar] [CrossRef]
- Qiao, C.; Li, L.; Johns, R.T.; Xu, J. A Mechanistic Model for Wettability Alteration by Chemically Tuned Waterflooding in Carbonate Reservoirs. SPE J. 2015, 20, 767–783. [Google Scholar] [CrossRef]
- Liu, P.; Yao, J.; Couples, G.D.; Huang, Z.; Sun, H.; Ma, J. Numerical modelling and analysis of reactive flow and wormhole formation in fractured carbonate rocks. Chem. Eng. Sci. 2017, 172, 143–157. [Google Scholar] [CrossRef]
- Yuan, T.; Ning, Y.; Qin, G. Numerical Modeling and Simulation of Coupled Processes of Mineral Dissolution and Fluid Flow in Fractured Carbonate Formations. Transp. Porous Media 2016, 114, 747–775. [Google Scholar] [CrossRef]
- Yuan, T.; Ning, Y.; Qin, G. Numerical Modeling of Mineral Dissolution of Carbonate Rocks During Geological CO2 Sequestration Processes. In Proceedings of the SPE Europec Featured at 79th EAGE Conference and Exhibition, Paris, France, 12–15 June 2017. [Google Scholar]
- Popov, P.; Efendiev, Y.; Qin, G. Multiscale modeling and simulations of flows in naturally fractured Karst reservoirs. Commun. Comput. Phys. 2009, 6, 162–184. [Google Scholar] [CrossRef]
- Bi, L.; Qin, G.; Popov, P. An Efficient Upscaling Process Based on a Unified Fine-scale Multi-Physics Model for Flow Simulation in Naturally Fracture Carbonate Karst Reservoirs. In Proceedings of the SPE/EAGE Reservoir Characterization and Simulation Conference, Abu Dhabi, UAE, 19–21 October 2009. [Google Scholar]
- Qin, G.; Bi, L.; Popov, P.; Efendiev, Y.; Espedal, M.S. An Efficient Upscaling Process Based on a Unified Fine-scale Multi-Physics Model for Flow Simulation in Naturally Fracture Carbonate Karst Reservoirs. In Proceedings of the CPS/SPE International Oil & Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010. [Google Scholar]
- Brinkman, H.C. A Calculation of the Viscous Force Exerted By a Flowing Fluid on a Dense Swarm of Particles. Appl. Sci. Res. 1947, 1, 27–34. [Google Scholar] [CrossRef]
- Durlofsky, L.; Brady, J.F. Analysis of the Brinkman equation as a model for flow in porous media. Phys. Fluids 1987, 30, 3329–3341. [Google Scholar] [CrossRef]
- Hwang, W.R.; Advani, S.G. Numerical simulations of Stokes-Brinkman equations for permeability prediction of dual scale fibrous porous media. Phys. Fluids 2010, 22, 113101. [Google Scholar] [CrossRef]
- Popov, P.; Qin, G.; Bi, L.; Efendiev, Y.; Kang, Z.; Jianglong, L. Multiphysics and multiscale methods for modeling fluid flow through naturally fractured carbonate karst reservoirs. SPE Reserv. Eval. Eng. 2009, 12, 218–231. [Google Scholar] [CrossRef]
- Beavers, G.S.; Joseph, D.D. Boudary conditions at a naturally permeable wall. J. Fluid Mech. 1967, 30, 197–207. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical Calculation of Time-Dependent Viscous Incompressible Flow of Fluid with Free Surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Bell, J.B.; Colella, P.; Glaz, H.M. A Second-Order Incompressible Projection Method for the Navier-Stokes Equations. J. Comput. Phys. 1989, 283, 257–283. [Google Scholar] [CrossRef]
- Ge, L.; Fotis, S. A Numerical Method for Solving the 3D Unsteady Incompressible Navier-Stokes Equations in Curvilinear Domains with Complex Immersed Boundaries. J. Comput. Phys. 2007, 225, 1782–1809. [Google Scholar] [CrossRef] [PubMed]
- FASP User Guide. 2018. Available online: www.multigrid.org/fasp (accessed on 20 December 2018).
- Baker, A.H.; Jessup, E.R.; Kolev, T.V. A simple strategy for varying the restart parameter in GMRES(m). J. Comput. Appl. Math. 2009, 230, 751–761. [Google Scholar] [CrossRef] [Green Version]
- Tardy, P.; Lecerf, B.; Christanti, Y. An Experimentally Validated Wormhole Model for Self-Diverting and Conventional Acids in Carbonate Rocks Under Radial Flow Conditions. In Proceedings of the European Formation Damage Conference, Scheveningen, The Netherlands, 30 May–1 June 2007. [Google Scholar]
- Martys, N.; Bentz, D.P.; Garboczi, E.J. Computer simulation study of the effective viscosity in Brinkman’s equation. Phys. Fluids 1994, 6, 1434–1439. [Google Scholar] [CrossRef]
- Berg, R.R. Method for determining permeability from reservoir rock properties. Trans. Coast Assoc. Geol. Soc. 1970, 20, 303–317. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Pub. Co.: New York, NY, USA, 1972. [Google Scholar]
- Van Baaren, J.P. Quick-look permeability estimates using sidewall samples and porosity logs. In Proceedings of the Trans, 6th Annual European Logging Symposium, Society of Professional Well Log Analysts, London, UK, 26–27 March 1979. [Google Scholar]
- Glover, P.W.J.; Zadjali, I.I.; Frew, K.A. Using an Electrokinetic Approach. Geophysics 2006, 71, F49–F60. [Google Scholar] [CrossRef]
- Rashid, F.; Glover, P.W.J.; Lorinczi, P.; Collier, R.; Lawrence, J. Porosity and permeability of tight carbonate reservoir rocks in the north of Iraq. J. Pet. Sci. Eng. 2015, 133, 147–161. [Google Scholar] [CrossRef] [Green Version]
- Mavis, F.T.; Wilsey, E.F. A Study of the Permeability of Sand; State Univeristy Iowa Bullletin: Iowa, IA, USA, 1936. [Google Scholar]
- Nelson, P.H. Permeability-porosity relationships in sedimentary rocks. Log Anal. 1994, 35, 38–62. [Google Scholar]
- Chapuis, R.P. Sand–bentonite liners: Predicting permeability from laboratory tests. Can. Geotech. J. 1990, 27, 47–57. [Google Scholar] [CrossRef]
- Chapuis, R.P. The 2000 R.M. Hardy Lecture: Full-scale hydraulic performance of soil-bentonite and compacted clay liners. Can. Geotech. J. 2002, 39, 417–439. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Aubertin, M. Predicting the Coefficient Permeability of Soils Using the Kozeny-Carman Équation; École Polytech. Montréal: Montreal, QC, Canada, 2003. [Google Scholar]
- Ehrenberg, S.N.; Eberli, G.P.; Baechle, G. Porosity-permeability relationships in Miocene carbonate platforms and slopes seaward of the Great Barrier Reef, Australia (ODP Leg 194, Marion Plateau). Sedimentology 2006, 53, 1289–1318. [Google Scholar] [CrossRef]
- Ghommem, M.; Zhao, W.; Dyer, S.; Qiu, X.; Brady, D. Carbonate acidizing: Modeling, analysis, and characterization of wormhole formation and propagation. J. Pet. Sci. Eng. 2015, 131, 18–33. [Google Scholar] [CrossRef]
- Brunet, J.P.L.; Li, L.; Karpyn, Z.T.; Huerta, N.J. Fracture opening or self-sealing: Critical residence time as a unifying parameter for cement-CO2-brine interactions. Int. J. Greenh. Gas Control 2016, 47, 25–37. [Google Scholar] [CrossRef]
- Brandt, A.; Dinar, N. Multigrid Solutions to Elliptic Flow Problems. In Numerical Methods for Partial Differential Equations; Parter, S., Ed.; Academic Press: Cambridge, MA, USA, 1979; pp. 53–147. [Google Scholar]
- Bramble, J.H.; Pasciak, J.E. Iterative techniques for time dependent Stokes problems. Comput. Math. Applic. 1997, 33, 13–30. [Google Scholar] [CrossRef] [Green Version]
- Shen, L.; Xu, J. On A Schur Complement Operator Arisen from Navier-Stokes Equations and Its Preconditioning. In Proceedings of the Guangzhou International Symposium on Computational Mathematics; Chen, Z., Li, Y., Micchelli, C., Xu, Y., Eds.; Marcel Dekker: New York, NY, USA, 1998; pp. 481–490. [Google Scholar]
- Xu, J.; Zikatanov, L.T. Algebraic Multigrid Methods. Acta Numer. 2016, 1–128. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2 ed.; SIAM: Philadelphia, PA, USA, 2003; Volume 3, ISBN 0898715342. [Google Scholar]
- Ghommem, M.; Brady, D. Multifidelity Modeling and Analysis of Matrix Acidizing Under Radial Flow Conditions. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 25–28 April 2016. [Google Scholar]
- Suarez, D.; Wood, J. Simultaneous determination of calcite surface area and content in soils. Soil Sci. Soc. Am. J. 1984, 48, 1232–1235. [Google Scholar] [CrossRef]
| pH | |||||
|---|---|---|---|---|---|
| Initial Condition (mol/L) | 7 | ||||
| Injected CO2-saturated brine (mol/L) | 1.03 | 3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, T.; Wei, C.; Zhang, C.-S.; Qin, G. A Numerical Simulator for Modeling the Coupling Processes of Subsurface Fluid Flow and Reactive Transport Processes in Fractured Carbonate Rocks. Water 2019, 11, 1957. https://doi.org/10.3390/w11101957
Yuan T, Wei C, Zhang C-S, Qin G. A Numerical Simulator for Modeling the Coupling Processes of Subsurface Fluid Flow and Reactive Transport Processes in Fractured Carbonate Rocks. Water. 2019; 11(10):1957. https://doi.org/10.3390/w11101957
Chicago/Turabian StyleYuan, Tao, Chenji Wei, Chen-Song Zhang, and Guan Qin. 2019. "A Numerical Simulator for Modeling the Coupling Processes of Subsurface Fluid Flow and Reactive Transport Processes in Fractured Carbonate Rocks" Water 11, no. 10: 1957. https://doi.org/10.3390/w11101957
APA StyleYuan, T., Wei, C., Zhang, C.-S., & Qin, G. (2019). A Numerical Simulator for Modeling the Coupling Processes of Subsurface Fluid Flow and Reactive Transport Processes in Fractured Carbonate Rocks. Water, 11(10), 1957. https://doi.org/10.3390/w11101957





