Evaluation of Return Period and Risk in Bivariate Non-Stationary Flood Frequency Analysis
Abstract
1. Introduction
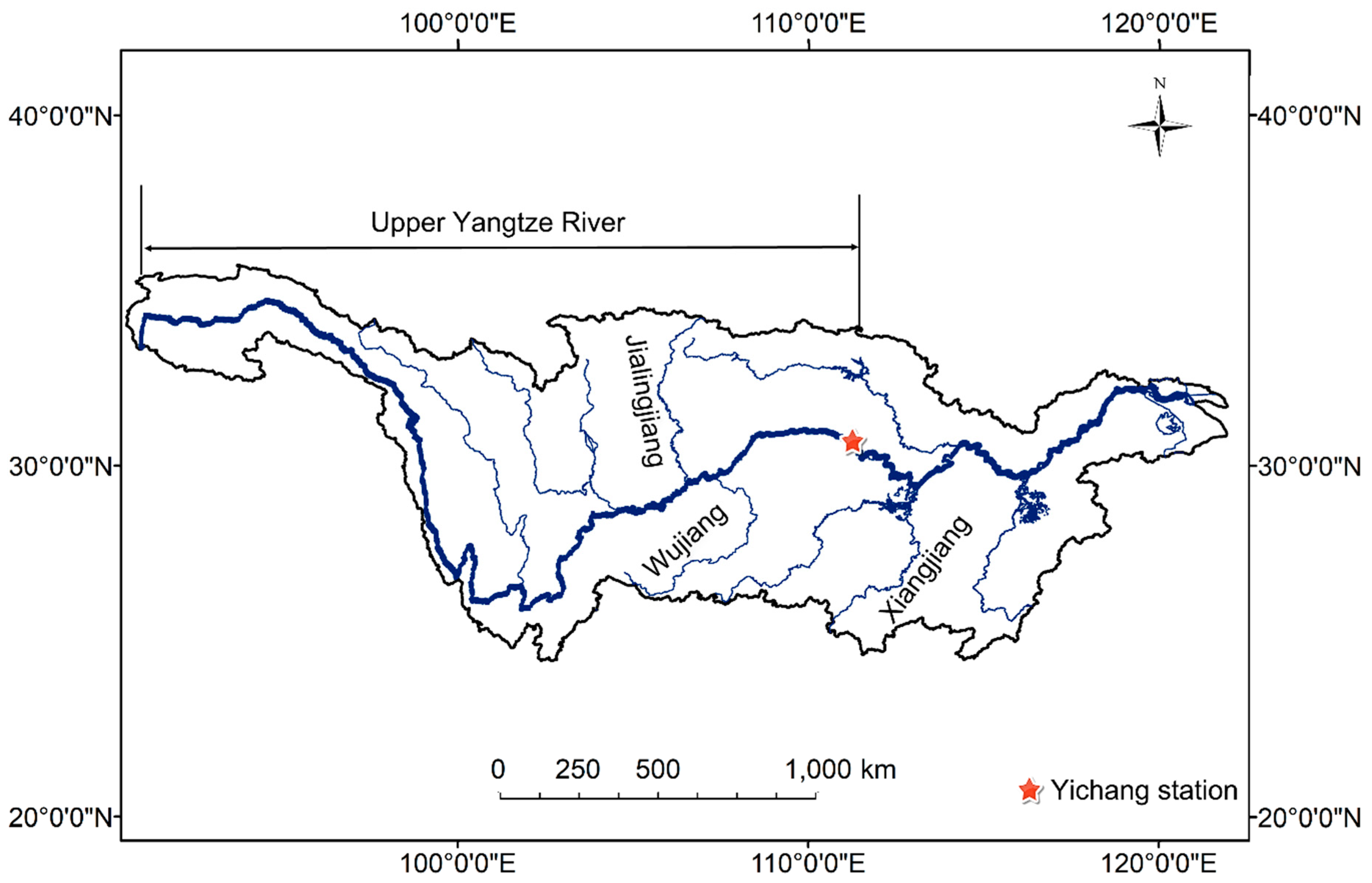
2. Study Area and Data
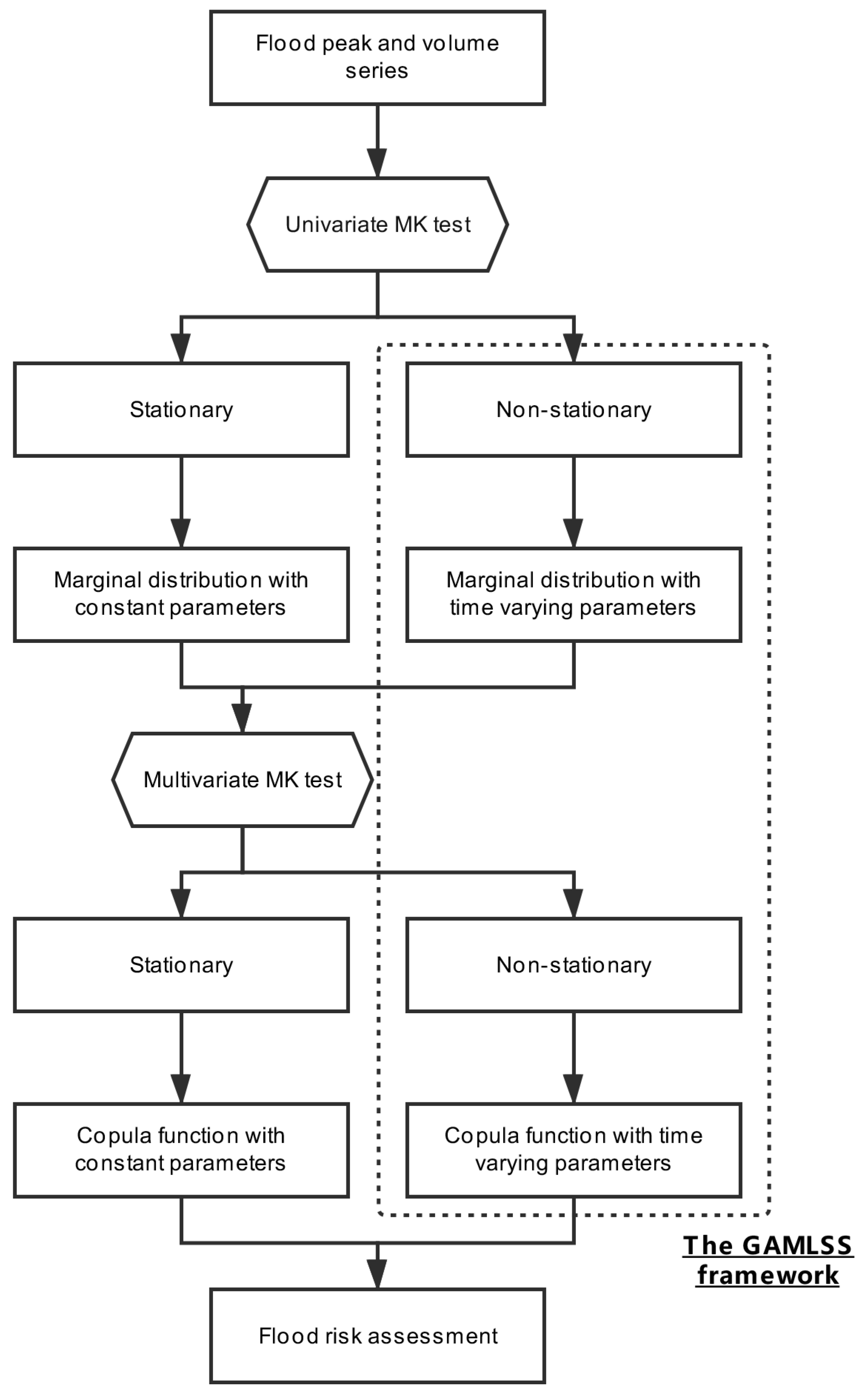
3. Methodology
3.1. Trend Analysis
3.1.1. Univariate Trend Test
3.1.2. Multivariate Trend Test
3.2. Time Varying Copula
3.2.1. Marginal Distribution
3.2.2. Copula Function
3.3. Return Period, Risk of Failure and Reliability
3.3.1. Non-Stationary Return Period
3.3.2. Risk of Failure and Reliability
4. Results
4.1. The Trend Test
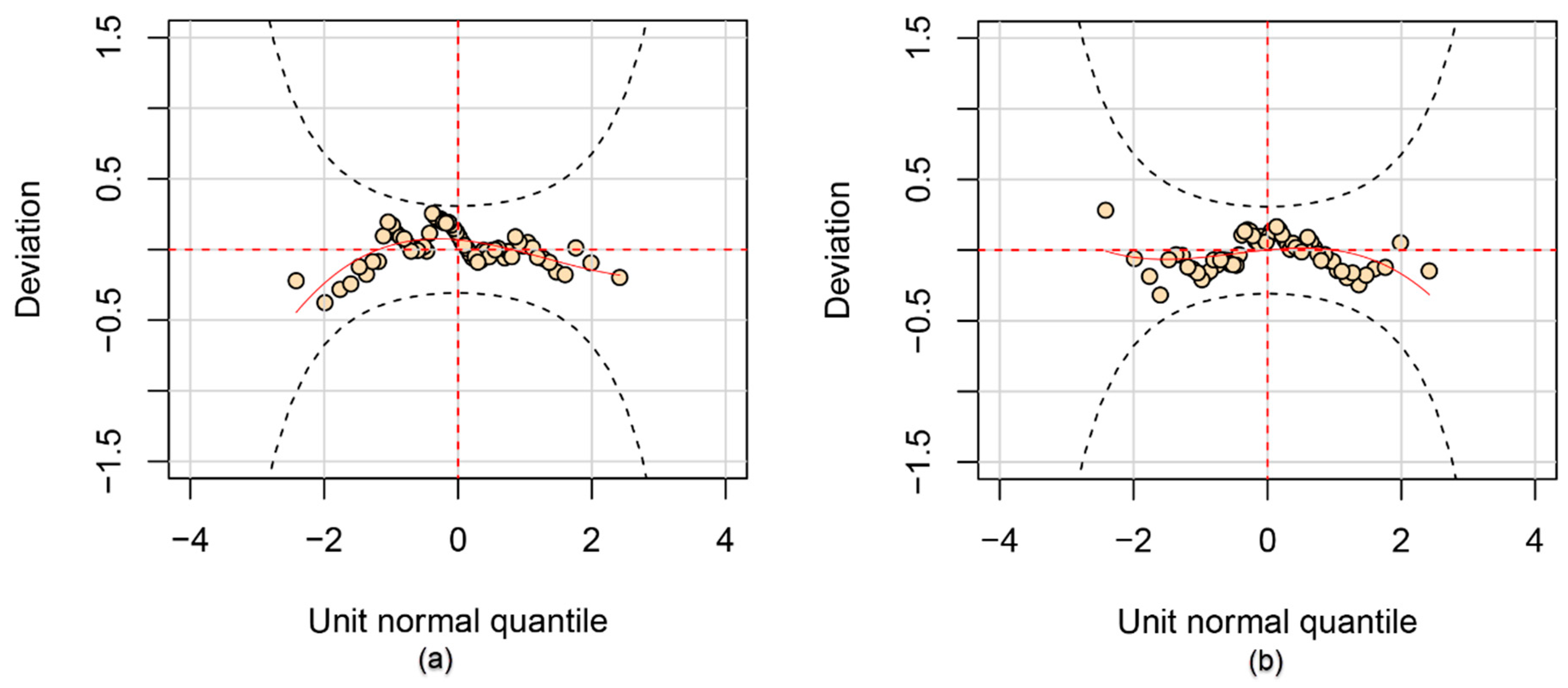
4.2. Marginal Distribution
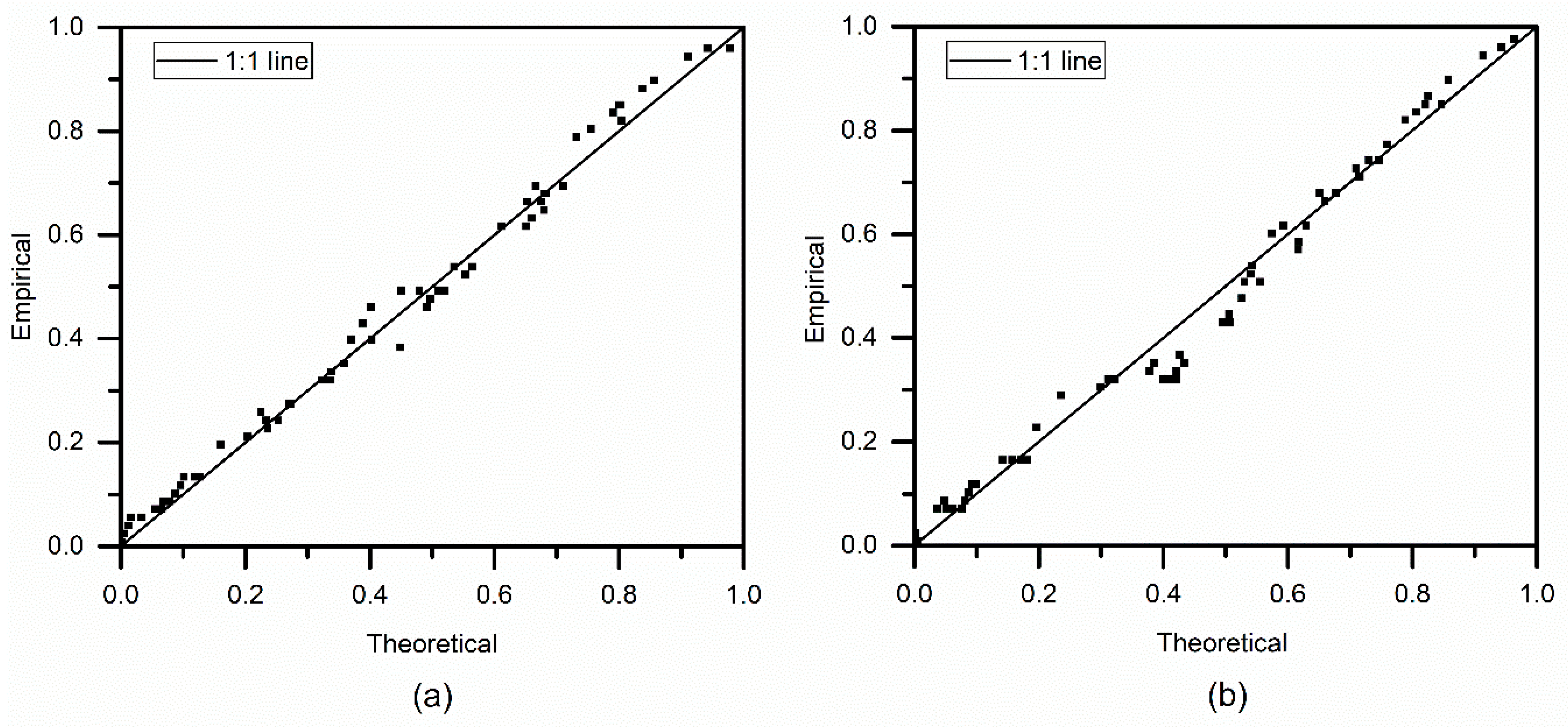
4.3. Copula Modeling
4.4. Flood Risk Assessment
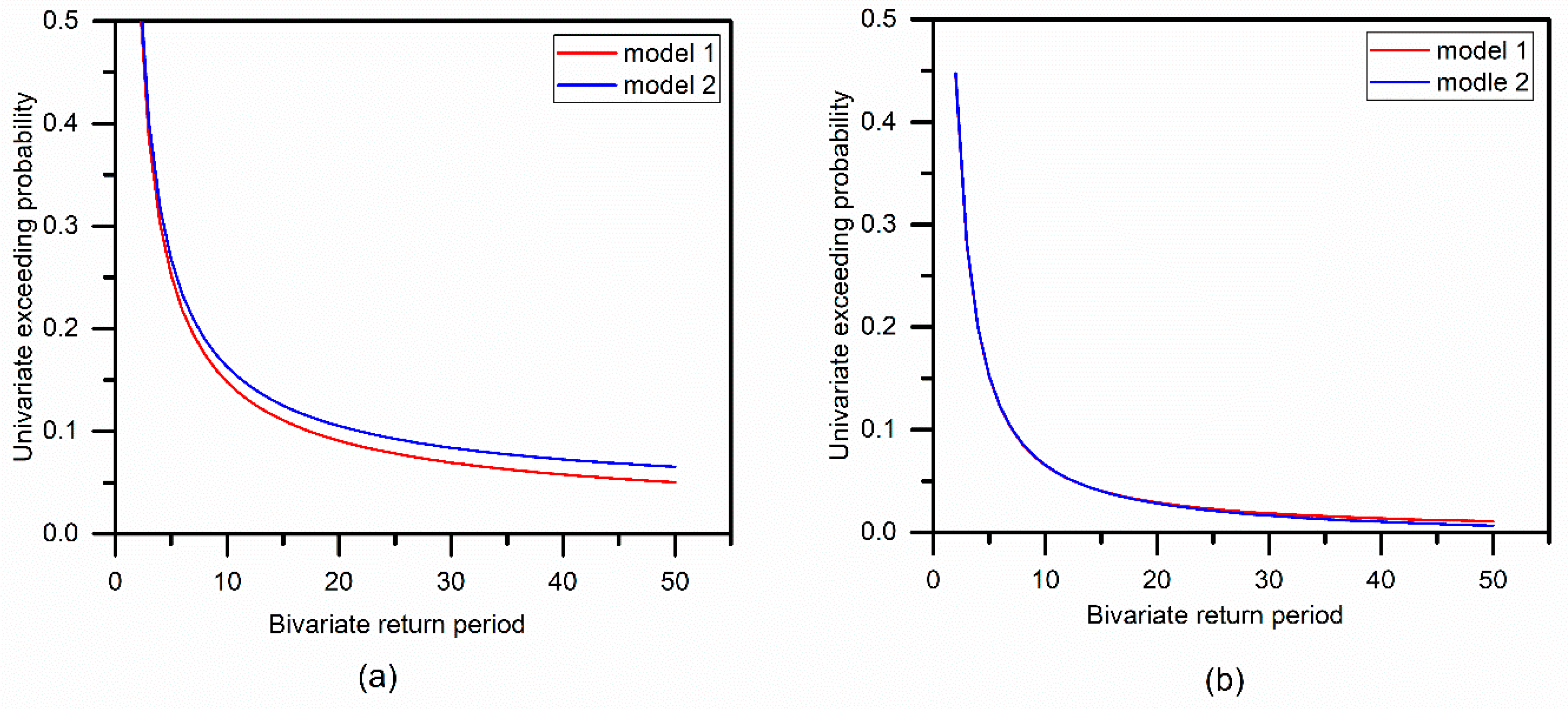
4.4.1. The Non-Stationary Return Period
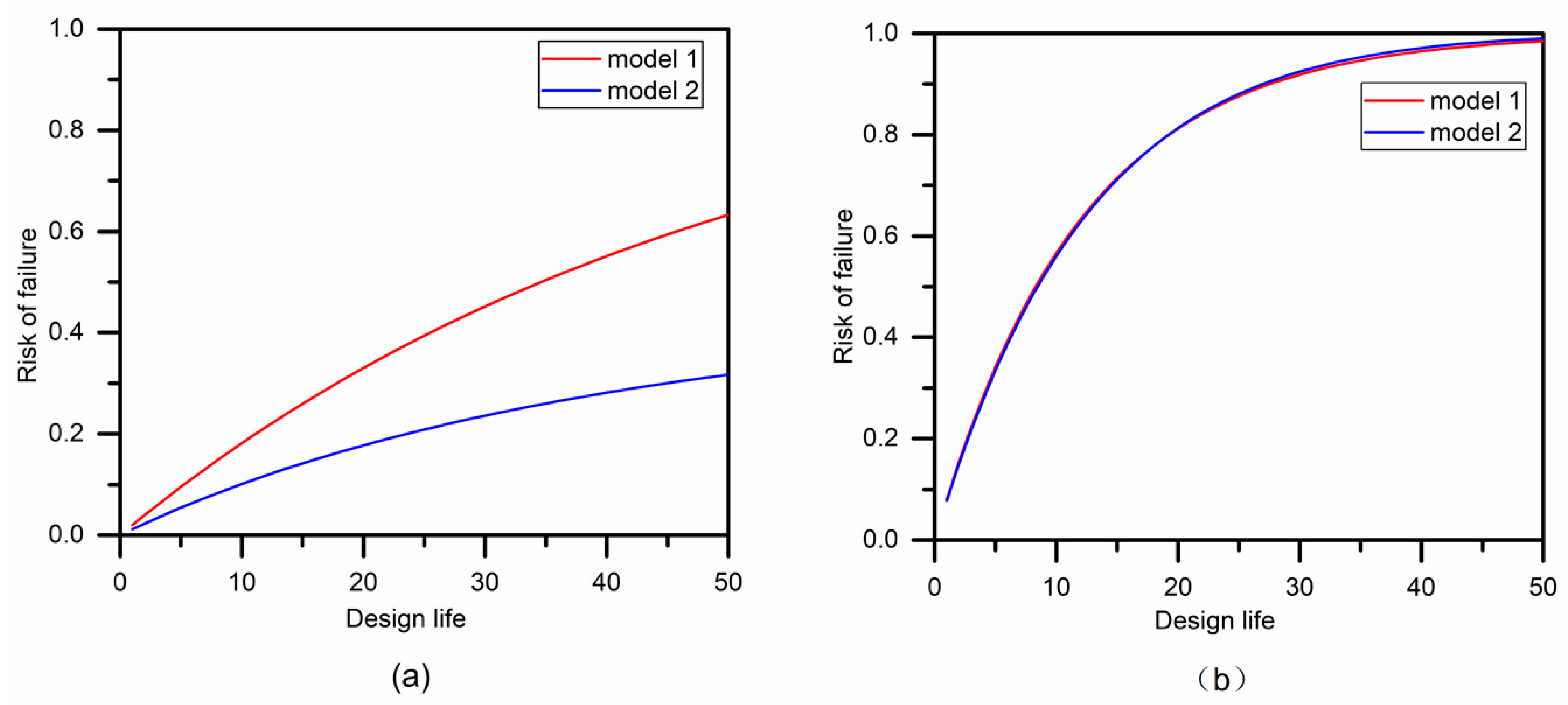
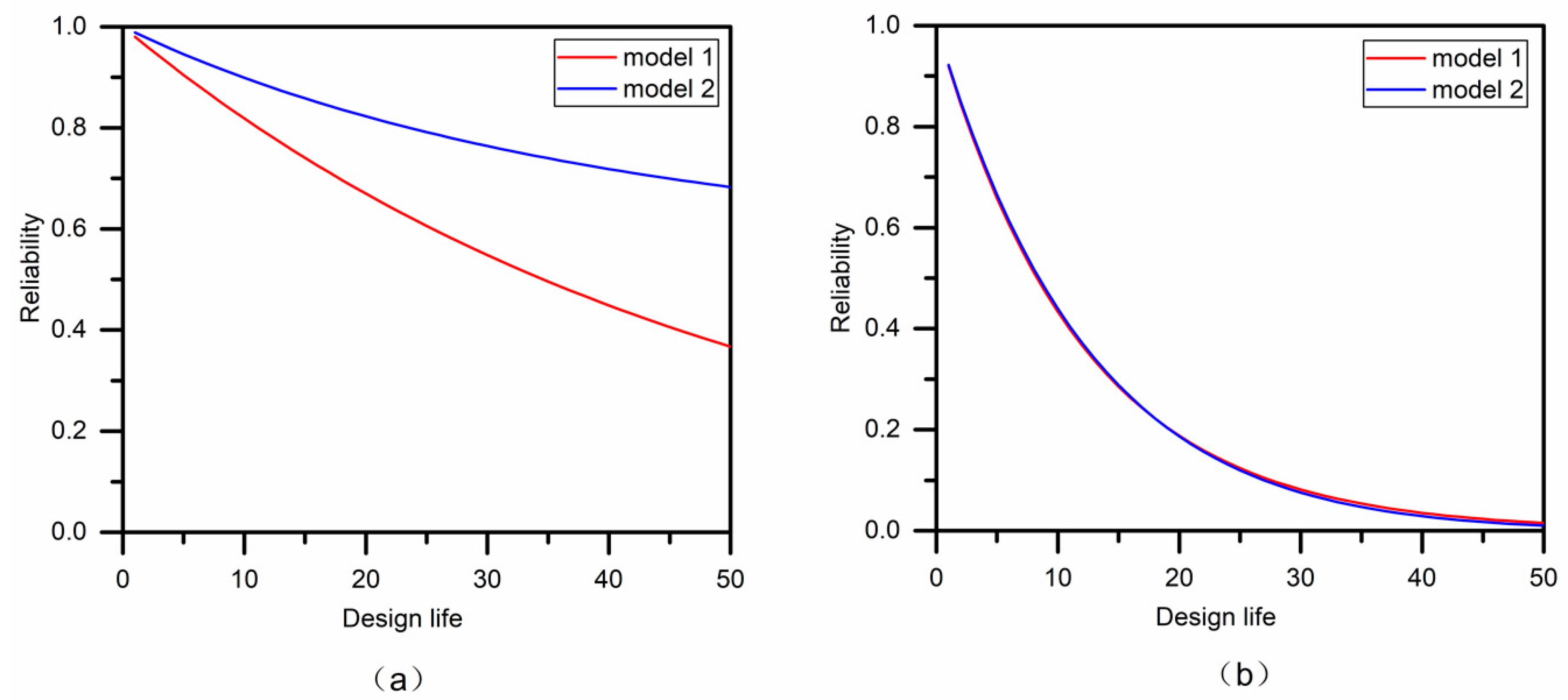
4.4.2. Risk of Failure and Reliability
5. Discussion
6. Conclusions
- (1)
- Both univariate and multivariate M-K trend tests were used to examine the temporal variations between flood characteristics, and the results revealed severe non-stationary properties, indicating that the stationary assumption is invalid, and a non-stationary copula model is needed for hydrological modeling in this region.
- (2)
- The flood peak and volume series were fitted by 6 marginal distributions under stationary and non-stationary situations, and the appropriate distributions vary correspondingly. The Weibull and Logistic distributions were selected for flood peak and volume under the stationary assumption, while the Gamma and Logistic distributions were selected under the non-stationary assumption. The flood peak and volume series presented decreasing trends in their location parameters. Four copula functions were applied to investigate the dependence structure between flood variables, and the Frank copula was selected as the most appropriate. The non-stationary model performs better than the copula with constant parameters according to AIC values. The copula parameters of the non-stationary model detected a decreasing trend, which means the dependence structure between flood variables also weakened over time.
- (3)
- The joint non-stationary return period was calculated for comparison, and the results varied with different design flood events. Compared with the stationary model, in case AND, the flood risk of non-stationary models decreased as a result of the decreased parameters of both marginal distributions and copula functions. While in case OR, the effect of the non-stationary properties is almost negligible. As for the design values, the non-stationary model is characterized by a higher flood peak and lower flood volume. The bivariate risk of failure of 50 years of design life was also estimated, and the conclusions were similar to those obtained by the return period. The effect of non-stationarity is more inclined to case AND rather than case OR, and the non-stationary model is safer than the stationary model in case AND.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Selenica, A.; Kuriqi, A.; Ardicioglu, M. Risk assessment from floodings in the rivers of albania. In Proceedings of the International Balkans Conference on Challenges of Civil Engineering, Tirana, Albania, 23–25 May 2013. [Google Scholar]
- Kuriqi, A.; Ardiçlioǧlu, M. Investigation of hydraulic regime at middle part of the loire river in context of floods and low flow events. Pollack Period. 2018, 13, 145–156. [Google Scholar] [CrossRef]
- Deng, X.; Ren, W.; Feng, P. Design flood recalculation under land surface change. Nat. Hazards 2016, 80, 1153–1169. [Google Scholar] [CrossRef]
- Oliver, J.; Qin, X.S.; Larsen, O.; Meadows, M.; Fielding, M. Probabilistic flood risk analysis considering morphological dynamics and dike failure. Nat. Hazards 2018, 91, 287–307. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Zhou, Y.; Singh, V.P.; Chen, X. The influence of dam and lakes on the yangtze river streamflow: Long-range correlation and complexity analyses. Hydrol. Process. 2012, 26, 436–444. [Google Scholar] [CrossRef]
- Ishak, E.H.; Rahman, A.; Westra, S.; Sharma, A.; Kuczera, G. Evaluating the non-stationarity of australian annual maximum flood. J. Hydrol. 2013, 494, 134–145. [Google Scholar] [CrossRef]
- O’Brien, N.L.; Burn, D.H. A nonstationary index-flood technique for estimating extreme quantiles for annual maximum streamflow. J. Hydrol. 2014, 519, 2040–2048. [Google Scholar] [CrossRef]
- Li, J.; Tan, S. Nonstationary flood frequency analysis for annual flood peak series, adopting climate indices and check dam index as covariates. Water Resour. Manag. 2015, 29, 5533–5550. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the concepts of return period and risk for nonstationary hydrologic extreme events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Serinaldi, F. Dismissing return periods! Stoch. Environ. Res. Risk Assess. 2014, 29, 1179–1189. [Google Scholar] [CrossRef]
- Du, T.; Xiong, L.; Xu, C.-Y.; Gippel, C.J.; Guo, S.; Liu, P. Return period and risk analysis of nonstationary low-flow series under climate change. J. Hydrol. 2015, 527, 234–250. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, L.; Guo, S.; Xu, C.-Y.; Xia, J.; Du, T. Comparison of four nonstationary hydrologic design methods for changing environment. J. Hydrol. 2017, 551, 132–150. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Xu, C.Y.; Guo, S. Bivariate frequency analysis of nonstationary low-flow series based on the time-varying copula. Hydrol. Process. 2015, 29, 1521–1534. [Google Scholar] [CrossRef]
- Ahn, K.H.; Palmer, R.N. Use of a nonstationary copula to predict future bivariate low flow frequency in the connecticut river basin. Hydrol. Process. 2016, 30, 3518–3532. [Google Scholar] [CrossRef]
- Sarhadi, A.; Burn, D.H.; Ausín, M.C.; Wiper, M.P. Time varying nonstationary multivariate risk analysis using a dynamic bayesian copula. Water Resour. Res. 2016, 52. [Google Scholar] [CrossRef]
- Yu, F.; Chen, Z.; Ren, X.; Yang, G. Analysis of historical floods on the yangtze river, china: Characteristics and explanations. Geomorphology 2009, 113, 210–216. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Shenglian, G.; Hao, Z.; Li, T. Flood coincidence risk analysis using multivariate copula functions. J. Hydrol. Eng. 2012, 17, 742–755. [Google Scholar] [CrossRef]
- Su, B.; Huang, J.; Zeng, X.; Gao, C.; Jiang, T. Impacts of climate change on streamflow in the upper yangtze river basin. Clim. Chang. 2017, 141, 533–546. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975. [Google Scholar]
- Hirsch, R.M.; Slack, J.R. A nonparametric trend test for seasonal data with serial dependence. Water Resour. Res. 1984, 20, 727–732. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T.B.M.J.; Duong, T.C. Testing for multivariate trends in hydrologic frequency analysis. J. Hydrol. 2013, 486, 519–530. [Google Scholar] [CrossRef]
- Rizwan, M.; Guo, S.; Xiong, F.; Yin, J. Evaluation of various probability distributions for deriving design flood featuring right-tail events in pakistan. Water 2018, 10, 1603. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. C-Appl. Stat. 2005, 54, 507–544. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, L.; Liu, D.; Hu, T.; Xu, C.-Y. Frequency analysis of nonstationary annual maximum flood series using the time-varying two-component mixture distributions. Hydrol. Process. 2017, 31, 69–89. [Google Scholar] [CrossRef]
- Zhang, D.-D.; Yan, D.-H.; Wang, Y.-C.; Lu, F.; Liu, S.-H. Gamlss-based nonstationary modeling of extreme precipitation in Beijing–Tianjin–Hebei region of china. Nat. Hazards 2015, 77, 1037–1053. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Buuren, S.; Van Fredriks, M. Worm plot: A simple diagnostic device for modelling growth reference curves. Stat. Med. 2010, 20, 1259–1277. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.; Jiang, S. Bivariate frequency analysis of hydrological drought using a nonstationary standardized streamflow index in the Yangtze river. J. Hydrol. Eng. 2019, 24, 05018031. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; Chapman and Hall/CRC: New York, NY, USA, 1997. [Google Scholar]
- Zhang, Q.; Gu, X.; Singh, V.P.; Xiao, M.; Chen, X. Evaluation of flood frequency under non-stationarity resulting from climate indices and reservoir indices in the east river basin, china. J. Hydrol. 2015, 527, 565–575. [Google Scholar] [CrossRef]
- Cooley, D. Return periods and return levels under climate change. In Extremes in a Changing Climate; Springer: Dordrecht, The Netherlands, 2013; pp. 97–114. [Google Scholar]
- Salvadori, G.; De Michele, C.; Kottegoda, N.T.; Rosso, R. Extremes in Nature: An. Approach using Copulas; Springer Science & Business Media: Dordrecht, The Netherlands, 2007; Volume 56. [Google Scholar]
- Ministry of Water Resources. Regulation for Calculating Design Flood of Water Resources and Hydropower Projects; China Water&Power Press: Beijing, China, 2006. [Google Scholar]
- Li, T.; Guo, S.; Chen, L.; Guo, J. Bivariate flood frequency analysis with historical information based on copula. J. Hydrol. Eng. 2012, 18, 1018–1030. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Wang, B.; Tan, S.; Feng, P. Nonstationary flood frequency analysis using univariate and bivariate time-varying models based on gamlss. Water 2018, 10, 819. [Google Scholar] [CrossRef]
| Distribution | Probability Density Function, f(x) | Link Function | |
|---|---|---|---|
| g(μ) | g(σ) | ||
| Gamma | ln(μ) | ln(σ) | |
| Weibull | ln(μ) | ln(σ) | |
| Gumbel | μ | ln(σ) | |
| Logistic | μ | ln(σ) | |
| Lognormal | μ | ln(σ) | |
| Pearson III | ln(μ) | ln(σ) | |
| Copula | C(u,v) | Range of θ | g(θ) |
|---|---|---|---|
| Clayton | θ > 0 | ln(θ) | |
| GH | θ ≥ 1 | ln(θ) | |
| Frank | θ ≠ 0 | ln(θ) | |
| Joe | θ ≥ 1 | ln(θ) |
| Series | Type | Distribution | μ | σ | AIC |
|---|---|---|---|---|---|
| P (m3/s) | Stationary | Weibull | 53,585.83 | 6.74 | 1341.9 |
| Non-stationary | Gamma | exp(10.90 − 0.0026t) | exp(−2.20 + 0.0116t) | 1339.9 | |
| V (106 m3) | Stationary | Logistic | 26,542.00 | 2444.02 | 1258.4 |
| Non-stationary | Logistic | 28,239.69 − 53.43t | 2387.50 | 1256.6 |
| Model | Copula Function | θ | AIC |
|---|---|---|---|
| 1 | Clayton | 3.70 | −94.31 |
| GH | 3.06 | −87.33 | |
| Frank | 12.88 | −101.80 | |
| Joe | 3.43 | −63.52 | |
| 2 | Clayton | exp(−0.0064t + 1.24) | −76.98 |
| GH | exp(−0.0048t + 1.34) | −98.05 | |
| Frank | exp(−0.0039t + 2.69) | −102.36 | |
| Joe | exp(−0.0052t + 1.55) | −77.45 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, L.; Jiang, S.; Hu, X.; Li, C. Evaluation of Return Period and Risk in Bivariate Non-Stationary Flood Frequency Analysis. Water 2019, 11, 79. https://doi.org/10.3390/w11010079
Kang L, Jiang S, Hu X, Li C. Evaluation of Return Period and Risk in Bivariate Non-Stationary Flood Frequency Analysis. Water. 2019; 11(1):79. https://doi.org/10.3390/w11010079
Chicago/Turabian StyleKang, Ling, Shangwen Jiang, Xiaoyong Hu, and Changwen Li. 2019. "Evaluation of Return Period and Risk in Bivariate Non-Stationary Flood Frequency Analysis" Water 11, no. 1: 79. https://doi.org/10.3390/w11010079
APA StyleKang, L., Jiang, S., Hu, X., & Li, C. (2019). Evaluation of Return Period and Risk in Bivariate Non-Stationary Flood Frequency Analysis. Water, 11(1), 79. https://doi.org/10.3390/w11010079





