Flooding Related Consequences of Climate Change on Canadian Cities and Flow Regulation Infrastructure
Abstract
1. Introduction
2. Methodology
2.1. CaMa-Flood Hydrodynamic Model
2.2. Future Projected Changes in Flood Risk in Canadian Cities
2.2.1. Projected Changes in Flood Hazard
2.2.2. Population Exposed to Flooding
- A retrospective simulation of a land surface model MATSIRO [37] forced by climate variables obtained from gauges and reanalysis datasets, and with CaMa-Flood river routing is performed for the time-period 1979–2010 for the entire Canadian landmass at 0.005° spatial resolution to simulate daily discharges, water levels and other flood inundation related variables. The estimated discharge and hydrologic variables from this retrospective run has been validated against observations from Gravity Recovery and Climate Experiment (GRACE) based terrestrial water storage data in Kim et al. [38].
- The annual maximum discharge and water levels obtained from this retrospective run are fitted to a Generalized Extreme Value (GEV) distribution and their 100 and 250 year return period estimates are obtained.
- The water levels corresponding to 100 and 250 year return period flooding events are used to obtain the fraction of CaMa-Flood grids encompassing different cities that are flooded as a consequence of these events.
- The flooded area fraction is then multiplied to the total population of the cities to obtain the total population exposed to flooding.
2.2.3. Projected Changes in Flood Risk
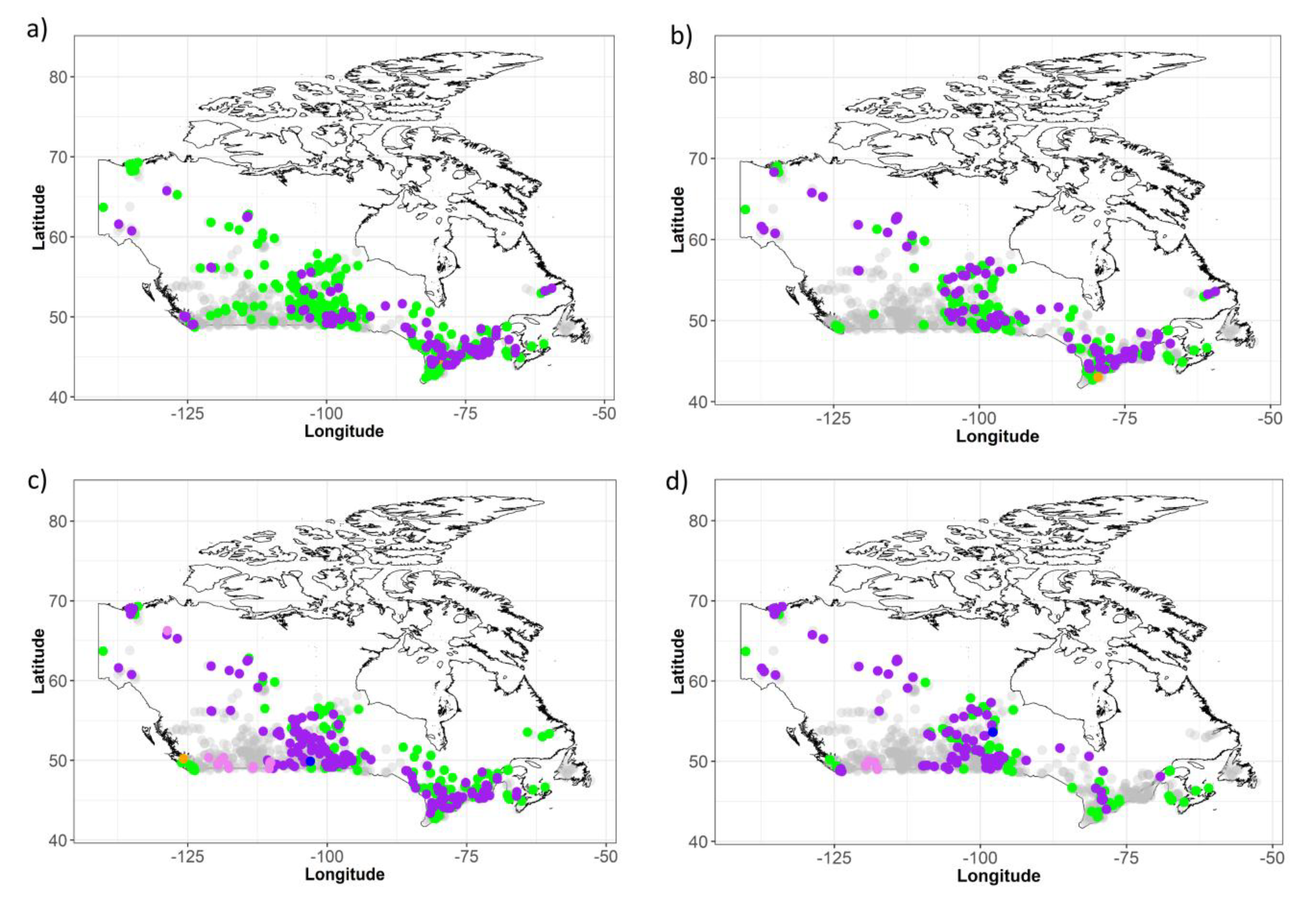
2.3. Future Changes in Flood Hazard at Flow Regulation Infrastructure Locations in Canada
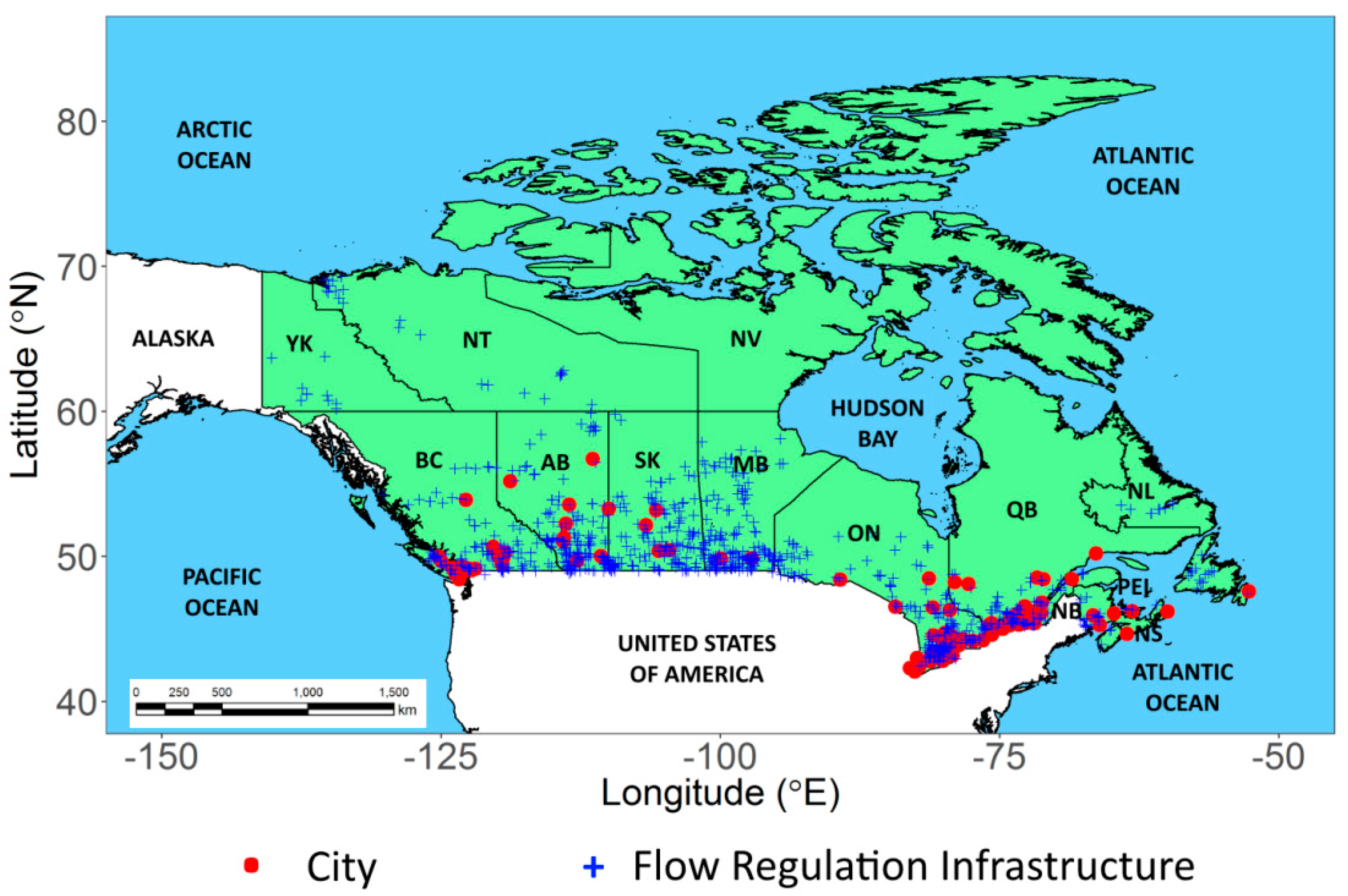
3. Study Region and Data Used
4. Results and Discussion
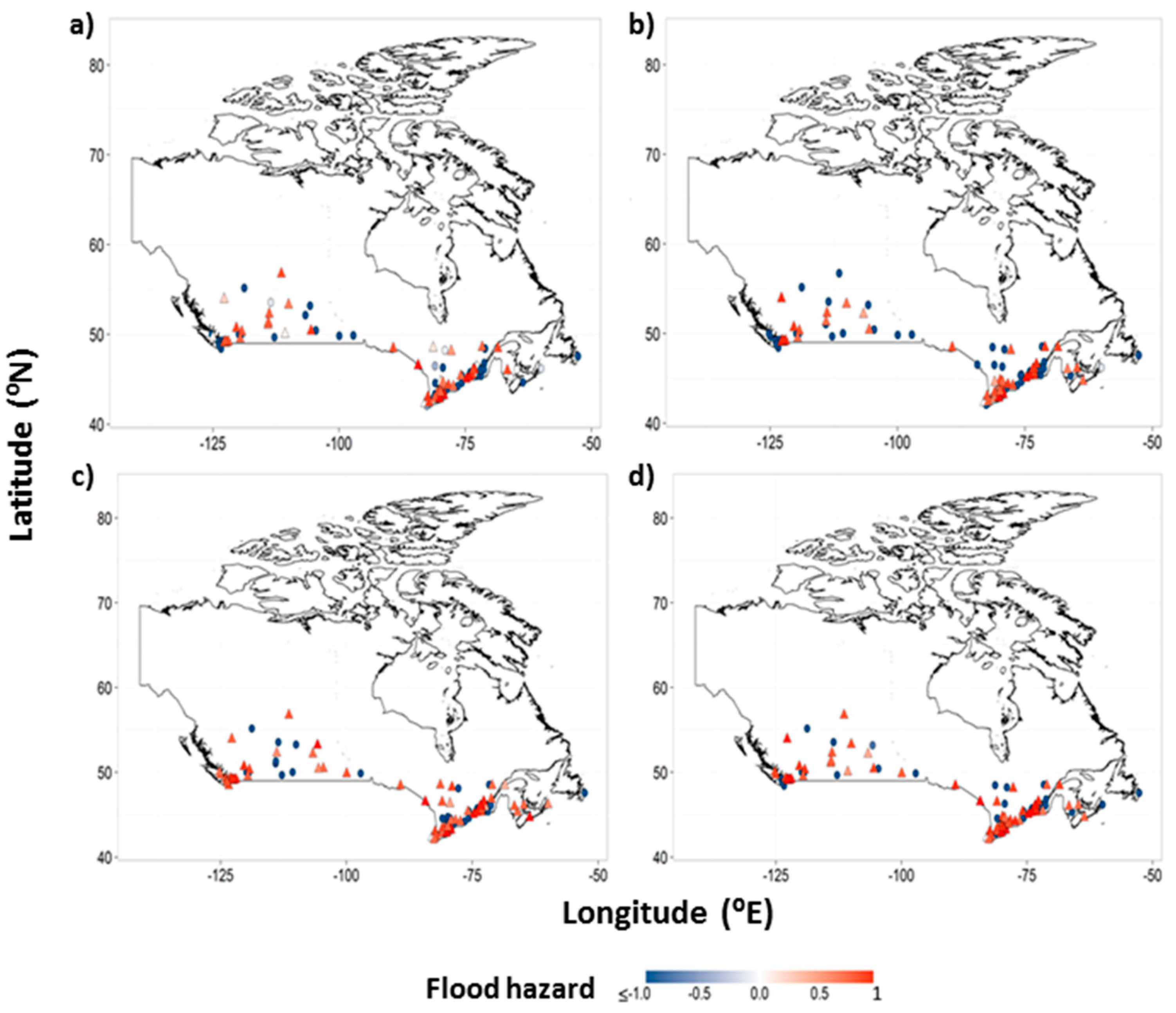
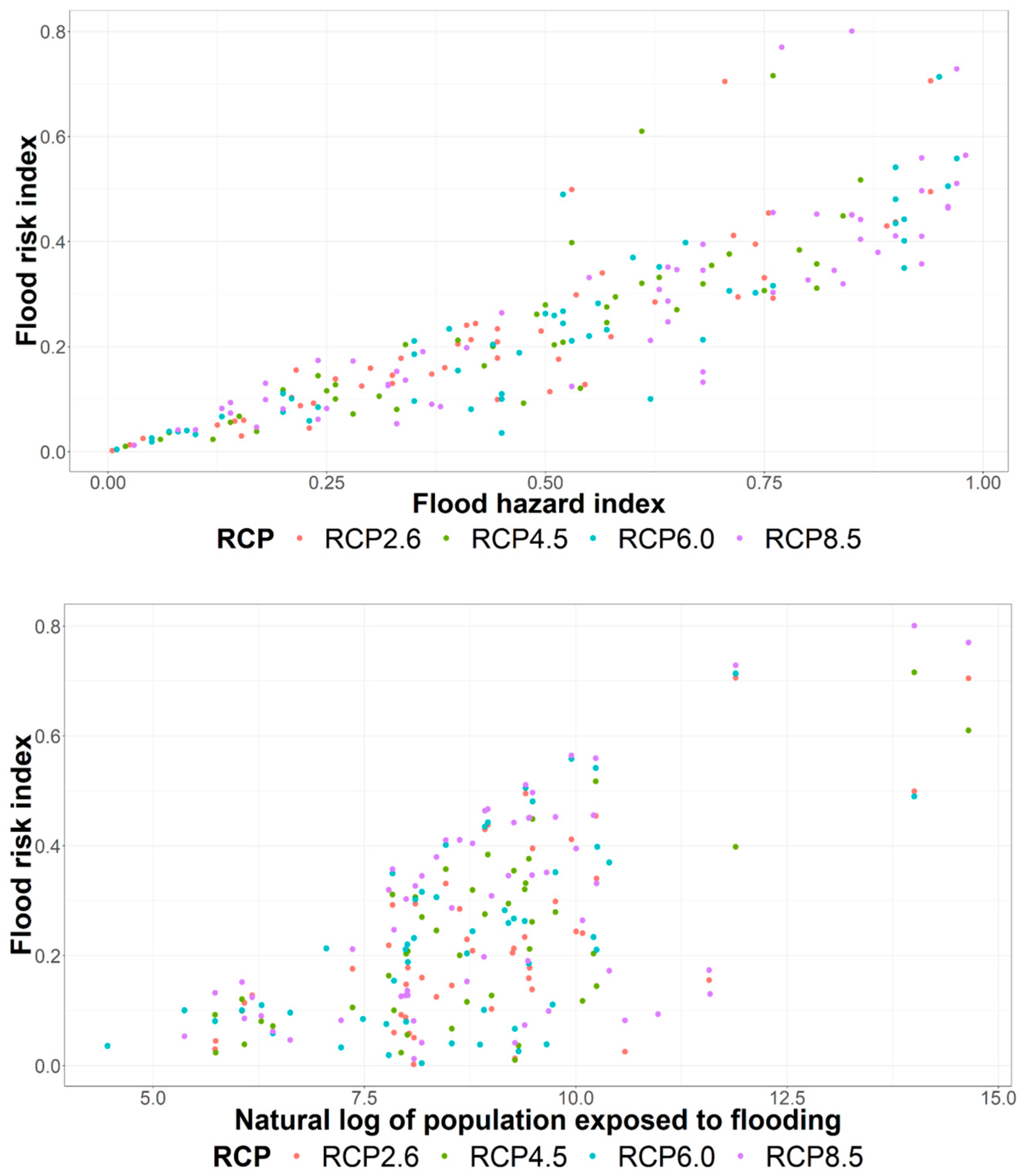
4.1. Projected Changes in Flood-Risk in Canadian Cities
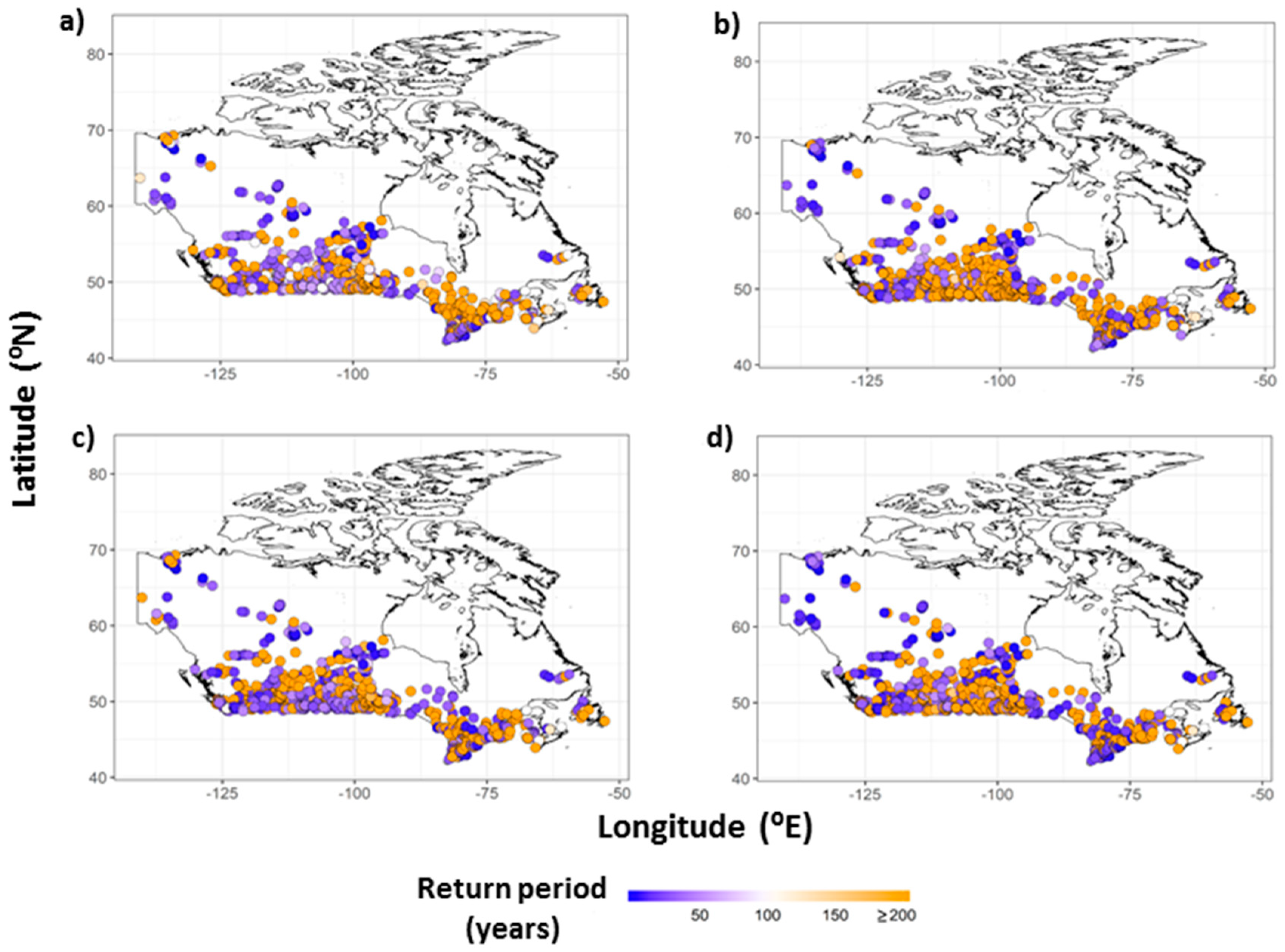
4.2. Flooding Related Impacts on Flow Regulation Infrastructures (FRIs)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Summary for Policymakers. In: Climate Change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation. In A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V., Stocker, T.F., Qin, D., Dokken, D.J., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.K., Allen, S.K., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012; p. 582. [Google Scholar]
- Watt, W.E.; Lathem, K.W.; Neill, C.R.; Richards, T.L.; Rousselle, J. Hydrology of Floods in Canada: A Guide to Planning and Design; National Research Council of Canada: Ottawa, ON, Canada, 1989. [Google Scholar]
- Andrews, J. Flooding: Canada Water Year Book; Ministry of Supply and Services: Ottawa, ON, USA, 1993.
- Burn, D.H.; Elnur, M.A. Detection of hydrological trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
- Burn, D.H.; Fan, L.; Bell, G. Identification and quantification of streamflow trends on the Canadian Prairies. Hydrol. Sci. 2008, 53, 538–549. [Google Scholar] [CrossRef]
- Déry, S.J.; Stahl, K.; Moore, R.D.; Whitfield, P.H.; Menounos, B.; Burford, J.E. Detection of runoff timing changes in pluvial, nival and glacial rivers of western Canada. Water Resour. Res. 2009, 45, W04426. [Google Scholar] [CrossRef]
- Burn, D.H.; Sharif, M.; Zhang, K. Detection of trends in hydrological extremes for Canadian watersheds. Hydrol. Process. 2010, 24, 1781–1790. [Google Scholar] [CrossRef]
- Sandink, D. Urban Flooding in Canada; Institute for Catastrophic Loss Reduction: London, ON, Canada, 2013; Volume 52, pp. 1–94. [Google Scholar]
- Gaur, A.; Simonovic, S.P. Projected Changes in the Dynamics of Flood Hazard in the Grand River Basin, Canada. Br. J. Environ. Clim. Chang. 2015, 5, 37–51. [Google Scholar] [CrossRef]
- Fiorentino, M.; Gioia, A.; Iacobellis, V.; Manfreda, S. Regional analysis of runoff thresholds behaviour in Southern Italy based on theoretically derived distributions. Adv. Geosci. 2011, 26, 139–144. [Google Scholar] [CrossRef]
- Gioia, A.; Manfreda, S.; Iacobellis, V.; Fiorentino, M. Performance of a theoretical model for the description of water balance and runoff dynamics in Southern Italy. J. Hydrol. Eng. 2014, 19, 1113–1123. [Google Scholar] [CrossRef]
- Devkota, L.P.; Gyawali, D.R. Impacts of climate change on hydrological regime and water resources management of the Koshi River Basin, Nepal. J. Hydrol. Reg. Stud. 2015, 4B, 502–515. [Google Scholar] [CrossRef]
- Qin, X.S.; Lu, Y. Study of Climate Change Impact on Flood Frequencies: A Combined Weather Generator and Hydrological Modeling Approach. J. Hydrometeorol. 2014, 15, 1205–1219. [Google Scholar] [CrossRef]
- Das, S.; Millington, N.; Simonovic, S.P. Distribution choice for the assessment of design rainfall for the city of London (Ontario, Canada) under climate change. Can. J. Civ. Eng. 2012, 40, 121–129. [Google Scholar] [CrossRef]
- Gaur, A.; Gaur, A.; Simonovic, S.P. Future Changes in Flood Hazards across Canada under a Changing Climate. Water 2018, 10, 1441. [Google Scholar] [CrossRef]
- Ranger, N.; Hallegatte, S.; Bhattacharya, S.; Bachu, M.; Priya, S.; Dhore, K.; Rafique, F.; Mathur, P.; Naville, N.; Henriet, F.; et al. An assessment of the potential impact of climate change on flood risk in Mumbai. Clim. Chang. 2011, 104, 139–167. [Google Scholar] [CrossRef]
- Kundzewicz, Z.; Kanae, S.; Seneviratne, S.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: Global and regional perspectives [le risque d’inondation et les perspectives de changement climatique mondial et regional]. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Pappenberger, F.; Dutra, E.; Wetterhall, F.; Cloke, H.L. Deriving global flood hazard maps of fluvial floods through a physical model cascade. Hydrol. Earth Syst. Sci. 2012, 16, 4143–4156. [Google Scholar] [CrossRef]
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kanae, S. Global flood risk under climate change. Nat. Clim. Chang. 2013, 3, 816–821. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Van Beek, L.P.H.; Jongman, B.; Ward, P.J.; Bouwman, A. A framework for global river flood risk assessments. Hydrol. Earth Syst. Sci. 2013, 17, 1871–1892. [Google Scholar] [CrossRef]
- Yamazaki, D.; Lee, H.; Alsdorf, E.; Dutra, E.; Kim, H.; Kanae, S.; Oki, T. Analysis of the water level dynamics simulated by a global river model: A case study in the Amazon River. Water Resour. Res. 2012, 48, W09508. [Google Scholar] [CrossRef]
- Dankers, R.; Feyen, L. Climate change impact on flood hazard in Europe: An assessment based on high resolution climate simulations. J. Geophys. Res. 2008, 113, D19105. [Google Scholar] [CrossRef]
- Yamazaki, D.; Kanae, S.; Kim, H.; Oki, T. A physically based description of floodplain inundation dynamics in a global river routing model. Water Resour. Res. 2011, 47, 1–21. [Google Scholar] [CrossRef]
- Jongman, B.; Ward, P.J.; Aerts, J.C.J.H. Global exposure to river and coastal flooding: Long term trends and changes. Glob. Environ. Chang. 2012, 22, 823–835. [Google Scholar] [CrossRef]
- Peduzzi, P.; Dao, H.; Herold, C.; Mouton, F. Assessing global exposure and vulnerability towards natural hazards: The Disaster Risk Index. Nat. Hazards Earth Syst. Sci. 2009, 9, 1149–1159. [Google Scholar] [CrossRef]
- de Moel, H.; Aerts, J.C.J.H.; Koomen, E. Development of flood exposure in the Netherlands during the 20th and 21st century. Glob. Environ. Chang. 2011, 21, 620–627. [Google Scholar] [CrossRef]
- Kleinen, T.; Petschel-Held, G. Integrated assessment of changes in flooding probabilities due to climate change. Clim. Chang. 2007, 81, 283–312. [Google Scholar] [CrossRef]
- Feyen, L.; Barredo, J.I.; Dankers, R. Implications of global warming and urban land use change on flooding in Europe. In Water and Urban Development Paradigms—Towards an Integration of Engineering, Design and Management Approaches; Feyen, J., Shannon, K., Neville, M., Eds.; CRC Press: London, UK, 2009; pp. 217–225. [Google Scholar]
- Feyen, L.; Dankers, R.; Bódis, K.; Salamon, P.; Barredo, J.I. Fluvial flood risk in Europe in present and future climates. Clim. Chang. 2012, 112, 47–62. [Google Scholar] [CrossRef]
- Van Vuuren, D.P. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Yamazaki, D.; Oki, T.; Kanae, S. Deriving a global river network map and its sub-grid topographic characteristics from a fine-resolution flow direction map. Hydrol. Earth Syst. Sci. 2009, 13, 2241–2251. [Google Scholar] [CrossRef]
- Ikeuchi, H.; Hirabayashi, Y.; Yamazaki, D.; Kiguchi, M.; Koirala, S.; Nagano, T.; Kotera, A.; Kanae, S. Modeling complex flow dynamics of fluvial floods exacerbated by sea level rise in the Ganges-Brahmaputra-Meghna delta. Environ. Res. Lett. 2015, 10, 124011. [Google Scholar] [CrossRef]
- Hu, X.; Hall, J.W.; Shi, P.; Lim, W.H. The spatial exposure of the Chinese infrastructure system to flooding and drought hazards. Nat. Hazards 2016, 80, 1083–1118. [Google Scholar] [CrossRef]
- Mateo, C.M.; Hanasaki, N.; Komori, D.; Tanaka, K.; Kiguchi, M.; Champathong, M.; Sukhapunnaphan, T.; Yamazaki, D.; Oki, T. Assessing the impacts of reservoir operation to floodplain inundation by combining hydrological, reservoir management, and hydrodynamic models. Water Resour. Res. 2014, 50, 7245–7266. [Google Scholar] [CrossRef]
- Koirala, S.; Hirabayashi, Y.; Mahendran, R.; Kanae, S. Global assessment of agreement among streamflow projections using CMIP5 model outputs. Environ. Res. Lett. 2014, 9, 064017. [Google Scholar] [CrossRef]
- Takata, K.; Emori, S.; Watanabe, T. Development of the minimal advanced treatments of surface interaction and runoff. Glob. Planet. Chang. 2003, 38, 209–222. [Google Scholar] [CrossRef]
- Kim, H.; Yeh, P.; Oki, T.; Kanae, S. Role of rivers in the seasonal variations of terrestrial water storage over global basins. Geophys. Res. Lett. 2009, 36, L17402. [Google Scholar] [CrossRef]
- Knutti, R.; Furrer, R.; Tebaldi, C.; Cermak, J.; Meehl, G.A. Challenges in Combining Projections from Multiple Climate Models. J. Clim. 2010, 23, 2739–2758. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera. Revisiting the Concepts of Return Period and Risk for Nonstationary Hydrologic Extreme Events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
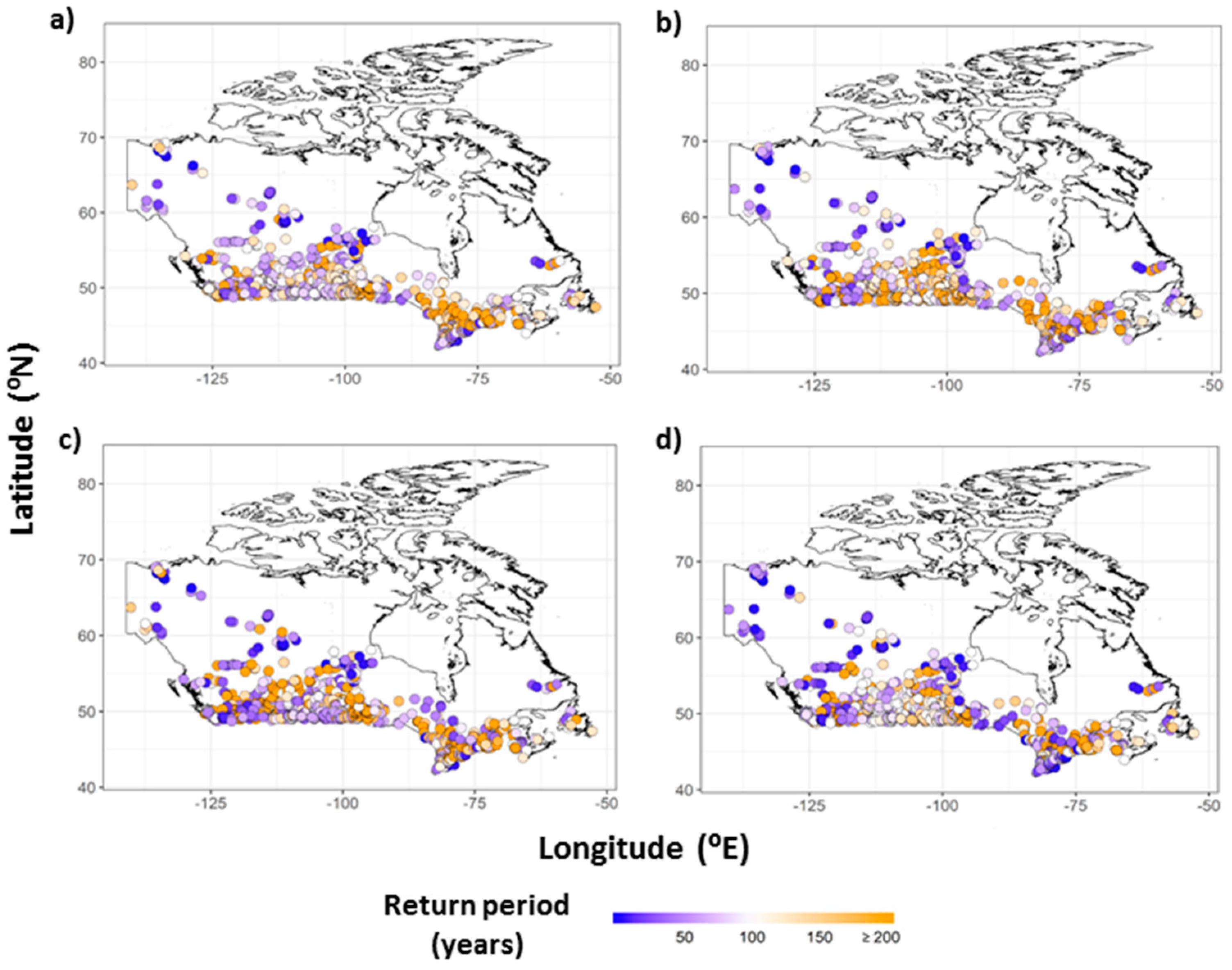
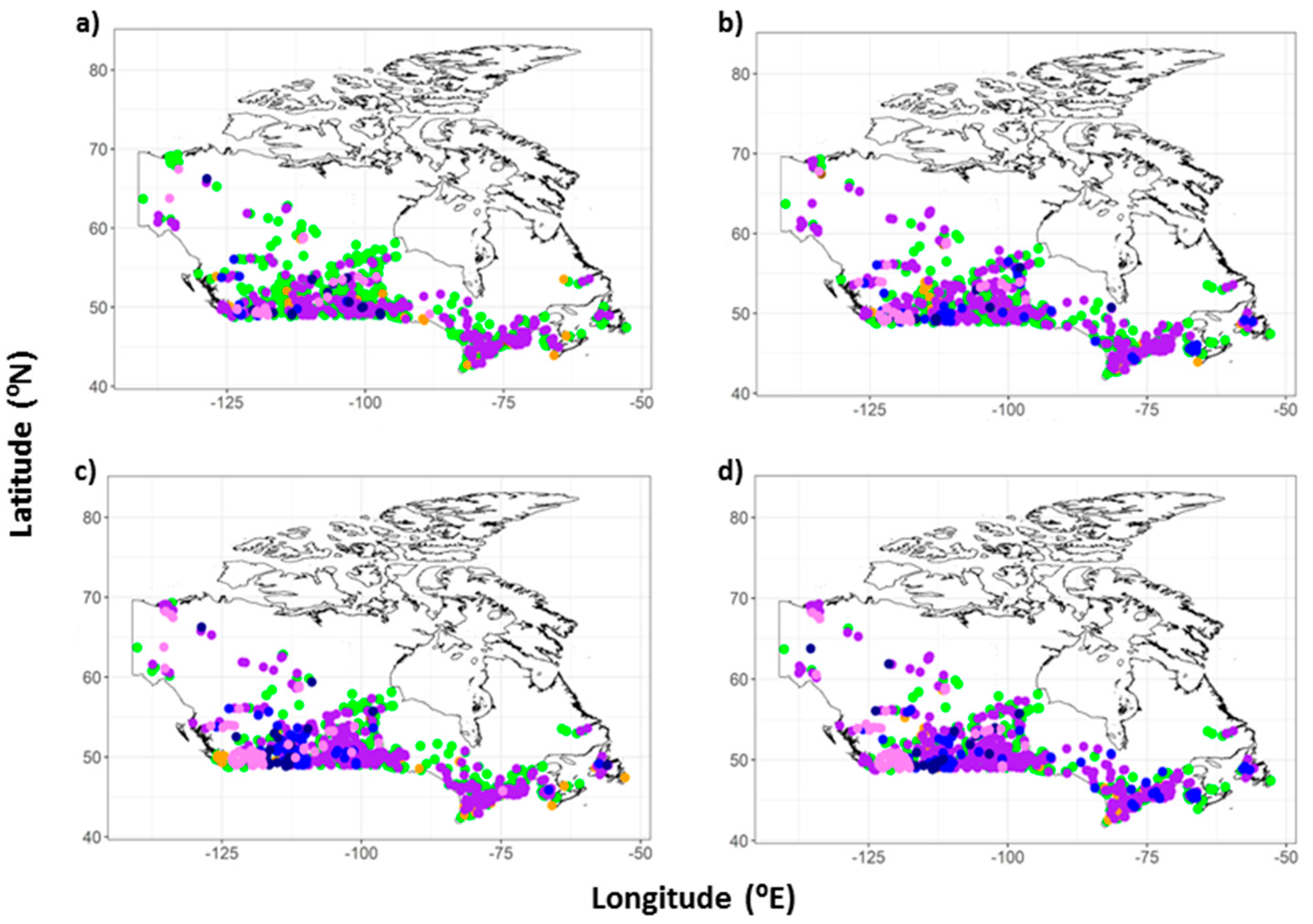
| RCP | 100-Year | 250-Year | ||||
|---|---|---|---|---|---|---|
| Decrease | Increase | No Change | Decrease | Increase | No Change | |
| All GCM Median | ||||||
| RCP 2.6 | 50 | 49 | 1 | 52 | 47 | 1 |
| RCP 4.5 | 55 | 43 | 2 | 51 | 48 | 1 |
| RCP 6.0 | 46 | 53 | 1 | 34 | 65 | 1 |
| RCP 8.5 | 34 | 60 | 6 | 32 | 63 | 5 |
| Robust GCM median | ||||||
| RCP 2.6 | 50 | 49 | 1 | 52 | 47 | 1 |
| RCP 4.5 | 56 | 43 | 1 | 51 | 48 | 1 |
| RCP 6.0 | 46 | 53 | 1 | 35 | 64 | 1 |
| RCP 8.5 | 39 | 60 | 1 | 35 | 63 | 1 |
| City | RCP 2.6 | RCP 4.5 | RCP 6.0 | RCP 8.5 | ||||
|---|---|---|---|---|---|---|---|---|
| 100-Year | 250-Year | 100-Year | 250-Year | 100-Year | 250-Year | 100-Year | 250-Year | |
| Toronto | 22 | 37 | 32 | 46 | 32 | 39 | 15 | 22 |
| Montreal | 26 | 38 | 22 | 32 | 18 | 25 | 11 | 16 |
| Vancouver | ≥200 | ≥500 | ≥200 | ≥500 | 20 | 28 | ≥200 | 32 |
| Calgary | 46 | 94 | ≥200 | ≥500 | ≥200 | ≥500 | 49 | 85 |
| Ottawa | ≥200 | ≥500 | ≥200 | ≥500 | ≥200 | ≥500 | ≥200 | ≥500 |
| Edmonton | 104 | 284 | ≥200 | ≥500 | ≥200 | ≥500 | ≥200 | ≥500 |
| Hamilton | 37 | 56 | 151 | 78 | ≥200 | 67 | 27 | 56 |
| Quebec | ≥200 | ≥500 | ≥200 | ≥500 | 27 | 49 | 26 | ≥500 |
| Winnipeg | ≥200 | ≥500 | ≥200 | ≥500 | ≥200 | ≥500 | ≥200 | ≥500 |
| Kitchener | 26 | 47 | ≥200 | 86 | ≥200 | 57 | 29 | 60 |
| City | RCP 2.6 | RCP 4.5 | RCP 6.0 | RCP 8.5 | ||||
|---|---|---|---|---|---|---|---|---|
| 100-Year | 250-Year | 100-Year | 250-Year | 100-Year | 250-Year | 100-Year | 250-Year | |
| Toronto | 30 | 63 | 39 | 86 | 116 | 227 | 23 | 35 |
| Montreal | 47 | 95 | 24 | 58 | 48 | 178 | 15 | 22 |
| Vancouver | ≥200 | ≥500 | 193 | ≥500 | 34 | 62 | 107 | 157 |
| Calgary | 96 | 199 | 133 | 254 | ≥200 | ≥500 | 87 | 156 |
| Ottawa | ≥200 | ≥500 | ≥200 | ≥500 | ≥200 | ≥500 | ≥200 | ≥500 |
| Edmonton | 104 | 284 | 189 | 476 | ≥200 | ≥500 | ≥200 | ≥500 |
| Hamilton | 79 | 142 | 102 | 223 | 125 | 198 | 76 | 174 |
| Quebec | 175 | ≥500 | ≥200 | ≥500 | 40 | 98 | 72 | 250 |
| Winnipeg | 151 | 416 | 191 | 393 | ≥200 | ≥500 | 121 | 319 |
| Kitchener | 58 | 108 | 103 | 231 | 126 | 188 | 32 | 74 |
| S. No. | RCP 2.6 | RCP 4.5 | RCP 6.0 | RCP 8.5 | ||||
|---|---|---|---|---|---|---|---|---|
| Hazard | Risk | Hazard | Risk | Hazard | Risk | Hazard | Risk | |
| 1 | Sault Ste. Marie (ON; 4) | Toronto (ON; 22) | Saint Catharines-Niagara (ON; 4) | Montreal (QB; 22) | Halifax (NS; 1) | Montreal (QB; 18) | Sault Ste. Marie (ON; 2) | Toronto (ON; 15) |
| 2 | Nanticoke (ON; 5) | Saint Catharines-Niagara (ON; 6) | Nanticoke (ON; 4) | Toronto (ON; 32) | Sault Ste. Marie (ON; 3) | Toronto (ON; 32) | Saint Catharines-Niagara (ON; 3) | Montreal (QB; 11) |
| 3 | Saint Catharines-Niagara (ON; 6) | Montreal (QB; 26) | Cornwall (ON; 7) | Saint Catharines-Niagara (ON; 4) | Saint Catharines-Niagara (ON; 4) | Vancouver (BC; 20) | Cornwall (ON; 3) | Saint Catharines-Niagara (ON; 3) |
| 4 | Cornwall (ON; 7) | Sault Ste. Marie (ON; 4) | Salaberry-de-Valleyfield (QB; 7) | Abbotsford (BC; 11) | Nanticoke (ON; 4) | Saint Catharines-Niagara (ON; 4) | Nanticoke (ON; 3) | Quebec (QB; 26) |
| 5 | Salaberry-de-Valleyfield (QB; 7) | Nanticoke (ON; 5) | Walnut Grove (BC; 10) | Barrie (ON; 31) | Cornwall (ON; 6) | Halifax (NB; 1) | Salaberry-de-Valleyfield (QB; 4) | Hamilton (ON; 27) |
| 6 | Brantford (ON; 18) | Abbotsford (BC; 21) | Abbotsford (BC; 11) | Chicoutimi-Jonquiere (QB; 21) | Shawinigan (QB; 7) | Quebec (QB; 27) | White rock (BC; 5) | London (ON; 20) |
| 7 | Chatham (ON; 18) | Sarnia (ON; 21) | White Rock (BC; 11) | Thunder Bay (ON; 32) | Sorel (QB; 8) | Victoria (BC; 30) | Abbotsford (BC; 6) | Kitchener (ON; 29) |
| 8 | Saint-Jean-Sur- Richelieu (QB; 20) | Chatham (ON; 18) | Chilliwack (BC; 11) | Peterborough (ON; 17) | Joliette (QB; 8) | Abbotsford (BC; 9) | Chilliwack (BC; 6) | Vancouver (BC; 49) |
| 9 | Beloeil (QB; 20) | Hamilton (ON; 37) | Shawinigan (QB; 13) | White Rock (BC; 11) | Prince Albert (SK; 8) | Saskatoon (SK; 38) | Joliette (QB; 6) | Calgary (AB; 25) |
| 10 | Kamloops (BC; 20) | Cornwall (ON; 7) | Sorel (QB; 14) | Brantford (ON; 31) | White Rock (BC; 9) | Regina (SK; 40) | Walnut Grove (BC; 6) | Halifax (NB; 24) |
| S. No. | RCP 2.6 | RCP 4.5 | RCP 6.0 | RCP 8.5 | ||||
|---|---|---|---|---|---|---|---|---|
| Hazard | Risk | Hazard | Risk | Hazard | Risk | Hazard | Risk | |
| 1 | Saint Catharines-Niagara (ON; 6) | Saint Catharines-Niagara (ON; 6) | Abbotsford (BC; 14) | Montreal (QB; 24) | Sault Ste. Marie (ON; 3) | Saint Catharines-Niagara (ON; 5) | Sault Ste. Marie (ON; 2) | Montreal (QB; 15) |
| 2 | Nanticoke (ON; 6) | Toronto (ON; 30) | Chilliwack (BC; 16) | Toronto (ON; 39) | Nanticoke (ON; 4) | Sault Ste. Marie (ON; 3) | Saint Catharines-Niagara (ON; 3) | Toronto (ON; 23) |
| 3 | Cornwall (ON; 10) | Montreal (QB; 47) | White Rock (BC; 19) | Abbotsford (BC; 14) | Saint Catharines-Niagara (ON; 5) | Abbotsford (BC; 10) | Nanticoke (ON; 3) | Saint Catharines-Niagara (ON; 3) |
| 4 | Salaberry-de-Valleyfield (QB; 11) | Nanticoke (ON; 6) | Walnut Grove (BC; 19) | Chilliwack (BC; 16) | White Rock (BC; 9) | Nanticoke (ON; 4) | Cornwall (ON; 4) | Sault Ste. Marie (ON; 2) |
| 5 | Walnut Grove (BC; 24) | Abbotsford (BC; 25) | Cornwall (ON; 21) | Saint Catharines-Niagara (ON; 47) | Cornwall (ON; 9) | Montreal (QB; 48) | Salaberry-de-Valleyfield (QB; 4) | Abbotsford (BC; 7) |
| 6 | Abbotsford (BC; 25) | Cornwall (ON; 10) | Montreal (QB; 24) | Cornwall (ON; 21) | Walnut Grove (BC; 9) | Chilliwack (BC; 10) | Abbotsford (BC; 7) | Nanticoke (ON; 3) |
| 7 | White Rock (BC; 25) | Salaberry-de-Valleyfield (QB; 11) | Kamloops (BC; 25) | Belleville (ON; 29) | Abbotsford (BC; 10) | Sorel (BC; 15) | White rock (BC; 7) | Chilliwack (BC; 7) |
| 8 | Chilliwack (BC; 26) | Sault Ste. Marie (ON; 29) | Belleville (ON; 29) | White Rock (BC; 19) | Chilliwack (BC; 10) | Cornwall (ON; 9) | Chilliwack (BC; 7) | Cornwall (ON; 4) |
| 9 | Kamloops (BC; 28) | Chilliwack (BC; 26) | Saint-jean-sur-richelieu (QB; 31) | Saint-jean-sur-richelieu (QB; 31) | Salaberry-de-Valleyfield (QB; 10) | Salaberry-de-Valleyfield (QB; 10) | Walnut Grove (BC; 7) | Salaberry-de-Valleyfield (QB; 4) |
| 10 | Sault Ste. Marie (ON; 29) | Thunder Bay (ON; 44) | Beloeil (QB; 32) | Nanticoke (ON; 37) | Joliette (QB; 10) | Joliette (QB; 10) | Joliette (QB; 10) | Sarnia (ON; 24) |
| RCP | 100-Year | 250-Year | ||||
|---|---|---|---|---|---|---|
| Increase | Decrease | No Change | Increase | Decrease | No Change | |
| All GCM median | ||||||
| RCP 2.6 | 532 | 518 | 22 | 538 | 509 | 25 |
| RCP 4.5 | 639 | 403 | 30 | 623 | 422 | 27 |
| RCP 6.0 | 520 | 523 | 29 | 507 | 544 | 21 |
| RCP 8.5 | 441 | 485 | 146 | 402 | 543 | 127 |
| Robust GCM median | ||||||
| RCP 2.6 | 543 | 518 | 11 | 553 | 509 | 10 |
| RCP 4.5 | 660 | 403 | 9 | 641 | 422 | 9 |
| RCP 6.0 | 540 | 523 | 9 | 519 | 544 | 9 |
| RCP 8.5 | 578 | 485 | 9 | 520 | 543 | 9 |
| S.No. | RCP 2.6 | RCP 4.5 | RCP 6.0 | RCP 8.5 |
|---|---|---|---|---|
| 1 | Reindeer River Above Devil Rapids (SK; 2) | Playgreen Lake At Entrance To East Nelson River (MB; 2) | Reindeer River Above Devil Rapids (SK; 2) | St. Marys River At Sault Ste. Marie (Above) (ON; 2) |
| 2 | Churchill River Above Leaf Rapids (MB; 2) | Sipiwesk Lake At Sipiwesk Landing (MB; 2) | Churchill River Above Leaf Rapid (MB; 2) | St. Marys River At Sault Ste. Marie (Below) (ON; 2) |
| 3 | Churchill River Below Fidler Lake (MB; 2) | Split Lake At Split Lake (MB; 2) | Churchill River Below Fidler Lake (MB; 2) | Churchill River Above Leaf Rapid (MB; 2) |
| 4 | Mackenzie River At Arctic Red River (NT; 2) | Nelson River At Kettle Generating Station (MB; 2) | Peace River Below Chenal Des Quatre Fourches (AB; 2) | Churchill River Below Fidler Lake (MB; 2) |
| 5 | Mackenzie River At Confluence East Channel (NT; 2) | Churchill River Below Fidler Lake (MB; 2) | Riviere Des Rochers Above Slave River (AB; 2) | Peace River Below Chenal Des Quatre Fourches (AB; 2) |
| 6 | Mackenzie River At Fort Good Hope (NT; 2) | Mackenzie River At Arctic Red River (NT; 2) | Mackenzie River At Arctic Red River (NT; 2) | Lake Athabasca Near Crackingstone Point (SK; 2) |
| 7 | Playgreen Lake At Entrance To East Nelson River (MB; 2.5) | Mackenzie River At Confluence East Channel (NT; 2) | Mackenzie River At Confluence East Channel (NT; 2) | Riviere Des Rochers Above Slave River (AB; 2) |
| 8 | Sipiwesk Lake At Sipiwesk Landing (MB; 2.5) | Mackenzie River At Fort Good Hope (NT; 2) | Mackenzie River At Fort Good Hope (NT; 2) | Riviere Des Rochers East Of Little Rapids (AB; 2) |
| 9 | Mackenzie River (Peel Channel) Above Aklavik (NT; 2.5) | Mackenzie River (Peel Channel) Above Aklavik (NT; 2) | Mackenzie River (Peel Channel) Above Aklavik (NT; 2) | Riviere Des Rochers West Of Little Rapids (AB; 2) |
| 10 | Cedar Lake Near Oleson Point (MB; 3) | Churchill River Above Leaf Rapids (MB; 2.5) | St. Marys River At Sault Ste. Marie (Above) (ON; 3) | Mackenzie River At Arctic Red River (NT; 2) |
| S.No | RCP 2.6 | RCP 4.5 | RCP 6.0 | RCP 8.5 |
|---|---|---|---|---|
| 1 | Mackenzie River At Fort Good Hope (NT; 2) | Churchill River Below Fidler Lake (MB; 2) | Reindeer River Above Devil Rapids (SK; 2) | St. Marys River At Sault Ste. Marie (Above) (ON; 2) |
| 2 | Churchill River Above Leaf Rapids (MB; 2.5) | Mackenzie River At Arctic Red River (NT; 2) | Churchill River Above Leaf Rapids (MB; 2) | St. Marys River At Sault Ste. Marie (Below) (ON; 2) |
| 3 | Churchill River Below Fidler Lake (MB; 2.5) | Mackenzie River At Confluence East Channel (NT; 2) | Peace River Below Chenal Des Quatre Fourches (AB; 2) | Churchill River Above Leaf Rapids (MB; 2) |
| 4 | Playgreen Lake At Entrance To East Nelson River (MB; 3) | Mackenzie River At Fort Good Hope (NT; 2) | Riviere Des Rochers Above Slave River (AB; 2) | Churchill River Below Fidler Lake (MB; 2) |
| 5 | Peace River Below Chenal Des Quatre Fourches (AB; 3) | Mackenzie River (Peel Channel) Above Aklavik (NT; 2) | Mackenzie River At Arctic Red River (NT; 2) | Peace River Below Chenal Des Quatre Fourches (AB; 2) |
| 6 | Riviere Des Rochers Above Slave River (AB; 3) | Reindeer River Above Devil Rapids (SK; 3) | Mackenzie River At Confluence East Channel (NT; 2) | Riviere Des Rochers Above Slave River (AB; 2) |
| 7 | Mackenzie River At Arctic Red River (NT; 3) | Churchill River Above Leaf Rapids (MB; 3) | Mackenzie River At Fort Good Hope (NT; 2) | Mackenzie River At Arctic Red River (NT; 2) |
| 8 | Mackenzie River At Confluence East Channel (NT; 3) | Peace River Below Chenal Des Quatre Fourches (AB; 3) | Mackenzie River (Peel Channel) Above Aklavik (NT; 2) | Mackenzie River At Confluence East Channel (NT; 2) |
| 9 | Mackenzie River (Peel Channel) Above Aklavik (NT; 3) | Riviere Des Rochers Above Slave River (AB; 3) | St. Marys River At Sault Ste. Marie (Above) (ON; 3) | Mackenzie River At Fort Good Hope (NT; 2) |
| 10 | Sipiwesk Lake At Sipiwesk Landing (MB; 3.5) | Lake Athabasca Near Crackingstone Point (SK; 4) | St. Marys River At Sault Ste. Marie (Below) (ON; 3) | Mackenzie River (Peel Channel) Above Aklavik (NT; 2) |
| RCP | All GCM Median | Robust GCM Median | ||||
|---|---|---|---|---|---|---|
| Change | No Change | Uncertain | Change | No Change | Uncertain | |
| RCP 2.6 | 417 | 655 | 0 | 126 | 352 | 594 |
| RCP 4.5 | 510 | 562 | 0 | 124 | 167 | 781 |
| RCP 6.0 | 638 | 434 | 0 | 209 | 178 | 685 |
| RCP 8.5 | 676 | 396 | 0 | 115 | 83 | 874 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaur, A.; Gaur, A.; Yamazaki, D.; Simonovic, S.P. Flooding Related Consequences of Climate Change on Canadian Cities and Flow Regulation Infrastructure. Water 2019, 11, 63. https://doi.org/10.3390/w11010063
Gaur A, Gaur A, Yamazaki D, Simonovic SP. Flooding Related Consequences of Climate Change on Canadian Cities and Flow Regulation Infrastructure. Water. 2019; 11(1):63. https://doi.org/10.3390/w11010063
Chicago/Turabian StyleGaur, Ayushi, Abhishek Gaur, Dai Yamazaki, and Slobodan P. Simonovic. 2019. "Flooding Related Consequences of Climate Change on Canadian Cities and Flow Regulation Infrastructure" Water 11, no. 1: 63. https://doi.org/10.3390/w11010063
APA StyleGaur, A., Gaur, A., Yamazaki, D., & Simonovic, S. P. (2019). Flooding Related Consequences of Climate Change on Canadian Cities and Flow Regulation Infrastructure. Water, 11(1), 63. https://doi.org/10.3390/w11010063






