Capturing the Motion of the Free Surface of a Fluid Stored within a Floating Structure
Abstract
1. Introduction
2. Experimental Method
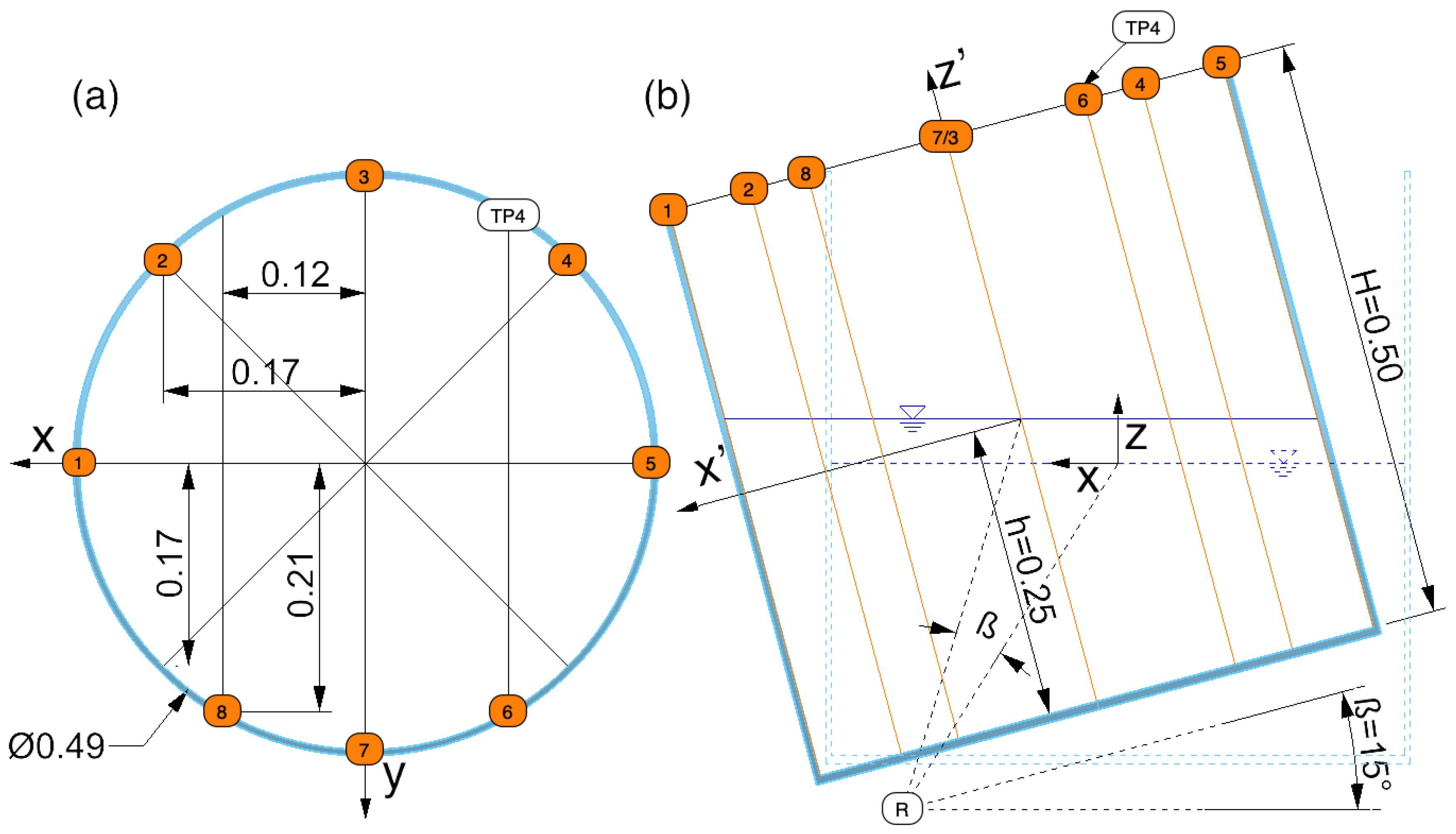
2.1. Overview
2.2. Floating Infra-Red Reflective Markers
2.3. Copper Tape Resistive Wave Gauges
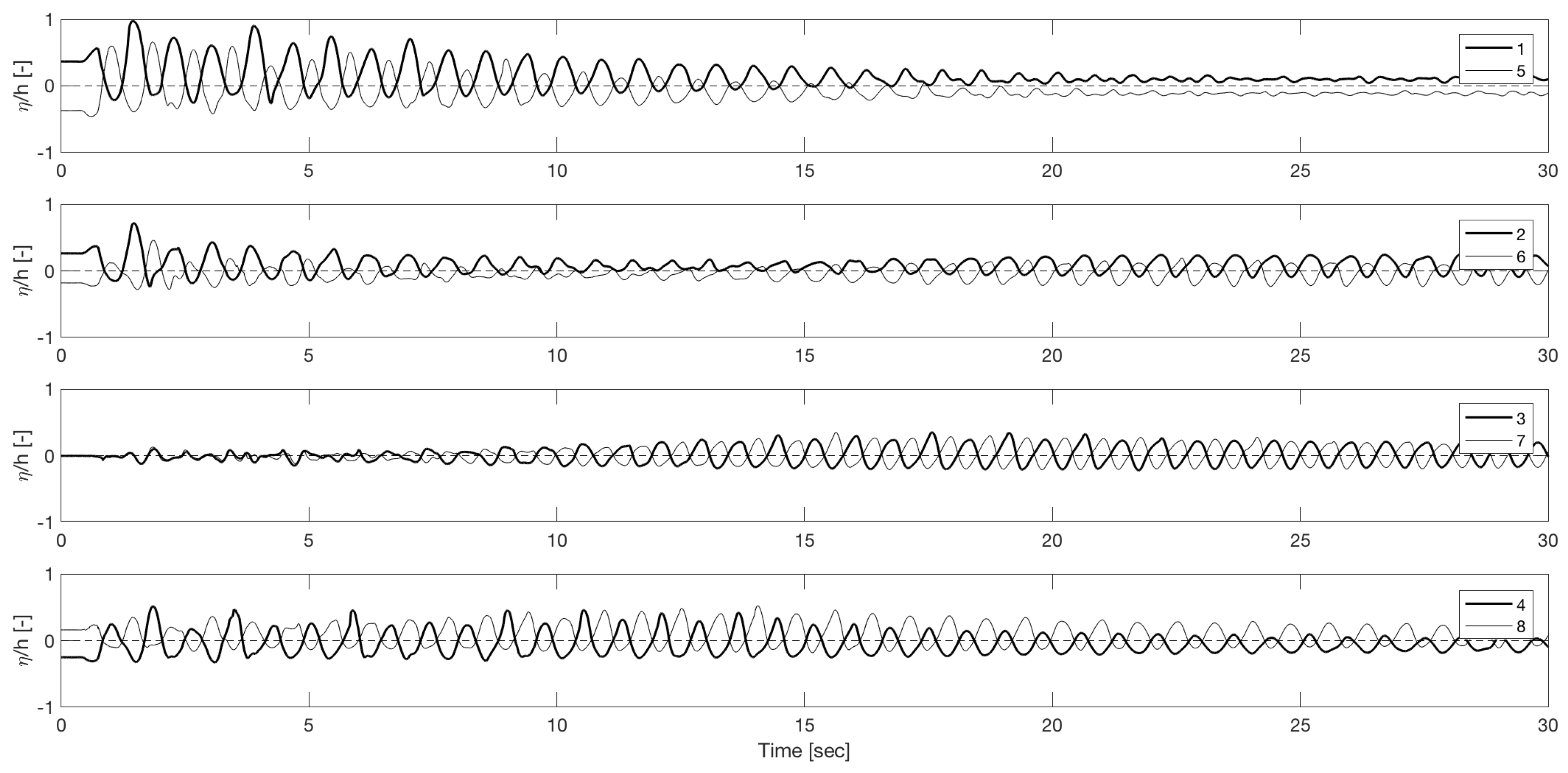
3. Results
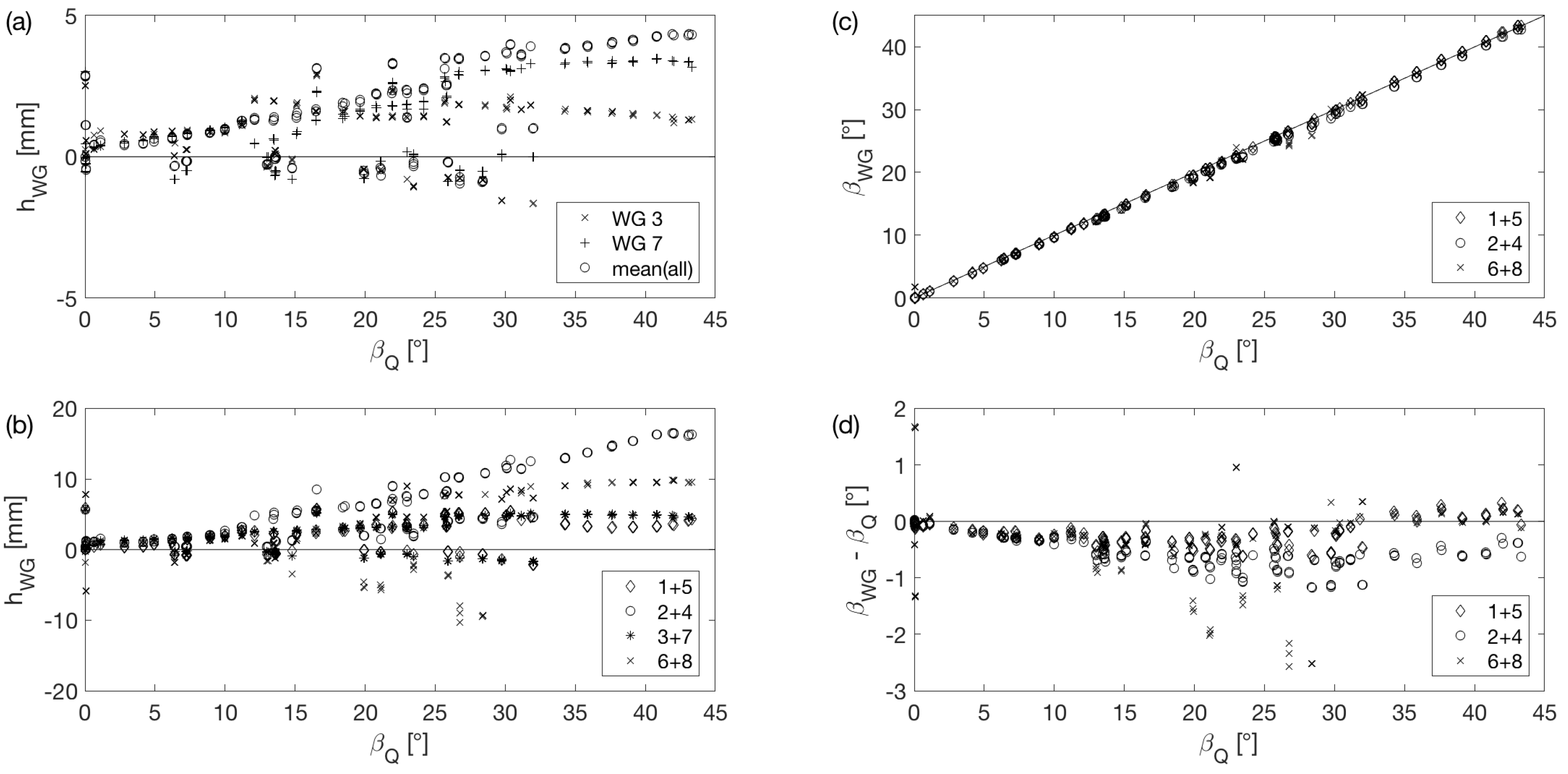
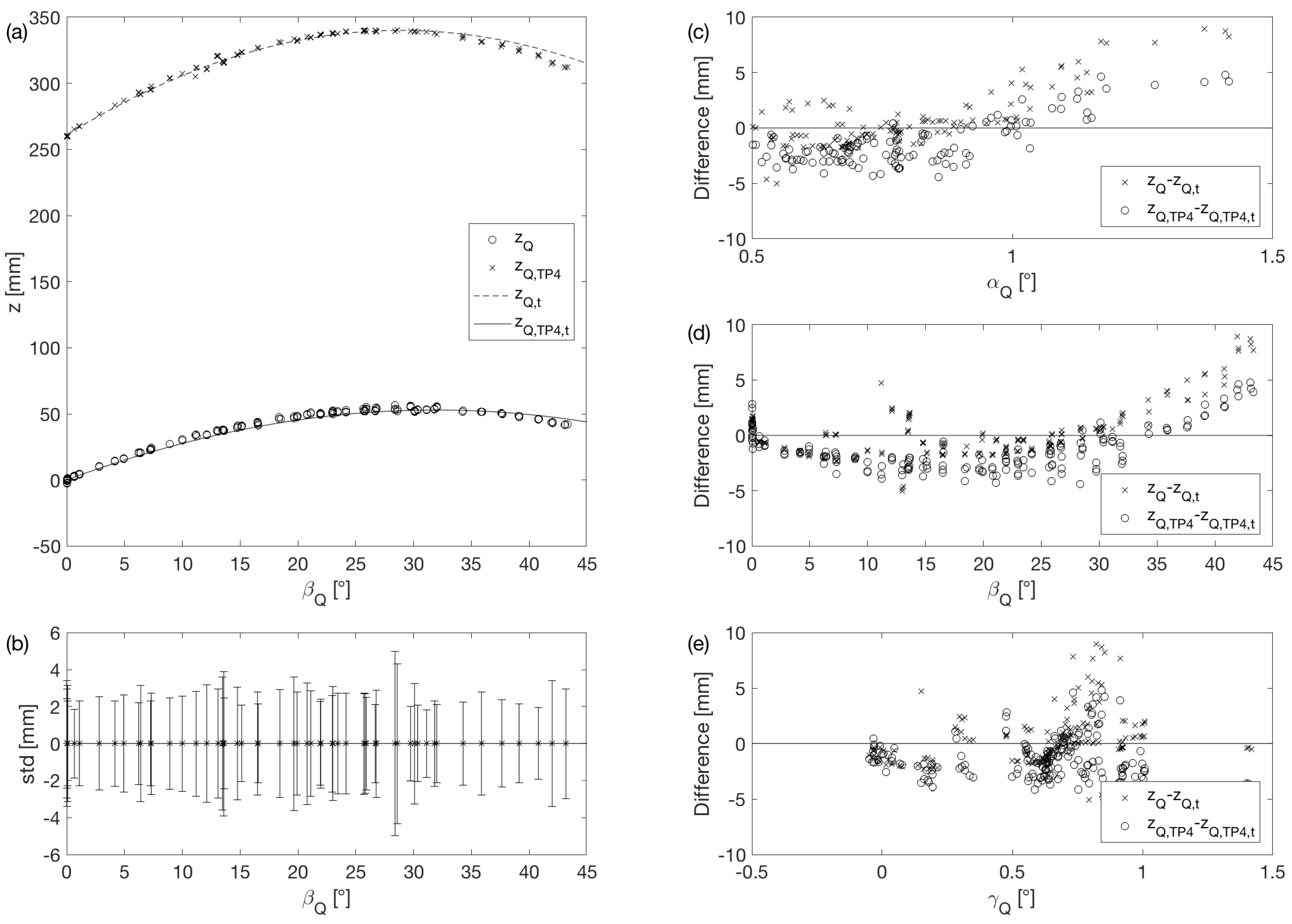
3.1. Influence of Variable Inner Water Depth h
3.2. Influence of Variable Inclination Angle of the Tank
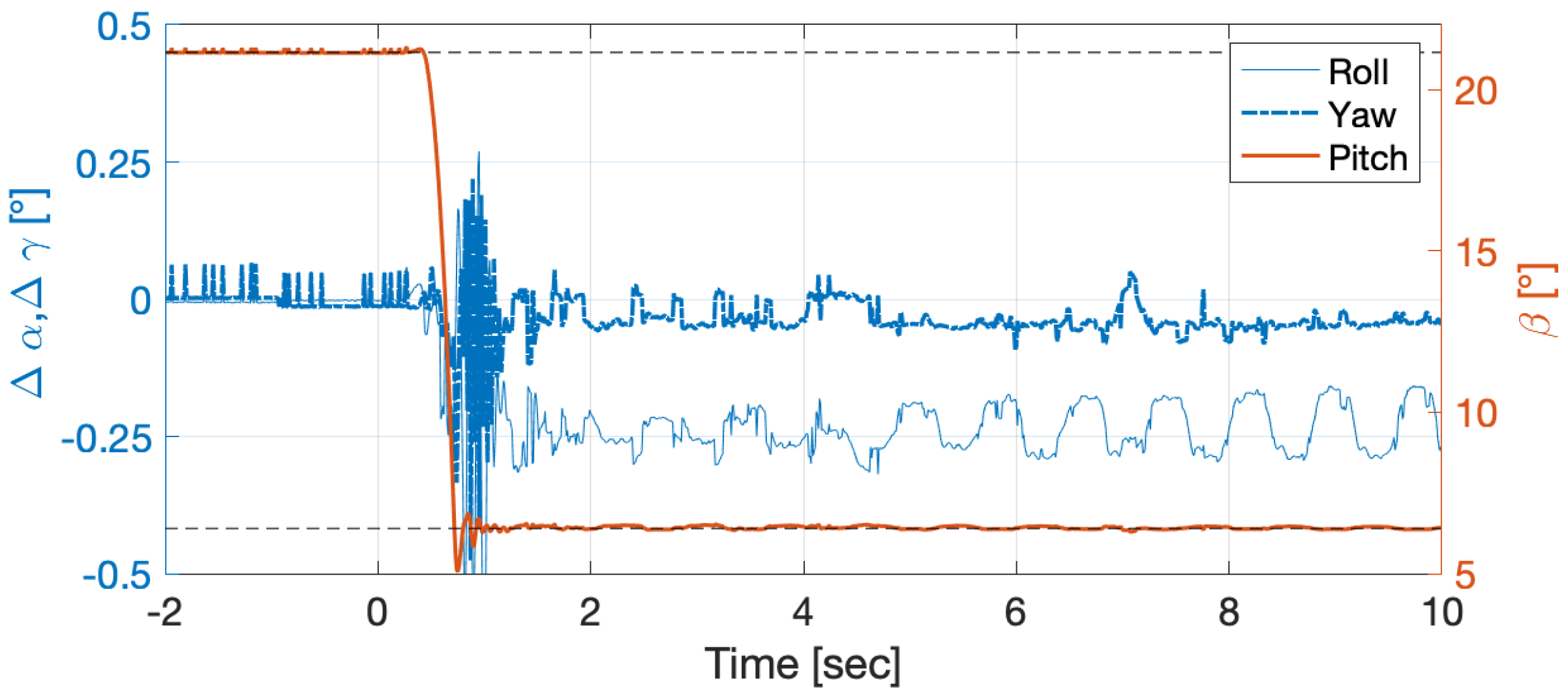
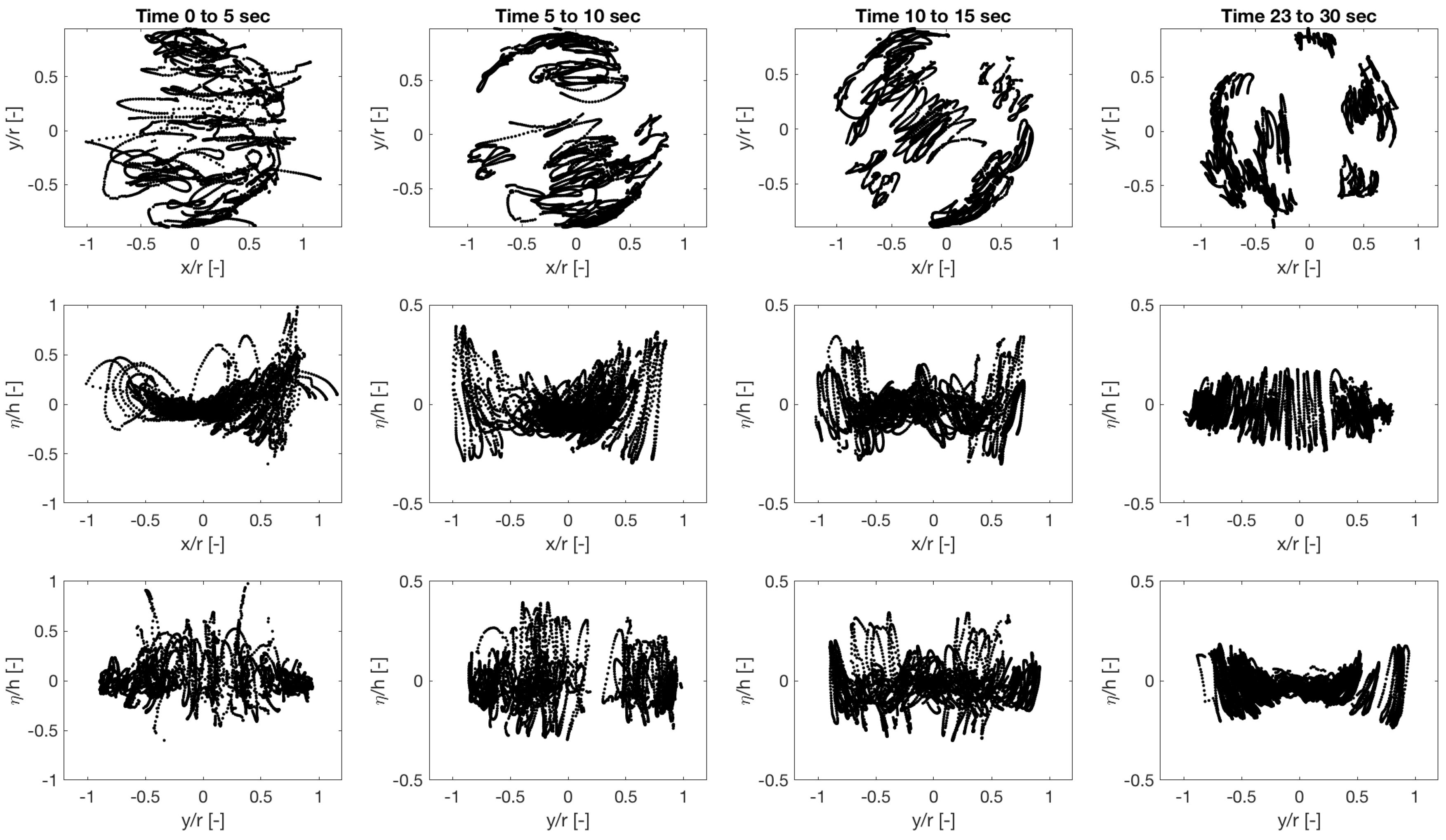
3.3. Transient Behaviour
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LNG | liquefied natural gas |
| Q | Qualisys |
| VLFS | very large floating structures |
| WG | wave gauge |
References
- Chaplin, J.R.; Heller, V.; Farley, F.J.M.; Hearn, G.E.; Rainey, R.C.T. Laboratory testing the Anaconda. Philos. Trans. R. Soc. A 2012, 370, 403–424. [Google Scholar] [CrossRef]
- Farley, F.J.M.; Rainey, R.C.T.; Chaplin, J.R. Rubber tubes in the sea. Philos. Trans. R. Soc. A 2012, 370, 381–402. [Google Scholar] [CrossRef] [PubMed]
- Hirdaris, S.E.; Bai, W.; Dessi, D.; Ergin, A.; Gu, X.; Hermundstad, O.A.; Huijsmans, R.; Iijima, K.; Nielsen, U.D.; Parunov, J.; et al. Loads for use in the design of ships and offshore structures. Ocean Eng. 2014, 78, 131–174. [Google Scholar] [CrossRef]
- Jiao, J.; Ren, H.; Chen, C. Model testing for ship hydroelasticity: A review and future trends. J. Shanghai Jiaotong Univ. 2017, 22, 641–650. [Google Scholar] [CrossRef]
- Sharma, R.; Kim, T.W.; Storch, R.L.; Hopman, H.; Erikstad, S.O. Challenges in computer applications for ship and floating structure design and analysis. CAD Comput. Aided Des. 2012, 44, 166–185. [Google Scholar] [CrossRef]
- Bureau Veritas (BV). Design Sloshing Loads for LNG Membrane Tanks—Guidance Note NI 554 DT R00 E; Bureau Veritas (BV): Paris, France, 2010. [Google Scholar]
- ITTC—Seakeeping Committee of the 28th ITTC. ITTC Quality System Manual Recommended Procedures and Guidelines—Procedure Sloshing Model Tests, Revision 00, Section: 7.5-02-07-02.7. Available online: https://ittc.info/media/7625/75-02-07-027.pdf (accessed on 27 December 2018).
- Lyu, W.; Moctar, O.E.; Potthoff, R.; Neugebauer, J. Experimental and numerical investigation of sloshing using different free surface capturing methods. Appl. Ocean Res. 2017, 68, 307–324. [Google Scholar] [CrossRef]
- Song, Y.K.; Chang, K.A.; Ryu, Y.; Kwon, S.H. Experimental study on flow kinematics and impact pressure in liquid sloshing. Exp. Fluids 2013, 54, 1592. [Google Scholar] [CrossRef]
- Ariyarathne, K.; Chang, K.-A.; Mercier, R. Green water impact pressure on a three-dimensional model structure. Exp. Fluids 2012, 53, 1879–1894. [Google Scholar] [CrossRef]
- Chuang, W.L.; Chang, K.A.; Mercier, R. Impact pressure and void fraction due to plunging breaking wave impact on a 2D TLP structure. Exp. Fluids 2017, 58, 68. [Google Scholar] [CrossRef]
- Kim, S.Y.; Kim, K.H.; Kim, Y. Comparative study on pressure sensors for sloshing experiment. Ocean Eng. 2015, 94, 199–212. [Google Scholar] [CrossRef]
- Kim, K.-T.; Lee, P.-S.; Park, K.C. A direct coupling method for 3D hydroelastic analysis of floating structures. Int. J. Numer. Methods Eng. 2013, 96, 842–866. [Google Scholar] [CrossRef]
- Wei, W.; Fu, S.; Moan, T.; Lu, Z.; Deng, S. A discrete-modules-based frequency domain hydroelasticity method for floating structures in inhomogeneous sea conditions. J. Fluids Struct. 2017, 74, 321–339. [Google Scholar] [CrossRef]
- Yoon, J.S.; Cho, S.P.; Jiwinangun, R.G.; Lee, P.S. Hydroelastic analysis of floating plates with multiple hinge connections in regular waves. Mar. Struct. 2014, 36, 65–87. [Google Scholar] [CrossRef]
- Lee, K.H.; Cho, S.; Kim, K.T.; Kim, J.G.; Lee, P.S. Hydroelastic analysis of floating structures with liquid tanks and comparison with experimental tests. Appl. Ocean Res. 2015, 52, 167–187. [Google Scholar] [CrossRef]
- Klar, R.; Steidl, B.; Sant, T.; Aufleger, M.; Farrugia, R.N. Buoyant Energy—Balancing wind power and other renewables in Europe’s oceans. J. Energy Storage 2017, 14, 246–255. [Google Scholar] [CrossRef]
- Klar, R.; Steidl, B.; Aufleger, M. A floating energy storage system based on fabric. Ocean Eng. 2018, 165, 328–335. [Google Scholar] [CrossRef]
- Gabl, R.; Achleitner, S.; Neuner, J.; Aufleger, M. Accuracy analysis of a physical scale model using the example of an asymmetric orifice. Flow Meas. Instrum. 2014, 36, 36–46. [Google Scholar] [CrossRef]
- Hughes, S.A. Physical Models and Laboratory Techniques in Coastal Engineering; Advanced Series on Ocean Engineering; World Scientific: Singapore, 1993. [Google Scholar] [CrossRef]
- Lykke Andersen, T.; Frigaard, P.; Damsgaard, M.L.; De Vos, L. Wave run-up on slender piles in design conditions - Model tests and design rules for offshore wind. Coast. Eng. 2011, 58, 281–289. [Google Scholar] [CrossRef]
- Mavrakos, S.A.; Chatjigeorgiou, I.K.; Lentziou, D.M. Wave Run-Up and Second-Order Wave Forces on a Truncated Circular Cylinder Due to Monochromatic Waves. In Proceedings of the 24th International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Greece, 12–17 June 2005; pp. 231–238. [Google Scholar]
- Teh, H.M.; Venugopal, V.; Bruce, T. Hydrodynamic characteristics of a free-surface semicircular breakwater exposed to irregular waves. J. Waterway Port Coast. Ocean Eng. 2012, 138, 149–163. [Google Scholar] [CrossRef]
- Tripepi, G.; Aristodemo, F.; Veltri, P. On-Bottom Stability Analysis of Cylinders under Tsunami-Like Solitary Waves. Water 2018, 10, 487. [Google Scholar] [CrossRef]
- Peruzzo, P.; De Serio, F.; Defina, A.; Mossa, M. Wave Height Attenuation and Flow Resistance Due to Emergent or Near-Emergent Vegetation. Water 2018, 10, 402. [Google Scholar] [CrossRef]
- Chiapponi, L.; Longo, S.; Tonelli, M. Experimental study on oscillating grid turbulence and free surface fluctuation. Exp. Fluids 2012, 53, 1515–1531. [Google Scholar] [CrossRef]
- Caron, P.A.; Cruchaga, M.A.; Larreteguy, A.E. Study of 3D sloshing in a vertical cylindrical tank. Phys. Fluid 2018, 30, 082112. [Google Scholar] [CrossRef]
- Longo, S. Experiments on turbulence beneath a free surface in a stationary field generated by a Crump weir: Free-Surface characteristics and the relevant scales. Exp. Fluids 2010, 49, 1325–1338. [Google Scholar] [CrossRef]
- Longo, S.; Liang, D.; Chiapponi, L.; Jimenez, L.A. Turbulent flow structure in experimental laboratory wind-generated gravity waves. Coast. Eng. 2012, 64, 1–15. [Google Scholar] [CrossRef]
- Sellar, B.; Harding, S.; Richmond, M. High-resolution velocimetry in energetic tidal currents using a convergent-beam acoustic Doppler profiler. Meas. Sci. Technol. 2015, 26, 085801. [Google Scholar] [CrossRef]
- Bonakdar, L.; Oumeraci, H.; Etemad-Shahidi, A. Run-up on vertical piles due to regular waves: Small-scale model tests and prediction formulae. Coast. Eng. 2016, 118, 1–11. [Google Scholar] [CrossRef]
- Tosun, U.; Aghazadeh, R.; Sert, C.; Özer, M.B. Tracking free surface and estimating sloshing force using image processing. Exp. Thermal Fluid Sci. 2017, 88, 423–433. [Google Scholar] [CrossRef]
- Bechle, A.J.; Wu, C.H. Virtual wave gauges based upon stereo imaging for measuring surface wave characteristics. Coast. Eng. 2011, 58, 305–316. [Google Scholar] [CrossRef]
- Gomit, G.; Chatellier, L.; Calluaud, D.; David, L. Free surface measurement by stereo-refraction. Exp. Fluids 2013, 54, 1540. [Google Scholar] [CrossRef]
- Bregoli, F.; Bateman, A.; Medina, V. Tsunamis generated by fast granular landslides: 3D experiments and empirical predictors. J. Hydraul. Res. 2017, 55, 743–758. [Google Scholar] [CrossRef]
- Chang, K.-A.; Liu, P.L.-F. Pseudo turbulence in PIV breaking-wave measurements. Exp. Fluids 2000, 29, 331–338. [Google Scholar] [CrossRef]
- Fritz, H.M.; Hager, W.H.; Minor, H.E. Landslide generated impulse waves. 1. Instantaneous flow fields. Exp. Fluids 2003, 35, 505–519. [Google Scholar] [CrossRef]
- Heller, V.; Bruggemann, M.; Spinneken, J.; Rogers, B.D. Composite modelling of subaerial landslide-tsunamis in different water body geometries and novel insight into slide and wave kinematics. Coast. Eng. 2016, 109, 20–41. [Google Scholar] [CrossRef]
- Weigand, A. Simultaneous mapping of the velocity and deformation field at a free surface. Exp. Fluids 1996, 20, 358–364. [Google Scholar] [CrossRef]
- Park, J.; Im, S.; Sung, H.J.; Park, J.S. PIV measurements of flow around an arbitrarily moving free surface. Exp. Fluids 2015, 56, 56. [Google Scholar] [CrossRef]
- Belden, J.; Techet, A.H. Simultaneous quantitative flow measurement using PIV on both sides of the air-water interface for breaking waves. Exp. Fluids 2011, 50, 149–161. [Google Scholar] [CrossRef]
- Blenkinsopp, C.E.; Turner, I.L.; Allis, M.J.; Peirson, W.L.; Garden, L.E. Application of LiDAR technology for measurement of time-varying free-surface profiles in a laboratory wave flume. Coast. Eng. 2012, 68, 1–5. [Google Scholar] [CrossRef]
- Montano, L.; Li, R.; Felder, S. Continuous measurements of time-varying free-surface profiles in aerated hydraulic jumps with a LIDAR. Exp. Thermal Fluid Sci. 2018, 93, 379–397. [Google Scholar] [CrossRef]
- Weitbrecht, V.; Kühn, G.; Jirka, G.H. Large Scale PIV Measurements at the Surface of Shallow Water Flows. Flow Meas. Instrum. 2002, 13, 237–245. [Google Scholar] [CrossRef]
- Akutina, Y.; Mydlarski, L.; Gaskin, S.; Eiff, O. Error analysis of 3D-PTV through unsteady interfaces. Exp. Fluids 2018, 59, 53. [Google Scholar] [CrossRef]
- Evers, F.M.; Hager, W.H. Videometric Water Surface Tracking: Towards Investigating Spatial Impulse Waves. In Proceedings of the 36th IAHR World Congress, Delft, The Netherlands, 28 June–3 July 2015; pp. 6618–6623. [Google Scholar]
- Evers, F.M.; Hager, W.H. Spatial impulse waves: Wave height decay experiments at laboratory scale. Landslides 2016, 13, 1395–1403. [Google Scholar] [CrossRef]
- Mignot, E.; Moyne, T.; Doppler, D.; Riviere, N. Clear-water scouring process in a flow in supercritical regime. J. Hydraul. Eng. 2016, 142, 04015063-1. [Google Scholar] [CrossRef]
- Przadka, A.; Cabane, B.; Pagneux, V.; Maurel, A.; Petitjeans, P. Fourier transform profilometry for water waves: How to achieve clean water attenuation with diffusive reflection at the water surface? Exp. Fluids 2012, 52, 519–527. [Google Scholar] [CrossRef]
- Heller, V.; Spinneken, J. On the effect of the water body geometry on landslide-tsunamis: Physical insight from laboratory tests and 2D to 3D wave parameter transformation. Coast. Eng. 2015, 104, 113–134. [Google Scholar] [CrossRef]
- Whittaker, C.N.; Fitzgerald, C.J.; Raby, A.C.; Taylor, P.H.; Orszaghova, J.; Borthwick, A.G.L. Optimisation of focused wave group runup on a plane beach. Coast. Eng. 2017, 121, 44–55. [Google Scholar] [CrossRef]
- Niedzwecki, J.M.; Duggal, A.S. Wave runup and forces on cylinders in regular and random waves. J. Waterway Port Coast. Ocean Eng. 1992, 118, 615–634. [Google Scholar] [CrossRef]
- Kang, Z.; Ni, W.; Zhang, L.; Ma, G. An experimental study on vortex induced motion of a tethered cylinder in uniform flow. Ocean Eng. 2017, 142, 259–267. [Google Scholar] [CrossRef]
- O’Connell, K.; Thiebaut, F.; Kelly, G.; Cashman, A. Development of a free heaving OWC model with non-linear PTO interaction. Renew. Energy 2018, 117, 108–115. [Google Scholar] [CrossRef]
- Sjökvist, L.; Wu, J.; Ransley, E.; Engström, J.; Eriksson, M.; Göteman, M. Numerical models for the motion and forces of point-absorbing wave energy converters in extreme waves. Ocean Eng. 2017, 145, 1–14. [Google Scholar] [CrossRef]
- Usherwood, J.R. The aerodynamic forces and pressure distribution of a revolving pigeon wing. Exp. Fluids 2009, 46, 991–1003. [Google Scholar] [CrossRef] [PubMed]
- Gyongy, I.; Richon, J.-B.; Bruce, T.; Bryden, I. Validation of a hydrodynamic model for a curved, multi-paddle wave tank. Appl. Ocean Res. 2014, 44, 39–52. [Google Scholar] [CrossRef]
- Draycott, S.; Noble, D.; Davey, T.; Bruce, T.; Ingram, D.; Johanning, L.; Smith, H.; Day, A.; Kaklis, P. Re-creation of site-specific multi-directional waves with non-collinear current. Ocean Eng. 2018, 152, 391–403. [Google Scholar] [CrossRef]
- Draycott, S.; Sutherland, D.; Steynor, J.; Sellar, B.; Venugopal, V. Re-creating waves in large currents for tidal energy applications. Energies 2017, 10, 1838. [Google Scholar] [CrossRef]
- Draycott, S.; Davey, T.; Ingram, D.M. Simulating Extreme Directional Wave Conditions. Energies 2017, 10, 1731. [Google Scholar] [CrossRef]
- Ingram, D.; Wallace, R.; Robinson, A.; Bryden, I. The design and commissioning of the first, circular, combined current and wave test basin. In Proceedings of the Oceans 2014 MTS/IEEE Taipei, Taiwan, 18–21 May 2015. [Google Scholar]
- Sutherland, D.R.J.; Noble, D.R.; Steynor, J.; Davey, T.; Bruce, T. Characterisation of current and turbulence in the FloWave Ocean Energy Research Facility. Ocean Eng. 2017, 139, 103–115. [Google Scholar] [CrossRef]
- Draycott, S.; Sellar, B.; Davey, T.; Noble, D.R.; Venugopal, V.; Ingram, D. Capture and Simulation of the Ocean Environment for Offshore Renewable Energy. Renew. Sustain. Energy Rev. 2019. under review. [Google Scholar]
- MARINET (2012) Work Package 2: Standards and Best Practice—D2.1 Wave Instrumentation Database. Revision: 05. Available online: http://www.marinet2.eu/wp-content/uploads/2017/04/D2.01-Wave-Instrumentation-Database.pdf (accessed on 23 November 2018).
- Heller, V.; Chen, F.; Brühl, M.; Gabl, R.; Chen, X.; Wolters, G.; Fuchs, H. Large-scale experiments into the tsunamigenic potential of different iceberg calving mechanisms. Sci. Rep. 2018. [Google Scholar] [CrossRef]
- Mai, T.; Greaves, D.; Raby, A.; Taylor, P.H. Physical modelling of wave scattering around fixed FPSO-shaped bodies. Appl. Ocean Res. 2016, 61, 115–129. [Google Scholar] [CrossRef]
- Wienke, J.; Oumeraci, H. Breaking wave impact force on a vertical and inclined slender pile—Theoretical and large-scale model investigations. Coast. Eng. 2005, 52, 435–462. [Google Scholar] [CrossRef]
- EDL-Edinburgh Designs Ltd. Available online: http://www.edesign.co.uk/product/wavegauges/ (accessed on 23 November 2018).
- Andersen, T.L.; Frigaard, P. Horns Rev II, 2D-Model Tests: Wave Run-Up on Pile. In DCE Contract Reports, No. 3; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2006. [Google Scholar]
- Liu, H.-T.; Katsaros, K.B.; Weissman, M.A. Dynamic response of thin-wire wave gauges. J. Geophys. Res. 1982, 87, 5686–5698. [Google Scholar] [CrossRef]
- Petti, M.; Longo, S. Turbulence experiments in the swash zone. Coast. Eng. 2001, 43, 1–24. [Google Scholar] [CrossRef]
- Bruce, T.; van der Meer, J.W.; Franco, L.; Pearson, J.M. Overtopping performance of different armour units for rubble mound breakwaters. Coast. Eng. 2009, 56, 166–179. [Google Scholar] [CrossRef]
- Pullen, T.; Allsop, W.; Bruce, T.; Pearson, J. Field and laboratory measurements of mean overtopping discharges and spatial distributions at vertical seawalls. Coast. Eng. 2009, 56, 121–140. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabl, R.; Steynor, J.; Forehand, D.I.M.; Davey, T.; Bruce, T.; Ingram, D.M. Capturing the Motion of the Free Surface of a Fluid Stored within a Floating Structure. Water 2019, 11, 50. https://doi.org/10.3390/w11010050
Gabl R, Steynor J, Forehand DIM, Davey T, Bruce T, Ingram DM. Capturing the Motion of the Free Surface of a Fluid Stored within a Floating Structure. Water. 2019; 11(1):50. https://doi.org/10.3390/w11010050
Chicago/Turabian StyleGabl, Roman, Jeffrey Steynor, David I. M. Forehand, Thomas Davey, Tom Bruce, and David M. Ingram. 2019. "Capturing the Motion of the Free Surface of a Fluid Stored within a Floating Structure" Water 11, no. 1: 50. https://doi.org/10.3390/w11010050
APA StyleGabl, R., Steynor, J., Forehand, D. I. M., Davey, T., Bruce, T., & Ingram, D. M. (2019). Capturing the Motion of the Free Surface of a Fluid Stored within a Floating Structure. Water, 11(1), 50. https://doi.org/10.3390/w11010050






