Three-Dimensional Turbulence Numerical Simulation of Flow in a Stepped Dropshaft
Abstract
1. Introduction
2. Numerical Simulation
2.1. Volume of Fluid Method
2.2. Turbulence Model
2.3. Numerical Algorithm
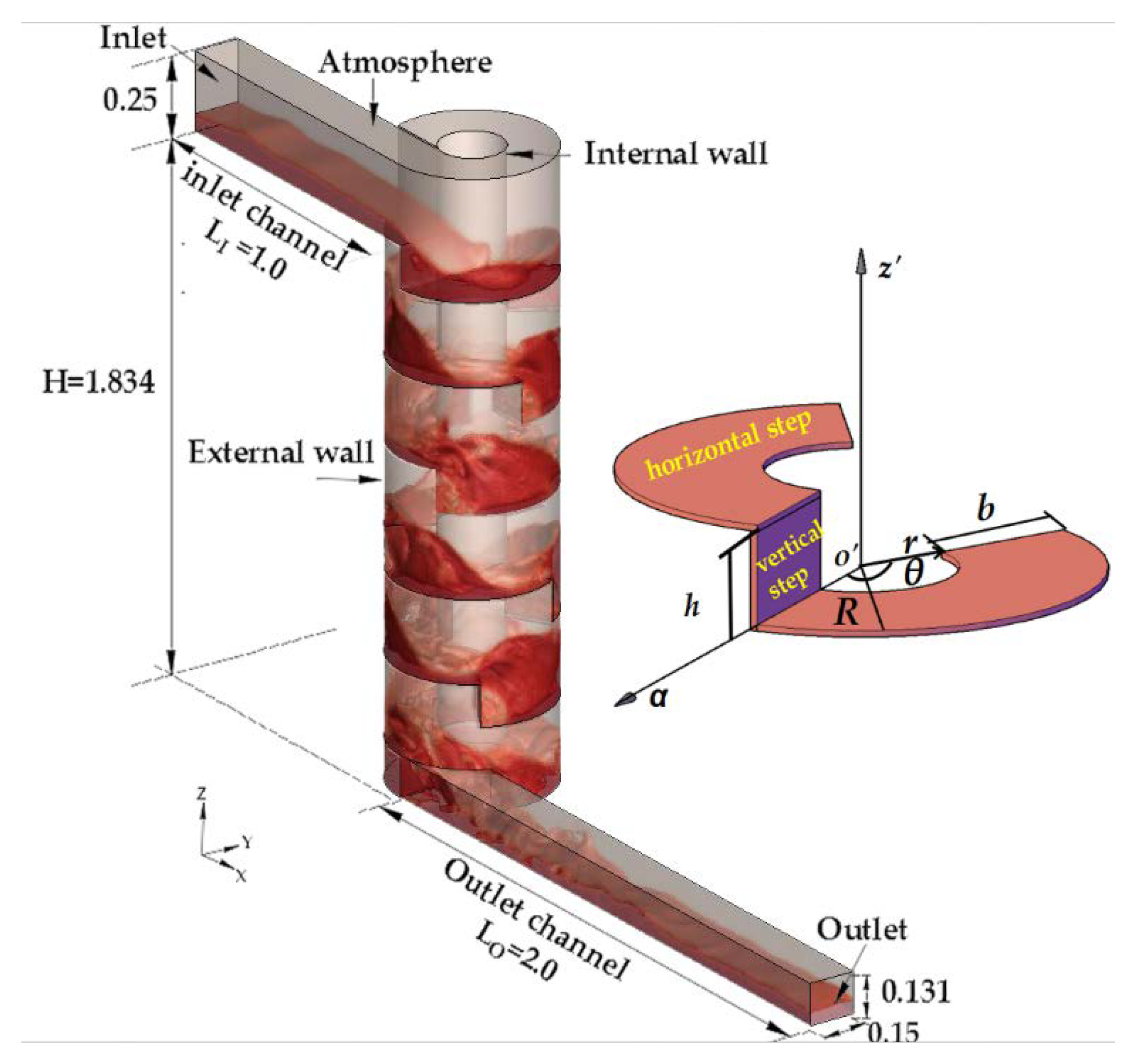
2.4. Geometric Model
2.5. Boundary Conditions and Cases
- (1)
- Inlet boundary: the velocity inlet was used for the intake, which was set at 0.89–2.69 m/s;
- (2)
- Outlet boundary: the outlet boundary was set as pressure outlet and the normal gradient of all variables was equal to 0;
- (3)
- Free surface: the free surface of water was assumed to be the pressure inlet and the pressure value was P = 0; and
- (4)
- Wall boundary: no-slip velocity boundary condition; the near-wall regions of the flow were analyzed using the method of standard wall function.
2.6. Verification
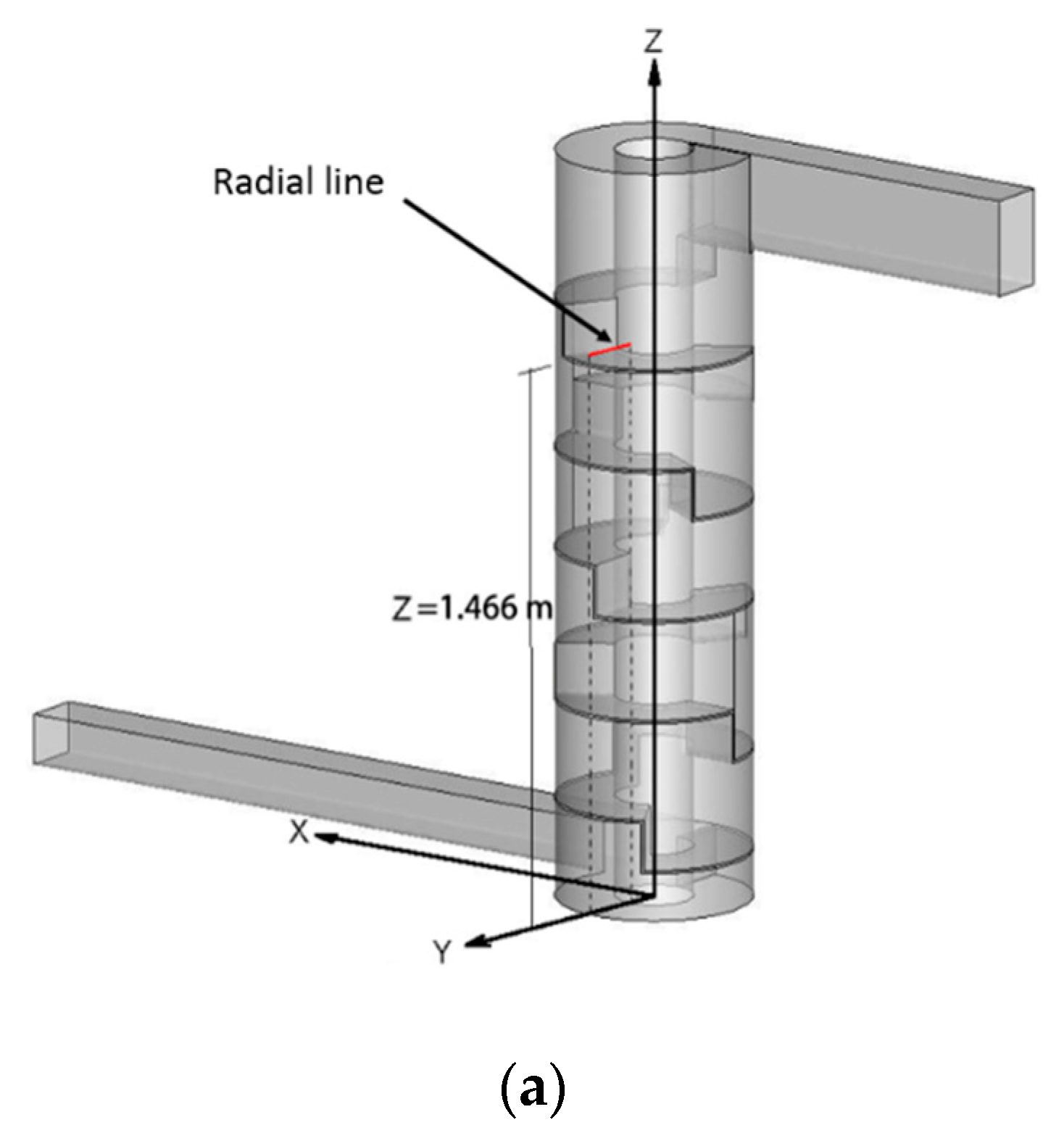
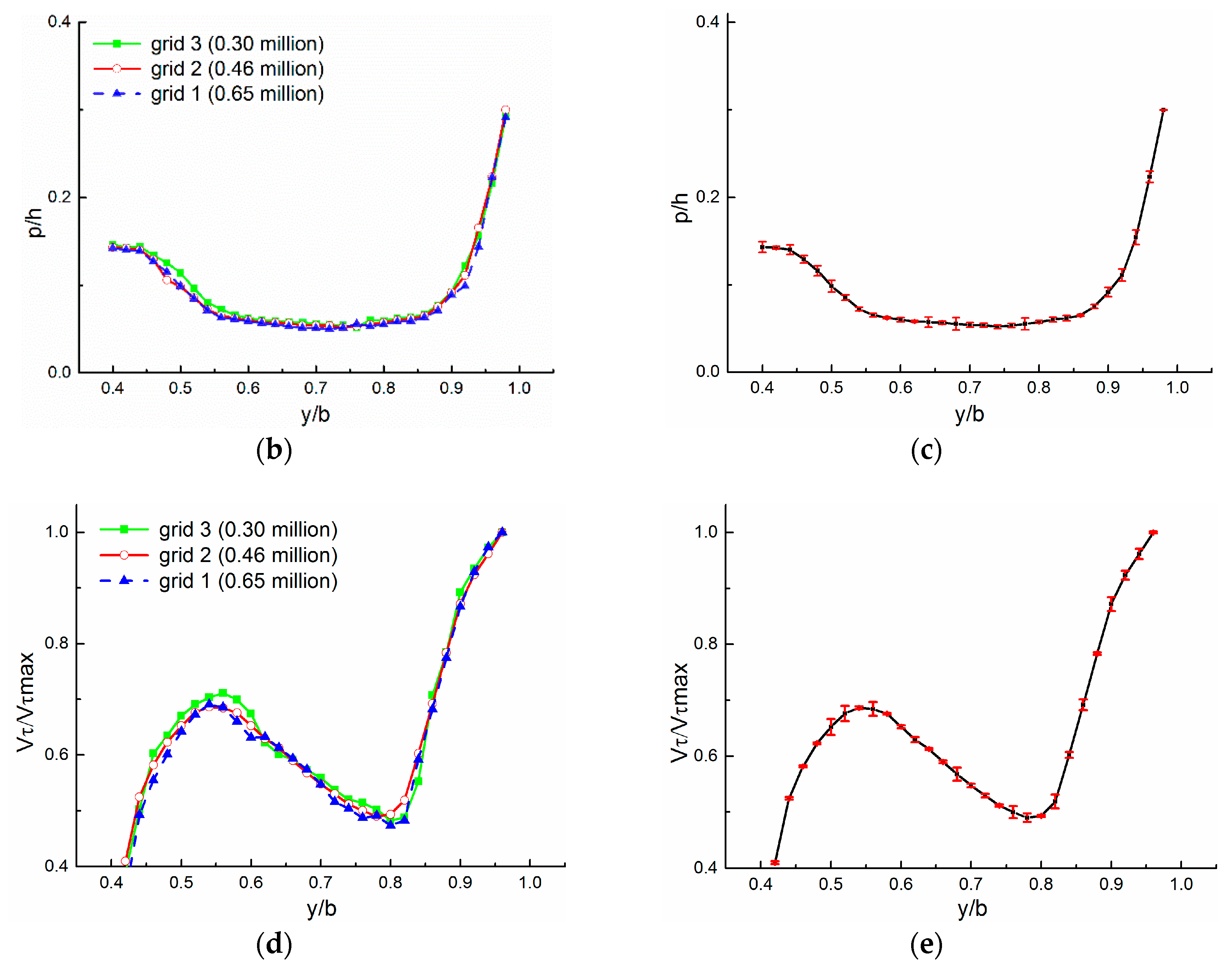
2.6.1. Grid Testing
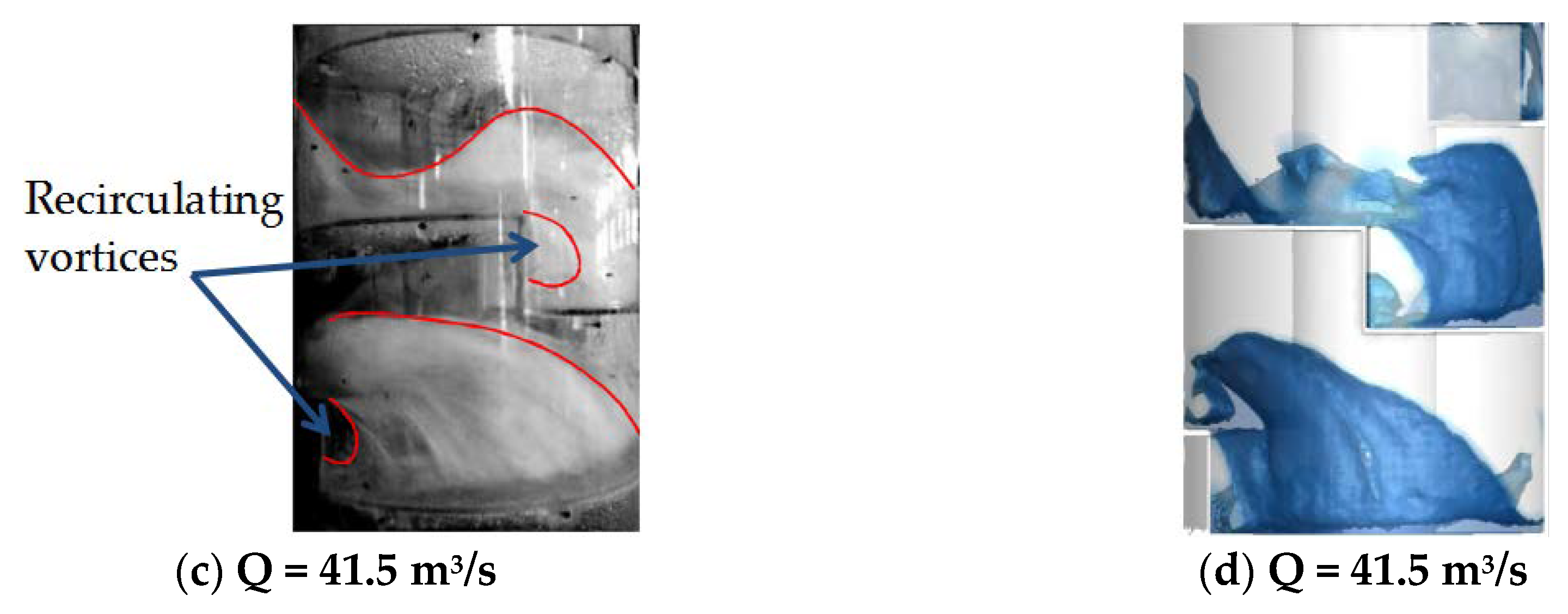
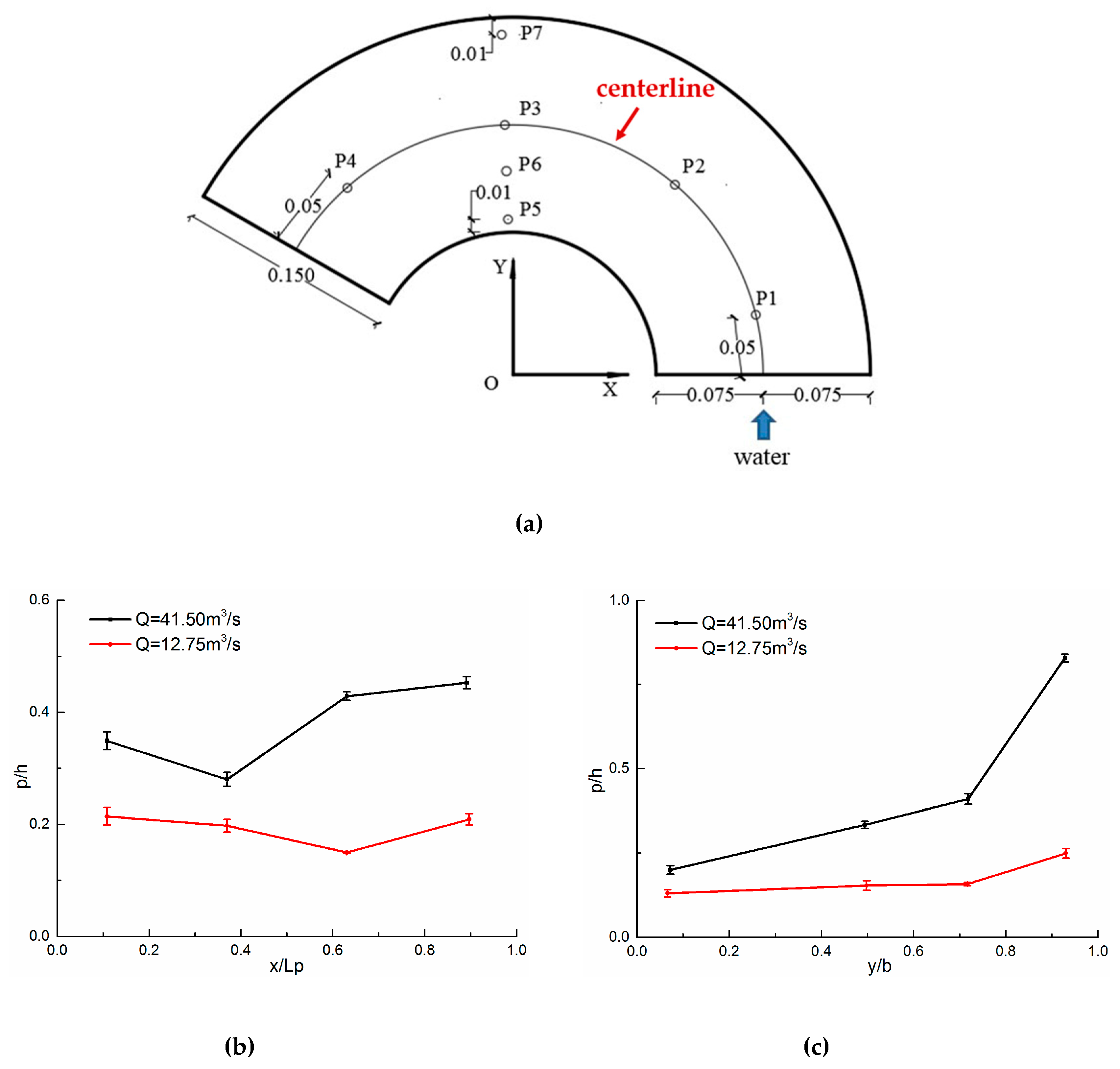
2.6.2. Model Verification
2.6.3. Fluctuation of Calculation Results
3. Results and Analysis
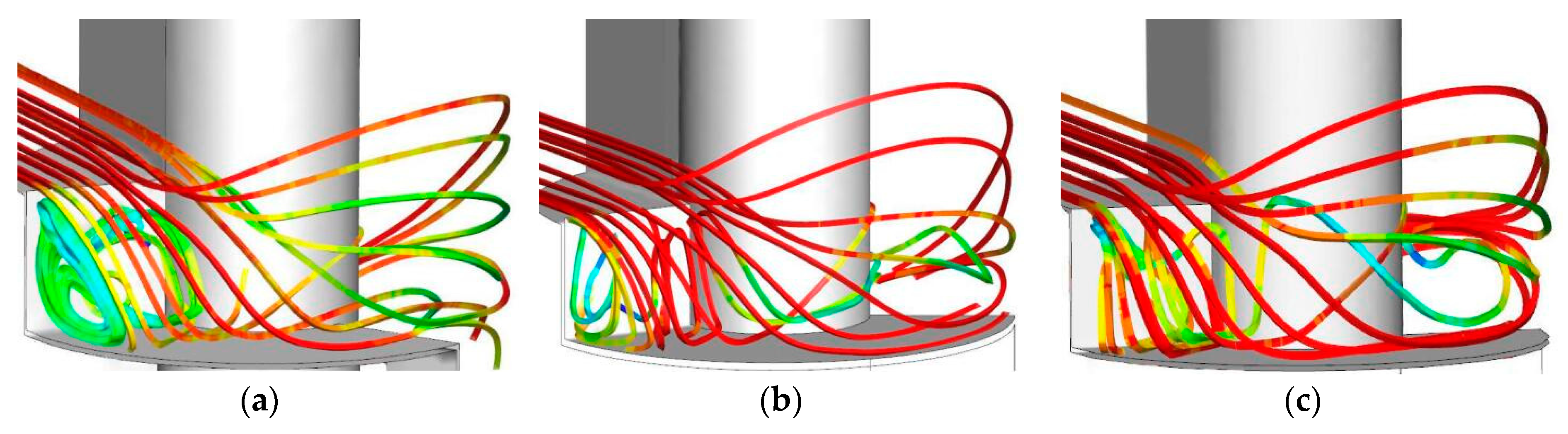
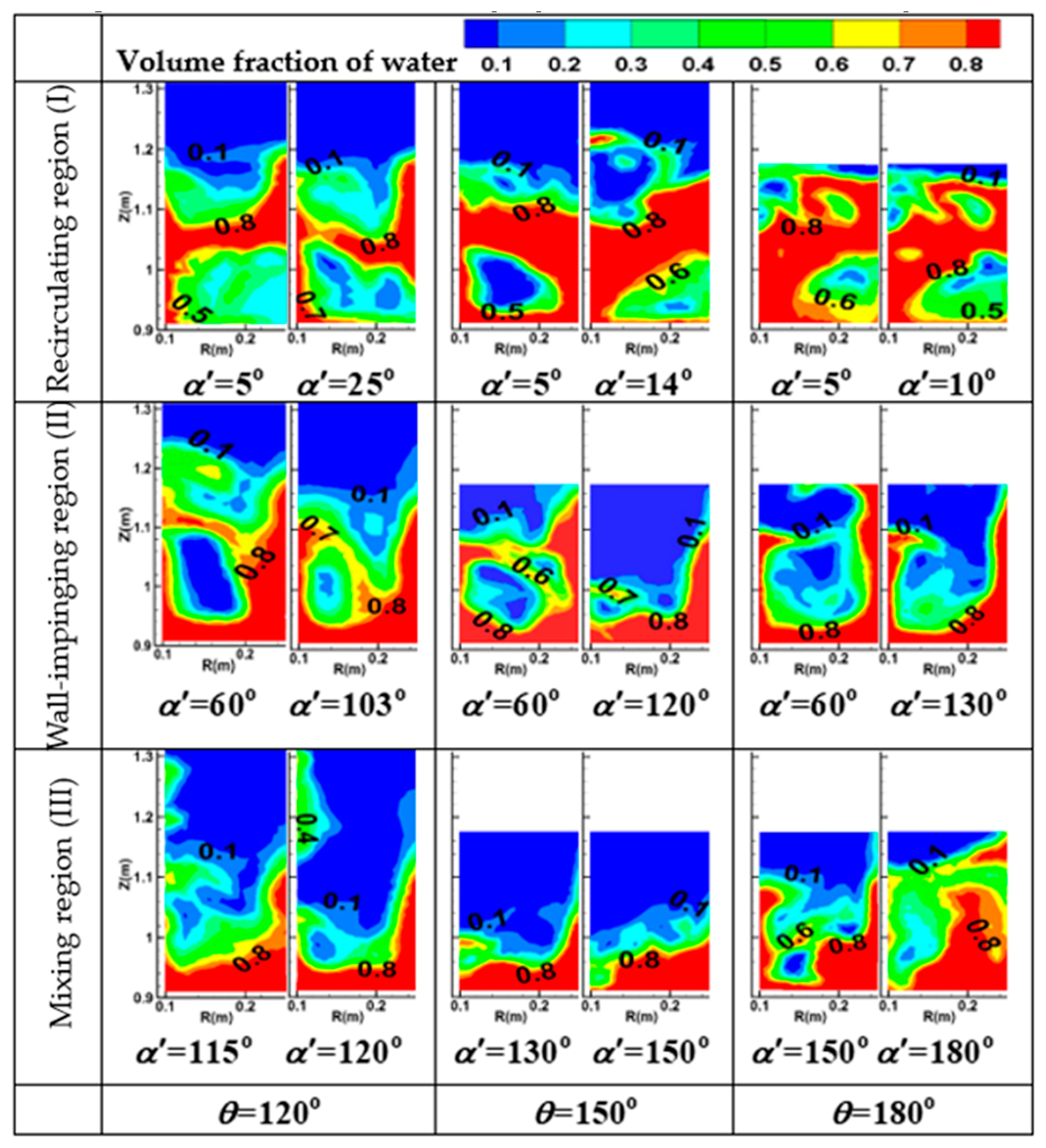
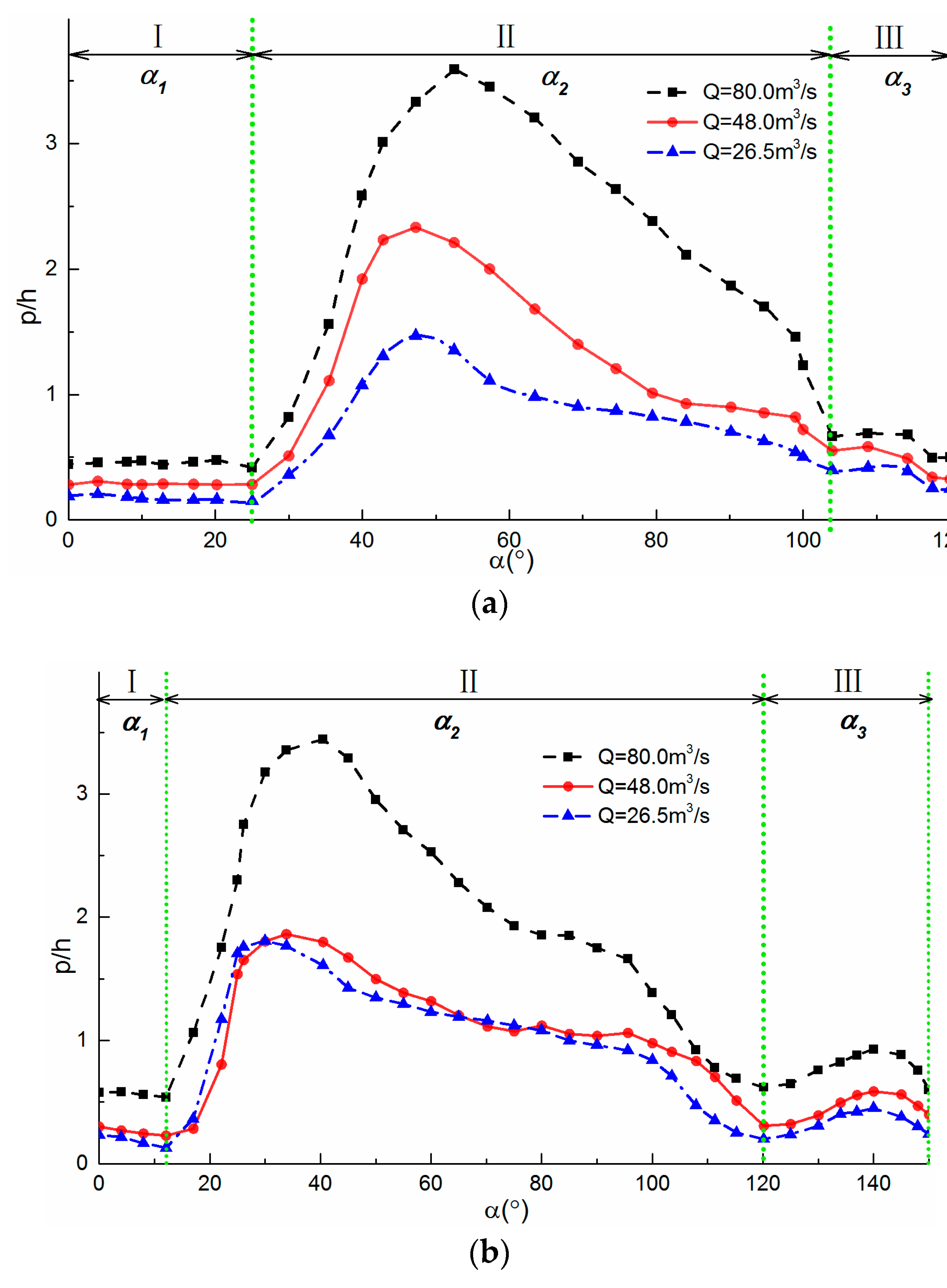
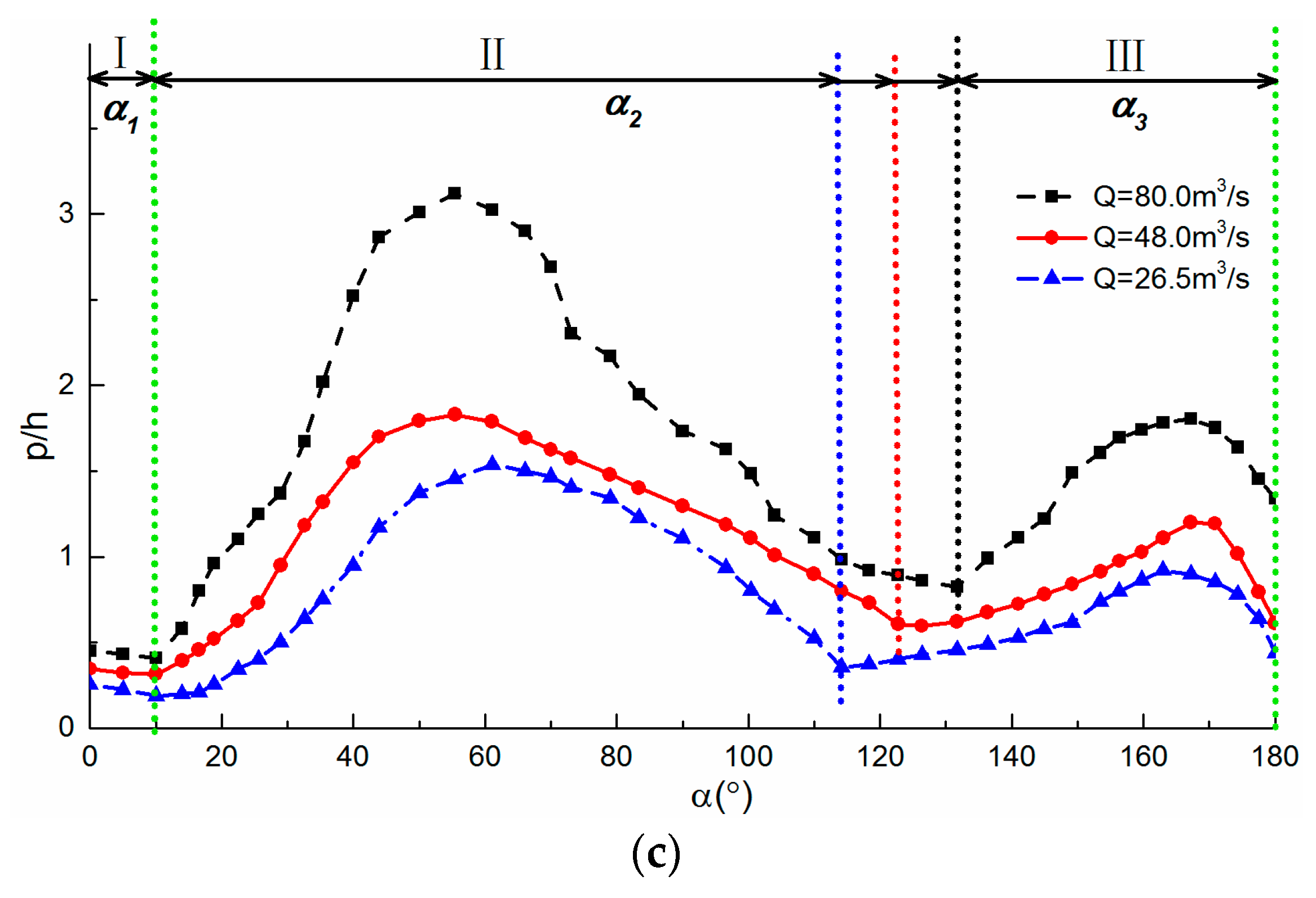
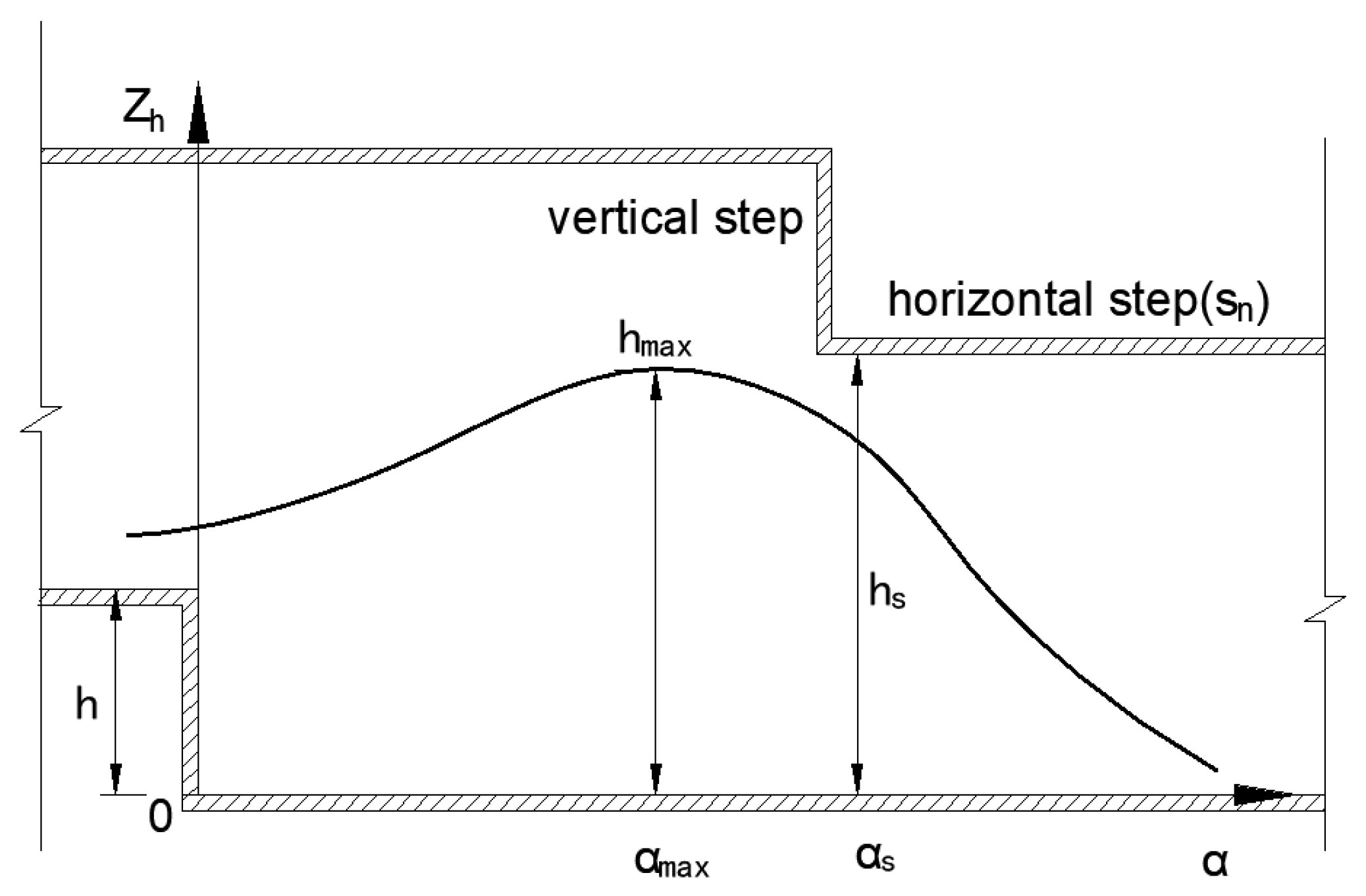
3.1. Region Division in the Flow
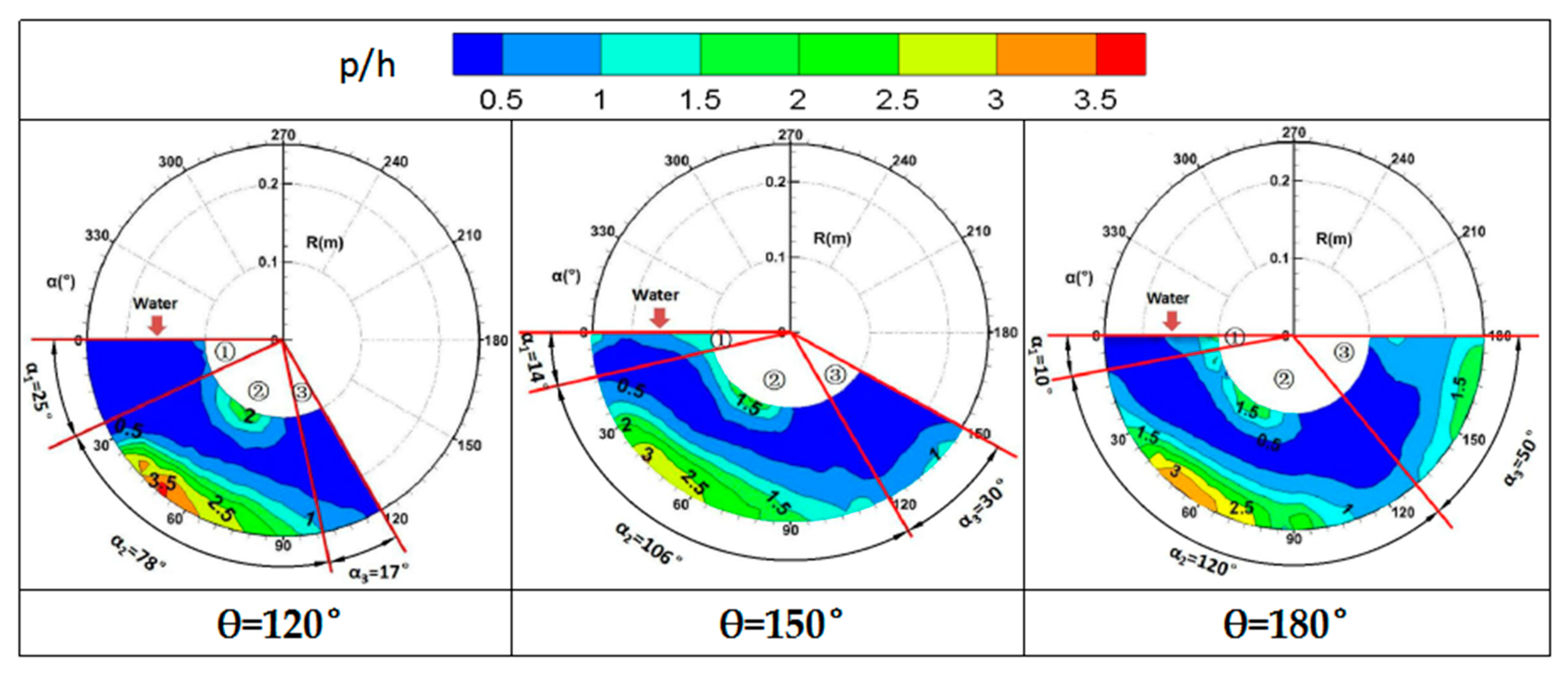
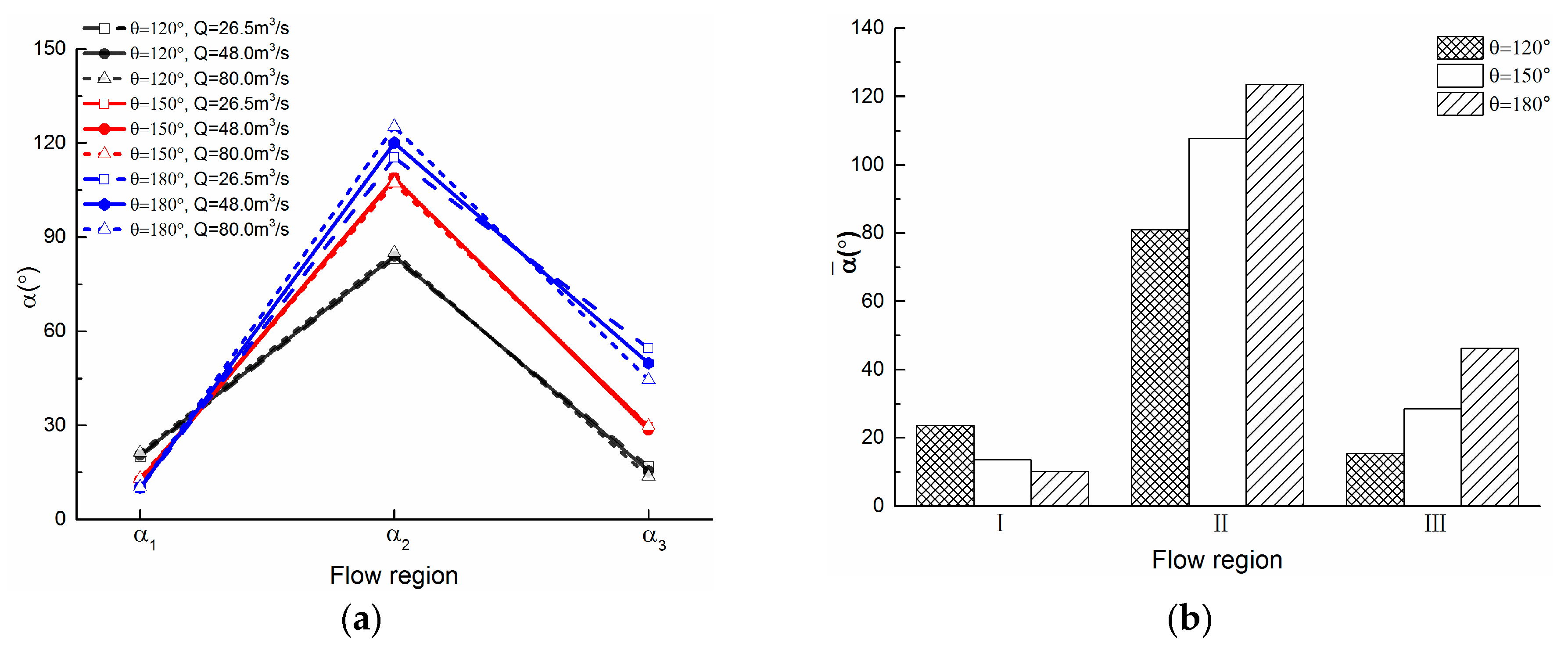
3.2. Regional Scope
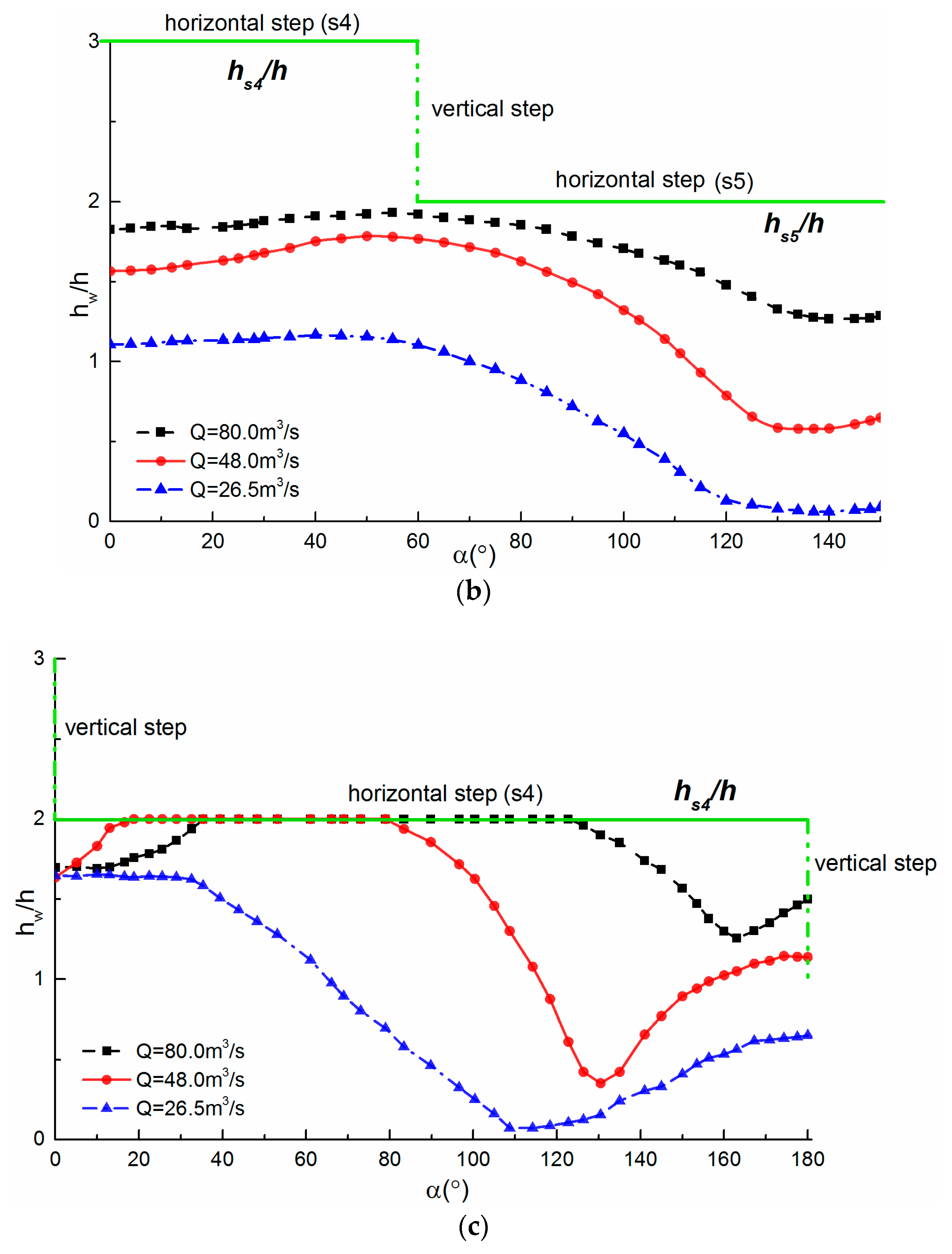
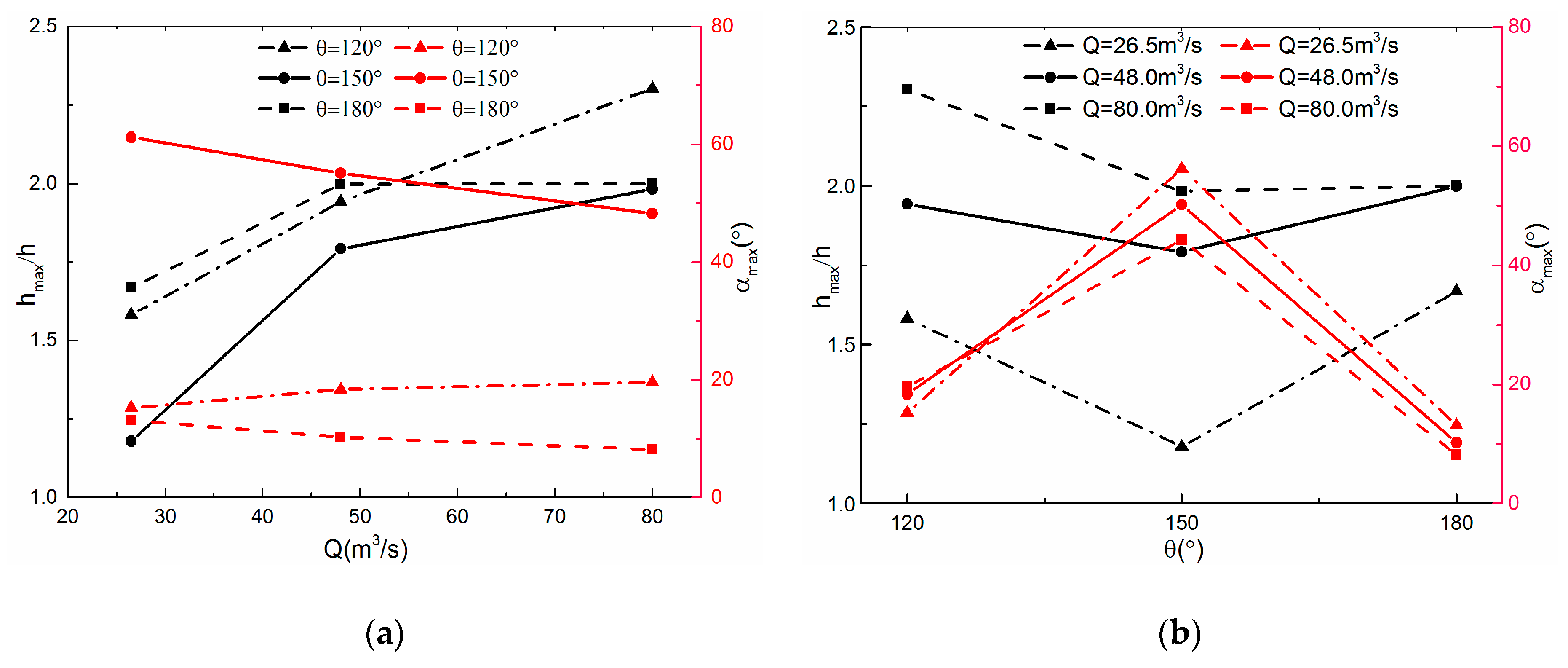
3.3. Water Depth
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rajaratnam, N.; Mainali, A.; Hsung, C. Observations on flow in vertical dropshafts in urban drainage systems. J. Environ. Eng. 1997, 123, 486–491. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of rectangular dropshafts. J. Irrig. Drain. Eng. 2004, 130, 523–529. [Google Scholar] [CrossRef]
- Chanson, H. Understanding air–water mass transfer in rectangular dropshafts. J. Environ. Eng. Sci. 2004, 3, 319–330. [Google Scholar] [CrossRef]
- Adriana Camino, G.; Zhu, D.Z.; Rajaratnam, N. Flow observations in tall plunging flow dropshafts. J. Hydraul. Eng. 2014, 141, 06014020. [Google Scholar] [CrossRef]
- Granata, F.; de Marinis, G.; Gargano, R.; Hager, W.H. Hydraulics of circular drop manholes. J. Irrig. Drain. Eng. 2010, 137, 102–111. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, D.Z.; Rajaratnam, N.; van Duin, B. Energy dissipation in circular drop manholes. J. Irrig. Drain. Eng. 2017, 143, 04017047. [Google Scholar] [CrossRef]
- Jain, S.C. Air transport in vortex-flow drop shafts. J. Hydraul. Eng. 1988, 114, 1485–1497. [Google Scholar] [CrossRef]
- Vischer, D.; Hager, W. Vortex drops. In Energy Dissipators; Routledge: Abingdon, UK, 2018; pp. 167–181. ISBN 9781351451345. [Google Scholar]
- Odgaard, A.J.; Lyons, T.C.; Craig, A.J. Baffle-drop structure design relationships. J. Hydraul. Eng. 2013, 139, 995–1002. [Google Scholar] [CrossRef]
- Stirrup, M.; Margevicius, T.; Hrkac, T.; Baca, A. A baffling solution to Sewage Conveyance In York Region, Ontario. Proc. Water Environ. Fed. 2012, 2012, 74–90. [Google Scholar] [CrossRef]
- Kennedy, J.F.; Jain, S.C.; Quinones, R.R. Helicoidal-ramp dropshaft. J. Hydraul. Eng. 1988, 114, 315–325. [Google Scholar] [CrossRef]
- Tamura, S.; Matsushima, O.; Yoshikawa, S. Helicoidal-ramp type drop shaft to deal with high head drop works in manholes. Proc. Water Environ. Fed. 2010, 2010, 4991–5002. [Google Scholar] [CrossRef]
- Jain, S.C.; Kennedy, J.F. Vortex-Flow Drop Structures for the Milwaukee Metropolitan Sewerage District Inline Storage System; Iowa Institute of Hydraulic Research, The University of Iowa: Iowa City, IA, USA, 1983. [Google Scholar]
- Hager, W.H. Wastewater Hydraulics: Theory and Practice; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Zhao, C.H.; Zhu, D.Z.; Sun, S.K.; Liu, Z.P. Experimental study of flow in a vortex drop shaft. J. Hydraul. Eng. 2006, 132, 61–68. [Google Scholar] [CrossRef]
- Del Giudice, G.; Gisonni, C. Vortex dropshaft retrofitting: Case of Naples city (Italy). J. Hydraul. Res. 2011, 49, 804–808. [Google Scholar] [CrossRef]
- Natarius, E.M. Aeration performance of vortex flow insert assemblies in sewer drop structures. Proc. Water Environ. Fed. 2008, 2008, 842–851. [Google Scholar] [CrossRef]
- Yu, D.; Lee, J.H. Hydraulics of tangential vortex intake for urban drainage. J. Hydraul. Eng. 2009, 135, 164–174. [Google Scholar] [CrossRef]
- Wu, J.H.; Yang, T.; Sheng, J.Y.; Ren, W.C.; Fei, M.A. Hydraulic characteristics of stepped spillway dropshafts with large angle. Chin. J. Hydrodyn. 2018, 33, 176–180. (In Chinese) [Google Scholar] [CrossRef]
- Christodoulou, G.C. Energy dissipation on stepped spillways. J. Hydraul. Eng. 1993, 119, 644–650. [Google Scholar] [CrossRef]
- Sorensen, R.M. Stepped spillway hydraulic model investigation. J. Hydraul. Eng. 1985, 111, 1461–1472. [Google Scholar] [CrossRef]
- Frizell, K.W.; Renna, F.M.; Matos, J. Cavitation potential of flow on stepped spillways. J. Hydraul. Eng. 2012, 139, 630–636. [Google Scholar] [CrossRef]
- Wu, J.H.; Ren, W.C.; Ma, F. Standing wave at dropshaft inlets. J. Hydrodyn. Ser. B 2017, 29, 524–527. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Burrows, R. Modelling the free surface flow in rectangular shallow basins by lattice Boltzmann method. J. Hydrau. Eng. 2011, 137, 1680–1685. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Burrows, R. Modelling solute transport in shallow water with the lattice Boltzmann method. Comput. Fluids. 2011, 50, 181–188. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, J.M.; Zhou, J.G. Lattice Boltzmann Model Using Two-Relaxation-Time for Shallow Water Equations. J. Hydrau. Eng. 2016, 142, 06015017. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, J.M.; Meng, J.P. Second order force scheme for lattice Boltzmann model of shallow water flows. J. Hydraul. Res. 2017, 55, 592–597. [Google Scholar] [CrossRef]
- Peng, Y.; Mao, Y.F.; Wang, B.; Xie, B. Study on C-S and P-R EOS in pseudo-potential lattice Boltzmann model for two-phase flows. Int. J. Mod. Phys. C 2017, 28, 1750120. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, B.; Mao, Y.F. Study on force schemes in pseudopotential lattice Boltzmann model for two-phase flows. Math. Probl. Eng. 2018. [Google Scholar] [CrossRef]
- Galván, S.; Reggio, M.; Guibault, F. Assessment study of k-ε turbulence models and near-wall modeling for steady state swirling flow analysis in draft tube using fluent. Eng. Appl. Comput. Fluid 2011, 5, 459–478. [Google Scholar] [CrossRef]
- Morovati, K.; Eghbalzadeh, A.; Javan, M. Numerical investigation of the configuration of the pools on the flow pattern passing over pooled stepped spillway in skimming flow regime. Acta Mech. 2015, 227, 1–14. [Google Scholar] [CrossRef]
- Devolder, B.; Troch, P.; Rauwoens, P. Performance of a buoyancy-modified k-ω and k-ω SST turbulence model for simulating wave breaking under regular waves using OpenFOAM®. Coast. Eng. 2018, 138, 49–65. [Google Scholar] [CrossRef]
- Fuhrman, D.R.; Dixen, M.; Jacobsen, N.G. Physically-consistent wall boundary conditions for the k-ω turbulence model. J. Hydraul. Res. 2010, 48, 793–800. [Google Scholar] [CrossRef]
- Bai, Z.L.; Zhang, J.M. Comparison of different turbulence models for numerical simulation of pressure distribution in V-shaped stepped spillway. Math. Probl. Eng. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Li, S.; Zhang, J. Numerical investigation on the hydraulic properties of the skimming flow over pooled stepped spillway. Water 2018, 10, 1478. [Google Scholar] [CrossRef]
- Chan, S.; Qiao, Q.; Lee, J.H. On the three-dimensional flow of a stable tangential vortex intake. J. Hydro-Environ. Res. 2018, 21, 29–42. [Google Scholar] [CrossRef]
- Gao, X.P.; Zhang, H.; Liu, J.J.; Sun, B.; Tian, Y. Numerical investigation of flow in a vertical pipe inlet/outlet with a horizontal anti-vortex plate: Effect of diversion orifices height and divergence angle. Eng. Appl. Comput. Fluid Mech. 2018, 12, 182–194. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 57, 1722. [Google Scholar] [CrossRef]
- Liu, Z.P.; Guo, X.L.; Xia, Q.F.; Fu, H.; Wang, T.; Dong, X.L. Experimental and numerical investigation of flow in a newly developed vortex drop shaft spillway. J. Hydraul. Eng. 2018, 144, 04018014. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Zhou, C.; Dong, Z.; Zhou, Z. Numerical simulation of hydraulic characteristics in a vortex drop shaft. Water 2018, 10, 1393. [Google Scholar] [CrossRef]
- Guo, X.L.; Xia, Q.F.; Fu, H.; Yang, K.L.; Li, S.J. Numerical study on flow of newly vortex drop shaft spillway. J. Hydraul. Eng. 2016, 47, 733–741. (In Chinese) [Google Scholar] [CrossRef]
- ANSYS Fluent Theory Guide; Release 16.0; ANSYS Inc.: Canonsburg, PA, USA, 2015.
- Celik, I.B.; Ghia, U.; Roache, P.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130. [Google Scholar] [CrossRef]
- Iaccarino, G.; Mishra, A.A.; Ghili, S. Eigenspace perturbations for uncertainty estimation of single-point turbulence closures. Phys. Rev. Fluids 2017, 2, 024605. [Google Scholar] [CrossRef]
- Mishra, A.A.; Iaccarino, G. Uncertainty Estimation for Reynolds-Averaged Navier–Stokes Predictions of High-Speed Aircraft Nozzle Jets. AIAA J. 2017, 3999–4004. [Google Scholar] [CrossRef]
- Del Giudice, G.; Gisonni, C.; Rasulo, G. Design of a scroll vortex inlet for supercritical approach flow. J. Hydraul. Eng. 2010, 136, 837–841. [Google Scholar] [CrossRef]
- Hager, W.H. Vortex drop inlet for supercritical approaching flow. J. Hydraul. Eng. 1990, 116, 1048–1054. [Google Scholar] [CrossRef]
- Kawagoshi, N.; Hager, W. Wave type flow at abrupt drops Wave type flow at abrupt drops: I. Flow geometry. J. Hydraul. Res. 1990, 28, 235–252. [Google Scholar] [CrossRef]


| h (m) | D | (°) | i | Q (m3/s) | Fr | Case |
|---|---|---|---|---|---|---|
| 0.131 | 0.6 | 150 | 0.20 | 12.75 | 0.58 | test1 |
| 41.50 | 1.90 | test2 | ||||
| 120 | 0.25 | 80.00 | 3.67 | 1 | ||
| 48.00 | 2.20 | 2 | ||||
| 26.50 | 1.22 | 3 | ||||
| 150 | 0.20 | 80.00 | 3.67 | 4 | ||
| 48.00 | 2.20 | 5 | ||||
| 26.50 | 1.22 | 6 | ||||
| 180 | 0.17 | 80.00 | 3.67 | 7 | ||
| 48.00 | 2.20 | 8 | ||||
| 26.50 | 1.22 | 9 |
| (%) | 10° | 30° | 60° | 90° | 120° | ||
|---|---|---|---|---|---|---|---|
| case1 | 8.25 | 0.0707 | 0.0692 | 0.0723 | 0.0818 | 0.0726 | |
| 0.0852 | 0.0912 | 0.0823 | 0.0797 | 0.0906 | |||
| case2 | 7.18 | 0.0675 | 0.0704 | 0.0681 | 0.0619 | 0.0621 | |
| 0.0823 | 0.0834 | 0.0885 | 0.0818 | 0.0911 | |||
| case3 | 4.58 | 0.0754 | 0.0652 | 0.0801 | 0.0781 | 0.0702 | |
| 0.0925 | 0.0922 | 0.0879 | 0.0921 | 0.0942 | |||
| case4 | 7.32 | 0.0583 | 0.0621 | 0.0612 | 0.0565 | 0.0669 | |
| 0.0725 | 0.0822 | 0.0850 | 0.0818 | 0.0861 | |||
| case5 | 7.07 | 0.0754 | 0.0689 | 0.0692 | 0.0717 | 0.0722 | |
| 0.0628 | 0.0587 | 0.0603 | 0.0614 | 0.0592 | |||
| case6 | 5.68 | 0.0718 | 0.0782 | 0.0811 | 0.0777 | 0.0798 | |
| 0.0823 | 0.0898 | 0.0912 | 0.0884 | 0.0879 | |||
| case7 | 8.12 | 0.0905 | 0.0972 | 0.0883 | 0.0878 | 0.0928 | |
| 0.0923 | 0.0985 | 0.0984 | 0.1008 | 0.0954 | |||
| case8 | 7.22 | 0.0661 | 0.0622 | 0.0704 | 0.0683 | 0.0688 | |
| 0.0921 | 0.0918 | 0.0856 | 0.0885 | 0.0892 | |||
| case9 | 6.64 | 0.0775 | 0.0721 | 0.0605 | 0.0644 | 0.0786 | |
| 0.0858 | 0.0805 | 0.0734 | 0.0713 | 0.0728 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Y.; Wang, Y.; Zhang, J. Three-Dimensional Turbulence Numerical Simulation of Flow in a Stepped Dropshaft. Water 2019, 11, 30. https://doi.org/10.3390/w11010030
Qi Y, Wang Y, Zhang J. Three-Dimensional Turbulence Numerical Simulation of Flow in a Stepped Dropshaft. Water. 2019; 11(1):30. https://doi.org/10.3390/w11010030
Chicago/Turabian StyleQi, Yongfei, Yurong Wang, and Jianmin Zhang. 2019. "Three-Dimensional Turbulence Numerical Simulation of Flow in a Stepped Dropshaft" Water 11, no. 1: 30. https://doi.org/10.3390/w11010030
APA StyleQi, Y., Wang, Y., & Zhang, J. (2019). Three-Dimensional Turbulence Numerical Simulation of Flow in a Stepped Dropshaft. Water, 11(1), 30. https://doi.org/10.3390/w11010030





