Abstract
In this study an analysis of the water supply variability for three towns in Puglia (Southern Italy), Roccaforzata, Palagianello and Palagiano, was carried out, based on time series continuously recorded over two years. The towns’ population ranges between 1800 and 16,000 inhabitants and the flow data, collected with time steps of 10 min, are referred to drinking water in an urban environment. The frequency analysis was conducted on the hourly and instantaneous peak factors and confirmed that the Gumbel distribution is able to represent the stochastic behavior of the peak water demand. A physically based formulation of the distribution parameters was exploited in order to investigate the regional distribution of the peak factor for towns with a different population.
1. Introduction
Water demand is the driving force for water distribution networks (WDNs) operation and its correct assessment is an essential and crucial task in the context of their design [1]. The technical literature has tried to define the peak water demand adopting several approaches since many years. Firstly, a deterministic or top-down approach [2] has been adopted, several researchers starting from the water sources and working down to the nodal water demands, defined and proposed peak values within a range depending on climate variability, geographical position etc. [3,4,5], or depending on population by means of empirical expressions [6,7,8,9,10,11] Recently the path taken by scientific literature is more focused on probabilistic variability, considering the random nature of water demand [12,13,14,15].
Since water demand is characterized by a pulsed nature, the temporal scale adopted for its analysis is very important for a correct peak demand estimation. Water demand is described by a random fluctuation at fine temporal scales. The increase of the time scale leads to neglect major peaks that could arise during the time interval adopted [15]. The effect of the sampling interval has been widely investigated [11,16] showing that a finest temporal scale (1s) is essential for a single household or few households water peak detection. A larger sampling resolution can be adopted for numerous households and for towns since the entity of these fluctuations decreases with the spatial scale increase [1].
Buchberger and Wu [17] proposed a Poisson Rectangular Pulse (PRP) model to estimate the probability distribution of water demand for final branches of a WDN. Four single-family residences monitored for one year [18] showed how residential water demand can be represented with rectangular pulses thanks to a signal smoothing and pulse separation. Pulses subdivided into deterministic (washing machines, dishwashers, water closets etc.) and random servers (showers, cleaning, cooking etc.) were analyzed in terms of intensity, duration and frequency, however the variance of the daily pulse counts appeared to be too high for a Poisson process. With the aim to go beyond this limit, Creaco et al. [14] presented a Poisson model for water demand generation where, unlike the previously mentioned work, mutual dependence of pulse duration and intensity is proposed.
Nevertheless, water demand for several users may still arise from the overlapping of several rectangular pulses and more or less complicated Pulse based approaches could be feasible when the purpose is the water peak demand estimation for large residential areas [19]. On the other hand, the scientific literature [12,19,20,21] also shows that the marginal distribution of peak factor data may be satisfactorily represented by a Log-Normal, a Gumbel or a Log-Logistic distribution, all laws that are usually adopted to describe extreme events and which well-fit the recorded time series of water maximum demands.
Starting from these considerations and given the availability of randomly (not continuously) sampled flow data at aggregation intervals of 3, 5, and 10 min for about 150 municipalities in Puglia, Balacco et al. [15] have defined a regional relationship between a fixed peak coefficient quantile and population. Such a study was inspired by Zhang et al. [22] which derived the Gumbel asymptotic distribution of extreme values of a Poisson Rectangular Pulse (PRP) representation of residential water demand. The approach proposed by Reference [22] offers interesting perspectives with regard to the physical parametrization of the peak factors distribution. On the other hand, it leaves open the problem of assessing the verification of the hypothesis that lies beneath the adopted stochastic structure of the process.
In this framework the continuously recorded time series of three towns in Puglia (Southern Italy), Roccaforzata, Palagianello and Palagiano, with population ranging between 1800 and 16,000 where exploited to verify the fit of a Gumbel distribution to recorded data and to check the validity of the regional relationship derived from the pulse based representation of the water use process.
2. Case Study
Acquedotto Pugliese (Puglia Aqueduct, AQP in the following lines) supplies drinking water and manages the whole WDN of Puglia in Southern Italy. Today AQP is the biggest water supply network in Europe. AQP derives water from the Sele spring (superficial water and groundwater), located in the western hillslope of the Apennine watershed and from another source in contiguous regions. This study exploits the dataset recorded in three small towns, Palagiano, Palagianello and Roccaforzata, located in Puglia (Southern Italy), and including continuous flow data of drinking water demand for two years: 2015 and 2016.
The flow data are extracted from the remote-control system of AQP. Records have been collected every 10 min by flow meters positioned on feeding pipes of networks. The field campaigns were performed after intense works for leak reduction thus we assume the presence of a physiological level of leaks.
A preliminary analysis of data [23] highlighted the daily periodicity, as well as a weekly periodicity in water demand. As is well known, daily variability and peak water demand are strongly influenced by habits and activities of inhabitants, however, an analysis of the daily demand pattern (Figure 1) shows a certain synchronicity of the main daily peak in all the three towns. Observing the daily pattern for Palagiano a singular peak can be observed in the morning (05:00–06:00) probably due to the dominant working activity represented by agriculture.
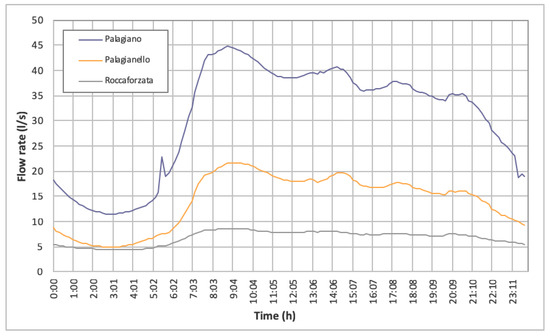
Figure 1.
Typical daily patterns in hourly water demand [23].
Moreover, a peak demand was always detected in the morning during either the week working days and the weekends (Figure 2), even if for the latter the peak is delayed by about one hour. The highest peak occurs on Sundays, while the water demand becomes more uniform during the remaining hours of the day; instead the maximum water volume is observed on Saturdays.
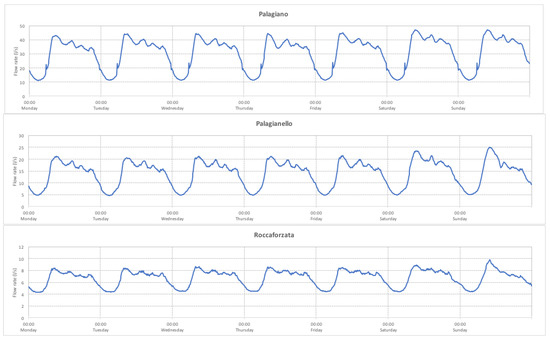
Figure 2.
Typical daily patterns in hourly water demand for the seven days of the week [23].
3. Hourly Peaks Frequency Analysis
Given the random nature of the factors that influence the peak water demand, it seems suitable to consider the peak coefficients as random variables and then to characterize their behavior through a probabilistic approach. Recent scientific studies, aimed at improving the WDN design procedures, use this type of approach to provide the peak coefficient evaluation for the assigned frequency of occurrence [19]. In particular, they show cases where either the log-normal or the Gumbel law are able to represent the trend of the peak coefficient for a small town of about 1200 inhabitants. Within such a framework, for each of the time series here considered, we estimated the hourly peak coefficient as defined by the following expression:
where Qmax(h) is the daily maximum of the hourly flow rate and Qm is the average daily flow (reported in Table 1).

Table 1.
Sample mean and standard deviation of the hourly peak coefficients.
We compared the observed values of each annual series of data available with those deriving from the application of the Gumbel law. Figure 3 shows a good fit between the empirical quantiles of the peak coefficient and the Gumbel distribution in every annual observed time series. The Gumbel parameters, where estimated by means of the classical method of moments assuming the sample values of the mean μ and the standard deviation σ reported in Table 1.
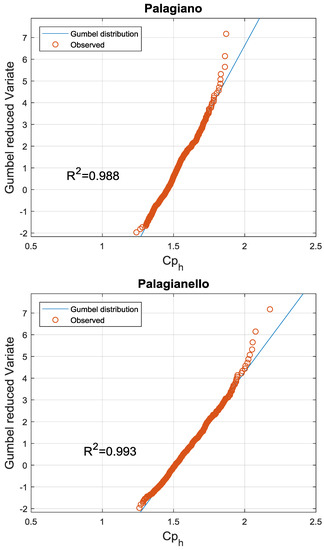
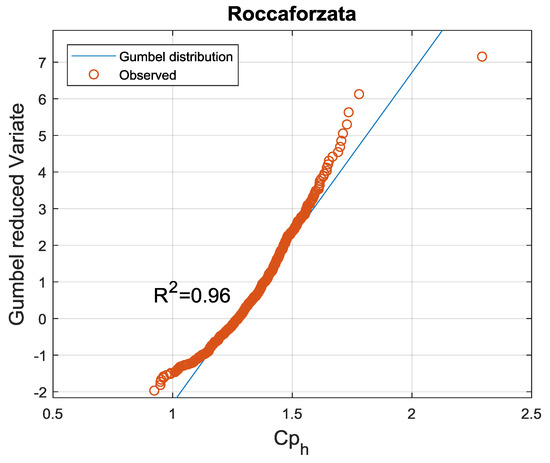
Figure 3.
Hourly peak coefficients and fitted Gumbel distribution.
4. Instantaneous Peaks Frequency Analysis
In order to investigate the instantaneous variability of water demand, the instantaneous peak flow factor is defined as:
where Qmax(i) is the instantaneous peak flow and Qm is the average daily flow (reported in Table 1). Considering for each of the towns investigated the observed two years of peak factor data, good performances are obtained by fitting the Gumbel probability distribution (see Figure 4) with parameters obtained through the method of moments. The sample mean (μ) and standard deviation (σ) are reported in Table 2.
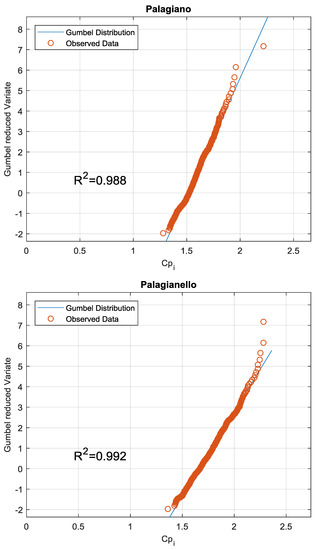
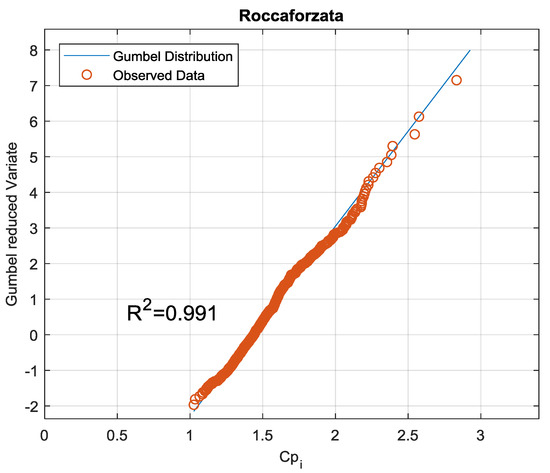
Figure 4.
Comparison between the instantaneous peak observed data and the Gumbel distribution.

Table 2.
Sample mean and standard deviation of the instantaneous peak factors.
5. Regional Distribution of the Instantaneous Peak Factor
Due to the randomness of water demand, recent literature, see for example Reference [24], shows how is today considered less acceptable evaluating the peak factor by using a deterministic approach. This consideration can be confirmed observing sample data and their dispersion reported in Figure 5. Apart from empirical evidence, in this context Zhang et al. [22], developed a theoretical reliability-based methodology for the estimation of an instantaneous peak factor (Cpi) for residential water use, using a probabilistic approach based on the Poisson Rectangular Pulse (PRP) representation, leading to an extreme value distribution of the Gumbel type. Under this hypothesis the water consumption is characterized by a rectangular water pulse of random duration, with mean equal to τ, mean intensity equal to α and mean arrival rate of water pulses at a single home equal to λ; so ρ = λ × τ is daily average utilization factor for a single-family home.
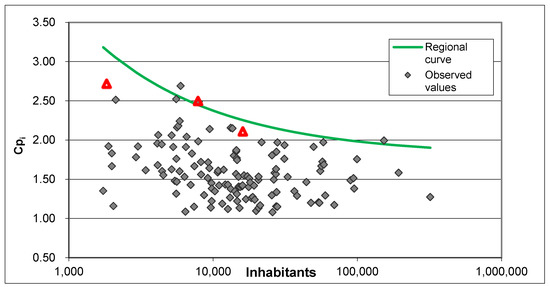
Figure 5.
Comparison between Cpi sample values (grey rhombs), regional curve (in green) and 99.9th percentile peak factors (red triangles) obtained from the at-site Gumbel distributions.
Following this approach, the instantaneous peak flow factor is evaluated as follows:
where N is the number of homes in the neighborhood; F is the pth percentile (frequency factor) of Gumbel distribution given by Chow et al. [25] and ρ is the daily average utilization factor for a single-family home θq is the coefficient of variation of PRP indoor water demand pulse, ψ* is the dimensionless peak hourly demand factor. It is worth noting that, due to the structure of such equation, the instantaneous peak demand factor, Cpi, tends to ψ*, the dimensionless hourly peak factor, for increasing N. In other terms the instantaneous peak factor converges to the hourly peak coefficient for growing population.
Considering the 99.9th percentile and assuming ψ* equal to 1.8, suitable value for Italian towns of large population [23], θq equal to 0.55 as in Zhang et al. [22], a regional behavior (using data extracted from 150 towns in Puglia) of the instantaneous peak flow factor was found by Balacco et al. [15].
where P is the population in thousands.
In Figure 5 the regional relationship (green curve) is shown along with the observed values extracted from the measurement campaign conducted on 150 towns in Puglia data (grey rhombs) and with the Peak flow factors (red triangles) evaluated as the 99.9th percentile of the at-site Gumbel distribution (described in Section 4) fitted to the time series recorded in Roccaforzata, Palagianello and Palagiano. The behavior represented in Figure 5 confirms the good behavior of the theoretical regional curve and also allow for other considerations to be discussed in the following section.
6. Fitting the Probability Distribution of the Peak Factor to the Observed Local Values
By exploiting Equation (3) we derived the peak factor probability distribution F(Cpi), for a town with N number of homes; considering that such expression can be easily turned into town population (P) if an average number of inhabitants for home is known.
We derived also the theoretical relationships between the parameters of the theoretical Cpi distribution and the mean and standard deviation of the population of the peak factors:
Then, in order to apply such a model to our data we assumed ρ equal to 0.045, as in Reference [22], and we evaluated N from the population by considering that in Italy the average number of people for home is 2.6. Finally, we evaluated the remaining two parameters θq and ψ* as a function of the sample mean, and standard deviation of instantaneous peak factors reported in Table 2 by means of Equations (6) and (7). The resulting values of θq and ψ* are reported in Table 3.

Table 3.
Parameters of the Cpi distribution according to the data series recorded at Roccaforzata, Palagianello and Palagiano.
Values shown in Table 3 seem to suggest an interesting dependence of the coefficient of variation of the PRP process on population, that any way need to be further assessed in future research involving time series recorded in other towns. Moreover, the estimated ψ* value is always lower than the value of 1.8 adopted in Equation (4) assumed equal to the asymptotical hourly peak factor for a growing population. In both cases such variability could be due to sample inter-annual variability of the average peak factor. Nevertheless the 99.9th percentile estimates provided by the regional relationship in Equation (4) still looks a robust and reliable value to be suggested for design purpose.
7. Conclusions
In the last few decades, the improvement of living conditions and the large infrastructure investments of industrialized countries has led to a significant increase in water consumption; in particular due to the growth of population, increasing energy demand. Improving living standards, changes in the global food system and land use, freshwater demand is significantly increasing in many areas of the world. Systems of water supply are also expected to be affected by fluctuations of climate and changes in variability of temperature and precipitation. In this context global or local variations of spatial and temporal dynamics of the water cycle may greatly increase the gaps between water supply and water demand.
In this study instantaneous flow data of water consumption for three towns located in Puglia Region (Southern Italy) were exploited and collected at time steps of 10 min for two years: 2015 and 2016. As expected, an analysis of the two years observed data revealed the existence of patterns in which it is possible to identify daily periodicities in hourly water demands, as well as weekly periodicities in daily water demands.
Moreover, the frequency analysis conducted on the instantaneous peak factors confirmed that the Gumbel distribution is suitable to represent the stochastic behavior of the peak water demand; in particular, exploiting the approach proposed by Zhang et al. [22], we derived a physically based regional relationship able to provide a robust evaluation for the design value of the instantaneous peak factor depending on population and suitable for refinements based on deeper at-site investigations about variability of water demand.
Author Contributions
The authors’ contribution is equal.
Funding
This research received no external funding.
Acknowledgments
The Authors thank AQP for providing water demand data and in particular Antonio Carbonara for his kind and absolute willingness to provide information and details on the data provided. In addition, the Authors thank the anonymous Reviewers for their valuable comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Creaco, E.; Signori, P.; Papiri, S.; Ciaponi, C. Peak demand assessment and hydraulic analysis in WDN design. J. Water Resour. Plan. Manag. 2018, 144, 6. [Google Scholar] [CrossRef]
- Bentley, S.; Walski, T.; Chase, D.; Savic, D.; Grayman, W.; Beckwith, S.; Koelle, E. Advanced Water Distribution Modelling and Management; Haestad: Waterbury, CT, USA, 2007. [Google Scholar]
- Fair, G.M.; Geyer, J.C. Elements of Water Supply and Waste-Water Disposal; John Wiley & Sons Inc.: London, UK, 1958. [Google Scholar]
- Linaweaver, F.P.; Geyer, J.C.; Wolff, J.B. A Study of Residential Water Use; John Hopkins University: Baltimore, MD, USA, 1967. [Google Scholar]
- Barnes, D.; Bliss, P.J.; Gould, B.W.; Vallentine, H.R. Water and Wastewater Engineering Systems; Pitman Books Ltd.: London, UK, 1981. [Google Scholar]
- Harmon, W.G. Forecasting Sewage at Toledo under Dry Weather Conditions. Eng. News Rec. 1918, 80, 1233. [Google Scholar]
- Babbitt, H.E. Sewerage and Sewage Treatment, 3rd ed.; Wiley: New York, NY, USA, 1928; pp. 20–33. [Google Scholar]
- Metcalf, L.; Eddy, H.P. American Sewerage Practice, Volume III: Design of Sewers, 3rd ed.; McGraw-Hill: New York, NY, USA, 1935; Volume I. [Google Scholar]
- Johnson, C.F. Relation between Average and extreme sewage flow rates. Eng. News Rec. 1942, 129, 500–501. [Google Scholar]
- Rich, L.G. Low Maintenance Mechanically Simple Wastewater Treatment Systems; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Tricarico, C.; De Marinis, G.; Gargano, R.; Leopardi, A. Peak residential water demand. Water Manag. 2007, 60, 115–121. [Google Scholar] [CrossRef]
- Blokker, E.J.M.; Vreeburg, J.H.G.; van Dijk, J.C. Simulating Residential Water Demand with a Stochastic End-Use Model. J. Water Resour. Plan. Manag. ASCE 2010, 136, 19–26. [Google Scholar] [CrossRef]
- Omaghomi, T.; Buchberger, S. Estimating water demands in buildings. Procedia Eng. 2014, 89, 1013–1022. [Google Scholar] [CrossRef]
- Creaco, E.; Farmani, R.; Kapelan, Z.; Vamvakeridou-Lyroudia, L.; Savic, D. Considering the mutual dependence of pulse duration and intensity in models for generating residential water demand. J. Water Resour. Plan. Manag. 2015, 141. [Google Scholar] [CrossRef]
- Balacco, G.; Carbonara, A.; Gioia, A.; Iacobellis, V.; Piccinni, A.F. Evaluation of Peak Water Demand Factors in Puglia (Southern Italy). Water 2017, 9, 96. [Google Scholar] [CrossRef]
- Gato-Trinidad, S.; Gan, K. Characterizing maximum residential water demand. Urban Water 2012, 122, 15–24. [Google Scholar]
- Buchberger, S.G.; Wu, L. Model for instantaneous residential residential water demands. J. Hydraul. Eng. 1995, 121, 232–246. [Google Scholar] [CrossRef]
- Buchberger, S.G.; Wells, G.J. Intensity, duration and frequency of residential water demands. J. Water Resour. Plan. Manag. 1996, 122, 11–19. [Google Scholar] [CrossRef]
- Gargano, R.; Tricarico, C.; Granata, F.; Santopietro, S.; de Marinis, G. Probabilistic Models for the Peak Residential Water Demand. Water 2017, 9, 417. [Google Scholar] [CrossRef]
- Buchberger, S.G.; Nadimpalli, G. Leak estimation in water distribution systems by statistical analysis of flow readings. J. Water Resour. Plan. Manag. 2004, 130, 321–329. [Google Scholar] [CrossRef]
- Pallavicini, I.; Magini, R. Experimental analysis of residential water demand data: Probabilistic estimation of peak coefficients at small time scales. In Water Management Challenges in Global Change; Ulanicki, B., Vairavamoorthy, K., Butler, D., Bounds, P.L.M., Memon, F.A., Eds.; Taylor & Francis Group: London, UK, 2007; ISBN 978-0-415-45415-5. [Google Scholar]
- Zhang, X.; Buchberger, S.; Van Zyl, J. A theoretical explanation for peaking factors. In Proceedings of the ASCE EWRI Conferences, Anchorage, AK, USA, 15–19 May 2005. [Google Scholar]
- Balacco, G.; Carbonara, A.; Gioia, A.; Iacobellis, V.; Piccinni, A.F. Investigation of Peak Water Consumption Variability at Local Scale in Puglia (Southern Italy). Proceedings 2018, 11, 674. [Google Scholar] [CrossRef]
- Gargano, R.; Di Palma, F.; De Marinis, G.; Granata, F.; Greco, R. A stochastic approach for the water demand of residential end users. Urban Water J. 2016, 13, 569–582. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill Inc.: New York, NY, USA, 1988; p. 572. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).