Evaluation of Design Flow Rate of Water Supply Systems with Low Flow Showering Appliances
Abstract
:1. Introduction
2. Reviews on Design Flow Rate
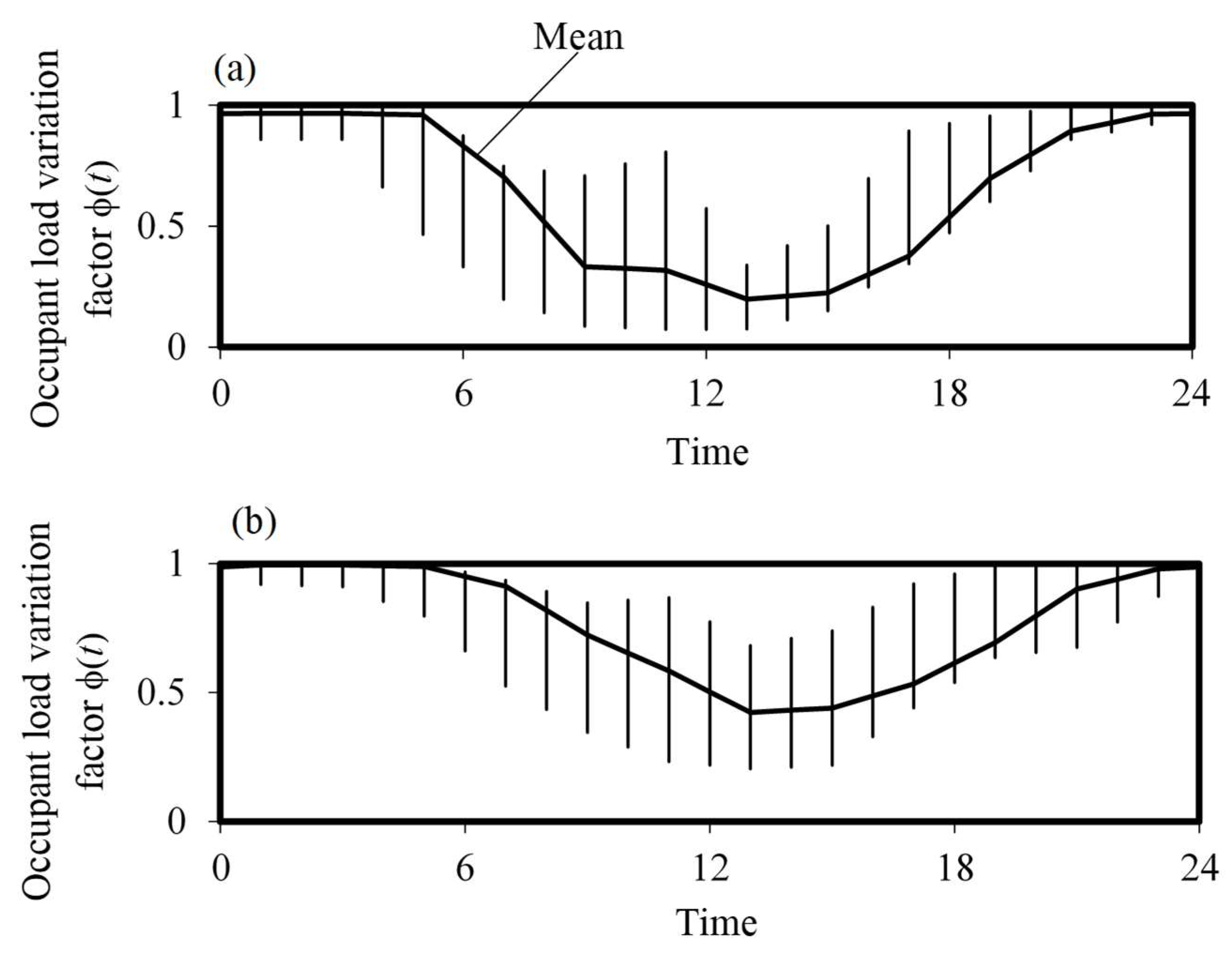
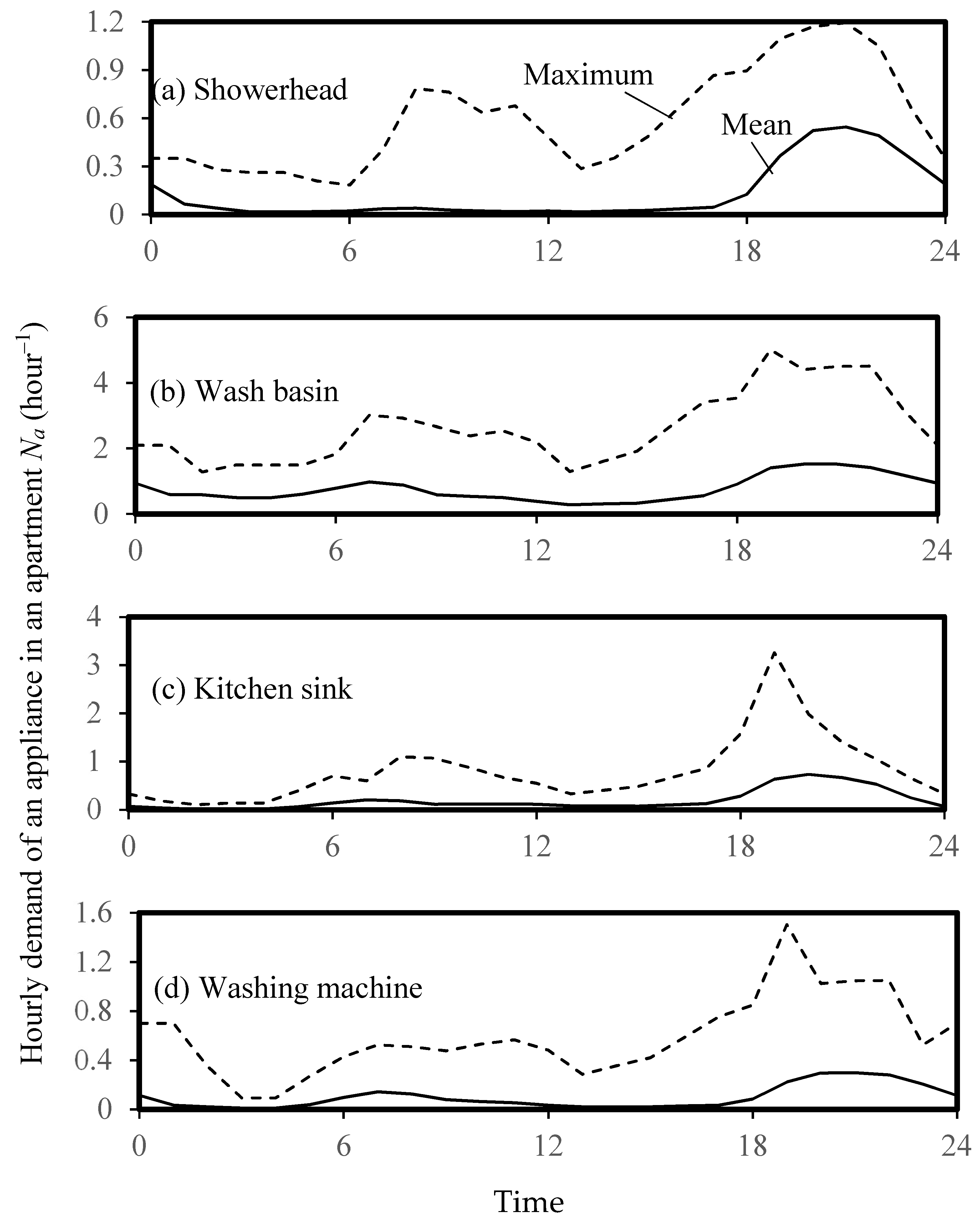
3. Occupant Loads and Water Demand Patterns in High-Rise Buildings in Hong Kong
4. Methodology
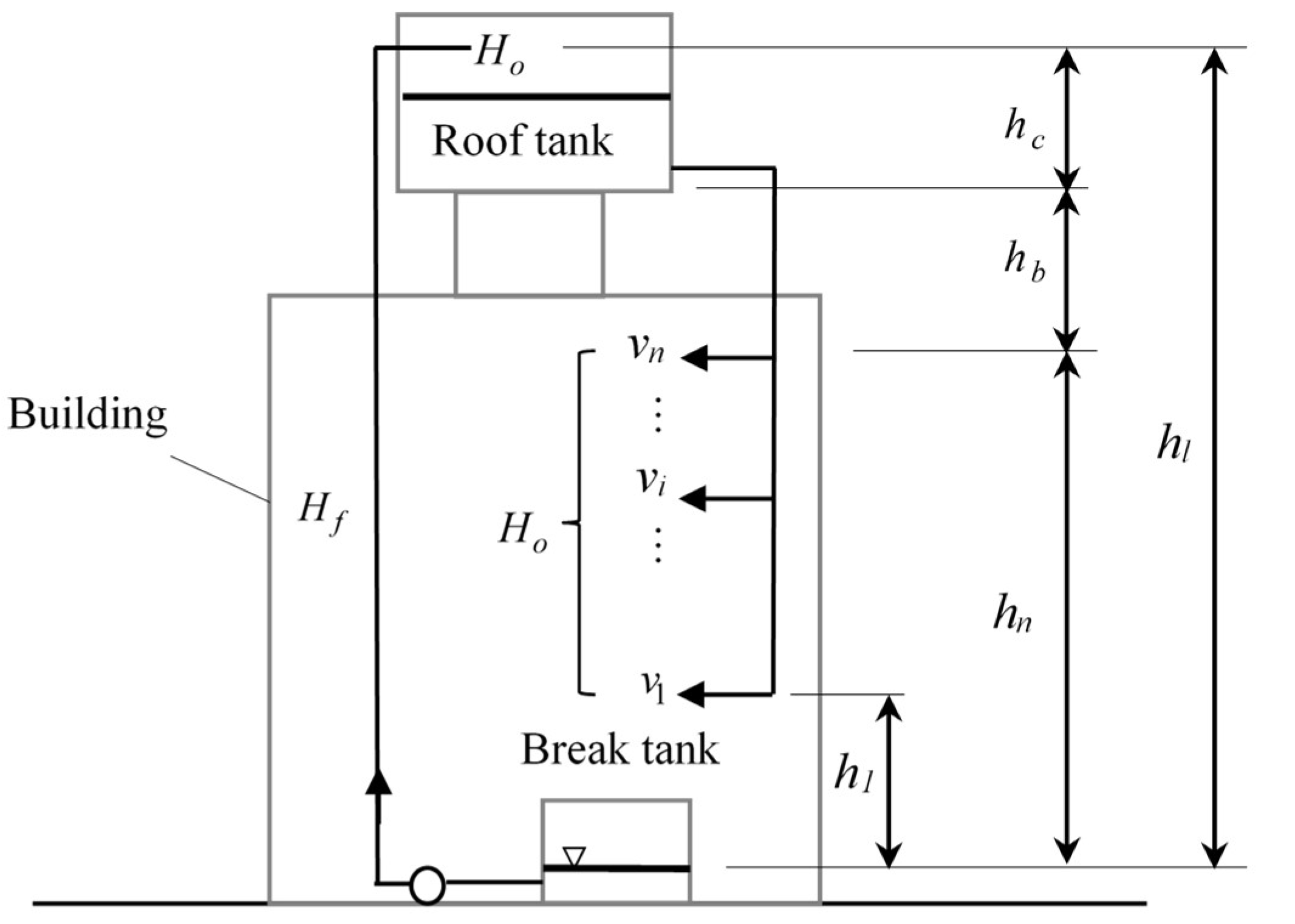
4.1. Models of Design Flow Rate
4.2. Energy Efficiency of a Water Supply System
5. Results and Discussion
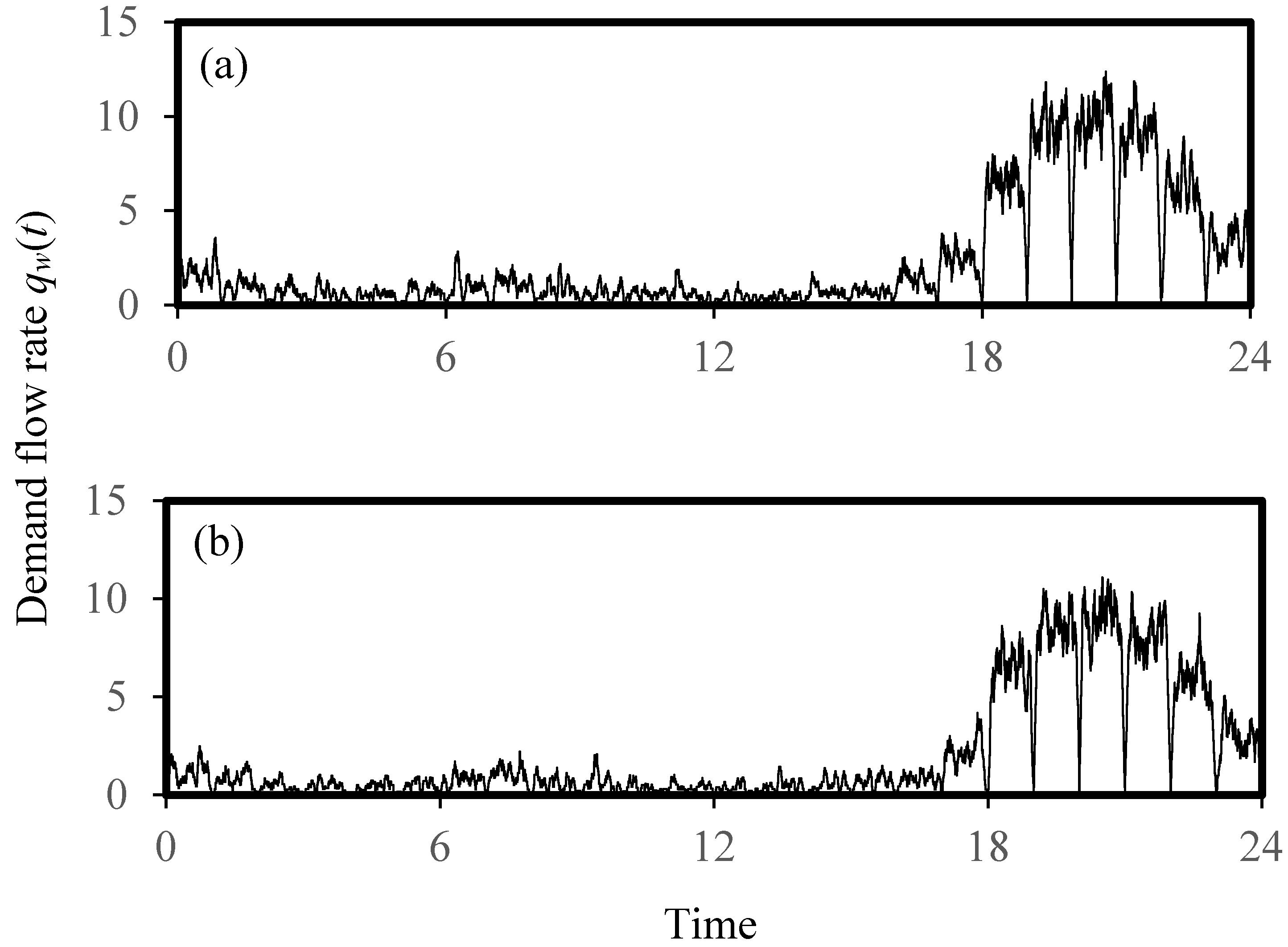
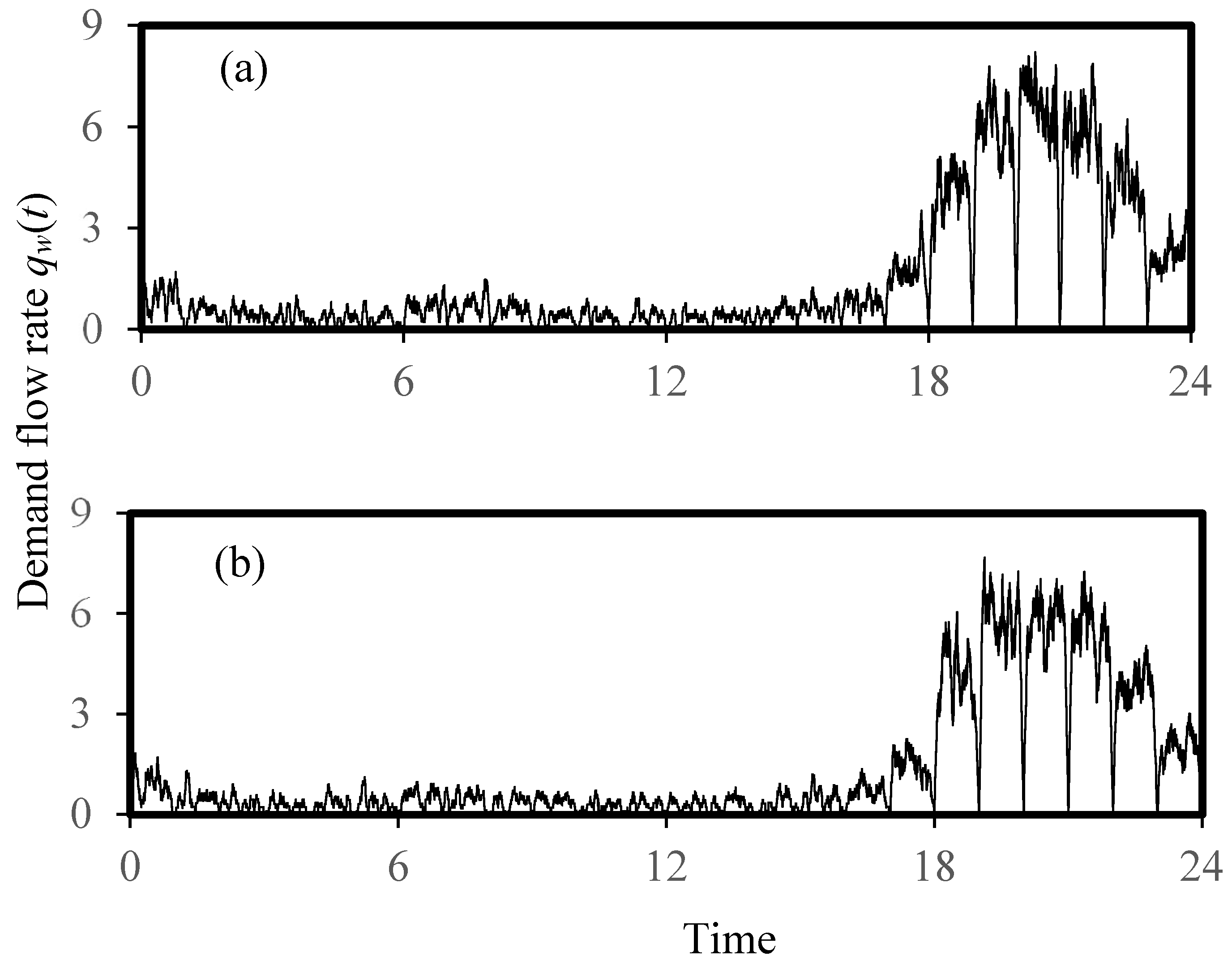
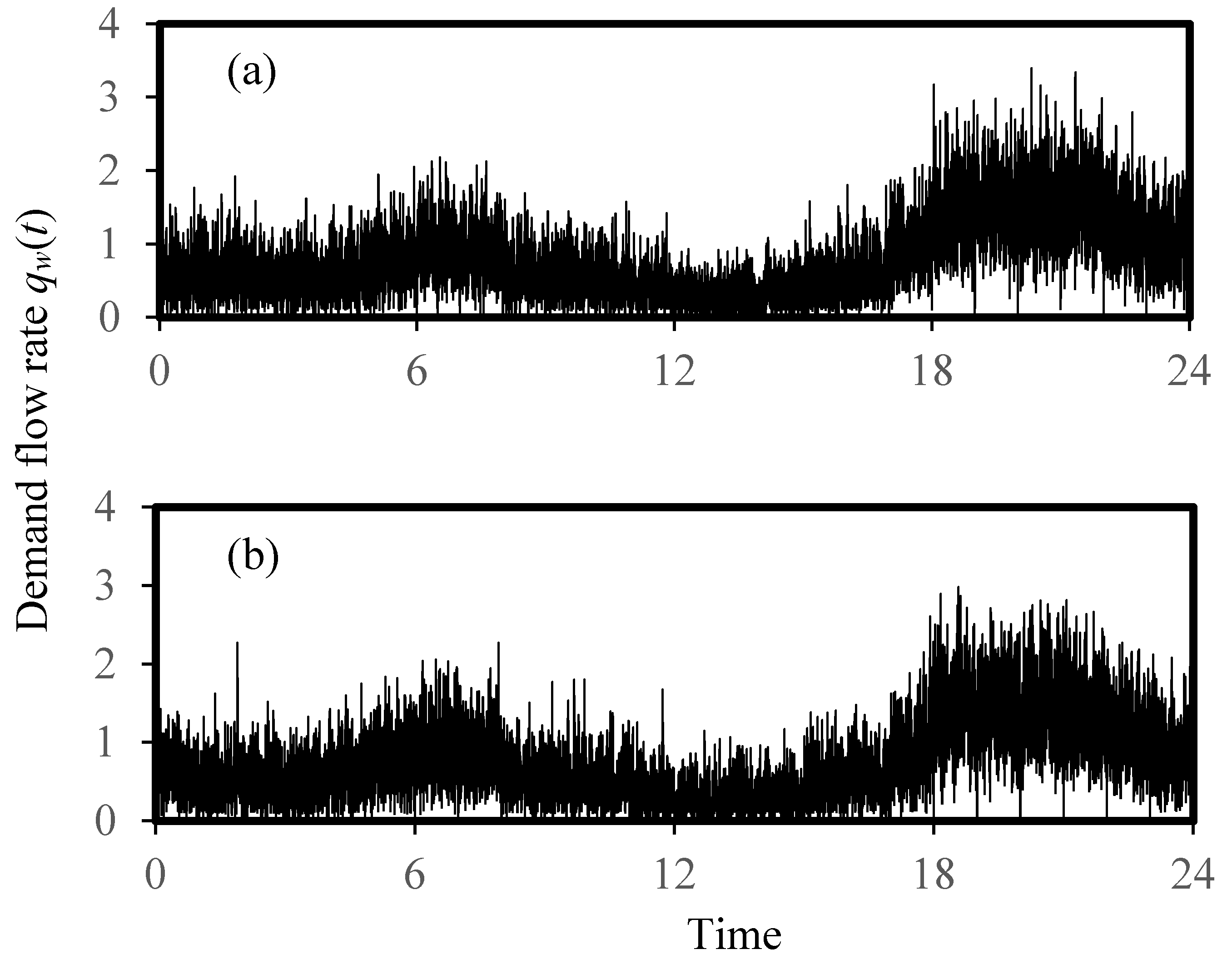
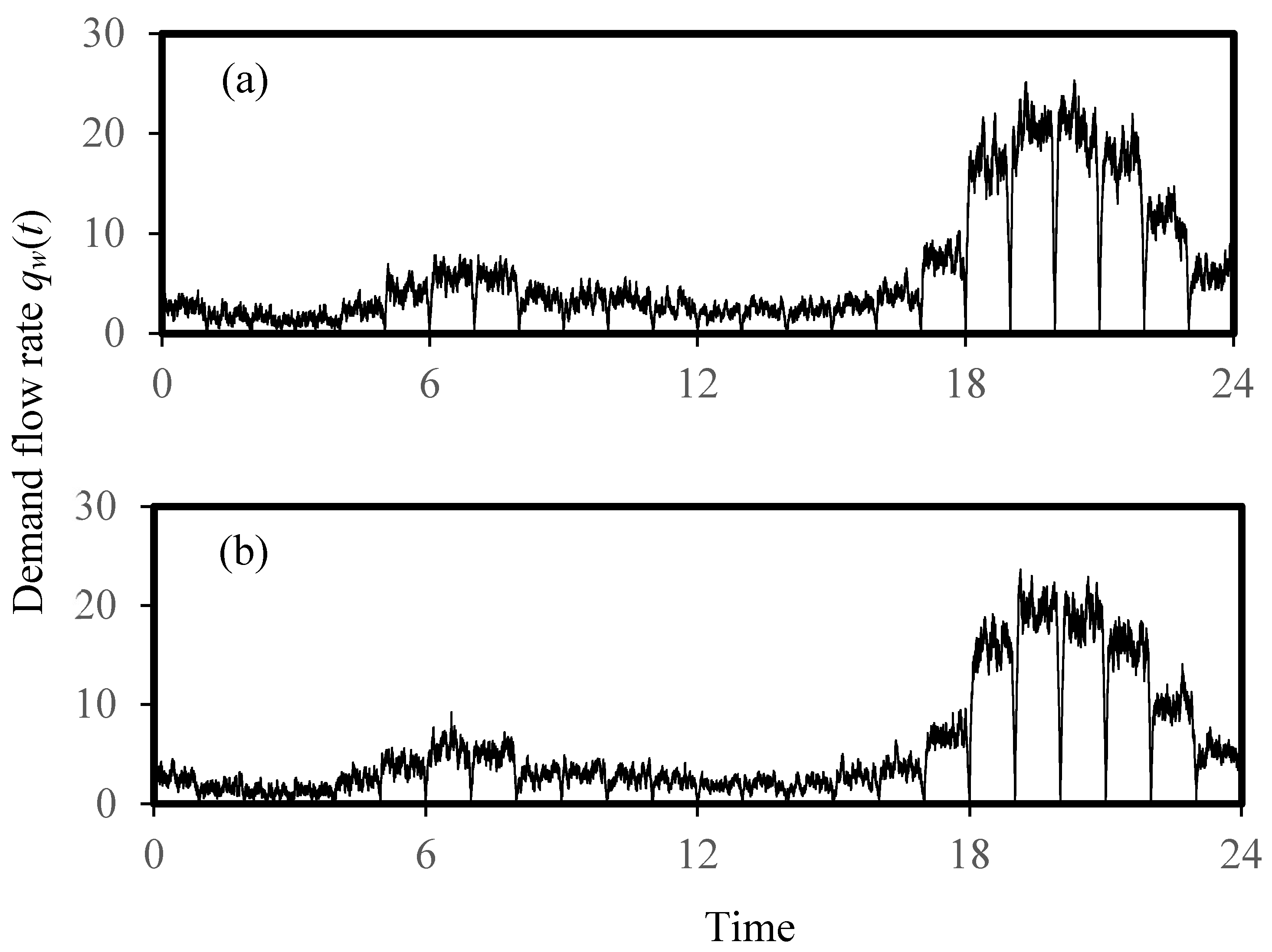
5.1. Simulated Water Demand Time Series
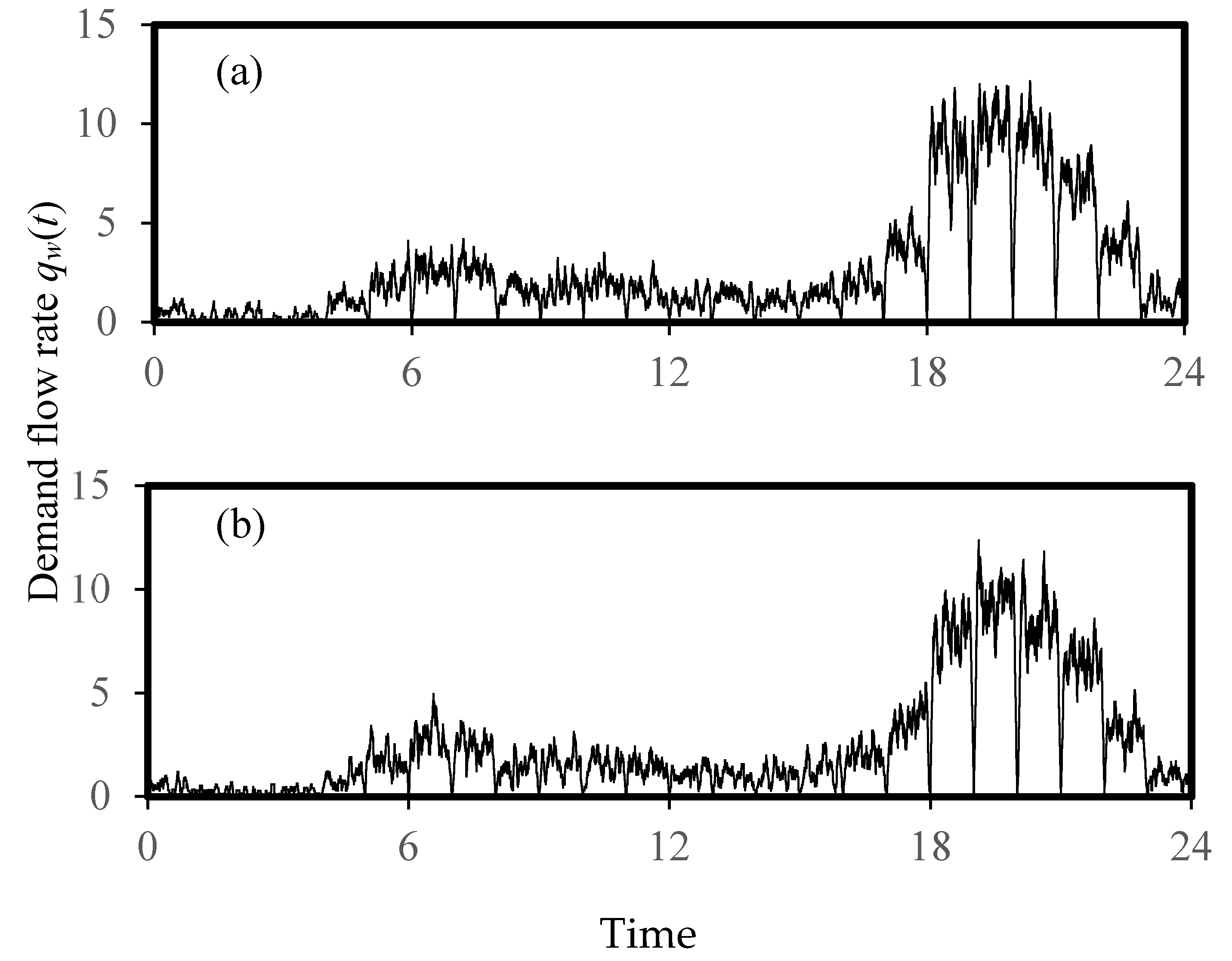
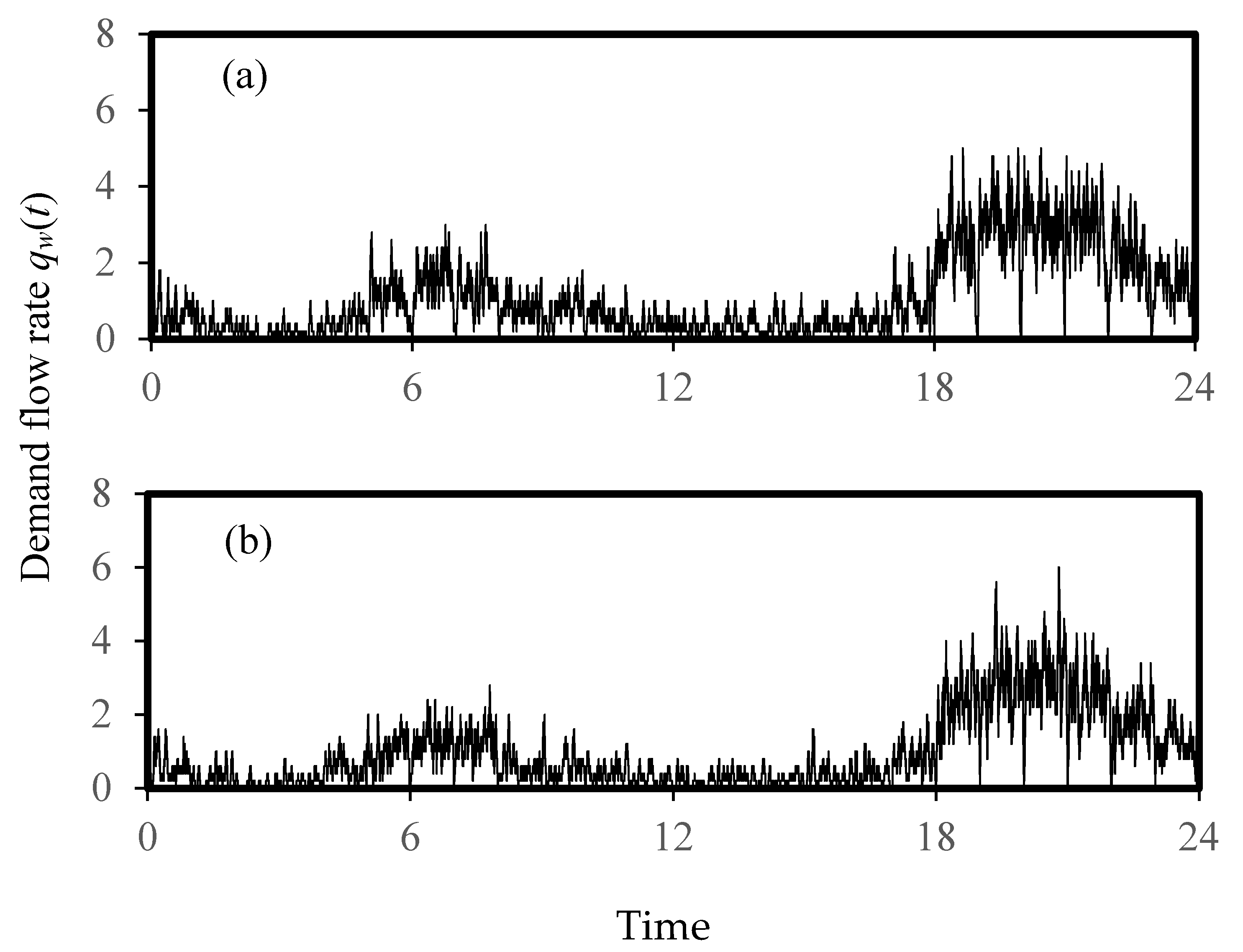
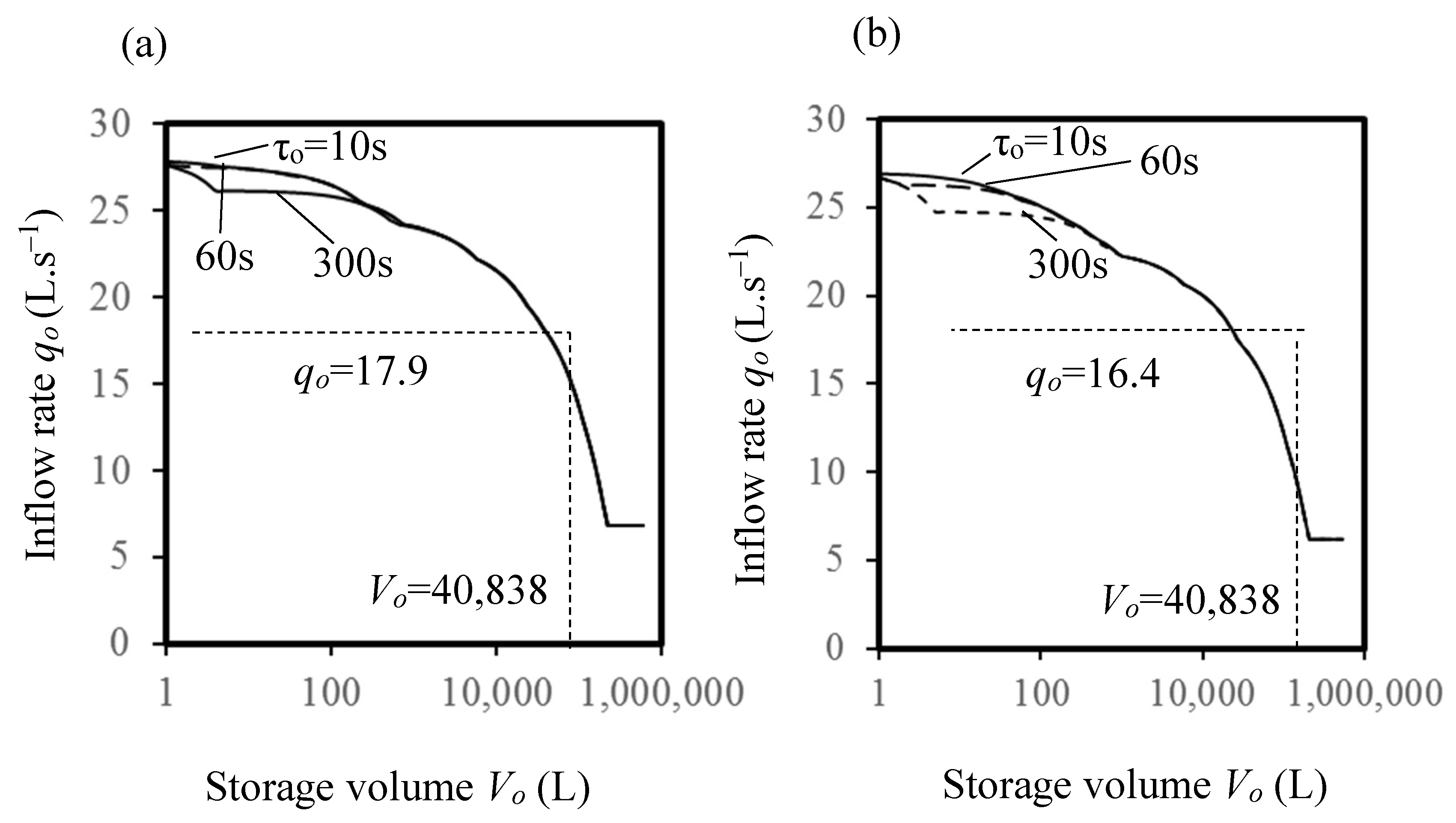
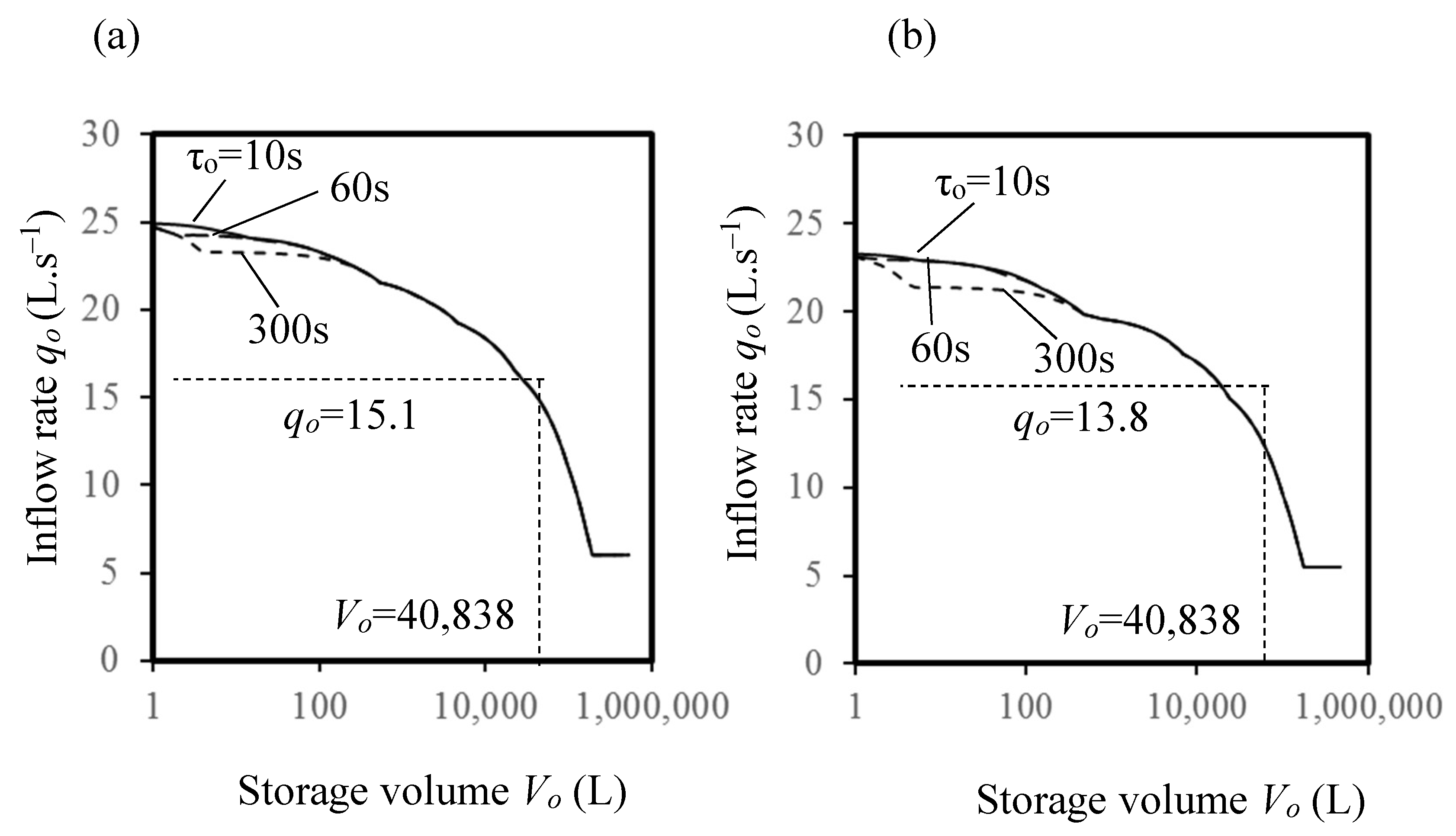
5.2. Simulated Design Flow Rates for Water Supply Systems
5.3. Evaluation of Energy Efficiency for Water Supply Systems with Different Design Flow Rates
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations. Available online: http://www.un.org/en/sections/issues-depth/global-issues-overview/ (accessed on 3 March 2017).
- Hong Kong Water Supplies Department. Combat against Climate Change: Exploit New Water Resources and Foster Water Conservation Culture; Annual Report 2014/15; HKSAR: Hong Kong, China, 2015.
- Hong Kong Water Supplies Department. Domestic Water Consumption Survey—Key Survey Findings—Fact Sheet; HKSAR: Hong Kong, China, 2011.
- Singapore’s National Water Agency. Available online: https://www.pub.gov.sg/watersupply/singaporewaterstory (accessed on 30 October 2017).
- Willis, R.M.; Stewart, R.A.; Giurco, D.P.; Talebpour, M.R.; Mousavinejad, A. End use water consumption in households: Impact of socio-demographic factors and efficient devices. J. Clean. Prod. 2013, 60, 107–115. [Google Scholar] [CrossRef]
- Renwick, M.E.; Archibald, S.O. Demand side management policies for residential water use: Who bears the conservation burden? Land Econ. 1998, 74, 343–359. [Google Scholar] [CrossRef]
- Millock, K.; Nauges, C. Household adoption of water-efficient equipment: The role of socio-economic factors, environmental attitudes and policy. Environ. Resour. Econ. 2010, 46, 539–565. [Google Scholar] [CrossRef]
- Hong Kong Water Supplies Department. Available online: http://www.wsd.gov.hk/en/plumbing-engineering/water-efficiency-labelling-scheme/index.html (accessed on 29 October 2017).
- Australian Government. Available online: http://www.waterrating.gov.au/about-wels (accessed on 16 March 2017).
- Public Unities Board. Water Efficiency Labelling Scheme (Voluntary & Mandatory); Public Unities Board: Singapore, 2013. [Google Scholar]
- United States Environmental Protection Agency (EPA). Available online: https://www.epa.gov/watersense/about-watersense (accessed on 29 October 2017).
- The Water Label Company Limited. Available online: http://www.water-efficiencylabel.org.uk/home.asp (accessed on 2 November 2017).
- Yamazaki, H.; Toyosada, K.; Shimizu, Y.; Dejima, S. Potential for CO2 reductions in Viet Nam by the introduction of water-saving showers. In Proceedings of the 39th International Symposium of CIB W062 Water Supply and Drainage for Buildings, Nagano, Japan, 17–20 September 2013. [Google Scholar]
- Lee, M.; Chen, C.; Cheng, C.; Liao, W.; Nagata, K.; Sato, M. Shower comfort in different water supply pressure conditions in Taiwan. In Proceedings of the 41st International Symposium of CIB W062 Water Supply and Drainage for Buildings, Beijing, China, 18–20 August 2015. [Google Scholar]
- Wong, L.T.; Mui, K.W. A Review of Demand Models for Water Systems in Buildings including a Bayesian Approach. Water 2018, 10, 1078. [Google Scholar] [CrossRef]
- Hunter, R.B. Methods of Estimating Loads in Plumbing Systems; US Dept. of Commerce, National Bureau of Standards: Gaithersburg, MD, USA, 1940.
- Wise, A.F.E.; Swaffield, J. Water, Sanitary and Waste Services for Buildings; Routledge: London, UK, 2012. [Google Scholar]
- CIBSE. Public Health Engineering; CIBSE: Norfolk, UK, 2004. [Google Scholar]
- Murakawa, S.; Takata, H. Development of the calculating method for cold and hot water consumption based on the fixture usage in the time series through a day—A case study of apartment houses. In Proceedings of the CIB W062 International Symposium on Water Supply and Drainage for Buildings, Iasi, Romania, 18–19 September 2002; pp. 1–13. [Google Scholar]
- Murakawa, S.; Takata, H.; Saito, C.; Abe, M.; Toyosada, K. Development of the calculating method for the loads of cold and hot water consumption in a business hotel (Part 2) Dynamic estimation for the loads of cold and hot water demands. In Proceedings of the 41st International Symposium of CIB W062 Water Supply and Drainage for Buildings, Beijing, China, 18–20 August 2015. [Google Scholar]
- Murakawa, S.; Takata, H. Development of the calculating method for the loads of cold and hot water consumption in the apartment houses. In Proceedings of the 2003 CIB W062 International Symposium Water Supply and Drainage for Buildings, Ankara, Turkey, 11–12 September 2003. [Google Scholar]
- Wu, G.; Sakaue, K.; Hayakawa, K.; Murakawa, S.; Inada, T. Verification of calculating method using the Monte Carlo method for water supply demands: The water consumption of mixed-use building for rent. In Proceedings of the 41st International Symposium of CIB W062 Water Supply and Drainage for Buildings, Beijing, China, 18–20 August 2015. [Google Scholar]
- The Institute of Plumbing. Plumbing Engineering Services Design Guide; The Institute of Plumbing: Essex, UK, 2002. [Google Scholar]
- CEN-European Committee for Standardization. EN 806-3:2006 Specifications for Installations Inside Buildings Conveying Water for Human Consumption—Part 3: Pipe Sizing—Simplified Method; CEN: Brussels, Belgium, 2006. [Google Scholar]
- Wong, L.T.; Mui, K.W.; Zhou, Y. Design of tank water supply systems in buildings. In Proceedings of the CIB W062 International Symposium on Water Supply and Drainage for Buildings, Sao Paulo, Brazil, 8–10 September 2014; pp. 223–230. [Google Scholar]
- Bleys, B.; Van den Bossche, P.; Kuborn, X. Measurements of water consumption in apartment buildings. In Proceedings of the 38th International Symposium CIB W062 on Water Supply and Drainage for Buildings, Edinburgh, Scotland, 27–30 August 2012. [Google Scholar]
- Vrana, J.; Jaron, Z.; Kucharik, M. Peak flow rates measured in residential building. In Proceedings of the 42nd International Symposium of CIB W062 on Water Supply and Drainage for Buildings, Kosice, Slovakia, 29 August–1 September 2016. [Google Scholar]
- Blokker, M. Stochastic Water Demand Modelling, Hydraulics in Water Distribution Networks; IWA Publishing: London, UK, 2011. [Google Scholar]
- Wong, L.T. Occupant load assessment for old residential high-rise buildings. Archit. Sci. Rev. 2003, 46, 273–277. [Google Scholar] [CrossRef]
- Wong, L.T.; Mui, K.W. A survey of the sanitation load for domestic high-rise building estates in Hong Kong. In Proceedings of the 30th International Symposium on Water Supply and Drainage for Buildings, CIBW062, CSTB, Paris, France, 16–17 September 2004; pp. 16–17. [Google Scholar]
- Wong, L.T.; Mui, K.W. Determining the domestic drainage loads for high-rise buildings. Archit. Sci. Rev. 2004, 47, 347–354. [Google Scholar] [CrossRef]
- Cheng, C.; Yen, C.; Wong, L.; Ho, K. An evaluation tool of infection risk analysis for drainage systems in high-rise residential buildings. Build. Serv. Eng. Res. Technol. 2008, 29, 233–248. [Google Scholar] [CrossRef]
- Mui, K.W.; Wong, L.T. Modelling occurrence and duration of building drainage discharge loads from random and intermittent appliance flushes. Build. Serv. Eng. Res. Technol. 2013, 34, 381–392. [Google Scholar] [CrossRef]
- Wong, L.T.; Mui, K.W.; Zhou, Y. Impact evaluation of low flow showerheads for Hong Kong residents. Water 2016, 8, 305. [Google Scholar] [CrossRef]
- Hong Kong Water Supplies Department. Available online: https://www.wsd.gov.hk/en/plumbing-engineering/water-efficiency-labelling-scheme/wels-on-showers-for-bathing/voluntary-water-efficiency-labelling-scheme-on-sho/index.html (accessed on 29 September 2017).
- Wong, L.T.; Liu, W. Demand analysis for residential water supply systems in Hong Kong. HKIE Trans. 2008, 15, 24–28. [Google Scholar] [CrossRef]
- Cheung, C.; Mui, K.W.; Wong, L.T. Energy efficiency of elevated water supply tanks for high-rise buildings. Appl. Energy 2013, 103, 685–691. [Google Scholar] [CrossRef]
- Kaya, D.; Yagmur, E.A.; Yigit, K.S.; Kilic, F.C.; Eren, A.S.; Celik, C. Energy efficiency in pumps. Energy Convers. Manag. 2008, 49, 1662–1673. [Google Scholar] [CrossRef]
- Wong, L.T.; Mui, K.W.; Lau, C.; Zhou, Y. Pump efficiency of water supply systems in buildings of Hong Kong. Energy Procedia 2014, 61, 335–338. [Google Scholar] [CrossRef]
- Ingle, S.; King, D.; Southerton, R. Design and sizing of water supply systems using loading units—Time for a change. In Proceedings of the 40th CIBW062 International Symposium of Water Supply and Drainage for Buildings, Sao Paulo, Brazil, 4–10 September 2014; pp. 8–10. [Google Scholar]
- Price, J.I.; Chermak, J.M.; Felardo, J. Low-flow appliances and household water demand: An evaluation of demand-side management policy in Albuquerque, New Mexico. J. Environ. Manag. 2014, 133, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Hong Kong Water Supplies Department. Handbook on Plumbing Installation for Buildings; HKSAR: Hong Kong, China, 2014.
- Moody, L.F. Friction factors for pipe flow. Trans. ASME 1944, 66, 671–684. [Google Scholar]


| Appliance | Parameter | Value | Reference | ||
|---|---|---|---|---|---|
| Conventional | Showerhead | Flow rate (L/s) | Max | 0.20 | [34] |
| Min | 0.10 | [34] | |||
| Mean | 0.16 | [34] | |||
| Discharge time (s) | Max | 359 | [34] | ||
| Min | 240 | [34] | |||
| Mean | 310.2 | [34] | |||
| Wash basin | Flow rate (L/s) | Max | 0.23 | [30] | |
| Min | 0.03 | [35] | |||
| AM1 | 0.13 | [36] | |||
| Discharge time (s) | GM2 | 23.2 | [36] | ||
| Kitchen sink | Flow rate (L/s) | Max | 0.26 | [30] | |
| Min | 0.03 | [35] | |||
| AM1 | 0.15 | [36] | |||
| Discharge time (s) | GM2 | 257 | [36] | ||
| Washing machine | Flow rate (L/s) | AM1 | 0.2 | [36] | |
| Discharge time (s) | GM2 | 150 | [36] | ||
| Low flow | Showerhead | Flow rate (L/s) | Max | 0.15 | [35] |
| Min | 0.07 | [35] | |||
| Mean | 0.11 | ||||
| Discharge time (s) | Mean | 310.2 | [34] | ||
| Parameter | Case A | Case B |
|---|---|---|
| Total tank size (m3) Vo | 41 | 41 |
| Daily consumption (m3) V∞ | 535–590 | 474–521 |
| Design inflow rate (L·s−1) qo | 17.9 | 15.1 |
| Feed pipe water velocity (m·s−1) vo | 1.95 | 1.60 |
| Friction head loss (m) Hf | 5.55 | 4.05 |
| System energy efficiency αt | 0.266 | 0.270 |
| Total electricity power (kW) Pt | 1.77 | 1.09 |
| Daily pumping energy (kWh) Epump | 274–302 | 239–263 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Mui, K.-w.; Wong, L.-t. Evaluation of Design Flow Rate of Water Supply Systems with Low Flow Showering Appliances. Water 2019, 11, 100. https://doi.org/10.3390/w11010100
Zhou Y, Mui K-w, Wong L-t. Evaluation of Design Flow Rate of Water Supply Systems with Low Flow Showering Appliances. Water. 2019; 11(1):100. https://doi.org/10.3390/w11010100
Chicago/Turabian StyleZhou, Yang, Kwok-wai Mui, and Ling-tim Wong. 2019. "Evaluation of Design Flow Rate of Water Supply Systems with Low Flow Showering Appliances" Water 11, no. 1: 100. https://doi.org/10.3390/w11010100
APA StyleZhou, Y., Mui, K.-w., & Wong, L.-t. (2019). Evaluation of Design Flow Rate of Water Supply Systems with Low Flow Showering Appliances. Water, 11(1), 100. https://doi.org/10.3390/w11010100







