Improving the Muskingum Flood Routing Method Using a Hybrid of Particle Swarm Optimization and Bat Algorithm
Abstract
1. Introduction
1.1. Background
1.2. Innovation and Objectives
2. Methods
2.1. Muskingum Model
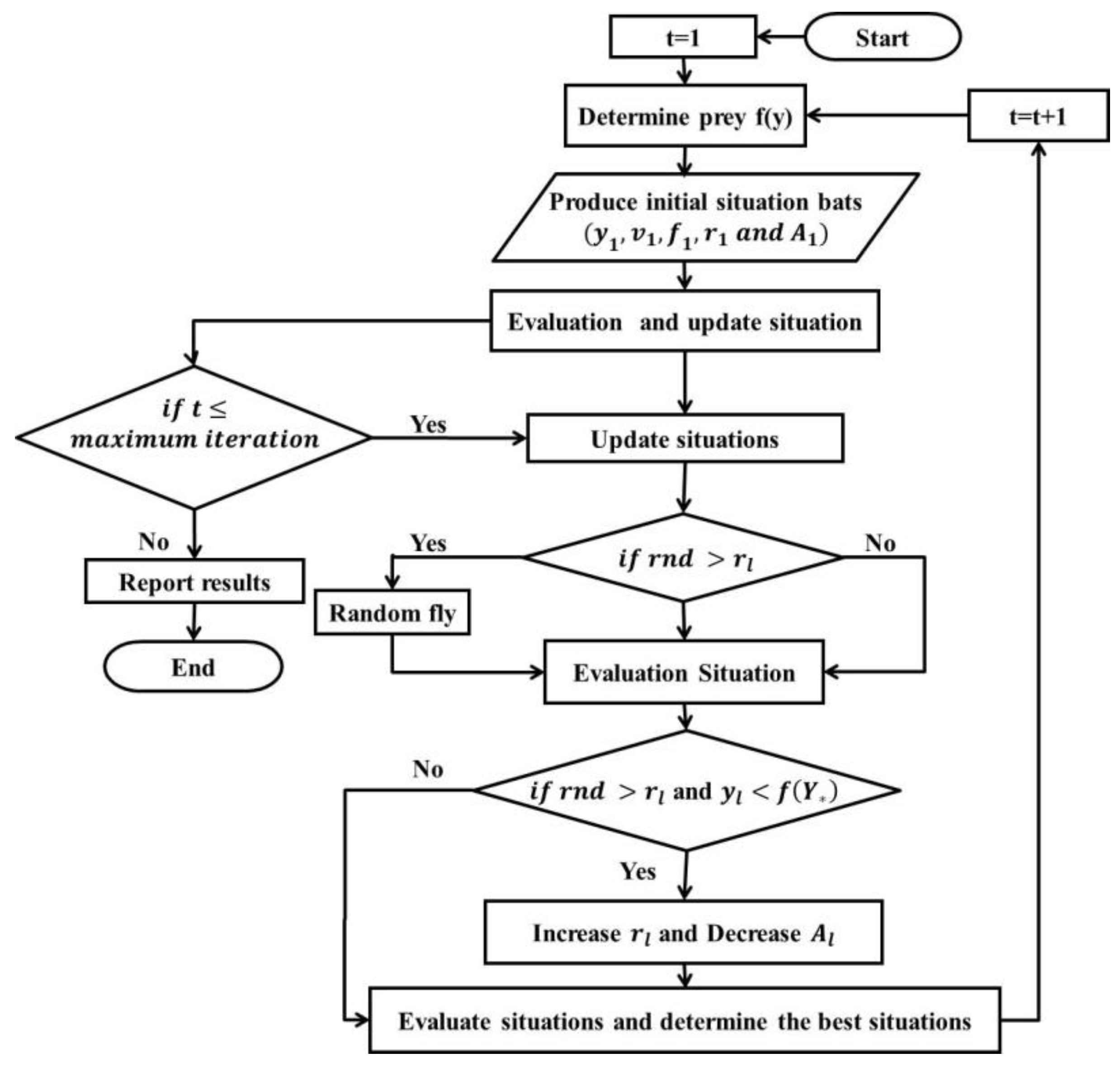
2.2. Bat Algorithm
- (1)
- All bats use echolocation to identify prey and obstacles based on received sound frequencies.
- (2)
- All bats fly randomly with the velocity (vl) at position (yl), and the frequency, loudness and wavelength values are , and , respectively.
- (3)
- The loudness changes from a large positive (A0) to a small positive value (Amin).
2.3. Particle Swarm Optimization
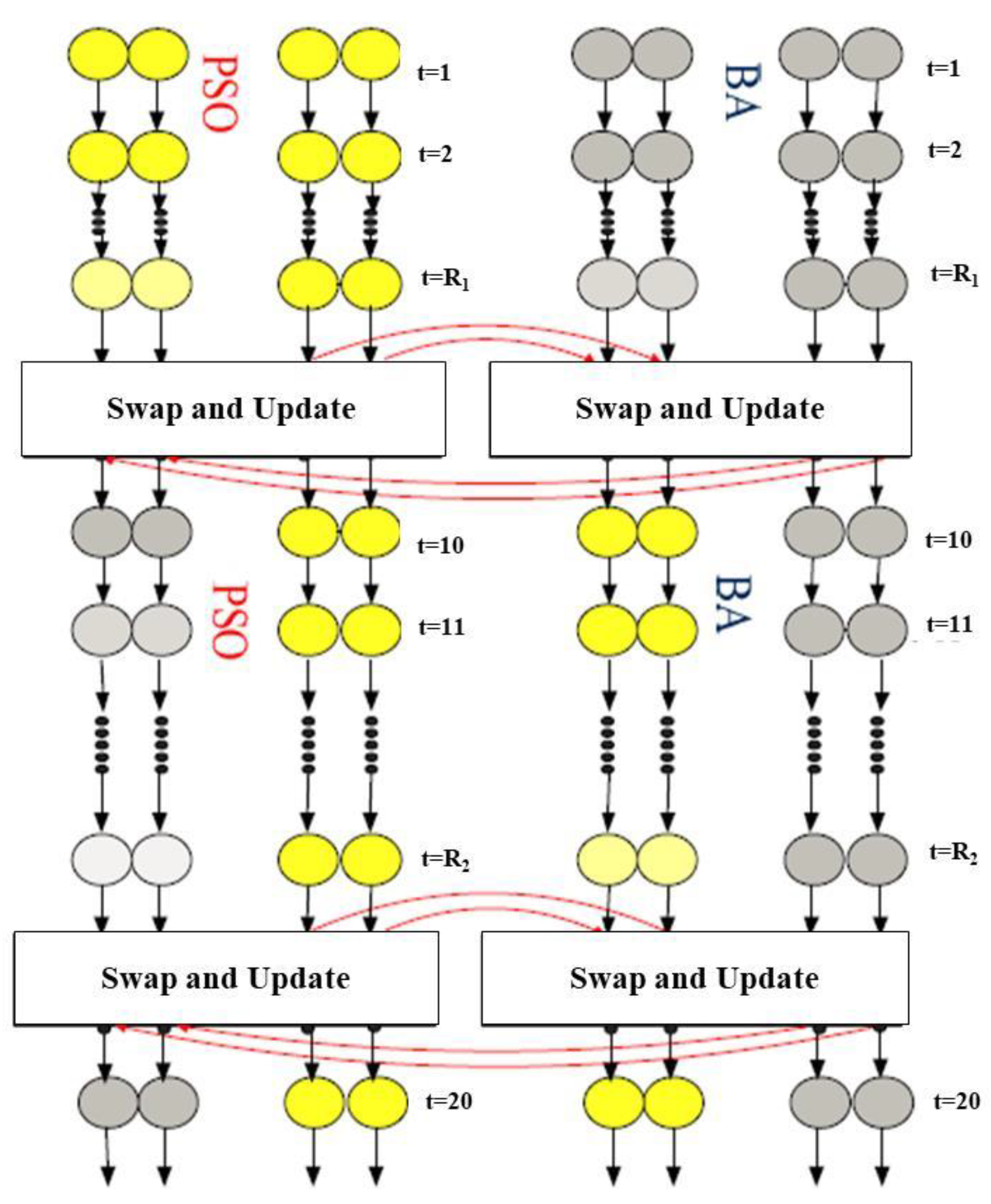
2.4. Hybrid PSO and BA
- (1)
- The random parameters for both algorithms (PSO + BA) are initialized, and the initial populations for the two algorithms are considered.
- (2)
- The first initial values for the hydrological parameters (K, x, m and ) are considered at the start of the algorithm.
- (3)
- The variation in storage is computed based on Equation (7). The initial outflow is the same as inflow.
- (4)
- The accumulated storage is computed based on Equation (8).
- (5)
- The outflow is computed based on Equation (6).
- (6)
- The time step is compared with the total flood time. If it is less than the total time, the algorithm goes to step 3; otherwise, the algorithm goes to the next level.
- (7)
- The objective function is computed for the two algorithms and all members that can be seen in the algorithms.
- (8)
- The velocity and position for the PSO algorithm are updated based on Equations (14) and (15), and the velocity, frequency and position are updated based on Equations (9)–(11).
- (9)
- The best particles migrate from the PSO algorithm to the BA, and there is a condition for BA similarity. In fact, the specific number of best members for each algorithm is known and is substituted for the worst solutions of the other algorithm.
- (10)
- The convergence criteria are considered. If the criteria are satisfied, the algorithm finishes; otherwise, the algorithm returns to the second step.
- (1)
- The sum of the squared deviations between observed and estimated discharges is considered the objective function and is computed based on the following equation:
- (2)
- The SAD between estimated and observed discharges is computed based on the following equation:
- (3)
- The mean absolute error (MARE) between estimated and observed discharges is computed based on the following equation:
- (4)
- The error for peak discharge (EO) is computed based on the following equation:
- (5)
- The error for peak time is computed based on the following equation:where is the simulated discharge, is the observed discharge, is the peak time of observed discharge, is the peak time of simulated discharge, and N is the number of data.
3. Case Studies
4. Results and Discussion
4.1. Wilson Flood
4.1.1. Sensitivity Analysis for Different Algorithms for the Wilson Flood
4.1.2. Ten Random Results for Different Algorithms for Wilson Flood
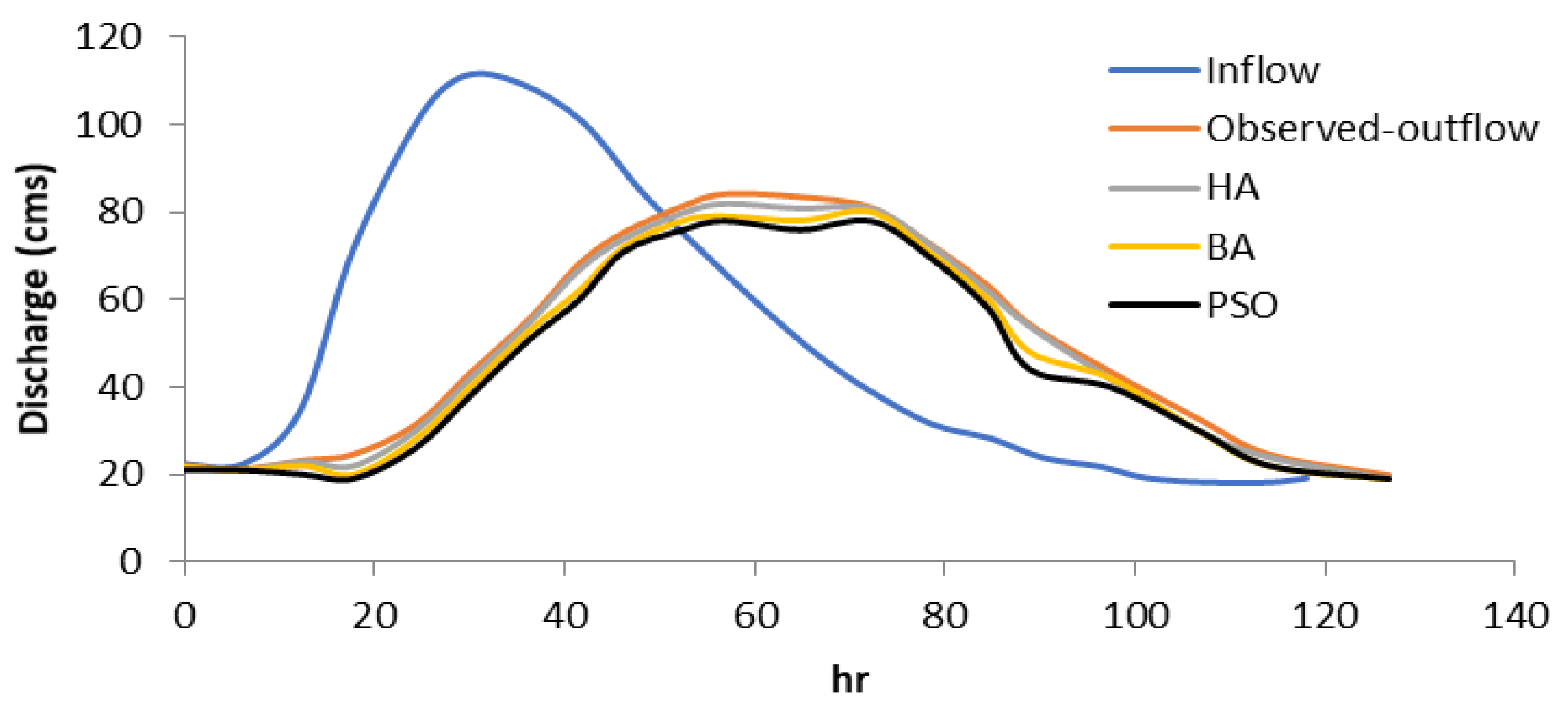
4.1.3. Discussion of the Wilson Flood Results
4.2. Karahan Flood
4.2.1. Discussion of the Karahan Results
4.2.2. Ten Random Results for Karahan Flood
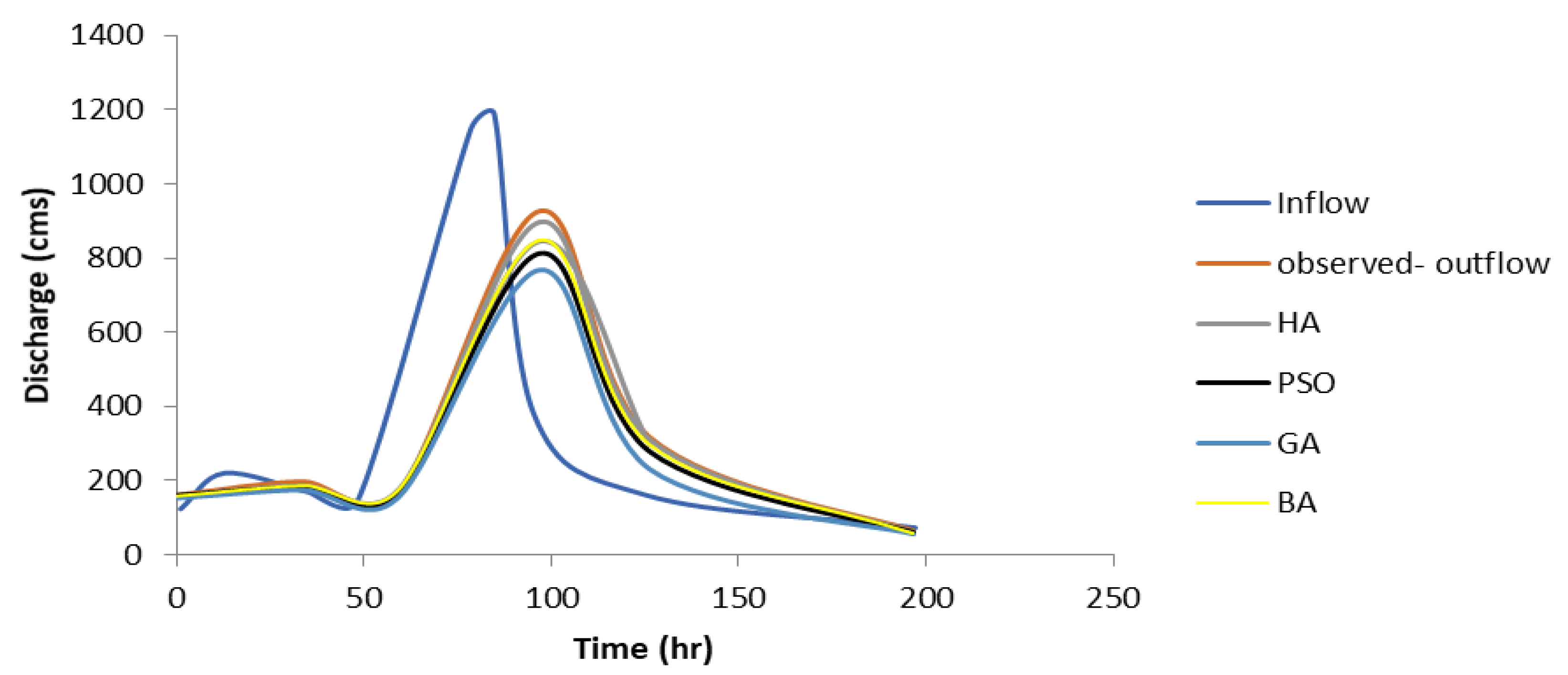
4.3. Discussion of the Viessman and Lewis Flood Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bagatur, T.; Onen, F. Development of predictive model for flood routing using genetic expression programming. J. Flood Risk Manag. 2018, 11, S444–S454. [Google Scholar] [CrossRef]
- El-shafie, A.; Noureldin, A.; Taha, M.; Hussain, A.; Mukhlisin, M. Dynamic versus static neural network model for rainfall forecasting at Klang River Basin, Malaysia. Hydrol. Earth Syst. Sci. 2012, 16, 1151–1169. [Google Scholar] [CrossRef]
- Mazzoleni, M.; Noh, S.J.; Lee, H.; Liu, Y.; Seo, D.J.; Amaranto, A.; Alfonso, L.; Solomatine, D.P. Real-time assimilation of streamflow observations into a hydrological routing model: Effects of model structures and updating methods. Hydrol. Sci. J. 2018, 63, 386–407. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Chang, F.J.; Liu, P.; Chen, A.B. Methodology that improves water utilization and hydropower generation without increasing flood risk in mega cascade reservoirs. Energy 2018, 143, 785–796. [Google Scholar] [CrossRef]
- El-shafie, A.; Mukhlisin, M.; Najah, A.A.; Taha, M.R. Performance of artificial neural network and regression techniques for rainfall-runoff prediction. Int. J. Phys. Sci. 2011, 6, 1997–2003. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Discussion of “Assessment of Modified Honey Bee Mating Optimization for Parameter Estimation of Nonlinear Muskingum Models” by Majid Niazkar and Seied Hosein Afzali. J. Hydrol. Eng. 2018, 23, 07018002. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Pati, A.; Sen, S.; Perumal, M. Modified Channel-Routing Scheme for SWAT Model. J. Hydrol. Eng. 2018, 23, 1–8. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016. [Google Scholar] [CrossRef]
- Barati, R. Comment on “Evaluation of a physically based quasi-linear and a conceptually based nonlinear Muskingum methods” by Muthiah Perumal, Gokmen Tayfur, C. Madhusudana Rao and Gurhan Gurarslan. J. Hydrol. 2017, 550, 218–219. [Google Scholar] [CrossRef]
- Barbetta, S.; Moramarco, T.; Perumal, M. A Muskingum-based methodology for river discharge estimation and rating curve development under significant lateral inflow conditions. J. Hydrol. 2017, 554, 216–232. [Google Scholar] [CrossRef]
- Barati, R.; Badfar, M.; Azizyan, G.; Akbari, G.H. Discussion of “Parameter Estimation of Extended Nonlinear Muskingum Models with the Weed Optimization Algorithm” by Farzan Hamedi, Omid Bozorg-Haddad, Maryam Pazoki, Hamid-Reza Asgari, Mehran Parsa and Hugo A. Loáiciga. J. Irrig. Drain. Eng. 2018, 144, 07017021. [Google Scholar] [CrossRef]
- Yoo, C.; Lee, J.; Lee, M. Parameter Estimation of the Muskingum Channel Flood-Routing Model in Ungauged Channel Reaches. J. Hydrol. Eng. 2017, 22, 05017005. [Google Scholar] [CrossRef]
- Zhang, S.; Kang, L.; Zhou, B. Parameter estimation of nonlinear Muskingum model with variable exponent using adaptive genetic algorithm. In Environmental Conservation, Clean Water, Air & Soil (CleanWAS); IWA Publishing: London, UK, 2017; pp. 231–237. [Google Scholar]
- Luo, J.; Xie, J. Parameter Estimation for Nonlinear Muskingum Model Based on Immune Clonal Selection Algorithm. J. Hydrol. Eng. 2010, 15, 844–851. [Google Scholar] [CrossRef]
- Barati, R. Parameter Estimation of Nonlinear Muskingum Models Using Nelder-Mead Simplex Algorithm. J. Hydrol. Eng. 2011, 16, 946–954. [Google Scholar] [CrossRef]
- Barati, R.; Rahimi, S.; Akbari, G.H. Analysis of dynamic wave model for flood routing in natural rivers. Water Sci. Eng. 2012, 5, 243–258. [Google Scholar] [CrossRef]
- Karahan, H.; Gurarslan, G.; Geem, Z.W. Parameter Estimation of the Nonlinear Muskingum Flood-Routing Model Using a Hybrid Harmony Search Algorithm. J. Hydrol. Eng. 2013, 18, 352–360. [Google Scholar] [CrossRef]
- Orouji, H.; Haddad, O.B.; Fallah-Mehdipour, E.; Mariño, M.A. Estimation of Muskingum parameter by meta-heuristic algorithms. In Proceedings of the Institution of Civil Engineers: Water Management; Institution of Civil Engineers (ICE): London, UK, 2013; Volume 166, pp. 315–324. [Google Scholar]
- Easa, S.M.; Barati, R.; Shahheydari, H.; Nodoshan, E.J.; Barati, T. Discussion: New and improved four-parameter non-linear Muskingum model. Proc. Inst. Civ. Eng. Water Manag. 2014, 167, 612–615. [Google Scholar] [CrossRef]
- Ouyang, A.; Li, K.; Truong, T.K.; Sallam, A.; Sha, E.H.M. Hybrid particle swarm optimization for parameter estimation of Muskingum model. Neural Comput. Appl. 2014, 25, 1785–1799. [Google Scholar] [CrossRef]
- Niazkar, M.; Afzali, S.H. Assessment of modified honey bee mating optimization for parameter estimation of nonlinear Muskingum models. J. Hydrol. Eng. 2015, 20, 04014055. [Google Scholar] [CrossRef]
- Talatahari, S.; Sheikholeslami, R.; Farahmand Azar, B.; Daneshpajouh, H. Optimal Parameter Estimation for Muskingum Model Using a CSS-PSO Method. Adv. Mech. Eng. 2013, 5, 480954. [Google Scholar] [CrossRef]
- Karahan, H.; Gurarslan, G.; Geem, Z.W. A new nonlinear Muskingum flood routing model incorporating lateral flow. Eng. Optim. 2015, 47, 737–749. [Google Scholar] [CrossRef]
- Bozorg Haddad, O.; Hamedi, F.; Orouji, H.; Pazoki, M.; Loáiciga, H.A. A Re-Parameterized and Improved Nonlinear Muskingum Model for Flood Routing. Water Resour. Manag. 2015, 29, 3419–3440. [Google Scholar] [CrossRef]
- Niazkar, M.; Afzali, S.H. Parameter estimation of new improved Muskingum model using new hybrid model. Hydrol. Res. 2016, 49, nh2016089. [Google Scholar] [CrossRef]
- Dhar, S.; Kundu, M.K. A novel method for image thresholding using interval type-2 fuzzy set and Bat algorithm. Appl. Soft Comput. 2018, 63, 1–37. [Google Scholar] [CrossRef]
- Cui, Z.; Cao, Y.; Cai, X.; Cai, J.; Chen, J. Optimal LEACH protocol with modified bat algorithm for big data sensing systems in Internet of Things. J. Parallel Distrib. Comput. 2018. [Google Scholar] [CrossRef]
- Bekdaş, G.; Nigdeli, S.M.; Yang, X.S. A novel bat algorithm based optimum tuning of mass dampers for improving the seismic safety of structures. Eng. Struct. 2018, 159, 89–98. [Google Scholar] [CrossRef]
- Mihoubi, M.; Rahmoun, A.; Lorenz, P.; Lasla, N. An effective Bat algorithm for node localization in distributed wireless sensor network. Secur. Priv. 2017, 1, e7. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O.; Karimirad, I.; Seifollahi-Aghmiuni, S.; Loáiciga, H.A. Development and Application of the Bat Algorithm for Optimizing the Operation of Reservoir Systems. J. Water Resour. Plan. Manag. 2015, 141, 04014097. [Google Scholar] [CrossRef]
- Gill, M.A. Flood routing by the Muskingum method. J. Hydrol. 1978, 36, 353–363. [Google Scholar] [CrossRef]
- Tung, Y. River Flood Routing by Nonlinear Muskingum Method. J. Hydraul. Eng. 1985, 111, 1447–1460. [Google Scholar] [CrossRef]
- Geem, Z.; Kim, J.; Loganathan, G. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Elzwayie, A.; El-shafie, A.; Yaseen, Z.M.; Afan, H.A.; Allawi, M.F. RBFNN-based model for heavy metal prediction for different climatic and pollution conditions. Neural Comput. Appl. 2017, 28, 1991–2003. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Fu, M.; Wang, C.; Hanna, W.; Wan, M.; Deo, R.C.; El-shafie, A. Application of the Hybrid Artificial Neural Network Coupled with Rolling Mechanism and Grey Model Algorithms for Streamflow Forecasting Over Multiple Time Horizons. Water Res. Manag. 2018, 32, 1883–1899. [Google Scholar] [CrossRef]
- Diop, L.; Bodian, A.; Djaman, K.; Yaseen, Z.M.; Deo, R.C.; El-shafie, A.; Brown, L.C. The influence of climatic inputs on stream-flow pattern forecasting: Case study of Upper Senegal River. Environ. Earth Sci. 2018, 77, 182. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Deo, R.C.; Yaseen, Z.M.; Kashani, M.H. Pan evaporation prediction using a hybrid multilayer perceptron-firefly algorithm (MLP-FFA) model : Case study in North Iran. Theor. Appl. Climatol. 2017, 1–13. [Google Scholar] [CrossRef]
- Warrren, V.; Gary, L.L. Introduction to Hydrology; Prentice Hall India (P) Ltd.: Delhi, India, 2003. [Google Scholar]
- Moghaddam, A.; Behmanesh, J.; Farsijani, A. Parameters Estimation for the New Four-Parameter Nonlinear Muskingum Model Using the Particle Swarm Optimization. Water Resour. Manag. 2016, 30, 2143–2160. [Google Scholar] [CrossRef]
| Population Size | Objective Function | Maximum Frequency (Hz) | Objective Function | Minimum Frequency (Hz) | Objective Function | Maximum Loudness (dB) | Objective Function | c1 | Objective Function | c2 | Objective Function | w | Objective Function |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 5.123 | 3 | 5.254 | 1 | 5.565 | 0.20 | 4.999 | 1.6 | 5.145 | 1.6 | 5.011 | 0.3 | 5.133 |
| 40 | 4.789 | 5 | 4.884 | 2 | 4.987 | 0.40 | 4.845 | 1.8 | 4.933 | 1.8 | 4.987 | 0.5 | 4.654 |
| 60 | 4.234 | 7 | 4.233 | 3 | 4.234 | 0.60 | 4.234 | 2.0 | 4.234 | 2.0 | 4.234 | 0.70 | 4.235 |
| 80 | 4.312 | 9 | 4.679 | 4 | 4.789 | 0.80 | 4.565 | 2.2 | 4.555 | 2.2 | 4.445 | 0.90 | 4.512 |
| Population Size | Objective Function | c1 | Objective Function | c2 | Objective Function | w | Objective Function |
|---|---|---|---|---|---|---|---|
| 20 | 5.981 | 1.60 | 5.891 | 1.60 | 5.954 | 0.30 | 5.845 |
| 40 | 5.785 | 1.80 | 5.654 | 1.80 | 5.878 | 0.50 | 5.764 |
| 60 | 5.555 | 2.0 | 5.554 | 2.0 | 5.554 | 0.70 | 5.555 |
| 70 | 5.894 | 2.2 | 5.892 | 2.2 | 5.891 | 0.90 | 5.789 |
| Population Size | Objective Function | Maximum Frequency (Hz) | Objective Function | Minimum Frequency (Hz) | Objective Function | Loudness (dB) | Objective Function |
|---|---|---|---|---|---|---|---|
| 20 | 5.765 | 3 | 5.812 | 1 | 5.911 | 0.3 | 5.912 |
| 40 | 5.455 | 5 | 5.691 | 2 | 5.783 | 0.5 | 5.678 |
| 60 | 5.342 | 7 | 5.342 | 3 | 5.343 | 0.70 | 5.343 |
| 70 | 5.694 | 9 | 5.611 | 4 | 5.455 | 0.90 | 5.678 |
| Run Number | HA | BA | PSO |
|---|---|---|---|
| 1 | 4.234 | 5.342 | 5.555 |
| 2 | 4.233 | 5.348 | 5.555 |
| 3 | 4.234 | 5.342 | 5.555 |
| 4 | 4.234 | 5.342 | 5.555 |
| 5 | 4.234 | 5.342 | 5.559 |
| 6 | 4.233 | 5.342 | 5.560 |
| 7 | 4.234 | 5.342 | 5.555 |
| 8 | 4.234 | 5.342 | 5.555 |
| 9 | 4.234 | 5.342 | 5.555 |
| 10 | 4.234 | 5.342 | 5.555 |
| Average | 4.234 | 5.342 | 5.555 |
| Computational time | 20 s | 27 s | 25 s |
| Variation coefficient | 0.00007 | 0.0003 | 0.0004 |
| Method | SSQ | SAD | MARE | EO | ET |
|---|---|---|---|---|---|
| HA | 4.234 | 3.125 | 0.012 | 0.00111 | 0 |
| PSO | 5.555 | 4.128 | 0.017 | 0.00251 | 0 |
| BA | 5.342 | 4.117 | 0.015 | 0.00167 | 0 |
| Method | SSQ | SAD | MARE | EO | ET |
|---|---|---|---|---|---|
| GA [40] (Three-parameter Muskingum) | 38.230 | 23.00 | 0.0912 | 0.0083 | 0 |
| HS [40] (Three-parameter Muskingum) | 36.780 | 23.40 | 0.0878 | 0.0107 | 0 |
| ICA [40] (Three-parameter Muskingum) | 36.801 | 23.46 | 0.0745 | 0.0105 | 0 |
| BA (current research) (Three-parameter Muskingum) | 12.25 | 10.95 | 0.0215 | 0.0079 | 0 |
| PSO (current research) (Three-parameter Muskingum) | 14.78 | 12.72 | 0.0325 | 0.0081 | 0 |
| HA (current research) (Three-parameter Muskingum) | 8.215 | 6.515 | 0.0205 | 0.0043 | 0 |
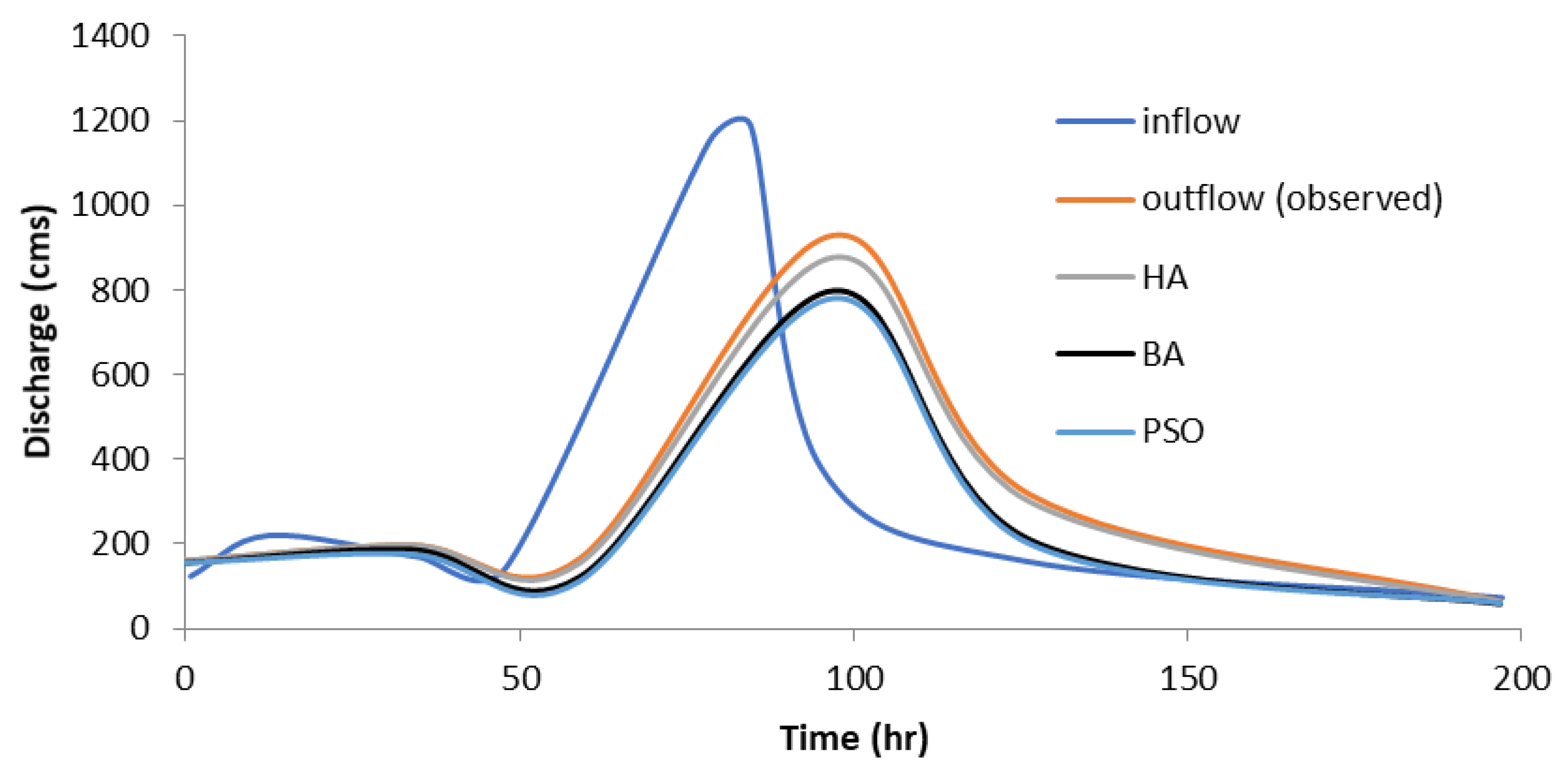
| Time | Inflow (cm) | Outflow (Observed-cm) | Hybrid Method (cm) | BA (cm) | PSO |
|---|---|---|---|---|---|
| 0 | 22 | 22 | 22.0 | 22.0 | 22.0 |
| 6 | 23 | 21 | 22.0 | 23.0 | 23.0 |
| 12 | 35 | 21 | 21.0 | 22.5 | 23.5 |
| 18 | 71 | 26 | 25.0 | 25.0 | 26.0 |
| 24 | 103 | 34 | 34.0 | 35.0 | 35.5 |
| 30 | 111 | 44 | 43.5 | 44.0 | 44.0 |
| 36 | 109 | 55 | 54.0 | 55.0 | 55.5 |
| 42 | 100 | 66 | 66.0 | 67.0 | 68.0 |
| 48 | 86 | 75 | 74.0 | 74.0 | 75.0 |
| 54 | 71 | 82 | 81.5 | 82.0 | 83.0 |
| 60 | 59 | 85 | 85.0011 | 85.00251 | 85.00267 |
| 66 | 47 | 84 | 84.0 | 84.0 | 84.0 |
| 72 | 39 | 80 | 81.0 | 80.5 | 81.0 |
| 78 | 32 | 73 | 74.0 | 73.0 | 74.0 |
| 84 | 28 | 64 | 64.0 | 65.0 | 66.0 |
| 90 | 24 | 54 | 54.0 | 55.0 | 56.0 |
| 96 | 22 | 44 | 44.0 | 44.0 | 45.0 |
| 102 | 21 | 36 | 36.0 | 37.0 | 38.0 |
| 108 | 20 | 30 | 30.5 | 31.0 | 31.0 |
| 114 | 19 | 25 | 25.5 | 26.2 | 26.9 |
| 120 | 19 | 22 | 23.0 | 24.0 | 25.0 |
| 126 | 18 | 19 | 20.0 | 21.0 | 22.0 |
| Method | K | x | m | |
|---|---|---|---|---|
| HA | 0.164 | 0.2879 | 3.781 | 0.4678 |
| BA | 0.152 | 0.2768 | 3.567 | 0.4567 |
| PSO | 0.144 | 0.2645 | 3.123 | 0.3789 |
| Method | SSQ | SAD | MARE | EO | ET |
|---|---|---|---|---|---|
| HA | 30,235 | 625 | 0.22 | 0.101 | 0 |
| PSO | 32,119 | 697 | 0.25 | 0.109 | 0 |
| BA | 31,112 | 676 | 0.24 | 0.108 | 0 |
| Method | SSQ | SAD | MARE | EO | ET |
|---|---|---|---|---|---|
| GA [40] (Three-parameter Muskingum) | 35,123 | 1980 | 0.910 | 0.701 | 0 |
| HS [40] (Three-parameter Muskingum) | 37,944 | 2161 | 0.924 | 0.798 | 0 |
| ICA [40] (Three-parameter Muskingum) | 37,825 | 2054 | 0.914 | 0.787 | 0 |
| BA (current research) (Three-parameter Muskingum) | 32,228 | 712 | 0.420 | 0.115 | 0 |
| PSO (current research) (Three-parameter Muskingum) | 33,229 | 735 | 0.454 | 0.125 | 0 |
| HA (current research) (Three-parameter Muskingum) | 31,125 | 697 | 0.254 | 0.105 | 0 |
| Time | Inflow (cm) | Outflow (Observed-cm) | Hybrid Method (cm) | BA (cm) | PSO (cm) |
|---|---|---|---|---|---|
| 0 | 154 | 102 | 102.0 | 102.0 | 102.0 |
| 6 | 150 | 140 | 139.23 | 138.23 | 154.2 |
| 12 | 219 | 169 | 170.21 | 171.24 | 152.1 |
| 18 | 182 | 190 | 185.12 | 183.24 | 179.4 |
| 24 | 182 | 209 | 202.34 | 200.11 | 190.9 |
| 30 | 192 | 218 | 212.23 | 198.23 | 185.4 |
| 36 | 165 | 210 | 207.11 | 192.32 | 186.9 |
| 42 | 150 | 194 | 192.12 | 189.23 | 180.2 |
| 48 | 128 | 172 | 170.21 | 169.24 | 164.1 |
| 54 | 168 | 149 | 147.21 | 146.74 | 143.7 |
| 60 | 260 | 136 | 137.21 | 139.23 | 152.8 |
| 66 | 471 | 228 | 219.21 | 212.23 | 196.3 |
| 72 | 717 | 303 | 300.11 | 298.21 | 267.3 |
| 78 | 1092 | 366 | 358.11 | 354.23 | 351.4 |
| 84 | 1145 | 456 | 436.32 | 426.73 | 431.8 |
| 90 | 600 | 615 | 612.21 | 623.24 | 617.4 |
| 96 | 365 | 830 | 830.101 | 830.108 | 830.109 |
| 102 | 277 | 969 | 894.12 | 879.12 | 836.70 |
| 108 | 227 | 665 | 665.101 | 665.108 | 665.109 |
| 114 | 187 | 519 | 519.21 | 523.12 | 549.10 |
| 120 | 161 | 444 | 435.68 | 424.32 | 416.90 |
| 126 | 143 | 321 | 315.23 | 312.11 | 305.0 |
| 132 | 126 | 208 | 210.21 | 212.21 | 221.40 |
| 138 | 115 | 176 | 169.21 | 166.24 | 163.38 |
| 144 | 102 | 148 | 142.12 | 139.23 | 131.20 |
| 150 | 93 | 125 | 119.21 | 115.67 | 110.0 |
| 156 | 88 | 114 | 109.21 | 100.21 | 96.40 |
| 162 | 82 | 106 | 110.21 | 112.11 | 89.20 |
| 168 | 76 | 97 | 92.21 | 89.23 | 82.70 |
| 174 | 73 | 89 | 82.12 | 79.43 | 76.30 |
| 180 | 70 | 81 | 80.23 | 78.12 | 73.00 |
| 186 | 67 | 76 | 79.14 | 75.12 | 69.80 |
| 192 | 63 | 71 | 70.14 | 70.11 | 66.7 |
| 198 | 59 | 66 | 70.23 | 69.12 | 62.40 |
| Method | K | x | m | |
|---|---|---|---|---|
| HA | 0.610 | 0.404 | 3.781 | 1.125 |
| BA | 0.578 | 0.311 | 2.896 | 1.112 |
| PSO | 0.578 | 0.309 | 2.789 | 1.105 |
| Run Number | HA | BA | PSO |
|---|---|---|---|
| 1 | 30,235 | 31,112 | 32,119 |
| 2 | 30,237 | 31,117 | 32,119 |
| 3 | 30,235 | 31,112 | 32,119 |
| 4 | 30,235 | 31,112 | 32,119 |
| 5 | 30,235 | 31,112 | 32,119 |
| 6 | 30,235 | 31,112 | 32,119 |
| 7 | 30,237 | 31,112 | 32,122 |
| 8 | 30,235 | 31,117 | 32,112 |
| 9 | 30,235 | 31,112 | 32,119 |
| 10 | 30,235 | 31,112 | 32,119 |
| Average | 30,235.4 | 31,113 | 32,119 |
| Computational time | 19 s | 23 s | 27 s |
| Variation coefficient | 0.00002 | 0.00005 | 0.00007 |
| Population Size | Objective Function | Maximum Frequency (Hz) | Objective Function | Minimum Frequency (Hz) | Objective Function | Maximum Loudness (dB) | Objective Function | c1 | Objective Function | c2 | Objective Function | w | Objective Function |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 34,231 | 3 | 33,278 | 1 | 32,278 | 0.20 | 31,124 | 1.6 | 32,112 | 1.6 | 32,114 | 0.3 | 31,127 |
| 40 | 32,278 | 5 | 32,211 | 2 | 31,112 | 0.40 | 30,298 | 1.8 | 31,214 | 1.8 | 31,289 | 0.5 | 31,119 |
| 60 | 30,235 | 7 | 30,235 | 3 | 30,235 | 0.60 | 30,235 | 2.0 | 30,235 | 2.0 | 30,235 | 0.70 | 30,235 |
| 80 | 31,112 | 9 | 31,265 | 4 | 31,112 | 0.80 | 30,236 | 2.2 | 31,112 | 2.2 | 31,112 | 0.90 | 30,254 |
| Method | SSQ | SAD | MARE | EO | ET |
|---|---|---|---|---|---|
| HA (4PMM) | 45,225 | 998.24 | 0.794 | 0.111 | 0 |
| PSO (4PMM) | 55,124 | 1012.22 | 0.812 | 0.209 | 0 |
| BA (4PMM) | 47,224 | 1001.14 | 0.798 | 0.118 | 0 |
| HA (3PMM) | 48,225 | 1002.23 | 0.812 | 0.115 | 0 |
| PSO (3PMM) | 56,712 | 1014.45 | 0.867 | 0.288 | 0 |
| BA (3PMM) | 49,112 | 1009.23 | 0.724 | 0.202 | 0 |
| WA (3PMM) | 73,312 | 1037.25 | 0.994 | 0.488 | 0 |
| Population Size | Objective Function | Maximum Frequency (Hz) | Objective Function | Minimum Frequency (Hz) | Objective Function | Maximum Loudness (dB) | Objective Function | c1 | Objective Function | c2 | Objective Function | w | Objective Function |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 47,229 | 3 | 47,312 | 1 | 49,278 | 0.20 | 46,124 | 1.6 | 47,119 | 1.6 | 48,124 | 0.3 | 48,119 |
| 40 | 46,214 | 5 | 47,001 | 2 | 47,112 | 0.40 | 45,298 | 1.8 | 46,224 | 1.8 | 47,211 | 0.5 | 47,015 |
| 60 | 45,225 | 7 | 45,225 | 3 | 45,225 | 0.60 | 45,225 | 2.0 | 45,225 | 2.0 | 45,225 | 0.70 | 45,225 |
| 80 | 49,112 | 9 | 45,287 | 4 | 48,112 | 0.80 | 47,119 | 2.2 | 46,179 | 2.2 | 46,117 | 0.90 | 46,119 |
| Run Number | HA | PSO | BA |
|---|---|---|---|
| 1 | 45,225 | 55,124 | 47,224 |
| 2 | 45,226 | 55,124 | 47,226 |
| 3 | 45,225 | 55,127 | 47,224 |
| 4 | 45,225 | 55,124 | 47,224 |
| 5 | 45,225 | 55,124 | 47,224 |
| 6 | 45,225 | 55,124 | 47,224 |
| 7 | 45,225 | 55,124 | 47,224 |
| 8 | 45,225 | 55,124 | 47,224 |
| 9 | 45,225 | 55,124 | 47,224 |
| 10 | 45,225 | 55,124 | 47,224 |
| Average | 45,225 | 31113 | 47,224 |
| Computational time | 15 s | 17 s | 19 s |
| Variation coefficient | 0.000004 | 0.000006 | 0.00005 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ehteram, M.; Binti Othman, F.; Mundher Yaseen, Z.; Abdulmohsin Afan, H.; Falah Allawi, M.; Bt. Abdul Malek, M.; Najah Ahmed, A.; Shahid, S.; P. Singh, V.; El-Shafie, A. Improving the Muskingum Flood Routing Method Using a Hybrid of Particle Swarm Optimization and Bat Algorithm. Water 2018, 10, 807. https://doi.org/10.3390/w10060807
Ehteram M, Binti Othman F, Mundher Yaseen Z, Abdulmohsin Afan H, Falah Allawi M, Bt. Abdul Malek M, Najah Ahmed A, Shahid S, P. Singh V, El-Shafie A. Improving the Muskingum Flood Routing Method Using a Hybrid of Particle Swarm Optimization and Bat Algorithm. Water. 2018; 10(6):807. https://doi.org/10.3390/w10060807
Chicago/Turabian StyleEhteram, Mohammad, Faridah Binti Othman, Zaher Mundher Yaseen, Haitham Abdulmohsin Afan, Mohammed Falah Allawi, Marlinda Bt. Abdul Malek, Ali Najah Ahmed, Shamsuddin Shahid, Vijay P. Singh, and Ahmed El-Shafie. 2018. "Improving the Muskingum Flood Routing Method Using a Hybrid of Particle Swarm Optimization and Bat Algorithm" Water 10, no. 6: 807. https://doi.org/10.3390/w10060807
APA StyleEhteram, M., Binti Othman, F., Mundher Yaseen, Z., Abdulmohsin Afan, H., Falah Allawi, M., Bt. Abdul Malek, M., Najah Ahmed, A., Shahid, S., P. Singh, V., & El-Shafie, A. (2018). Improving the Muskingum Flood Routing Method Using a Hybrid of Particle Swarm Optimization and Bat Algorithm. Water, 10(6), 807. https://doi.org/10.3390/w10060807











