Trunk Network Rehabilitation for Resilience Improvement and Energy Recovery in Water Distribution Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Trunk Network
2.2. Resilience Index
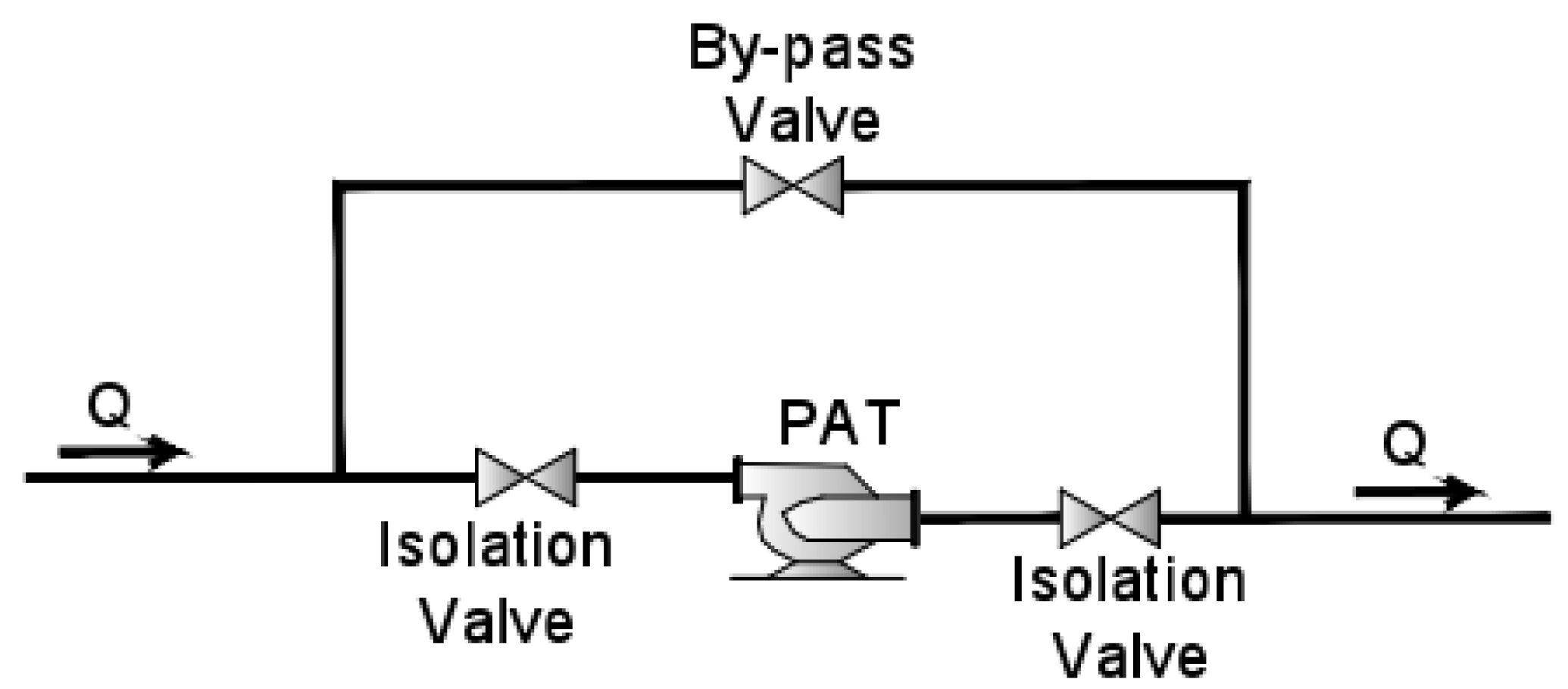
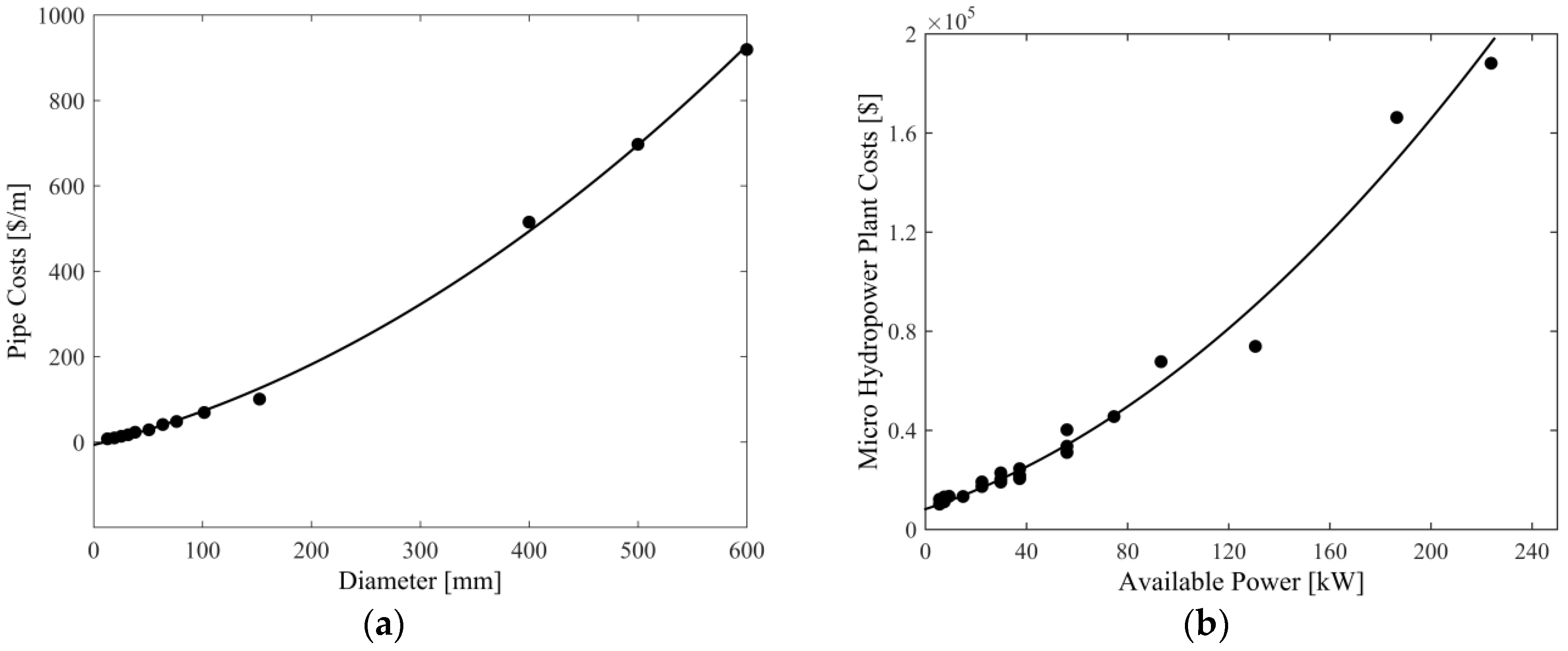
2.3. Trunk Network Design and Energy Recovery
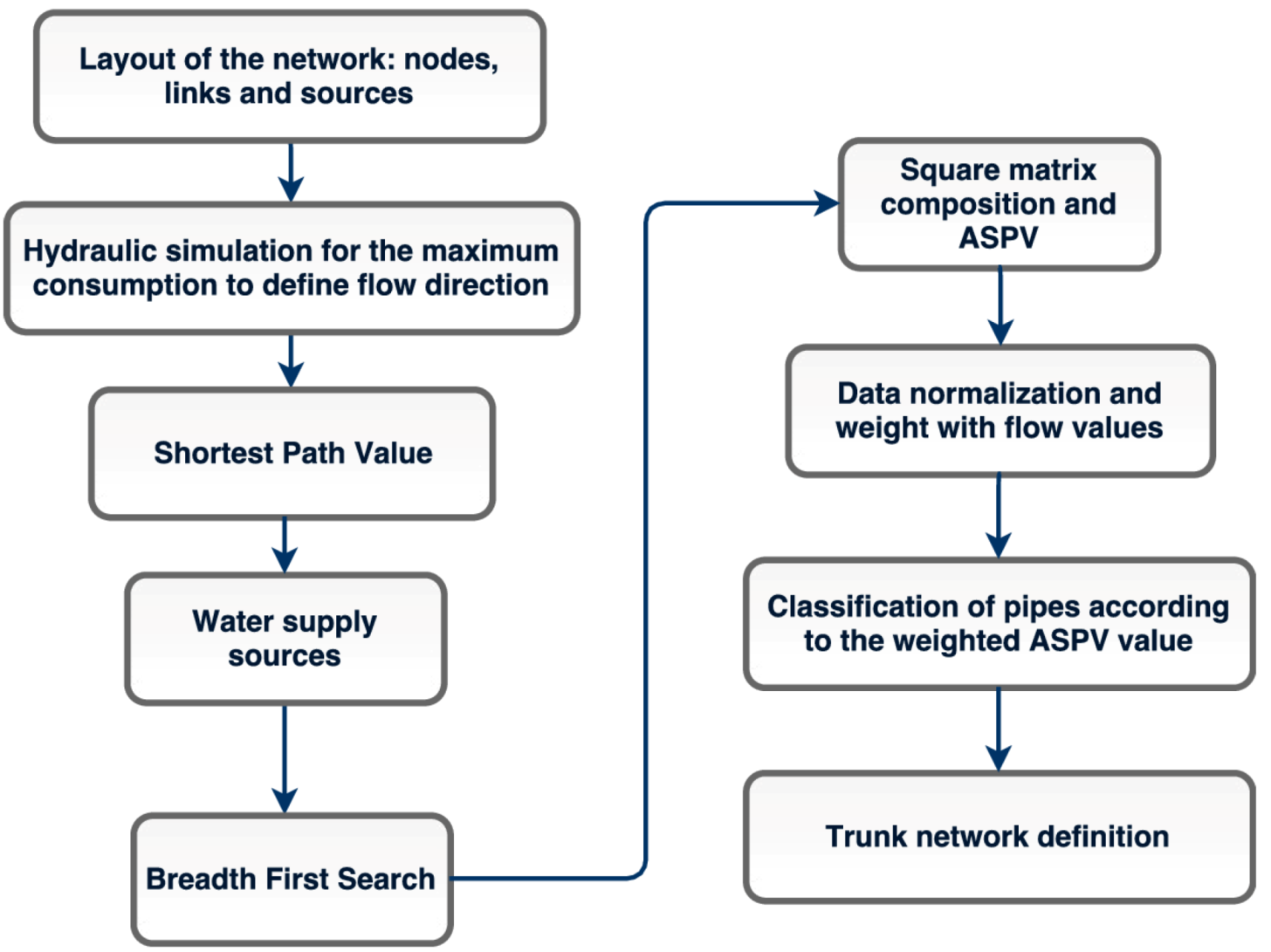
2.4. Optimization and TN Design Procedure
3. Results
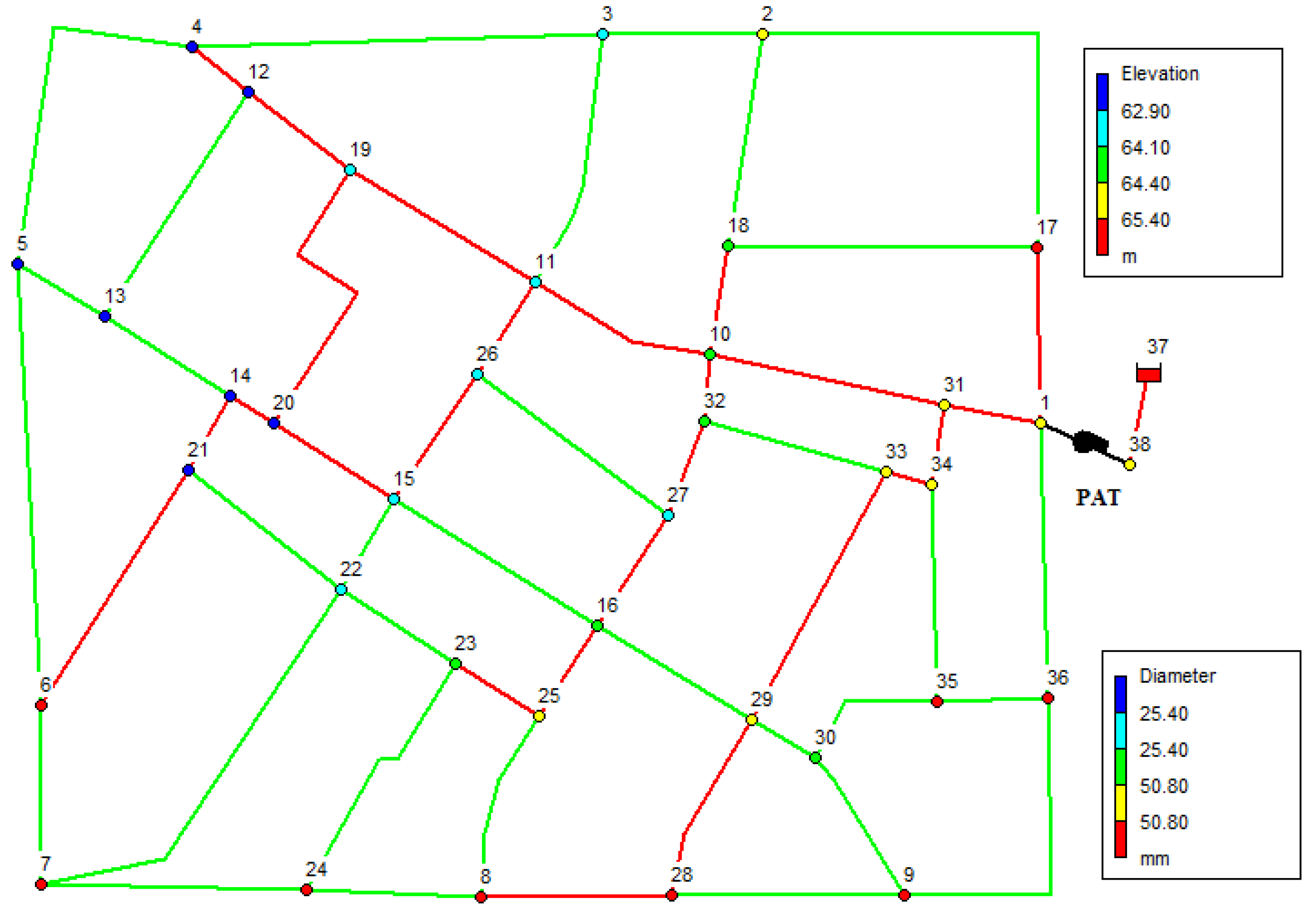
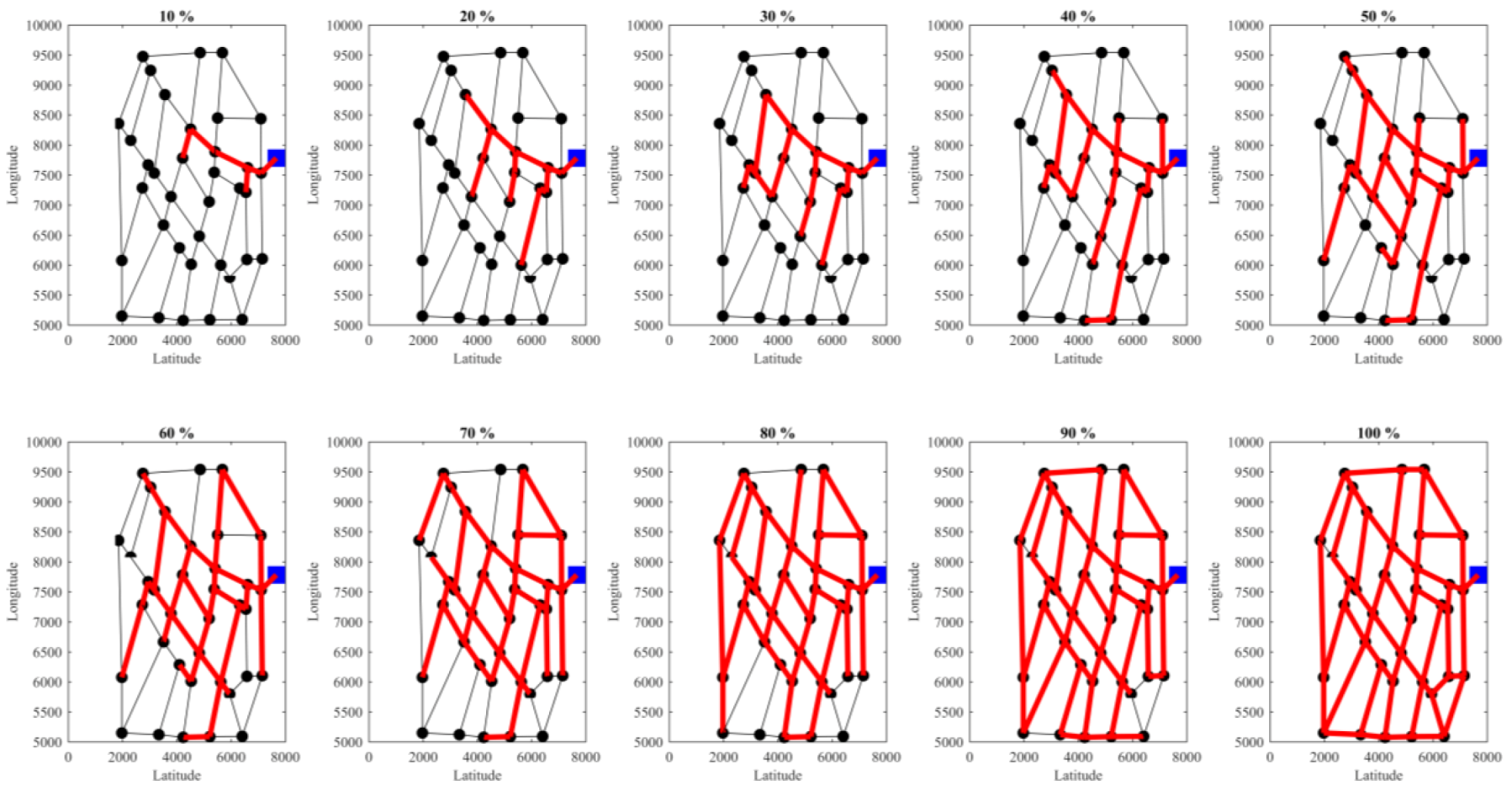
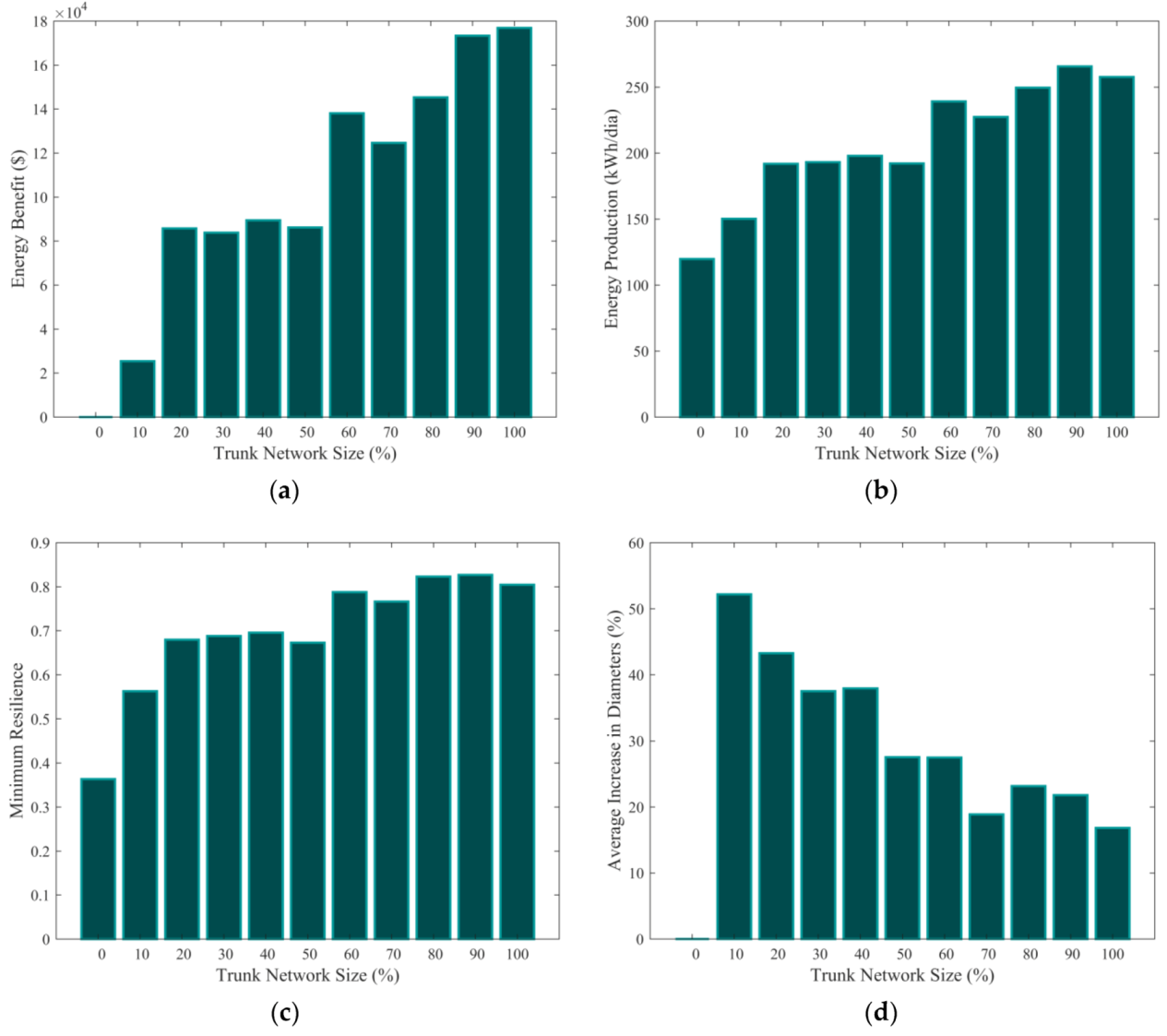
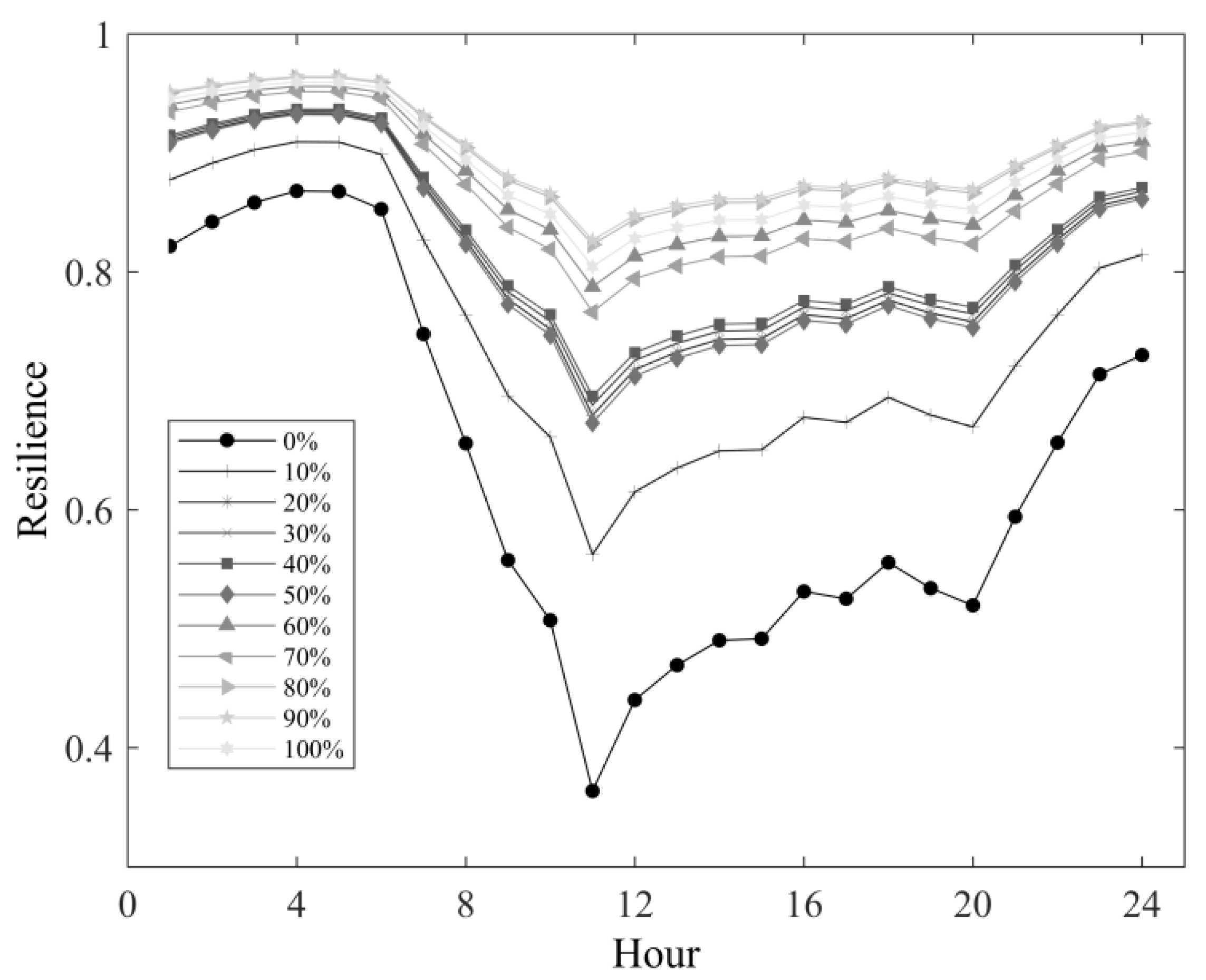
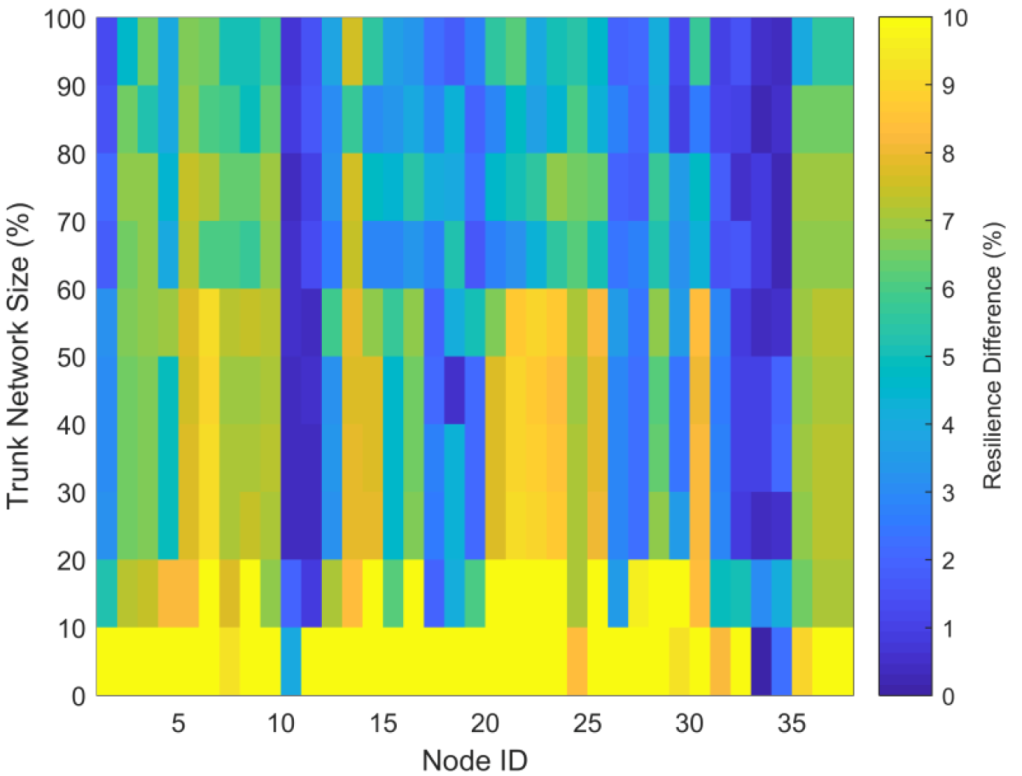
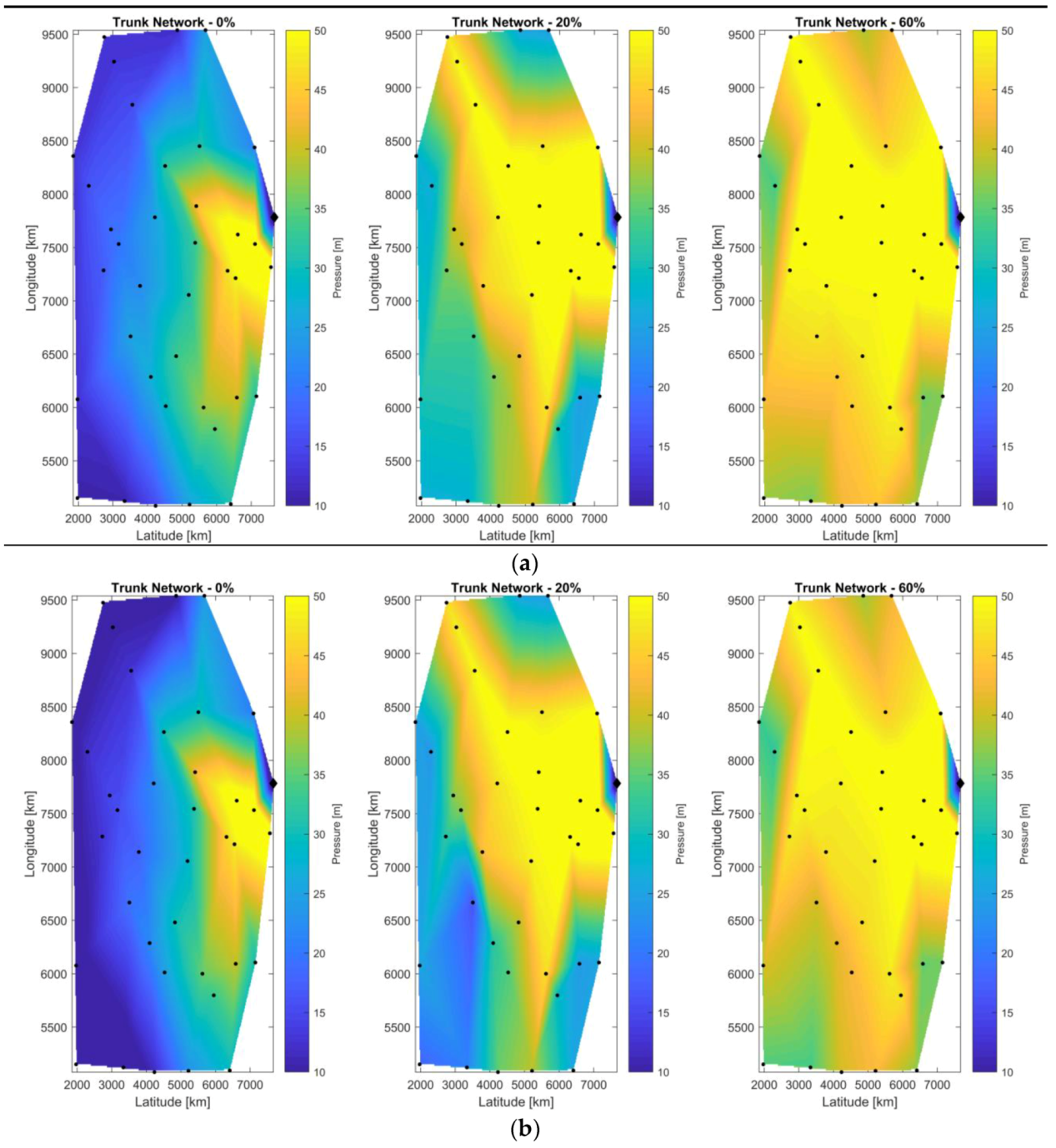
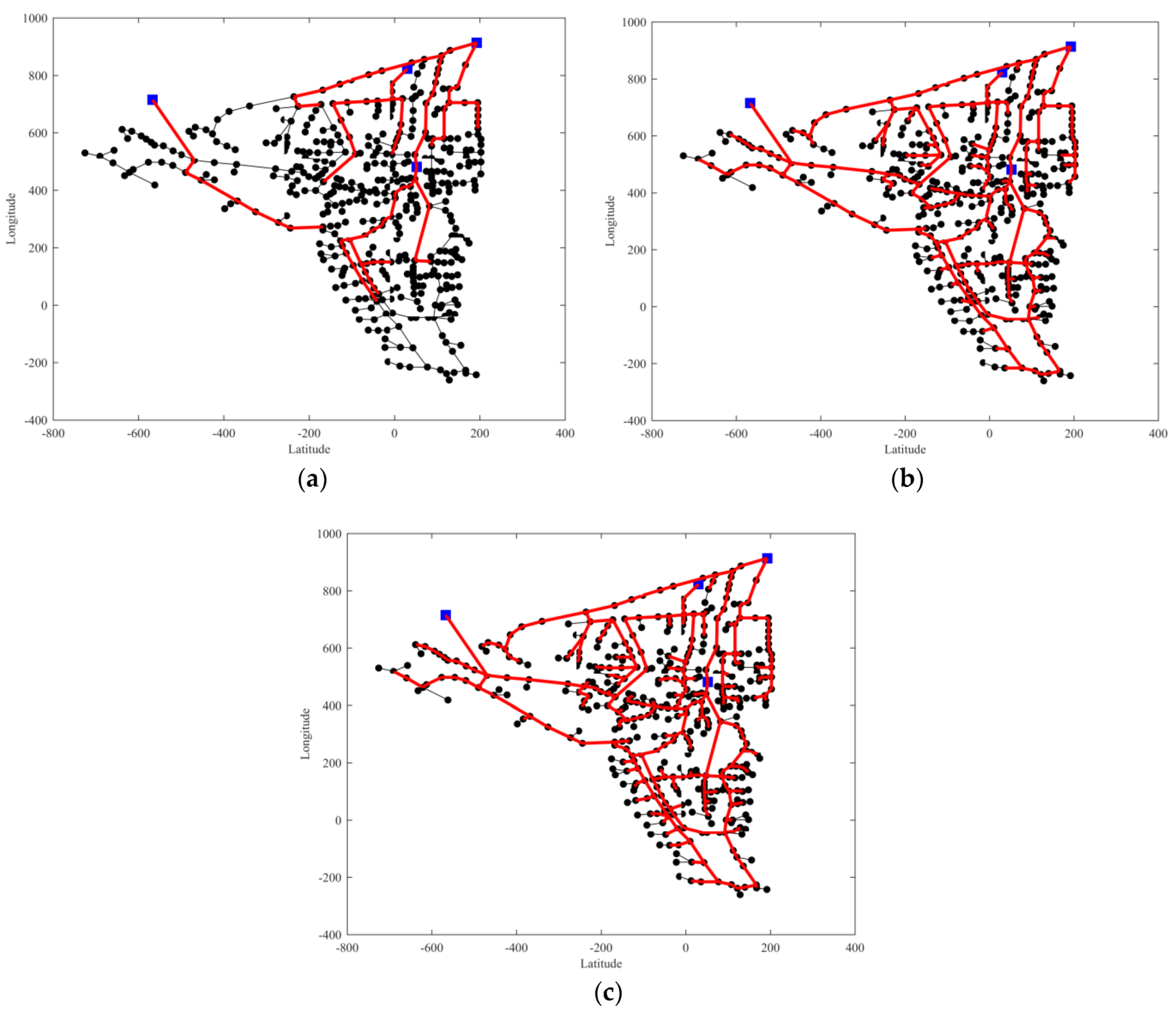
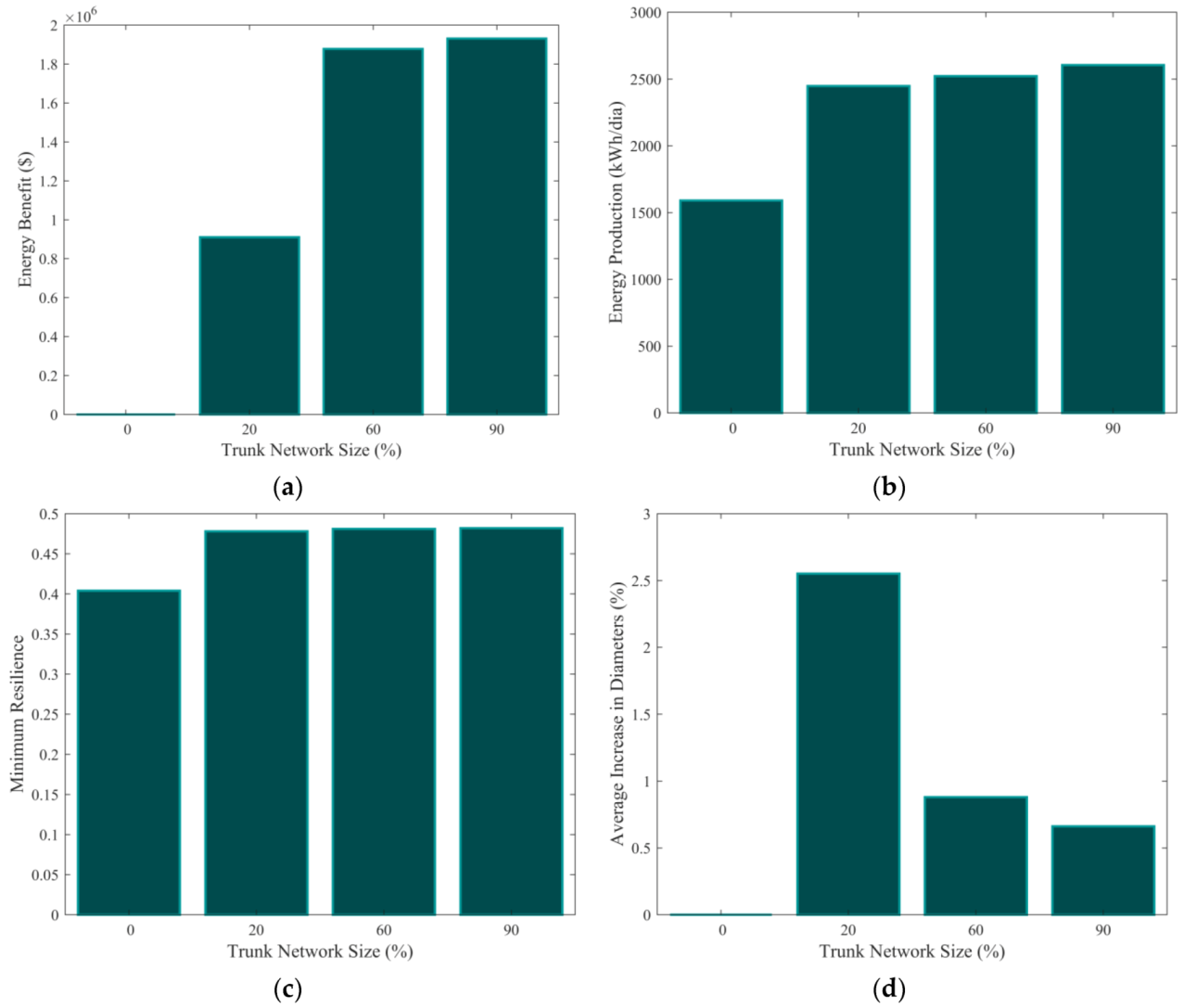
3.1. Fossolo Network
3.2. Balerma Irrigation Network
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Maier, H.R.; Simpson, A.R.; Zecchin, A.C.; Foong, W.K.; Phang, K.Y.; Seah, H.Y.; Tan, C.L. Ant colony optimization for design of water distribution systems. J. Water Res. Plan. Manag. 2003, 139, 200–209. [Google Scholar] [CrossRef]
- Suribabu, C.R.; Neelakantan, T.R. Design of water distribution networks using particle swarm optimization. Urban Water J. 2006, 3, 111–120. [Google Scholar] [CrossRef]
- Baños, R.; Reca, J.; Martínez, J.; Gil, C.; Márquez, A.L. Resilience indexes for water distribution network design: A performance analysis under demand uncertainty. Water Res. Manag. 2011, 25, 2351–2366. [Google Scholar] [CrossRef]
- Shokoohi, M.; Tabesh, M.; Nazif, S.; Dini, M. Water quality based multi-objective optimal design of water distribution systems. Water Res. Manag. 2017, 31, 93–108. [Google Scholar] [CrossRef]
- Marques, J.; Cunha, M.; Savić, D. Using real options in the optimal design of water distribution networks. J. Water Res. Plan. Manag. 2014, 141, 1–10. [Google Scholar] [CrossRef]
- Schwartz, R.; Housh, M.; Ostfeld, A. Least-Cost Robust Design Optimization of Water Distribution Systems under Multiple Loading. J. Water Res. Plan. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Giustolisi, O.; Laucelli, D.; Colombo, A.F. Deterministic versus stochastic design of water distribution networks. J. Water Res. Plan. Manag. 2009, 135, 117–127. [Google Scholar] [CrossRef]
- Lansey, K.E.; Duan, N.; Mays, L.W.; Tung, Y.K. Water distribution system design under uncertainties. J. Water Res. Plan. Manag. 1989, 115, 630–645. [Google Scholar] [CrossRef]
- Zheng, F.; Simpson, A.; Zecchin, A. Improving the efficiency of multi-objective evolutionary algorithms through decomposition: An application to water distribution network design. Environ. Model. Softw. 2015, 69, 240–252. [Google Scholar] [CrossRef]
- Geem, Z.W. Multiobjective optimization of water distribution networks using fuzzy theory and harmony search. Water 2015, 7, 3613–3625. [Google Scholar] [CrossRef]
- Prasad, T.D.; Park, N.S. Multiobjective genetic algorithms for design of water distribution networks. J. Water Res. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Ramos, H.M.; Borga, A.; Simão, M. New design solutions for low-power energy production in water pipe systems. Water Sci. Eng. 2009, 2, 69–84. [Google Scholar]
- Carravetta, A.; Houreh, S.D.; Ramos, H.M. Pumps as Turbines: Fundamentals and Applications, 1st ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Energy recovery in existing water networks: Towards greater sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- De Marchis, M.; Freni, G. Pump as turbine implementation in a dynamic numerical model: cost analysis for energy recovery in water distribution network. J. Hydroinform. 2015, 17, 347–360. [Google Scholar] [CrossRef]
- Carravetta, A.; del Giudice, G.; Fecarotta, O.; Ramos, H.M. PAT design strategy for energy recovery in water distribution networks by electrical regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Meirelles, G., Jr.; Luvizotto, E.; Brentan, B.M.; Ramos, H.M. Leakage Control and Energy Recovery Using Variable Speed Pumps as Turbines. J. Water Res. Plan. Manag. 2017, 144. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. Energy production in water distribution networks: A PAT design strategy. Water Res. Manag. 2012, 26, 3947–3959. [Google Scholar] [CrossRef]
- Lydon, T.; Coughlan, P.; McNabola, A. Pump-as-turbine: Characterization as an energy recovery device for the water distribution network. J. Hydraul. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Afshar, A.; Jemaa, F.B.; Marino, M.A. Optimization of hydropower plant integration in water supply system. J. Water Res. Plan. Manag. 1990, 116, 665–675. [Google Scholar] [CrossRef]
- Meirelles, G.; Brentan, B.M., Jr.; Luvizotto, E. Optimal design of water supply networks using an energy recovery approach. Renew. Energy 2018, 117, 404–413. [Google Scholar] [CrossRef]
- Campbell, E.; Izquierdo, J.; Montalvo, I.; Ilaya-Ayza, A.; Pérez-García, R.; Tavera, M. A flexible methodology to sectorize water supply networks based on social network theory concepts and multi-objective optimization. J. Hydroinform. 2016, 18, 62–76. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Complex network and fractal theory for the assessment of water distribution network resilience to pipe failures. Water Sci. Technol. Water Supply 2018, 18, 767–777. [Google Scholar] [CrossRef]
- Bragalli, C.; D'Ambrosio, C.; Lee, J.; Lodi, A.; Toth, P. On the optimal design of water distribution networks: A practical MINLP approach. Optim. Eng. 2012, 13, 219–246. [Google Scholar] [CrossRef]
- Reca, J.; Martínez, J. Genetic algorithms for the design of looped irrigation water distribution networks. Water Resour. Res. 2006, 42, 1–9. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Tzatchkov, V.G.; Alcocer-Yamanaka, V.H. Water network sectorization based on graph theory and energy performance indices. J. Water Resour. Plan. Manag. 2013, 140, 620–629. [Google Scholar] [CrossRef]
- Hajebi, S.; Temate, S.; Barrett, S.; Clarke, A.; Clarke, S. Water distribution network sectorisation using structural graph partitioning and multi-objective optimization. Proc. Eng. 2014, 89, 1144–1151. [Google Scholar] [CrossRef]
- Moore, E.F. The Shortest Path through a Maze; Part II: The Annals of the Computation Laboratory of Harvard University Volume XXX; Harvard University Press: Cambridge, MA, USA, 1959; pp. 285–292. [Google Scholar]
- Todini, E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, 1995 (MHS ’95), Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Brentan, B.M.; Campbell, E.; Meirelles, G.L.; Luvizotto, E.; Izquierdo, J. Social Network Community Detection for DMA Creation: Criteria Analysis through Multilevel Optimization. Math. Probl. Eng. 2017, 2017. [Google Scholar] [CrossRef]
- Meirelles, G., Jr.; Luvizotto, E.; Brentan, B.M. Selection and location of Pumps as Turbines substituting pressure reducing valves. Renew. Energy 2017, 109, 392–405. [Google Scholar]
- Letting, L.K.; Hamam, Y.; Abu-Mahfouz, A.M. Estimation of Water Demand in Water Distribution Systems Using Particle Swarm Optimization. Water 2017, 9, 593. [Google Scholar] [CrossRef]
- Rossman, A.L. EPANET 2.0 User’s Manual; EPA/600/R-00/057; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2000.
- ABNT–Brazilian Association of Technical Standards. Project of Water Distribution Network for Public Supply; NBR 12218; ABNT–Brazilian Association of Technical Standards: Rio de Janeiro, Brazil, 1994. (In Portuguese) [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meirelles, G.; Brentan, B.; Izquierdo, J.; Ramos, H.; Luvizotto, E., Jr. Trunk Network Rehabilitation for Resilience Improvement and Energy Recovery in Water Distribution Networks. Water 2018, 10, 693. https://doi.org/10.3390/w10060693
Meirelles G, Brentan B, Izquierdo J, Ramos H, Luvizotto E Jr. Trunk Network Rehabilitation for Resilience Improvement and Energy Recovery in Water Distribution Networks. Water. 2018; 10(6):693. https://doi.org/10.3390/w10060693
Chicago/Turabian StyleMeirelles, Gustavo, Bruno Brentan, Joaquín Izquierdo, Helena Ramos, and Edevar Luvizotto, Jr. 2018. "Trunk Network Rehabilitation for Resilience Improvement and Energy Recovery in Water Distribution Networks" Water 10, no. 6: 693. https://doi.org/10.3390/w10060693
APA StyleMeirelles, G., Brentan, B., Izquierdo, J., Ramos, H., & Luvizotto, E., Jr. (2018). Trunk Network Rehabilitation for Resilience Improvement and Energy Recovery in Water Distribution Networks. Water, 10(6), 693. https://doi.org/10.3390/w10060693








