Abstract
The outer banks of meadow-type meandering river bends in the source zone of the Yellow River are especially vulnerable to bank failure. This study aims to understand how vegetation affects bank stability and the mechanism of bank failure, especially via a prediction of the width of a collapsed block of small rivers through a proposed bank stability equilibrium as well as field sampling. Soil and vegetation properties were surveyed at four sites near the riverbank in 2013–2016. It was found that the failed blocks had, on average, a dimension of 0.865 m (width) by 0.817 m (thickness) by 2.228 m (length). The variability in the size of all the failed blocks was attributed predominantly to the roots of plants. Block thickness could be logarithmically predicted by root length at R2 ≥ 0.76. The block width predicted from the proposed equilibrium equation deviated from in situ measurements by approximately 22.1%, a discrepancy highly subject to the overestimation of root reinforcement using Wu’s model. By reducing the coefficient of Wu’s model from 1.2 to 0.85, the proposed equilibrium equation was reliable to predict the width of bank collapse. However, its applicability to other study areas needs to be verified in further studies.
1. Introduction
A complex interplay exists between bank failure and riparian vegetation in meandering rivers. Riparian vegetation improves the stability of riverbanks by increasing the shear strength of the soil and armoring the bank [1,2,3,4,5,6]. The mechanical effects are largely beneficial; however, the height and weight of vegetation can negatively impact bank stability, particularly mature or large trees [7]. Plant roots enhance bank substrate strength, thereby helping restrain banks from mass failure. The root system can enhance bank stability [8], and the stability factor of the riverbank by about 60% [9]. Thus, riparian vegetation plays a key role in determining bank failure patterns and reducing the frequency of bank collapse [10,11,12]. Because the proportion of channel width and bank erosion of small meandering rivers is greater than those of large rivers, it is especially important to study how and by how much riparian vegetation protects bank stability in small meandering rivers by increasing bank strength. This can be achieved through a prediction of the width of a collapsed block of small rivers through a proposed bank stability equilibrium and field sampling.
As many concave banks are composed of multiple layers of deposits, the mechanism and rates of bank failure are likely to vary according to both the type of deposit materials and riparian vegetative cover. Previous studies have analyzed the stability of cohesive sediments in a riverbank [1,13,14,15,16]. The most critical cause of cohesive bank collapse is a steepening of the concave bank, which can result from lateral erosion [17,18]. Indeed, any factor that steepens the bank or increases the height of a riverbank is likely to increase its instability. For instance, if a bank exceeds a critical height threshold, its upper parts are no longer supported and can topple over (e.g., slump or fall). For example, a channel bank acts as an overhanging wall, which often comprises an unsupported hillslope, from which the removal of supporting toe sediments induces bank failure [8].
The failure of composite banks (i.e., cohesive, suspended load materials in the upper layer, overlying non-cohesive (bedload) deposits in lower layers) has been studied extensively [19,20] and, in particular, the patterns and mechanisms of composite bank failure have been studied quantitatively [1,16,18,21]. Thorne and Tovey differentiated three collapse patterns of two-layered (composite) banks: Shear failure, beam failure, and tensile failure [1]. Fukuoka identified three stages in the erosion of natural banks [22]: Erosion of noncohesive sediments in the lower layer, collapse of the overhanging deposit in the upper cohesive layer, and the breakup and transport of the collapsed soil mass. If the erosion width exceeds a certain threshold, the cantilever failure occurs under the weight of the overhanging material [23]. Bank slope stability can be studied using the Bank Stability and Toe Erosion Model (BSTEM), which was proposed and modified by Pollen-Bankhead and Simon [24] and Simon and Collison [25]. This model can be used not only to simulate the stability of the riverbank and the dynamics of different layers but also to estimate the amount of erosion according to riverbank material composition and slope geometry [4]. This model is limited in that its performance depends on the precise definition of several river channel parameters that are not easily obtained accurately, such as the soil boundary shear stress of the riverbank, collapse angle, and the variation of water level. Thus, new models are needed to predict the properties of slope failure.
Despite recent efforts to explain the mechanism and process of bank failure, many issues surrounding the manner and rate of small meandering riverbank failure still require in-depth investigation [4,26]. In contrast to large meandering rivers, in which riverbank collapse occurs primarily by shear failure because of bank toe scour, the mechanism of meadow-type meandering riverbank collapse is largely attributable to tensile failure; this can result from basal erosion at the toe of the bank, in which plants roots play an important role. To date, no study has examined how the morphological and mechanical characteristics of the root system through the failure plane affects the dimension of the failure blocks; simultaneously, how the soil-root composite of riparian vegetation affects the morphology of cantilever, outer bank failures of meandering rivers has not been clearly revealed. This study aims to overcome these deficiencies by developing initial insights into the failure process and the interrelationships between plant roots and bank failure through field investigations and a proposed equilibrium equation. This study has three objectives: (1) To explore the properties (e.g., mechanical strength) of riparian vegetation roots and the soil-root composite; (2) to assess the physical dimension of the failed blocks and its relationship with plant root properties; and (3) to propose and test an equilibrium equation for predicting the width of failure blocks for a small meadow-type meandering river at upstream parts of the Yellow River.
2. Study Area
The meandering river under consideration is the Lanmucuo River, a small tributary of the Yellow River Source Zone, approximately 50 km southeast of the Henan County Town in the Huangnan Tibetan Autonomous Prefecture, Qinghai Province, on the Qinghai-Tibet Plateau (Figure 1a). A 5 km stretch of the river located on the open, flat plateau (34°24.317′ N–34°26.695′ N; 101°25.807′ E–101°29.444′ E) was selected for this study (Figure 1b). It drains a catchment of about 80 km2 in size. The river channel lies at an elevation of 3400–4200 m.a.s.l. with a mean channel gradient of 0.19%. This area has a plateau, periglacial humid climate with a mean annual temperature of −4 °C. It has two distinct seasons, a warm and rainy season from May to October and a cold, dry, and windy season from November to April. Mean annual precipitation is 329–560 mm, only a fraction of the mean annual evaporation of 1278 mm [27]. The vegetation of the area is predominantly alpine meadow and alpine grassland meadows [28]. These meadows comprise perennial Cyperaceae plants, Gramineae plants, forbs, and a small variety of shrubs. Soil type is alpine meadow soil, while swamp meadow soil is also common. Soil layer is thin with a coarse texture, and the soil organic matter is predominantly distributed in the surface layer.
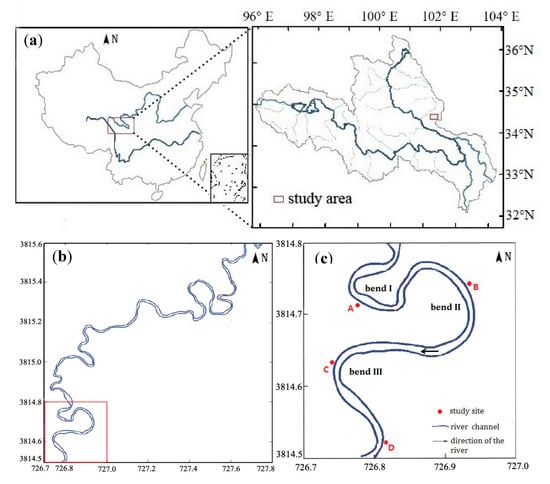
Figure 1.
Location of the Lanmucuo River and its highly sinuous bends. (a) location of the study site; (b) the channel stretch within which bank failures were inspected and measured; (c) A, B, C, and D: sites from where soil samples were collected and in situ soil and root properties tests were carried out.
Numerous tributary meandering rivers in the source zone of the Yellow River are characterized by regular, highly sinuous (tortuous) bends. The outer bank of the meadow-type meandering river has a composite structure, with fine sediments at the top and coarse sediments at the bottom. The upper layer is composed of soils and roots of meadow vegetation, with densely tangled roots concentrated at 0–60 cm beneath the surface (Figure 2a). The cohesive upper layer is more resistant to erosion than the non-cohesive lower layer, which is made up of sand and gravel (Figure 2a). The upper layer produces a cantilever because of the different erosion rates of the upper and lower bank by fluvial entrainment. The steep riverbank tensile failure under the effect of its own weight can cause the soil-root block to topple (e.g., slump) near the riverbank. Because of the varying stages of the failure process, the blocks were divided into two types, namely critical blocks and slump blocks. The former refers to the separation of the block from the bank by longitudinal riparian cracks; the block does not topple and is not completely destroyed but lies in a critical condition (Figure 2b). The latter refers to the failed block onto the riverbed (Figure 2b). The outer bank of the Lanmucuo River is prone to failure because of the strong destabilization factors attributable to sand and gravel deposits resulting from channel flow, which stem from the high sinuosity in this stretch of the channel. The vegetation is predominantly composed of perennial (cold climate) mesophyte herbs, often accompanied by mesophyte perennial forbs found in the study area. A wide variety of plants include Cyperaceae, Gramineae, and forb. Predominant species found include: Blysmus sinocompressus, Poa annua, Elymus nutans, Kobresia capillifolia, Kobresia tibetica, Carex moorcroftii, Potentilla fruticosa, Potentilla glabra, Hippophae thibetana, Polygonum viviparum, Ligularia virgaurea, Nardostachys chinensis, and Geranium pylzowianum.

Figure 2.
The outer bank of the meandering bend. (a) The exposed soil-root layer after bank failure; (b) the cantilever slump blocks and critical blocks.
3. Methods
3.1. Field Sample Collection
Over the 5 km stretch of the channel, all failed blocks were identified by their type in the field (Figure 1b). Their three dimensions and root length were measured with a tape to an accuracy of 0.1 cm. To characterize the field site, the hydraulic parameters included water depth, velocity, and channel width and were measured with tape, box staff, and current meter at 5 km stretches of the channel in July of 2015. In addition, the measurements of root diameters, root numbers, and root tensile strength of Blysmus sinocompressus, etc. were performed at the recently collapsed outer bank profile of three typical bends in 2015 (Figure 1c). The collapsed slump blocks near the bank (Figure 2) provided exposed the plant roots, providing an ideal setting for studying the impact of plant roots on bank failure. Measurements of root diameters and root numbers were performed at four sites (two in one bend) within a collapsed surface of 20 cm × 20 cm in each of the three bends (Figure 1c). The collapsed surface of 20 cm × 20 cm initially was divided into 100 small plots of 2 cm × 2 cm by strings; subsequently, root diameters were measured in situ using a vernier caliper to an accuracy of 0.02 mm in every small spot. Roots passing through the collapsed surface were also measured. Simultaneously, root numbers were counted in every small spot. In addition, the number of exposed roots within the sampling surface was tallied to calculate the root area ratio.
Soil samples were also collected at each of the four sites. These samples were used to determine soil density and soil moisture content. After the root diameter was measured in situ using a vernier caliper, a pulling test was carried out on the single plant root passing through the collapsed surface. Root tensile strength was measured in situ using the HF-2K-type digital push-pull dynamometer (Leqing Aidebao Instruments Co. Ltd., Leqing, China). The measurement was performed on the roots of Blysmus sinocompressus, the dominant plant in the collapsed riparian block in the study area.
At these bends, the channel width ranged from 8 m to 12 m. At each bend, the properties of plants and their roots were studied along a longitudinal distance of approximately 80–120 m on the riverbank. They included plant height, coverage, and proportion as well as the diameter of plant roots and root length. Both aboveground plants and their roots were sampled at three randomly selected plots at each of the bends (Figure 1c). First, the aboveground plants within the sampling plot of 50 cm × 50 cm in size were surveyed to determine vegetation type, coverage, proportion, and height. Plant coverage refers to the ratio of the perpendicular projection area of aboveground plants to the sample. The adopted method was the eyeball method. To facilitate the measurements, every sampling plot was divide into 25 small plots of 10 cm × 10 cm with string. The main plant coverage in each sample was counted. In this study, plant proportion was the ratio of total coverage to coverage by all species. The natural height of plant was plant height, which was measured by tape as the distance between ground surface to the top of the stem.
The soil at the same location was sampled within a smaller plot of 10 cm × 10 cm using a ring sampler 5–15 cm below the surface. Because all plant roots were also collected, they were commonly referred to as soil-root samples. Sampling was replicated three times at each location. Samples were brought back to the laboratory for additional analysis. To determine the properties of the plant roots, all plants which were 10 cm in diameter by 6.37 cm in depth within the ring sampler were gently dug out of the ground using a small shovel. After the soil had been removed from the samples, root properties including root number, root branches, and length were counted or measured using a ruler. At selected sampling points of the four study sites, 500–800 g sediment was removed with a shovel within the range of 5–15 cm on the surface; the removed sediment was labelled and put into a bag and brought back to the laboratory for a soil particle gradation test. Additionally, samples of both the cantilever slump blocks and the river bed were taken for a grain size distribution test. The manual sieving method was used for materials coarser than 2 mm; particles smaller than 2 mm were measured using a Mastersizer 2000 (Malvern Panalytical, Malvern, UK).
3.2. Laboratory Analysis
The shear strength of the soil without roots was determined by the indoor remodelling method [29], in which the soil sample was provided the same moisture and density as the in situ soil. Measurement was conducted using the ZJ strain controlled electric direct shear device (Nanjing Soil Instrument Factory Co., Ltd., Nanjing, China) connected to a computer. Its geotechnical test software could automatically yield the results. After the soil-root samples were naturally dried, the roots contained in each ring sampler were weighed, and the density of the composite soil-root and the roots was calculated. Water content of the soil was determined by calculating the weight difference of the soil samples before and after oven-drying.
4. Theoretical Foundations
The outer bank of the river bends comprise two layers (the soil-root composite and the sandy layers) (Figure 3) [18]. As a result of lateral scour of the sandy layer, the slump block fails. Under the assumption that the critical block is nearly cubically shaped, the moment balance equation for critical tensile failure can be expressed in Equation (1) [30] based on the force of the unit length critical block.
where d1 and d2 are the vertical thickness of the soil-root composite and the transitional sandy block, respectively; bc refers to the width of the collapsed block; G1 and G2 are the self-weight of the soil-root composite and sand layer, respectively. They are calculated as:
where , and are the density of the soil-root composite, the sand layer, and water, respectively; g is the gravitational acceleration.
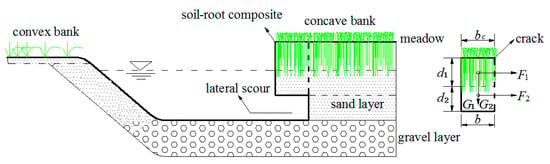
Figure 3.
A schematic diagram illustrating the failure of the outer bank as a slump block in the presence of plant roots (green) (refer to section 4 for the meaning of the symbols).
F1 and F2 in Equation (1) are the critical shear strength of the soil-root composite and the maximum cohesion of the transitional sandy layer, respectively. (c2 is the cohesion of the sandy layer that can be determined through shear strength tests of the field samples).
in which S0 is the shear strength of the soil without roots; represents the reinforced shear strength caused by the roots traversing through the collapsed surface. If most of the roots have reached their critical tensile strength, the entire undermined block will collapse, which follows the assumption that the root surface of the collapsed site bears enough friction and binding force and that it has enough anchoring length to protect the root from being pulled out. According to the root reinforcement model proposed by Wu et al. [31], ΔS1 can be approximated as
in which TN is the average tensile strength of roots in unit soil, which is also called the root area ratio, Ar/As is the ratio of the sum of the cross-sectional area of the roots on the collapsed surface to the collapsed area.
After the expressions of G1, G2, F1 and F2 are plugged into Equation (1), it is transformed to the following form:
After simplification of Equation (6), the critical shear strength of the soil-root composite F1 can be expressed as:
The equilibrium function f of the critical tensile strength of the meandering river outer bank at any moment can be expressed as:
Equation (8) is transformed to Equation (9) after all the relevant terms are plugged into it.
After simplification Equation (9) becomes:
in which g, ρ1, ρ2, and ρw have been determined from an analysis of the in situ collected soil samples; S0, TN, and Ar vary with soil structure and plant species on the failed surface, which can be measured in situ; As, d1, d2, and bc can also be measured in the field. d2 = 0 when water scour reaches the soil-root composite. In this case, Equation (10) can be further simplified as follows:
If the equilibrium is tipped (e.g., the soil-root block slumps, and f = 0), bc can be obtained from Equation (11) as follows:
The derivation of Equation (12) ignores coarse sands and pebbles in the lower soil-root composite layer near the bank. Most of these materials can erode completely or to a very thin layer in case of bank failure; accordingly, it is reasonable to ignore their self-weight and cohesion.
5. Results
5.1. Characteristics of Vegetation, Its Roots, Soil, and River
The alpine meadows in the Yellow River Source Zone are predominantly composed of perennial (cold climate) mesophyte herbs, often accompanied with mesophyte perennial forbs. A wide variety of plant species, such as Cyperaceae, Gramineae, and Kobresia, are distributed in the outer bank of the river. They are perennial herbs and 0.17 m in mean height. These plants have a variable dominance in the bank; the dominant species is Blysmus sinocompressus (16%–20%), followed by Kobresia capillifolia at 11%–14%. The third most dominant plants are Kobresia tibetica at 8%–10% (Table 1). In comparison to the three most dominant species, all others are significantly less abundant (e.g., less than 10%). Their maximum height is approximately 0.50 m; however, many species are dwarf plants, which are lower than 0.20 m. All herbaceous plants have well-developed roots and a strong capacity of propagation and competition [32].

Table 1.
Characteristics of aboveground riparian vegetation in the outer bank.
Root lengths for riparian vegetation range from 20 cm to 110 cm. Plant roots can adhere to the rhizome type with nodes, such as the roots of the dominant plant Blysmus sinocompressus. Rhizomes can be dense and short (e.g., the roots of Cyperaceae, Gramineae, and Kobresia species). Additionally, some plants have developed cross branch roots, such as Potentilla fruticosa and Carex moorcroftii. These dense, thin roots have a diameter that is less than 3 mm (Table 1). For instance, the average root diameter of Poa annua, Kobresia tibetica, and Blysmus sinocompressus is considerably small. On the other hand, such shrubs as Potentilla fruticosa and Hippophae thibetana have a relatively large diameter. Their roots are shorter than 1 m in length, with a common average length of 0.55 m; however, non-herbaceous plants do not have well-developed roots. with lengths shorter than 0.22 m. Root length of shrubs such as Potentilla fruticosa and Potentilla glabra is considerably longer than that of other plants.
Spatially, the plant roots exhibited a widely variable diameter across the four sample sites, from 0.58 mm at site A to 1.16 mm at site D (Table 2). On average, the mean diameter was 0.82 ± 0.25 mm. Such a wide variation contributed to a high variability of root tensile strength. The physical dimension of a root is related closely to its tensile strength. The tensile strength of roots in the four sites varied from 13,530 kPa at site D to 15,480 kPa at site A, with an average of 14,792 kPa. Root tensile strength is closely but inversely correlated to root diameter Droot (Figure 4). This relationship can be expressed as:
Tensile strength (kPa) = 12521Droot−1.297 (R2 = 0.713)

Table 2.
Physical parameters of soil-root composite (SRC), soil, and roots in the undisturbed samples.
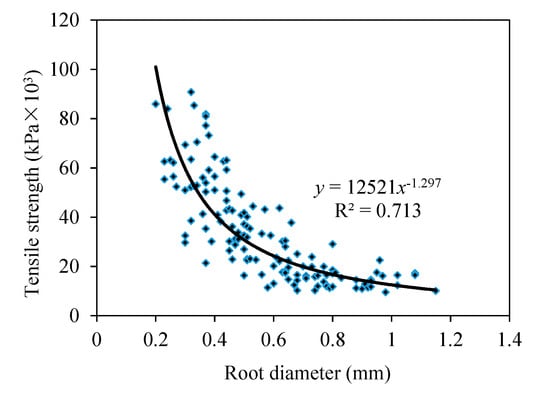
Figure 4.
Relationship between root tensile strength and root diameter of Blysmus sinocompressus Tang et Wang.
Thus, if the average diameter of plant roots is larger, such as Potentilla fruticosa and Hippophae thibetana, its tensile strength is lower. In contrast, the average shear strength of the soil is low, with a small variation from 3.41 kPa to 5.03 kPa (mean = 4.11 ± 0.58 kPa). The composition of soil particles was similar at the four sites (Table 2); accordingly, the soil shear strength was similar.
The mean water depth of these small meandering river in the study area was 0.59 m, and the mean channel width was 7.6 m. The velocity ranged from 0.6 m∙s−1 to 1.9 m∙s−1 (Table 3).

Table 3.
Hydraulic parameters and morphological parameters of the study area.
5.2. Impact of Plant Roots on Bank Failure
A total of 63 slump blocks were observed in the 5 km stretch of the Lanmucuo River (Table 4). The in situ measured width of the slump blocks ranged from 0.40 to 1.30 m, with an average of 0.865 ± 0.06 m. Length ranged from 1.00 to 6.30 m, with a mean of 2.228 ± 0.15 m. Blocks were considerably thick (mean thickness = 0.817 ± 0.10 m). In comparison, critical blocks exhibited a marginally smaller dimension. They measured, on average, 2.053 ± 1.33 m long, 0.799 ± 0.26 m wide, and 0.699 ± 0.18 m thick. Thus, both width and thickness were very close to each other, but they were both much lower than block length. The three dimensions of a block are related, i.e., a longer block is also wider and thicker (Figure 5). The correlation can be as high as (r = 0.537, R2 = 0.289) between the length and width of critical blocks. However, the correlation is slightly looser for slump blocks (r = 0.531, R2 = 0.282 with a linear relationship); R-squared values showed a lack of correlation between the length and width of collapsed blocks.

Table 4.
In situ measured average dimensions of failed blocks by failure manner in comparison with root length.
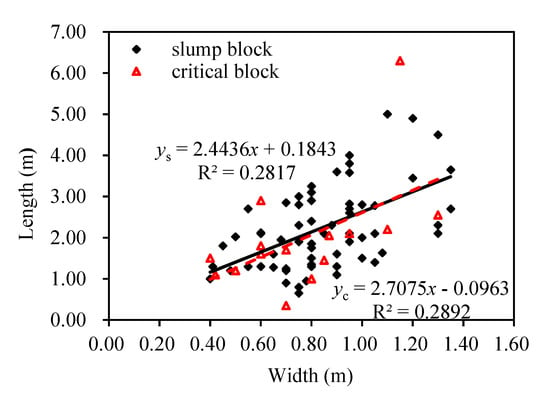
Figure 5.
Relationship between width and corresponding length of slump and critical blocks.
The aforementioned morphological properties of both slump and critical blocks are closely associated to their root properties (Figure 6). For instance, the width of the slump blocks increases with root length (Figure 6a). The longer the roots, the wider the slump blocks. The root length Lr of both slump and critical blocks was in good agreement with the thickness d1 of the failed blocks after natural logarithmic transformation (Figure 6b). This relationship can be expressed as Equation (13) for slump blocks and Equation (14) for critical blocks:
d1 = 0.4965 lnLr + 1.1816 (R2 = 0.892, n = 63)
d1 = 0.4637 lnLr + 1.1342 (R2 = 0.757, n = 15)
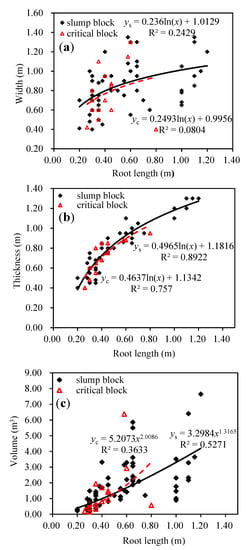
Figure 6.
Relationship between root length and corresponding dimensions and volume of failed blocks. (a) block width; (b) block thickness; and (c) block volume.
As shown in Figure 6c, the volume of the slump blocks is correlated exponentially with root length. This relationship can be expressed as:
Vols = 0.3298 Lr1.3165 (R2 = 0.527)
This correlation (r = 0.726, R2 = 0.5271) derived for the slump blocks is closer than that for the critical blocks (r = 0.603, R2 = 0.3633), like attributable to the role of plant roots. However, this relationship does suggest that the volume of the failed blocks is associated with the root length of riparian vegetation. It demonstrates that the root system of the soil-root composite has a strong reinforcing and binding effect on vertical bank deposits.
5.3. Predicted Width of the Failed Blocks
The figures in Table 4 were used to predict the width (bc) of the failed blocks using Equation (12) that has been transformed to Equation (17) after the root area ratio Ar/As was expressed in terms of root diameter.
where di is the diameter of root i; n stands for the total number of roots on a collapsed surface (0.20 m × 0.20 m in size); the root area ratio Ar/As of the study area ranges from 0.11% to 0.13% with an average of 0.12% (Table 2, column 7); d1 is the thickness of the collapsed block at the four study sites. It was measured at 0.65–1.22 m from the field samples; the average d1 was calculated from weighted averaging of the thickness of both critical and slump blocks (Table 4, column 5). Notably, the overall slump blocks and critical blocks in each of the sites were used to derive the average thickness of the riverbank soil-root composite (Table 5, column 2). The average thickness of the collapsed block was calculated to be 0.81 m; S0 was the average shear strength of the soil, with a mean of S0 = 4.11 kPa (Table 2, column 9); TN was the tensile strength of plant roots within the collapsed riparian blocks at the four sites (Table 2, column 8). The average soil-root composite density ρ1 was calculated as 1536 kg/m3 from in situ measurements (Table 2, column 2).

Table 5.
Comparison of in situ measured and predicted width of the collapsed block at four sites.
To some extent, horizontal roots of riparian plants on a collapsed surface can reinforce the soil-root composite and restrain the bank from failure. In contrast, vertical roots provide only minimal enhancement to the tensile strength of the soil-root composite (Figure 7). This finding contrasts with the important role of vertical roots considered in Wu’s model [31]. Given the varying contributions of roots which are oriented in different directions to ΔS, Wu’s original model (Equation (18)) can be modified as Equation (19):
where Tr is the tensile strength of plant roots per unit area, θ is the angle of tensile distortion, and φ is the angle of friction. According to the results of in situ shear strength tests, θ and φ were found to vary from 40° < θ < 80° and 10° < φ < 25°, resulting in ΔS varying from 0.61 to 1.15. Thus, a middle value of 0.85 was used in this study to calibrate the predicted width of blocks.
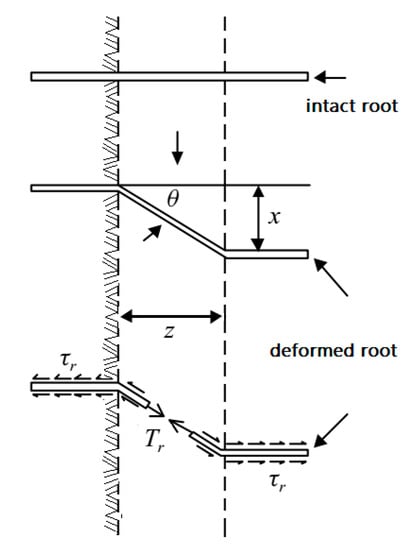
Figure 7.
Root reinforcement model with a flexible elastic root aligned horizontally to the shear zone prior to bank failure [33] (adapted from Gray and Leiser (1982) (z: Thickness of shear zone; x: Deflection of root; τr: Interface friction between root and soil).
The width bc of the collapsed block at each of the four study sites was predicted by applying all the above relevant values into Equation (17). It ranged from 0.989 m at site B to 1.158 m at site D, with an average of 1.056 m (Table 5, column 4). The four in situ measured widths of the collapsed slump and critical blocks had an average of 0.865 m (see Table 5, column 3), which was slightly smaller than the predicted bc of 1.056 m, resulting in an overall relative error of 22.1%. Furthermore, all four predicted widths were larger than their in situ measured counterparts because Equation (17) was underpinned by the assumption that all the roots passing through the collapsed surface snapped simultaneously at the moment of failure. In reality, the plant roots were entangled with one another in the soil. In the case of bank failure, the roots on the collapsed surface are gradually pulled away under gravity. Some are also connected to other fibrous roots that do not pass through the collapsed surface. Their tensile effect has been ignored in the prediction, resulting in an average overestimated value of 22.1%.
6. Discussion
Bank failure in meadow-type meandering rivers occurs as a cantilever collapse under gravity, in which plant roots exert a vital influence. In this study a bank equilibrium equation (Equation (1)) was proposed on the basis of the root enhancement model [31]; the equation was used to predict the width of cantilever blocks collapse. The theoretical width of blocks predicted using the equation was in close agreement with field measurements, demonstrating that this equation was highly reliable. This is significant in the study of transverse migration of meadow-type meandering channels and the duration that the slump/critical blocks can protect the outer bank. Nevertheless, the reliability of the equation needs to be further verified under different hydrodynamic conditions. The accurate prediction was achieved for the study area where the outer bank was composed of two layers of drastically different deposit materials. Thus, the equilibrium equation may not be applicable to other areas of different riparian bank deposits, such as the middle and lower Yangtze River or the lower Mississippi River [34]. In the study area, the thickness of the sand layers ranged 30–50 cm of collapsed banks, and the occurrence of bank failure was rare in cases in which the thickness was thinner or thicker than 30–50 cm. The thickness of the sand layers affected the thickness of the blocks, and the failure mechanism of sand layers requires further study. When the effect of geomorphological collapse was introduced into the simulation by a simple mass conservative mechanism of slope sliding failure, the failure mechanism was applied by comparison between the bed slope in each computational cell [35]. The overestimation of the width of bank failure block predicted by the proposed equilibrium equation was 22.1% (Table 5). This overestimation is similar to what has been reported in the literature [36,37,38,39]. Loades et al. overestimated the reinforcement of shear strength by 79% using the same (Wu’s) model [37]. Zhu et al. reported an average overestimation of 21.8% using the same model, approximately the same magnitude of overestimation obtained in this study (22.1%) [39]. Zhu et al. calibrated the overestimation by reducing the coefficient in Equation (5) from 1.2 to 0.63 for the study area of Jinyun Mountain of Chongqing City, western China [39]. To accurately predict the width of the block, it is recommended that the coefficient be reduced to 0.85 for the study area. After calibration using this value, the predicted bc (Table 5, column 6) was much closer to the in situ measured counterparts, resulting in an average overestimation of only 2.7% (Table 5, column 7).
The mode of slump blocks in meadow-type meandering riverbanks is characterized chiefly by stretching-pulling failure. During this process, tensile cracks initially form on the outer bank surface; they then gradually progress to the deeper root-soil layer under the action of self-weight, until the outmost cantilever topples. During the process of failure, the shear strength of the soil plays a less important role than that of root tensile strength. The roots of the soil-root composite are intertwined to form a tensile structure network with a high tensile strength. Clearly, it can reduce bank erosion. The mechanical properties of the soil-root composite and the tensile action exerted by the plant roots are critical forces in slowing down and preventing riverbank collapse. The morphology of the failed block is related to the properties of meadow plant roots, suggesting that certain plants with dense roots are more effective at stabilizing the bank than others. For instance, Blysmus sinocompressus, with its extensive lateral roots and strong tensile strength, should be planted at numerous spots along the bank to enhance bank stability and minimize soil erosion.
Finally, the comprehensive effect of plant roots on outer bank stability was not restricted to its ability to reinforce and bind the slope soil in the study area of a perennially cold climate. The ground can freeze up to a depth of 1.38 m from late October to early April. In early spring, when the ground thaws, cracks can form as a result of ground expansion. The formation of such cracks can be reduced by plant roots. In addition, the binding effect of the plant roots can also restrain the cracks from expanding further [21], thus effectively reducing the occurrence of bank failure.
7. Conclusions
Cantilever failures are widespread in the outer bank of meadow-type meandering rivers in the Yellow River Source Zone. They occur as either slump blocks or critical blocks. The former was more common (63 identified) than the latter (only 15 observed) within a 5-km area of study. Typically, a failed block has a dimension of 0.865 m (width) by 0.817 m (thickness) by 2.228 m (length). Accordingly, their width is highly connected to their thickness, despite the fact that both are much smaller than their length. The length of failed blocks is correlated with their width (R2 = 0.26 to 0.29). The dimension of the failed blocks varies according to site. Such variations in the morphology of the failed blocks are linked closely to plant root length. In particular, block thickness can be accurately predicted from root length (R2 ≥ 0.76) but not block width. The thickness of slump blocks is logarithmically related to root length. Similarly, the volume of the displaced blocks is also closely related to root length for slump blocks (R2 = 0.527) but not for critical blocks, attributable to the action of plant roots. The block width predicted from the proposed equilibrium equation differed from the in situ measured width by an average of 22.1% among the four sites. The constrained equilibrium formula for predicting the width of blocks suggests that alpine meadow vegetation can increase the amount of time required to undermine, detach, and remove bank failure blocks. It can be concluded that the proposed equilibrium equation is reliable for predicting the width of collapsed blocks from in situ measured soil and vegetation properties. It facilitates the understanding of the mechanism of cantilever bank collapse. However, its applicability to other study areas requires further investigation, where bank deposits may comprise different materials.
Author Contributions
This research was conceptualized by H.Z., Z.L., and X.H. during the funding acquisition. The methodology for the field investigation was a joint effort of H.Z. and Z.L. H.Z., Z.L., L.S., K.L. and G.L. were responsible for the collection and analysis of field data. H.Z. wrote the first draft of the paper, X.H., Z.L. and X.L. contributed in reviewing and editing the manuscript.
Funding
This research was funded by [National Natural Science Foundation of China] grant number [41762023, 41302258, 41662023 and 91547112]; [Qinghai Science and Technology Department] grant number [2017-ZJ-776]; [Hundred Talents Program of the Chinese Academy of Sciences] grant number [Y110091025]; [Open Project of State Key Laboratory of Plateau Ecology and Agriculture] grant number [2017-KF-01]; [Natural Science Foundation of Hunan Province] grant number [2018JJ3547]; [Qinghai Science and Technology Department] grant number [2015-SF-117] and [Changjiang Scholar Program and Innovative Research Team Building, MOE] Grant Number [IRT_17R62].
Acknowledgments
The authors thank undergraduate students D.C., X.C., G.Y., and X.Z. for data collection in the field. G.B. from the University of Auckland provided insightful comments on the original manuscript. G.J. from the University of Auckland gave constructive guidance and valuable help of the manuscript. Thanks are extended to three anonymous reviewers and the Editor for useful comments that improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Thorne, C.R.; Tovey, N.K. Stability of composite river banks. Earth Surf. Process. Landf. 1981, 6, 469–484. [Google Scholar] [CrossRef]
- Hickin, E.J. Vegetation and river channel dynamics. Can. Geogr. 1984, 28, 111–126. [Google Scholar] [CrossRef]
- Abernethy, B.; Rutherfurd, I.D. Where along a river’s length will vegetation most effectively stabilise stream banks? Geomorphology 1998, 23, 55–75. [Google Scholar] [CrossRef]
- Simon, A.; Curini, A.; Darby, S.E.; Langendoen, E.J. Bank and near-bank processes in an incised channel. Geomorphology 2000, 35, 193–217. [Google Scholar] [CrossRef]
- Gray, D.H.; Barker, D. Root-soil mechanics and interactions. In Riparian Vegetation and Fluvial Geomorphology; American Geophysical Union: Washington, DC, USA, 2004; pp. 113–123. [Google Scholar]
- Wiel, M.J.; Darby, S.E. A new model to analyse the impact of woody riparian vegetation on the geotechnical stability of riverbanks. Earth Surf. Process. Landf. 2007, 32, 2185–2198. [Google Scholar] [CrossRef]
- Pollen, N. Temporal and spatial variability in root reinforcement of streambanks: Accounting for soil shear strength and moisture. Catena 2007, 69, 197–205. [Google Scholar] [CrossRef]
- Eaton, B.; Millar, R. Predicting gravel bed river response to environmental change: The strengths and limitations of a regime-based approach. Earth Surf. Process. Landf. 2017, 42, 994–1008. [Google Scholar] [CrossRef]
- Abernethy, B.; Rutherfurd, I.D. The effect of riparian tree roots on the mass-stability of riverbanks. Earth Surf. Process. Landf. 2000, 25, 921–937. [Google Scholar] [CrossRef]
- Kirchner, J.W.; Micheli, L.; Farrington, J.D. Effects of Herbaceous Riparian Vegetation on Streambank Stability; University of California Water Resources Center: Berkeley, CA, USA, 1998. [Google Scholar]
- Langendoen, E.J.; Simon, A. Modeling the evolution of incised streams. II: Streambank erosion. J. Hydraul. Eng. 2008, 134, 905–915. [Google Scholar] [CrossRef]
- Perucca, E.; Camporeale, C.; Ridolfi, L. Significance of the riparian vegetation dynamics on meandering river morphodynamics. Water Resour. Res. 2007, 43, W03430-1–W03430-10. [Google Scholar] [CrossRef]
- Thorne, C. Processes and mechanisms of river bank erosion. In Gravel-bed Rivers; Hey, J.B., Thorne, R.D., Eds.; John, Wiley and Sons: Chichester, UK, 1982; pp. 227–272. [Google Scholar]
- Page, K.; Nanson, G. Concave-bank benches and associated floodplain formation. Earth Surf. Process. Landf. 1982, 7, 529–543. [Google Scholar] [CrossRef]
- Huang, B.; Bai, Y.; Wan, Y. Model for dilapidation mechanism of riverbank. J. Hydraul. Eng. 2002, 33, 49–54. [Google Scholar]
- Wang, Y.G.; Kuang, S.F. Critical height of bank collapse. J. Hydraul. Eng. 2007, 38, 1158–1165. [Google Scholar]
- Osman, A.M.; Thorne, C.R. Riverbank stability analysis. I: Theory. J. Hydraul. Eng. 1988, 114, 134–150. [Google Scholar] [CrossRef]
- Wang, Y.G.; Kuang, S.F.; Su, J.L. Critical caving erosion width for cantilever failures of river bank. Int. J. Sediment Res. 2016, 31, 220–225. [Google Scholar] [CrossRef]
- Gregory, K.J.; Gurnell, A.M. Vegetation and river channel form and process. In Biogeomorphology; Basil Blackwell: Oxford, UK, 1988; pp. 11–42. [Google Scholar]
- Wynn, T.M.; Mostaghimi, S.; Burger, J.A.; Harpold, A.A.; Henderson, M.B.; Henry, L.A. Variation in root density along stream banks. J. Environ. Qual. 2004, 33, 2030–2039. [Google Scholar] [CrossRef] [PubMed]
- Konsoer, K.M.; Rhoads, B.L.; Langendoen, E.J.; Best, J.L.; Ursic, M.E.; Abad, J.D.; Garcia, M.H. Spatial variability in bank resistance to erosion on a large meandering, mixed bedrock-alluvial river. Geomorphology 2016, 252, 80–97. [Google Scholar] [CrossRef]
- Fukuoka, S. Erosion processes of natural riverbank. In Proceedings of the 1st International Symposium on Hydraulic Measurement (CHES and IAHR), Beijing, China, 15 September 1994; pp. 222–229. [Google Scholar]
- Samadi, A.; Amiri-Tokaldany, E.; Davoudi, M.H.; Darby, S.E. Experimental and numerical investigation of the stability of overhanging riverbanks. Geomorphology 2013, 184, 1–19. [Google Scholar] [CrossRef]
- Pollen-Bankhead, N.; Simon, A. Hydrologic and hydraulic effects of riparian root networks on streambank stability: Is mechanical root-reinforcement the whole story? Geomorphology 2010, 116, 353–362. [Google Scholar] [CrossRef]
- Simon, A.; Collison, A.J. Quantifying the mechanical and hydrologic effects of riparian vegetation on streambank stability. Earth Surf. Process. Landf. 2002, 27, 527–546. [Google Scholar] [CrossRef]
- Xia, J.Q.; Wu, B.S.; Wang, Y.P.; Zhao, S.G. An analysis of soil composition and mechanical properties of riverbanks in a braided reach of the Lower Yellow River. Chin. Sci. Bull. 2008, 53, 2400–2409. [Google Scholar] [CrossRef]
- Lin, C.Y.; Li, X.L.; Liu, K.; Xue, Z.P. Vegetation change characteristics during degradation succession in floodplain wetlands of the Yellow River Source Zone. Chin. Agric. Sci. Bull. 2016, 32, 115–119. [Google Scholar]
- Zhu, H.L.; Wang, Z.Y.; Li, Z.W. Influence of riparian meadow to the meandering rivers evolution in the yellow river source region. Yellow River 2013, 35, 41–44. [Google Scholar]
- Fu, J.T.; Hu, X.S.; Brierley, G.; Qiao, N.; Yu, Q.Q.; Lu, H.J.; Li, G.R.; Zhu, H.L. The influence of plant root system architectural properties upon the stability of loess hillslopes, Northeast Qinghai, China. J. Mt. Sci. 2016, 13, 785–801. [Google Scholar] [CrossRef]
- Li, Z.W. Fluvial Processes and Wetland Degradation Mechanism of the Sanjiangyuan Source. Ph.D. Thesis, Tsinghua University, Beijing, China, 1 November 2013. [Google Scholar]
- Wu, T.H.; McKinnell, W.P., III; Swanston, D.N. Strength of tree roots and landslides on Prince of Wales Island, Alaska. Can. Geotech. J. 1979, 16, 19–33. [Google Scholar] [CrossRef]
- Liu, S.W. Qinghai Flora; People’s Publishing House of Qinghai: Xining, China, 1996. [Google Scholar]
- Gray, D.H.; Leiser, A.T. Biotechnical Slope Protection and Erosion Control; Nostrand Reinhold Co.: New York, NY, USA, 2001; p. 40. [Google Scholar]
- Xia, J.Q.; Zong, Q.L.; Xu, Q.X.; Deng, C.Y. Soil properties and erosion mechanisms of composite riverbanks in lower Jingjiang reach. Adv. Water Sci. 2013, 24, 810–820. [Google Scholar]
- Juez, C.; Murillo, J.; García-Navarro, P. Numerical assessment of bed-load discharge formulations for transient flow in 1D and 2D situations. J. Hydroinform. 2013, 15, 1234–1257. [Google Scholar] [CrossRef]
- Abernethy, B.; Rutherfurd, I.D. The distribution and strength of riparian tree roots in relation to riverbank reinforcement. Hydrol. Process. 2001, 15, 63–79. [Google Scholar] [CrossRef]
- Loades, K.W.; Bengough, A.G.; Bransby, M.F.; Hallett, P.D.; Stokes, A. Planting density influence on fibrous root reinforcement of soils. Ecol. Eng. 2010, 36, 276–284. [Google Scholar] [CrossRef]
- Zhu, J.Q.; Wang, Y.Q.; Wang, Y.J.; Zhang, H.L.; Li, Y.P.; Li, Y. Analysis of root system enhancing shear strength based on experiment and model. Rock Soil Mech. 2014, 35, 449–458. [Google Scholar]
- Zhu, J.Q.; Wang, Y.Q.; Wang, Y.J.; Zhang, H.L.; Li, Y.P.; Li, Y. An analysis on soil physical enhancement effects of root system of Pinus Tabulae formis and Acer Truncatum based on two models. Bull. Soil Water Conserv. 2015, 35, 277–282. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).