Numerical Study of Spatial Behavior of Solute Particle Transport in Single Fracture with Variable Apertures
Abstract
:1. Introduction
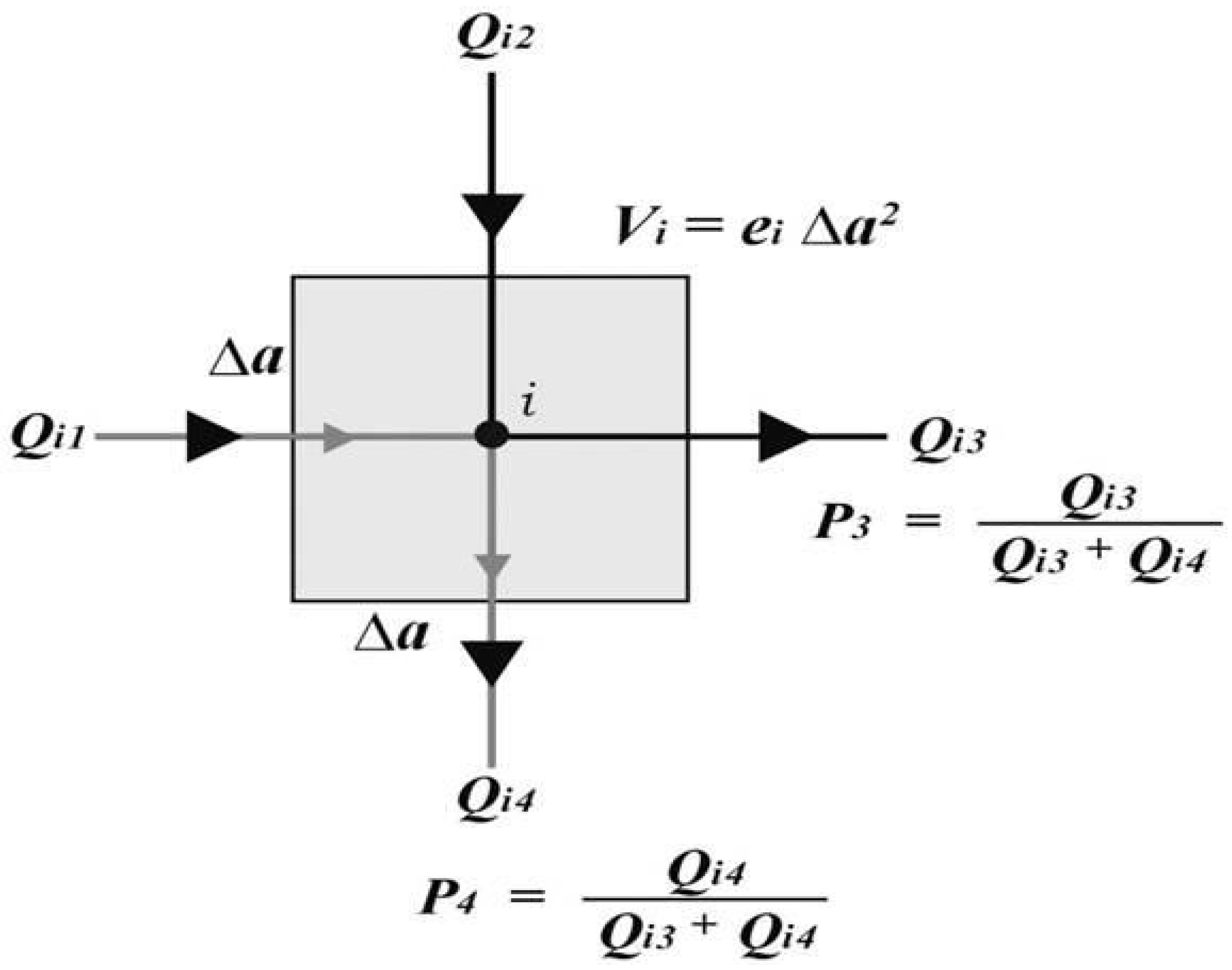
2. Solute Transport Model: Random Walk Particle Following (RWPF) Model
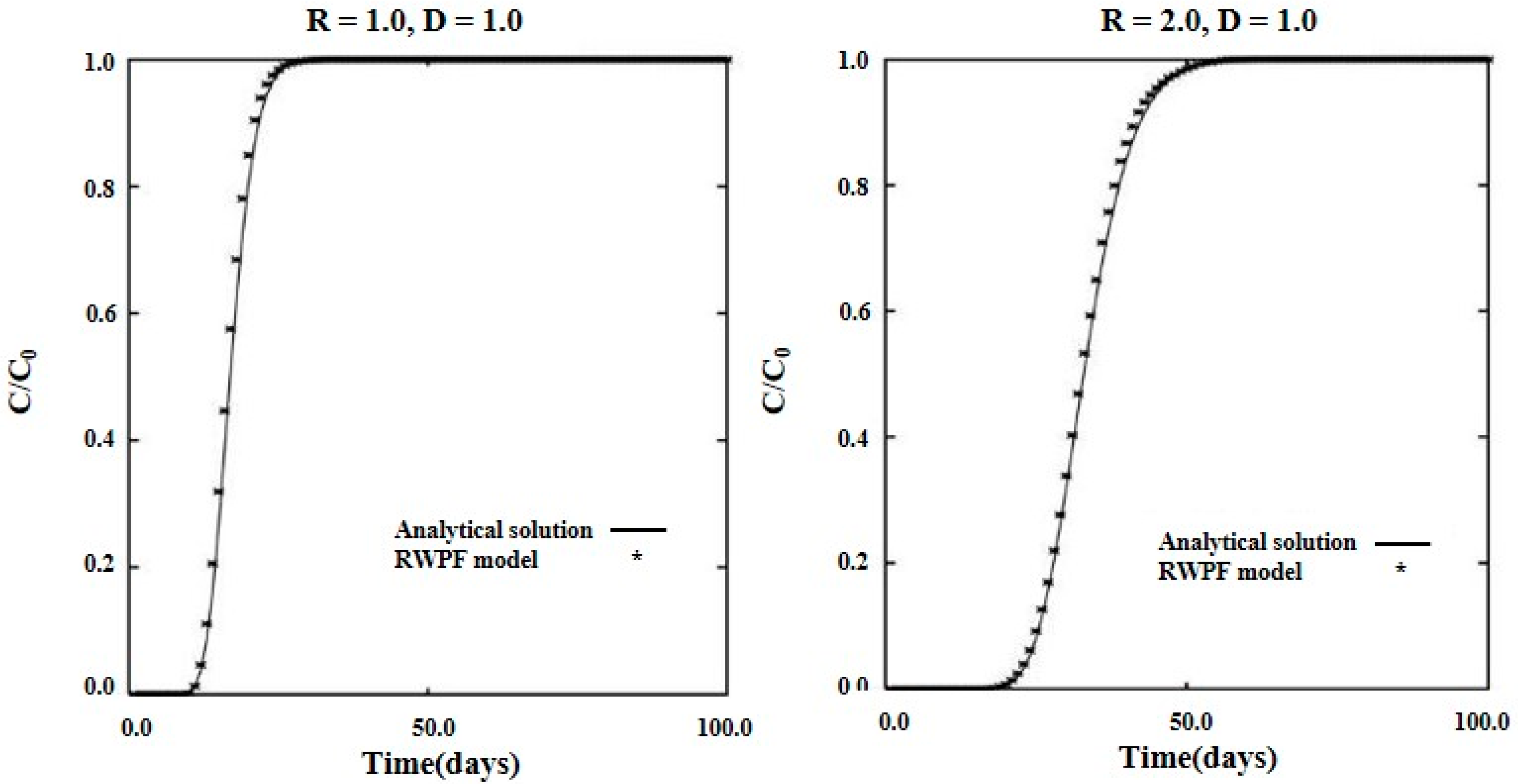
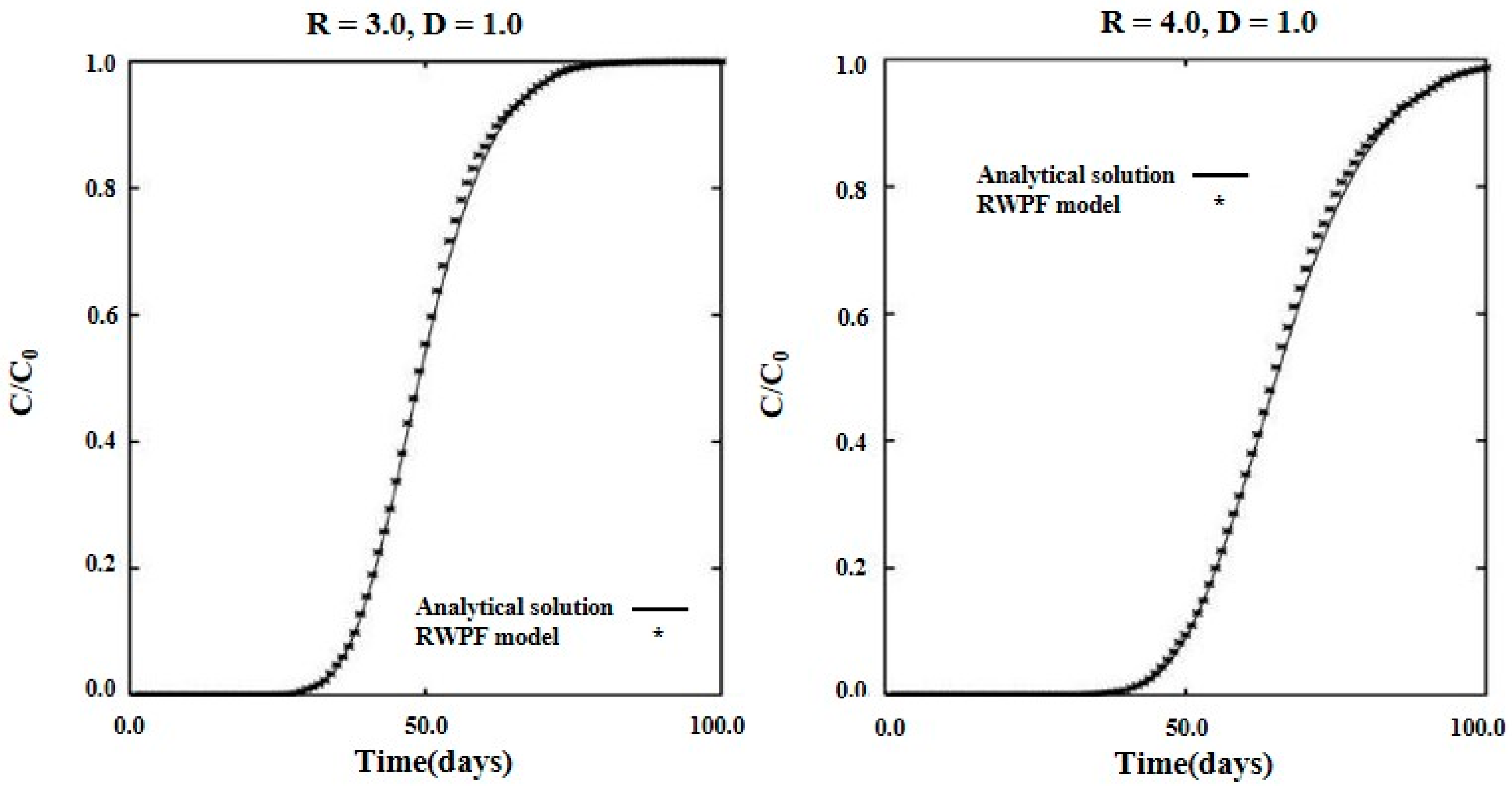
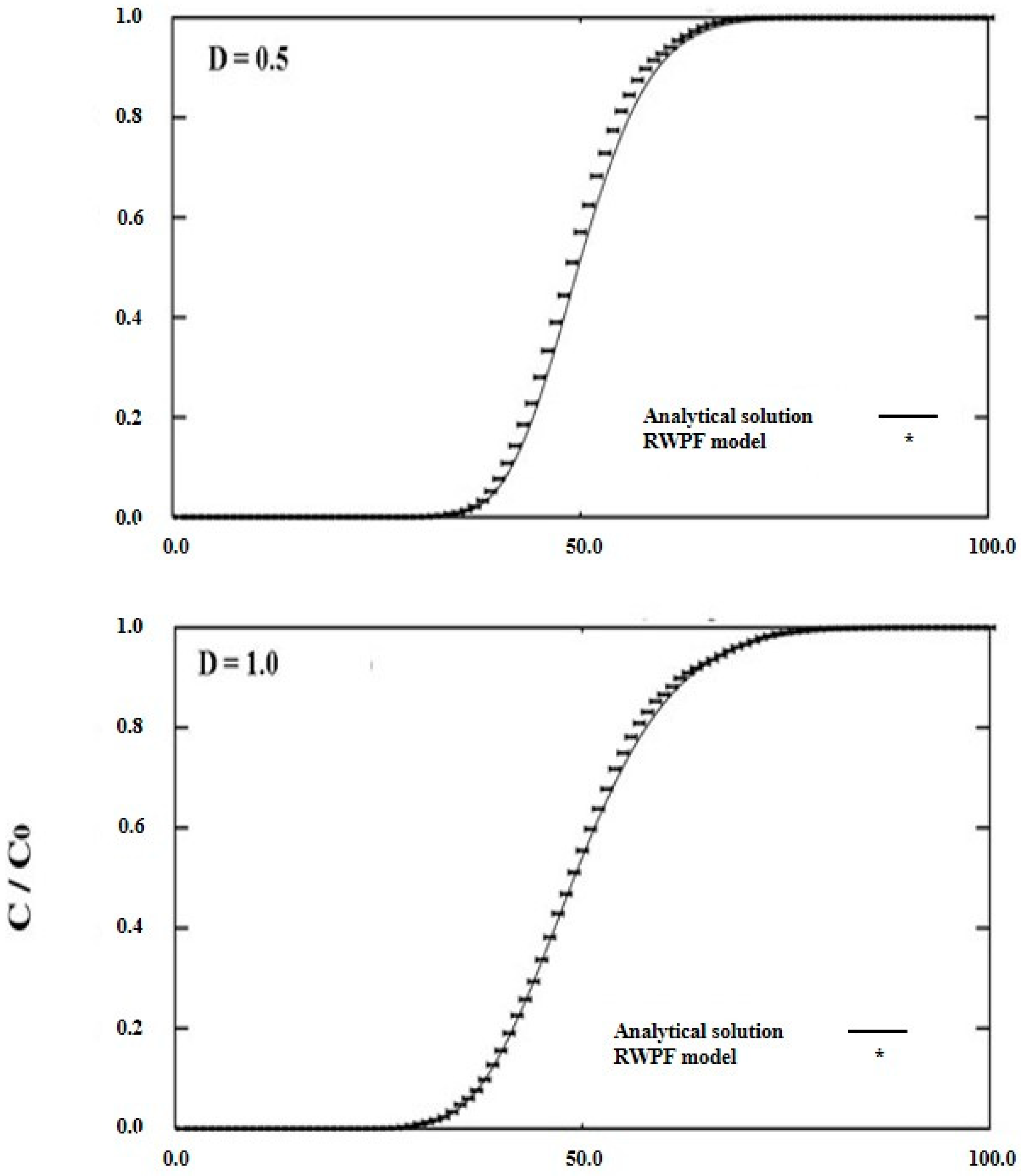
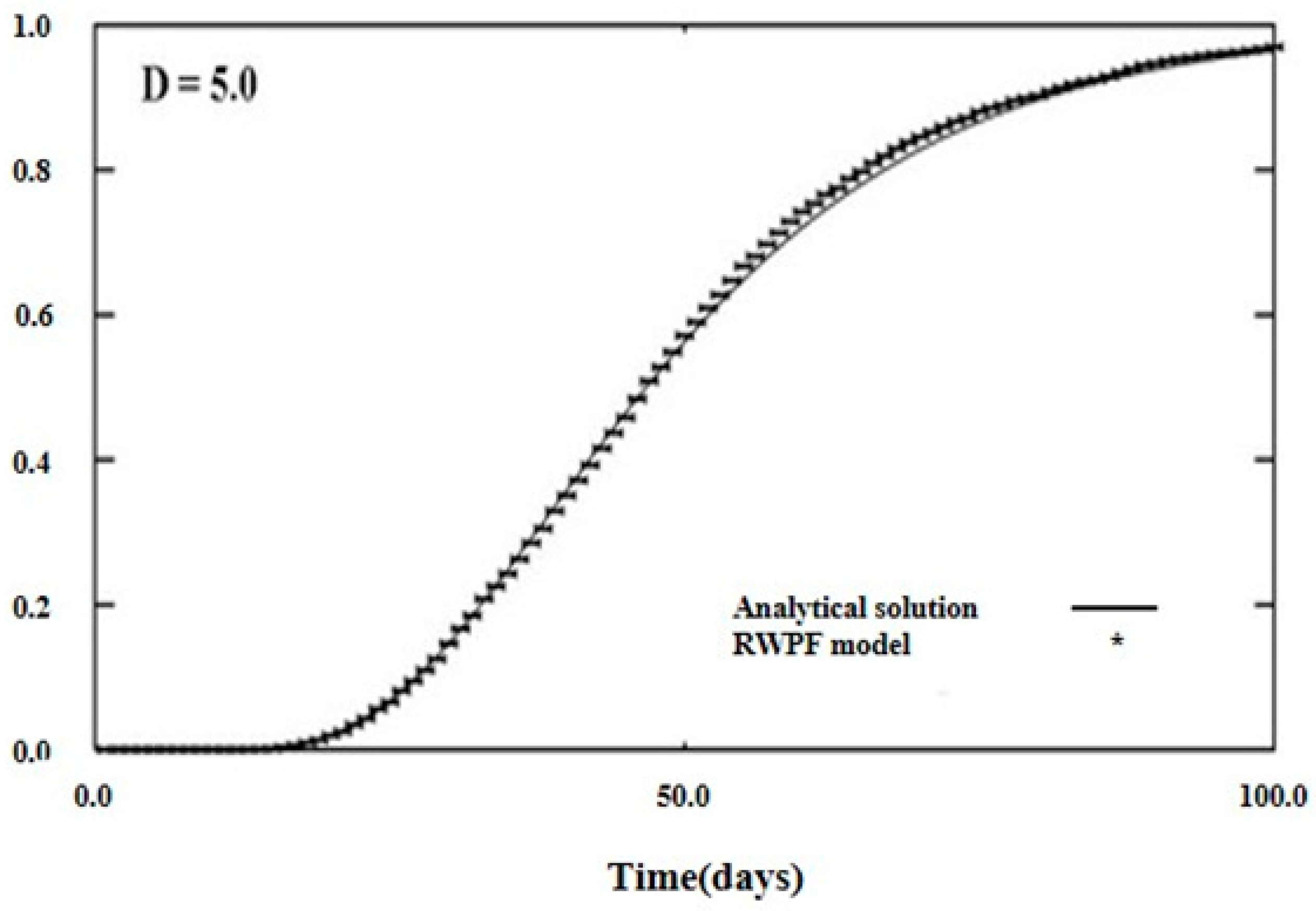
3. Verification of RWPF Model
4. Solute Transport Simulation with Spatial Correlation Length and Effective Normal Stress
4.1. Simulation Condition
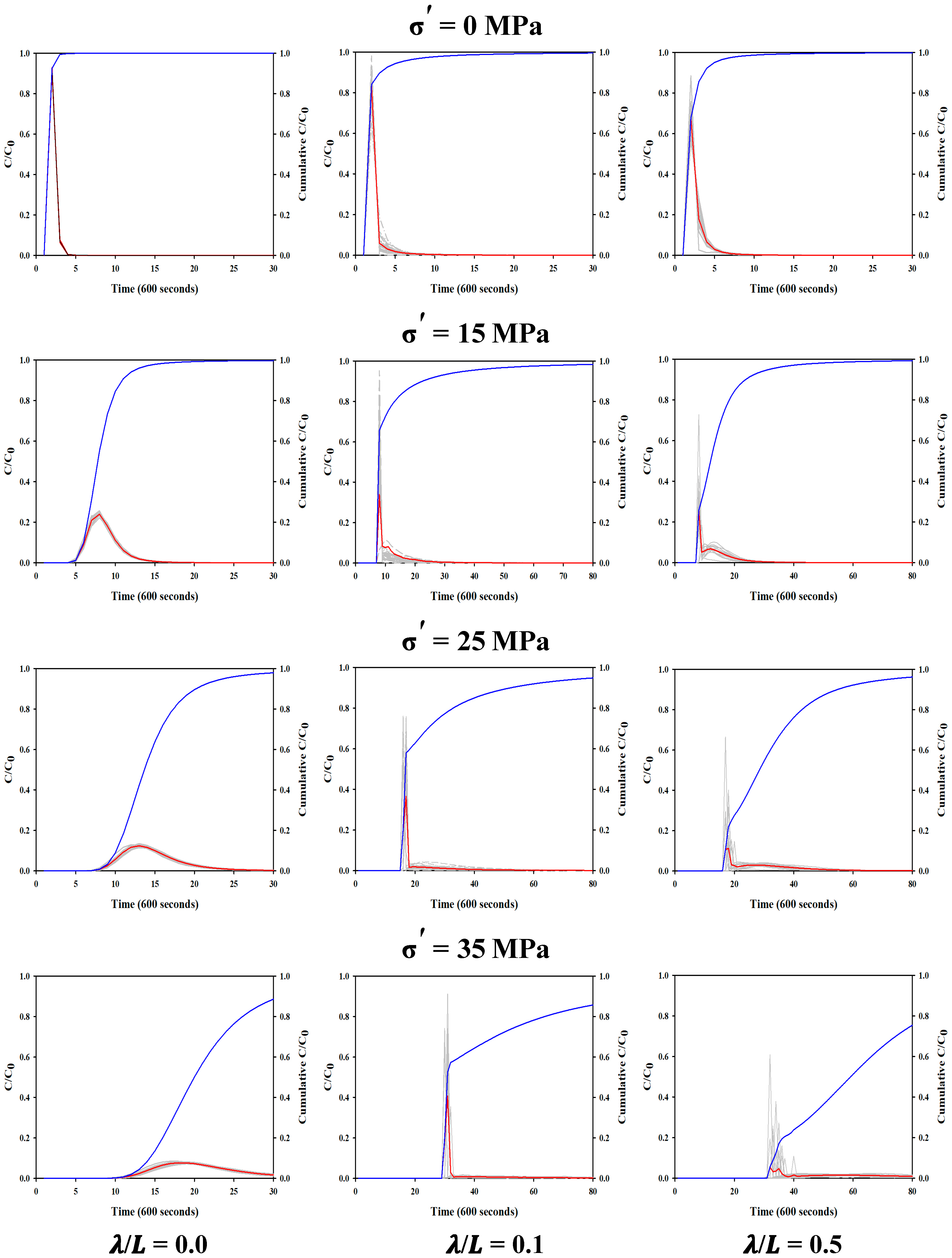
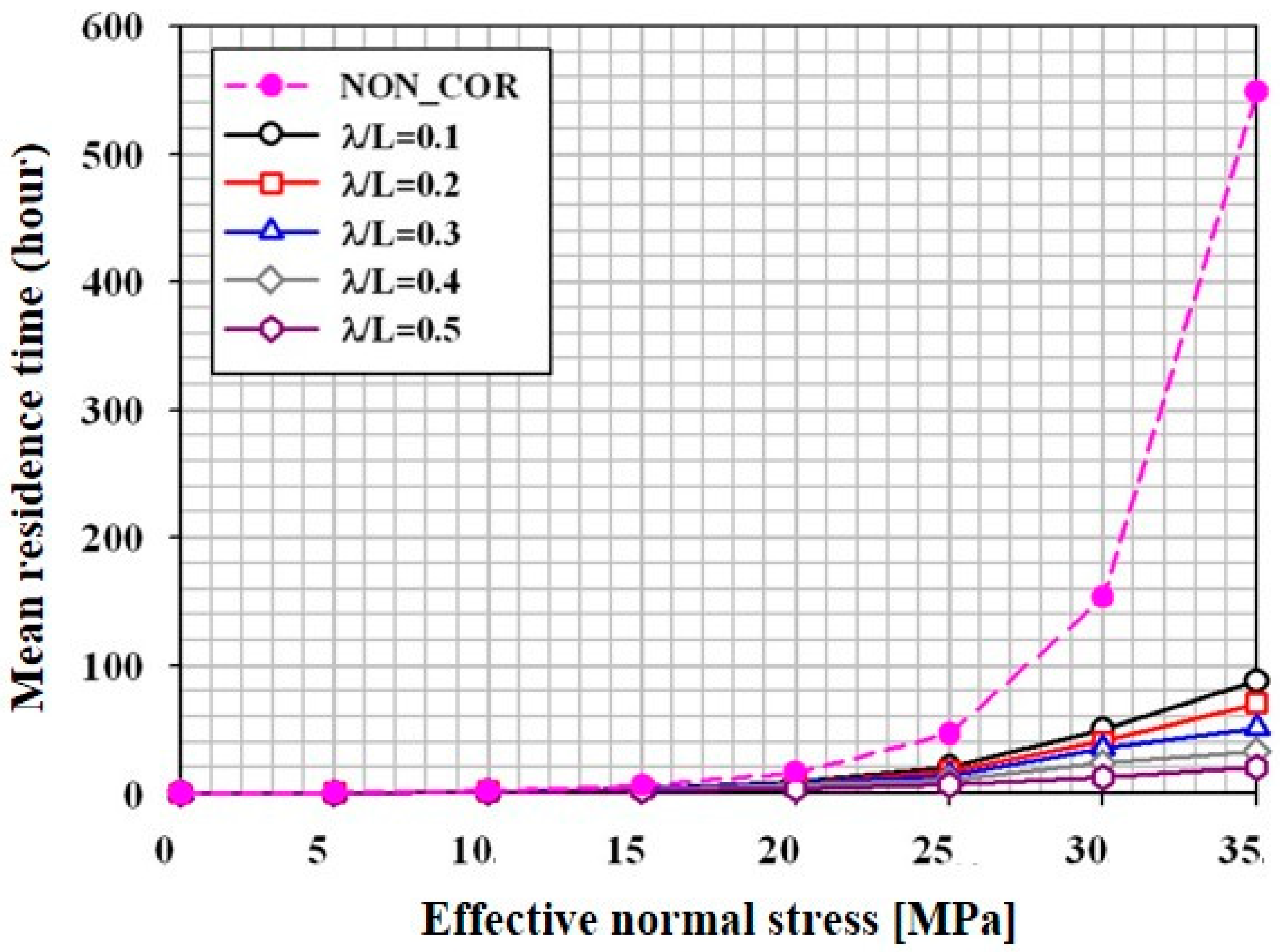
4.2. Breakthrough Curves and Mean Residence Time
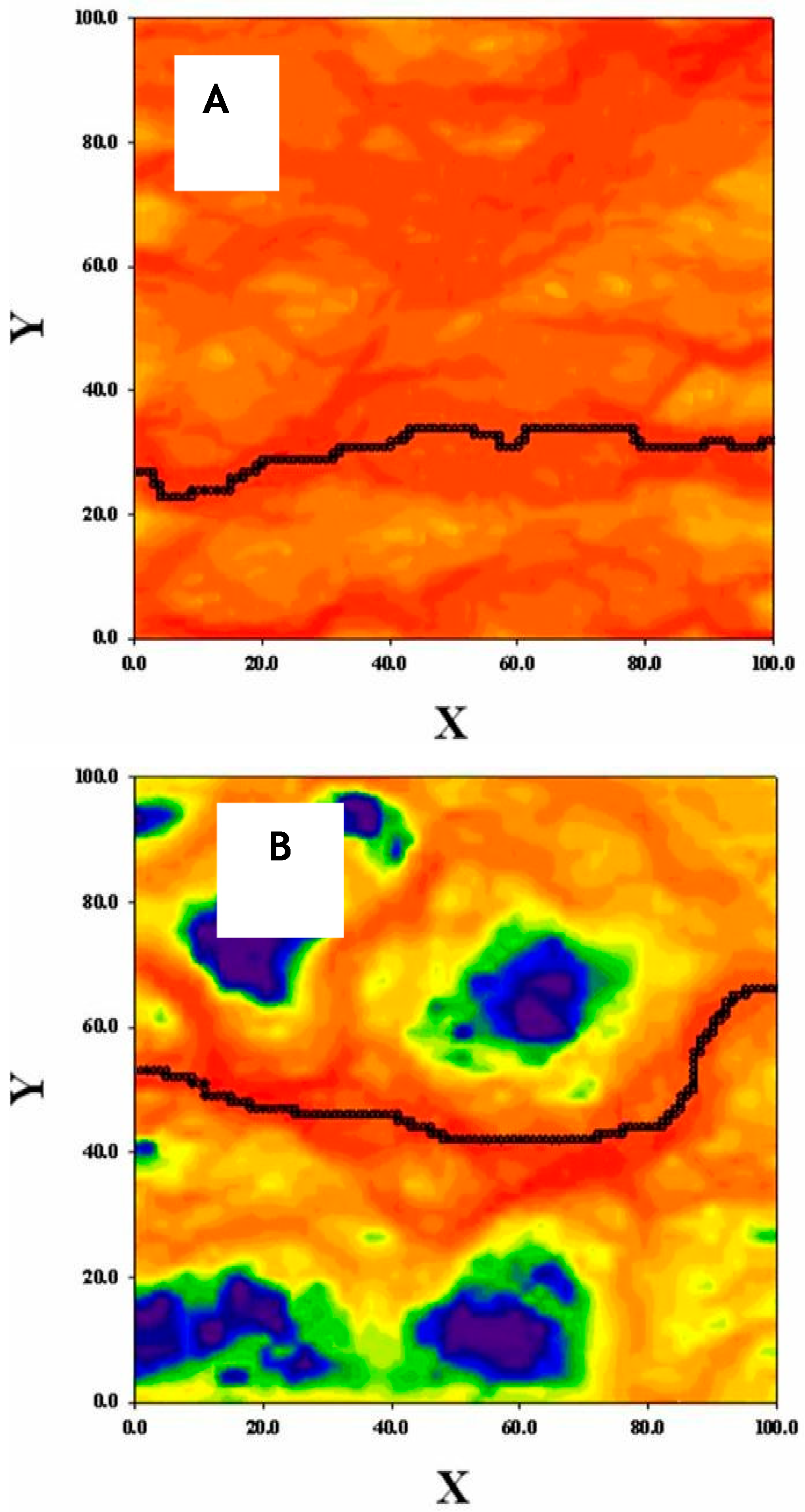
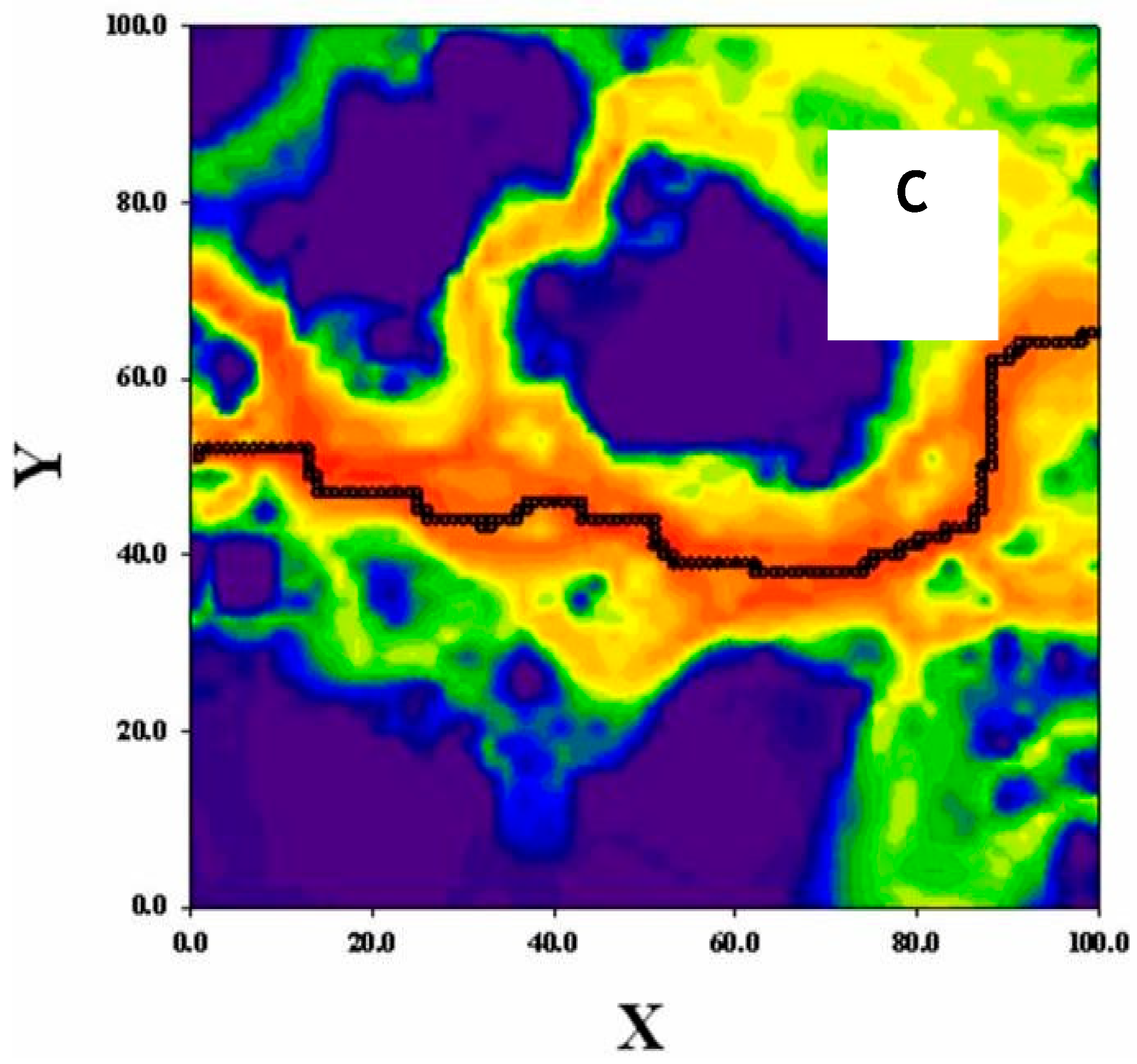
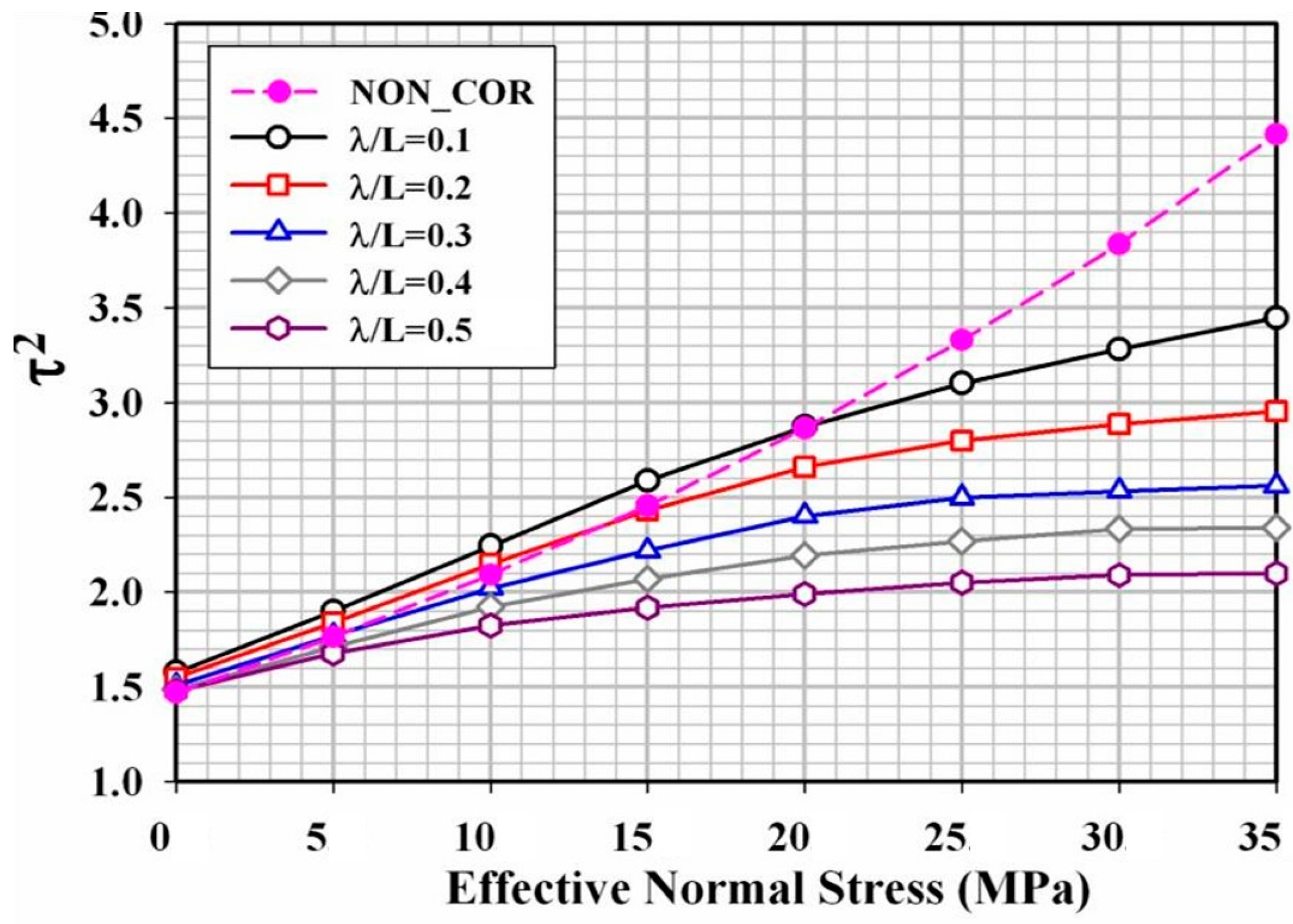
4.3. Tortuosity of Solute Particles
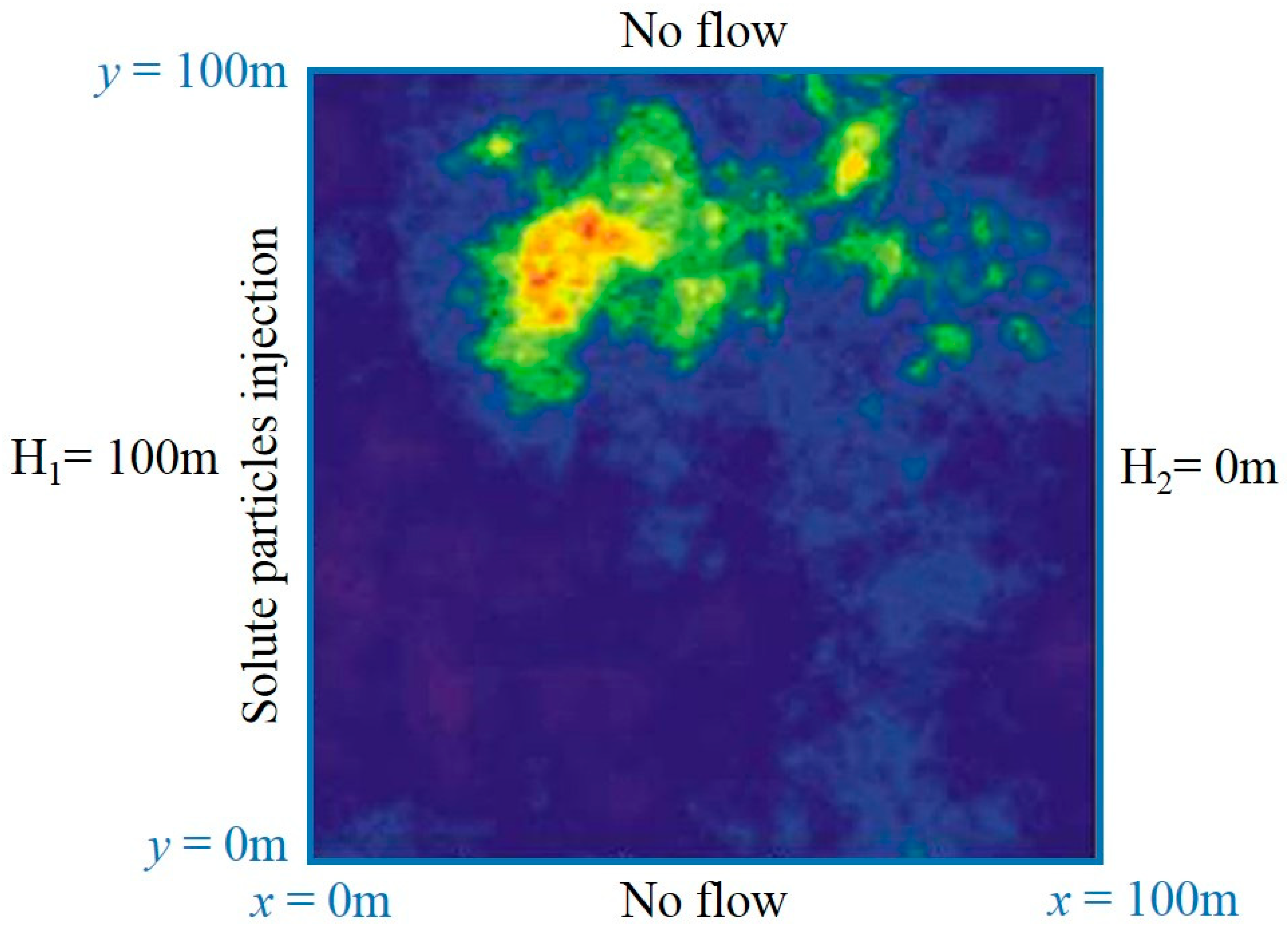
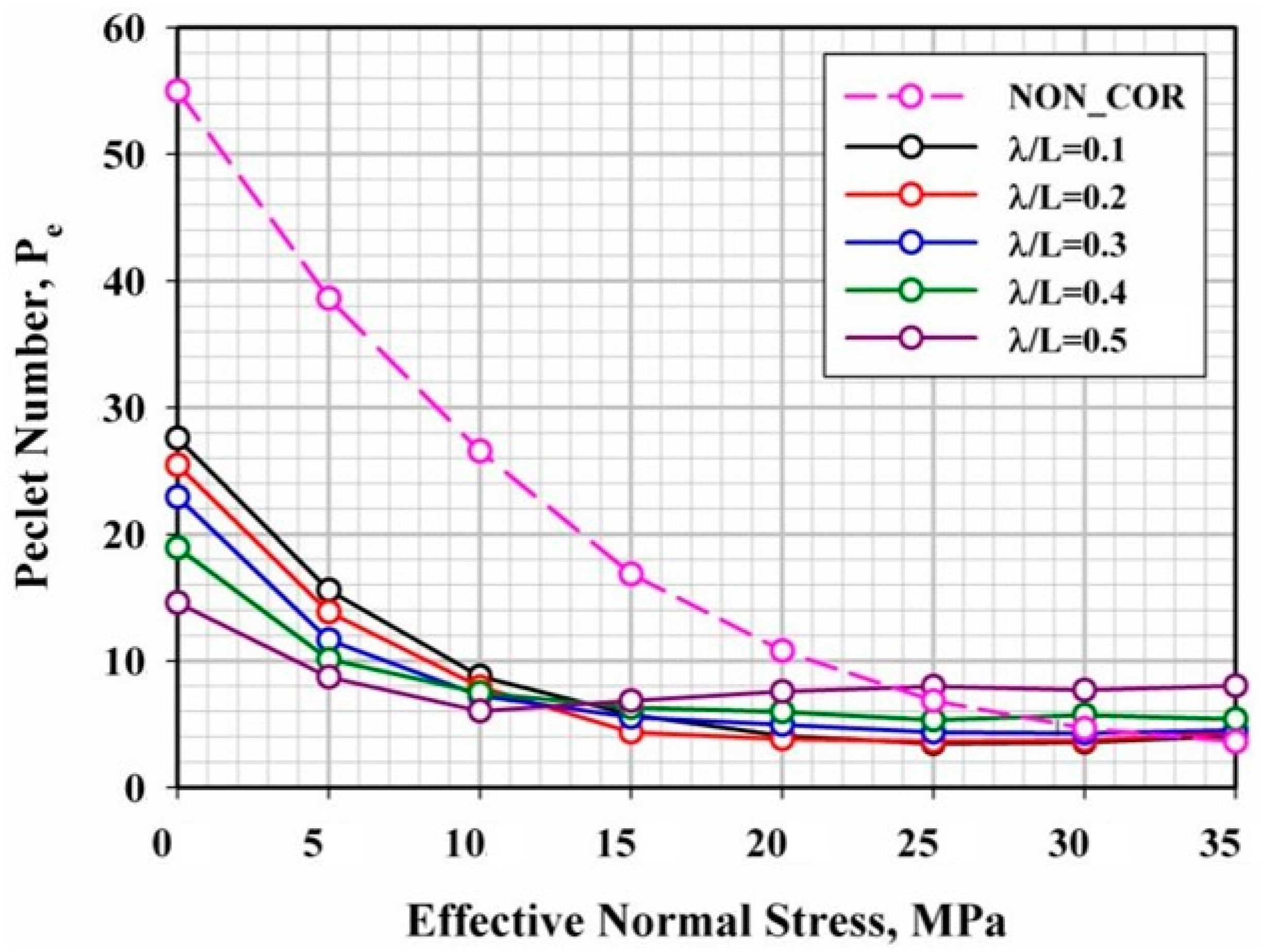
4.4. Spatial Dispersion of Solute Particles
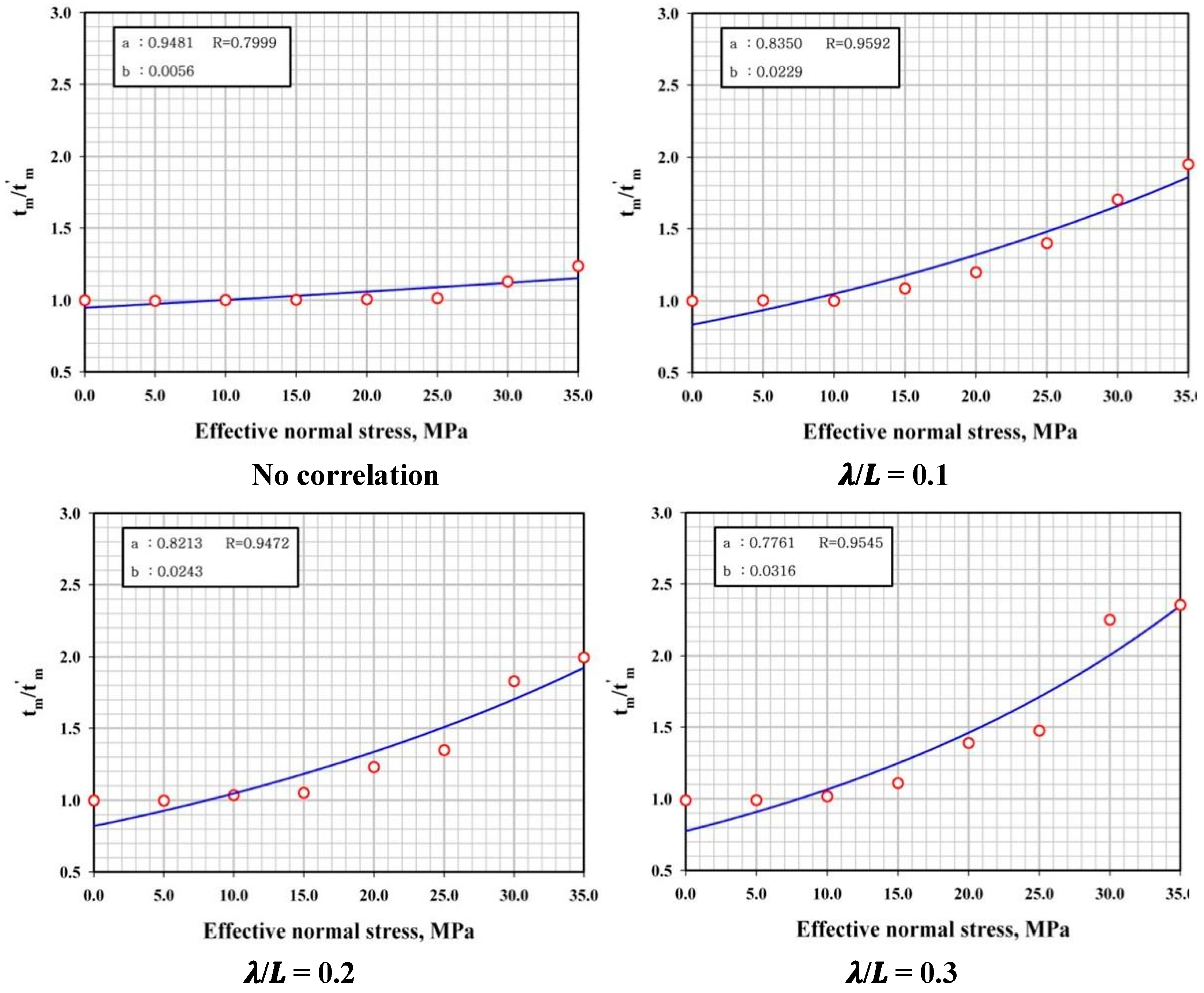
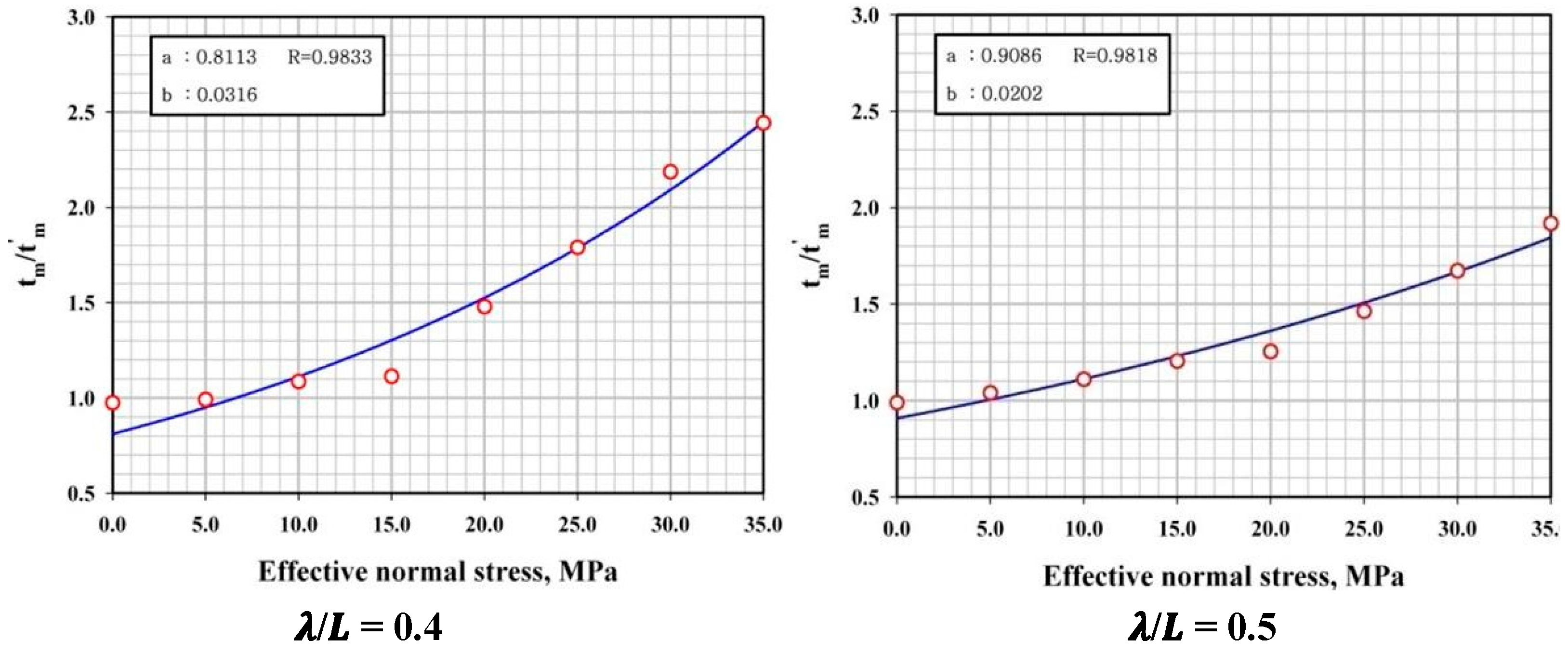
4.5. Empirical Formula for Calculating Mean Residence Time of Solutes
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Abelin, H.; Gidlund, J.; Neretnieks, I. Migration in a single fracture. Proc. Mater. Res. Soc. Symp. 1982, 11, 529–538. [Google Scholar] [CrossRef]
- Gale, J. Hydraulic behavior of rock joints. In Rock Joints; Barton, N., Stephansson, O., Eds.; Balkema: Rotterdam, The Netherlands, 1987; pp. 623–630. [Google Scholar]
- Gentier, S. Morphologie et Comportement Hydromécanique D’une Fracture Naturelle Dans un Granite sous Contrainte Normale: Étude Expérimentale et Théorique. Ph.D. Dissertation, University of Orleans, Orleans, France, 1986; pp. 1–350. [Google Scholar]
- Hakami, E.; Larsson, E. Aperture measurements and flow experiments on a single natural fracture. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 395–404. [Google Scholar] [CrossRef]
- Haldeman, W.; Chuang, Y.; Rasmussen, T.; Evans, D. Laboratory analysis of fluid flow and solute transport through a fracture embedded in porous tuff. Water Resour. Res. 1985, 27, 53–65. [Google Scholar] [CrossRef]
- Pyrak-Nolte, L.; Myer, L.; Cook, N.; Witherspoon, R. Hydraulic and mechanical properties of natural fractures in low permeability rock. In Proceedings of 6th International Congress of Rock Mechanics; Balkema: Rotterdam, The Netherlands, 1987; pp. 789–798. [Google Scholar]
- Raven, K.; Gale, J. Water flow in a natural rock fracture as a function of stress and sample size. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 251–261. [Google Scholar] [CrossRef]
- Witherspoon, P.; Wang, J.; Iwai, K.; Gale, J. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- Brown, S. Fluid flow through rock joints: The effect of surface roughness. J. Geophys. Res. 1987, 92, 1337–1347. [Google Scholar] [CrossRef]
- Jeong, W.; Song, J. A numerical study on flow and transport in a rough fracture with self-affine fractal variable apertures. Energy Sources 2008, 30, 606–619. [Google Scholar] [CrossRef]
- LaBolle, E.M.; Fogg, G.E.; Tompson, A.F.B. Random-walk simulation of transport in heterogeneous porous media: Local mass-conservation problem and implementation methods. Water Resour. Res. 1996, 32, 583–593. [Google Scholar] [CrossRef]
- Moreno, L.; Tsang, C.; Tsang, Y.; Hale, F.; Neretnieks, I. Flow and tracer transport in a single fracture: A stochastic model and its relation to some field observations. Water Resour. Res. 1988, 24, 2033–2048. [Google Scholar] [CrossRef]
- Thompson, M. Numerical simulation of solute transport in rough fractures. J. Geophys. Res. 1991, 96, 6. [Google Scholar] [CrossRef]
- Tsang, Y.; Tsang, C.; Neretnieks, I.; Moreno, L. Flow and tracer transport in fractured media: A variable aperture channel model and its properties. Water Resour. Res. 1988, 24, 2049–2060. [Google Scholar] [CrossRef]
- Tsang, Y.; Tsang, C. Channel model of flow through fractured media. Water Resour. Res. 1987, 23, 467–479. [Google Scholar] [CrossRef]
- Ewing, P.; Jaynes, D. Issue in single-fracture transport modeling: Scales, algorithms and grid types. Water Resour. Res. 1995, 31, 303–312. [Google Scholar] [CrossRef]
- Vogler, D.; Settgast, R.; Annavarapu, C.; Madonna, C.; Bayer, P.; Amann, F. Experiments and simulations of fully hydro-mechanicallly coupled response of rough fractures exposed to high-pressure fluid injection. J. Geophys. Res. 2018, 123, 1186–1200. [Google Scholar] [CrossRef]
- Cacas, M.; Ledoux, E.; de Marsily, G.; Barbreau, A.; Calmels, P.; Gaillard, B.; Margrite, R. Modelling fracture flow with a discrete fracture network: Calibration and validation 2. The transport model. Water Resour. Res. 1990, 26, 491–500. [Google Scholar]
- Fetter, C. Contaminant Hydrogeology, 2nd ed.; Prentice Hall: New York, NY, USA, 1999; pp. 60–61. ISBN 0-13-751215-5. [Google Scholar]
- Jeong, W. Numerical Study on Behavior of groundwater flow in single rough fractures under mechanical effect. Groundwater 2017, 55, 38–50. [Google Scholar] [CrossRef] [PubMed]
- Matheron, G. The intrinsic random function and their applications. Adv. Appl. Prob. 1973, 5, 439–468. [Google Scholar] [CrossRef]
- Brown, S. Simple transport of fluid and electric current through a single fracture. J. Geophys. Res. 1989, 94, 9429–9438. [Google Scholar] [CrossRef]
- Neretnieks, I.; Eriksen, T.; Tahtien, P. Tracer movement in a single fissure in granitic rock: Some experimental results and their interpretation. Water Resour. Res. 1982, 18, 849–858. [Google Scholar] [CrossRef]
- Moreno, L.; Neretnieks, I.; Eriksen, T. Analysis of some laboratory tracer runs in natural fissures. Water Resour. Res. 1985, 21, 951–958. [Google Scholar] [CrossRef]
- Nordqvist, A.; Tsang, Y.; Tsang, C.; Dverstorp, B.; Anderson, J. A variable aperture fracture network model for flow and transport in fractured rocks. Water Resour. Res. 1992, 28, 1703–1713. [Google Scholar] [CrossRef]

| Effective Normal Stress | Closure |
|---|---|
| 0.0 | 0.0 |
| 5.0 | 139.0 |
| 10.0 | 212.0 |
| 15.0 | 258.0 |
| 20.0 | 289.0 |
| 25.0 | 312.0 |
| 30.0 | 329.0 |
| 35.0 | 342.0 |
| No Correlation | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
|---|---|---|---|---|---|---|
| a | 0.9481 | 0.8350 | 0.8213 | 0.7761 | 0.8113 | 0.9086 |
| b | 0.0056 | 0.0229 | 0.0243 | 0.0316 | 0.0316 | 0.0202 |
| CR | 0.7999 | 0.9592 | 0.9472 | 0.9545 | 0.9833 | 0.9818 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, Y.-W.; Jeong, W. Numerical Study of Spatial Behavior of Solute Particle Transport in Single Fracture with Variable Apertures. Water 2018, 10, 673. https://doi.org/10.3390/w10060673
Jeong Y-W, Jeong W. Numerical Study of Spatial Behavior of Solute Particle Transport in Single Fracture with Variable Apertures. Water. 2018; 10(6):673. https://doi.org/10.3390/w10060673
Chicago/Turabian StyleJeong, Yong-Wook, and Woochang Jeong. 2018. "Numerical Study of Spatial Behavior of Solute Particle Transport in Single Fracture with Variable Apertures" Water 10, no. 6: 673. https://doi.org/10.3390/w10060673
APA StyleJeong, Y.-W., & Jeong, W. (2018). Numerical Study of Spatial Behavior of Solute Particle Transport in Single Fracture with Variable Apertures. Water, 10(6), 673. https://doi.org/10.3390/w10060673





