Modeling Soil Water Dynamics and Pasture Growth in the Montado Ecosystem Using MOHID Land
Abstract
1. Introduction
2. Material and Methods
2.1. Field Site Description and Data
2.2. Model Description
2.2.1. Soil Water Dynamics
2.2.2. Plant Growth
2.3. Model Setup, Calibration, and Validation
2.4. Simulation Scenarios
3. Results and Discussion
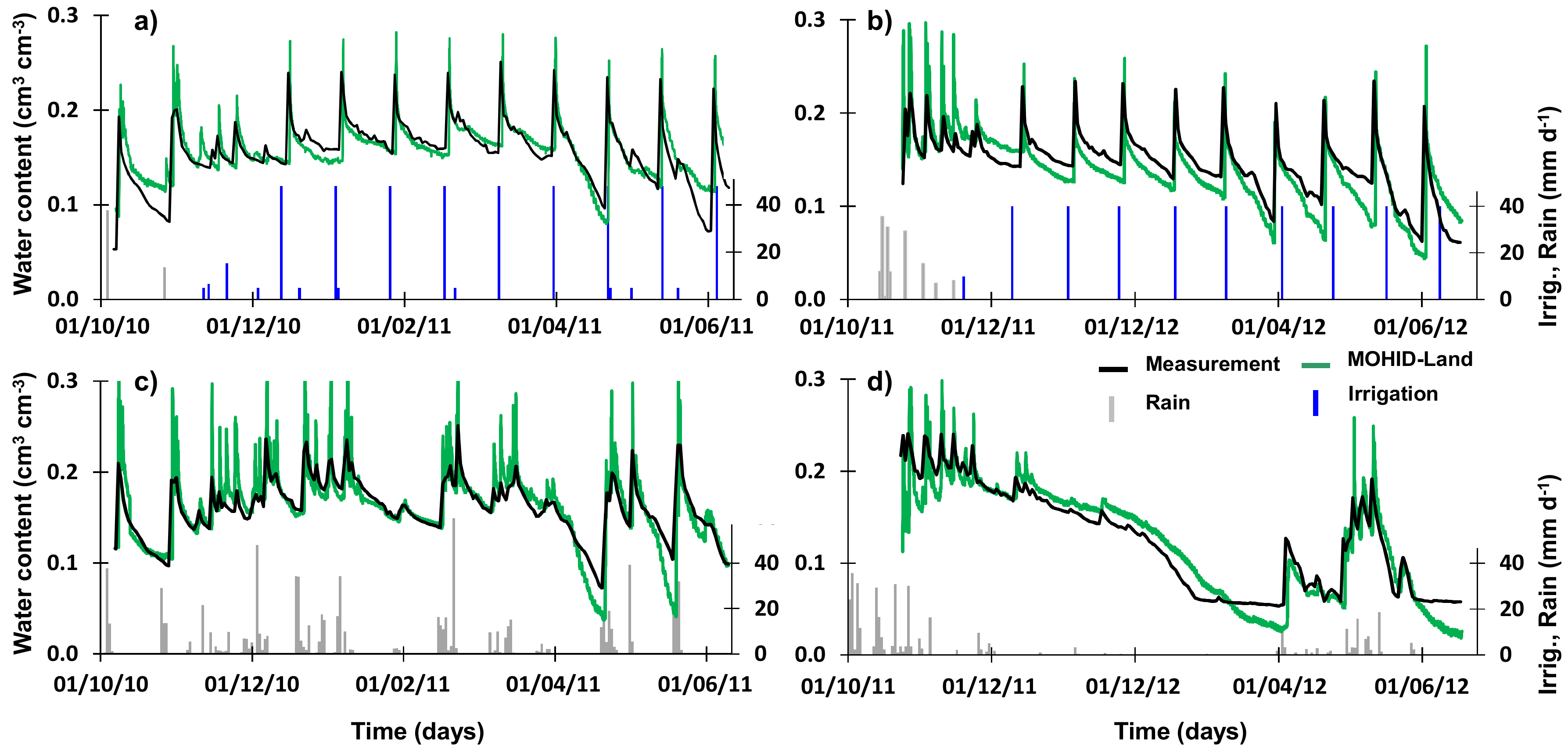
3.1. Soil Water Contents
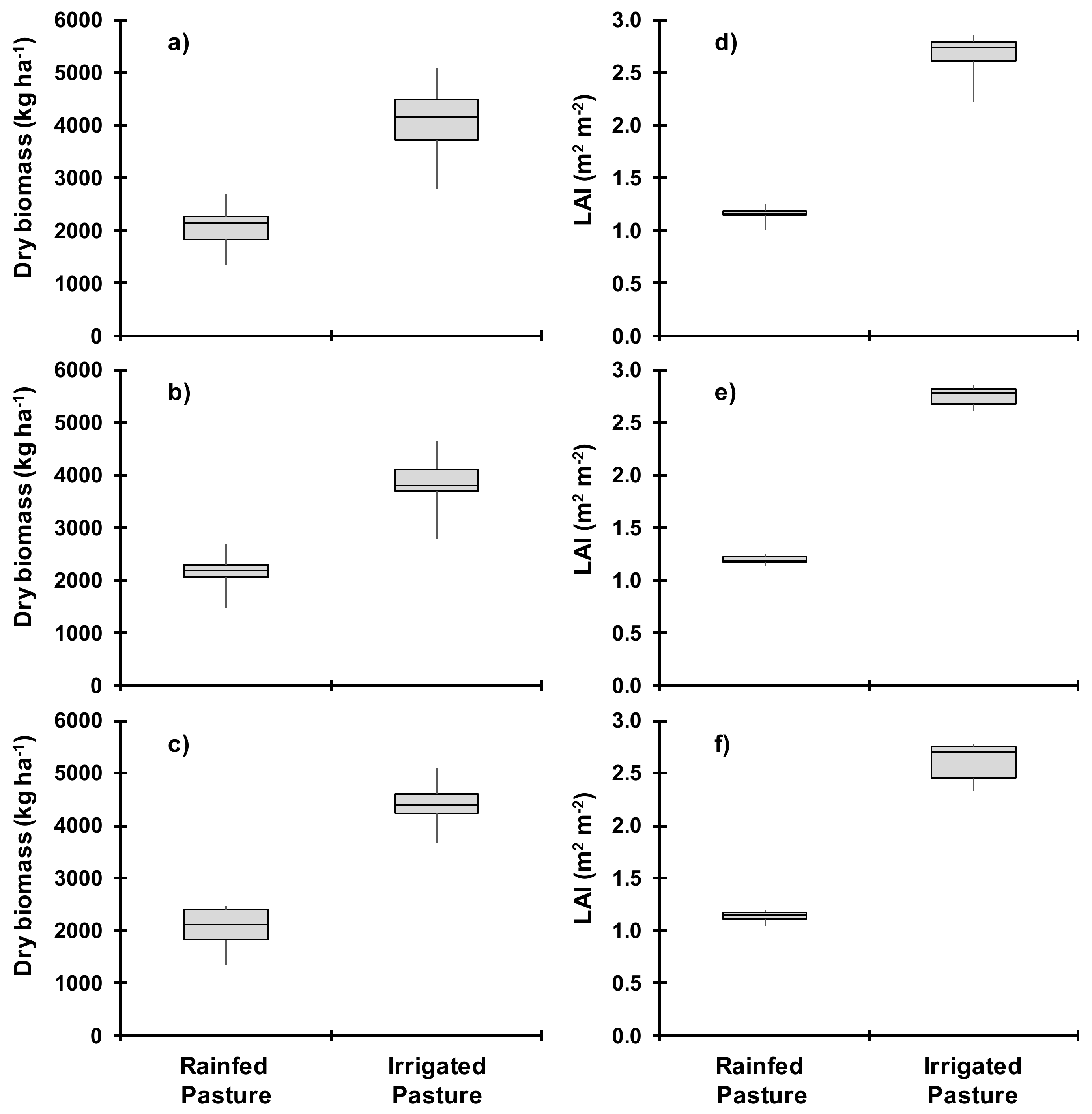
3.2. Pasture Growth
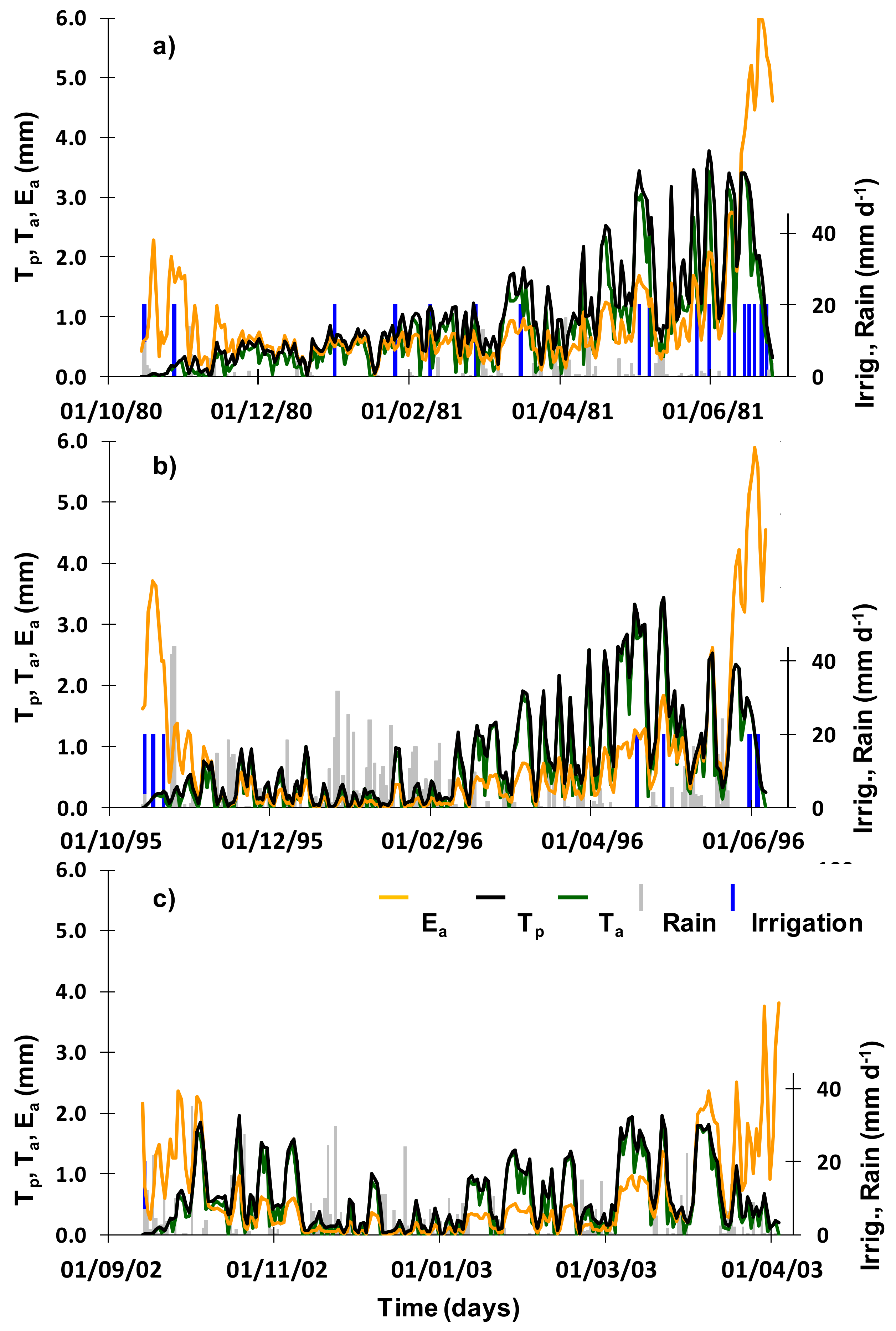
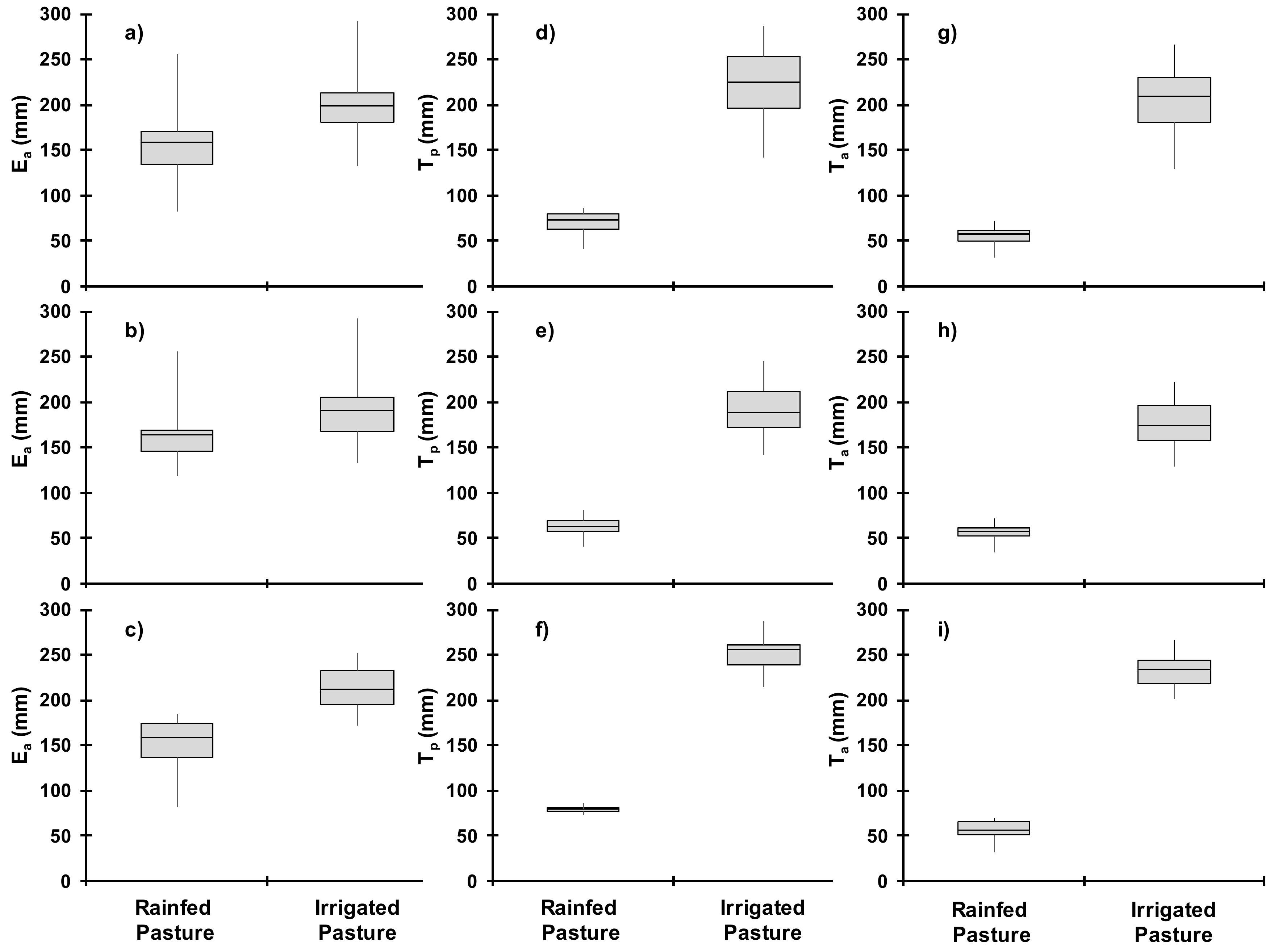
3.3. Soil Water Balance
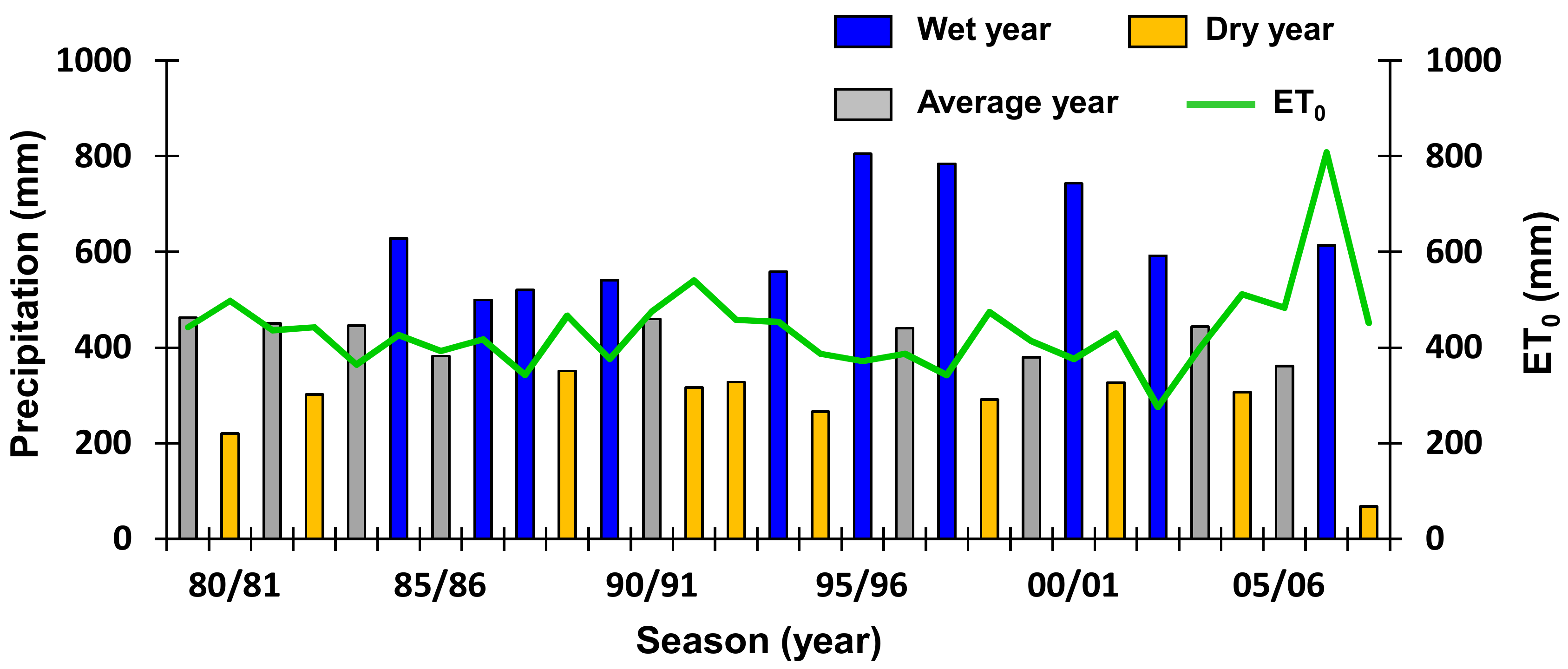
3.4. Dry Biomass and Water Balance Estimates in Wet and Dry Seasons
3.5. Future Research Needs Direction
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aronson, J.; Santos-Pereira, J.; Pausas, J.G. (Eds.) Cork Oak Woodlands on the Edge: Ecology, Adaptive Management, and Restoration; Island Press: Washington, DC, USA, 2009; pp. 1–10. [Google Scholar]
- Pinto-Correia, T.; Ribeiro, N.; Sá-Sousa, P. Introducing the montado, the cork and holm oak agroforestry system of Southern Portugal. Agrofor. Syst. 2011, 82, 99–104. [Google Scholar] [CrossRef]
- Pinto-Correia, T.; Mascarenhas, J. Contribution to the extensification/intensification debate: New trends in the Portuguese montado. Landsc. Urban Plan. 1999, 46, 125–131. [Google Scholar] [CrossRef]
- Santos, R.; Clemente, P.; Brouwer, R.; Antunes, P.; Pinto, R. Landowner preferences for agri-environmental agreements to conserve the montado ecosystem in Portugal. Ecol. Econ. 2015, 118, 159–167. [Google Scholar] [CrossRef]
- Guerra, C.A.; Pinto-Correia, T. Linking farm management and ecosystem service provision: Challenges and opportunities for soil erosion prevention in Mediterranean silvo-pastoral systems. Land Use Policy 2016, 51, 54–65. [Google Scholar] [CrossRef]
- Garrido, P.; Elbakidze, M.; Angelstam, P.; Plieninger, T.; Pulido, F.; Moreno, G. Stakeholder perspectives of wood-pasture ecosystem services: A case study from Iberian dehesas. Land Use Policy 2017, 60, 324–333. [Google Scholar] [CrossRef]
- Pinto-Correia, T.; Azeda, C. Public policies creating tensions in Montado management models: Insights from farmers’ representations. Land Use Policy 2017, 64, 76–82. [Google Scholar] [CrossRef][Green Version]
- Fragoso, R.; Marques, C.; Lucas, M.R.; Martins, M.B.; Jorge, R. The economic effects of common agricultural policy on Mediterranean montado/dehesa ecosystem. J. Policy Model. 2011, 33, 311–327. [Google Scholar] [CrossRef]
- Sándor, R.; Barcza, Z.; Hidy, D.; Lellei-Kovács, E.; Ma, S.; Bellocchi, G. Modelling of grassland fluxes in Europe: Evaluation of two biogeochemical models. Agric. Ecosyst. Environ. 2016, 215, 1–19. [Google Scholar] [CrossRef]
- Tenhunen, J.D.; Serra, A.S.; Harley, P.C.; Dougherty, R.L.; Reynolds, J.F. Factors influencing carbon fixation and water use by mediterranean sclerophyll shrubs during summer drought. Oecologia 1990, 82, 381–393. [Google Scholar] [CrossRef] [PubMed]
- Hussain, M.Z.; Otieno, D.O.; Mirzae, H.; Li, Y.L.; Schmidt, M.W.T.; Siebke, L.; Tenhunen, J.D. CO2 exchange and biomass development of the herbaceous vegetation in the Portuguese montado ecosystem during spring. Agric. Ecosyst. Environ. 2009, 132, 143–152. [Google Scholar] [CrossRef]
- Jongen, M.; Pereira, J.S.; Aires, L.M.I.; Pio, C.A. The effects of drought and timing of precipitation on the inter-annual variation in ecosystem-atmosphere exchange in a Mediterranean grassland. Agric. For. Meteorol. 2011, 151, 595–606. [Google Scholar] [CrossRef]
- Jongen, M.; Lecomte, X.; Unger, S.; Pintó-Marijuan, M.; Pereira, J.S. The impact of changes in the timing of precipitation on the herbaceous understorey of Mediterranean evergreen oak woodlands. Agric. For. Meteorol. 2013, 171, 163–173. [Google Scholar] [CrossRef]
- Jongen, M.; Unger, S.; Fangueiro, D.; Cerasoli, S.; Silva, J.M.N.; Pereira, J.S. Resilience of montado understorey to experimental precipitation variability fails under severe natural drought. Agric. Ecosyst. Environ. 2013, 178, 8–30. [Google Scholar] [CrossRef]
- Christensen, J.H.; Hewitson, B.; Busuioc, A.; Chen, A.; Gao, X.; Held, I.; Jones, R.; Kolli, R.K.; Kwon, W.-T.; Laprise, R.; et al. Regional climate projections. In Climate Change 2007: The Physical Science Basis; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC); Cambridge University Press: Cambridge, UK, 2007; pp. 847–940. [Google Scholar]
- IPCC. Climate Change 2007: The Physical Science Basis; Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- White, M.A.; Thornton, P.E.; Running, S.W.; Nemani, R.R. Parameterization and Sensitivity Analysis of the BIOME–BGC Terrestrial Ecosystem Model: Net Primary Production Controls. Earth Interact. 2000, 4, 1–85. [Google Scholar] [CrossRef]
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Sinoquet, H. An overview of the crop model STICS. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Wu, L.; McGechan, M.B.; McRoberts, N.; Baddeley, J.A.; Watson, C.A. SPACSYS: Integration of a 3D root architecture component to carbon, nitrogen and water cycling—Model description. Ecol. Model. 2007, 200, 343–359. [Google Scholar] [CrossRef]
- Williams, J.R.; Izaurralde, R.C.; Steglich, E.M. Agricultural Policy/Environmental eXtender Model: Theoretical Documentation Version 0604; Texas AgriLIFE Research, Texas A & M University: Temple, TX, USA, 2008; Available online: http://epicapex.brc.tamus.edu (accessed on 15 January 2018).
- Perego, A.; Giussani, A.; Sanna, M.; Fumagalli, M.; Carozzi, M.; Alfieri, L.; Brenna, S.; Acutis, M. The ARMOSA simulation crop model: Overall features, calibration and validation results. Ital. J. Agrometeorol. 2013, 18, 23–38. [Google Scholar]
- Ma, S.; Lardy, R.; Graux, A.-I.; Ben Touhami, H.; Klumpp, K.; Martin, R.; Bellocchi, G. Regional-scale analysis of carbon and water cycles on managed grassland systems. Environ. Model. Softw. 2015, 72, 356–371. [Google Scholar] [CrossRef]
- Trancoso, A.R.; Braunschweig, F.; Chambel Leitão, P.; Obermann, M.; Neves, R. An advanced modelling tool for simulating complex river systems. Sci. Total Environ. 2009, 407, 3004–3016. [Google Scholar] [CrossRef] [PubMed]
- FAO. World Reference Base for Soil Resources. A Framework for International Classification, Correlation and Communication; World Soil Resources Report 103; Food and Agriculture Organization of the United Nations: Rome, Italy, 2006. [Google Scholar]
- Soil Survey Staff. Soil Survey Laboratory Information Manual; Soil Survey Investigations Report No. 45; Version 2.0.; Burt, R., Ed.; U.S. Department of Agriculture, Natural Resources Conservation Service: Washington, DC, USA, 2011. [Google Scholar]
- Gomes, M.P.; Silva, A.A. Um novo diagrama triangular para a classificação básica da textura do solo. Garcia Orta 1962, 10, 171–179. [Google Scholar]
- Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon, and organic matter. In Methods of Soil Analysis, Part 3. Chemical Methods; Sparks, D.L., Page, A.L., Helmke, P.A., Loeppert, R.H., Soltanpour, P.N., Tabatabai, M.A., Johnston, C.T., Sumner, M.E., Eds.; Soil Science Society of America Inc., American Society of Agronomy Inc.: Madison, WI, USA, 1996; pp. 961–1010. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; Wiley: Hoboken, NJ, USA, 1978. [Google Scholar]
- Skaggs, T.H.; van Genuchten, M.T.; Shouse, P.J.; Poss, J.A. Macroscopic approaches to root water uptake as a function of water and salinity stress. Agric. Water Manag. 2006, 86, 140–149. [Google Scholar] [CrossRef]
- Šimůnek, J.; Hopmans, J.W. Modeling compensated root water and nutrient uptake. Ecol. Model. 2009, 220, 505–521. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; Irrigation & Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- American Society of Civil Engineers (ASCE). Hydrology Handbook Task Committee on Hydrology Handbook; II Series, GB 661.2. H93; ASCE: Reston, VA, USA, 1996; pp. 96–104. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool; Theoretical Documentation; Version 2009; Texas Water Resources Institute; Technical Report No. 406; Texas A&M University System: College Station, TX, USA, 2011. [Google Scholar]
- Ramos, T.B.; Simionesei, L.; Jauch, E.; Almeida, C.; Neves, R. Modelling soil water and maize growth dynamics influenced by shallow groundwater conditions in the Sorraia Valley region, Portugal. Agric. Water Manag. 2017, 185, 27–42. [Google Scholar] [CrossRef]
- Monsi, M.; Saeki, T. Uber den Lictfaktor in den Pflanzengesellschaften und sein Bedeutung fur die Stoffproduktion. Jpn. J. Bot. 1953, 14, 22–52. [Google Scholar]
- Stockle, C.O.; Williams, J.R.; Rosenberg, N.J.; Jones, C.A. A method for estimating the direct and climatic effects of rising atmospheric carbon dioxide on growth and yield of crops: Part I—Modification of the EPIC model for climate change analysis. Agric. Syst. 1992, 38, 225–238. [Google Scholar] [CrossRef]
- Jones, C.A. C-4 Grasses and Cereals; John Wiley & Sons: New York, NY, USA, 1985; p. 419. [Google Scholar]
- Purser, R.J.; Leslie, L.M. A Semi-Implicit, Semi-Lagrangian Finite-Difference Scheme Using Hligh-Order Spatial Differencing on a Nonstaggered Grid. Mon. Weather Rev. 1988, 116, 2069–2080. [Google Scholar] [CrossRef]
- Wesseling, J.G.; Elbers, J.A.; Kabat, P.; van den Broek, B.J. SWATRE: Instructions for Input Report; Winand Staring Centre: Wageningen, The Netherlands, 1991. [Google Scholar]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Transaction of the ASABE: St. Joseph, MI, USA, 2007; Volume 50, pp. 885–900. [Google Scholar]
- Wang, X.; Williams, J.R.; Gassman, P.W.; Baffaut, C.; Izaurralde, R.C.; Jeong, J.; Kiniry, J.R. EPIC and APEX: Model Use, Calibration, and Validation; Transaction of the ASABE: St. Joseph, MI, USA, 2012; Volume 55, pp. 1447–1462. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Ramos, T.B.; Šimůnek, J.; Gonçalves, M.C.; Martins, J.C.; Prazeres, A.; Pereira, L.S. Two-dimensional modeling of water and nitrogen fate from sweet sorghum irrigated with fresh and blended saline waters. Agric. Water Manag. 2012, 111, 87–104. [Google Scholar] [CrossRef]
- Dabach, S.; Lazarovitch, N.; Šimůnek, J.; Shani, U. Numerical investigation of irrigation scheduling based on soil water status. Irrig. Sci. 2013, 31, 27–36. [Google Scholar] [CrossRef]
- Sándor, R.; Barcza, Z.; Acutis, M.; Doro, L.; Hidy, D.; Köchy, M.; Bellocchi, G. Multi-model simulation of soil temperature, soil water content and biomass in Euro-Mediterranean grasslands: Uncertainties and ensemble performance. Eur. J. Agron. 2017, 88, 22–40. [Google Scholar] [CrossRef]
- Yu, Q.; Saseendran, S.A.; Ma, L.; Flerchinger, G.N.; Green, T.R.; Ahuja, L.R. Modeling a wheat–maize double cropping system in China using two plant growth modules in RZWQM. Agric. Syst. 2006, 89, 457–477. [Google Scholar] [CrossRef]
- Xu, X.; Huang, G.; Sun, C.; Pereira, L.S.; Ramos, T.B.; Huang, Q.; Hao, Y. Assessing the effects of water table depth on water use, soil salinity and wheat yield: Searching for a target depth for irrigated areas in the upper Yellow River basin. Agric. Water Manag. 2013, 125, 46–60. [Google Scholar] [CrossRef]
- Wang, X.; Huang, G.; Yang, J.; Huang, Q.; Liu, H.; Yu, L. An assessment of irrigation practices: Sprinkler irrigation of winter wheat in the North China Plain. Agric. Water Manag. 2015, 159, 197–208. [Google Scholar] [CrossRef]
- Hou, L.; Zhou, Y.; Bao, H.; Wenninger, J. Simulation of maize (Zea mays L.) water use with the HYDRUS-1D model in the semi-arid Hailiutu River catchment, Northwest China. Hydrol. Sci. J. 2016, 62, 93–103. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting; I: Factors governing measurement accuracy. Agric. Water Manag. 2012, 98, 899–920. [Google Scholar] [CrossRef]
- Huxman, T.E.; Wilcox, B.P.; Breshears, D.D.; Scott, R.L.; Snyder, K.A.; Small, E.E.; Hultine, K.; Pockman, W.T.; Jackson, R.B. Ecohydrological implications of woody plant encroachment. Ecology 2005, 86, 308–319. [Google Scholar] [CrossRef]
- Kurc, S.A.; Small, E.E. Soil moisture variations and ecosystem-scale fluxes of water and carbon in semiarid grassland and shrubland. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Graham, S.L.; Kochendorfer, J.; McMillan, A.M.S.; Duncan, M.J.; Srinivasan, M.S.; Hertzog, G. Effects of agricultural management on measurements, prediction, and partitioning of evapotranspiration in irrigated grasslands. Agric. Water Manag. 2016, 177, 340–347. [Google Scholar] [CrossRef]
- Chapman, D.F.; Rawnsley, R.P.; Cullen, B.R.; Clark, D.A. Inter-annual variability in pasture herbage accumulation in temperate dairy regions: Causes, consequences, and management tools. In Proceedings of the 22nd International Grassland Congress: Revitalising Grasslands to Sustain Our Communities, Sydney, Australia, 15–19 September 2013; pp. 798–805. [Google Scholar]
- Van der Molen, M.K.; Dolman, A.J.; Ciais, P.; Eglin, T.; Gobron, N.; Law, B.E.; Wang, G. Drought and ecosystem carbon cycling. Agric. For. Meteorol. 2011, 151, 765–773. [Google Scholar] [CrossRef]
- Dane, J.J.; Topp, G.C. (Eds.) Methods of Soil Analysis Part 4. Physical Methods; Soil Science Society of America, Inc.: Madison, WI, USA, 2002. [Google Scholar]
- Ramos, T.B.; Gonçalves, M.C.; Brito, D.; Martins, J.C.; Pereira, L.S. Development of class pedotransfer functions for integrating water retention properties into Portuguese soil maps. Soil Res. 2013, 51, 262–277. [Google Scholar] [CrossRef]


| Soil Properties | Soil Layers | ||
|---|---|---|---|
| Depth (m) | 0–0.2 | 0.2–0.8 | >0.8 |
| Coarse sand, 2000–200 μm (%) | 65.83 | 56.18 | 63.43 |
| Fine sand, 200–20 μm (%) | 21.70 | 21.64 | 13.91 |
| Silt, 20–2 μm (%) | 10.98 | 17.34 | 9.35 |
| Clay, <2 μm (%) | 1.49 | 9.35 | 13.30 |
| Texture | Loamy-sand | Sandy-loam | Sandy-loam |
| Bulk density (g cm−3) | 1.65 | 1.57 | - |
| Organic matter (%) | 1.39 | 0.32 | 0.02 |
| Parameter | Soil Layers | ||
|---|---|---|---|
| Depth (m) | 0–0.2 | 0.2–0.8 | >0.8 |
| Irrigated Plots: | |||
| θr (cm3 cm−3) | 0.035 | 0.035 | 0.067 |
| θs (cm3 cm−3) | 0.300 | 0.300 | 0.450 |
| α (cm−1) | 0.015 | 0.015 | 0.020 |
| η (-) | 1.80 | 1.80 | 1.41 |
| ℓ (-) | 0.50 | 0.50 | 0.50 |
| Ks (cm d−1) | 62.4 | 27.8 | 4.5 |
| Rainfed Plots: | |||
| θr (cm3 cm−3) | 0.035 | 0.035 | 0.067 |
| θs (cm3 cm−3) | 0.290 | 0.300 | 0.450 |
| α (cm−1) | 0.015 | 0.015 | 0.020 |
| η (-) | 1.85 | 1.80 | 1.41 |
| ℓ (-) | 0.50 | 0.50 | 0.50 |
| Ks (cm d−1) | 62.4 | 27.8 | 4.5 |
| Crop Parameter | Irrigated Plot | Rainfed Plot |
|---|---|---|
| Optimal temperature for plant growth, Topt (°C) | 20.0 | 20.0 |
| Minimum temperature for plant growth, Tbase (°C) | 5.0 | 5.0 |
| Plant radiation-use efficiency, RUE [(kg ha−1) (MJ m−2)−1] | 8.0 | 8.0 |
| Total heat units required for plant maturity, PHU (°C) | 1800 | 1800 |
| Fraction of PHU to reach the end of stage 1 (initial crop stage), frPHU,init (-) | 0.05 | 0.05 |
| Fraction of PHU to reach the end of stage 2 (canopy development stage), frPHU,dev (-) | 0.20 | 0.60 |
| Fraction of PHU after which LAI starts to decline, frPHU,sen (-) | 0.70 | 0.70 |
| Maximum leaf area index, LAImax (m2 m−2) | 3.0 | 3.0 |
| Fraction of LAImax at the end of stage 1 (initial crop stage), frLAImax,ini (-) | 0.05 | 0.05 |
| Fraction of LAImax at the end of stage 2 (canopy development stage), frLAImax,dev (-) | 0.55 | 0.40 |
| Maximum canopy height, hc,max (m) | 0.30 | 0.30 |
| Maximum root depth, Zroot,max (m) | 0.40 | 0.40 |
| Statistic | Irrigated Plot | Rainfed Plot | ||
|---|---|---|---|---|
| Water Content (cm3 cm−3) | Aboveground Dry Biomass (kg ha−1) | Water Content (cm3 cm−3) | Aboveground Dry Biomass (kg ha−1) | |
| Calibration set (2010–2011) | ||||
| ME | 0.001 | −870.8 | −0.002 | −739.4 |
| RMSE | 0.015 | 1286.5 | 0.018 | 1125.5 |
| NRMSE | 0.039 | 0.210 | 0.030 | 0.372 |
| EF | 0.632 | 0.869 | 0.780 | 0.584 |
| Validation set (2011–2012) | ||||
| ME | −0.010 | −667.6 | −0.003 | 120.9 |
| RMSE | 0.026 | 1088.1 | 0.022 | 279.8 |
| NRMSE | 0.047 | 0.375 | 0.024 | 0.243 |
| EF | 0.481 | 0.718 | 0.863 | 0.882 |
| Season | Inputs | Outputs | |||||
|---|---|---|---|---|---|---|---|
| P (mm) | I (mm) | ΔSS (mm) | Ea (mm) | Ta (mm) | Ta/Tp (-) | DP (mm) | |
| Irrigated plot: | |||||||
| 2010–2011 | 134 | 454 | −31 | 128 | 143 | 0.95 | 296 |
| 2011–2012 | 152 | 370 | 56 | 155 | 166 | 0.86 | 257 |
| Rainfed plot: | |||||||
| 2010–2011 | 873 | 0 | −263 | 182 | 65 | 0.94 | 362 |
| 2011–2012 | 413 | 0 | 65 | 198 | 53 | 0.60 | 226 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simionesei, L.; Ramos, T.B.; Oliveira, A.R.; Jongen, M.; Darouich, H.; Weber, K.; Proença, V.; Domingos, T.; Neves, R. Modeling Soil Water Dynamics and Pasture Growth in the Montado Ecosystem Using MOHID Land. Water 2018, 10, 489. https://doi.org/10.3390/w10040489
Simionesei L, Ramos TB, Oliveira AR, Jongen M, Darouich H, Weber K, Proença V, Domingos T, Neves R. Modeling Soil Water Dynamics and Pasture Growth in the Montado Ecosystem Using MOHID Land. Water. 2018; 10(4):489. https://doi.org/10.3390/w10040489
Chicago/Turabian StyleSimionesei, Lucian, Tiago B. Ramos, Ana R. Oliveira, Marjan Jongen, Hanaa Darouich, Kirsten Weber, Vânia Proença, Tiago Domingos, and Ramiro Neves. 2018. "Modeling Soil Water Dynamics and Pasture Growth in the Montado Ecosystem Using MOHID Land" Water 10, no. 4: 489. https://doi.org/10.3390/w10040489
APA StyleSimionesei, L., Ramos, T. B., Oliveira, A. R., Jongen, M., Darouich, H., Weber, K., Proença, V., Domingos, T., & Neves, R. (2018). Modeling Soil Water Dynamics and Pasture Growth in the Montado Ecosystem Using MOHID Land. Water, 10(4), 489. https://doi.org/10.3390/w10040489






