Spatial Downscaling of Satellite Precipitation Data in Humid Tropics Using a Site-Specific Seasonal Coefficient
Abstract
:1. Introduction
2. Materials and Methods
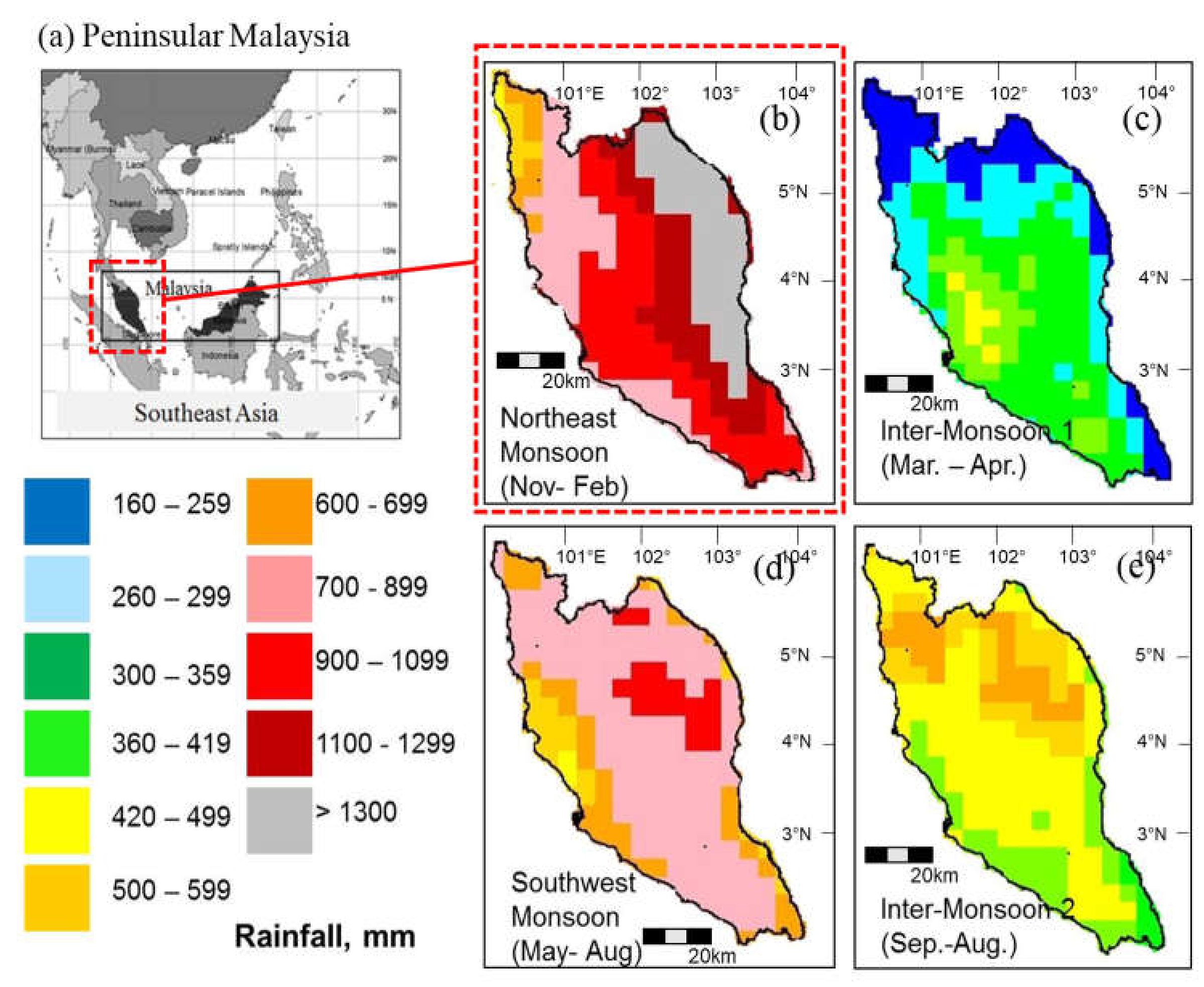
2.1. Study Site
2.2. Data
2.2.1. Tropical Rainfall Measuring Mission Satellite Data
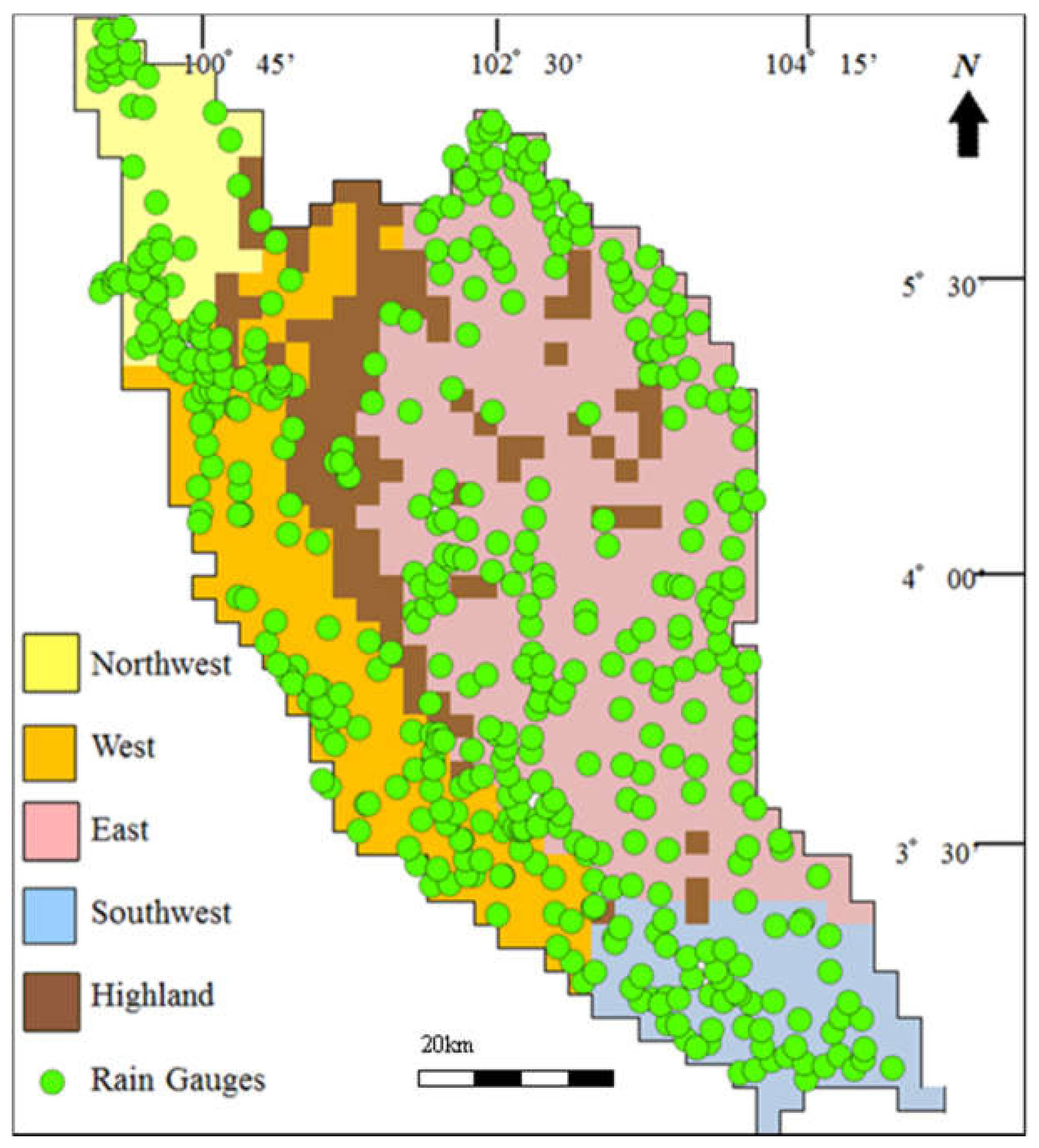
2.2.2. Rain Gauge Data
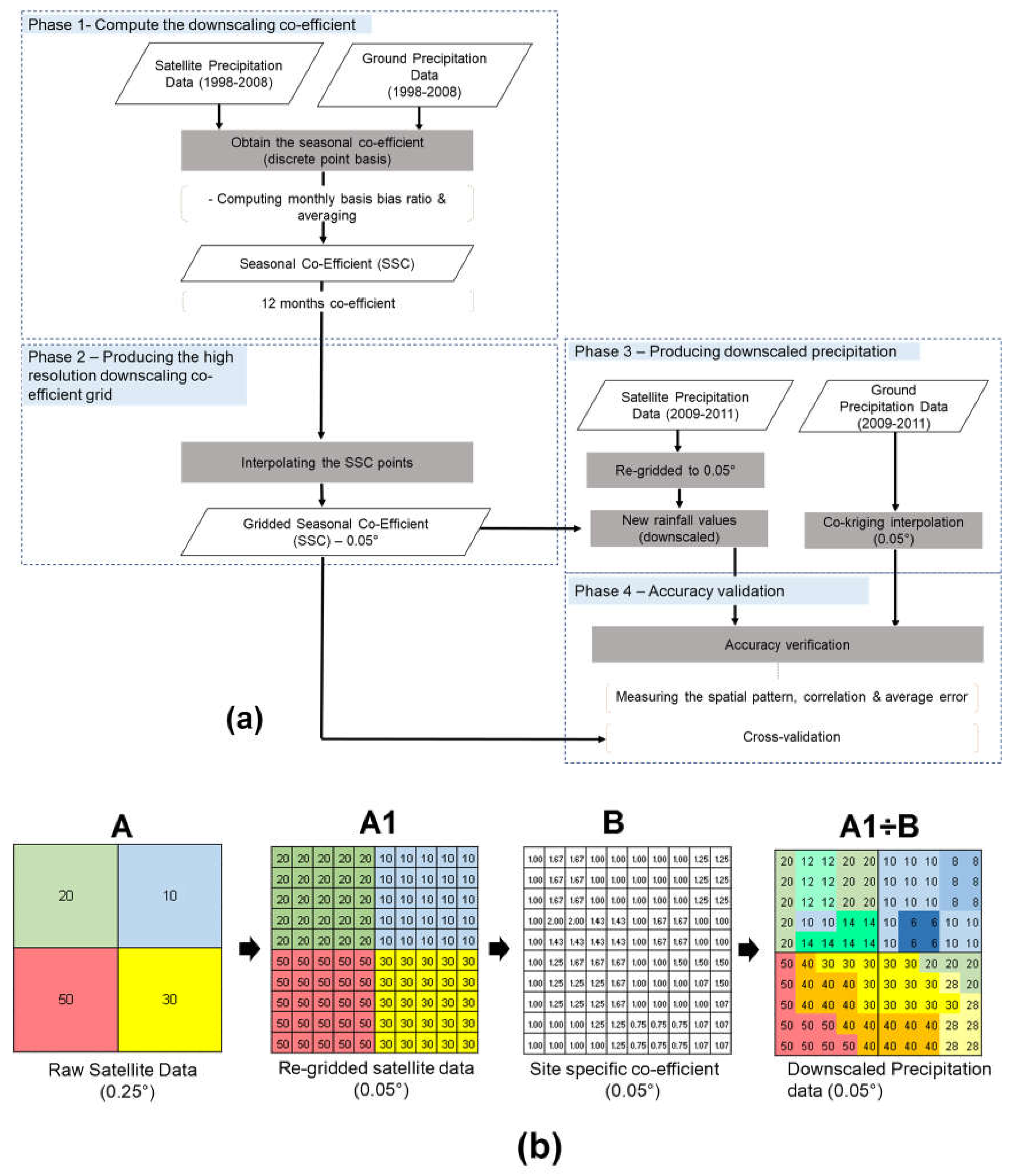
2.3. Downscaling Tropical Rainfall Measuring Mission Data Using the Seasonal Site-Specific Coefficient
2.3.1. Phase 1: Preparation of the High-Resolution Precipitation Data for Coefficient Derivation
2.3.2. Phase 2: Deriving the Seasonal Site-Specific Coefficient
2.3.3. Phase 3: Downscaling the Tropical Rainfall Measuring Mission Satellite Data Using the Site-Specific Coefficient
2.3.4. Phase 4: Accuracy Validation
2.4. Determining the Effect of Interpolation to the Gridded Areal Ground Rainfall
3. Results
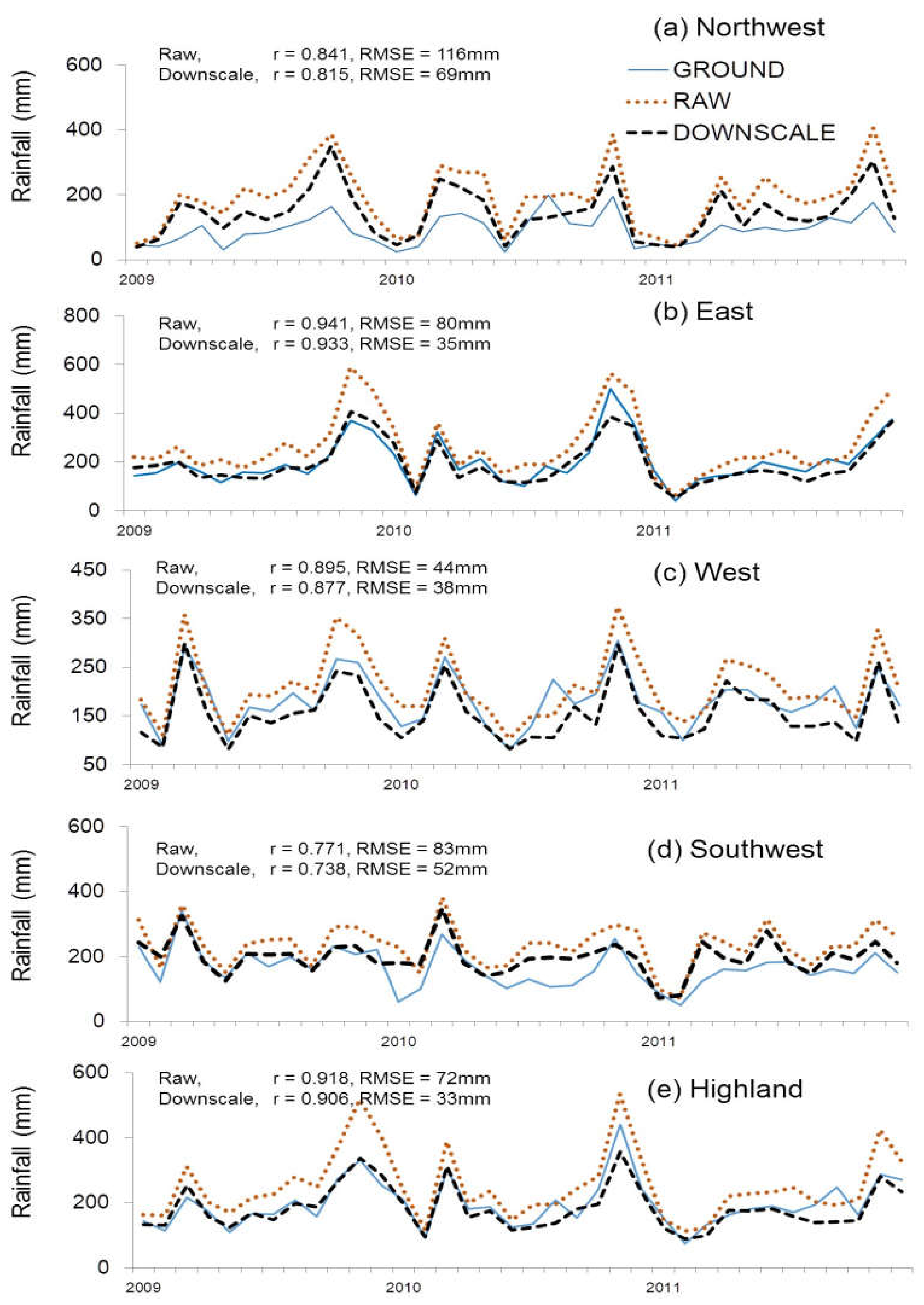
3.1. Performance of the Site-Specific Coefficient Tropical Rainfall Measuring Mission Downscaled Precipitation
3.2. Coefficient of Variance of Historical Bias Ratio Records and Downscaling Performance
3.3. Comparison of the Site-Specific Coefficient-Downscale and Other Satellite Precipitation Products
3.4. Effects of the Interpolation Process
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Behrangi, A.; Khakbaz, B.; Jaw, T.C.; AghaKouchak, A.; Hsu, K.; Sorooshian, S. Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrol. 2011, 360, 225–237. [Google Scholar] [CrossRef]
- Mahmud, M.R.; Numata, S.; Hosaka, T.; Matsuyama, H.; Hashim, M. Preliminary study for effective seasonal downscaling of TRMM precipitation data in Peninsular Malaysia: Local scale validation using high resolution areal precipitation. Remote Sens. 2015, 7, 4092–4111. [Google Scholar] [CrossRef]
- Bidin, K.; Chappell, N.A. First evidence of a structured and dynamic spatial pattern of rainfall within a small humid tropical catchment. Hydrol. Earth Syst. Sci. 2003, 7, 245–253. [Google Scholar] [CrossRef]
- Chadwick, R.; Boutle, I.; Martin, G. Spatial patterns of precipitation change in CMIP5: Why the rich do not get richer in the tropics. J. Clim. 2013, 26, 3803–3822. [Google Scholar] [CrossRef]
- Chen, F.; Liu, Y.; Liu, Q.; Li, X. Spatial downscaling of TRMM 3B43 precipitation considering spatial heterogeneity. Int. J. Remote Sens. 2014, 35, 3074–3093. [Google Scholar] [CrossRef]
- Cho, H.; Choi, M. Spatial downscaling of TRMM precipitation using MODIS product in the Korean Peninsula. In Proceedings of the AGU 2013 Fall Meeting, Francisco, CA, USA, 9–13 December 2013. Abstract, H43G-1537. [Google Scholar]
- Immerzeel, W.W.; Rutten, M.M.; Droogers, P. Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula. Remote Sens. Environ. 2009, 113, 362–370. [Google Scholar] [CrossRef]
- Jian, F.; Du, J.; Xu, W.; Shi, P.; Li, M.; Ming, X. Spatial downscaling of TRMM data based on orographic effect and meteorological condition of mountainous region. Adv. Water Resour. 2013, 61, 42–50. [Google Scholar]
- Park, N.-W. Spatial downscaling of TRMM precipitation using geostatistics and fine scale environmental variables. Adv. Meteorol. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Shi, Y.; Song, L.; Xia, Z.; Lin, Y.; Myeni, R.B.; Choi, S.; Was, L.; Ni, X.; Lao, C.; Yang, F. Mapping annual precipitation across mainland China in the period of 2001–2010 from TRMM 3B43 product using spatial downscaling approach. Remote Sens. 2015, 7, 5849–5878. [Google Scholar] [CrossRef]
- Park, N.-W.; Kyriakidis, P.C.; Hong, S. Geostatistical integration of coarse resolution satellite precipitation products and rain gauge data to map precipitation at fine spatial resolutions. Remote Sens. 2017, 9, 255. [Google Scholar] [CrossRef]
- Ulloa, J.; Ballari, D.; Campozano, L.; Samaniego, E. Two-step downscaling of TRMM 3B43 V7 precipitation in contrasting climatic regions with sparse monitoring: The case of Ecuador in tropical South America. Remote Sens. 2017, 9, 758. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Ji, X.; Luo, X.; Li, X. Fine-Resolution Precipitation Mapping in a Mountainous Watershed: Geostatistical Downscaling of TRMM Products Based on Environmental Variables. Remote Sens. 2018, 10, 119. [Google Scholar] [CrossRef]
- Yatagai, A.; Krishnamurti, T.N.; Kumar, V.; Mishra, A.K.; Simon, A. Use of APHRODITE rain gauge–based precipitation and TRMM 3B43 products for improving Asian monsoon seasonal precipitation forecasts by the superensemble method. J. Clim. 2014, 27, 1062–1069. [Google Scholar] [CrossRef]
- Tao, K.; Barros, P. Using fractal downscaling of satellite precipitation products for hydrometeorological applications. J. Atmos. Ocean. Technol. 2010, 27, 409–427. [Google Scholar] [CrossRef]
- Anders, A.; Nesbitt, S.W. Altitudinal precipitation gradients in the tropics from Tropical Rainfall Measuring Mission (TRMM) Precipitation Radar. J. Hydrometeor. 2015, 16, 441–448. [Google Scholar] [CrossRef]
- Muller, C.J.; Back, L.E.; O’Gorman, P.A.; Emanuel, K.A. A model for the relationship between tropical precipitation and column water vapor. Geophys. Res. Lett. 2009, 36, L16804. [Google Scholar] [CrossRef]
- Chang, C.; Ding, Y.; Lau, N.; Johnson, R.H.; Wang, B.; Yasunari, T. The Global Monsoon System; World Scientific Series on Asia-Pacific Weather and Climate; World Scientific: Singapore, 2011; Volume 5. [Google Scholar]
- Lee, H.S. General rainfall patterns in Indonesia and the potential impacts of local season rainfall intensity. Water 2015, 7, 1751–1768. [Google Scholar] [CrossRef]
- Singhrattna, N.; Rajagopalan, B.; Kumar, K.K.; Clark, M. Interannual and interdecadal variability of Thailand Summer Monsoon Season. J. Clim. 2005, 18, 1697–1708. [Google Scholar] [CrossRef]
- Varikoden, H.; Preethi, B.; Samah, A.A.; Babu, C.A. Seasonal variation of rainfall characteristics in different intensity classes over Peninsular Malaysia. J. Hydrol. 2011, 404, 99–108. [Google Scholar] [CrossRef]
- Aldrian, E.; Dumenil, G.L.; Widodo, F.H. Seasonal variability of Indonesian rainfall in ECHAM4 simulations and in the reanalyses: The role of ENSO. Theor. Appl. Climatol. 2007, 87, 41–59. [Google Scholar] [CrossRef]
- Fein, J.S.; Stephens, P.L. Monsoons; John Wiley and Sons: New York, NY, USA, 1988. [Google Scholar]
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; Rudolf, B.; McNab, A.; Schneider, U. The Global Precipitation Climatology Project (GPCP) combined precipitation dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Manzanas, R. Statistical downscaling in the tropics can be sensitive to reanalysis choice: A Case Study for Precipitation in the Philippines. J. Clim. 2015, 28, 4171–4184. [Google Scholar] [CrossRef]
- Thompson, R.D. Atmospheric Processes and Systems, 1st ed.; Routledge: River Thames, UK, 1998. [Google Scholar]
- Wong, C.L.; Venneker, R.; Uhlenbrook, S.; Jamil, A.B.M.; Zhou, Y. Variability of rainfall in Peninsular Malaysia. Hydrol. Earth Syst. Discuss. 2009, 6, 5471–5503. [Google Scholar] [CrossRef]
- MACRES & UTM. Satellite Atlas Malaysia; Malaysian Centre for Remote Sensing: Kuala Lumpur, Malaysia, 2000. [Google Scholar]
- Okamoto, K.; Iguchi, T.; Takahashi, N.; Iwanami, K.; Ushio, T. The Global Satellite Mapping of Precipitation (GSMaP) project. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 25–29 July 2005; pp. 3414–3416. [Google Scholar]
- Hsu, K.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Chen, M.; Xie, P.; CPC Precipitation Working Group CPC/NCEP/NOAA. CPC Unified Gauge-based Analysis of Global Daily Precipitation. In Proceedings of the Western Pacific Geophysics Meeting, Cairns, Australia, 29 July–1 August 2008. [Google Scholar]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Xie, P.; Arkin, P.A. Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull. Am. Meteorol. Soc. 1996, 78, 2539–2558. [Google Scholar] [CrossRef]
- Reynolds, R.W. A real-time global sea surface temperature analysis. J. Clim. 1988, 1, 75–86. [Google Scholar] [CrossRef]
- Wagesho, N.; Goel, N.K.; Jain, M.K. Temporal and spatial variability of annual and seasonal rainfall over Ethiopia. Hydrol. Sci. J. 2013, 58, 354–373. [Google Scholar] [CrossRef]
- Mitchell, A. The ESRI Guide to GIS Analysis; ESRI Press: Redlands, CA, USA, 2005; Volume 2. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Mair, A.; Fares, A. Comparison of rainfall interpolation methods in a mountainous region of a tropical island. J. Hydrol. Eng. 2011, 16, 371–383. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Kishtawal, C.M.; Simon, A.; Yatagai, A. Use of a dense gauge network over India for improving blended TRMM products and downscaled weather models. J. Meteorol. Soc. Jpn. 2009, 87, 395–416. [Google Scholar] [CrossRef]
- Prasetia, R.; As-syakur, A.R.; Osawa, T. Validation of TRMM precipitation radar satellite data over Indonesian region. Theor. Appl. Climatol. 2013, 112, 575–587. [Google Scholar] [CrossRef]
- Roongroj, C.; Long, S.C. Thailand daily rainfall and comparison with TRMM products. J. Hydrometeorol. 2008, 9, 256–266. [Google Scholar]
- Endo, N.; Jun Matsumoto, J.; Lwin, T. Trends in Precipitation Extremes over Southeast Asia. SOLA 2009, 5, 168–171. [Google Scholar] [CrossRef]
- Ono, K.; Kazama, S. Analysis of extreme daily rainfall in Southeast Asia with a gridded daily rainfall data set. Hydro-climatology: Variability and Change In Proceedings of Symposium J-H02 Held During IUGG2011 in Melbourne, Melbourne, Australia, 28 June–7 July 2011; p. 344. [Google Scholar]
- Mahmud, M.R.; Hashim, M.; Mohd Reba, M.N. How effective is the new generation of GPM satellite precipitation in characterizing the rainfall variability over Malaysia? Asia-Pac. J. Atmos. Sci. 2017, 53, 375–384. [Google Scholar] [CrossRef]
- Sidle, R.C.; Tani, M.; Zeigler, A.D. Catchment processes in Southeast Asia: Atmospheric, hydrologic, erosion, nutrient cycling, and management effects. For. Ecol. Manag. 2006, 224, 1–4. [Google Scholar] [CrossRef]
- Liu, X.; Liu, F.M.; Wang, X.X.; Li, X.D.; Fan, Y.Y.; Cai, S.X.; Ao, T.Q. Combining rainfall data from rain gauges and TRMM in hydrological modelling of Laotian data-sparse basins. Appl. Water Sci. 2017, 7, 1487–1496. [Google Scholar] [CrossRef]
- Musiake, K. Hydrology and water resources in monsoon Asia: A consideration of the necessity of establishing a standing research community of hydrology and water resources in the Asia Pacific region. Hydrol. Process. 2003, 17, 2701–2709. [Google Scholar] [CrossRef]
- Jobard, I.; Desbois, M. Satellite estimation of the tropical precipitation using the METEOSTAT and SSM/I data. Atmos. Res. 1994, 34, 285–298. [Google Scholar] [CrossRef]
- Levizzani, V. Precipitation estimates using METEOSAT second generation (MSG): New perspectives from geostationary orbit. In Proceedings of the 1999 EUMETSAT meteorological Satellite Data users’ Conference, Copenhagen, Denmark, 6–10 September 1999; pp. 121–128. [Google Scholar]
- Turpeinin, O.M. Monitoring of precipitation with METEOSAT. Adv. Space Res. 1989, 9, 347–353. [Google Scholar] [CrossRef]
- Hendon, H.H. Indonesian rainfall variability: Impacts of ENSO and local air-sea interaction. J. Clim. 2003, 16, 1775–1790. [Google Scholar] [CrossRef]
- Loo, Y.Y.; Billa, L.; Singh, A. Effect of climate change on seasonal monsoon in Asia and its impact on the variability of monsoon rainfall in Southeast Asia. Geosci. Front. 2014, 6, 817–823. [Google Scholar] [CrossRef]
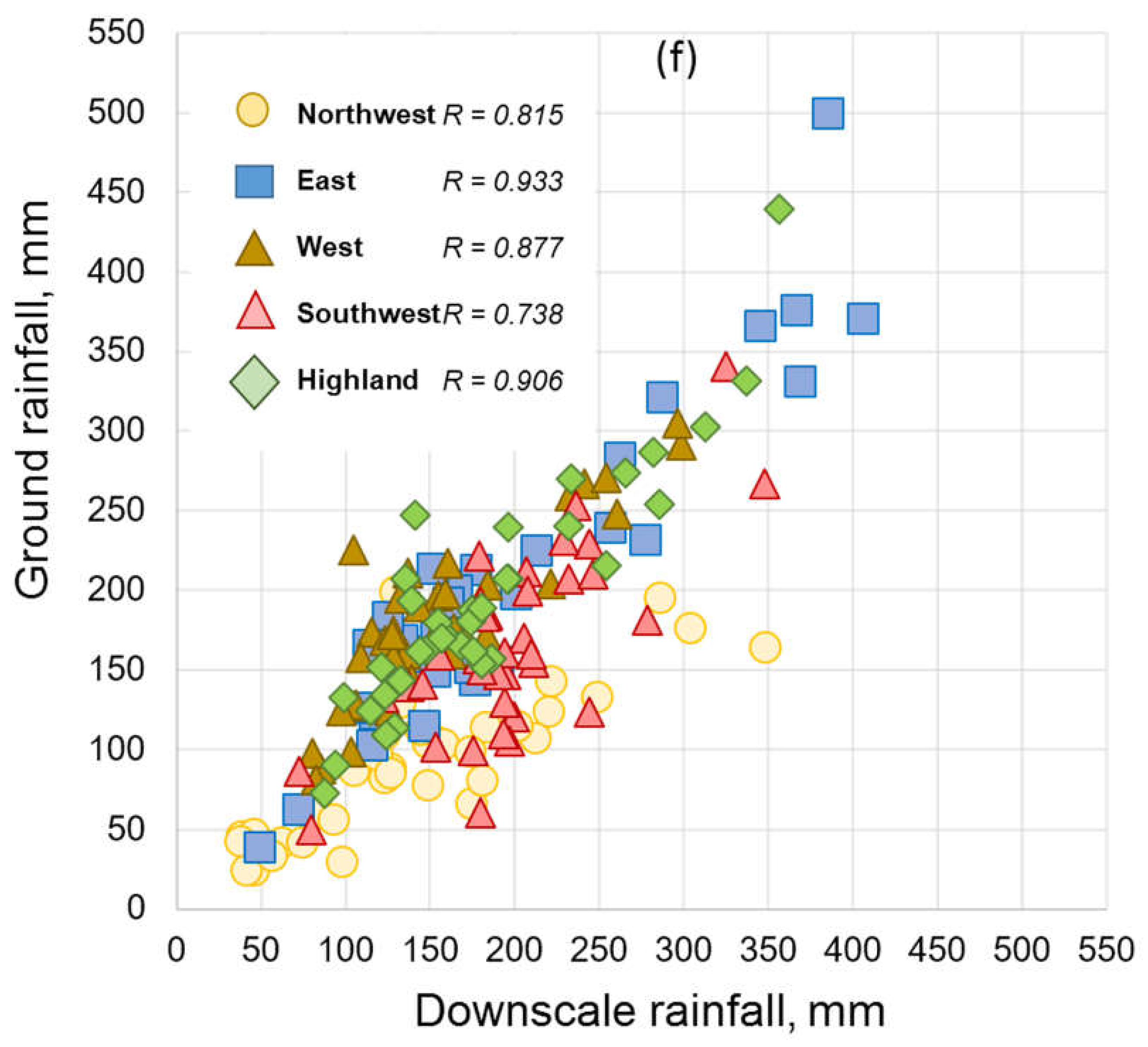
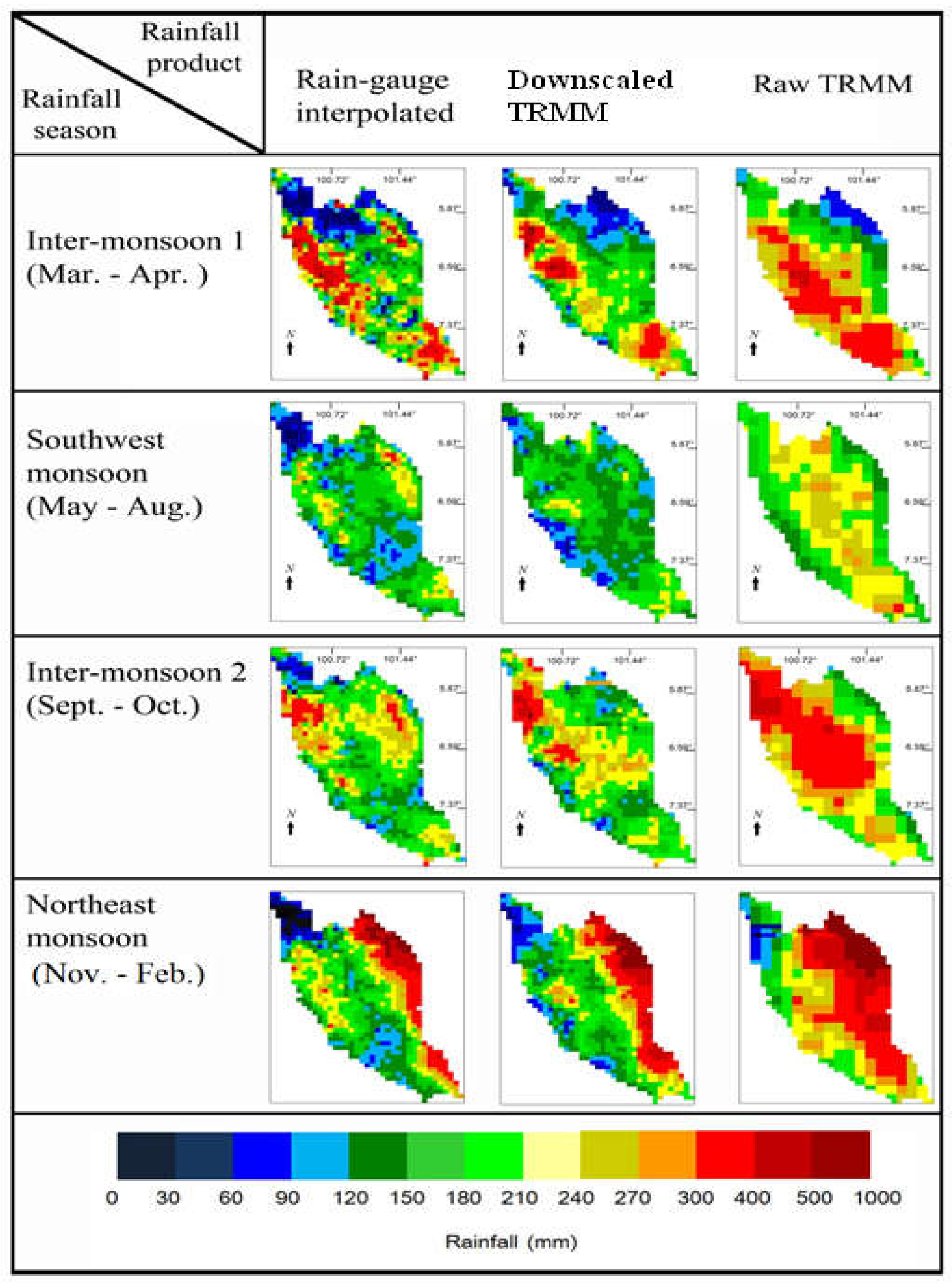
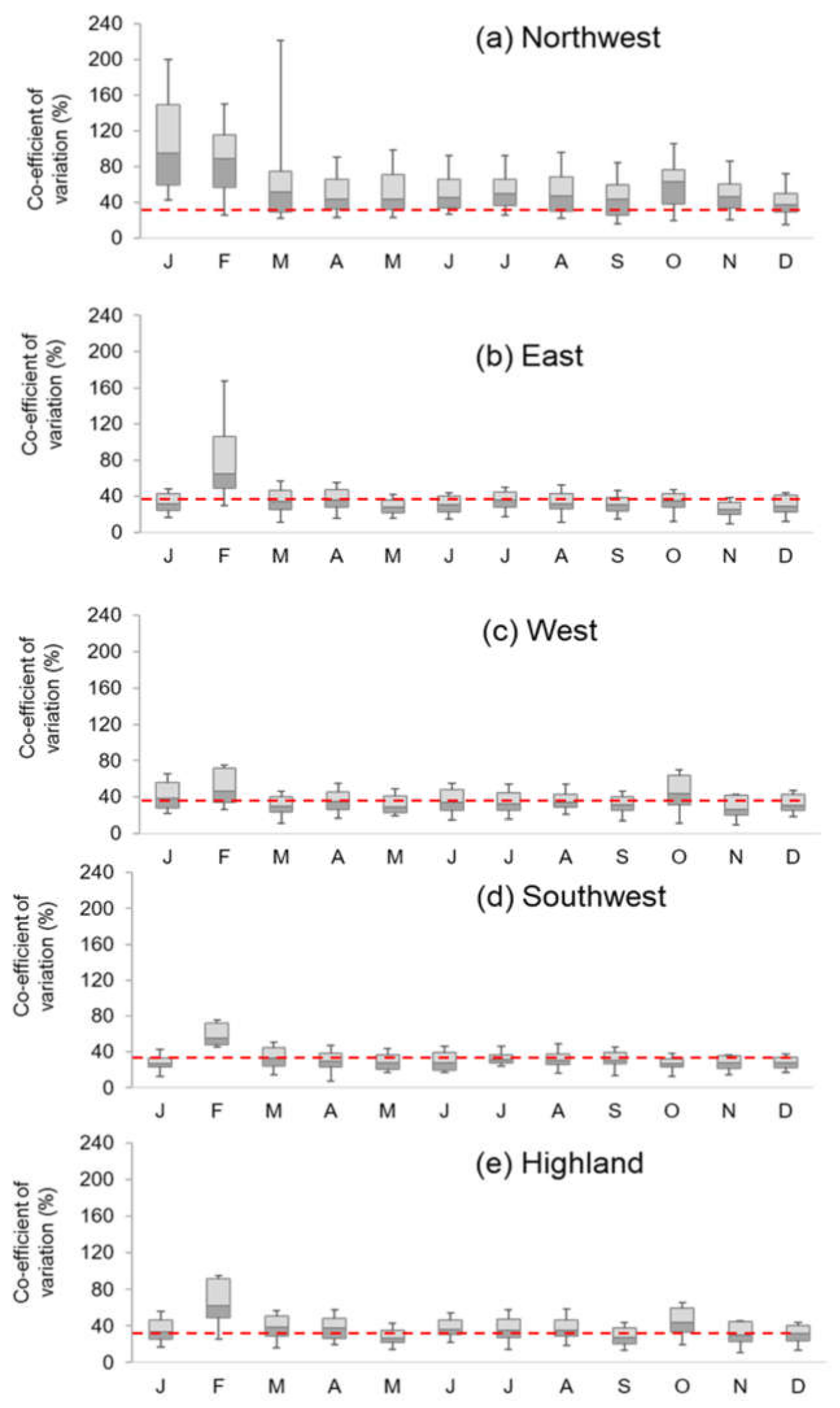
| Region | 2009 | 2010 | 2011 | Average Bias Ratio Reduction Capacity (%) | Average SSC Ratio * | |||
|---|---|---|---|---|---|---|---|---|
| Raw | SSC | Raw | SSC | Raw | SSC | |||
| Northwest | 3.14 | 2.01 | 3.59 | 1.52 | 2.70 | 1.30 | 94 | 1.6 |
| East | 2.70 | 1.70 | 1.60 | 1.03 | 1.34 | 0.86 | 49 | 1.2 |
| West | 1.28 | 0.83 | 1.39 | 0.85 | 1.35 | 0.84 | 53 | 0.8 |
| Southwest | 1.45 | 1.09 | 2.16 | 1.57 | 1.72 | 1.31 | 31 | 1.3 |
| Highland | 1.04 | 0.97 | 1.43 | 0.91 | 1.35 | 0.85 | 41 | 0.9 |
| Monsoon Season | Rain Gauge-Interpolated (a) | SSC-Downscale TRMM (b) | Raw TRMM (c) | Differences (%) | |
|---|---|---|---|---|---|
| (‖a − b‖/a) × 100 | (‖a − c‖/a) × 100 | ||||
| NEM | 36.75 | 35.35 | 37.22 | 3.8 | 1.3 |
| IM1 | 33.80 | 33.49 | 36.14 | 0.9 | 6.9 |
| SWM | 33.81 | 33.50 | 31.44 | 0.9 | 7.0 |
| IM2 | 34.73 | 33.49 | 30.74 | 3.6 | 11.5 |
| Satellite Precipitation Products * | Grid Size (Deg.) | Ratio | ||||
|---|---|---|---|---|---|---|
| N | E | W | S | H | ||
| TRMM V7—SSC | 0.05 | 2.2 | 0.9 | 0.8 | 1.5 | 0.8 |
| GsMAP | 0.10 | 1.5 | 1.4 | 19.8 | 0.9 | 1.0 |
| PERSIANN | 0.25 | 15.0 | 1.8 | 43.5 | 1.9 | 1.4 |
| CMORPH | 0.25 | 10.6 | 1.8 | 20.5 | 2.0 | 1.3 |
| CPC | 0.50 | 21.0 | 1.9 | 23.7 | 1.4 | 0.8 |
| GPCP | 1.00 | 27.0 | 25.0 | 24.0 | 24.0 | 23.0 |
| CMAP | 2.50 | 15.0 | 1.8 | 43.5 | 1.9 | 1.4 |
| Monsoon Season | Cross-Validation Metrics |
|---|---|
| MPE (%) | |
| NEM (November–January) | 5 |
| IM1 (March–April) | 3 |
| SWM (May–August) | 3 |
| IM2 (September–October) | 4 |
| Average | 4 |
| Monsoon Season | Cross-Validation Metrics | Average Ground Rainfall (mm) | |
|---|---|---|---|
| RMSE (mm) | MPE (%) | ||
| NEM (November–January) | 24 | 13 | 200 |
| IM1 (March–April) | 13 | 8 | 115 |
| SWM (May–August) | 11 | 9 | 118 |
| IM2 (September–October) | 21 | 10 | 176 |
| Average | 17 | 10 | 152 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmud, M.R.; Hashim, M.; Matsuyama, H.; Numata, S.; Hosaka, T. Spatial Downscaling of Satellite Precipitation Data in Humid Tropics Using a Site-Specific Seasonal Coefficient. Water 2018, 10, 409. https://doi.org/10.3390/w10040409
Mahmud MR, Hashim M, Matsuyama H, Numata S, Hosaka T. Spatial Downscaling of Satellite Precipitation Data in Humid Tropics Using a Site-Specific Seasonal Coefficient. Water. 2018; 10(4):409. https://doi.org/10.3390/w10040409
Chicago/Turabian StyleMahmud, Mohd. Rizaludin, Mazlan Hashim, Hiroshi Matsuyama, Shinya Numata, and Tetsuro Hosaka. 2018. "Spatial Downscaling of Satellite Precipitation Data in Humid Tropics Using a Site-Specific Seasonal Coefficient" Water 10, no. 4: 409. https://doi.org/10.3390/w10040409
APA StyleMahmud, M. R., Hashim, M., Matsuyama, H., Numata, S., & Hosaka, T. (2018). Spatial Downscaling of Satellite Precipitation Data in Humid Tropics Using a Site-Specific Seasonal Coefficient. Water, 10(4), 409. https://doi.org/10.3390/w10040409







