Low Frequency Waves Detected in a Large Wave Flume under Irregular Waves with Different Grouping Factor and Combination of Regular Waves
Abstract
1. Introduction
2. Experimental Setup
- random waves with different Grouping Factors (GF);
- combination of free partial standing long waves plus monochromatic short waves (hereinafter, combined waves);
- regular monochromatic;
- bichromatic waves (including bound long waves).
3. Methods
3.1. Spectral Analysis
3.2. Eigen Analysis
4. Results and Discussion
5. Additional Considerations
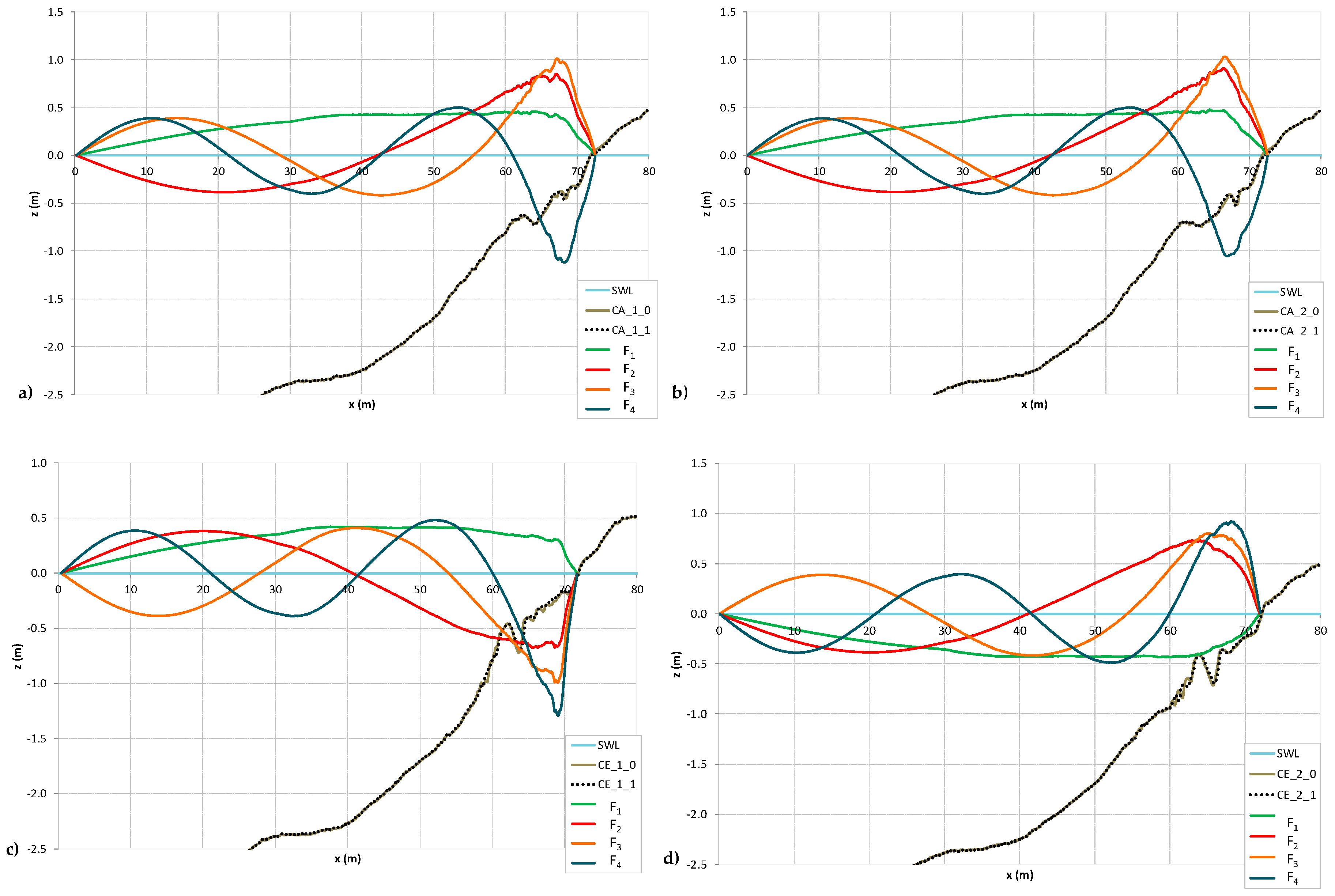
- A strong non-linear pattern of F1–F4 is identified for all the tests in proximity of breaking zone;
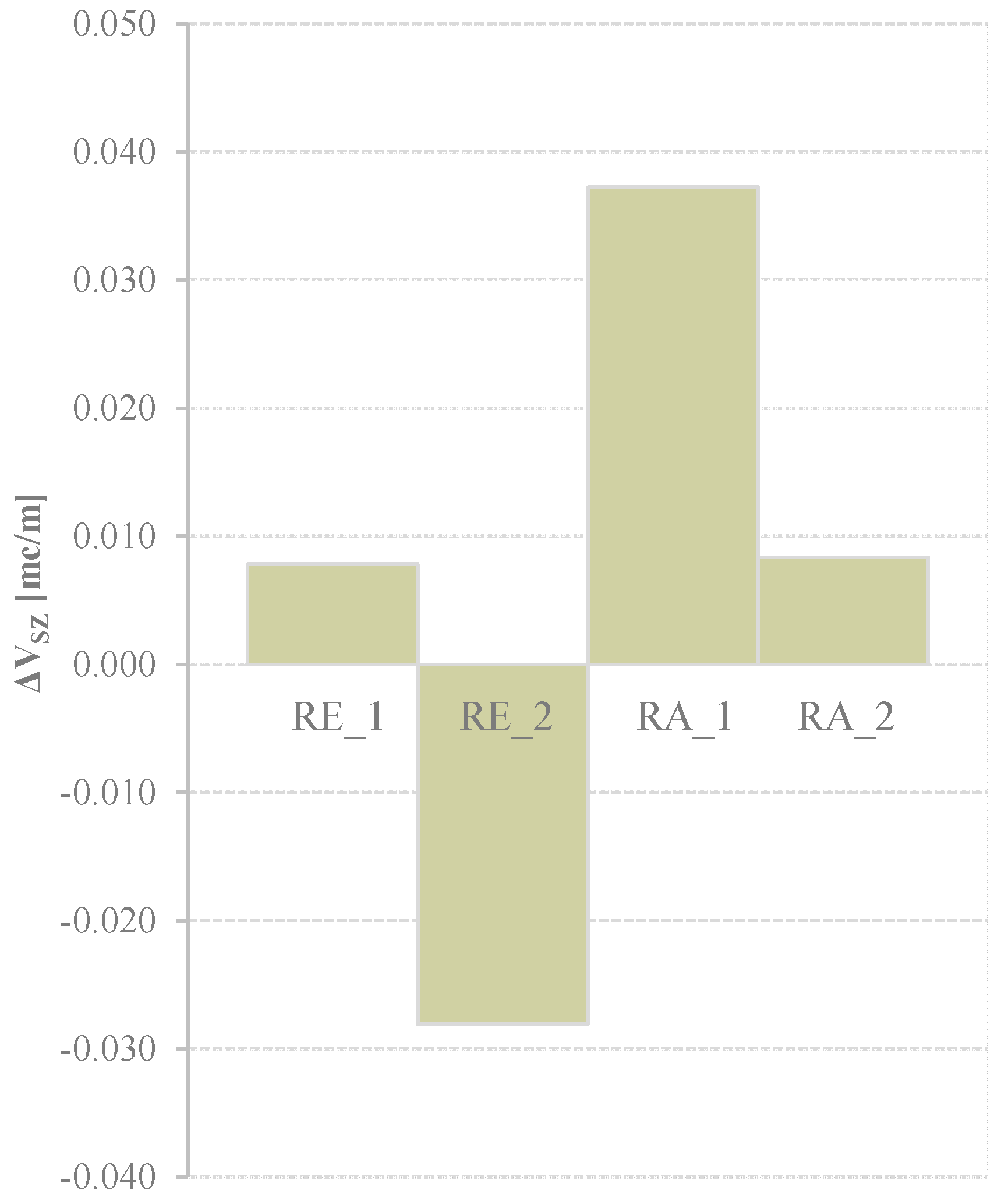
- Clear opposite behaviours of volume flux eigenmodes are shown for accretive and erosive wave conditions in the case of random and combination waves, except for the test CE_2;
- A different variation of the Eigenmodes for the combination tests in the erosive, clearly, due to the non-linearity effects;
- The monochromatic wave perturbed with the larger long waves for the erosive condition (CE_1) has an opposite variation of the Eigenmodes, than the monochromatic wave perturbed with smaller long waves (CE_2).
- specific eigenmode of the wave flume (generated seiches) induces spreading or downshift of carrier wave frequency, as foreseen;
- grouping of short waves in the inner surf zone could directly induce low-frequency oscillations of the shoreline.
5.1. Influence on Morphodynamic
5.2. Influence on Swash Hydrodynamics
- “accretive” conditions do not necessarily involve smaller runup;
- despite comparable energy levels, random waves give a runup twice higher than combination cases;
- the higher the grouping factor the higher the maximum runup.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Budillon, F.; Vicinanza, D.; Ferrante, V.; Iorio, M. Sediment transport and deposition during extreme sea storm events at the Salerno Bay (Tyrrhenian Sea): Comparison of field data with numerical model results. Nat. Hazards Earth Syst. Sci. 2006, 6, 839–852. [Google Scholar] [CrossRef]
- Brocchini, M.; Bellotti, G. Integral flow properties of the swash zone and averaging. Part 2. Shoreline boundary conditions for wave-averaged models. Int. J. Fluid Mech. Res. 2002, 458, 269–281. [Google Scholar] [CrossRef]
- Oltman-Shay, J.; Howd, P.A.; Birkemeier, W.A. Shear instabilities of the mean longshore current: 2. Field observations. J. Geophys. Res. Oceans 1989, 94, 18031–18042. [Google Scholar] [CrossRef]
- Miles, J.R.; Russell, P.E.; Ruessink, B.G.; Huntley, D.A. Field observations of the effect of shear waves on sediment suspension and transport. Cont. Shelf Res. 2002, 22, 657–681. [Google Scholar] [CrossRef]
- Watson, G.; Barnes, T.C.D.; Peregrine, D.H. The generation of low-frequency waves by a single wave group incident on a beach. Coast. Eng. 1994, 1995, 776–790. [Google Scholar]
- Mase, H. Frequency down-shift on swash oscillations compared to incident waves. J. Hydraul. Res. 1995, 33, 397–411. [Google Scholar] [CrossRef]
- Suhayda, J.N. Standing waves on beaches. J. Geophys. Res. 1974, 79, 3065–3071. [Google Scholar] [CrossRef]
- Huntley, D.A.; Guza, R.T.; Bowen, A.J. A universal form for shoreline run-up spectra. J. Geophys. Res. 1977, 82, 2577–2581. [Google Scholar] [CrossRef]
- Guza, R.T.; Thornton, E.B. Swash oscillations on a natural beach. J. Geophys. Res. 1982, 87, 483–491. [Google Scholar] [CrossRef]
- Holland, K.T.; Raubenheimer, B.; Guza, R.T.; Holman, R.A. Runup kinematics on a natural beach. J. Geophys. Res. 1995, 100, 4985–4993. [Google Scholar] [CrossRef]
- Raubenheimer, B.; Guza, R.T. Observations and predictions of run-up. J. Geophys. Res. 1996, 101, 25575–25587. [Google Scholar] [CrossRef]
- Van Dongeren, A.; Lowe, R.; Pomeroy, A.; Trang, D.; Roelvink, D.; Symonds, G.; Ranasinghe, R. Numerical modeling of dynamics over a fringing coral reef. Coast. Eng. 2013, 73, 178–190. [Google Scholar] [CrossRef]
- Ruju, A.; Lara, J.L.; Losada, I.J. Numerical analysis of run-up oscillations under dissipative conditions. Coast. Eng. 2014, 86, 45–56. [Google Scholar] [CrossRef]
- De Bakker, A.T.M.; Tissier, M.F.S.; Ruessink, B.G. Beach steepness effects on nonlinear infragravity-wave interactions: A numerical study. J. Geophys. Res. Oceans 2015, 121. [Google Scholar] [CrossRef]
- Bowen, A.J.; Inman, D.L. Edge waves and crescentic bars. J. Geophys. Res. 1971, 76, 8662–8671. [Google Scholar] [CrossRef]
- Huntley, D.A.; Guza, R.T.; Thornton, E.B. Field observations of surf beat: 1. Progressive edge waves. J. Geophys. Res. 1981, 86, 6451–6466. [Google Scholar] [CrossRef]
- Guza, R.T.; Thornton, E. Observations of surf beat. J. Geophys. Res. 1985, 90, 3161–3172. [Google Scholar] [CrossRef]
- Oltman-Shay, J.; Guza, R.T. Infragravity edge wave observations on two California beaches. J. Phys. Oceanogr. 1987, 17, 644–663. [Google Scholar] [CrossRef]
- Holland, K.T.; Holman, R.A. Wavenumber-frequency structure of infragravity swash motions. J. Geophys. Res. 1999, 104, 13479–13488. [Google Scholar] [CrossRef]
- Baldock, T.E.; Alsina, J.; Caceres, I.; Vicinanza, D.; Contestabile, P.; Power, H.; Sanchez-Arcilla, A. Large-scale experiments on beach profile evolution and surf and swash zone sediment transport induced by long waves, wave groups and random waves. Coast. Eng. 2011, 58, 214–227. [Google Scholar] [CrossRef]
- Watson, G.; Peregrine, D.H.; Toro, E.F. Numerical solution of the shallow-water equations on a beach using the weighted average flux method. In Proceedings of the First European Computational Fluid Dynamics Conference, Brussels, Belgium, 7–11 September 1992; Volume 1, pp. 495–502. [Google Scholar]
- Baldock, T.E.; Holmes, P.; Horn, D.P. Low frequency swash motion induced by wave grouping. Coast. Eng. 1997, 32, 197–222. [Google Scholar] [CrossRef]
- Brocchini, M. Eulerian and Lagrangian aspects of the longshore drift in the surf and swash zones. J. Geophys. Res. Oceans 1997, 102, 23155–23168. [Google Scholar] [CrossRef]
- Masselink, G.; Puleo, J.A. Swash-zone morphodynamics. Cont. Shelf Res. 2006, 26, 661–680. [Google Scholar] [CrossRef]
- Brocchini, M.; Baldock, T.E. Recent advances in modeling swash zone dynamics: Influence of surf-swash interaction on nearshore hydrodynamics and morphodynamics. Rev. Geophys. 2008, 46. [Google Scholar] [CrossRef]
- Horn, D.P.; Baldock, T.E.; Li, L. The influence of groundwater on profile evolution of fine and coarse sand beaches. In Proceedings of the Sixth International Symposium on Coastal Engineering and Science of Coastal Sediment Process, New Orleans, LA, USA, 13–17 May 2007. [Google Scholar]
- Ciavola, P.; Vicinanza, D.; Fontana, E. Beach drainage as a form of shoreline stabilization: case studies in Italy. In Proceedings of the 31st International Conference on Coastal Engineering, Hamburg, Germany, 31 August–5 September 2008. [Google Scholar]
- Ciavola, P.; Vicinanza, D.; Aristodemo, F.; Contestabile, P. Large-scale morphodynamic experiments on a Beach Drainage System. J. Hydraul. Res. 2011, 49, 523–528. [Google Scholar] [CrossRef]
- Damiani, L.; Aristodemo, F.; Saponieri, A.; Verbeni, B.; Veltri, P.; Vicinanza, D. Full-scale experiments on a beach drainage system: Hydrodynamic effects inside beach. J. Hydraul. Res. 2011, 49, 44–54. [Google Scholar] [CrossRef]
- Contestabile, P.; Aristodemo, F.; Vicinanza, D.; Ciavola, P. Laboratory study on a beach drainage system. Coast. Eng. 2012, 66, 50–64. [Google Scholar] [CrossRef]
- Ciavola, P.; Contestabile, P.; Aristodemo, F.; Vicinanza, D. Beach sediment mixing under drained and undrained conditions. J. Coast. Res. 2013, 65, 1503–1508. [Google Scholar] [CrossRef]
- Mansard, E.P.D.; Sand, S.E. A Comparative Evaluation of Wave Grouping Measures. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994. [Google Scholar]
- Merrick, C.; Haller, C.; Dalrymple, R.A. Looking for Wave Groups in the Surf Zone. In Proceedings of the International Conference on Coastal Research in Terms of Large Scale Experiments, Gdansk, Poland, 4–8 September 1995; pp. 81–92. [Google Scholar]
- Baldock, T.E.; Manoonvoravong, P.; Pham, K.S. Sediment transport and beach morphodynamics induced by free long waves, bound long waves and wave groups. Coast. Eng. 2010, 57, 898–916. [Google Scholar] [CrossRef]
- Dally, W.R. Long Wave Effects in Laboratory Studies of Cross-Shore Transport. 1991. Available online: http://cedb.asce.org/CEDBsearch/record.jsp?dockey=0071660 (accessed on 21 February 2018).
- Baldock, T.E.; Huntley, D.A. Long-Wave Forcing by the Breaking of Random Gravity Waves on a Beach. Philos. Trans. R. Soc. Lond. Ser. A 2002, 458, 2177–2201. [Google Scholar] [CrossRef]
- Hydrolab III. EU Integrated Infrastructure Initiative, SUSCO Swash Zone Response under Grouping Storm Conditions. Available online: http://hydralab.eu/research--results/ta-projects/project/97/ (accessed on 21 February 2018).
- Haller, M.C.; Dalrymple, R.A. Rip current instabilities. J. Fluid Mech. 2001, 433, 161–192. [Google Scholar] [CrossRef]
- Sorensen, R.M. Basic Wave Mechanics: For Coastal and Ocean Engineers; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Bellotti, G.; Archetti, R.; Brocchini, M. Experimental validation of mean swash zone boundary conditions. J. Geophys. Res. 2003, 108, 3250. [Google Scholar] [CrossRef]
- Young, I. Observations of triad coupling of finite depth wind waves. Coast. Eng. 1998, 33, 137–154. [Google Scholar] [CrossRef]
- Losada, M.A.; Roldan, A.J.; Dalrymple, R.A. Eigenfunction analysis of water wave propagation down a wave flume. J. Hydraul. Res. 1994, 32, 371–385. [Google Scholar] [CrossRef]
- Van Dongeren, A.; Battjes, J.; Janssen, T.; van Noorloos, J.; Steenhauer, K.; Steenbergen, G.; Reniers, A. Shoaling and shoreline dissipation of low-frequency waves. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Patel, M.H.; Ionnaou, P.A. Comparative Performance Study of Paddle- and Wedge-Type Wave Generators. J. Hydronaut. 1980, 14, 5–9. [Google Scholar] [CrossRef]
- Riefolo, L.; Contestabile, P.; Ferrante, V.; Azzellino, A.; Centurioni, L.; Vicinanza, D. The role of spectral wave components, bandwidth and wave grouping on runup: Preliminary results from large-scale experiments. In Proceedings of the 5th International Conference on the Application of Physical Modelling to Port and Coastal Protection Coastlab14, Varna, Bulgaria, 29 September–2 October 2014. [Google Scholar]
- Moreno, L.J. Perfil de Playas Sustentadas: Estudio Hidrodinámico y Experimental. Directrices de Diseño. Ph.D. Thesis, Technical University of Madrid, Madrid, Spain, 2016. [Google Scholar]
- Dean, R.G. Heuristic models of sand transport in the surf zone. In Proceedings of the First Australian Conference on Coastal Engineering, Sydney, Australia, 14–17 May 1973. [Google Scholar]
- Vicinanza, D.; Baldock, T.E.; Contestabile, P.; Alsina, J.; Cáceres, I.; Brocchini, M.; Conley, D.; Andersen, T.L.; Frigaard, P.; Ciavola, P. Swash Zone Response under Grouping Storm Conditions. J. Hydraul. Res. 2011, 4, 55–63. [Google Scholar] [CrossRef]
- Wright, L.D.; Short, A.D. Morphodynamic variability of surf zones and beaches: A synthesis. Mar. Geol. 1984, 56, 93–118. [Google Scholar] [CrossRef]
- Aalborg University. Software for Wave Laboratories. Available online: http://hydrosoft.civil.aau.dk/AwaSys/ (accessed on 17 February 2018).
- Hald, T. Wave Group Analysis by Means of the Hilbert Transform Technique; Aalborg University: Aalborg, Denmark, 1995. [Google Scholar]
- Munoz-Perez, J.J.; Caballero, I.; Tejedor, B.; Gomez-Pina, G. Reversal in longshore sediment transport without variations in wave power direction. J. Coast. Res. 2010, 780–786. [Google Scholar] [CrossRef]
- Molloy, E. Seiching in Cockburn Sound. Master’s Thesis, University of Western Australia, Crawley, WA, Australia, November 2001. [Google Scholar]
- Rabinovich, A.B. Seiches and Harbor Oscillations. In Handbook of Coastal and Ocean Engineering; Kim, Y.C., Ed.; World Scientific: Singapore, 2009. [Google Scholar]
- Merian, J.R. Ueber die Bewegung tropfbarer Flüssigkeiten in Gefässen [On the Motion of Drippable Liquids in Containers]. Master’s Thesis, Göttingen University, Göttingen, Germany, 1828. (In German). [Google Scholar]
- Wilson, B. Seiches. In Advances in Hydrosciences; Academic Press: Urbana, IL, USA, 1972; Volume 8, pp. 1–94. [Google Scholar]
- Kirby, J.T.; Özkan-Haller, H.T.; Haller, M.C. Seiching in a large wave flume. In Proceedings of the 30th International Conference on Coastal Engineering, San Diego, CA, USA, 3–8 September 2006. [Google Scholar]
- Cáceres, I.; Alsina, J.M. Suspended sediment transport and beach dynamics induced by monochromatic conditions, long waves and wave groups. Coast. Eng. 2016, 108, 36–55. [Google Scholar] [CrossRef]
- Svendsen, I.A. Mass flux and undertow in a surf zone. Coast. Eng. 1984, 8, 347–365. [Google Scholar] [CrossRef]
- Riefolo, L.; Azzellino, A.; Ferrante, V.; Contestabile, P.; Vicinanza, D. Wave flume-generated seiching analysis. In Proceedings of the Twenty-fifth International Ocean and Polar Engineering Conference, Kona, Big Island, HI, USA, 21–26 June 2015. [Google Scholar]
- Russell, P.E. Mechanisms for beach erosion during storms. Cont. Shelf Res. 1993, 13, 1243–1265. [Google Scholar] [CrossRef]
- Smith, G.G.; Mocke, G.P. Interaction between breaking/broken waves and infragravity-scale phenomena to control sediment suspension transport in the surf zone. Mar. Geol. 2002, 187, 329–345. [Google Scholar] [CrossRef]
- Benassai, G.; Aucelli, P.; Budillon, G.; De Stefano, M.; Di Luccio, D.; Di Paola, G.; Montella, R.; Mucerino, L.; Sica, M.; Pennetta, M. Rip current evidence by hydrodynamic simulations, bathymetric surveys and UAV observation. Nat. Hazards Earth Syst. Sci. 2017, 17, 1493. [Google Scholar] [CrossRef]
- Nunziata, F.; Buono, A.; Migliaccio, M.; Benassai, G. Dual-polarimetric C-and X-band SAR data for coastline extraction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4921–4928. [Google Scholar] [CrossRef]
- Nunziata, F.; Migliaccio, M.; Li, X.; Ding, X. Coastline extraction using dual-polarimetric COSMO-SkyMed PingPong mode SAR data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 104–108. [Google Scholar] [CrossRef]
- Nunziata, F.; Buono, A.; Migliaccio, M.; Benassai, G. An Effective Method to Extract Coastline from Dual-Polarimetric C- and X-Band SAR Measurements. Available online: http://lps16.esa.int/page_paper0891.php (accessed on 21 February 2018).
- Benassai, G.; Migliaccio, M.; Montuori, A. Sea wave numerical simulations with COSMO-SkyMed© SAR data. J. Coast. Res. 2013, 65, 660–665. [Google Scholar] [CrossRef]

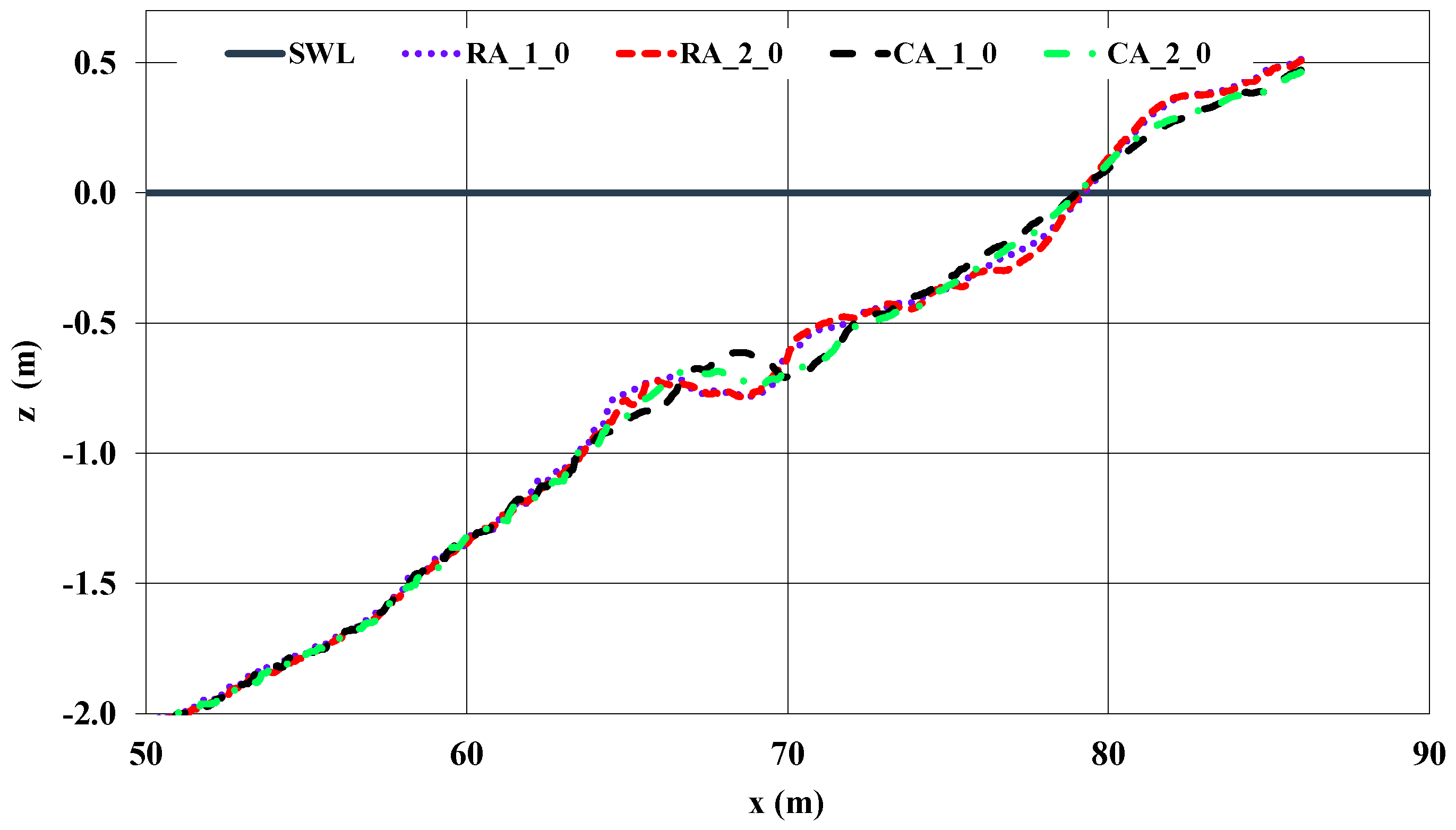

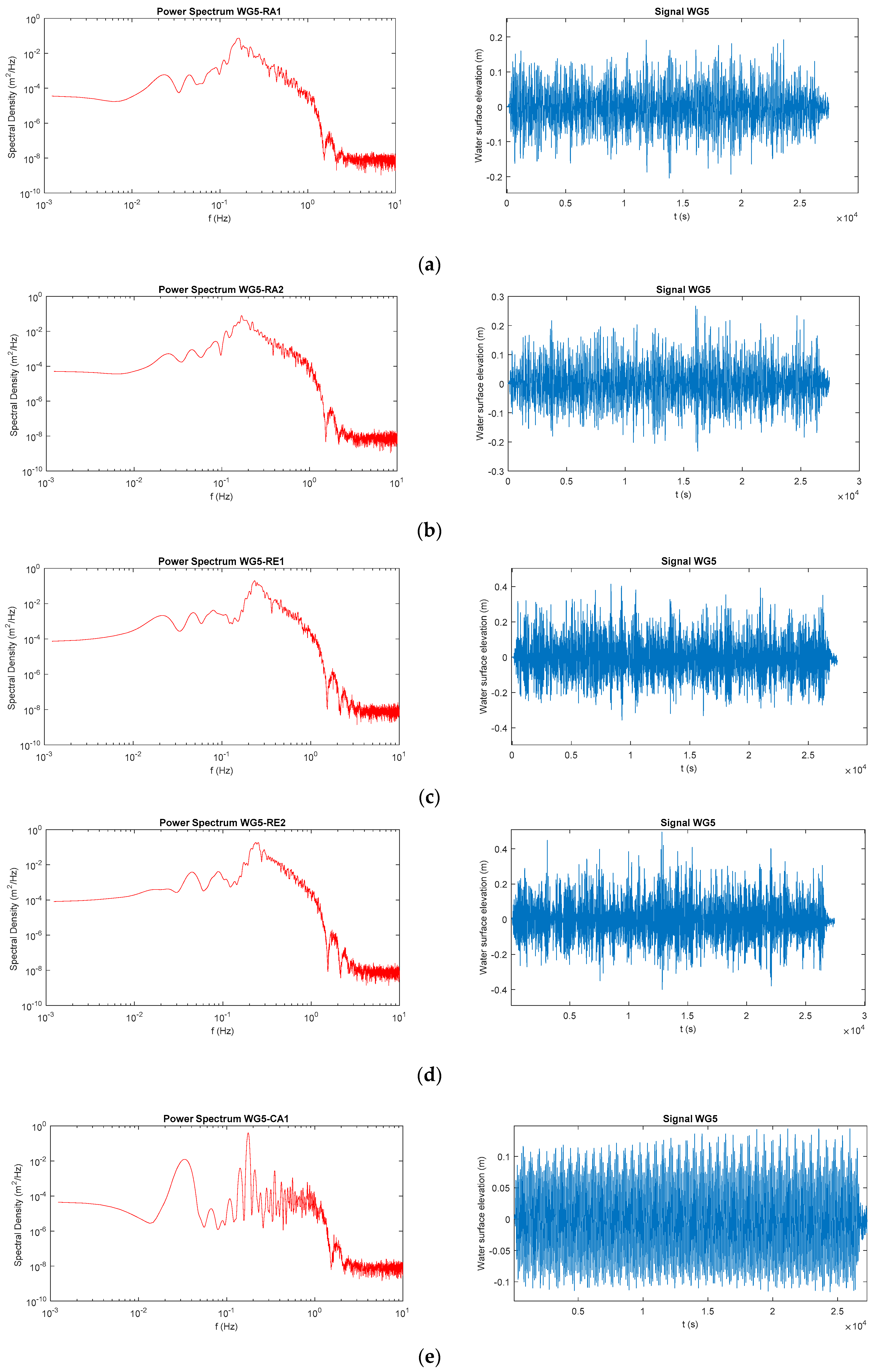
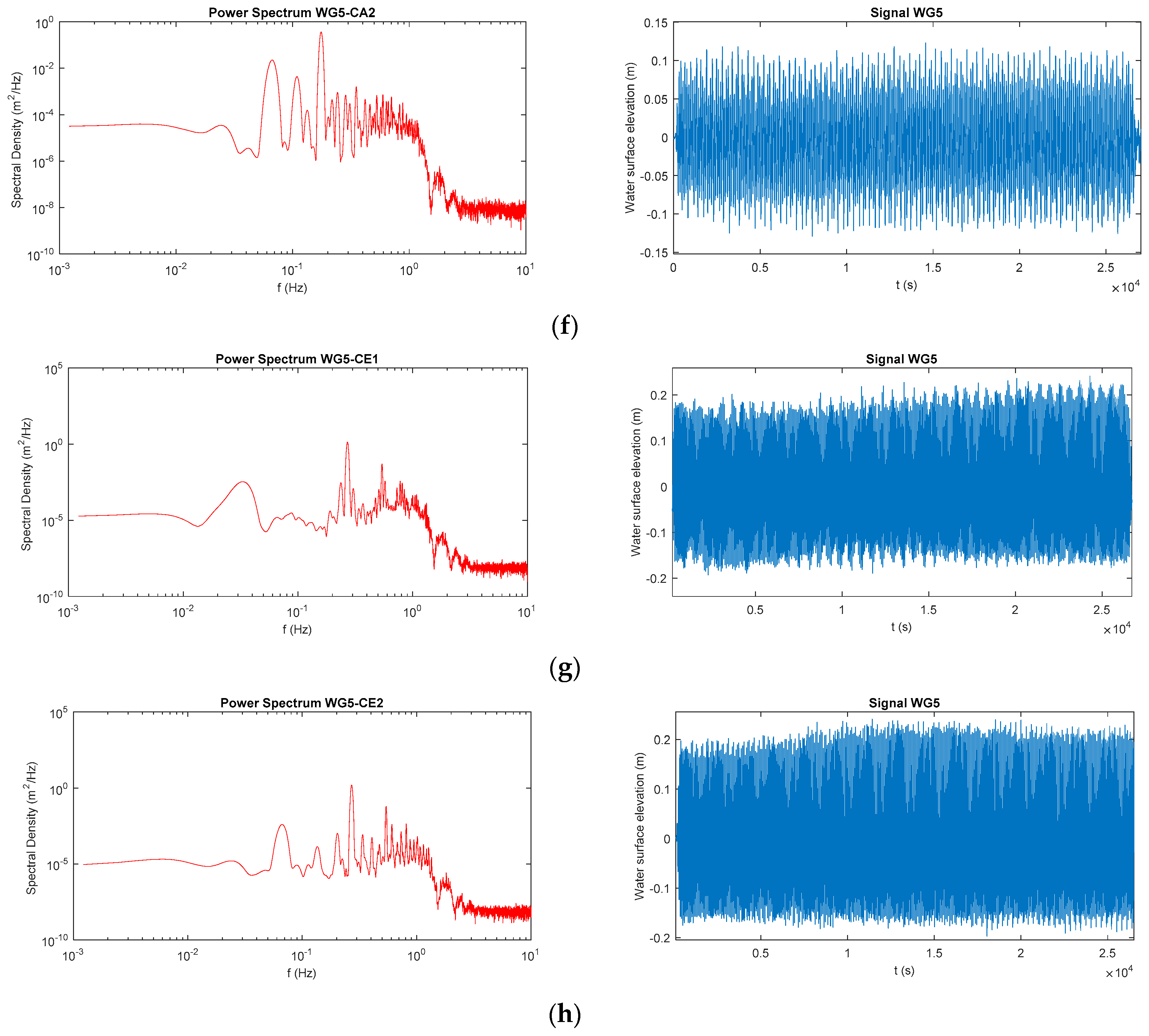
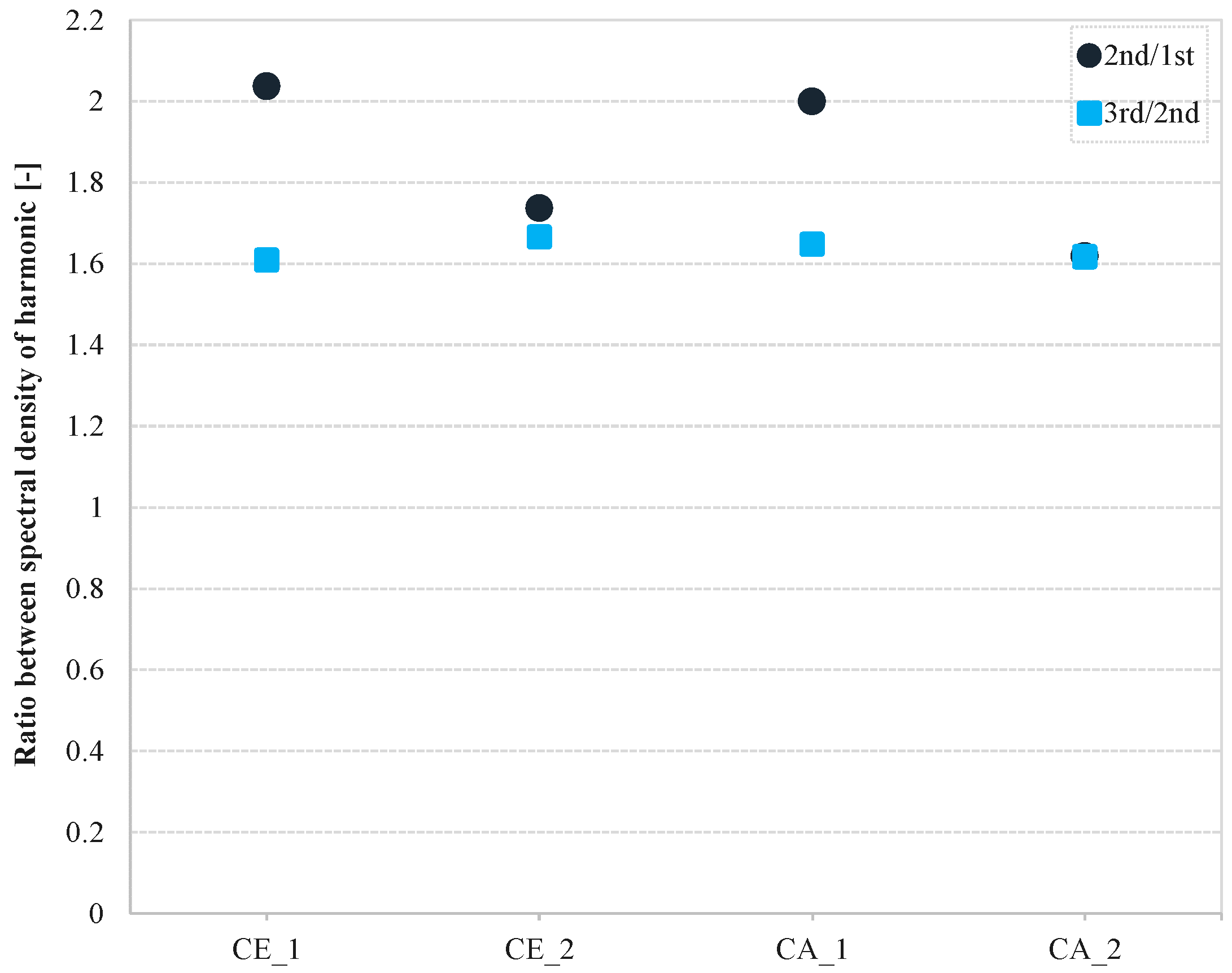
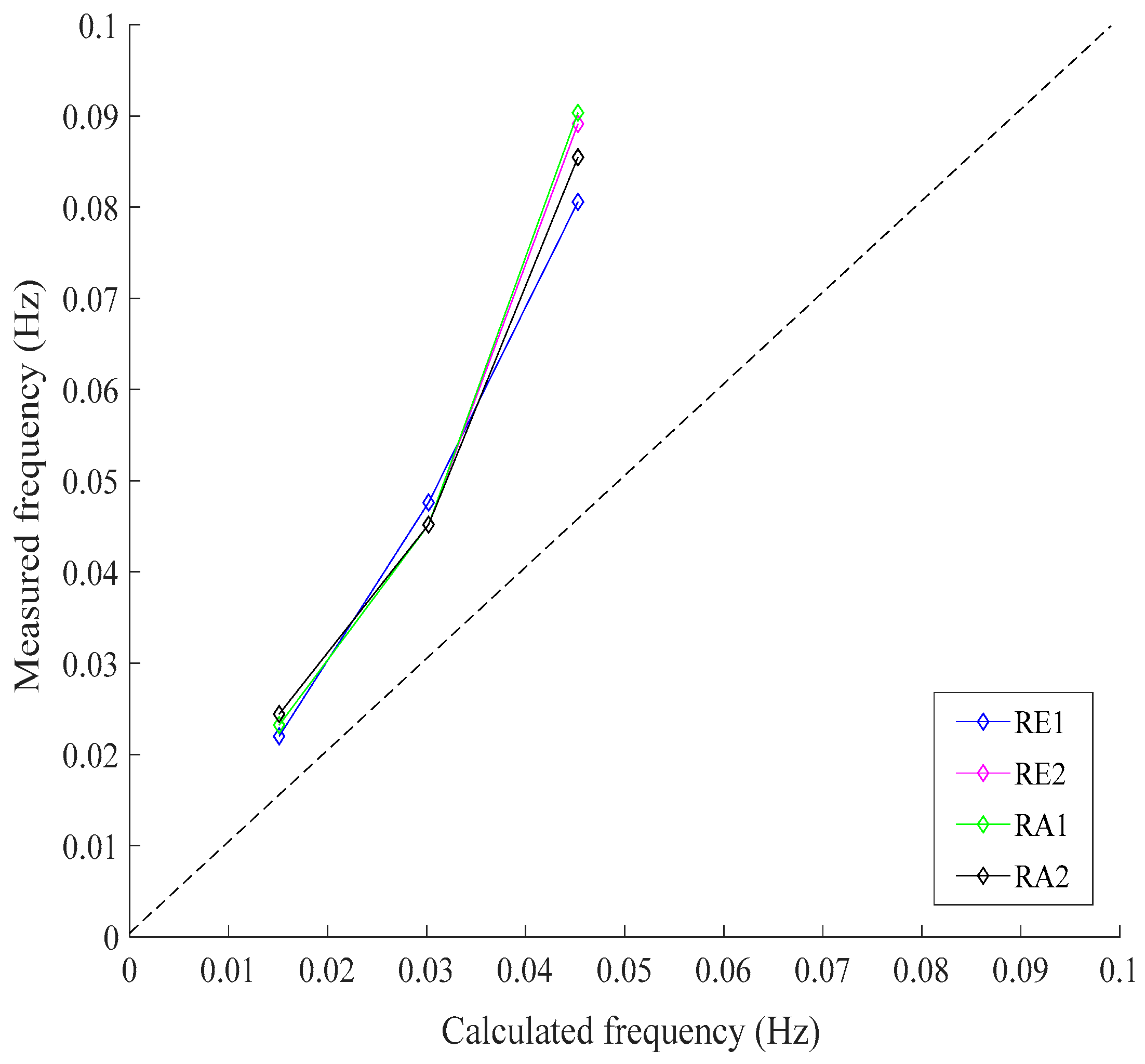
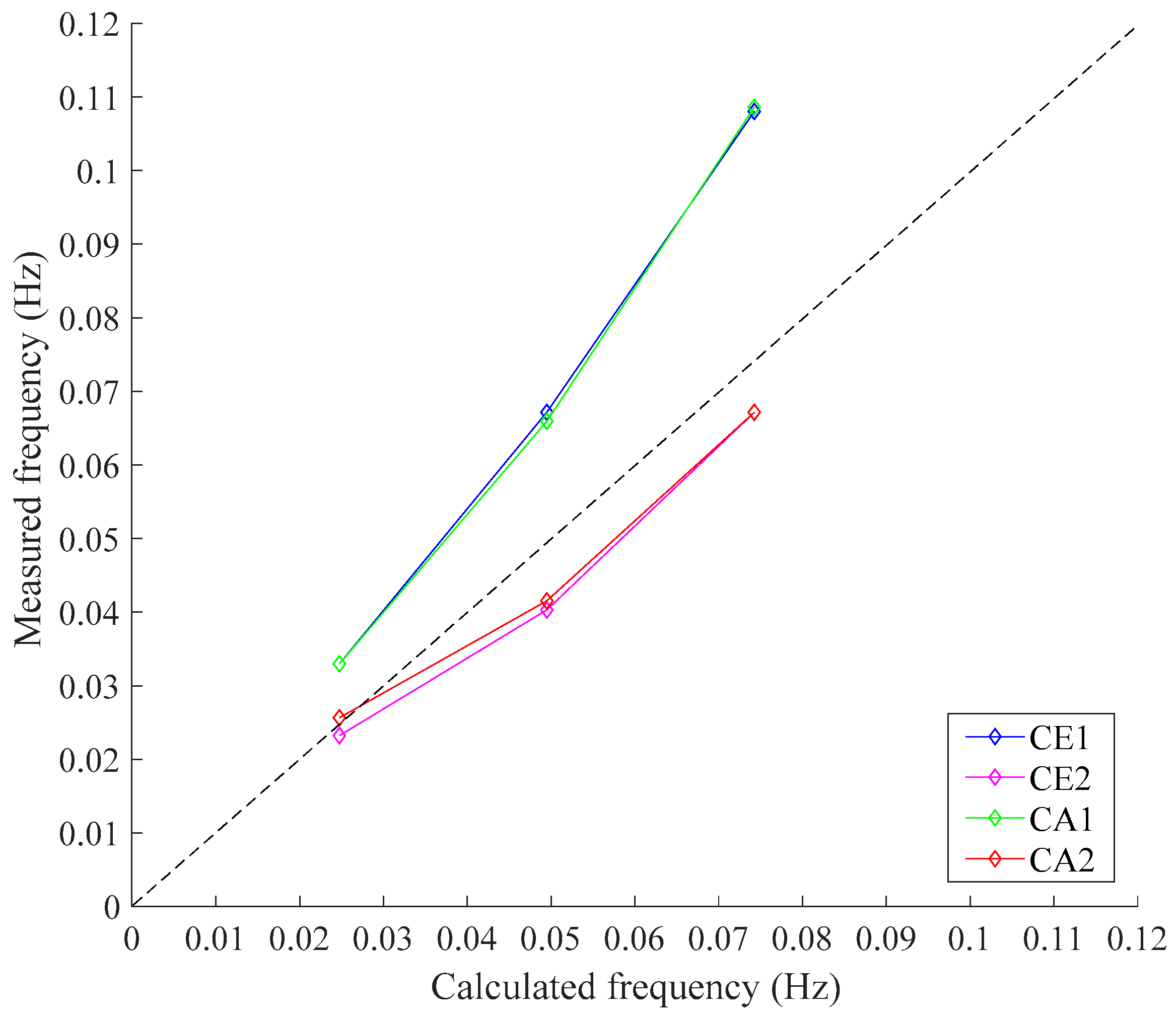
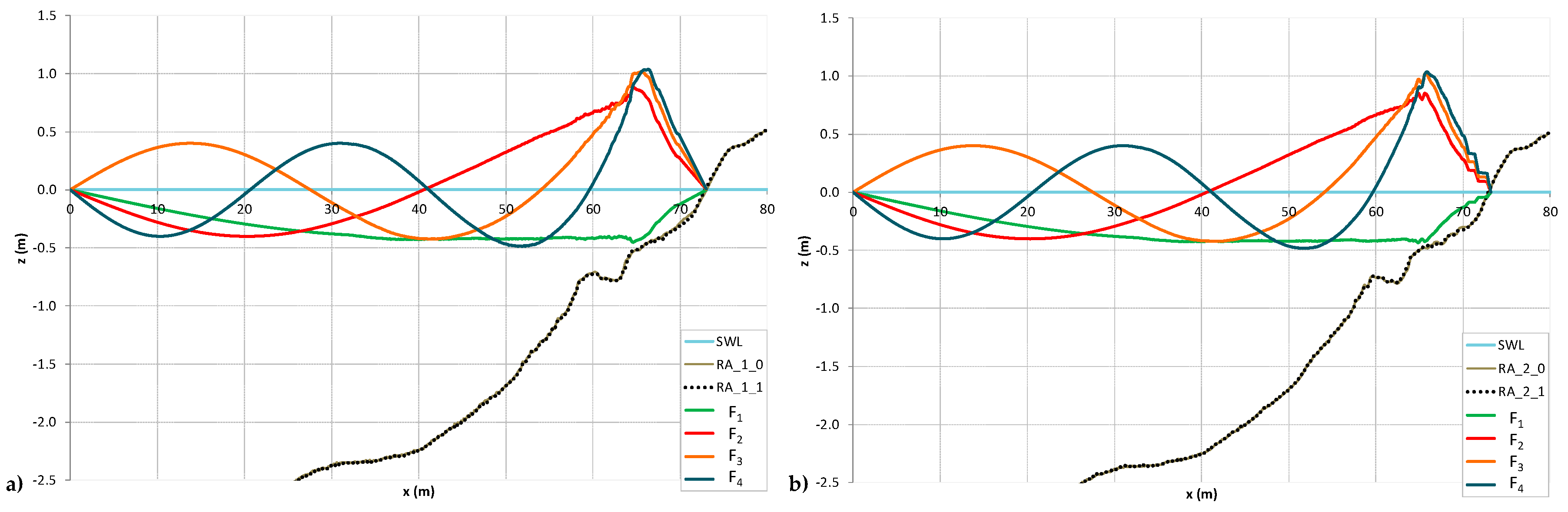

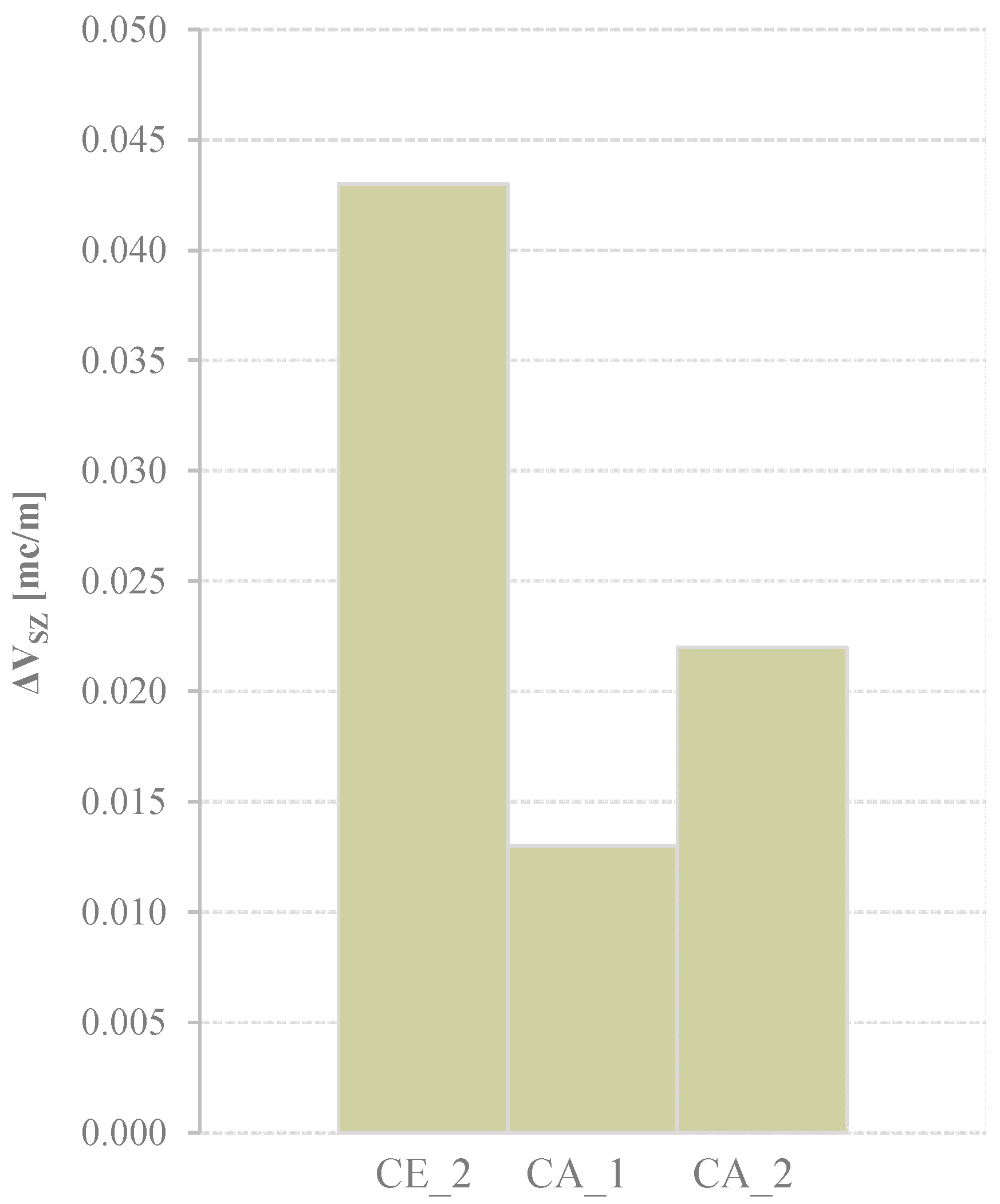
| Test | H (m) | T (s) | Wave Type |
|---|---|---|---|
| CA_1 | 0.226 0.038 | 6 30 | Combination |
| CA_2 | 0.226 0.038 | 6 15 | Combination |
| RA_1 | 0.319 | 6.7 | Random GF = 0.96 |
| RA_2 | 0.319 | 6.7 | Random GF = 1.08 |
| Test | H (m) | T (s) | Wave Type |
|---|---|---|---|
| CE_1 | 0.370 0.038 | 3.7 30 | Combination |
| CE_2 | 0.370 0.038 | 3.7 15 | Combination |
| RE_1 | 0.530 | 4.1 | Random GF = 1 |
| RE_2 | 0.530 | 4.1 | Random GF = 1.1 |
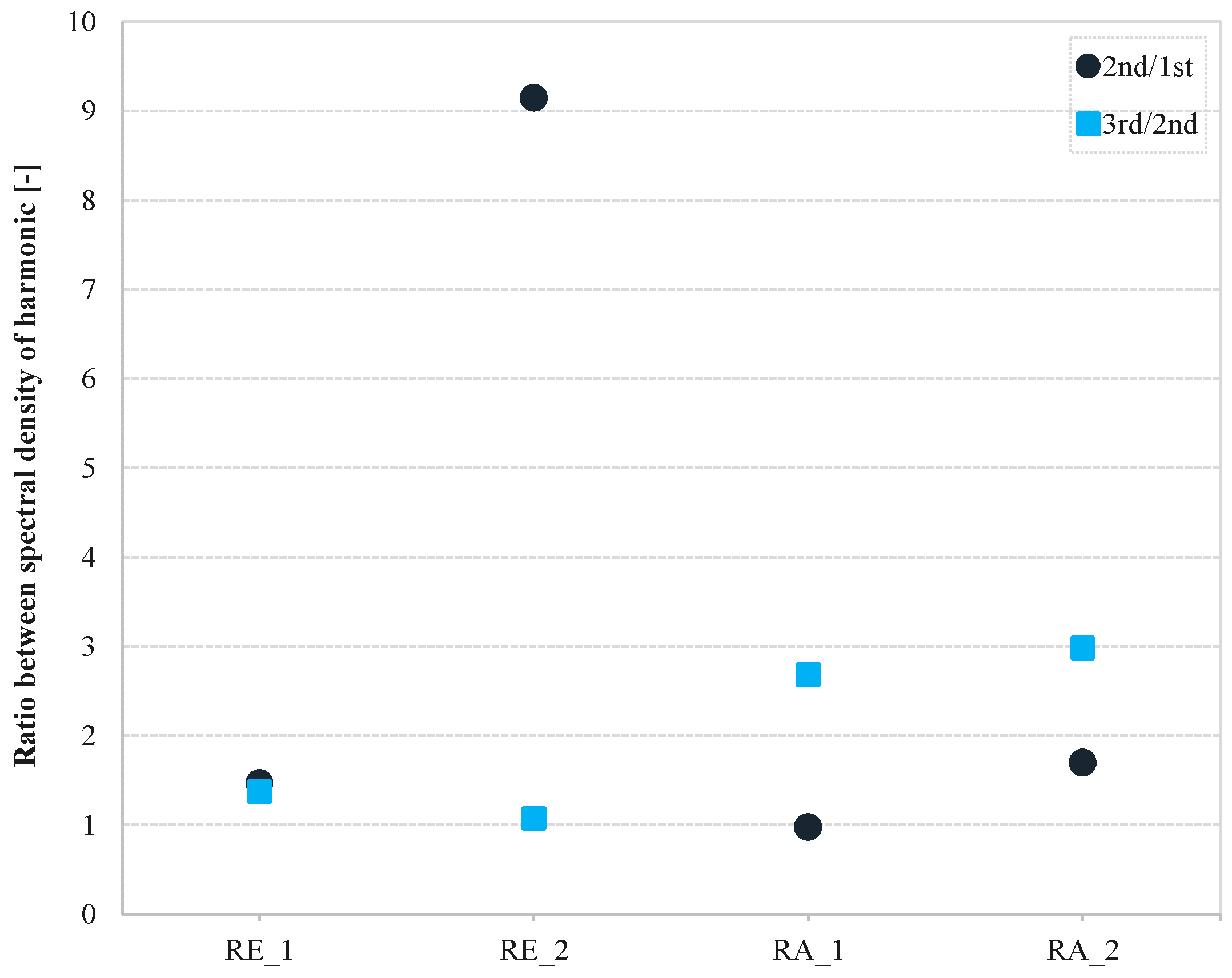
| Test RA_1 | Harmonics | f (Hz) | T(s) | E (m2/Hz) |
| 1st harmonic | 0.02319336 | 43.1157895 | 0.00059542 | |
| 2nd harmonic | 0.04516602 | 22.1405405 | 0.00058067 | |
| 3rd harmonic | 0.09033203 | 11.0702703 | 0.00155648 | |
| Test RA_2 | 1st harmonic | 0.02441406 | 40.9600042 | 0.00052997 |
| 2nd harmonic | 0.04516602 | 22.1405405 | 0.00089923 | |
| 3rd harmonic | 0.08544922 | 11.7028571 | 0.00267999 |
| Test RE_1 | Harmonics | f (Hz) | T(s) | E (m2/Hz) |
| 1st harmonic | 0.02197266 | 45.5111111 | 0.00211399 | |
| 2nd harmonic | 0.04760742 | 21.0051282 | 0.00310199 | |
| 3rd harmonic | 0.08056641 | 12.4121212 | 0.00424879 | |
| Test RE_2 | 1st harmonic | 0.02319336 | 43.1157895 | 0.00041757 |
| 2nd harmonic | 0.04516602 | 22.1405405 | 0.0038171 | |
| 3rd harmonic | 0.08911133 | 11.2219178 | 0.0040941 |
| E (m2/Hz) | RE_1 | RE_2 | RA_1 | RA_2 |
|---|---|---|---|---|
| total | 1.22 × 101 | 1.20 × 101 | 3.37 × 100 | 4.00 × 100 |
| <0.1 Hz | 1.45 × 10−1 | 1.19 × 10−1 | 3.97 × 10−2 | 6.34 × 10−2 |
| <0.03 Hz | 2.18 × 10−2 | 6.68 × 10−3 | 5.26 × 10−3 | 5.07 × 10−3 |
| Test CA_1 | Harmonics | f (Hz) | T(s) | E (m2/Hz) |
| 1st harmonic | 0.032958984 | 30.34074074 | 0.01233396 | |
| 2nd harmonic | 0.065917969 | 15.17037037 | 0.00001770 | |
| 3rd harmonic | 0.108642578 | 9.20449438 | 0.00004718 | |
| Test CA_2 | 1st harmonic | 0.025634766 | 39.00952381 | 0.00002758 |
| 2nd harmonic | 0.041503906 | 24.09411765 | 0.00000737 | |
| 3rd harmonic | 0.067138672 | 14.89454545 | 0.02348628 |
| Test CE_1 | Harmonics | f (Hz) | T(s) | E (m2/Hz) |
| 1st harmonic | 0.03295898 | 30.34074074 | 0.00314475 | |
| 2nd harmonic | 0.06713867 | 14.89454545 | 0.00000949 | |
| 3rd harmonic | 0.10805664 | 12.41212121 | 0.00002413 | |
| Test CE_2 | 1st harmonic | 0.023193359 | 43.11578947 | 0.00000319 |
| 2nd harmonic | 0.040283203 | 24.82424242 | 0.00000234 | |
| 3rd harmonic | 0.067138672 | 14.89454545 | 0.00393993 |
| E (m2/Hz) | CE_1 | CE_2 | CA_1 | CA_2 |
|---|---|---|---|---|
| total | 1.11 × 101 | 1.32 × 101 | 3.43 × 100 | 3.17 × 100 |
| <0.1 Hz | 2.53 × 10−2 | 3.14 × 10−2 | 9.80 × 10−2 | 1.86 × 10−1 |
| <0.03 Hz | 4.50 × 10−3 | 1.35 × 10−4 | 1.81 × 10−2 | 3.83 × 10−4 |
| Mode | f (Hz) |
|---|---|
| 1st | 0.02474874 |
| 2nd | 0.04949747 |
| 3rd | 0.07424621 |
| Test | Measured (m) | Test | Measured (m) |
|---|---|---|---|
| R_E1 | 0.36 | R_A1 | 0.30 |
| R_E2 | 0.41 | R_A2 | 0.37 |
| C_E1 | 0.16 | C_A1 | 0.18 |
| C_E2 | 0.12 | C_A2 | 0.23 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riefolo, L.; Contestabile, P.; Dentale, F.; Benassai, G. Low Frequency Waves Detected in a Large Wave Flume under Irregular Waves with Different Grouping Factor and Combination of Regular Waves. Water 2018, 10, 228. https://doi.org/10.3390/w10020228
Riefolo L, Contestabile P, Dentale F, Benassai G. Low Frequency Waves Detected in a Large Wave Flume under Irregular Waves with Different Grouping Factor and Combination of Regular Waves. Water. 2018; 10(2):228. https://doi.org/10.3390/w10020228
Chicago/Turabian StyleRiefolo, Luigia, Pasquale Contestabile, Fabio Dentale, and Guido Benassai. 2018. "Low Frequency Waves Detected in a Large Wave Flume under Irregular Waves with Different Grouping Factor and Combination of Regular Waves" Water 10, no. 2: 228. https://doi.org/10.3390/w10020228
APA StyleRiefolo, L., Contestabile, P., Dentale, F., & Benassai, G. (2018). Low Frequency Waves Detected in a Large Wave Flume under Irregular Waves with Different Grouping Factor and Combination of Regular Waves. Water, 10(2), 228. https://doi.org/10.3390/w10020228






