1. Introduction
The analysis of extremes arises in many branches of science and engineering. Hurricane winds for suspension bridge design and storm surge heights for coastal and offshore works are well-known examples in civil engineering. Extreme value analysis (EVA) is a branch of statistics dealing with the extreme deviations from the median of probability distributions. Knowledge of the value of an extreme event for a given return period TR is the result of the EVA.
In particular, in ocean and coastal engineering, extreme events are described in terms of the function H
S(T
R), which links the significant wave height (in the following: SWH, or H
S) of a sea state with different return periods T
R [
1,
2].
The traditional—and probably also the best—sources of data for such analyses are the historical in-situ (in the following: “direct” or “experimental”) wave measurements provided by wave buoy recorders. Buoys measure the motion of the sea surface, and modern buoys also measure slope and lateral motion [
3]. Properly analysed [
4,
5], these data allow an estimate of sea wave properties in terms of wave spectrum or, more simply, in terms of the main sea state parameters such as significant wave height H
S, mean and peak period T
m, T
p and mean direction θ
m.
However, the number of wave buoys is necessarily limited. For example, the entire Italian Data Buoy Network (in the following Rete Ondametrica Nazionale, RON), operational from 1989 until 2014, consisted of only 15 stations positioned along the more than 7000 km of Italian coasts [
6,
7].
As a consequence, it has become a common practice [
8,
9] to use data (in the following indicated as “indirect data” or “model data”) originated from global or regional wave models, which are in turn driven by meteorological wind models. Global and regional wave data are readily available and this favours their extensive use by ocean engineers and researchers. The wave part of the model chain implicitly takes into account the geographical and morphological aspects of the wave formation and propagation, such as the water depth (when applicable) and the variability of fetch, while the meteorological part includes all the information related both to large scale air circulation as well as to “regional” (in a meteorological sense) orography.
However, substantial differences can be found when performing an EVA that considers directly observed and model wave data [
10,
11,
12,
13,
14]. This difference is primarily due to the obvious fact that direct data, even though affected by errors—like any experiment—are still a more reliable estimate of the true values, compared to a model chain that, despite all the efforts and the care taken, is the result of enormously complicated calculations. The numerical diffusion [
13] present in all the models tends to smoothen the results and thus to decrease the peak values, particularly in areas with strong spatial horizontal gradients. Besides, most of the time the wave model results are only calibrated (“assimilated”) using of data from altimeter satellites, whose timing and location is uncorrelated with the weather or the sea state, so the calibration is biased against extreme weather or sea states.
It must also be noted here [
14] that the scatter of results for wind velocity is always larger than for waves: this implies that the atmospheric variability [
15] is the basic reason for the differences between model and experimental extreme data.
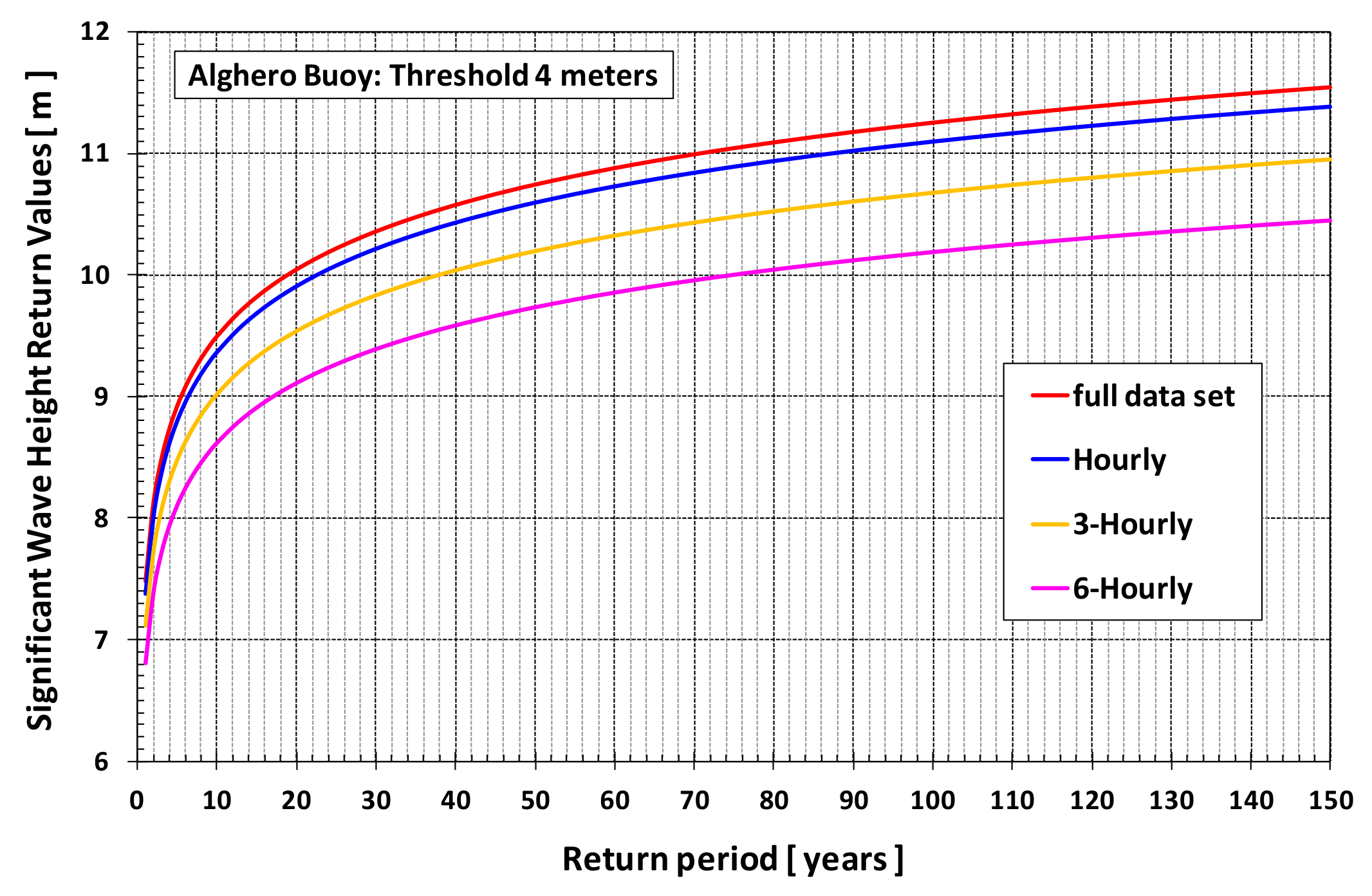
Another important aspect is the bias in the evaluation of extremes present in all sources of data whenever the sampling of the relevant parameter (SWH in our case) is carried out with too long a time interval compared with the inherent time constant of the phenomenon. The results shown for instance in [
10,
16], prove that use of data with a low time resolution (such as a 3 or 6 h) causes a considerable undervaluation of the extreme SWH values for a given return time T
R. The following
Figure 1 [
16] illustrates this point—by degrading the original buoy data from a sampling rate of 30′ (full data set) to a sampling rate of 6 h, there is an important reduction of the estimated H
S(T
R). This raises the problem of deciding what would be the “right” interval to choose in order to compute the H
S(T
R) curves. Current engineering practice is oriented towards 30′ or 1 h intervals, mostly because that is the commonly available sampling rate for buoy data, but also because what is normally important is not the extreme single wave, but some kind of average wave height; after all, this is the reason for adopting the concept of “significant wave height”. The opportunity of this choice seems to be confirmed by the apparent convergence of the curves (1 h curve in blue is very close to the 30′ curve in red).
Investigating the use of even shorter sampling rates would lead to a different problem, i.e., the determination of the probability of single extreme waves: an issue which also has relevance, but seems to be not yet clarified, see for instance [
17].
As a consequence of all this, the main problem in ocean and coastal engineering is that while long series of model data are available practically everywhere, the quality of such data is inadequate for the purpose of evaluating extreme SWHs; on the other hand, measurements taken at buoy wave meters provide reliable data, but for a limited number of sites.
The objective of this work is to propose a procedure by which model data can be integrated with experimental data in order to provide a better estimate of extreme SWH values. This is done by considering model-derived data at a given location as estimators—in a statistical sense—of the true values; and, in order to improve the estimate as well as to evaluate the error, information on their statistical distribution is obtained by analyzing the wave buoy data series in the area.
In the following such a procedure is discussed and applied to three different sea areas:
Global or regional wave datasets are provided by different organizations, i.e., ECMWF (European Centre for Medium-Range Weather Forecasts) and NOAA (National Oceanic and Atmospheric Administration).
The NOAA National Center for Environmental Prediction (NCEP) developed the Climate Forecast System (CFS), a fully coupled model representing the interaction between the Earth’s atmosphere, oceans, land and sea ice. A reanalysis of the sea and atmosphere state for the period of 1979–2009 has been conducted, resulting in the CFS Reanalysis (CFSR) dataset. Using the CFSR dataset, the NOAA Marine Modelling and Analysis Branch (MMAB) has produced a wave hindcast for the same period. The wave hindcast dataset has been generated using the WAVEWATCH III (WW3) model (v3.14) (NOAA/National Weather Service, College Park, MD, U.S.A.) and is suitable for use in climate studies. The wave model resolves 50 wave frequencies (from 0.035 to 0.963 Hz) and 36 wave directions (directional resolution of 10°). Data are given at a three-hourly time resolution and are available both on a global grid (spatial resolution of 0.5° × 0.5°) and on 16 different regional nested grids with a variable spatial resolution.
The ECMWF produces the ERA-Interim dataset, another global atmospheric reanalysis dataset starting from 1979 and continuously updated. It also models oceanographic variables, including waves. The wave model used by ECMWF is based on the WAM (WAve Model) approach [
18], resolving 30 wave frequencies and 24 wave directions. Furthermore, the wave model contains corrections for treating unresolved bathymetry effects and a reformulation of the dissipation source term. ERA-Interim produces four analysis data per day (at 00:00, 06:00, 12:00 and 18:00 UTC) and two 10-day forecast data per day, initialized from analysis at 00:00 and 12:00 UTC. Both wave products are distributed on a global 1.0° × 1.0° latitude/longitude grid.
Many commercial companies provide a model series with smaller sampling intervals, and often with a finer spatial resolution; however only NOAA and ECMWW provide well-tested and public reanalysis data, so in the following only those two sources have been considered.
3. Methods
As stated above, substantial differences can be found when performing an EVA considering directly observed and indirect wave data. Therefore, for practical coastal engineering purposes a procedure is necessary to correct and to evaluate the reliability of HS(TR) curves derived from model data for any location at sea. In the following, one such procedure is proposed and tested and shown to be reliable in areas where an adequate number of in situ wave buoys are available. Unlike most calibration or validation procedures currently being performed, all our elaborations were carried out on the HS(TR) functions rather than on the single raw extreme recorded significant wave heights HS. The basic concept is that the parameters of any HS(TR) function are themselves randomly distributed, and that the distribution of such parameters can be estimated by analyzing in situ data for any given area, thus providing a regional assessment of the error associated with such an estimate.
It is worth noting that the wave part of the model chain takes care of physical marine aspects such as fetch and depth, so that the difference between the data from the buoy and the data from the relevant model grid point depends partly on the meteorological uncertainty (i.e., the error of the wind part of the chain) and partly from the inherent error of the wave part of the model.
This approach is similar to what is done in many fields where distributed data (from a model or from a remote sensor) need to be assimilated and corrected with field data. In hydrology, for example, regional models for hydro-meteorological variables, such as extreme or annual rainfall, are often obtained by coupling a deterministic indicator, based on models, with a spatial model of the residuals measured at gauged sites [
19,
20,
21,
22]. A similar approach is also used for extracting the estimated rainfall rate at ground through meteorological radars and rain gauge measurements [
23,
24]. Several methods have been introduced to this purpose [
23,
24,
25,
26,
27]. In all such procedures, a regional assessment of statistical uncertainty is carried out by making use of spatial estimates of the error distributions.
For SWH extremes, the limited information coming from the historical data can be largely compensated by the available indirect model archive data. In order to do so, in this work the model data are used as indicators, and the buoy data are used for the correction of biases and the evaluation of uncertainties.
Extreme SWH values HM(TR) derived from model (indirect) time series are thus integrated with extreme SWH values HD(TR) derived from whatever wave buoy (direct) time series available in the same geographical area. This provides a tool to derive an estimated function HS(TR) for any point in the area, as well as an assessment of the quality of the whole model chain.
There are many possible alternatives which can be selected for this purpose—a first important decision to be taken is whether the observation period upon which the parameters are estimated should be the same for both the model and the wave buoy, or should encompass the whole length of the available period of observed or modeled data. On the one hand, for the sake of consistency, the time spans of the observation should coincide; on the other hand, since the final scope of the work is to provide a reliable tool, it would instead make sense to compare all the available in situ data with all the available model data (normally, the simulated data series are much longer than the experimental ones). As stated above, in the present paper, since the objective is to illustrate a procedure in the simplest possible way, the first alternative has been pursued so the series considered for each location overlap as much as possible.
A further choice is the actual threshold value to adopt if a POT (peak over threshold) procedure is used to compute the HD(T
R) and HM(T
R) functions. In this work, among the various possible alternatives, the thresholds were chosen by making sure that the number N
T of extreme events considered would be roughly equal for all the samples. Obviously, N
T increases by decreasing the threshold because more events are taken into account; on the other hand, if the threshold is too low the quality of the estimate is compromised, since the events will no longer be statistically independent. A compromise has to be found, and a measure of such compromise is given by the value of the parameter λ = N
T/
n,
n being the number of available observation years. This procedure is normally adopted in coastal engineering activities [
28] and is meant to provide a higher number of extremes, compared with annual maxima.
In any case, since the present paper is not aimed at evaluating, discussing or recommending one particular form of HS(TR), or any particular procedure to estimate its parameters, the only requirement is that such a form and procedure should be uniform throughout the whole analysis.
In the following, the peak over threshold (POT) method in the form described for instance in [
29,
30,
31,
32,
33] was followed to produce a set of extreme significant wave height values. There is here a choice to be made as to which extreme value distribution should be fitted to the data. For instance [
34,
35] suggest that a GPD (generalized Pareto distribution) should be employed for EVA. However, according to current ocean engineering practice [
28,
36], the Weibull distribution was adopted (Equation (1)):
where A, B and k are known respectively as scale, position and shape parameters. Once the distribution parameters are known, the H
S return value for a given return period T
R (in years) is computed by making use of Equation (2):
The λTR term derives from the POT techniques, where λ extreme values are considered on average for each observation year.
The same operation is carried out with both historical experimental direct datasets HD(T
R) and indirect data HM(T
R) at the same locations—naturally most of the time the positions do not exactly coincide with model grid points, so a spatial bi-linear interpolation (co-location) as described in [
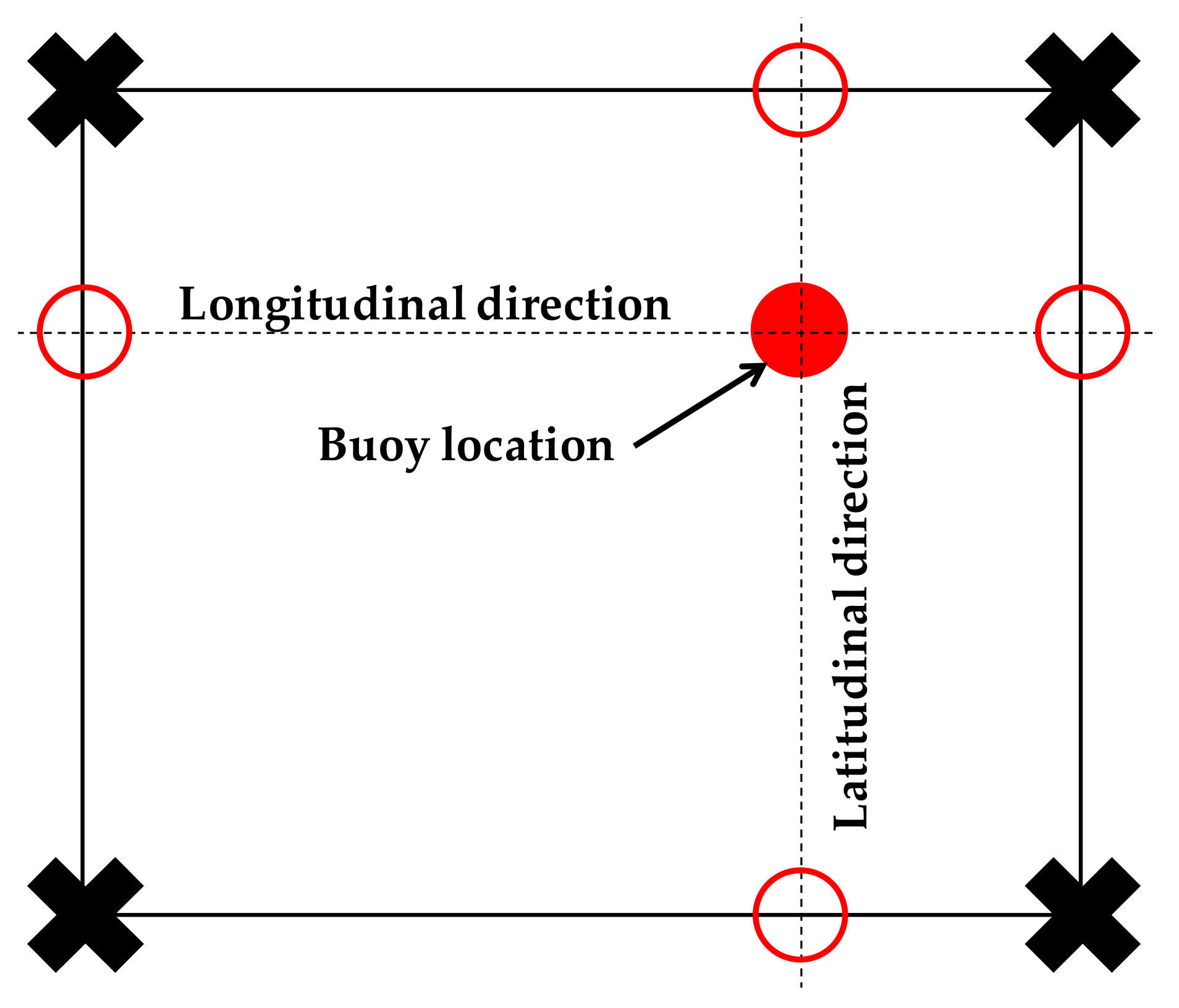
37] (pp. 10–11) has to be carried out. As shown in
Figure 5, for the four model grid points (black crosses) around each buoy location (filled red circle), a linear interpolation (red circles) between each pair of grid points has been computed. These two, in either the latitudinal or longitudinal direction, have then been used for linear interpolation to the requested boy location (filled red circle).
Since wave buoy time series are often incomplete, the experimental and model data series cannot be made to coincide exactly; some care must thus be taken to make sure that the extent of time they refer to are not too far apart. The mean rate values λ for the indirect data has been kept close enough to the λ value of the in-situ data, which generally means adopting a lower threshold.
Once the experimental HD(TR) and the model-derived HM(TR) curves have been computed, no matter how good the data or how careful their elaboration is, they will certainly differ for the reasons stated above.
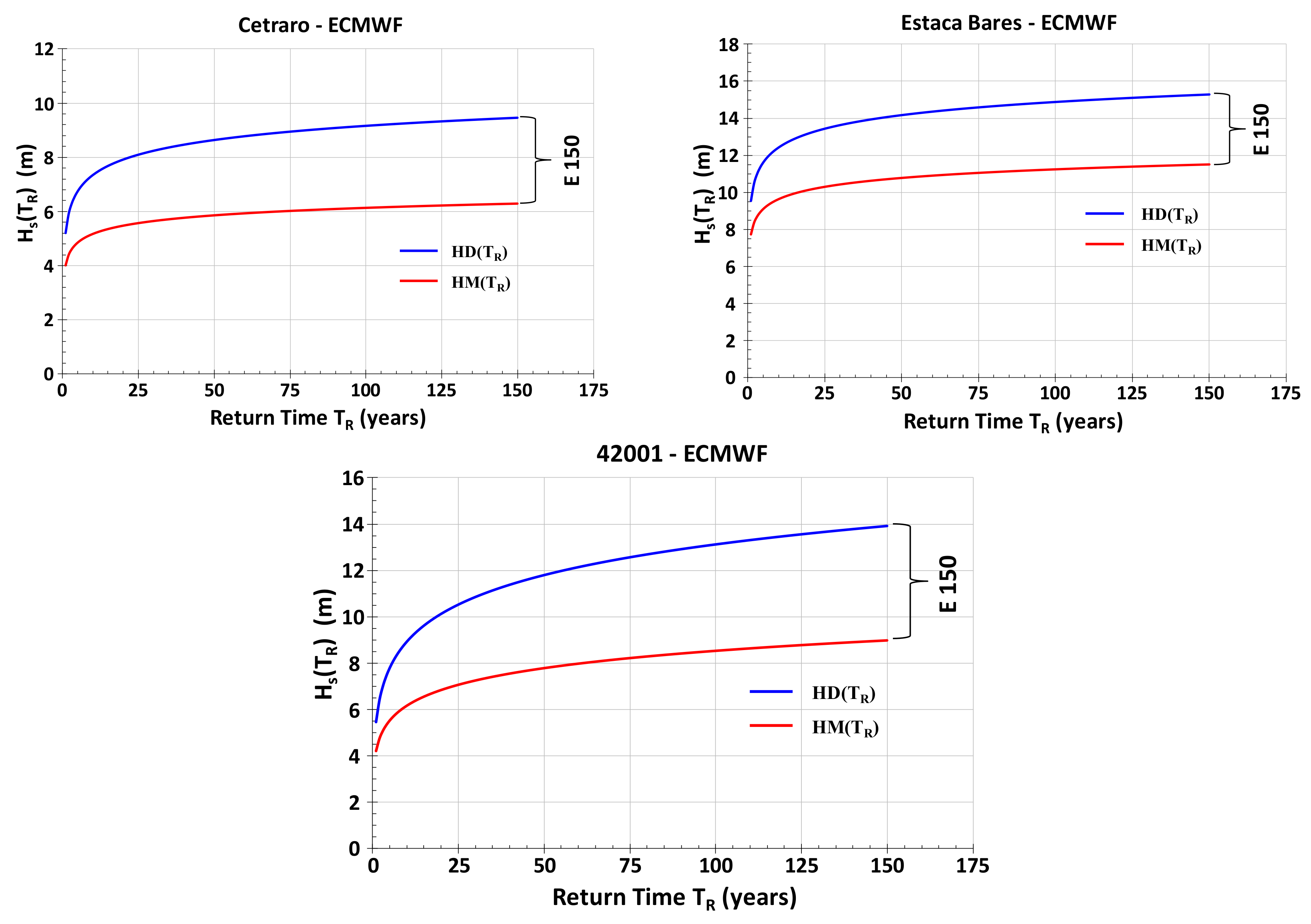
In the following
Figure 6, the results are shown for a test carried out in the three sea regions.
Models generally underestimate extreme values compared to experimental data, partly due to the inevitable smoothing of the results due to the numerical interpolation, and partly due to inherent limitations of the model chain, as it was shown quantitatively in [
13,
14,
15,
16]. As a consequence, it is to be expected for a given return time T
R that the corresponding significant wave height return value computed with the indirect data HM(T
R) is lower than the value obtained by making use of direct data HD(T
R).
The HM(T
R) values are then assumed to be indicators of the unknown true values, and a statistical correlation must thus be found between HM(T
R) and HD(T
R) in order to provide a reliable estimator H
S(T
R). We have then [
22]:
e(μ,σ) being the relative error distribution.
Following Equation (3), the expected values H
S for each T
R are:
and its upper and lower bounds of the 95% confidence intervals, corresponding at the 97.5% an 2.5% percentiles, are respectively:
e(μ,σ) represents the error caused by many reasons: meteorological uncertainty, model inaccuracy, and, as often happens, the different sampling rate between the experimental and the model data. The value of the parameters μ and σ can be evaluated by making use of a spatial analysis, i.e., by comparing the model result HM
i(T
R) with the experimental HD
i(T
R) values at the buoy location i of the m buoys available in the area. The relative error e
i(T
R) at location i is then given by Equation (6):
Its expected value μ(T
R) can be estimated as:
and its root mean square σ(T
R) as
the sums over the index i being extended to the m wave buoys in the region.
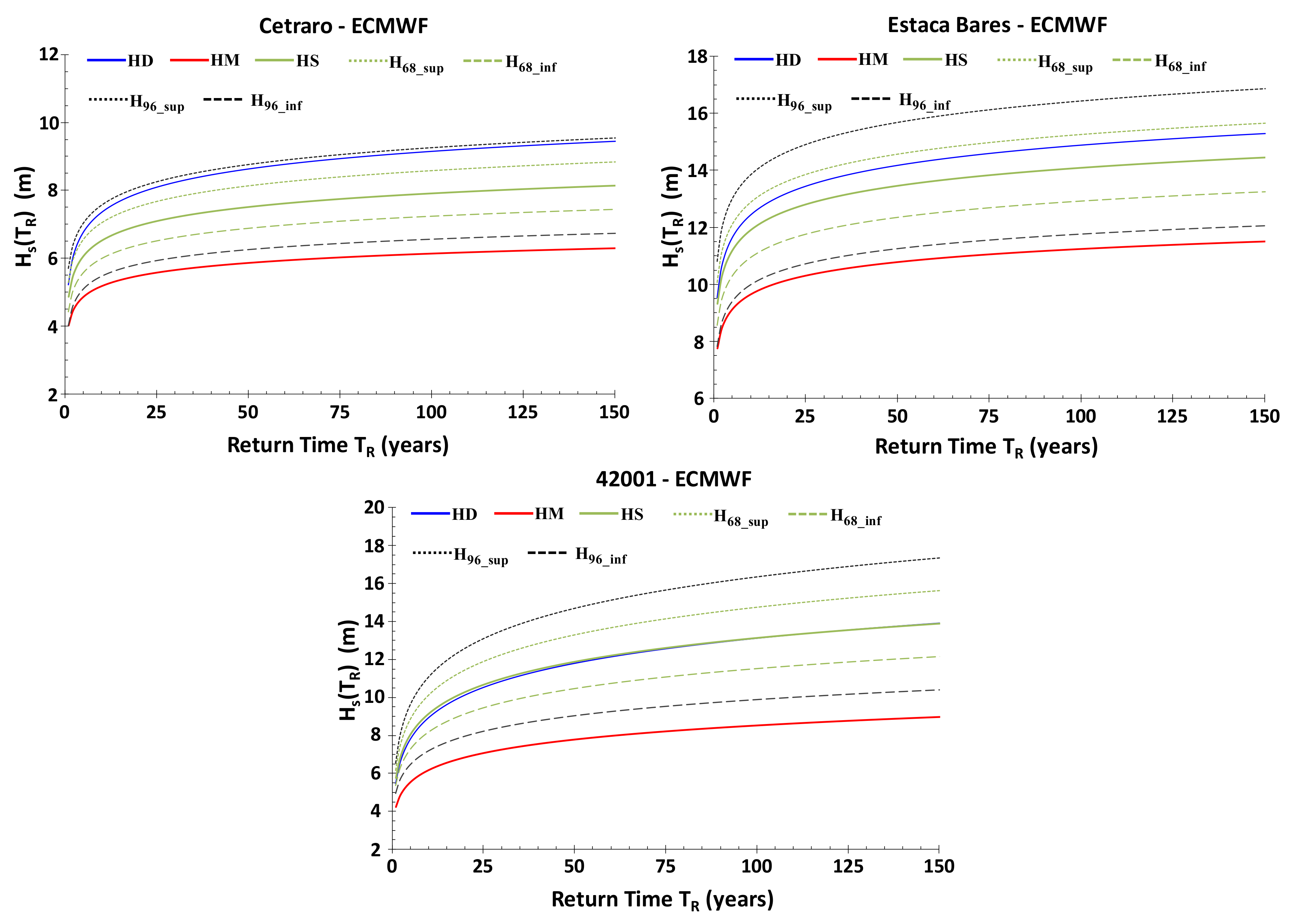
These estimates can be used to quantify the accuracy of the model chain, as well as to provide a way to compute HS(TR) curves for geographical locations not coinciding with wave buoys by making use of Equation (4), and of the standard deviation σ(TR) given by Equation (8).
Figure 7 reports some examples. Curves H
S(T
R) are shown together with the σ
68 and σ
96 confidence interval curves respectively equal to:
Similar analyses have been carried out for the three regions, and the results are reported in the following section.