Evaluation of Evapotranspiration Estimates in the Yellow River Basin against the Water Balance Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sets
2.2.1. ET Products
2.2.2. Precipitation, Streamflow, Soil Moisture, and Gravity Recovery and Climate Experiment (GRACE)
2.3. Methods
2.3.1. Water Balance Method
2.3.2. Error Metrics
2.3.3. Linear Trends
3. Results
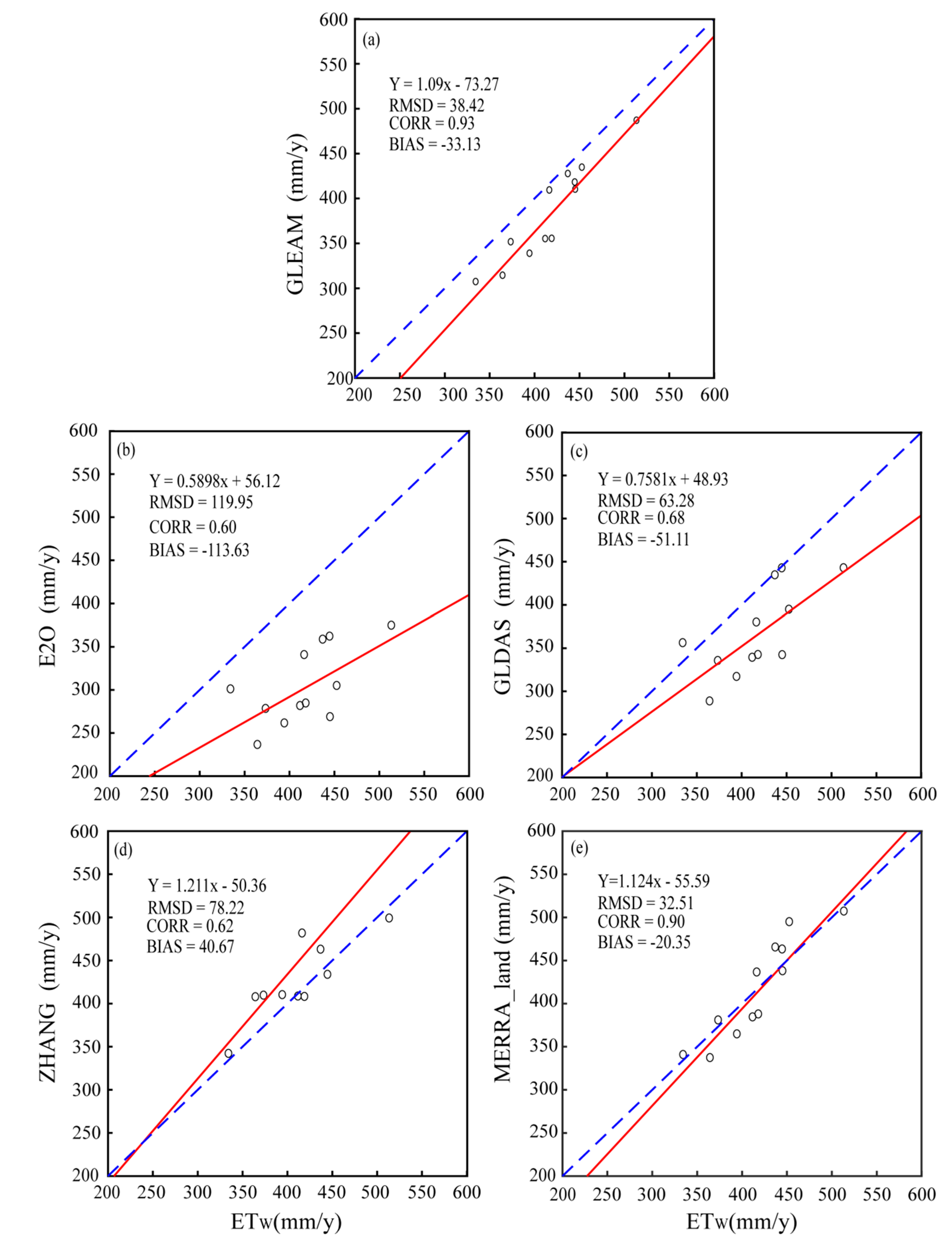
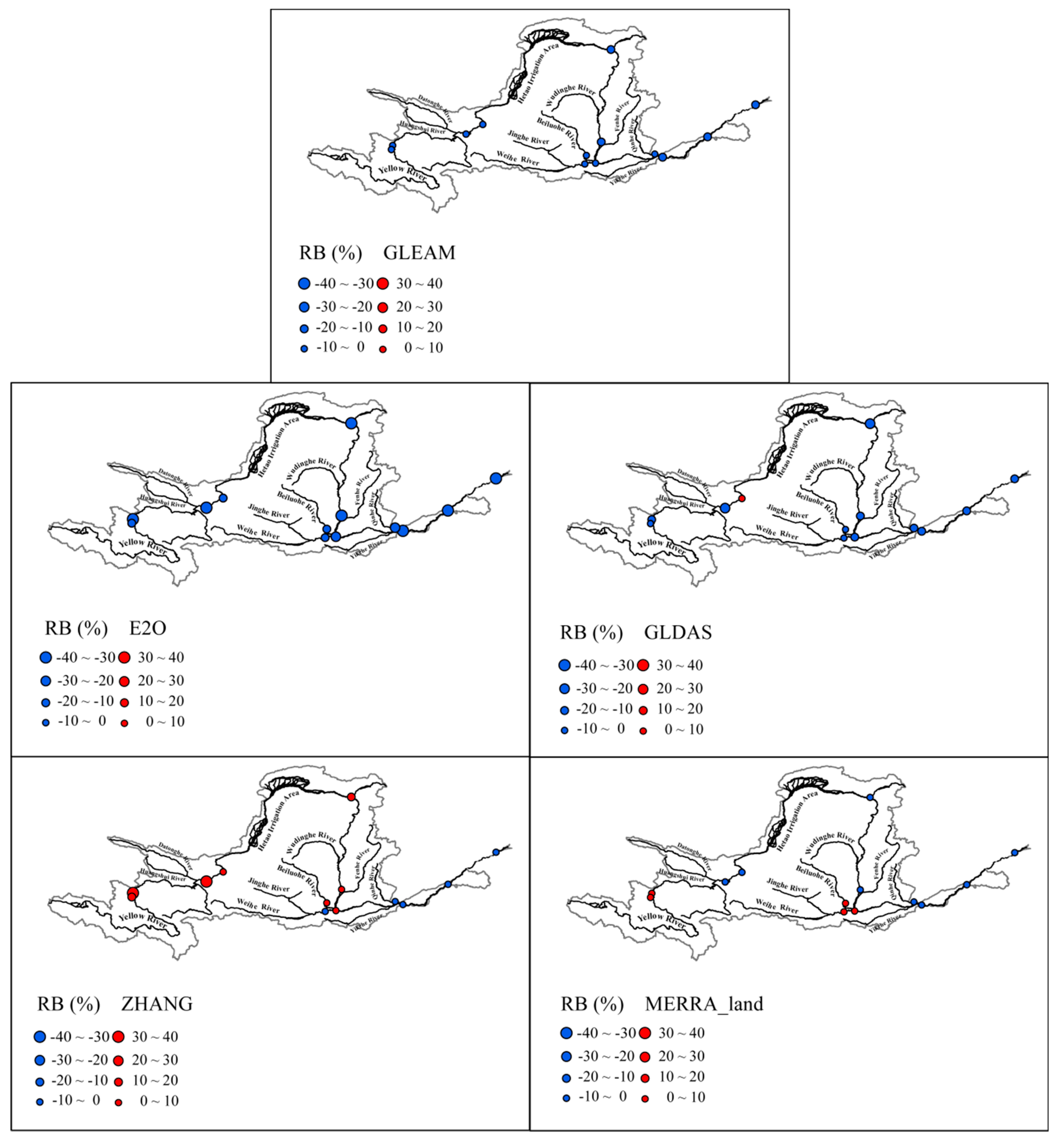
3.1. Long-Term Averages
3.2. Interannual Variations
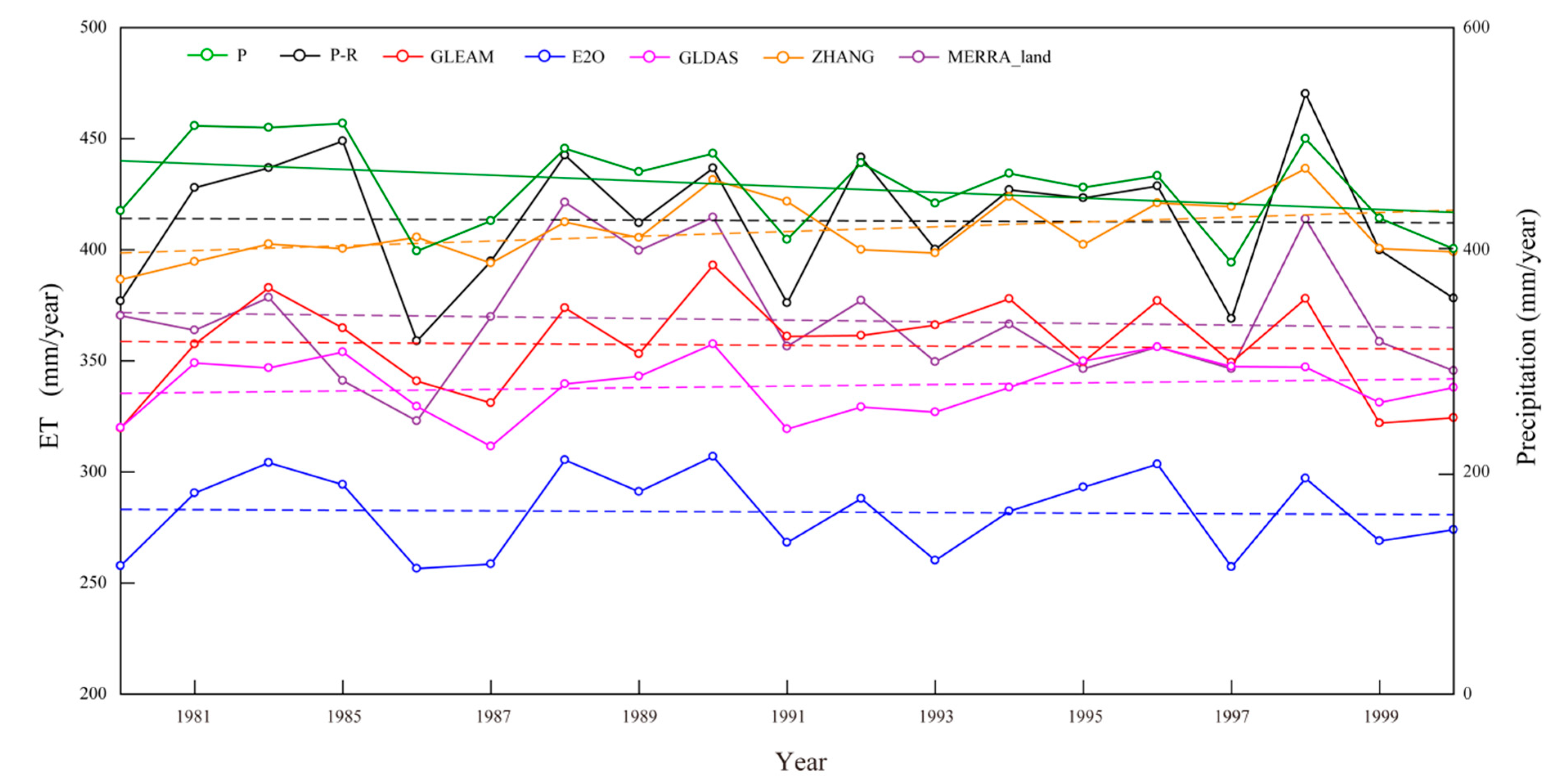
3.2.1. Estimations of Interannual ETw
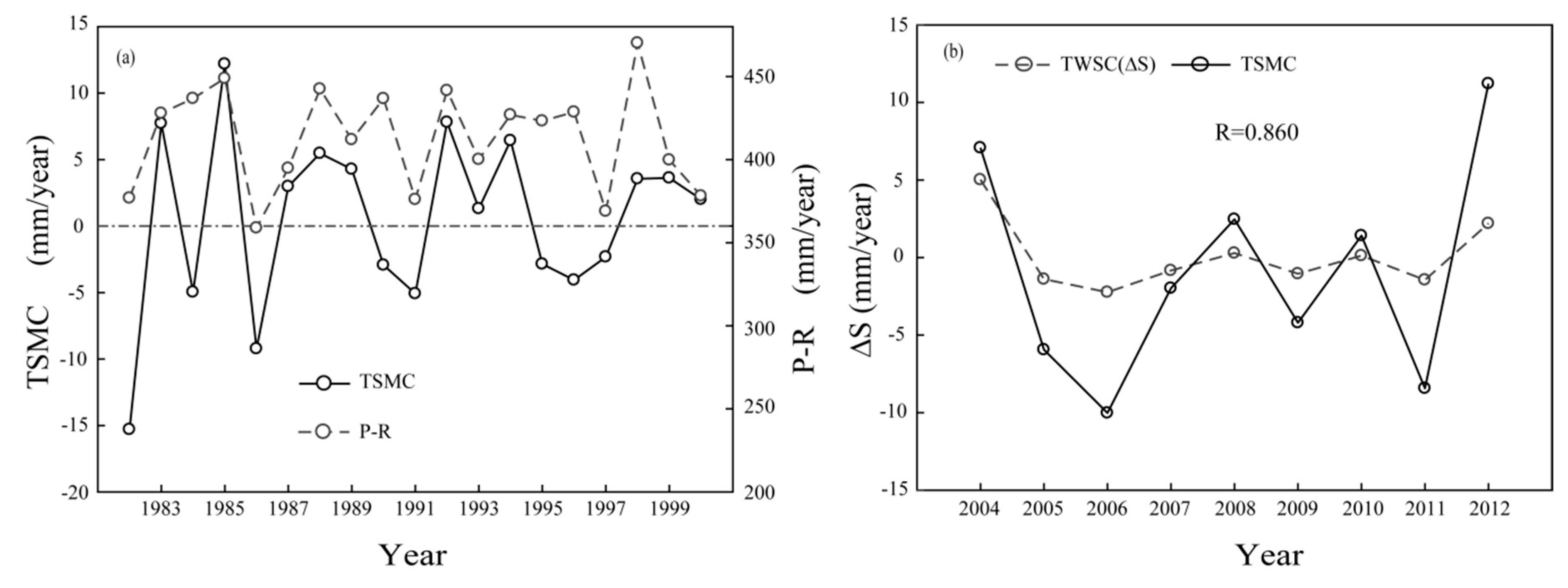
3.2.2. Interannual Variations and Trends
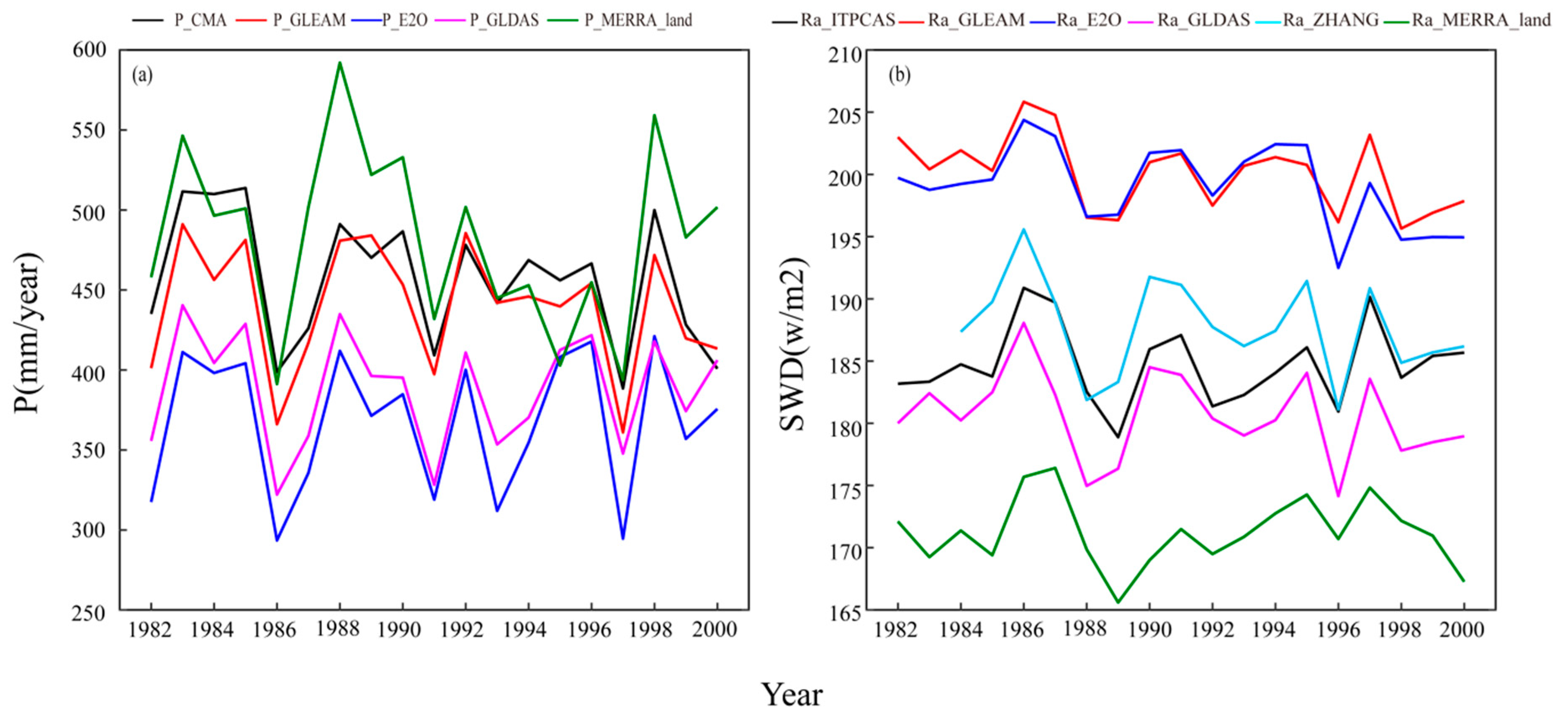
4. Discussion
Possible Reasons for the ET Product Performance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land-atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–323. [Google Scholar] [CrossRef]
- Xue, B.L.; Kumagai, T.O.; Iida, S.I.; Nakai, T.; Matsumoto, K.; Komatsu, H.; Otsuki, K.; Ohta, T. Influences of canopy structure and physiological traits on flux partitioning between understory and overstory in an eastern Siberian boreal larch forest. Ecol. Model. 2011, 222, 1479–1490. [Google Scholar] [CrossRef]
- Tang, X.G.; Li, H.P.; Desai, A.R.; Nagy, Z.; Luo, J.H.; Kolb, T.E.; Olioso, A.; Xu, X.B.; Yao, L.; Kutsch, W.; et al. How is water-use efficiency of terrestrial ecosystems distributed and changing on Earth? Sci. Rep. 2014, 4, 7483. [Google Scholar] [CrossRef] [PubMed]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Trajkovic, S. Testing hourly reference evapotranspiration approaches using lysimeter measurements in a semiarid climate. Hydrol. Res. 2010, 41, 38–49. [Google Scholar] [CrossRef]
- Liu, W.B.; Wang, L.; Zhou, J.; Li, Y.Z.; Sun, F.B.; Fu, G.B.; Li, X.P.; Sang, Y.F. A worldwide evaluation of basin-scale evapotranspiration estimates against the water balance method. J. Hydrol. 2016, 538, 82–95. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Chen, J.; Seneviratne, S.I.; Viterbo, P.; Holl, S.; Wilson, C.R. Basin scale estimates of evapotranspiration using GRACE and other observations. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Cai, X.T.; Yang, Z.L.; Xia, Y.L.; Huang, M.Y.; Wei, H.L.; Leung, R.; Ek, M.B. Assessment of simulated water balance from Noah, Noah-MP, CLM, and VIC over CONUS using the NLDAS test bed. J. Geophys. Res. Atmos. 2014, 119, 13751–13770. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; kamahori, H.; kobayashi, C.; Endo, H.; miyaoka, K.; Takahashi, K. The JRA-55 Reanalysis: General specifications and basic characteristics. J. Meteor. Soc. Jpn. 2015, 93, 5–58. [Google Scholar] [CrossRef]
- Wang, K.C.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, K.C.; Liu, X.M.; Liu, C.M. Water storage in reservoirs built from 1997 to 2014 significantly altered the calculated evapotranspiration trends over China. J. Geophys. Res. Atmos. 2016, 121, 10097–10112. [Google Scholar] [CrossRef]
- Xue, B.L.; Wang, L.; Li, X.P.; Yang, K.; Chen, D.L.; Sun, L.T. Evaluation of evapotranspriation estimates for two river basins on the Tibetan Plateau by a water balance method. J. Hydrol. 2013, 492, 290–297. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Krogh, S.A.; Pomeroy, J.W.; McPhee, J. Physically based mountain hydrological modeling using reanalysis data in Patagonia. J. Hydrometeorol. 2015, 16, 172–193. [Google Scholar] [CrossRef]
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; Dee, D.; Dutra, E.; Muñoz-Sabater, J.; Pappenberger, F.; et al. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef]
- Wang, S.; McKenney, D.W.; Shang, J.; Li, J. A national-scale assessment of long-term water budget closures for Canada’s watersheds. J. Geophys. Res. Atmos. 2014, 119, 8712–8725. [Google Scholar] [CrossRef]
- Li, X.P.; Wang, L.; Chen, D.L.; Yang, K.; Wang, A.H. Seasonal evapotranspiration changes (1983–2006) of four large basins on the Tibetan Plateau. J. Geophys. Res. 2014, 119, 13079–13095. [Google Scholar] [CrossRef]
- Zhang, Y.; Leuning, R.; Chiew, F.H.S.; Wang, E.; Zhang, L.; Liu, C.M.; Sun, F.B.; Peel, M.C.; Shen, Y.J.; Jung, M. Decadal trends in evaporation from global energy and water balances. J. Hydrometeorl. 2012, 13, 379–391. [Google Scholar] [CrossRef]
- Zeng, Z.Z.; Wang, T.; Zhou, F.; Ciais, P.; Mao, J.F.; Shi, X.Y.; Piao, S.L. A worldwide analysis of spatiotemporal changes in water balance-based evapotranspiration from 1982–2009. J. Geophys. Res. Atmos. 2014, 119, 1186–1202. [Google Scholar] [CrossRef]
- Li, Y.Z.; Kang, L.; Liu, C.M.; Liu, W.B.; Peng, B. Evaluation of different evapotranspiration products in the middle Yellow River Basin, China. J. Hydrol. Res. 2017, 48, 498–513. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.-Y.; Yang, T. Variability of water resource in the Yellow River basin of past 50 years, China. Water Resour. Manag. 2009, 23, 1157–1170. [Google Scholar] [CrossRef]
- Zhu, Y.; Chang, J.; Huang, S.; Huang, Q. Characteristics of integrated droughts based on a nonparametric standardized drought index in the Yellow River Basin, China. Hydrol. Res. 2015, 47, 454–467. [Google Scholar] [CrossRef]
- Ryberg, K.R.; Lin, W.; Vecchia, A.V. Impact of climate variability on runoff in the North Central United States. J. Hydrol. Eng. 2013, 19, 148–158. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, L.; Gallichand, J. Runoff responses to afforestation in a watershed of the Loess Plateau, China. Hydrol. Process. 2003, 17, 2599–2609. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; Schalie, R.V.D.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Schellekens, J.; Dutra, E.; Martínez-de la Torre, A.; Balsamo, G.; van Dijk, A.; Sperna-Weiland, F.; Minvielle, M.; Calvet, J.-C.; Decharme, B.; Eisner, S.; et al. A global water resources ensemble of hydrological models: The eartH2Observe Tier-1 dataset. Earth Syst. Sci. Data 2017, 9, 389–413. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D.; Lannoy, G.D.; Forman, B.A.; Liu, Q.; Mahanama, S.P.P.; Toure, A. Assessment and enhancement of MERRA land surface Hydrology estimates. J. Clim. 2011, 24, 6322–6338. [Google Scholar] [CrossRef]
- Hutchinson, M.F. Interpolation of rainfall data with thin plate smoothing splines. Part I: Two dimensional smoothing of data with short range correlation. J. Geogr. Inf. Decision Anal. 1998, 2, 139–151. [Google Scholar]
- Yuan, Z.; Yang, Z.; Yan, D.; Yin, J. Historical changes and future projection of extreme precipitation in China. Theor. Appl. Climatol. 2017, 127, 1–15. [Google Scholar]
- Zhang, X.; Tang, Q.; Pan, M.; Tang, Y. A long-term land surface hydrologic fluxes and states dataset for China. J. Hydrometeorol. 2014, 15, 2067–2084. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.J.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.T.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Swenson, S.C.; Wahr, J. Estimating large-scale precipitation minus evapotranspiration from GRACE satellite gravity measurements. J. Hydrometeorl. 2006, 7, 252–270. [Google Scholar] [CrossRef]
- Mo, X.; Wu, J.J.; Wang, Q.; Zhou, H. Variations in water storage in China over recent decades from GRACE observations and GLDAS. Nat. Hazards Earth Syst. Sci. 2016, 16, 469–482. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Gong, Z.; He, X.; Zhang, Y.; Andam-Akorful, S.A. Estimating total discharge in the Yangtze River Basin using satellite-based observations. Remote Sens. 2013, 5, 3415–3430. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Famiglietti, J.S. Hydrology: Water from on high. Nature 2006, 444, 562–563. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Wang, C.; Chen, Y.; Chen, X.; Yu, Z. Climate change and water storage variability over an arid endorheic region. J. Hydrol. 2015, 529, 330–339. [Google Scholar] [CrossRef]
- Theil, H. A rank invariant method of linear and polynomial regression analysis, Part 3. Proc. K. Ned. Akad. Wet. 1950, 53, 1397–1412. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Measures; Charles Griffin Inc.: London, UK, 1975. [Google Scholar]
- Liu, X.; Liu, W.; Xia, J. Comparison of the streamflow sensitivity to aridity index between the Danjiangkou Reservoir basin and Miyun Reservoir basin, China. Theor. Appl. Climatol. 2013, 111, 683–691. [Google Scholar] [CrossRef]
- Mateo, C.M.; Hanasaki, N.; Komori, D.; Tanaka, K.; Kiguchi, M.; Champathong, A.; Sukhapunnaphan, T.; Yamazaki, D.; Oki, T. Assessing the impacts of reservoir operation to floodplain inundation by combining hydrological, reservoir management, and hydrodynamic models. Water Resour. Res. 2014, 50, 7245–7266. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, K. Comparison of evapotranspiration estimates based on the surface water balance, modified Penman-Monteith model, and reanalysis data sets for continental China. J. Geophys. Res. Atmos. 2017, 122, 3228–3244. [Google Scholar] [CrossRef]
- Livneh, B.; Lin, C.; Mishra, V.; Andreadis, K.; Maurer, E.P.; Lettenmaier, D.P. A long-term hydrologically based dataset of land surface fluxes and states for the conterminous U.S.: Update and extensions. J. Clim. 2013, 26, 9384–9392. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Chaney, N.W.; Wood, E.F. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- Mueller, B.; Seneviratne, S.I.; Jimenez, C.; Corti, T.; Hirschi, M.; Balsamo, G.; Ciais, P.; Dirmeyer, P.; Fisher, J.B.; Guo, Z.; et al. Evaluation of global observations-based evapotranspriation datasets and IPCC AR4 simulations. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Teuling, A.J.; Seneviratne, S.I.; Stoeckli, R.; Reichstein, M.; Moors, E.; Ciais, P.; Luyssaert, S.; van den Hurk, B.; Ammann, C.; Bernhofer, C.; et al. Contrasting response of European forest and grassland energy exchange to heatwaves. Nat. Geosci. 2010, 3, 722–727. [Google Scholar] [CrossRef]
- Ukkola, A.M.; Prentice, I.C. A worldwide analysis of trends in water-balance evapotranspiration. Hydrol. Earth Syst. Sci. 2013, 17, 4177–4187. [Google Scholar] [CrossRef]
- Badgley, G.; Fisher, J.B.; Jiménez, C.; Tu, K.P.; Vinukollu, R. On uncertainty in global terrestrial evapotranspiration estimates from choice of input forcing datasets. J. Hydrometeorol. 2015, 16, 1449–1455. [Google Scholar] [CrossRef]
- Su, T.; Feng, T.C.; Feng, G.L. Evaporation variability under climate warming in five reanalyses and its association with pan evaporation over China. J. Geophys. Res. Atmos. 2015, 120, 8080–8098. [Google Scholar] [CrossRef]
- Lipton, A.E.; Liang, P.; Jiménez, C.; Moncet, J.L.; Aires, F.; Prigent, C.; Lynch, R.; Galantowicz, J.F.; d’Entremont, R.P.; Uymin, G. Sources of discrepancies between satellite-derived and land surface model estimates of latent heat fluxes. J. Geophys. Res. Atmos. 2015, 120, 2325–2341. [Google Scholar] [CrossRef]
- Hutyra, L.R.; Munger, J.W.; Saleska, S.R.; Gottlieb, E.; Daube, B.C.; Dunn, A.L.; Amaral, D.F.; de Camargo, P.B.; Wofsy, S.C. Seasonal controls on the exchange of carbon and water in an Amazonian rain forest. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Costa, M.H.; Biajoli, M.C.; Sanches, L.; Malhado, A.C.M.; Hutyra, L.R.; da Rocha, H.R.; Aguiar, R.G.; de Araújo, A.C. Atmospheric versus vegetation controls of Amazonian tropical rain forest evapotranspiration: Are the wet and seasonally dry rain forests any different? J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
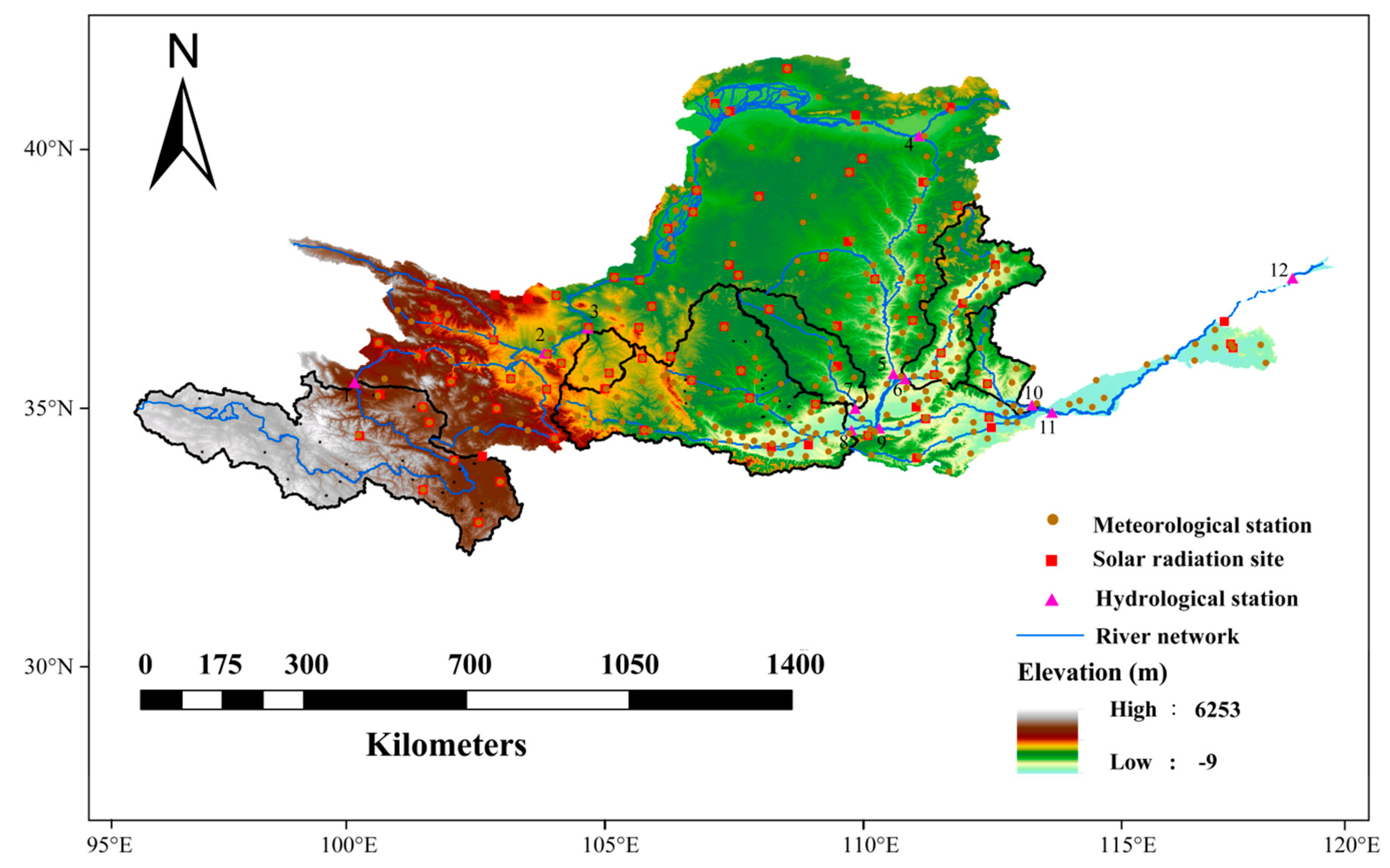

| No. | Station | Longitude | Latitude | Drainage Area (km2) |
|---|---|---|---|---|
| 1 | Tangnaihai | 100.15 | 35.50 | 117,605 |
| 2 | Lanzhou | 103.82 | 36.07 | 222,507 |
| 3 | Jinyuan | 104.66 | 36.55 | 10,496 |
| 4 | Toudaoguai | 111.07 | 40.27 | 367,898 |
| 5 | Longmen | 110.58 | 35.67 | 497,552 |
| 6 | Hejin | 100.09 | 35.30 | 38,486 |
| 7 | Zhuangtou | 109.84 | 35.00 | 25,648 |
| 8 | Huaxian | 109.76 | 34.58 | 106,000 |
| 9 | Tongguan | 110.30 | 34.62 | 682,144 |
| 10 | Wuzhi | 113.26 | 35.07 | 12,880 |
| 11 | Huayuankou | 113.65 | 34.92 | 730,036 |
| 12 | Lijin | 118.30 | 37.52 | 751,869 |
| Data Sets | Category | Scheme | Spatial Resolution | Reference |
|---|---|---|---|---|
| GLEAM | Diagnostic | Priestley-Taylor | 0.25° × 0.25° | Miralles et al. (2011) [31] |
| E2O | Reanalysis | Fusion of 10 different ET data | 0.5° × 0.5° | Jaap Schellekens et al (2017) [32] |
| GLDAS | LSM | Penman-Monteith | 1° × 1° | Rodell et al. (2004) [19] |
| ZHANG | Diagnostic | Modified Penman-Monteith | 8 km | Zhang et al. (2010) [9] |
| MERRA_land | Reanalysis | GEOS-5 (Goddard Earth Observing System Model, Version 5) Catchment LSM | 0.5° × 0.67° | Reichle et al. (2011) [33] |
| Product | RMSD | CORR | BIAS | MAE | Trend (mm /10a) |
|---|---|---|---|---|---|
| ETw | −2.35 | ||||
| GLEAM | 60.22 | 0.70 ** | −56.12 | 56.12 | 0.22 |
| E2O | 132.33 | 0.86 ** | −131.14 | 131.14 | 0.67 |
| GLDAS | 78.71 | 0.56 ** | −74.49 | 74.49 | 2.83 |
| ZHANG | 29.31 | 0.33 | −4.91 | 23.23 | 10.85 * |
| MERRA_land | 51.59 | 0.60 ** | −44.77 | 44.77 | −9.08 |
| Data Sets | Precipitation | Radiation | ||||
|---|---|---|---|---|---|---|
| RMSD | CORR | BIAS | RMSD | CORR | BIAS | |
| GLEAM | 24.02 | 0.90 | −16.80 | 15.53 | 0.74 | 15.38 |
| E2O | 92.80 | 0.80 | −89.11 | 14.65 | 0.56 | 14.35 |
| GLDAS | 72.87 | 0.78 | −68.48 | 4.90 | 0.75 | −4.10 |
| ZHANG | - | - | - | 3.70 | 0.78 | 2.88 |
| MERRA | 48.08 | 0.67 | 25.66 | 13.65 | 0.74 | v13.48 |
| Variable | GLEAM | E2O | GLDAS | ZHANG | MERRA |
|---|---|---|---|---|---|
| Precipitation | 0.61 * | 0.89 ** | 0.67 ** | 0.12 | 0.90 ** |
| Radiation | −0.23 | −0.39 | −0.13 | −0.06 | −0.37 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Pan, J.; Shen, C.; Li, S.; Lu, J.; Lou, D.; Hagan, D.F.T. Evaluation of Evapotranspiration Estimates in the Yellow River Basin against the Water Balance Method. Water 2018, 10, 1884. https://doi.org/10.3390/w10121884
Wang G, Pan J, Shen C, Li S, Lu J, Lou D, Hagan DFT. Evaluation of Evapotranspiration Estimates in the Yellow River Basin against the Water Balance Method. Water. 2018; 10(12):1884. https://doi.org/10.3390/w10121884
Chicago/Turabian StyleWang, Guojie, Jian Pan, Chengcheng Shen, Shijie Li, Jiao Lu, Dan Lou, and Daniel F. T. Hagan. 2018. "Evaluation of Evapotranspiration Estimates in the Yellow River Basin against the Water Balance Method" Water 10, no. 12: 1884. https://doi.org/10.3390/w10121884
APA StyleWang, G., Pan, J., Shen, C., Li, S., Lu, J., Lou, D., & Hagan, D. F. T. (2018). Evaluation of Evapotranspiration Estimates in the Yellow River Basin against the Water Balance Method. Water, 10(12), 1884. https://doi.org/10.3390/w10121884







