Vortex Cascade Features of Turbulent Flow in Hydro-Turbine Blade Passage with Complex Geometry
Abstract
1. Introduction
2. Numerical Setup
2.1. Computation Domain and Grid
2.2. Governing Equations
2.3. Calculation Method and Initial Condition
3. Results and Analysis
3.1. Transitional Process from Rated Load to No-Load
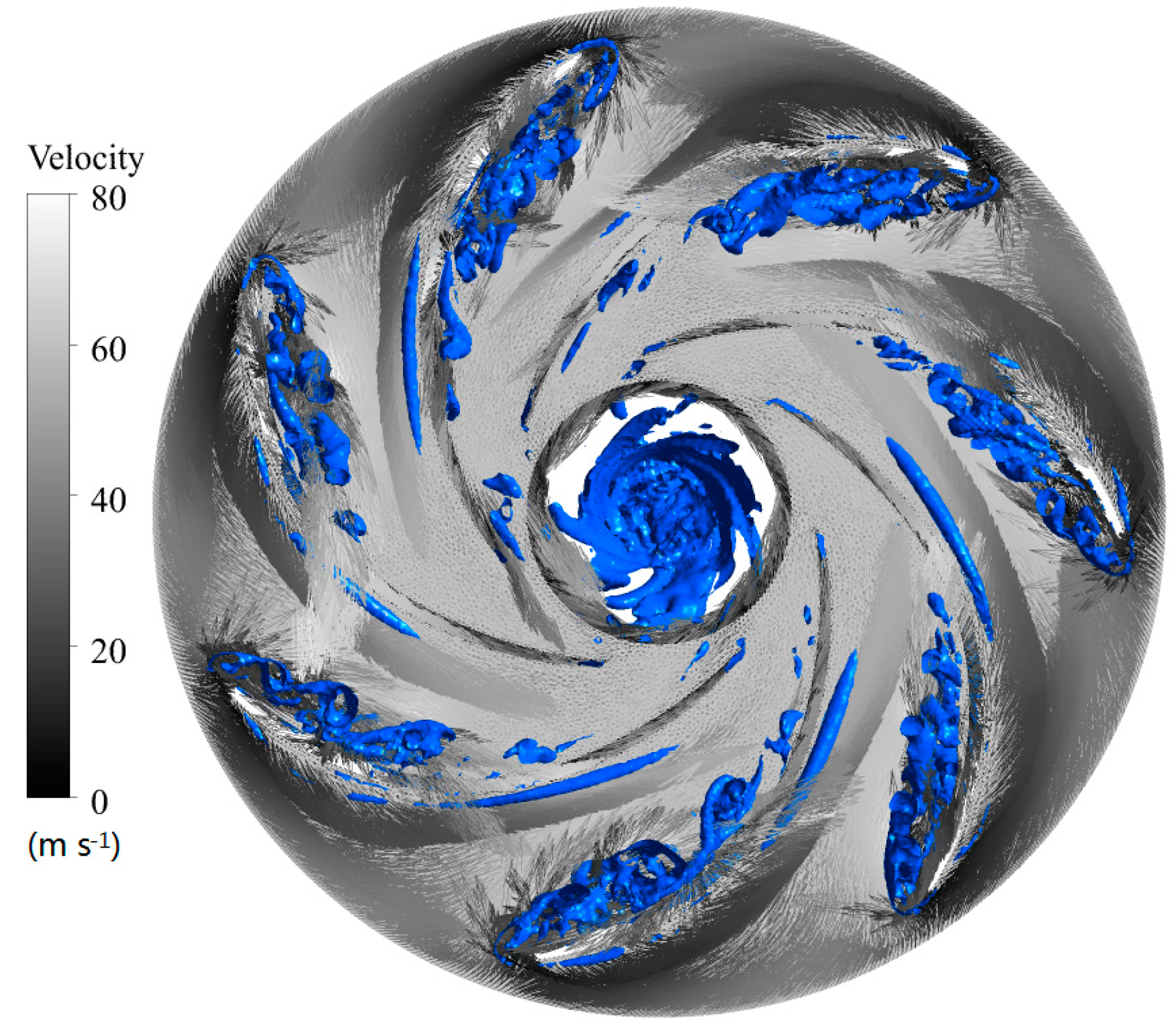
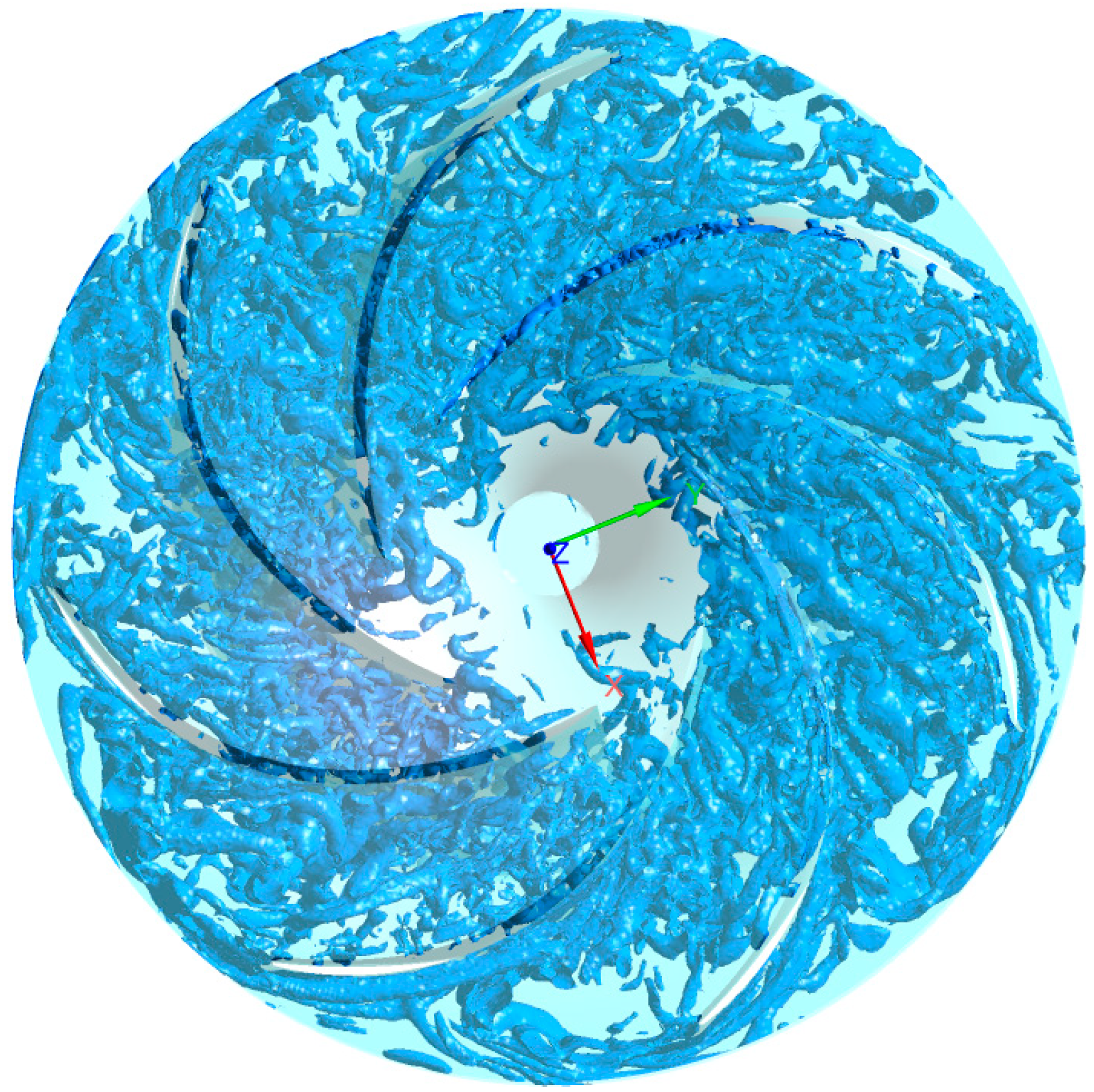
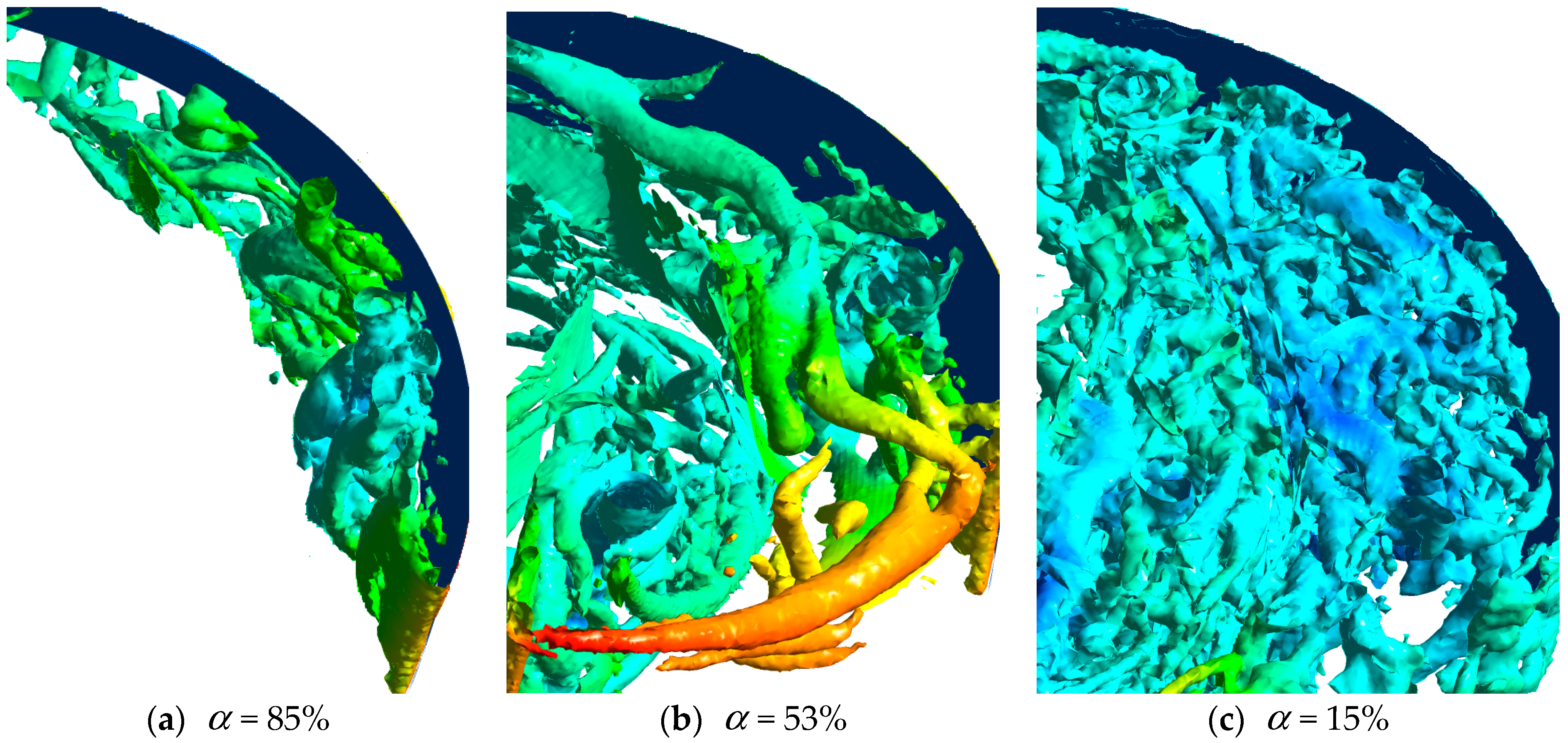
3.2. Different Forms of Channel Vortex
3.3. Cascade Characteristics of Vortex Structures
3.4. Similarity Analysis of Vortex Cascade and Dissipation Features
4. Conclusions
- (1)
- Due to the inconsistency between streamwise direction of the inlet flow and tangential direction of the bone line of the blade, angle of attack exists. Fluid flows through inner arc and back arc of the blade after the obstruction of the head of the blades. Under the influences of the viscous action of the curved blade surface and the inverse pressure gradient caused by the projecting objects, the flow separation is generated near the suction surface of the blade, and the flow state is unstable. The complex vortex structures caused by the dehydration are formed in the blade path, that is, the channel vortex. The vortex structure in the runner is different for the different angles of attack. When the angle of attack is small, the rupture of the tubular vortices will lead to developments of the spiral vortices into the horn vortex in the blade channel. When the angle of attack is large, it develops into a horseshoe vortex. When the angle of attack is medium, both horn vortex and horseshoe vortex are formed in the blade passage. The larger the angle of attack, the more complex the vortex system.
- (2)
- The “large scale” eddies at the blade passage have low survival rates, while “small scale” eddies have a high one. The volume ratio of the adjacent scale vortex is about 1.2–1.6.
- (3)
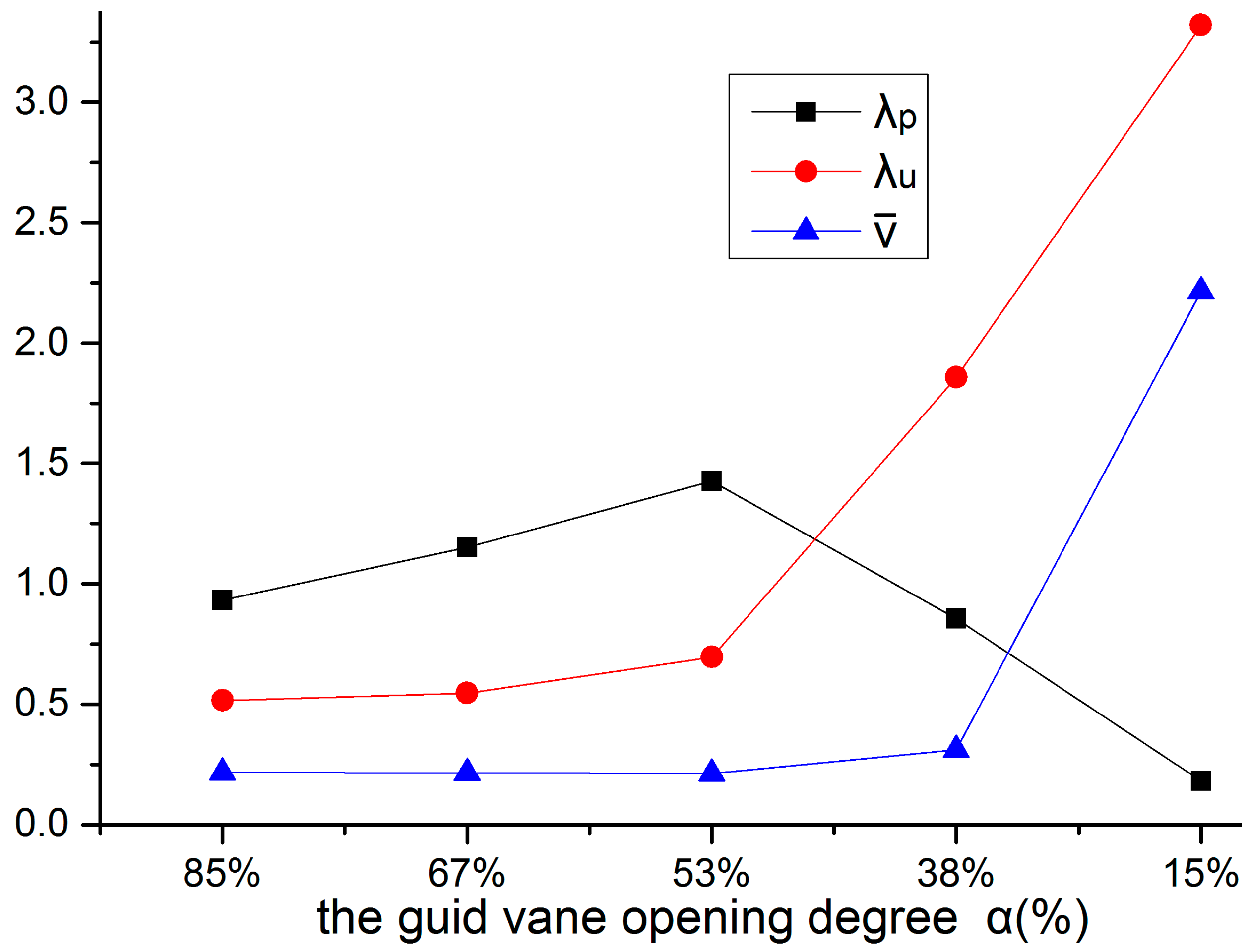
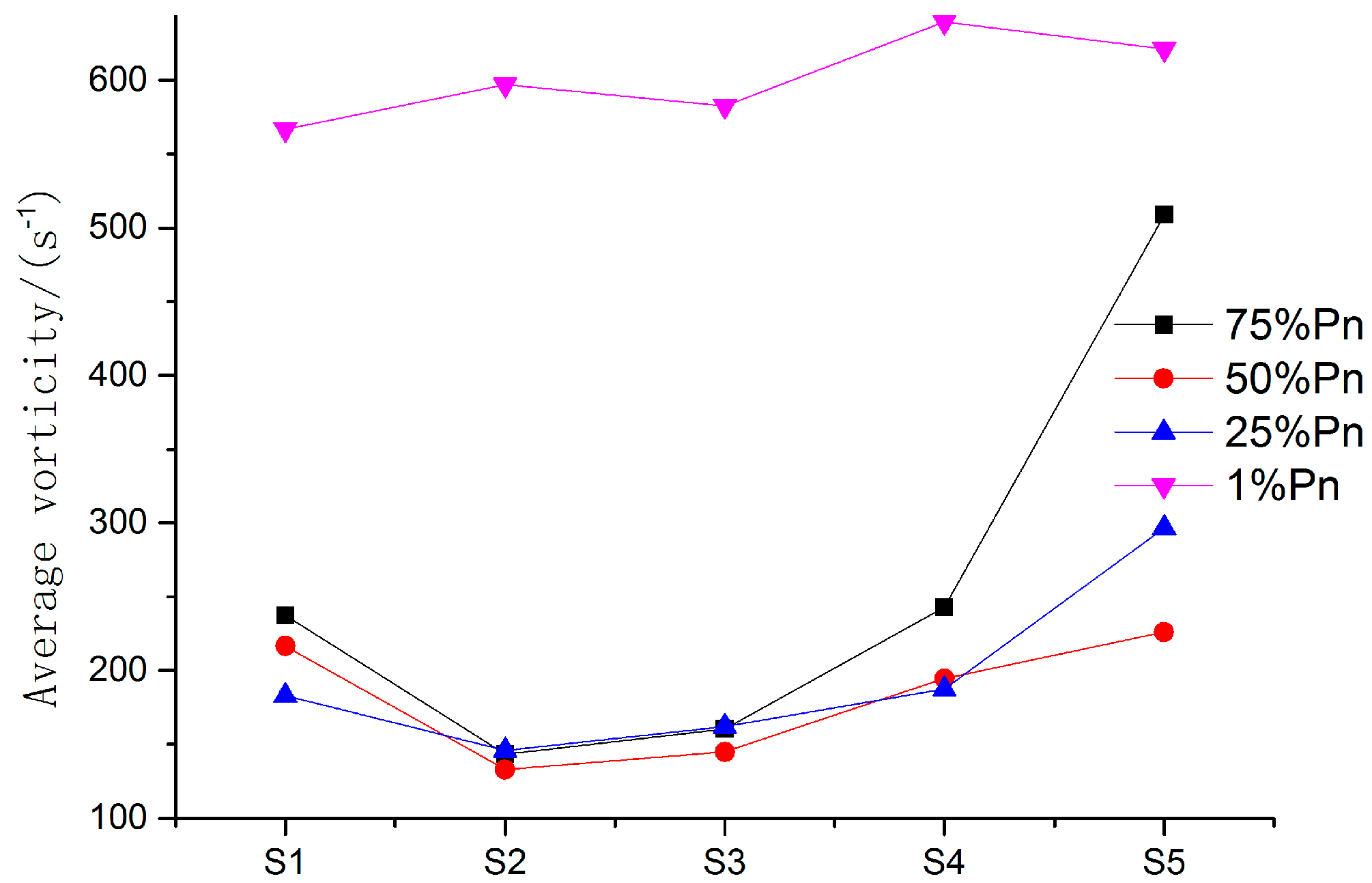
- The average vorticity near wall surfaces is large, and that of suction surface is higher than that of pressure surface. The flow separation near the surface is relatively significant. The average vorticity in the middle of the runner is secondary. The smaller the guide vane opening degree, the larger the energy loss of the vortex structure.
- (4)
- Turbulent kinetic energy near the outlet increases significantly. The existence of a large number of small-scale eddies which are formed in the middle of the channel increases turbulent viscosity in the flow field, causing the increase of the energy dissipation.
- (5)
- Large scale vortices evolve into large scale vortices, and small-scale vortices become more and more common in the blade passage along flow direction, especially in the rear segment of the bale passage.
- (6)
- Vorticity, eddy viscous, turbulent kinetic energy have similarities in their numerical values. The vortex cascade and dissipation features of the turbulent flow are also similar.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| —rotation speed of the runner (rpm) |
| —time (s) |
| —co-ordinate component of Cartesian system (m) |
| —component of flow velocity (m/s) |
| (m/s2) |
| —filtered component of flow velocity (-) |
| —test filtered component of flow velocity (-) |
| —kinetic viscosity of fluid (Pa·s) |
| —eddy viscosity of fluid (Pa·s) |
| —filtered pressure divided by mass density (-) |
| —pressure non-uniformity index (-) |
| —velocity non-uniformity index (-) |
| —eddy viscosity mean values (Pa·s) |
| —the maximum pressure in the surviving space of a certain scale vortex (Pa) |
| —the minimum pressure in the surviving space of a certain scale vortex (Pa) |
| —the maximum velocity in blade passage (m/s) |
| —the minimum velocity in blade passage (m/s) |
| —the eddy viscosity at the midline of blade passage (Pa·s) |
| —the reference pressure (Pa) |
| —the reference velocity (m/s) |
| —liquid mass density (kg/m3) |
| —Kronecker’s delta (-) |
| —strain rate tensor (-) |
| —grid width in i direction (m) |
| —SGS stress (-) |
| —Leonard stress (-) |
| —Cross stress (-) |
| —Reynolds stresses (-) |
| Pn—rated power (W) |
| T—rotation period (s) |
| —attack angle (°) |
| —survival volume ratio of adjacent scale vortex (-) |
| —survival volume of the eddy of scale A in space (m3) |
| —survival volume of the eddy of scale B in space (m3) |
| —dissipation coefficient of vortex energy (J·s·m4) |
| —vortex energy (J) |
| —fluid flow (m3/s) |
| —water head (m) |
| —the guide vane opening degree (%) |
References
- Richardson, L.F. Weather Prediction by Numerical Process; Cambridge University Press: Cambridge, UK, 1922. [Google Scholar]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds number. Proc. Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Davidson, P.A. A Voyage through Turbulence; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Deusebio, E.; Boffetta, G.; Lindborg, E.; Musacchio, S. Dimensional transition in rotating turbulence. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 90, 023005. [Google Scholar] [CrossRef] [PubMed]
- Marino, R.; Mininni, P.D.; Rosenberg, D.; Pouquet, A. Inverse cascades in rotating stratified turbulence: Fast growth of large scales. EPL 2013, 102, 44006. [Google Scholar] [CrossRef]
- Aluie, H.; Kurien, S. Joint downscale fluxes of energy and potential enstrophy in rotating stratified Boussinesq flows. EPL 2011, 96, 44006. [Google Scholar] [CrossRef]
- Nastrom, G.D.; Gage, K.S.; Jasperson, W.H. Kinetic energy spectrum of large-and mesoscale atmospheric processes. Nature 1984, 310, 36–38. [Google Scholar] [CrossRef]
- Gage, K.S.; Nastrom, G.D. Theoretical interpretation of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft during gasp. J. Atmos. Sci. 1986, 43, 729–740. [Google Scholar] [CrossRef]
- Byrne, D.; Zhang, J.A. Height-dependent transition from 3-D to 2-D turbulence in the hurricane boundary layer. Geophys. Res. Lett. 2013, 40, 1439–1442. [Google Scholar] [CrossRef]
- Young, R.M.B.; Read, P.L. Forward and inverse kinetic energy cascades in Jupiter’s turbulent weather layer. Nat. Phys. 2017, 13, 1135–1140. [Google Scholar] [CrossRef]
- Miloshevich, G.; Morrison, P.J.; Tassi, E. Direction of cascades in a magnetofluid model with electron skin depth and ion sound Larmor radius scales. Phys. Plasmas 2018, 25, 072303. [Google Scholar] [CrossRef]
- Alexakis, A.; Biferale, L. Cascades and transitions in turbulent flows. Phys. Rep. 2018, 767–769, 1–101. [Google Scholar] [CrossRef]
- Fortova, S.V. Eddy cascade of instabilities and transition to turbulence. Comput. Math. Math. Phys. 2014, 54, 553–560. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.; Guo, P.; Luo, X.; George, A. A novel surface-cluster approach towards transient modeling of hydro-turbine governing systems in the start-up process. Energy Convers. Manag. 2018, 165, 861–868. [Google Scholar] [CrossRef]
- Widmer, C.; Staubli, T.; Ledergerber, N. Unstable characteristics and rotating stall in turbine brake operation of pump-turbines. J. Fluids Eng. 2011, 133, 041101. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Gandhi, B.K.; Dahlhaug, O.G. Transient pressure measurements on a high head model francis turbine during emergency shutdown, total load rejection, and runaway. J. Fluids Eng. 2014, 136, 121107. [Google Scholar] [CrossRef]
- Hu, J.; Yang, J.; Zeng, W.; Yang, J. Transient pressure analysis of a prototype pump turbine: Field tests and simulation. J. Fluids Eng. 2018, 140, 071102. [Google Scholar] [CrossRef]
- Yang, J.; Hu, J.; Zeng, W.; Yang, J. Transient pressure pulsations of prototype Francis pump-turbines. J. Hydraul. Eng. 2016, 47, 858–864. [Google Scholar]
- Xia, L.; Cheng, Y.; Cai, F. Pressure pulsation characteristics of a model pump-turbine operating in the S-shaped Region: CFD simulations. Int. J. Fluid Mach. Syst. 2017, 10, 287–295. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, W.; Guo, Y. Numerical simulation of flow features and energy exchange physics in near-wall region with fluid-structure interaction. Int. J. Mod. Phys. B 2008, 22, 651–669. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, L. Numerical simulation of unsteady flow for a pump-turbine in transition cases with large-eddy simulation. J. Hydraul. Eng. 2018, 49, 492–500. [Google Scholar]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid scale eddy viscosity model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, Y.; Wang, W. Large eddy simulation of turbulent flow in a true 3D Francis hydro turbine passage with dynamical fluid-structure interaction. Int. J. Numer. Methods Fluids 2007, 54, 517–541. [Google Scholar] [CrossRef]
- Gabl, R.; Innerhofer, D.; Achleitner, S.; Righetti, M.; Aufleger, M. Evaluation criteria for velocity distributions in front of bulb hydro turbines. Renew. Energy 2018, 121, 745–756. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, L. Numerical study on turbulence characteristics in Francis turbine under small opening condition. Eng. Mech. 2015, 32, 222–230. [Google Scholar]
- Kudela, H.; Malecha, Z.M. Investigation of unsteady vorticity layer eruption induced by vortex patch using vortex particles method. J. Theor. Appl. Mech. 2007, 45, 785–800. [Google Scholar]
- Kudela, H.; Malecha, Z.M. Eruption of a boundary layer induced by a 2D vortex patch. Fluid Dyn. Res. 2009, 41, 055502. [Google Scholar] [CrossRef]
- Chen, Q.; Qi, M.; Li, J. Kinematic characteristics of horseshoe vortex upstream of circular cylinders in open channel flow. J. Hydraul. Eng. 2016, 47, 158–164. [Google Scholar]
- Cardesa, J.I.; Vela-Martín, A.; Jiménez, J. The turbulent cascade in five dimensions. Science 2017, 357, 782–784. [Google Scholar] [CrossRef]
- Dagan, Y.; Greenberg, J.B.; Katoshevski, D. Similarity solutions for the evolution of polydisperse droplets in vortex flows. Int. J. Multiph. Flow 2017, 97, 1–9. [Google Scholar] [CrossRef]
- Bosschers, J.; Janssen, A.A.; Hoeijmakers, H.W.M. Similarity solutions for viscous cavitating vortex cores. J. Hydrodyn. Ser. B. 2008, 20, 679–688. [Google Scholar] [CrossRef]
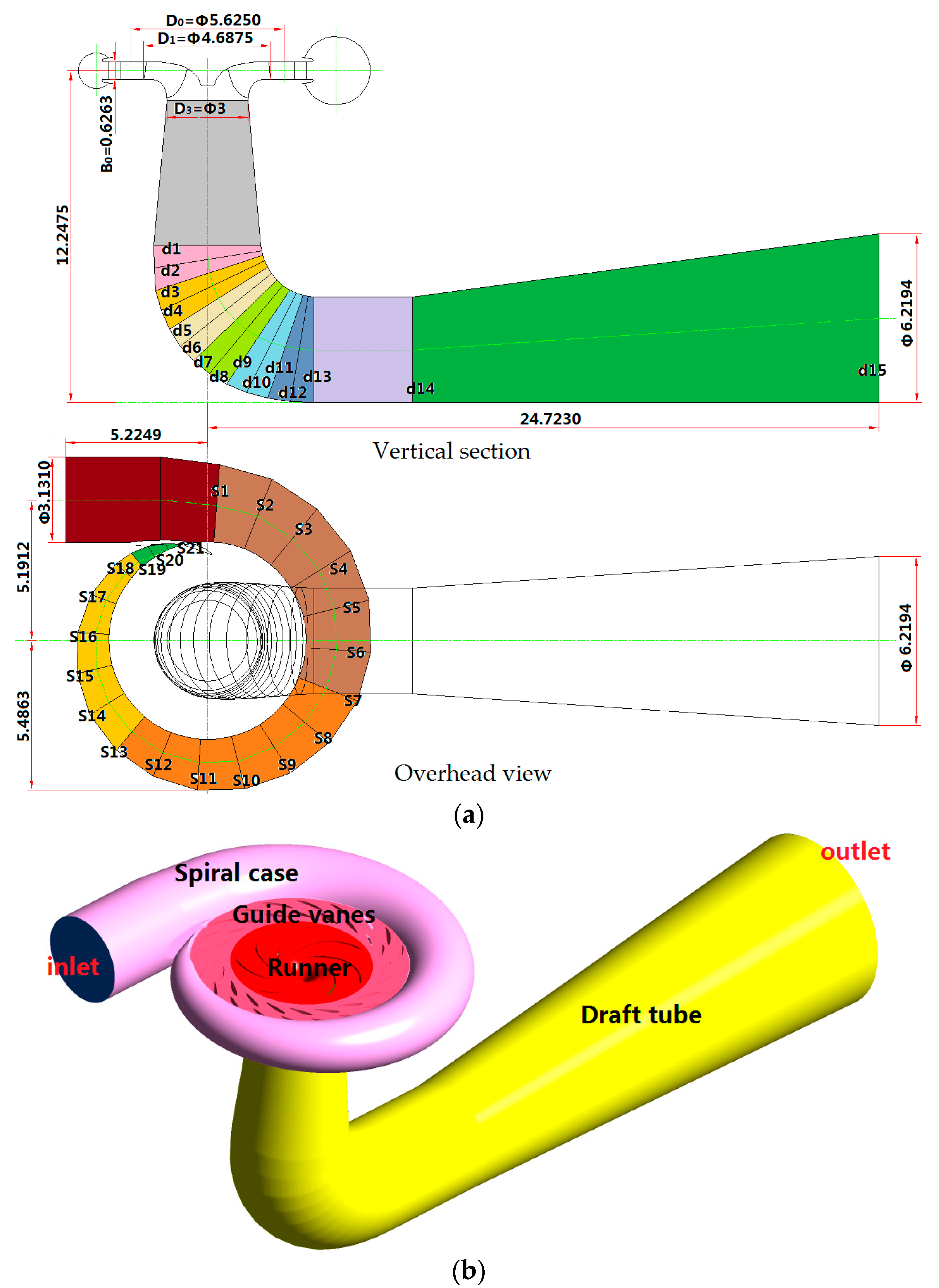
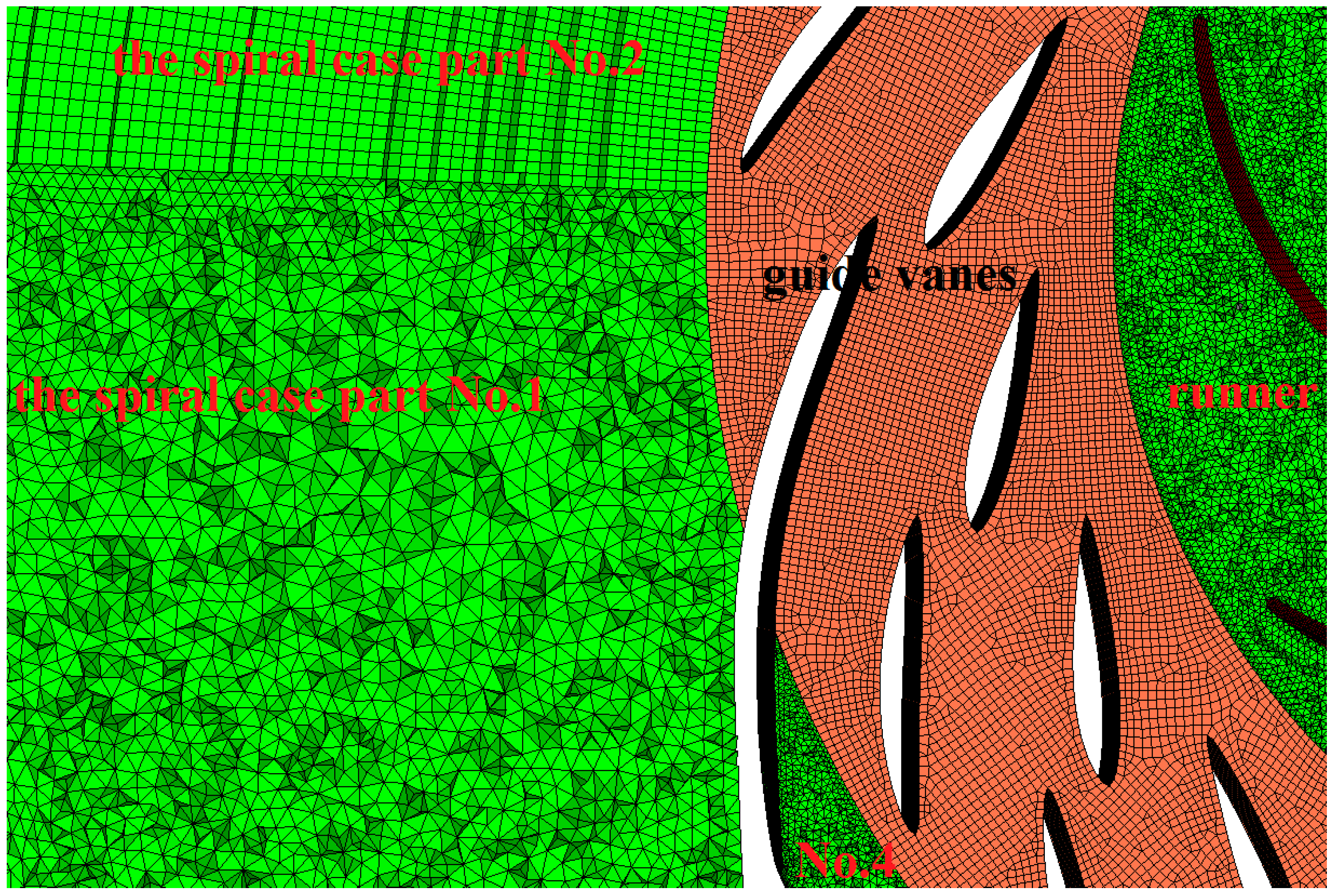




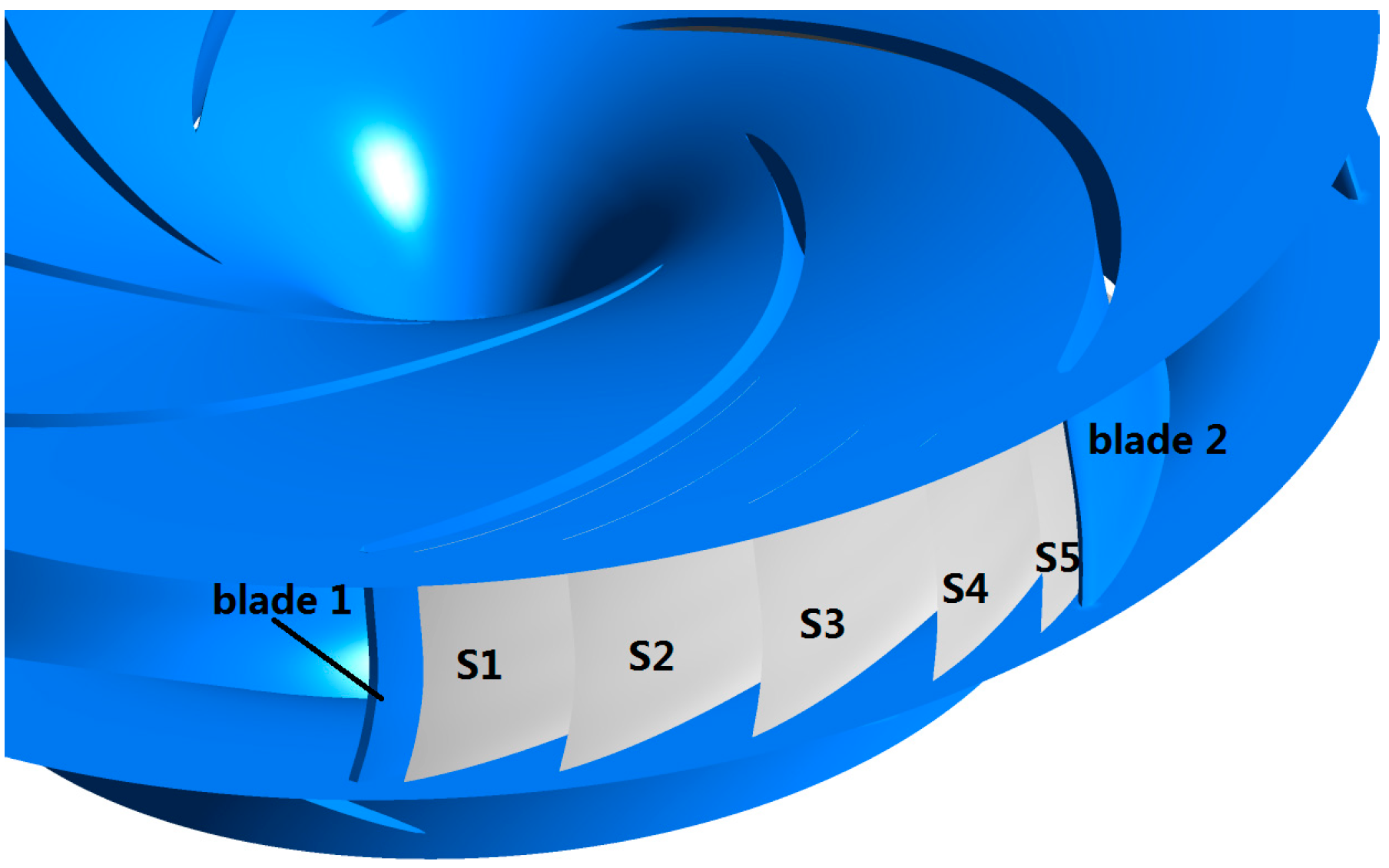

| Section | Radius (m) | Section | Radius (m) | Section | Radius (m) | Section | Radius (m) |
|---|---|---|---|---|---|---|---|
| S1 | 1.5009 | S10 | 1.0540 | S19 | 0.4173 | d7 | 2.1403 |
| S2 | 1.4553 | S11 | 0.9967 | S20 | 0.4088 | d8 | 2.1202 |
| S3 | 1.4096 | S12 | 0.9359 | S21 | 0.4066 | d9 | 2.0921 |
| S4 | 1.3644 | S13 | 0.8734 | d1 | 1.9670 | d10 | 2.0470 |
| S5 | 1.3176 | S14 | 0.8093 | d2 | 2.0064 | d11 | 2.0024 |
| S6 | 1.2677 | S15 | 0.7391 | d3 | 2.0719 | d12 | 1.9654 |
| S7 | 1.2161 | S16 | 0.6629 | d4 | 2.1124 | d13 | 1.9475 |
| S8 | 1.1637 | S17 | 0.5825 | d5 | 2.1404 | d14 | 1.9475 |
| S9 | 1.1103 | S18 | 0.4880 | d6 | 2.1469 | d15 | 3.1097 |
| Condition | 100%Pn | 75%Pn | 50%Pn | 25%Pn | 1%Pn |
|---|---|---|---|---|---|
| The guide vane opening degree (%) | 85% | 67% | 53% | 38% | 15% |
| Inlet velocity for the prototype (m/s) | 19.28 | 15.20 | 12.02 | 8.62 | 3.40 |
| Adjacent Scale | 0.25–0.2 | 0.2–0.15 | 0.15–0.1 | 0.1–0.05 | 0.05–0.01 |
|---|---|---|---|---|---|
| The survival volume ratio of adjacent vortex | 1.359 | 1.402 | 1.549 | 1.404 | 1.232 |
| Equal Points | P1 | P2 | P3 | P4 |
|---|---|---|---|---|
| Eddy viscosity for 100%Pn (Pa·s) | 0.1187 | 0.1434 | 0.2613 | 0.3413 |
| Eddy viscosity for 75%Pn (Pa·s) | 0.1242 | 0.1513 | 0.2485 | 0.3373 |
| Eddy viscosity for 50%Pn (Pa·s) | 0.1522 | 0.1619 | 0.2483 | 0.2840 |
| Eddy viscosity for 25%Pn (Pa·s) | 0.1742 | 0.2384 | 0.2941 | 0.5403 |
| Eddy viscosity for 1%Pn (Pa·s) | 1.4615 | 1.8220 | 2.7041 | 2.8693 |
| Turbulent kinetic energy for 100%Pn (m2·s−2) | 8.59 | 21.03 | 39.312 | 45.467 |
| Turbulent kinetic energy for 75%Pn (m2·s−2) | 9.68 | 22.63 | 24.09 | 25.92 |
| Turbulent kinetic energy for 50%Pn (m2·s−2) | 6.19 | 14.27 | 16.03 | 16.86 |
| Turbulent kinetic energy for 25%Pn (m2·s−2) | 3.46 | 9.45 | 19.66 | 20.97 |
| Turbulent kinetic energy for 1%Pn (m2·s−2) | 22.34 | 19.22 | 58.56 | 51.66 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Zhang, L. Vortex Cascade Features of Turbulent Flow in Hydro-Turbine Blade Passage with Complex Geometry. Water 2018, 10, 1859. https://doi.org/10.3390/w10121859
Hu X, Zhang L. Vortex Cascade Features of Turbulent Flow in Hydro-Turbine Blade Passage with Complex Geometry. Water. 2018; 10(12):1859. https://doi.org/10.3390/w10121859
Chicago/Turabian StyleHu, Xiucheng, and Lixiang Zhang. 2018. "Vortex Cascade Features of Turbulent Flow in Hydro-Turbine Blade Passage with Complex Geometry" Water 10, no. 12: 1859. https://doi.org/10.3390/w10121859
APA StyleHu, X., & Zhang, L. (2018). Vortex Cascade Features of Turbulent Flow in Hydro-Turbine Blade Passage with Complex Geometry. Water, 10(12), 1859. https://doi.org/10.3390/w10121859





