Qualifying Coordination Mechanism for Cascade-Reservoir Operation with a New Game-Theoretical Methodology
Abstract
1. Introduction
2. Study Area and Data
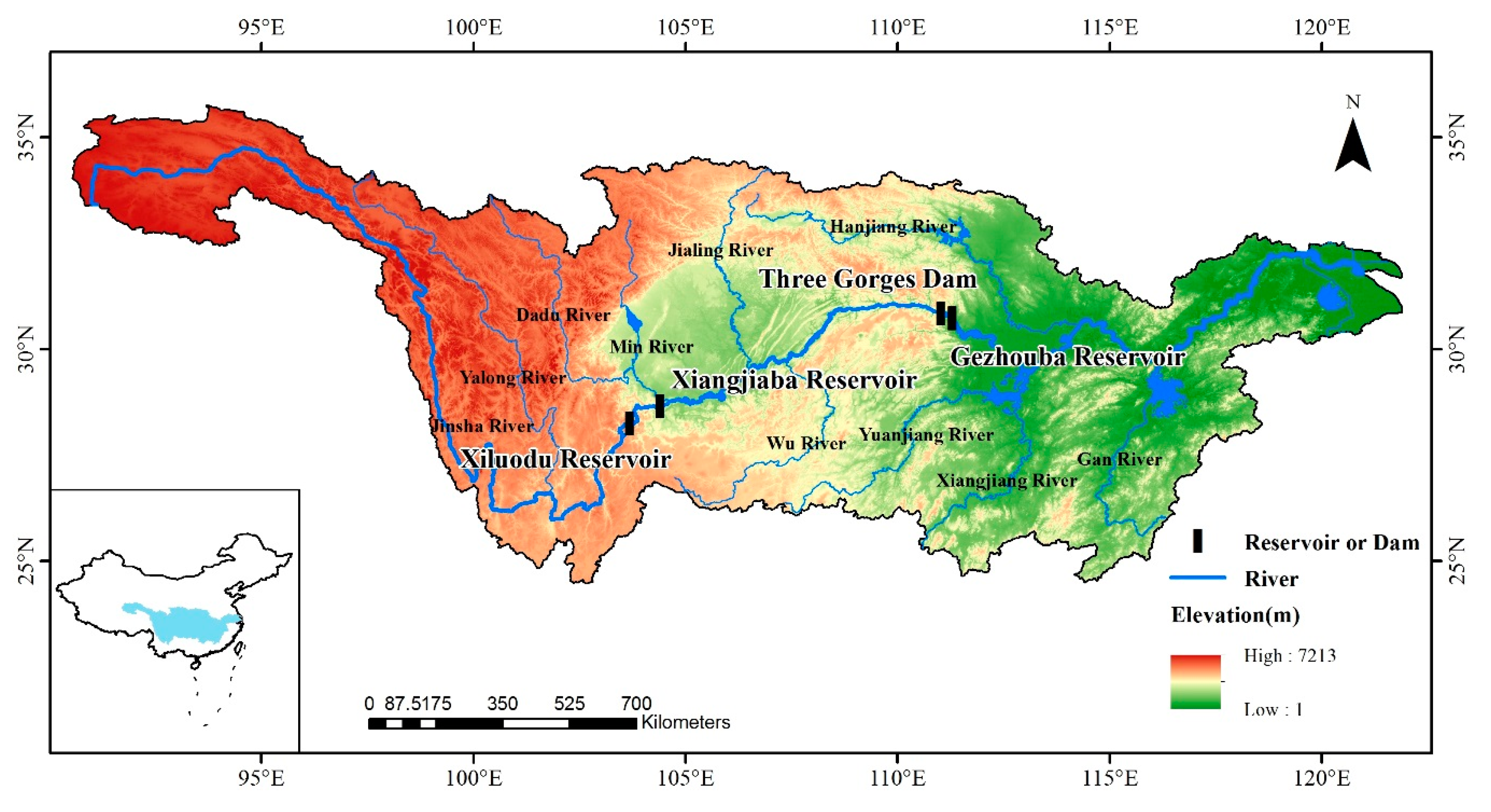
2.1. Study Area
2.2. Date Collection
3. Methodology
3.1. Centralized Model (Model I)
3.2. Non-Cooperative Model (Model II)
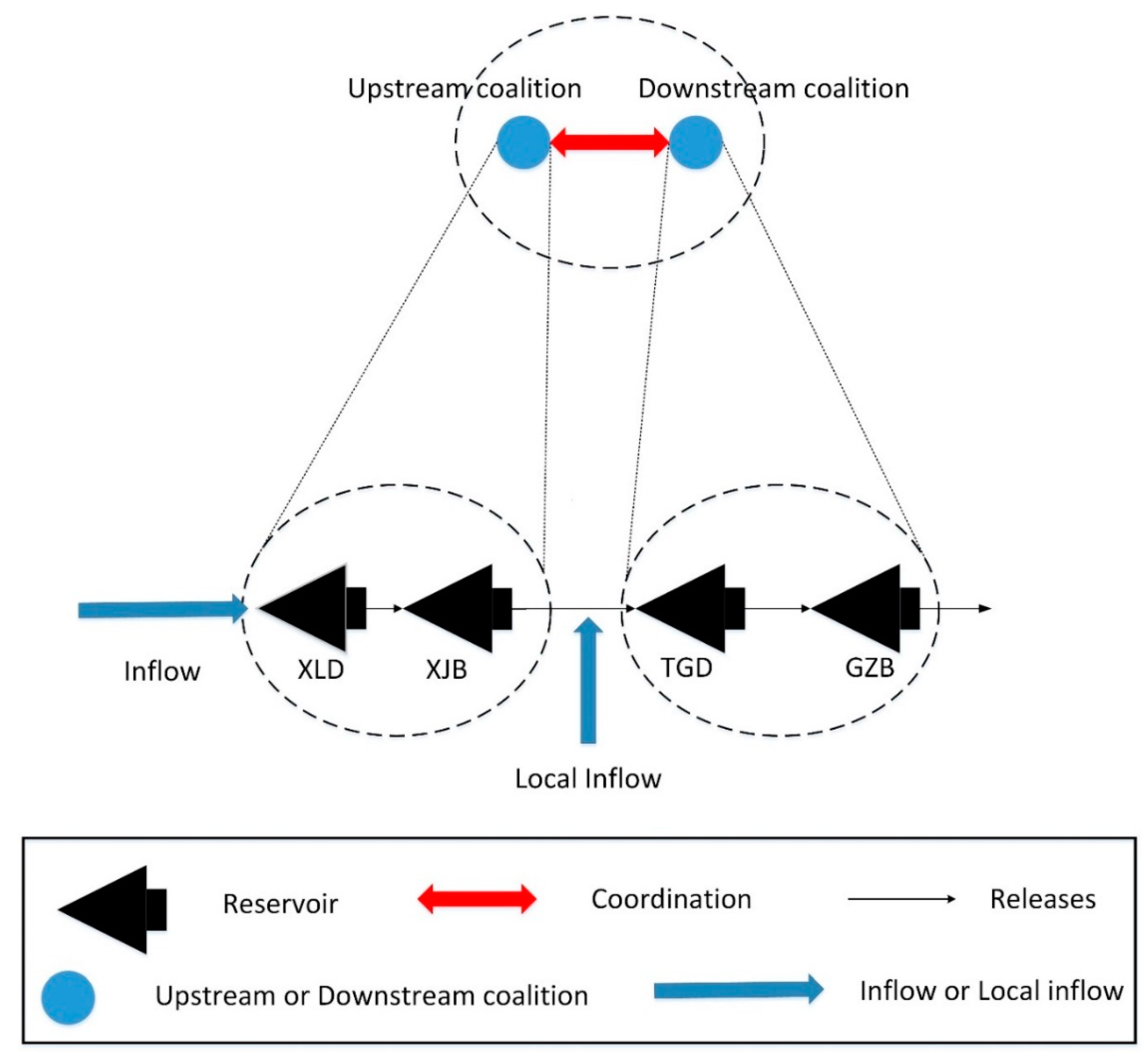
3.3. Integrated Game-Theoretical Model
3.3.1. Coordination Model (Model III(a))
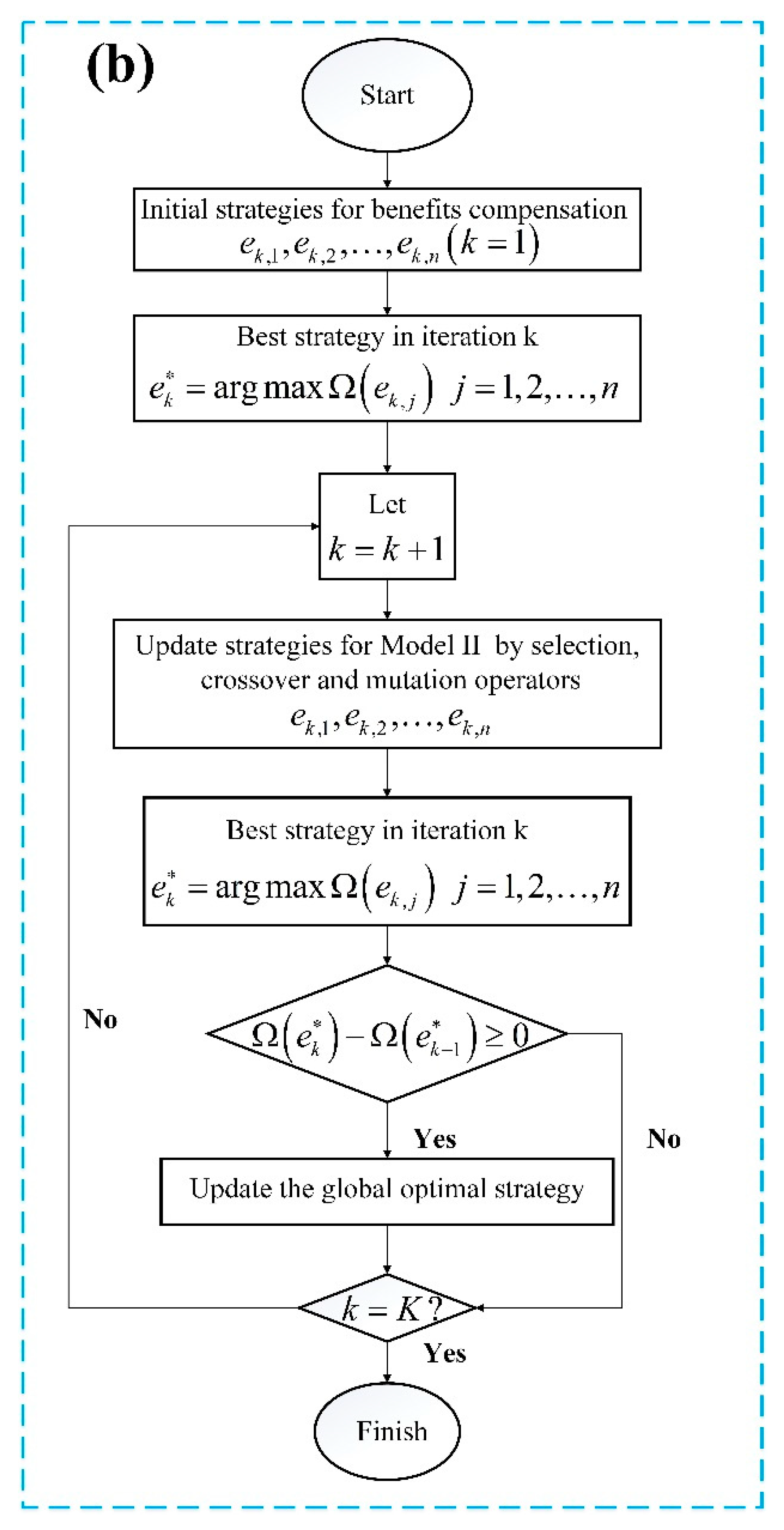
3.3.2. Benefits Compensation Model (Model III(b))
3.4. Evaluation Criterion
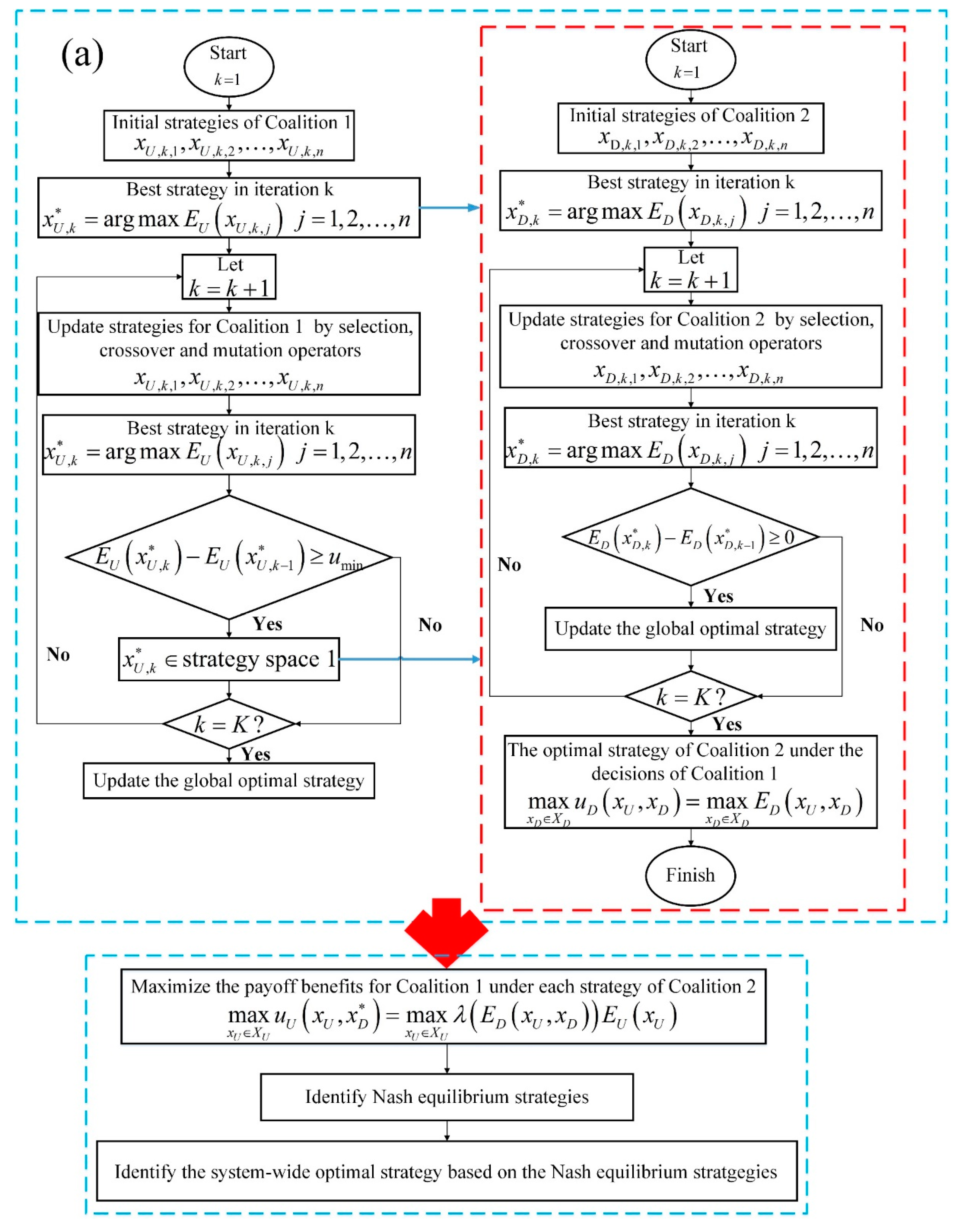
3.5. Solving Method
4. Results and Discussion
4.1. Nash Equilibrium Strategies of Multi-Reservoir Operation
4.2. Assessment of Game-Theoretical Model
4.2.1. Coordination Assessment
4.2.2. Benefits Compensation Assessment
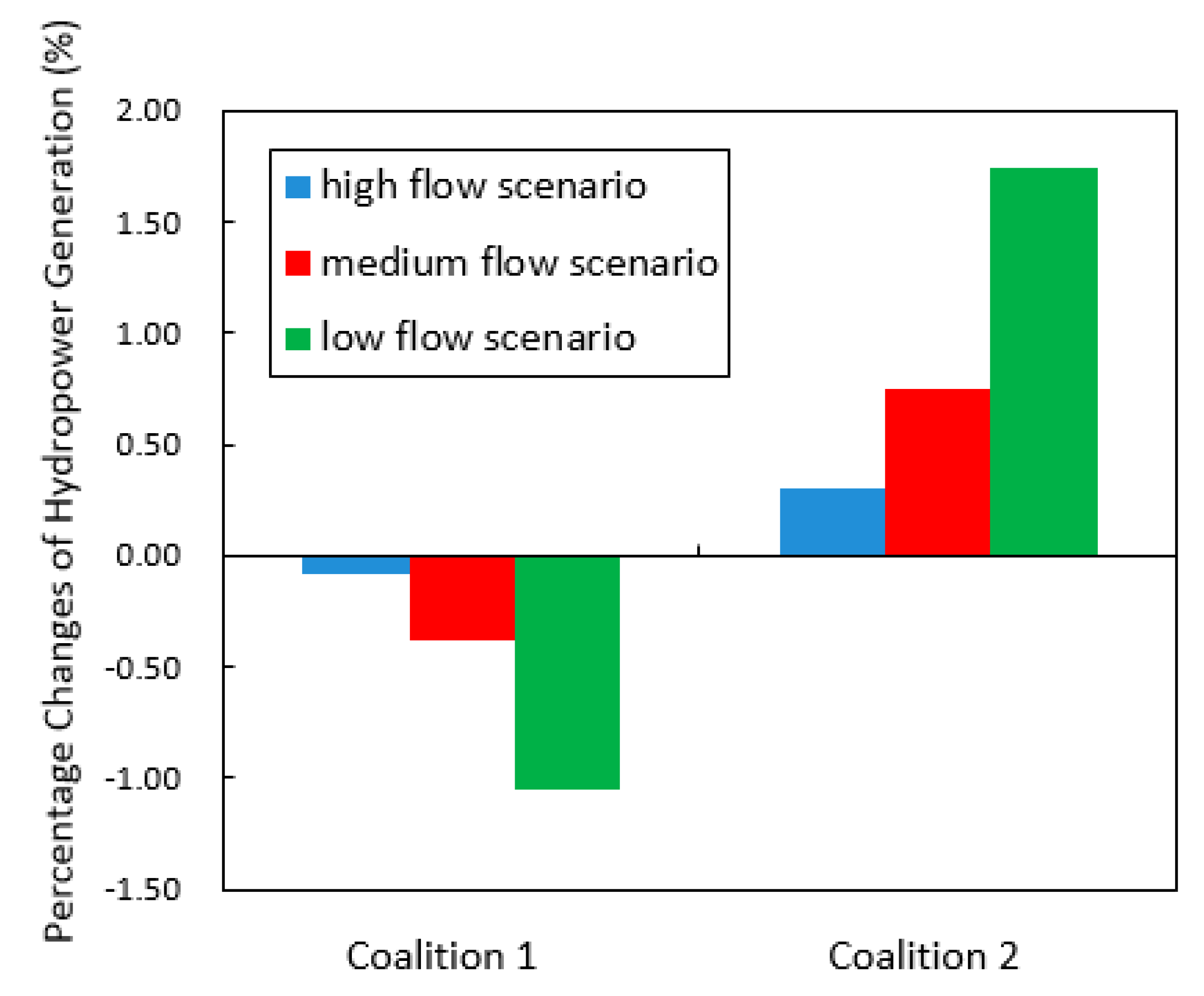
4.3. Factors Affecting the Efficiency of Coordination
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shen, Y.; Chen, Y. Global perspective on hydrology, water balance, and water resources management in arid basins. Hydrol. Process. 2010, 24, 129–135. [Google Scholar] [CrossRef]
- Zhang, R.; Duan, Z.; Tan, M.; Chen, X. The assessment of water stress with the water poverty index in the Shiyang River basin in China. Environ. Earth Sci. 2012, 67, 2155–2160. [Google Scholar] [CrossRef]
- Giuliani, M.; Castelletti, A. Assessing the value of cooperation and information exchange in large water resources systems by agent-based optimization. Water Resour. Res. 2013, 49, 3912–3926. [Google Scholar] [CrossRef]
- Cai, W.; Zhang, L.; Zhu, X.; Zhang, A.; Yin, J.; Wang, H. Optimized reservoir operation to balance human and environmental requirements: A case study for the Three Gorges and Gezhouba Dams, Yangtze River basin, China. Ecol. Inform. 2013, 18, 40–48. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S. Incorporating ecological requirement into multipurpose reservoir operating rule curves for adaptation to climate change. J. Hydrol. 2013, 498, 153–164. [Google Scholar] [CrossRef]
- Fallah-Mehdipour, E.; Haddad, O.B.; Mariño, M.A. Evaluation of stakeholder utility risk caused by the objective functions in multipurpose multireservoir systems. J. Irrig. Drain. Eng. 2014, 141, 04014047. [Google Scholar] [CrossRef]
- Xu, Y.; Mei, Y. A modified water cycle algorithm for long-term multi-reservoir optimization. Appl. Soft Comput. 2018, 71, 317–332. [Google Scholar] [CrossRef]
- Madani, K. Game theory and water resources. J. Hydrol. 2010, 381, 225–238. [Google Scholar] [CrossRef]
- Yang, Y.C.; Cai, X.; Stipanović, D.M. A decentralized optimization algorithm for multiagent system–based watershed management. Water Resour. Res. 2009, 45, W08430. [Google Scholar] [CrossRef]
- Yang, Y.C.E.; Zhao, J.; Cai, X. Decentralized optimization method for water allocation management in the Yellow River basin. J. Water Res. Plan. Man. 2012, 138, 313–325. [Google Scholar] [CrossRef]
- Akhbari, M.; Grigg, N.S. A framework for an agent-based model to manage water resources conflicts. Water Resour. Manag. 2013, 27, 4039–4052. [Google Scholar] [CrossRef]
- Giuliani, M.; Castelletti, A.; Amigoni, F.; Cai, X. Multiagent systems and distributed constraint reasoning for regulatory mechanism design in water management. J. Water Res. Plan. Man. 2015, 141, 04014068. [Google Scholar] [CrossRef]
- Madani, K. Hydropower licensing and climate change: Insights from cooperative game theory. Adv. Water Resour. 2011, 34, 174–183. [Google Scholar] [CrossRef]
- Salazar, R.; Szidarovszky, F.; Coppola, E., Jr.; Rojano, A. Application of game theory for a groundwater conflict in Mexico. J. Environ. Manag. 2007, 84, 560–571. [Google Scholar] [CrossRef]
- Chew, I.M.L.; Tan, R.R.; Foo, D.C.Y.; Chiu, A.S.F. Game theory approach to the analysis of inter-plant water integration in an eco-industrial park. J. Clean. Prod. 2009, 17, 1611–1619. [Google Scholar] [CrossRef]
- Salazar, R.; Szidarovszky, F.; Rojano, A. Water distribution scenarios in the Mexican valley. Water Resour. Manag. 2010, 24, 2959–2970. [Google Scholar] [CrossRef]
- Hipel, K.W.; Walker, S.B. Conflict analysis in environmental management. Environmetrics 2011, 22, 279–293. [Google Scholar] [CrossRef]
- Huang, X.; Chen, X.; Huang, P. Research on fuzzy cooperative game model of allocation of pollution discharge rights. Water 2018, 10, 662. [Google Scholar] [CrossRef]
- Madani, K.; Lund, J.R. A monte-carlo game theoretic approach for multi-criteria decision making under uncertainty. Adv. Water Resour. 2011, 34, 607–616. [Google Scholar] [CrossRef]
- Madani, K.; Hooshyar, M. A game theory–reinforcement learning (GT–RL) method to develop optimal operation policies for multi-operator reservoir systems. J. Hydrol. 2014, 519, 732–742. [Google Scholar] [CrossRef]
- Kicsiny, R.; Piscopo, V.; Scarelli, A.; Varga, Z. Dynamic stackelberg game model for water rationalization in drought emergency. J. Hydrol. 2014, 517, 557–565. [Google Scholar] [CrossRef]
- Wang, X.; Wang, G.; Wu, Y.; Xu, Y.; Gao, H. Comprehensive assessment of regional water usage efficiency control based on game theory weight and a matter-element model. Water 2017, 9, 113. [Google Scholar] [CrossRef]
- Yang, B.; Lai, C.; Chen, X.; Wu, X.; He, Y. Surface water quality evaluation based on a game theory-based cloud model. Water 2018, 10, 510. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, J.Z.; Yuan, L.; Zhang, Y.C. Study on dry season operation of cascade reservoir in Jinsha River. J. Hydraul. Eng. 2013, 44, 1399–1408. [Google Scholar] [CrossRef]
- Stackelberg, H.V. Marktform und Gleichgewicht; Springer: Vienna, Austria, 1934. [Google Scholar]
- Szidarovszky, F.; Molnár, S.; Okuguchi, K. An n-person stackelberg leader-leader model. Appl. Math. Comput. 1991, 46, 221–232. [Google Scholar] [CrossRef]
- Nie, P.Y.; Chen, L.H.; Fukushima, M. Dynamic programming approach to discrete time dynamic feedback Stackelberg games with independent and dependent followers. Eur. J. Oper. Res. 2006, 169, 310–328. [Google Scholar] [CrossRef]
- Nash, J. Two person cooperative games. Econometrica 1953, 21, 128–140. [Google Scholar] [CrossRef]
- Harsanyi, J.C. A Bargaining Model for Cooperative n-Person Games; Citeseer: State College, PA, USA, 1958. [Google Scholar]
- Madani, K.; Dinar, A. Cooperative institutions for sustainable common pool resource management: Application to groundwater. Water Resour. Res. 2012, 48, 57–76. [Google Scholar] [CrossRef]
- Fu, J.; Zhong, P.A.; Zhu, F.; Chen, J.; Wu, Y.; Xu, B. Water resources allocation in transboundary river based on asymmetric Nash-Harsanyi Leader-Follower game model. Water 2018, 10, 270. [Google Scholar] [CrossRef]
- Girard, C.; Rinaudo, J.; Pulido-Velazquez, M. Sharing the cost of a river basin adaptation portfolios to climate change: Insights from social justice and cooperative game theory. Water Resour. Res. 2016, 52, 7945–7962. [Google Scholar] [CrossRef]
- Han, Q.; Tan, G.; Fu, X.; Mei, Y.; Yang, Z. Water resource optimal allocation based on multi-agent game theory of HanJiang river basin. Water 2018, 10, 1184. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, MA, USA, 1992; Volume 6, pp. 126–137. [Google Scholar]
- Schlüter, M.; Leslie, H.; Levin, S. Managing water-use trade-offs in a semi-arid river delta to sustain multiple ecosystem services: A modeling approach. Ecol. Res. 2009, 24, 491–503. [Google Scholar] [CrossRef]
- Xiao, Y.; Fang, L.; Hipel, K.W. Centralized and decentralized approaches to water demand management. Water 2018, 10, 3466. [Google Scholar] [CrossRef]
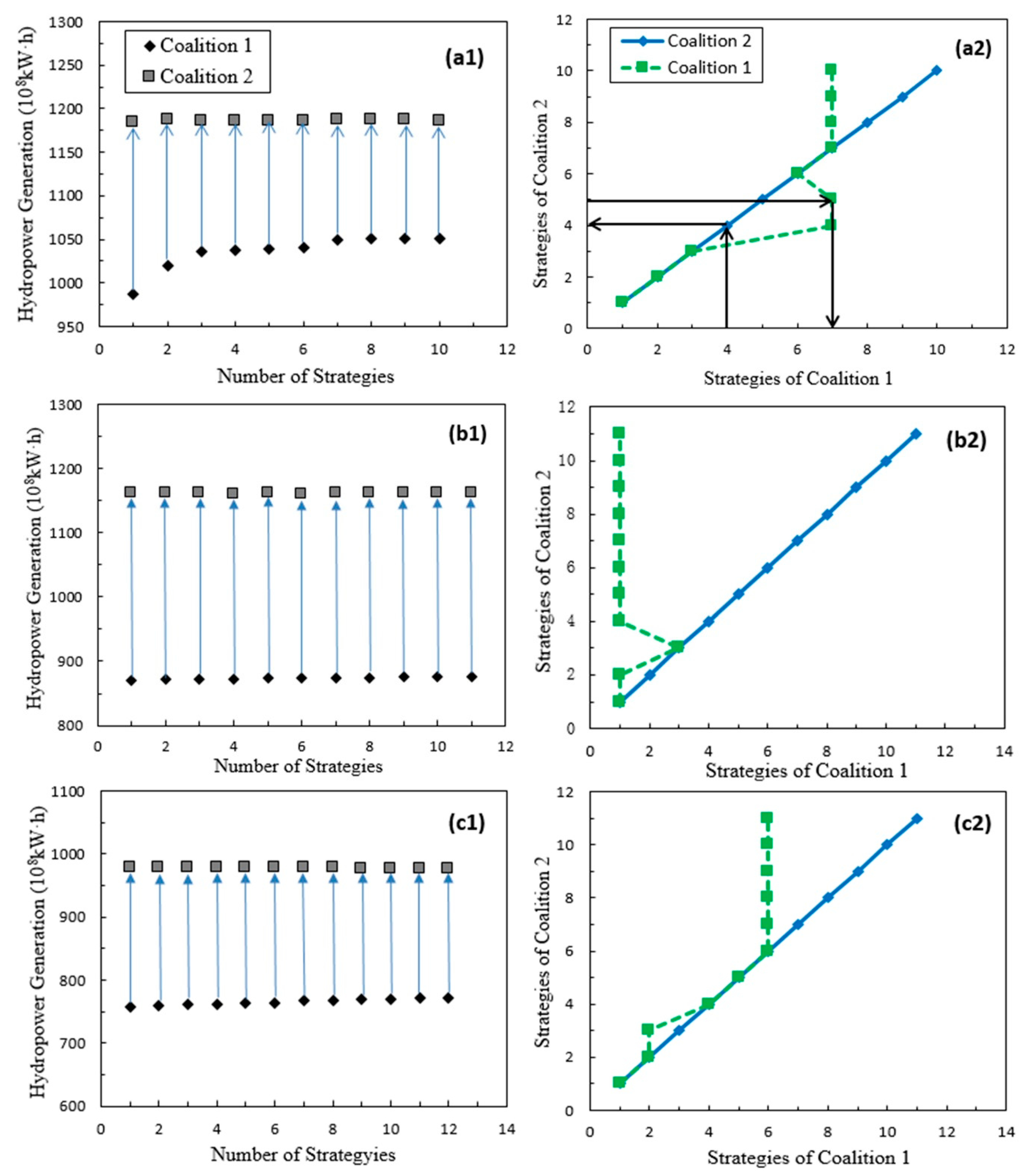
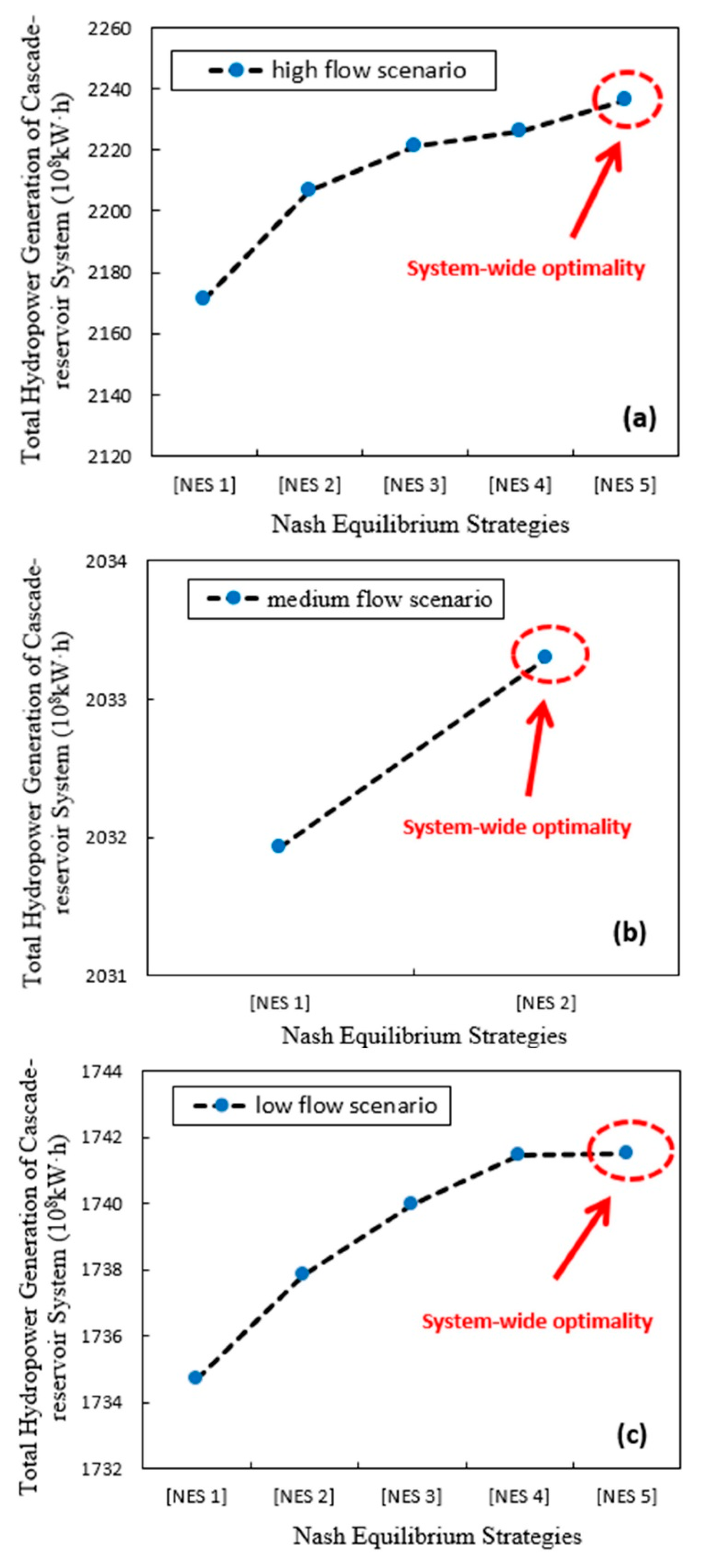
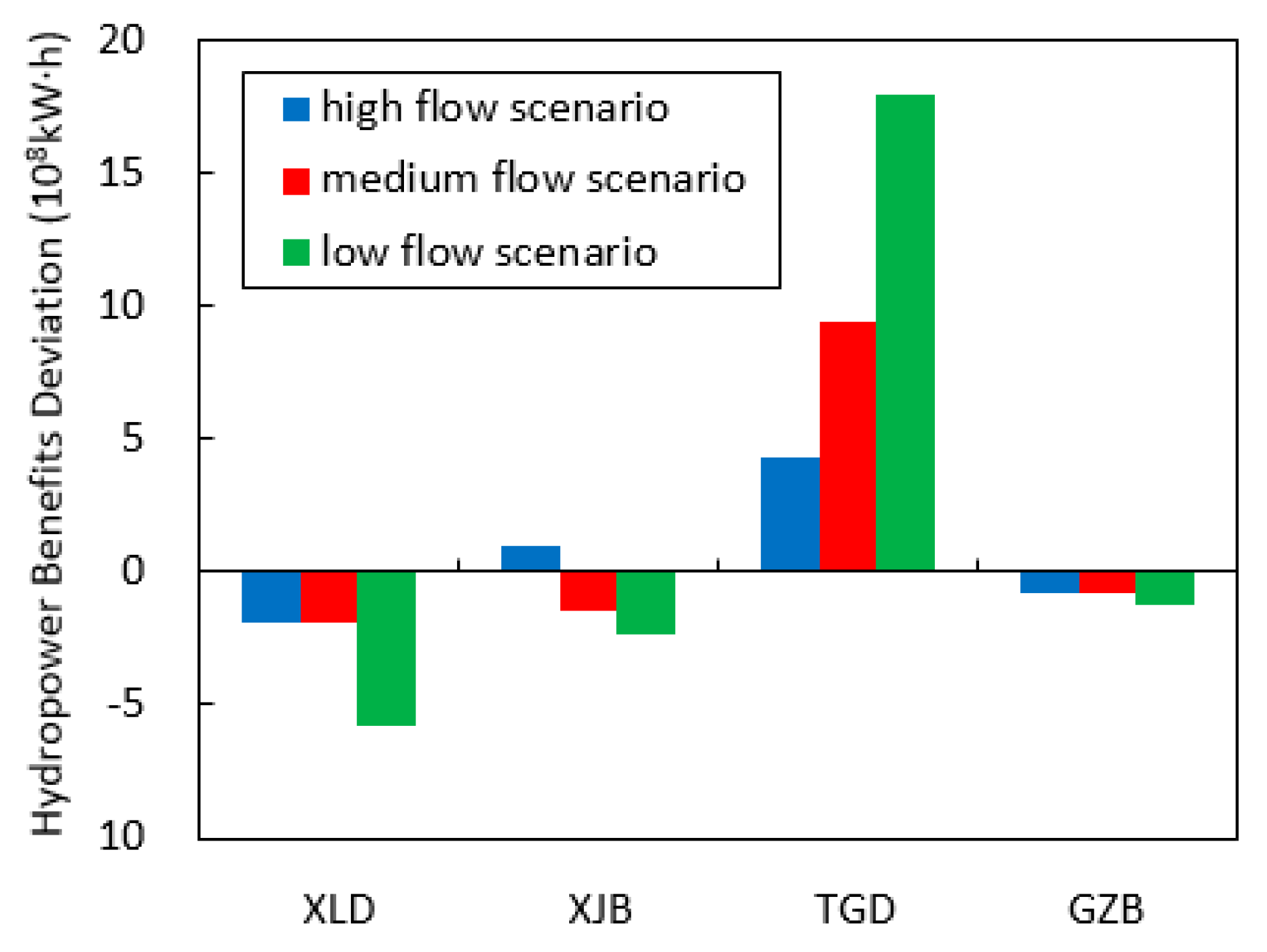
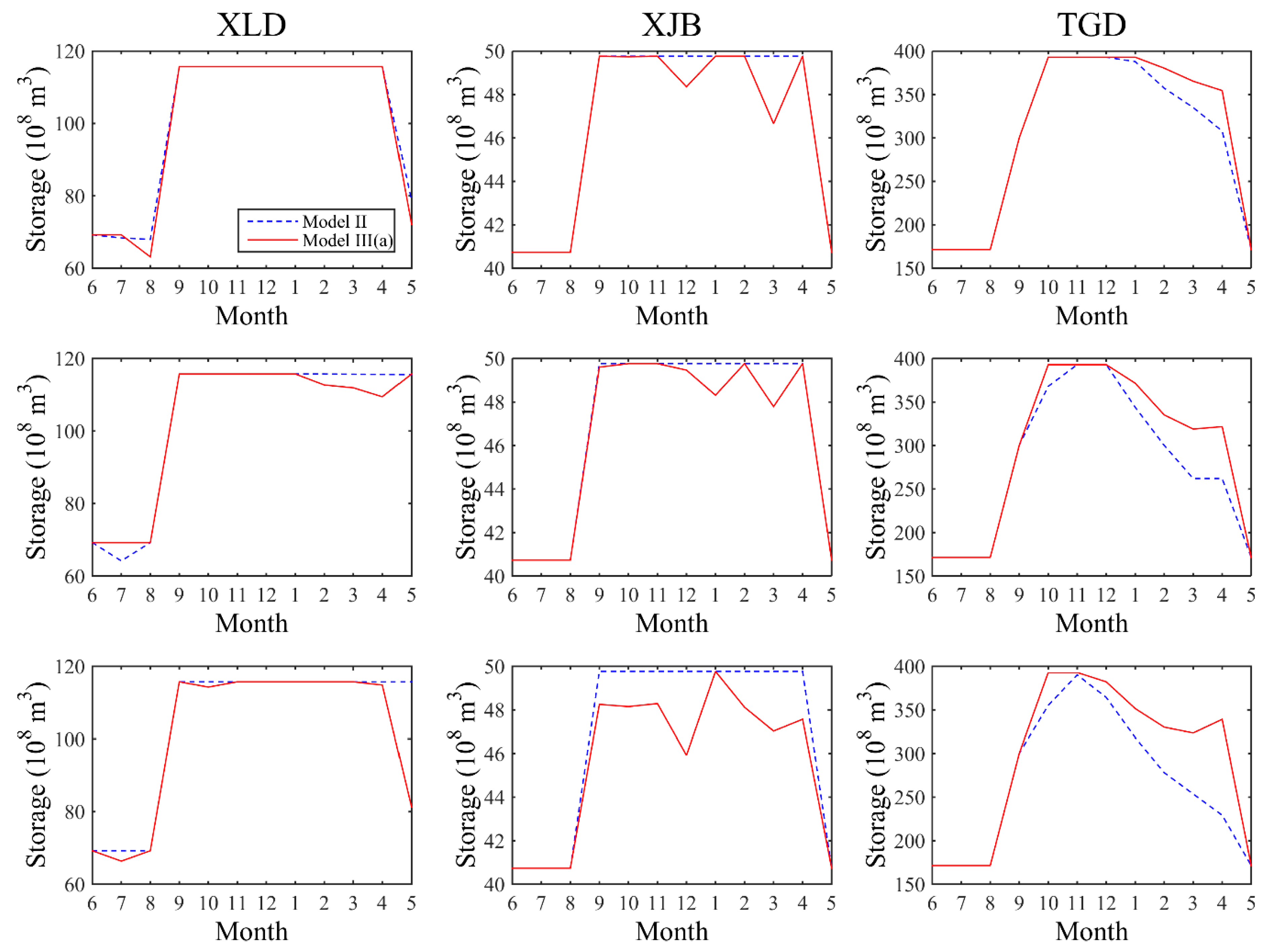
| Reservoir | XLD | XJB | TGD | GZB |
|---|---|---|---|---|
| Normal water level (m) | 600 | 380 | 175 | 66 |
| Flood limit water level (m) | 560 | 370 | 145 | 64.5 |
| Dead water level (m) | 540 | 370 | 145 | 62 |
| Firm power (MW) | 3790 | 2009 | 4990 | 1130.5 |
| Install capacity (MW) | 12,600 | 6000 | 22,500 | 2940 |
| Output coefficient | 8.7 | 8.7 | 8.8 | 8.5 |
| Statistics | Hydrological Station | |
|---|---|---|
| Pinshan Station | Yichang Station | |
| maximum daily flow (m3/s) | 16,964.52 | 50,312.90 |
| coefficient of variation | 0.15 | 0.10 |
| z test | 0.85 | −2.35 |
| Parameters | Value |
|---|---|
| Iteration | 500 |
| Population | 100 |
| Crossover rate | 0.8 |
| Mutation rate | 0.1 |
| Reservoirs | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model I | Model II | Model III(a) | Model I | Model II | Model III(a) | Model I | Model II | Model III(a) | |
| XLD | 702.96 | 705.19 | 703.33 | 581.93 | 582.74 | 580.87 | 512.01 | 513.77 | 508.00 |
| XJB | 346.23 | 344.99 | 345.98 | 292.50 | 292.42 | 291.00 | 258.38 | 258.28 | 255.97 |
| TGD | 1003.23 | 997.96 | 1002.26 | 981.93 | 973.39 | 982.81 | 810.17 | 795.36 | 813.28 |
| GZB | 184.71 | 185.68 | 184.92 | 179.04 | 179.37 | 178.61 | 164.61 | 165.45 | 164.22 |
| Total | 2237.13 | 2233.82 | 2236.49 | 2035.40 | 2027.92 | 2033.29 | 1745.17 | 1732.86 | 1741.47 |
| Reservoirs | ||||||
|---|---|---|---|---|---|---|
| Model III(a) | Model III(b) | Model III(a) | Model III(b) | Model III(a) | Model III(b) | |
| XLD | 703.33 | 705.86 (703.33 + 2.53) | 580.87 | 584.08 (580.87 + 3.21) | 508.00 | 515.92 (508.00 + 7.92) |
| XJB | 345.98 | 345.65 (345.98 − 0.33) | 291.00 | 293.76 (291.00 + 2.76) | 255.97 | 260.43 (255.97 + 4.46) |
| TGD | 1002.26 | 998.63 (1002.26 − 3.63) | 982.81 | 974.73 (982.81 − 8.08) | 813.28 | 797.52 (813.28 − 15.76) |
| GZB | 184.92 | 186.35 (184.92 + 1.43) | 178.61 | 180.72 (178.61 + 2.11) | 164.22 | 167.60 (164.22 + 3.38) |
| Patterns | Reservoir | High Flow (108 kW·h) | Medium Flow (108 kW·h) | Low Flow (108 kW·h) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model II | Model III(a) | Model III(b) | Model II | Model III(a) | Model III(b) | Model II | Model III(a) | Model III(b) | ||
| Pattern I | XLD | 705.19 | 696.98 | - | 582.74 | 573.42 | - | 513.77 | 504.14 | - |
| XJB | 344.99 | 347.92 | - | 292.42 | 293.56 | - | 258.28 | 259.51 | - | |
| Total | 1050.19 | 1044.90 | - | 875.16 | 866.98 | - | 772.05 | 763.65 | - | |
| Pattern II | XJB | 344.99 | 343.98 | 346.11 | 292.42 | 288.33 | 294.60 | 258.28 | 251.04 | 261.81 |
| Coalition 2 | 1183.64 | 1186.89 | 1184.76 | 1152.77 | 1161.23 | 1154.96 | 960.82 | 975.12 | 964.35 | |
| Total | 1528.63 | 1530.87 | 1530.87 | 1445.19 | 1449.56 | 1449.56 | 1219.10 | 1226.16 | 1226.16 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Fu, X.; Qin, J. Qualifying Coordination Mechanism for Cascade-Reservoir Operation with a New Game-Theoretical Methodology. Water 2018, 10, 1857. https://doi.org/10.3390/w10121857
Xu Y, Fu X, Qin J. Qualifying Coordination Mechanism for Cascade-Reservoir Operation with a New Game-Theoretical Methodology. Water. 2018; 10(12):1857. https://doi.org/10.3390/w10121857
Chicago/Turabian StyleXu, Yuni, Xiang Fu, and Jianan Qin. 2018. "Qualifying Coordination Mechanism for Cascade-Reservoir Operation with a New Game-Theoretical Methodology" Water 10, no. 12: 1857. https://doi.org/10.3390/w10121857
APA StyleXu, Y., Fu, X., & Qin, J. (2018). Qualifying Coordination Mechanism for Cascade-Reservoir Operation with a New Game-Theoretical Methodology. Water, 10(12), 1857. https://doi.org/10.3390/w10121857





