Integration of Remote Sensing Evapotranspiration into Multi-Objective Calibration of Distributed Hydrology–Soil–Vegetation Model (DHSVM) in a Humid Region of China
Abstract
1. Introduction
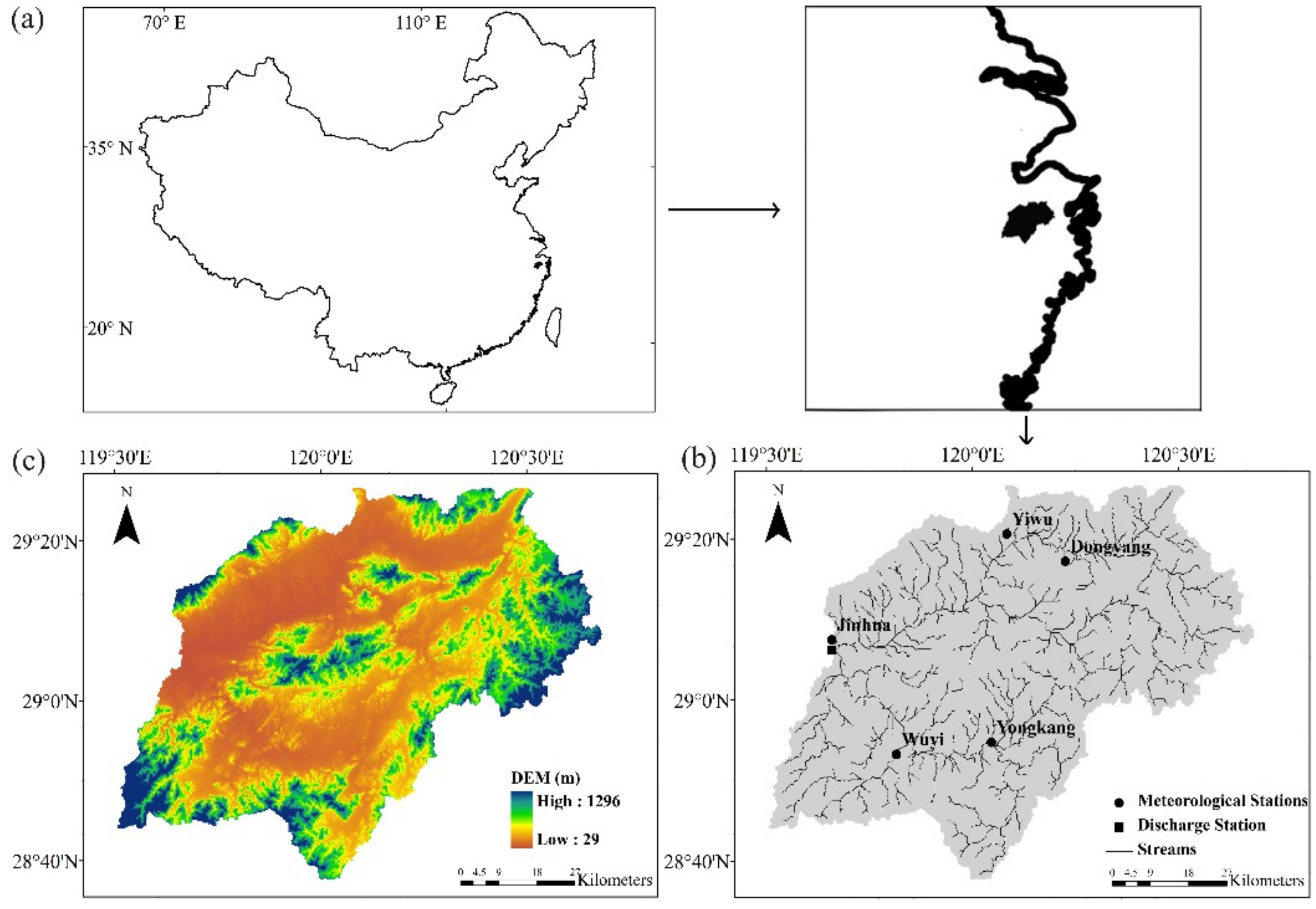
2. Study Area
3. Data and Methods
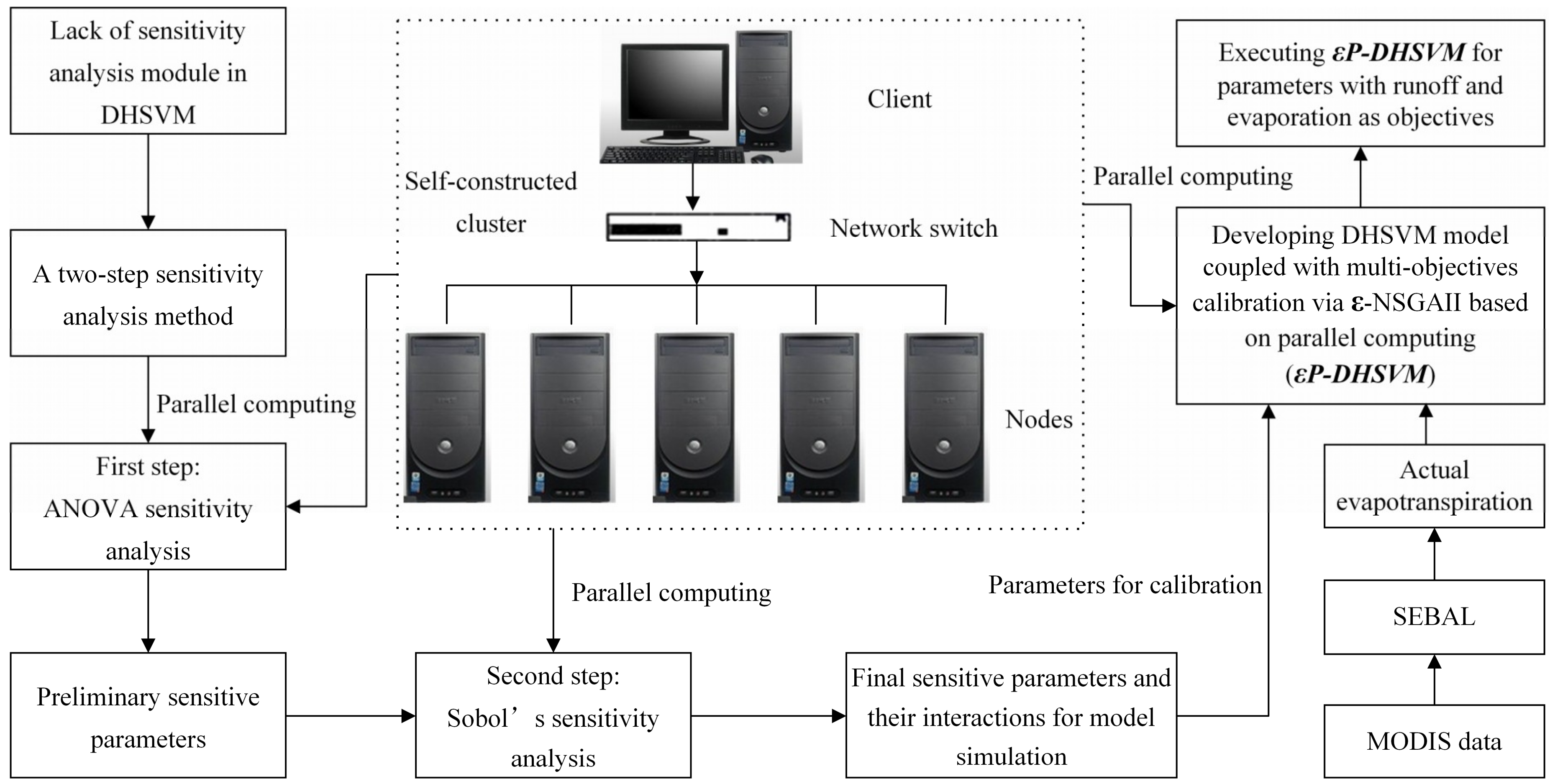
3.1. Experiment Design
3.2. Data
- (a)
- MOD09GA: 1-day, 500 m land surface reflectance;
- (b)
- MOD11A1: 1-day, 1-km land surface temperature;
- (c)
- MOD13A1: 16-day, 500 m vegetation indices (NDVI).
3.3. SEBAL Model
3.4. DHSVM
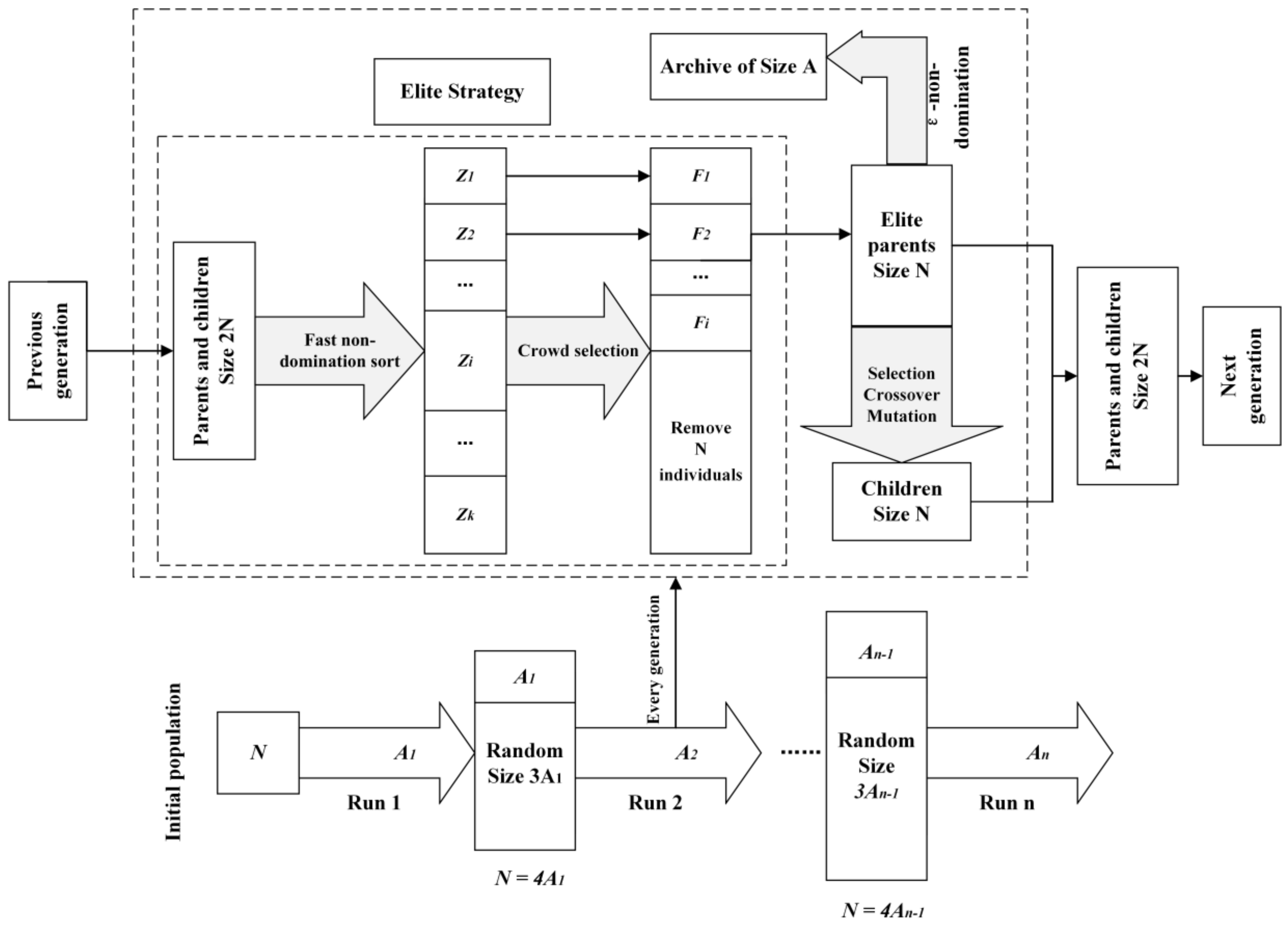
3.5. Multi-Objective Calibration
4. Results
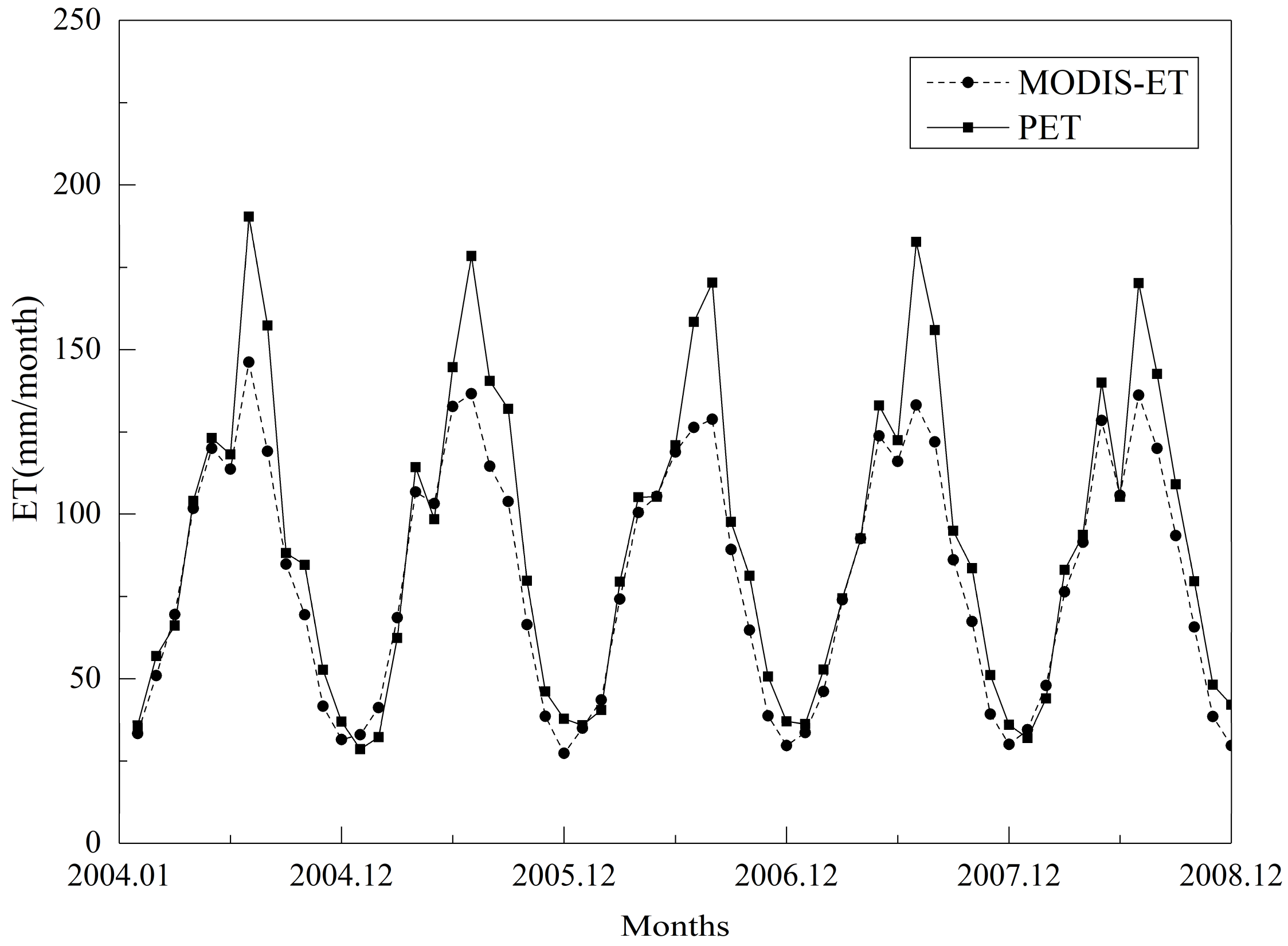
4.1. Time Series of Remote Sensing Evapotranspiration
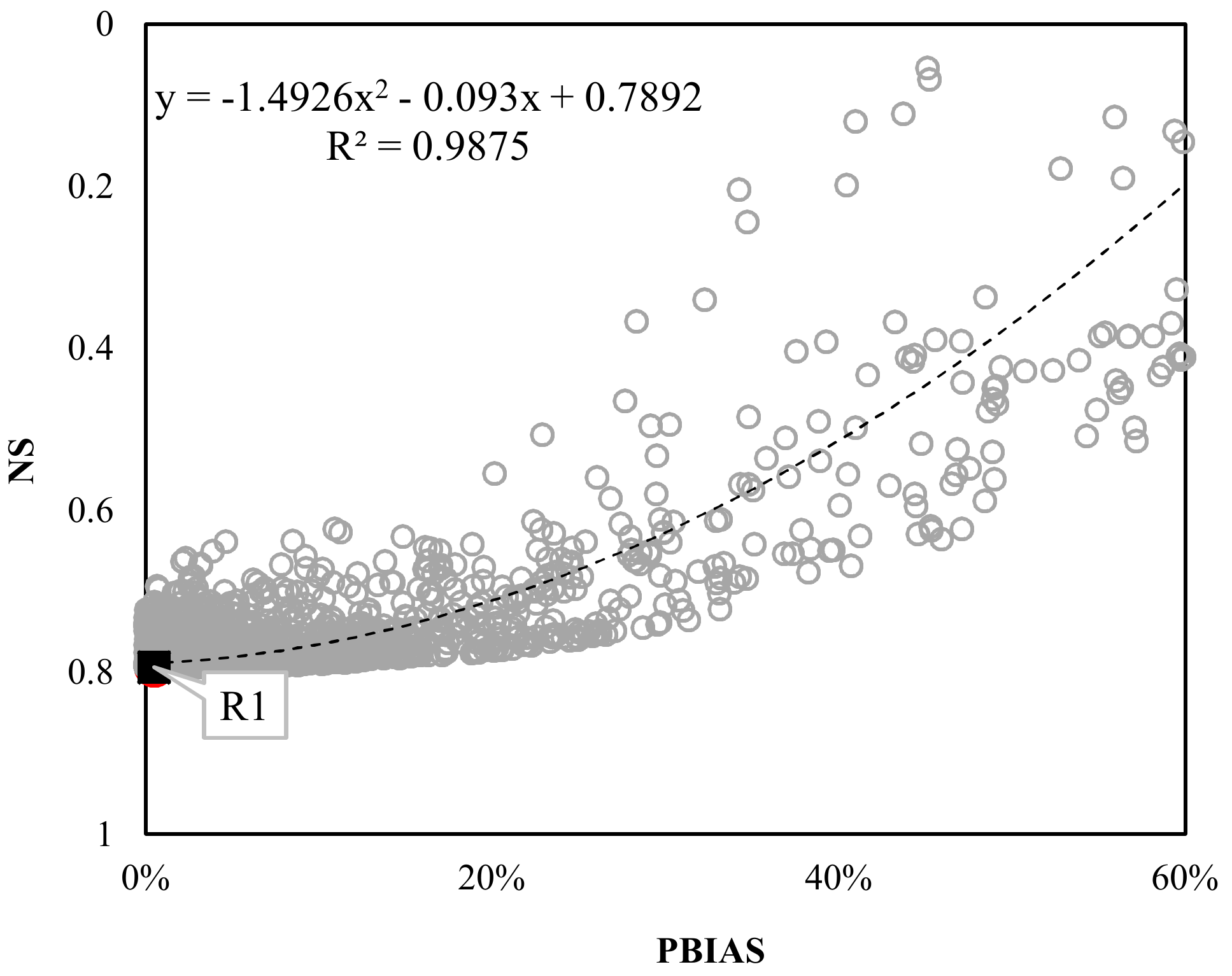
4.2. Single Objective Model Calibration Results
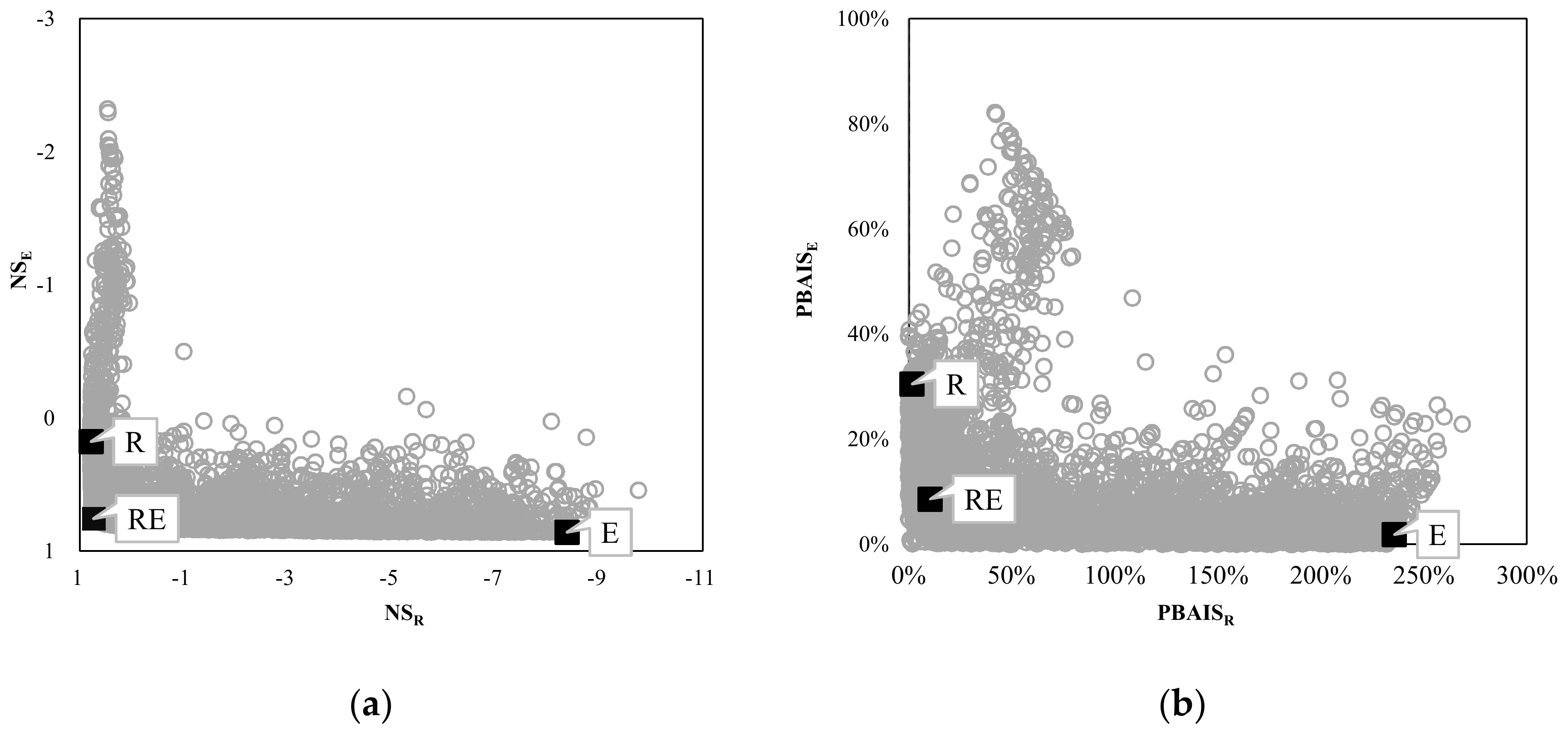
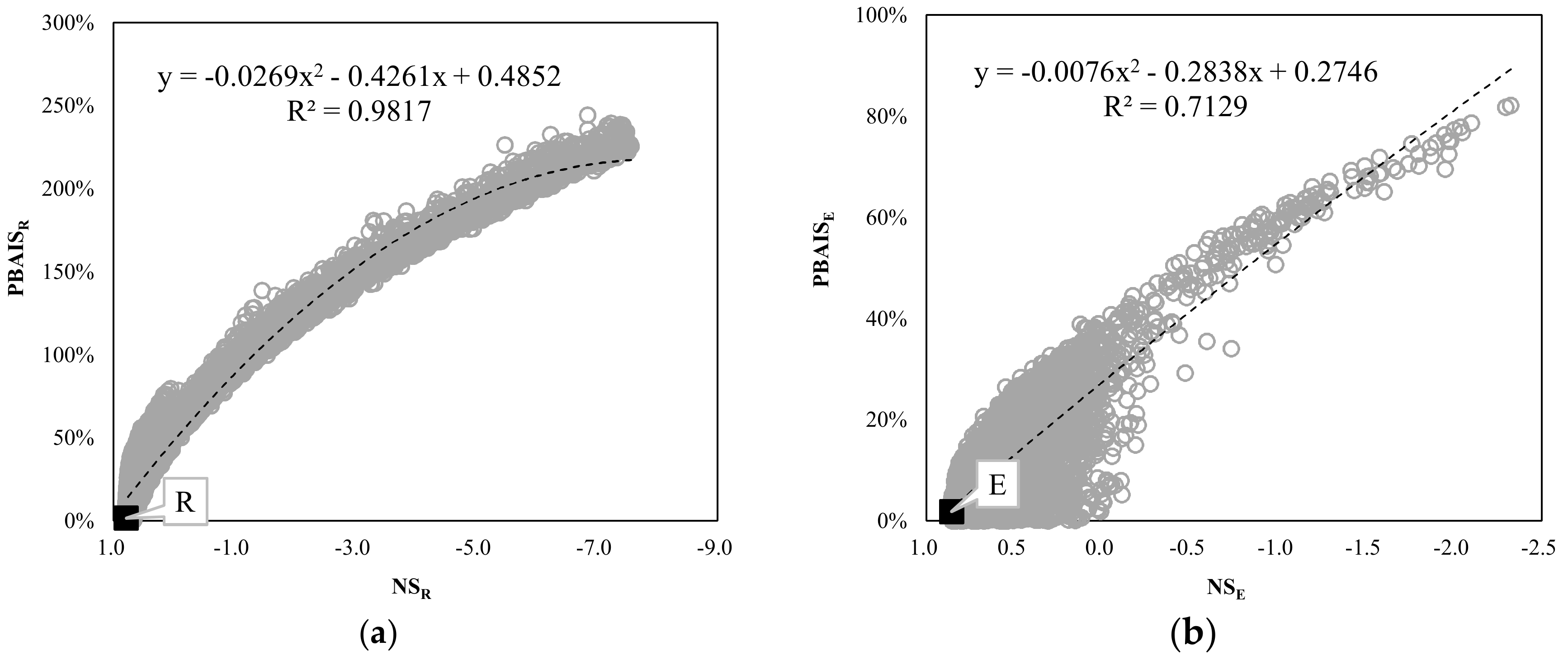
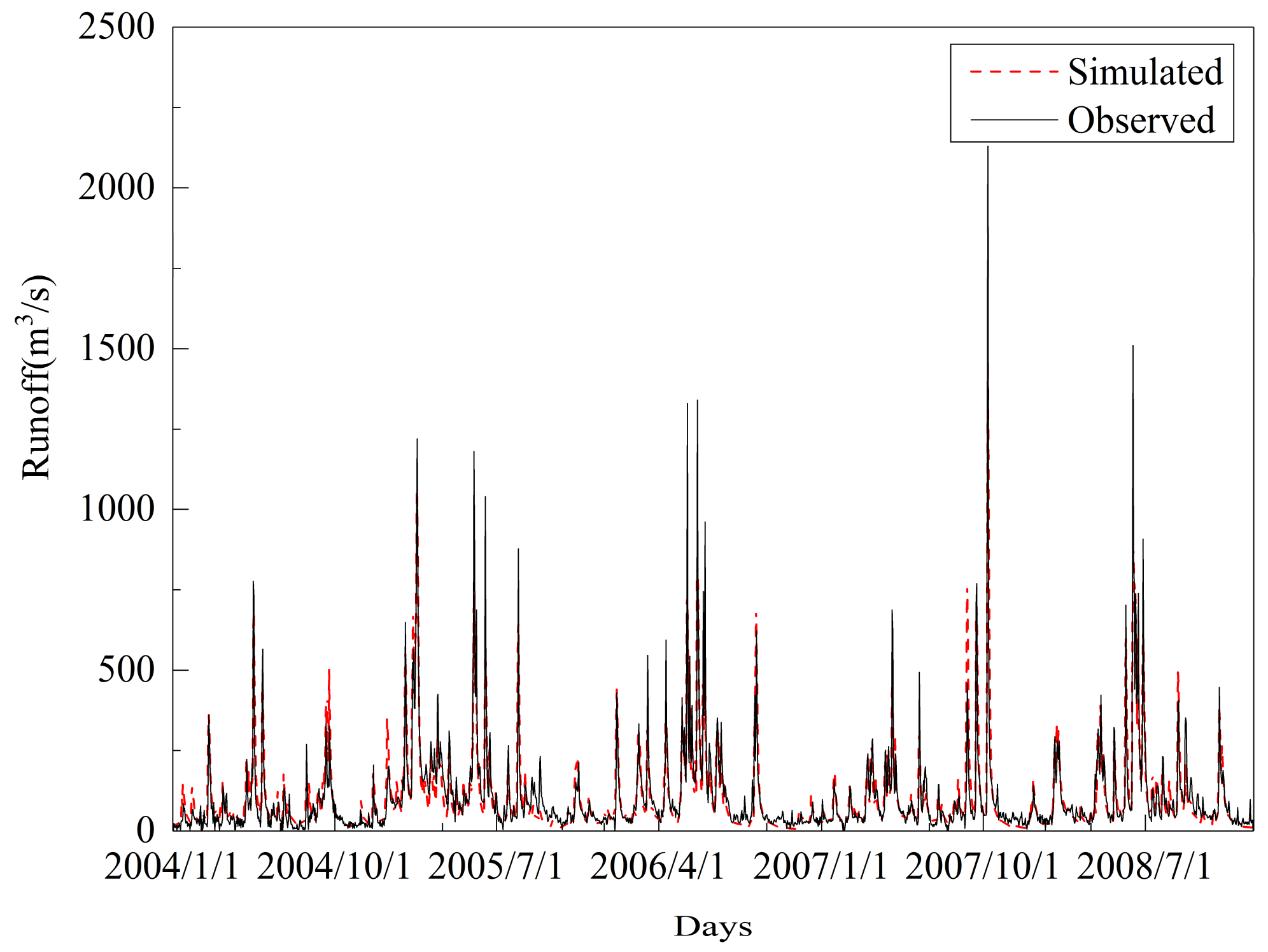
4.3. Multi-Objective Calibration Results
5. Discussion
6. Conclusions
- Compared with potential evapotranspiration, MODIS-ET estimated by SEBAL showed a satisfactory performance, with high values of efficiency coefficients on daily (0.89) and monthly (0.94) time scales, which illustrates the accuracy of MODIS-ET in the Jinhua River Basin.
- Runoff was simulated reasonably in single objective calibration with an NS value of 0.79 and a PBIAS value of 0.5%, whereas evapotranspiration was not. High equifinality occurred in single objective calibration.
- The multi-objective calibration by integrating remote sensing evapotranspiration showed good performance for runoff and evapotranspiration simulation with reasonable value of objective functions (NSR: 0.74, PBIASR: −10%, NSE: 0.76 and PBIASE: −8.6%). Furthermore, multi-objective calibration to a great extent alleviated the problem of equifinality.
- The self-developed model, εP-DHSVM, can implement multi-objective calibration effectively and efficiently, with its calculation speed improved more than 20 times.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward improved calibration of hydrologic models: Multiple and non-commensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
- Henriksen, H.J.; Troldborg, L.; Nyegaard, P.; Sonnenborg, T.O.; Refsgaard, J.C.; Madsen, B. Methodology for construction, calibration and validation of a national hydrological model for Denmark. J. Hydrol. 2003, 280, 52–71. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Klove, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Rajib, M.A.; Merwade, V.; Yu, Z. Multi-objective calibration of a hydrologic model using spatially distributed remotely sensed/in-situ soil moisture. J. Hydrol. 2016, 536, 192–207. [Google Scholar] [CrossRef]
- Daggupati, P.; Yen, H.; White, M.J.; Srinivasan, R.; Arnold, J.G.; Keitzer, C.S.; Sowa, S.P. Impact of model development, calibration and validation decisions on hydrological simulations in West Lake Erie Basin. Hydrol. Process. 2015, 29, 5307–5320. [Google Scholar] [CrossRef]
- Xu, Y.; Pan, S.; Fu, G.; Tian, Y.; Zhang, X. Future potential evapotranspiration changes and contribution analysis in Zhejiang Province, East China. J. Geophys. Res. Atmos. 2014, 119, 2174–2192. [Google Scholar] [CrossRef]
- Xie, H.; Zhu, X.; Yuan, D. Pan evaporation modelling and changing attribution analysis on the Tibetan Plateau (1970–2012). Hydrol. Process. 2015, 29, 2164–2177. [Google Scholar] [CrossRef]
- Xu, Y.; Pan, S.; Gao, C.; Fu, G.; Chiang, Y. Historical pan evaporation changes in the Qiantang River Basin, East China. Int. J. Climatol. 2016, 36, 1928–1942. [Google Scholar] [CrossRef]
- Chen, H.; Chandrasekar, V. The quantitative precipitation estimation system for Dallas-Fort Worth (DFW) urban remote sensing network. J. Hydrol. 2015, 531, 259–271. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Guo, L.; Liu, Z.; Bu, S.; Ren, J. Effective and Efficient Midlevel Visual Elements-Oriented Land-Use Classification Using VHR Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4238–4249. [Google Scholar] [CrossRef]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating soil moisture remote sensing with observations from the UK TechDemoSat-1 satellite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep Learning Classification of Land Cover and Crop Types Using Remote Sensing Data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 778–782. [Google Scholar] [CrossRef]
- Parajuli, P.B.; Jayakody, P.; Ouyang, Y. Evaluation of Using Remote Sensing Evapotranspiration Data in SWAT. Water Resour. Manag. 2018, 32, 985–996. [Google Scholar] [CrossRef]
- Sadeghi, M.; Jones, S.B.; Philpot, W.D. A linear physically-based model for remote sensing of soil moisture using short wave infrared bands. Remote Sens. Environ. 2015, 164, 66–76. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Z.; Chen, Q.; Bi, H.; Qiu, J.; Zou, P. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Chiew, F.H.S.; Zhang, L.; Leuning, R.; Cleugh, H.A. Estimating catchment evaporation and runoff using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; Moore, P.; Kilsby, C.G.; O’Donnell, G.M.; Hardy, A.J.; Berry, P.A.M. Daily discharge estimation at ungauged river sites using remote sensing. Hydrol. Process. 2014, 28, 1043–1054. [Google Scholar] [CrossRef]
- Faridzad, M.; Yang, T.; Hsu, K.; Sorooshian, S.; Xiao, C. Rainfall frequency analysis for ungauged regions using remotely sensed precipitation information. J. Hydrol. 2018, 563, 123–142. [Google Scholar] [CrossRef]
- Marra, F.; Morin, E.; Peleg, N.; Mei, Y.; Anagnostou, E.N. Intensity-duration-frequency curves from remote sensing rainfall estimates: Comparing satellite and weather radar over the eastern Mediterranean. Hydrol. Earth Syst. Sci. 2017, 29, 2389–2404. [Google Scholar] [CrossRef]
- Poortinga, A.; Bastiaanssen, W.; Simons, G.; Saah, D.; Senay, G.; Fenn, M.; Bean, B.; Kadyszewski, J. A Self-Calibrating Runoff and Streamflow Remote Sensing Model for Ungauged Basins Using Open-Access Earth Observation Data. Remote Sens. 2017, 9, 86. [Google Scholar] [CrossRef]
- Rhee, J.; Im, J. Meteorological drought forecasting for ungauged areas based on machine learning: Using long-range climate forecast and remote sensing data. Agric. For. Meteorol. 2017, 237, 105–122. [Google Scholar] [CrossRef]
- Sun, W.C.; Ishidaira, H.; Bastola, S. Towards improving river discharge estimation in ungauged basins: Calibration of rainfall-runoff models based on satellite observations of river flow width at basin outlet. Hydrol. Earth Syst. Sci. 2010, 14, 2011–2022. [Google Scholar] [CrossRef]
- Alton, P.B. Retrieval of seasonal Rubisco-limited photosynthetic capacity at global FLUXNET sites from hyperspectral satellite remote sensing: Impact on carbon modelling. Agric. For. Meteorol. 2017, 232, 74–88. [Google Scholar] [CrossRef]
- Gao, H.; Birkett, C.; Lettenmaier, D.P. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Hu, L.; Li, W.; Xu, B. The role of remote sensing on studying mangrove forest extent change. Int. J. Remote Sens. 2018, 39, 6440–6462. [Google Scholar] [CrossRef]
- Khan, S.I.; Hong, Y.; Wang, J.; Yilmaz, K.K.; Gourley, J.J.; Adler, R.F.; Brakenridge, G.R.; Policelli, F.; Habib, S.; Irwin, D. Satellite Remote Sensing and Hydrologic Modeling for Flood Inundation Mapping in Lake Victoria Basin: Implications for Hydrologic Prediction in Ungauged Basins. IEEE Trans. Geosci. Remote Sens. 2011, 49, 85–95. [Google Scholar] [CrossRef]
- Park, H.; Kim, Y.; Kimball, J.S. Widespread permafrost vulnerability and soil active layer increases over the high northern latitudes inferred from satellite remote sensing and process model assessments. Remote Sens. Environ. 2016, 175, 349–358. [Google Scholar] [CrossRef]
- Richardson, A.D.; Hufkens, K.; Milliman, T.; Frolking, S. Intercomparison of phenological transition dates derived from the PhenoCam Dataset V1.0 and MODIS satellite remote sensing. Sci. Rep. 2018, 8, 5679. [Google Scholar] [CrossRef]
- Yang, J.; Gong, P.; Fu, R.; Zhang, M.; Chen, J.; Liang, S.; Xu, B.; Shi, J.; Dickinson, R. The role of satellite remote sensing in climate change studies. Nat. Clim. Chang. 2013, 3, 875–883. [Google Scholar] [CrossRef]
- Bhattarai, N.; Shaw, S.B.; Quackenbush, L.J.; Im, J.; Niraula, R. Evaluating five remote sensing based single-source surface energy balance models for estimating daily evapotranspiration in a humid subtropical climate. Int. J. Appl. Earth Obs. 2016, 49, 75–86. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Menenti, M.; Feddes, R.A.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL)-1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)-Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Li, Z.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A Review of Current Methodologies for Regional Evapotranspiration Estimation from Remotely Sensed Data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Noordman, E.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Jaber, H.S.; Mansor, S.; Pradhan, B.; Ahmad, N. Evaluation of SEBAL model for Evapotranspiration mapping in Iraq using remote sensing and GIS. Int. J. Appl. Eng. Res. 2016, 11, 3950–3955. [Google Scholar]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Bouda, M.; Rousseau, A.N.; Gumiere, S.J.; Gagnon, P.; Konan, B.; Moussa, R. Implementation of an automatic calibration procedure for HYDROTEL based on prior OAT sensitivity and complementary identifiability analysis. Hydrol. Process. 2014, 28, 3947–3961. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Kollat, J.B.; Reed, P.M. The value of online adaptive search: A performance comparison of NSGAII, ε-NSGAII and εMOEA. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Guanajuato, Mexico, 9–11 March 2005; pp. 386–398. [Google Scholar]
- Kollat, J.B.; Reed, P.M. Comparing state-of-the-art evolutionary multi-objective algorithms for long-term groundwater monitoring design. Adv. Water Resour. 2006, 29, 792–807. [Google Scholar] [CrossRef]
- Du, E.; Link, T.E.; Gravelle, J.A.; Hubbart, J.A. Validation and sensitivity test of the distributed hydrology soil-vegetation model (DHSVM) in a forested mountain watershed. Hydrol. Process. 2014, 28, 6196–6210. [Google Scholar] [CrossRef]
- Pan, S.; Fu, G.; Chiang, Y.; Ran, Q.; Xu, Y. A two-step sensitivity analysis for hydrological signatures in Jinhua River Basin, East China. Hydrol. Sci. J. 2017, 62, 2511–2530. [Google Scholar] [CrossRef]
- Saltelli, A.; Chan, K.; Scott, E.M. Sensitivity Analysis; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Allen, R.G. An update for the calculation of potential evapotranspiration. ICID Bull. 1994, 43, 35–92. [Google Scholar]
- Ran, Y.; Li, X.; Lu, L. Evaluation of four remote sensing based land cover products over China. Int. J. Remote Sens. 2010, 31, 391–401. [Google Scholar] [CrossRef]
- Paul, G.; Gowda, P.H.; Prasad, P.V.V.; Howell, T.A.; Aiken, R.M.; Neale, C.M.U. Investigating the influence of roughness length for heat transport (z(oh)) on the performance of SEBAL in semi-arid irrigated and dryland agricultural systems. J. Hydrol. 2014, 509, 231–244. [Google Scholar] [CrossRef]
- Papadavid, G.; Hadjimitsis, D.G.; Toulios, L.; Michaelides, S. A Modified SEBAL Modeling Approach for Estimating Crop Evapotranspiration in Semi-arid Conditions. Water Resour. Manag. 2013, 27, 3493–3506. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.; Chen, K.; Jia, Y.; Li, C.; Sun, X. Spatial-scale effect on the SEBAL model for evapotranspiration estimation using remote sensing data. Agric. For. Meteorol. 2013, 174, 28–42. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Nijssen, B.; Storck, P.; Lettenmaier, D.P. The distributed hydrology soil vegetation model. Math. Model. Small Watershed Hydrol. Appl. 2002, 43, 7–42. [Google Scholar]
- Wigmosta, M.S.; Vail, L.W.; Lettenmaier, D.P. A distributed hydrology-vegetation model for complex terrain. Water Resour. Res. 1994, 30, 1665–1679. [Google Scholar] [CrossRef]
- Jost, G.; Moore, R.D.; Weiler, M.; Gluns, D.R.; Alila, Y. Use of distributed snow measurements to test and improve a snowmelt model for predicting the effect of forest clear-cutting. J. Hydrol. 2009, 376, 94–106. [Google Scholar] [CrossRef]
- Safeeq, M.; Fares, A. Hydrologic response of a Hawaiian watershed to future climate change scenarios. Hydrol. Process. 2012, 26, 2745–2764. [Google Scholar] [CrossRef]
- Sun, N.; Yearsley, J.; Baptiste, M.; Cao, Q.; Lettenmaier, D.P.; Nijssen, B. A spatially distributed model for assessment of the effects of changing land use and climate on urban stream quality. Hydrol. Process. 2016, 30, 4779–4798. [Google Scholar] [CrossRef]
- Sun, N.; Yearsley, J.; Voisin, N.; Lettenmaier, D.P. A spatially distributed model for the assessment of land use impacts on stream temperature in small urban watersheds. Hydrol. Process. 2015, 29, 2331–2345. [Google Scholar] [CrossRef]
- Tang, Y.; Reed, P.; Wagener, T.; Van Werkhoven, K. Comparing sensitivity analysis methods to advance lumped watershed model identification and evaluation. Hydrol. Earth Syst. Sci. Discuss. 2007, 11, 793–817. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ferringer, M.P.; Spencer, D.B.; Reed, P. Many-objective Reconfiguration of Operational Satellite Constellations with the Large-Cluster Epsilon Non-dominated Sorting Genetic Algorithm-II. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; p. 340. [Google Scholar]
- Reed, P.M.; Hadka, D.; Herman, J.D.; Kasprzyk, J.R.; Kollat, J.B. Evolutionary multiobjective optimization in water resources: The past, present, and future. Adv. Water Resour. 2013, 51, 438–456. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Wu, B.F.; Shao, J.H. Temporal and spatial extension of evaportranspiration estimated from remote sensing. J. Hydraul. Eng. 2006, 37, 286–292. [Google Scholar]
- Kelleher, C.; McGlynn, B.; Wagener, T. Characterizing and reducing equifinality by constraining a distributed catchment model with regional signatures, local observations, and process understanding. Hydrol. Earth Syst. Sci. 2017, 21, 3325–3352. [Google Scholar] [CrossRef]
- Kuras, P.K.; Alila, Y.; Weiler, M.; Spittlehouse, D.; Winkler, R. Internal catchment process simulation in a snow-dominated basin: Performance evaluation with spatiotemporally variable runoff generation and groundwater dynamics. Hydrol. Process. 2011, 25, 3187–3203. [Google Scholar] [CrossRef]
- Rientjes, T.H.M.; Muthuwatta, L.P.; Bos, M.G.; Booij, M.J.; Bhatti, H.A. Multi-variable calibration of a semi-distributed hydrological model using streamflow data and satellite-based evapotranspiration. J. Hydrol. 2013, 505, 276–290. [Google Scholar] [CrossRef]
- Wanders, N.; Bierkens, M.F.P.; de Jong, S.M.; de Roo, A.; Karssenberg, D. The benefits of using remotely sensed soil moisture in parameter identification of large-scale hydrological models. Water Resour. Res. 2014, 50, 6874–6891. [Google Scholar] [CrossRef]
- Fu, C.; James, A.L.; Yao, H. Investigations of uncertainty in SWAT hydrologic simulations: A case study of a Canadian Shield catchment. Hydrol. Process. 2015, 29, 4000–4017. [Google Scholar] [CrossRef]
- Qiao, L.; Pan, Z.; Herrmann, R.B.; Hong, Y. Hydrological variability and uncertainty of lower missouri river basin under changing climate. J. Am. Water Resour. Assoc. 2014, 50, 246–260. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Alsdorf, D.; Dozier, J.; Huffman, G.J.; Pan, M.; Wood, E.F. Inroads of remote sensing into hydrologic science during the WRR era. Water Resour. Res. 2015, 51, 7309–7342. [Google Scholar] [CrossRef]
- Yang, Y.; Long, D.; Guan, H.; Liang, W.; Simmons, C.; Batelaan, O. Comparison of three dual-source remote sensing evapotranspiration models during the MUSOEXE-12 campaign: Revisit of model physics. Water Resour. Res. 2015, 51, 3145–3165. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Fu, G.B.; Liu, C.M.; Chen, S.L.; Hong, E.L. Investigating the conversion coefficients for free water surface evaporation of different evaporation pans. Hydrol. Process. 2004, 18, 2247–2262. [Google Scholar] [CrossRef]
- Lim, W.H.; Roderick, M.L.; Hobbins, M.T.; Wong, S.C.; Farquhar, G.D. The energy balance of a US Class A evaporation pan. Agric. For. Meteorol. 2013, 182, 314–331. [Google Scholar] [CrossRef]
- Good, S.P.; Soderberg, K.; Guan, K.; King, E.G.; Scanlon, T.M.; Caylor, K.K. 2H isotopic flux partitioning of evapotranspiration over a grass field following a water pulse and subsequent dry down. Water Resour. Res. 2014, 50, 1410–1432. [Google Scholar] [CrossRef]
- Hu, Z.; Wen, X.; Sun, X.; Li, L.; Yu, G.; Lee, X.; Li, S. Partitioning of evapotranspiration through oxygen isotopic measurements of water pools and fluxes in a temperate grassland. J. Geophys. Res. Biogeosci. 2014, 119, 358–371. [Google Scholar] [CrossRef]
- Ma, Y.; Song, X. Applying stable isotopes to determine seasonal variability in evapotranspiration partitioning of winter wheat for optimizing agricultural management practices. Sci. Total Environ. 2018, 654, 633–642. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Yoshimura, K.; Okazaki, A.; Kim, W.; Liu, Z.; Yokoi, M. Partitioning of evapotranspiration using high-frequency water vapor isotopic measurement over a rice paddy field. Water Resour. Res. 2015, 51, 3716–3729. [Google Scholar] [CrossRef]
- Wen, X.; Yang, B.; Sun, X.; Lee, X. Evapotranspiration partitioning through in-situ oxygen isotope measurements in an oasis cropland. Agric. For. Meteorol. 2016, 230, 89–96. [Google Scholar] [CrossRef]
- Xiao, W.; Wei, Z.; Wen, X. Evapotranspiration partitioning at the ecosystem scale using the stable isotope method-A review. Agric. For. Meteorol. 2018, 263, 346–361. [Google Scholar] [CrossRef]
- Liou, Y.; Kar, S.K. Evapotranspiration Estimation with Remote Sensing and Various Surface Energy Balance Algorithms—A Review. Energies 2014, 7, 2821–2849. [Google Scholar] [CrossRef]
- Nouri, H.; Glenn, E.P.; Beecham, S.; Boroujeni, S.C.; Sutton, P.; Alaghmand, S.; Noori, B.; Nagler, P. Comparing Three Approaches of Evapotranspiration Estimation in Mixed Urban Vegetation: Field-Based, Remote Sensing-Based and Observational-Based Methods. Remote Sens. 2016, 8, 492. [Google Scholar] [CrossRef]
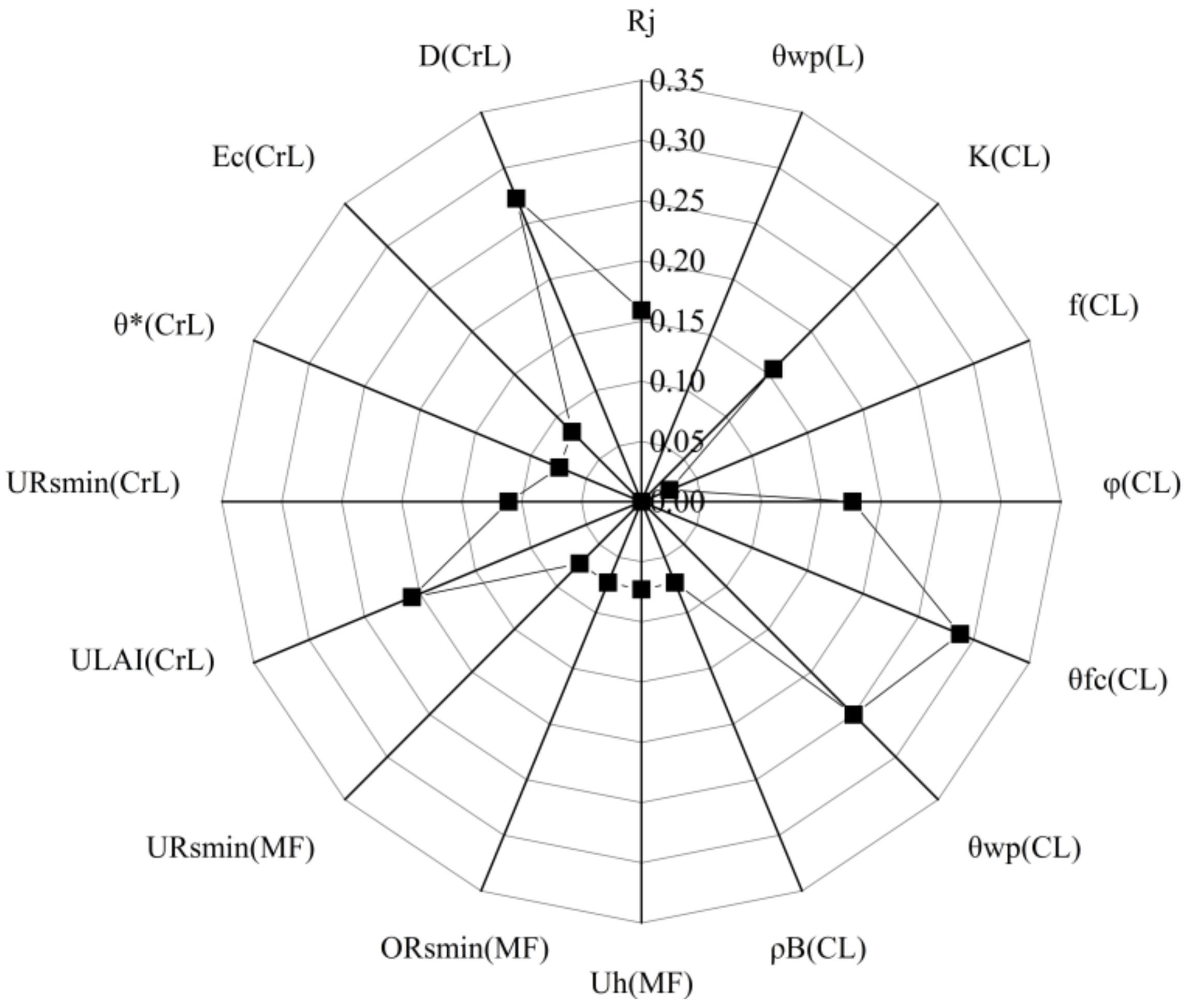
| Parameter | Meaning | Unit | Abbreviations | Range |
|---|---|---|---|---|
| Rain leaf area index (LAI) multiplier | Multiplier for LAI to determine interception capacity for rain | m | Rj | 0.00001~0.001 |
| Wilting point (L) | Wilting point for loam, used to calculate evapotranspiration | m3/m3 | θwp(L) | 0.05~0.25 |
| Lateral conductivity (CL) | Lateral saturated hydraulic conductivity for clay loam, used to calculate movement of lateral runoff | m/s | K(CL) | 0.00001~0.09 |
| Lateral conductivity exponential decrease (CL) | Exponent describing the decrease of lateral conductivity with soil depth for clay loam | / | f(CL) | 1~4 |
| Porosity (CL) | Porosity for clay loam, soil moisture content when soil is saturated | m3/m3 | φ(CL) | 0.35~0.6 |
| Field capacity (CL) | Field capacity for clay loam, used to estimate available water for subsurface layers | m3/m3 | θfc(CL) | 0.16~0.4 |
| Wilting point (CL) | Wilting point for clay loam, used to calculate evapotranspiration | m3/m3 | θwp(CL) | 0.05~0.25 |
| Bulk density (CL) | Bulk density for clay loam, used to estimate dry soil thermal conductivity | kg/m3 | ρB(CL) | 1000~3000 |
| Understory height (MF) | Understory height for mixed forests | m | Uh(MF) | 0.3~2.5 |
| Overstory minimum resistance (MF) | Overstory minimum stomatal resistance for understory of mixed forests | s/m | ORsmin(MF) | 300~800 |
| Understory minimum resistance (MF) | Understory minimum stomatal resistance for mixed forests | s/m | URsmin(MF) | 50~300 |
| Understory monthly LAI (CrL) | Understory leaf area index for croplands | m2/m2 | ULAI(CrL) | 0.3~3 |
| Understory minimum resistance (CrL) | Understory minimum stomatal resistance for croplands | s/m | URsmin(CrL) | 50~300 |
| Soil moisture threshold (CrL) | Soil moisture threshold above which soil moisture does not restrict transpiration for croplands | m3/m3 | θ*(CrL) | 0.1~0.35 |
| Vapor pressure deficit (CrL) | Vapor pressure deficit threshold above which stomatal closure occurs for each vegetation layer for croplands | pa | Ec(CrL) | 1000~6000 |
| Root zone depth (CrL) | These are in effect the depths of the various soil layers for croplands | m | D(CrL) | 0.1~0.8 |
| PBIAS (%) | 15% < PBIAS < 25% | 10% ≤ PBIAS ≤ 15% | PBIAS < 10% |
| average performance | good | very good | |
| NS | 0.35 < NS < 0.5 | 0.5 ≤ NS ≤ 0.7 | 0.7 < NS |
| average performance | good | very good | |
| R2 | 0.49 < R2 ≤ 0.64 | 0.64 < R2 ≤ 0.81 | R2 > 0.81 |
| average performance | good | very good |
| Parameters | R1 | R | E | RE |
|---|---|---|---|---|
| Rj | 0.0007 | 0.0004 | 0.0003 | 0.0003 |
| K(CL) | 0.02620 | 0.00008 | 0.00013 | 0.00012 |
| φ(CL) | 0.60 | 0.59 | 0.58 | 0.59 |
| θfc(CL) | 0.34 | 0.36 | 0.38 | 0.39 |
| θwp(CL) | 0.05 | 0.06 | 0.05 | 0.06 |
| ULAI(CrL) | 0.38 | 0.98 | 1.52 | 1.11 |
| URsmin(CrL) | 174 | 206 | 216 | 209 |
| D(CrL) | 0.02 | 0.17 | 0.17 | 0.17 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, S.; Liu, L.; Bai, Z.; Xu, Y.-P. Integration of Remote Sensing Evapotranspiration into Multi-Objective Calibration of Distributed Hydrology–Soil–Vegetation Model (DHSVM) in a Humid Region of China. Water 2018, 10, 1841. https://doi.org/10.3390/w10121841
Pan S, Liu L, Bai Z, Xu Y-P. Integration of Remote Sensing Evapotranspiration into Multi-Objective Calibration of Distributed Hydrology–Soil–Vegetation Model (DHSVM) in a Humid Region of China. Water. 2018; 10(12):1841. https://doi.org/10.3390/w10121841
Chicago/Turabian StylePan, Suli, Li Liu, Zhixu Bai, and Yue-Ping Xu. 2018. "Integration of Remote Sensing Evapotranspiration into Multi-Objective Calibration of Distributed Hydrology–Soil–Vegetation Model (DHSVM) in a Humid Region of China" Water 10, no. 12: 1841. https://doi.org/10.3390/w10121841
APA StylePan, S., Liu, L., Bai, Z., & Xu, Y.-P. (2018). Integration of Remote Sensing Evapotranspiration into Multi-Objective Calibration of Distributed Hydrology–Soil–Vegetation Model (DHSVM) in a Humid Region of China. Water, 10(12), 1841. https://doi.org/10.3390/w10121841





