Sensitivity Analysis to Investigate the Reliability of the Grid-Based Rainfall-Runoff Model
Abstract
:1. Introduction
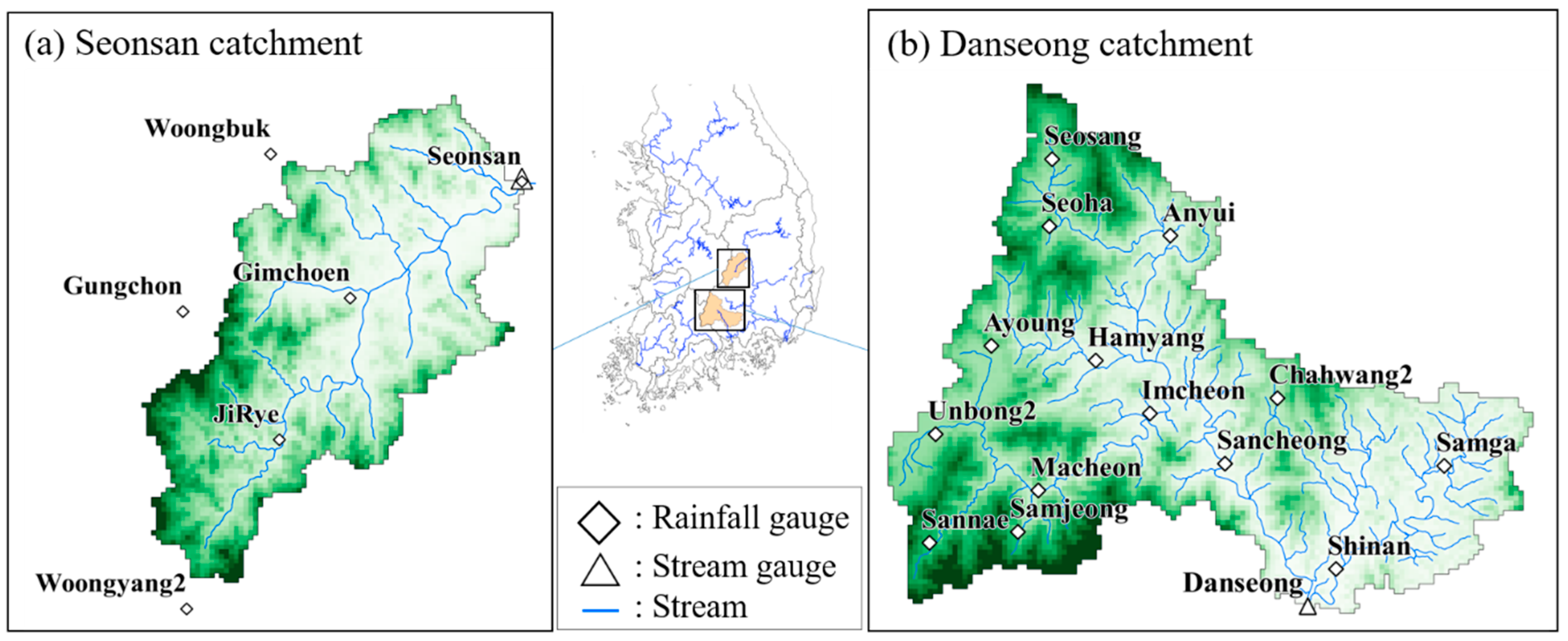
2. Catchment and Data
3. Material and Sensitivity Analysis Method
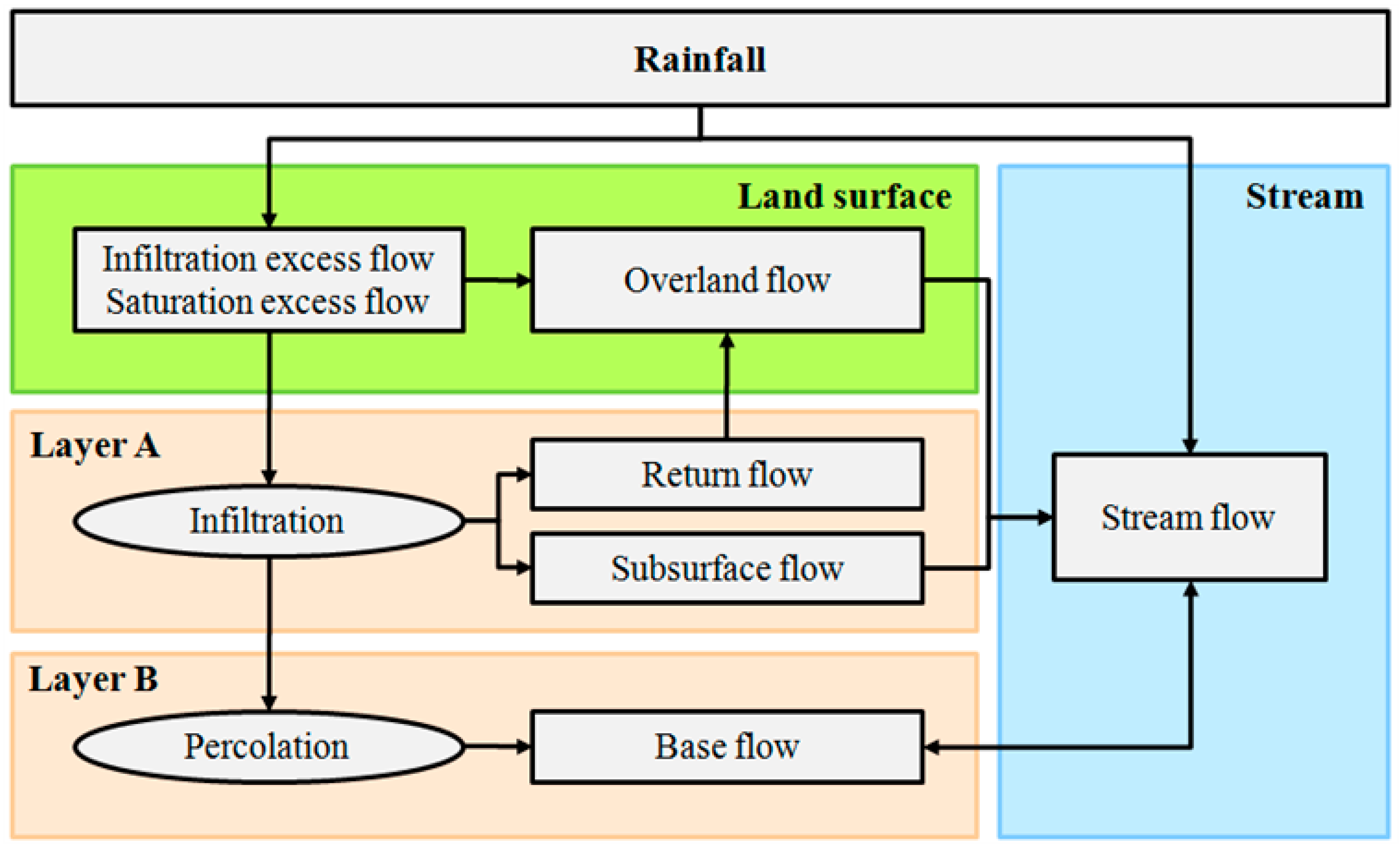
3.1. Grid-Based Rainfall-Runoff Model
3.2. The Sobol’ Method
4. Results and Discussion
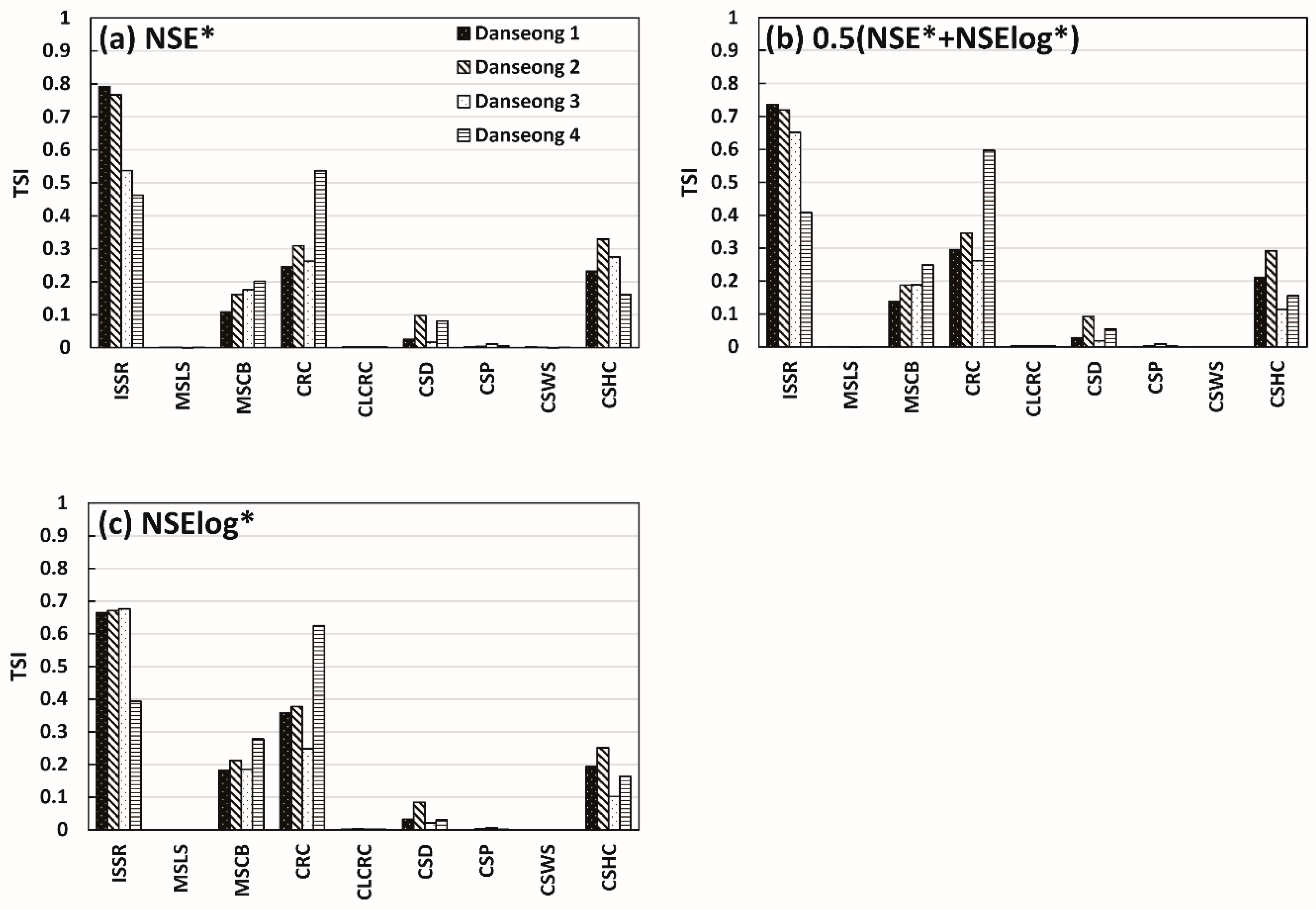
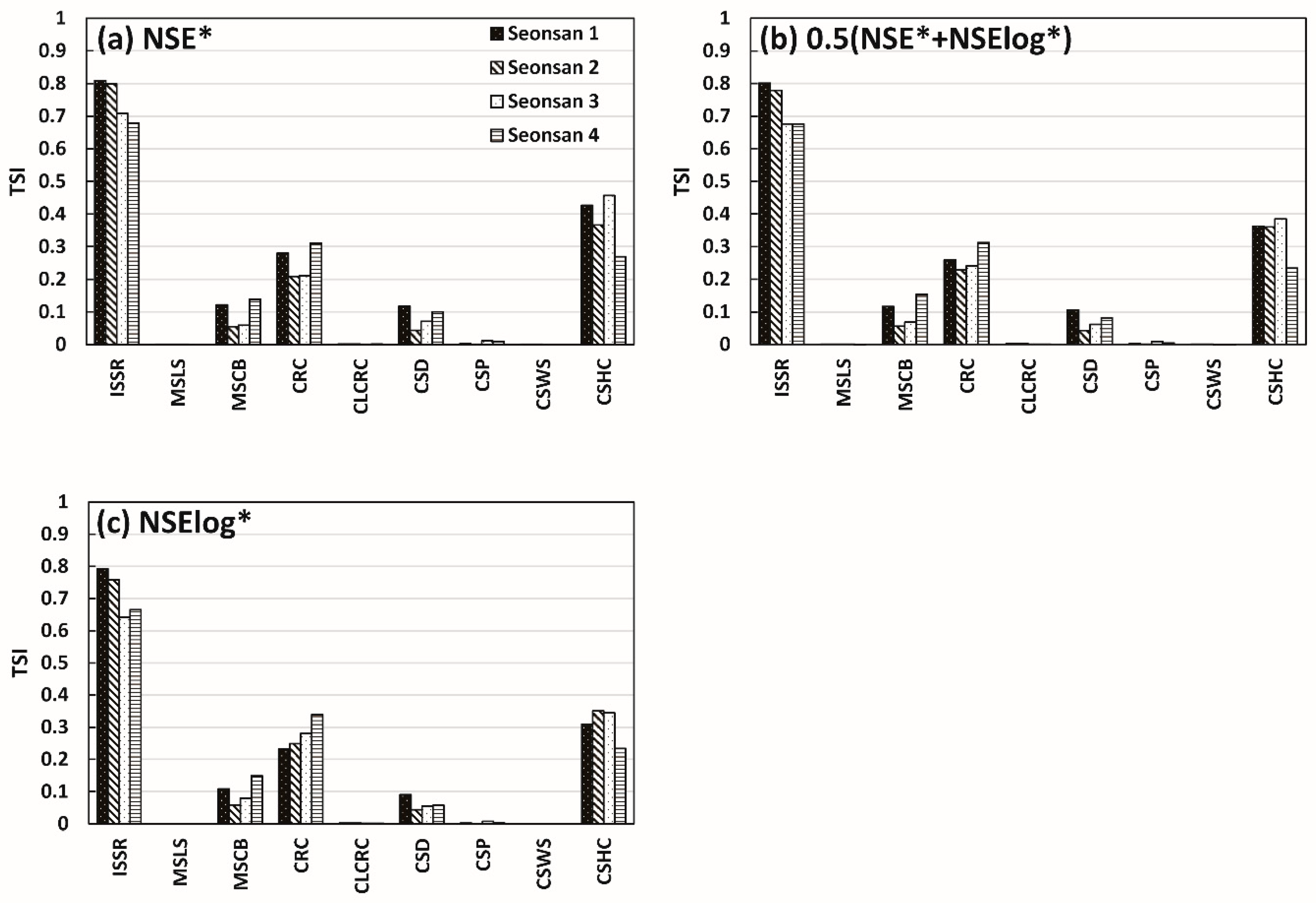
4.1. Parameter Sensitivity Analysis Reflecting the Scale of Rainfall Events
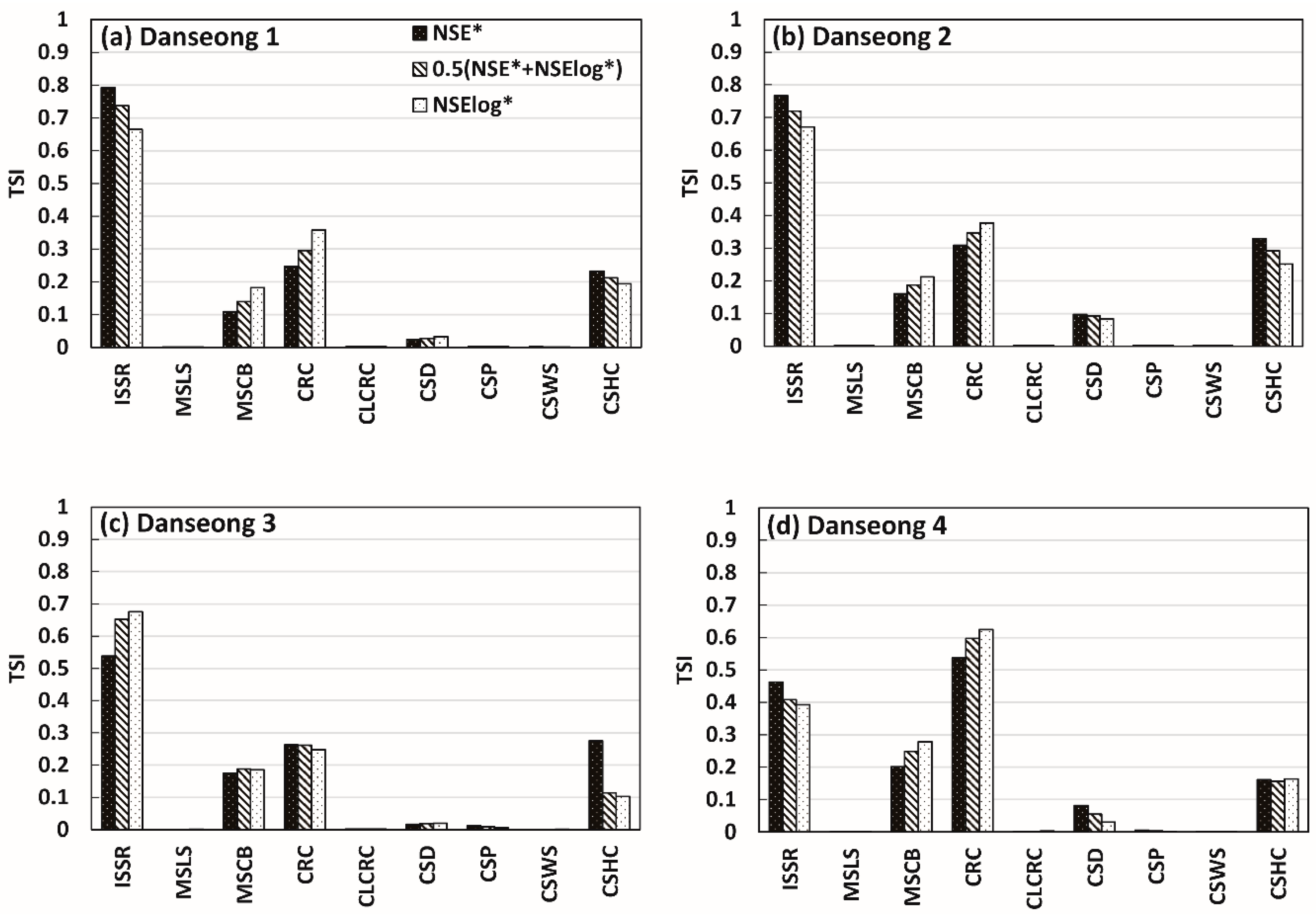
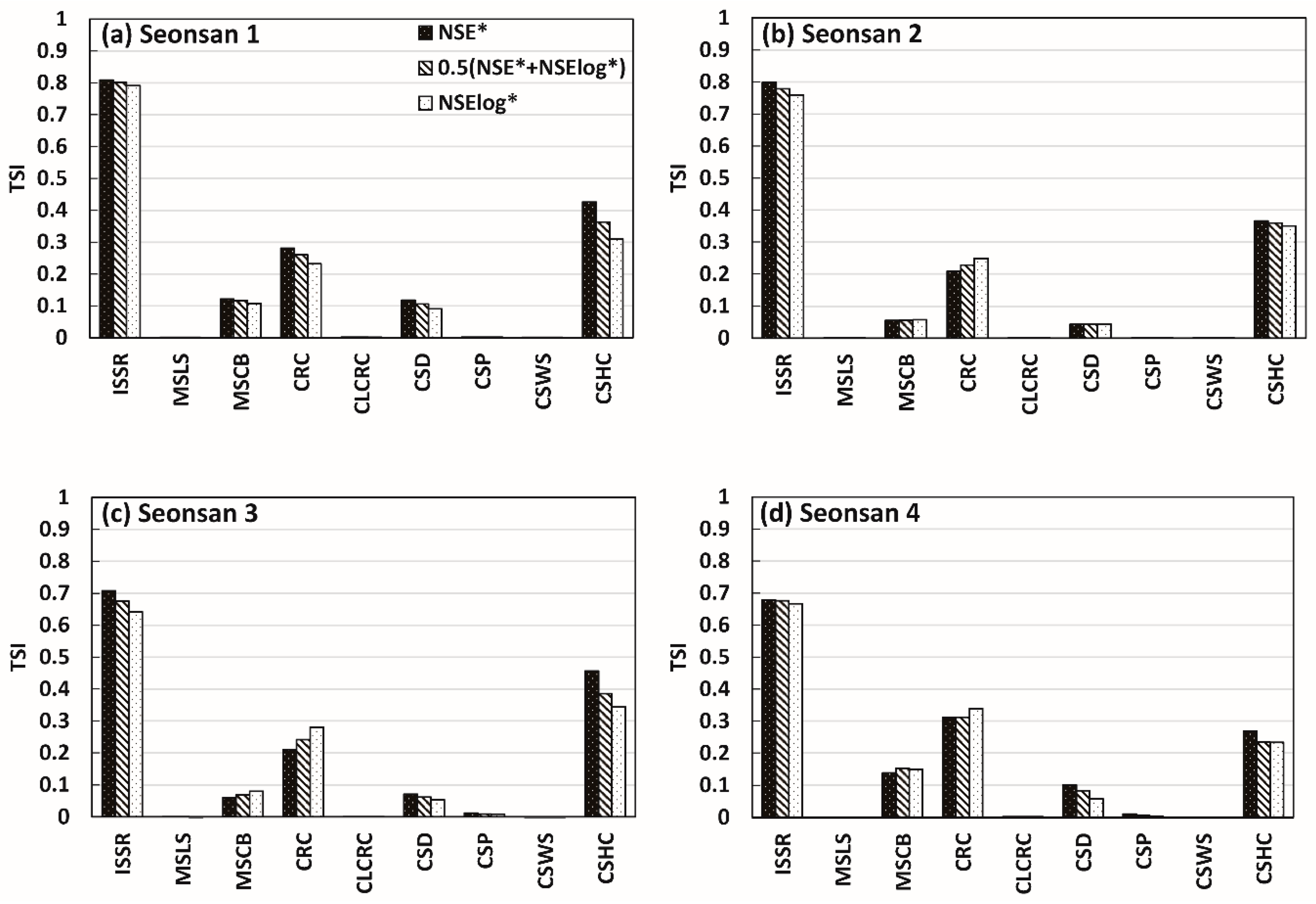
4.2. Parameter Sensitivity Analysis Reflecting Different Objective Functions
4.3. Parameter Sensitivity Analysis Reflecting Different Catchment Characteristics
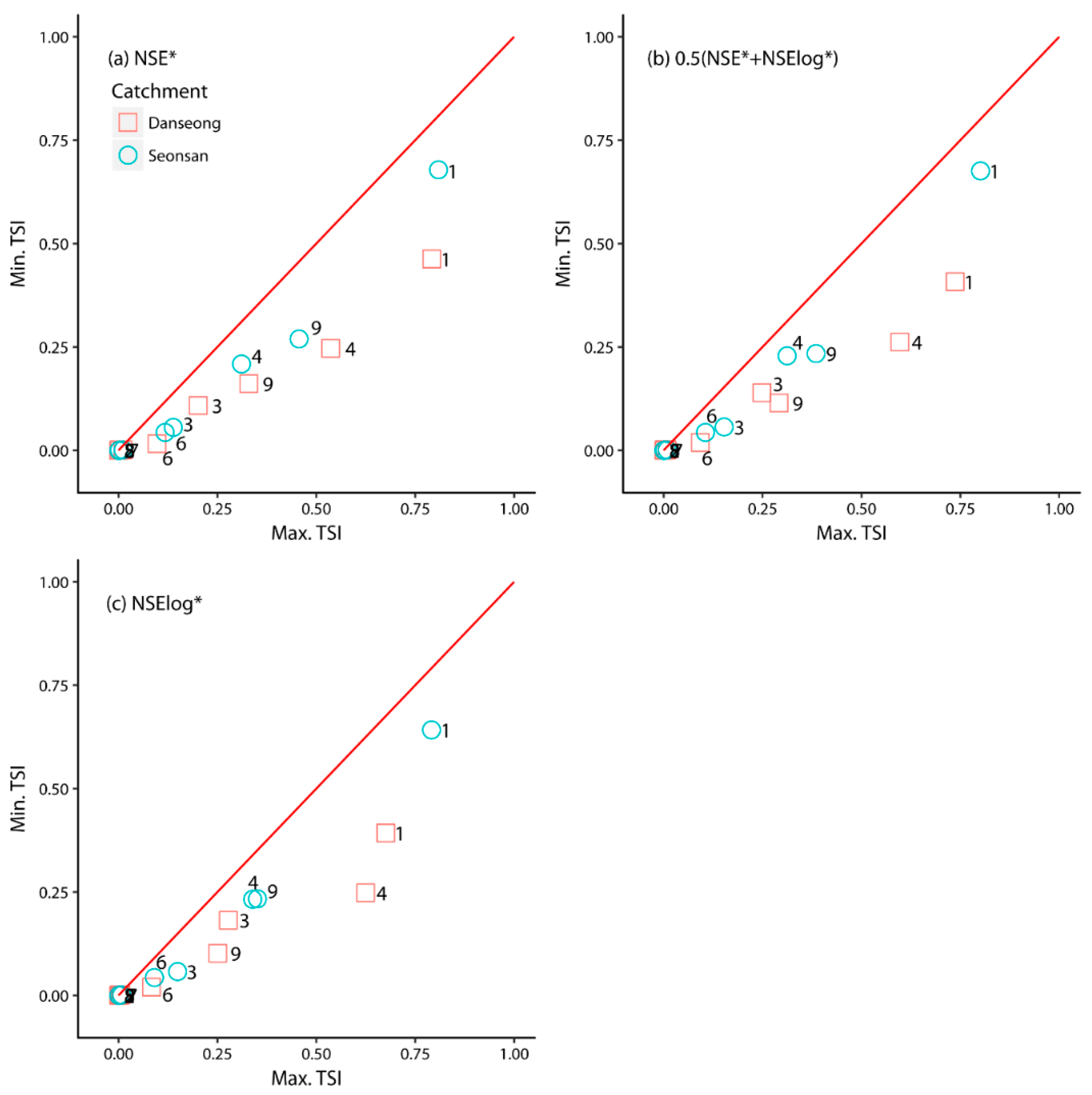
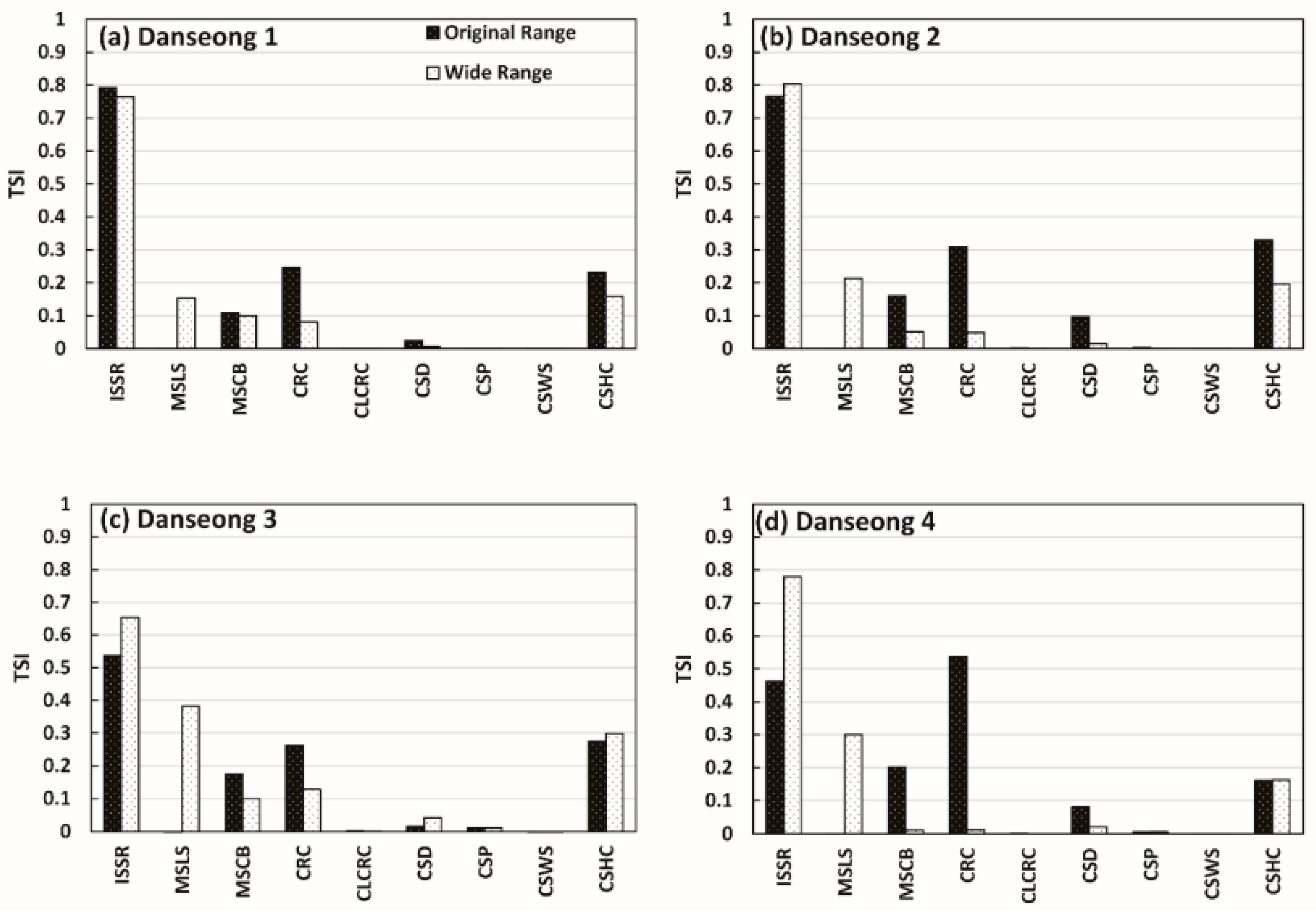
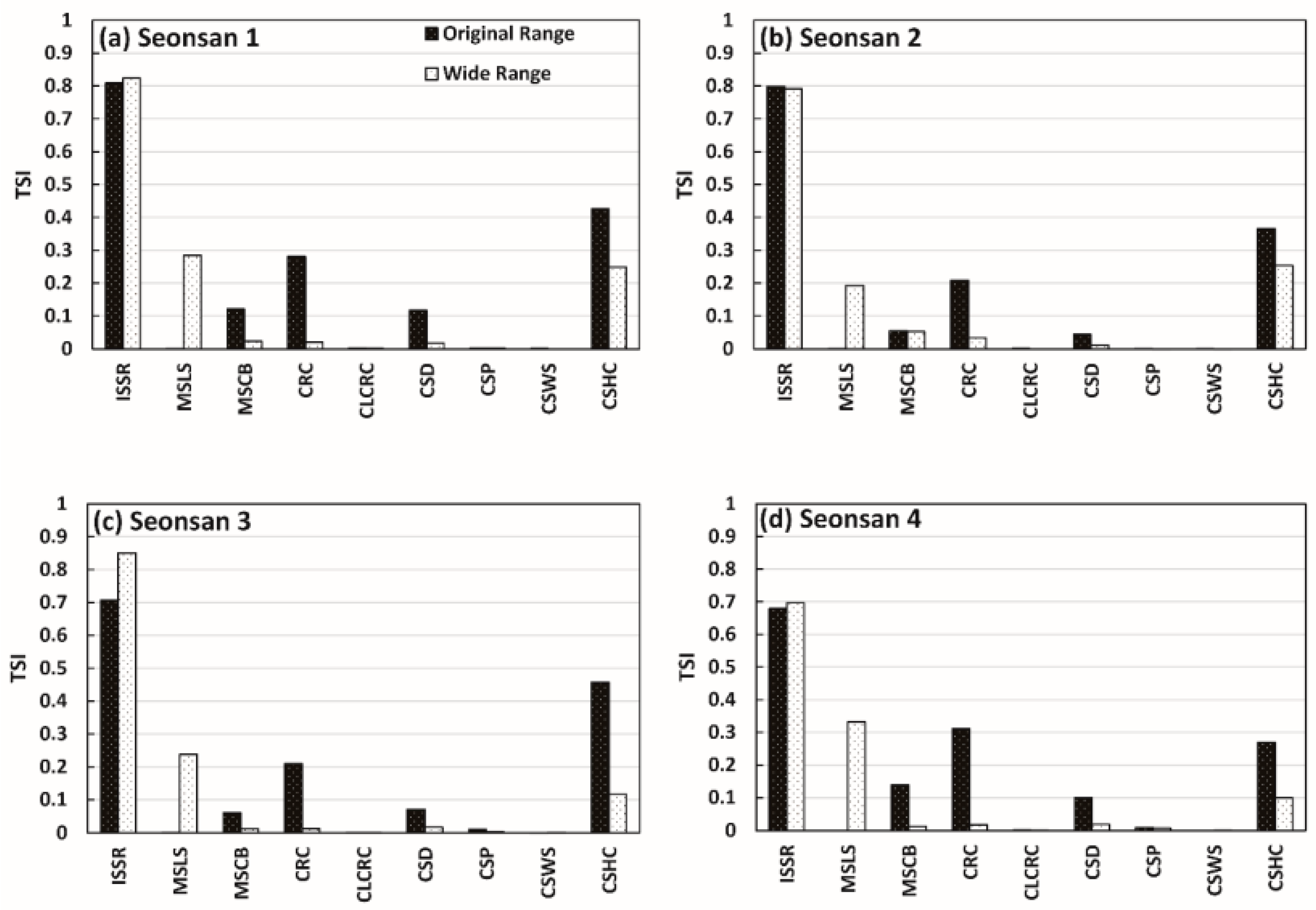
4.4. Effect of Parameter Range on Sensitivity
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Al-Qurashi, A.; McIntyre, N.; Wheater, H.; Unkrich, C. Application of the Kineros2 rainfall-runoff model to an arid catchment in Oman. J. Hydrol. 2008, 355, 91–105. [Google Scholar] [CrossRef]
- Herman, J.D.; Kollat, J.B.; Reed, P.M.; Wagener, T. Technical note: Method of morris effectively reduces the computational demands of global sensitivity analysis for distributed watershed models. Hydrol. Earth Syst. Sci. 2013, 17, 2893–2903. [Google Scholar] [CrossRef]
- Kannan, N.; White, S.M.; Worrall, F.; Whelan, M.J. Sensitivity analysis and identification of the best evapotranspiration and runoff options for hydrological modelling in SWAT-2000. J. Hydrol. 2007, 332, 456–466. [Google Scholar] [CrossRef]
- Wagener, T.; Van Werkhoven, K.; Reed, P.; Tang, Y. Multiobjective sensitivity analysis to understand the information content in streamflow observations for distributed watershed modeling. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- Chaubey, I.; Haan, C.T.; Grunwald, S.; Salisbury, J.M. Uncertainty in the model parameters due to spatial variability of rainfall. J. Hydrol. 1999, 220, 48–61. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Xie, S.; Xu, Y.; Xu, C.Y.; Singh, V.P. Development and testing of a simple physically-based distributed rainfall-runoff model for storm runoff simulation in humid forested basins. J. Hydrol. 2007, 336, 334–346. [Google Scholar] [CrossRef]
- Emmanuel, I.; Payrastre, O.; Andrieu, H.; Zuber, F. A method for assessing the influence of rainfall spatial variability on hydrograph modeling. First case study in the Cevennes Region, southern France. J. Hydrol. 2017, 555, 314–322. [Google Scholar] [CrossRef]
- Foglia, L.; Hill, M.C.; Mehl, S.W.; Burlando, P. Sensitivity analysis, calibration, and testing of a distributed hydrological model using error-based weighting and one objective function. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- Grayson, R.B.; Moore, I.D.; McMahon, T.A. Physically based hydrologic modeling: 1. A terrain-based model for investigative purposes. Water Resour. Res. 1992, 28, 2639–2658. [Google Scholar] [CrossRef]
- Jain, M.K.; Kothyari, U.C.; Raju, K.G.R. A GIS based distributed rainfall-runoff model. J. Hydrol. 2004, 299, 107–135. [Google Scholar] [CrossRef]
- Shah, S.M.S.; O’connell, P.E.; Hosking, J.R.M. Modelling the effects of spatial variability in rainfall on catchment response: 2. Experiments with distributed and lumped models. J. Hydrol. 1996, 175, 89–111. [Google Scholar] [CrossRef]
- Vansteenkiste, T.; Tavakoli, M.; Van Steenbergen, N.; De Smedt, F.; Batelaan, O.; Pereira, F.; Willems, P. Intercomparison of five lumped and distributed models for catchment runoff and extreme flow simulation. J. Hydrol. 2014, 511, 335–349. [Google Scholar] [CrossRef]
- Zhang, L.; Nan, Z.; Liang, X.; Xu, Y.; Hernández, F.; Li, L. Application of the MacCormack scheme to overland flow routing for high-spatial resolution distributed hydrological model. J. Hydrol. 2018, 558, 421–431. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. A dynamic top model. Hydrol. Process. 2001, 15, 1993–2011. [Google Scholar] [CrossRef]
- Choi, Y.S.; Choi, C.K.; Kim, H.S.; Kim, K.T.; Kim, S. Multi-site calibration using a grid-based event rainfallrunoff model: A case study of the upstream areas of the Nakdong River basin in Korea. Hydrol. Process. 2015, 29, 2089–2099. [Google Scholar] [CrossRef]
- Choi, Y.; Shin, M.-J.; Kim, K. Preliminary study of computational time steps in a physically based distributed rainfall-runoff model. Water 2018, 10, 1269. [Google Scholar] [CrossRef]
- Shin, M.-J.; Choi, Y. Combining an r-based evolutionary algorithm and hydrological model for effective parameter calibration. Water 2018, 10, 1339. [Google Scholar] [CrossRef]
- Abebe, N.A.; Ogden, F.L.; Pradhan, N.R. Sensitivity and uncertainty analysis of the conceptual HBV rainfall-runoff model: Implications for parameter estimation. J. Hydrol. 2010, 389, 301–310. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European hydrological system—Systeme hydrologique Europeen, “SHE”, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Bagarello, V.; Ferro, V.; Keesstra, S.; Comino, J.R.; Pulido, M.; Cerdà, A. Testing simple scaling in soil erosion processes at plot scale. Catena 2018, 167, 171–180. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modeling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Storm, B. Construction, Calibration and Validation of Hydrological Models. In Distributed Hydrological Modeling; Abbott, M.B., Refsgaard, J.C., Eds.; Kluwer Academic Publishers: Dordrecht, the Netherlands, 1996; pp. 41–54. [Google Scholar]
- Sahoo, G.B.; Ray, C.; De Carlo, E.H. Calibration and validation of a physically distributed hydrological model, MIKE SHE, to predict streamflow at high frequency in a flashy mountainous Hawaii stream. J. Hydrol. 2006, 327, 94–109. [Google Scholar] [CrossRef]
- Vieux, B.E. Distributed Hydrologic Modeling Using GIS; Kluwer Academic Publishers: Dordrecht, the Netherlands, 2004; pp. 197–215. [Google Scholar]
- Shin, M.-J.; Guillaume, J.H.A.; Croke, B.F.W.; Jakeman, A.J. A review of foundational methods for checking the structural identifiability of models: Results for rainfall-runoff. J. Hydrol. 2015, 520, 1–16. [Google Scholar] [CrossRef]
- Beven, K. Prophecy, reality and uncertainty in distributed hydrological modelling. Adv. Water Resour. 1993, 16, 41–51. [Google Scholar] [CrossRef]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Shao, Q.; Xu, Z.; Cai, X. Analysis of parameter uncertainty in semi-distributed hydrological models using bootstrap method: A case study of SWAT model applied to Yingluoxia watershed in northwest China. J. Hydrol. 2010, 385, 76–83. [Google Scholar] [CrossRef]
- Sieber, A.; Uhlenbrook, S. Sensitivity analyses of a distributed catchment model to verify the model structure. J. Hydrol. 2005, 310, 216–235. [Google Scholar] [CrossRef]
- Tang, Y.; Reed, P.; Van Werkhoven, K.; Wagener, T. Advancing the identification and evaluation of distributed rainfall-runoff models using global sensitivity analysis. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef] [Green Version]
- Lenhart, T.; Eckhardt, K.; Fohrer, N.; Frede, H.G. Comparison of two different approaches of sensitivity analysis. Phys. Chem. Earth. Pts. A/B/C 2002, 27, 645–654. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity analysis for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Spear, R.C.; Hornberger, G.M. Eutrophication in Peel Inlet-II. Identification of critical uncertainties via generalized sensitivity analysis. Water Res. 1980, 14, 43–49. [Google Scholar] [CrossRef]
- Zhang, C.; Chu, J.; Fu, G. Sobol’s sensitivity analysis for a distributed hydrological model of Yichun River Basin, China. J. Hydrol. 2013, 480, 58–68. [Google Scholar] [CrossRef]
- Choi, Y.S.; Kim, K.T. Grid based rainfall-runoff model user’s manual. Korea Inst. Civ. Eng. Build. Technol. Gyeonggi-do, Korea, 2017; pp. 1–21. Available online: https://github.com/floodmodel/GRM (accessed on 20 April 2018).
- Cuntz, M.; Mai, J.; Zink, M.; Thober, S.; Kumar, R.; Schäfer, D.; Schron, M.; Craven, J.; Rakovec, O.; Spieler, D.; et al. Computationally inexpensive identification of noninformative model parameters by sequential screening. Water Resour. Res. 2015, 51, 6417–6441. [Google Scholar] [CrossRef] [Green Version]
- Jepsen, S.M.; Harmon, T.C.; Ficklin, D.L.; Molotch, N.P.; Guan, B. Evapotranspiration sensitivity to air temperature across a snow-influenced watershed: Space-for-time substitution versus integrated watershed modeling. J. Hydrol. 2018, 556, 645–659. [Google Scholar] [CrossRef]
- Massmann, C.; Holzmann, H. Analysis of the behavior of a rainfall-runoff model using three global sensitivity analysis methods evaluated at different temporal scales. J. Hydrol. 2012, 475, 97–110. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Modell. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Rakovec, O.; Hill, M.C.; Clark, M.P.; Weerts, A.H.; Teuling, A.J.; Uijlenhoet, R. Distributed evaluation of local sensitivity analysis (DELSA), with application to hydrologic models. Water Resour. Res. 2014, 50, 409–426. [Google Scholar] [CrossRef]
- Sarrazin, F.; Pianosi, F.; Wagener, T. Global sensitivity analysis of environmental models: Convergence and validation. Environ. Modell. Softw. 2016, 79, 135–152. [Google Scholar] [CrossRef]
- Shin, M.-J.; Kim, C.S. Assessment of the suitability of rainfall-runoff models by coupling performance statistics and sensitivity analysis. Hydrol. Res. 2017, 48, 1192–1213. [Google Scholar] [CrossRef]
- Saltelli, A.; Chan, K.; Scott, E.M. Sensitivity Analysis; Wiley: New York, NJ, USA, 2008. [Google Scholar]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis? Environ. Modell. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Shin, M.-J.; Guillaume, J.H.A.; Croke, B.F.W.; Jakeman, A.J. Addressing ten questions about conceptual rainfall-runoff models with global sensitivity analyses in R. J. Hydrol. 2013, 503, 135–152. [Google Scholar] [CrossRef]
- Pujol, G.; Iooss, B.; Janon, A. Package ‘sensitivity’: Sensitivity Analysis. R package version 1.15.2. 2018. Available online: http://cran.r-project.org/package=sensitivity (accessed on 2 September 2018).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I––A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Oudin, L.; Andr-assian, V.; Mathevet, T.; Perrin, C.; Michel, C. Dynamic averaging of rainfall-runoff model simulations from complementary model parameterizations. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef] [Green Version]
- Mathevet, T.; Michel, C.; Andréassian, V.; Perrin, C. A Bounded Version of the Nash-Sutcliffe Criterion for Better Model Assessment on Large Sets of Basins. In Large Sample Basin Experiments for Hydrological Model Parameterization: Results of the Model Parameter Experiment—MOPEX; IAHS (International Association of Hydrological Sciences) Publications: London, UK, 2006; Volume 307, pp. 211–219. [Google Scholar]
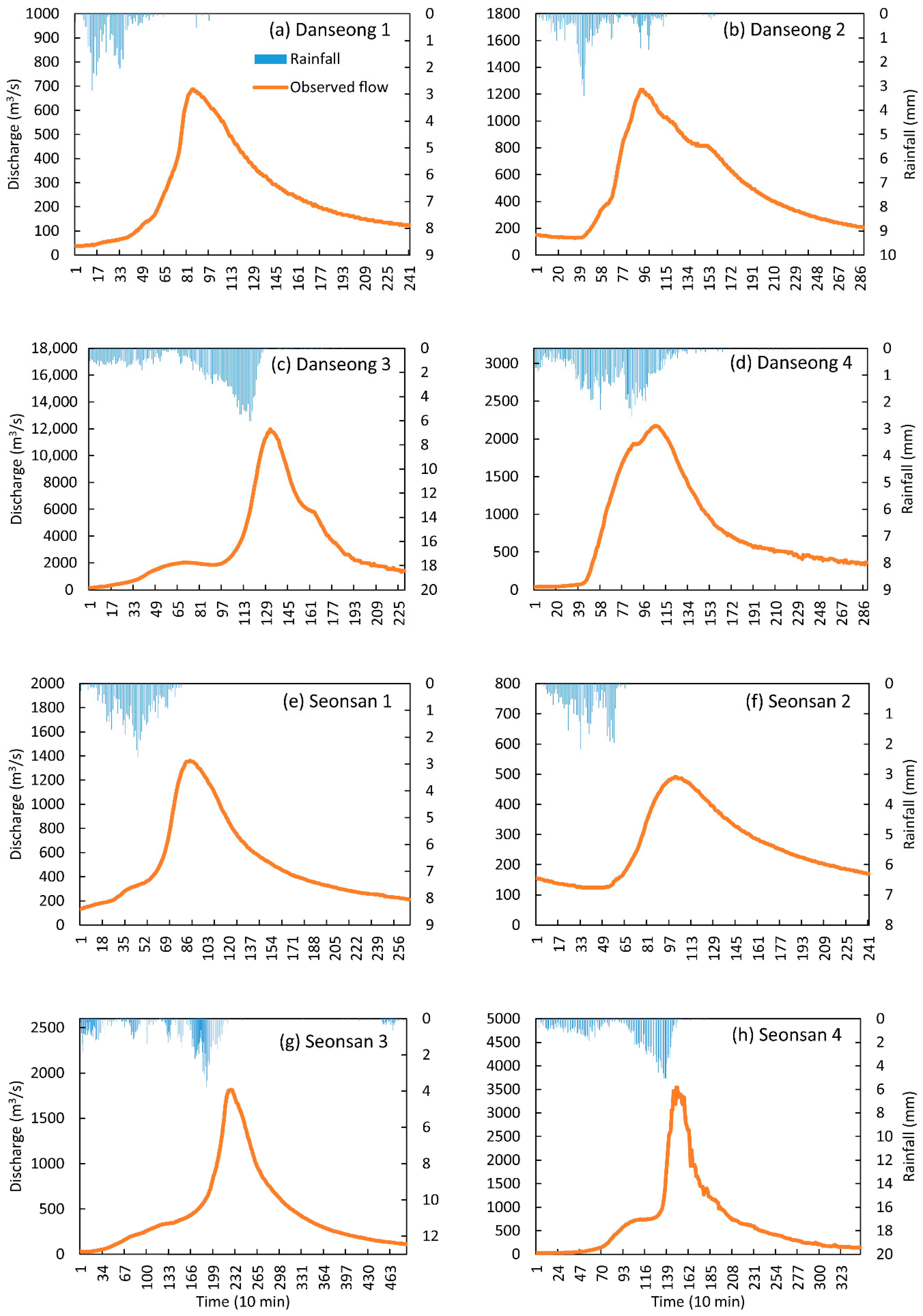
| Catchment | Event Number | Periods | Rainfall (mm) | Peak Flow (m3/s) |
|---|---|---|---|---|
| Danseong | 1 | 2011.07.03, 20:00– 2011.07.05, 12:00 | 43 | 687 |
| 2 | 2012.07.14, 15:00– 2012.07.16, 15:00 | 63 | 1232 | |
| 3 | 2012.09.16, 17:00– 2012.09.18, 07:00 | 225 | 11,970 | |
| 4 | 2015.07.12, 01:00– 2015.07.14, 01:00 | 123 | 2173 | |
| Seonsan | 1 | 2010.08.11, 00:00– 2010.08.12, 20:00 | 66 | 1361 |
| 2 | 2010.09.01, 20:00– 2010.09.03, 12:00 | 43 | 491 | |
| 3 | 2011.07.09, 11:00– 2011.07.12, 20:00 | 154 | 1814 | |
| 4 | 2012.09.16, 15:00– 2012.09.19, 00:00 | 198 | 3542 |
| Number | Parameter | Lower | Upper | Unit | Description |
|---|---|---|---|---|---|
| 1 | ISSR | 0 | 1 | - | Initial soil saturation ratio |
| 2 | MSLS | 0.0001 | 0.01 | - | Minimum slope of land surface |
| 3 | MSCB | 0.0001 | 0.01 | - | Minimum slope of channel bed |
| 4 | CRC | 0.008 | 0.2 | - | Channel roughness coefficient |
| 5 | CLCRC | 0.6 | 1.3 | - | Correction factor for land cover roughness coefficient |
| 6 | CSD | 0.8 | 1.2 | - | Correction factor for soil depth |
| 7 | CSP | 0.9 | 1.1 | - | Correction factor for soil porosity |
| 8 | CSWS | 0.25 | 4 | - | Correction factor for soil wetting front suction head |
| 9 | CSHC | 0.05 | 20 | - | Correction factor for soil hydraulic conductivity |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, M.-J.; Choi, Y.S. Sensitivity Analysis to Investigate the Reliability of the Grid-Based Rainfall-Runoff Model. Water 2018, 10, 1839. https://doi.org/10.3390/w10121839
Shin M-J, Choi YS. Sensitivity Analysis to Investigate the Reliability of the Grid-Based Rainfall-Runoff Model. Water. 2018; 10(12):1839. https://doi.org/10.3390/w10121839
Chicago/Turabian StyleShin, Mun-Ju, and Yun Seok Choi. 2018. "Sensitivity Analysis to Investigate the Reliability of the Grid-Based Rainfall-Runoff Model" Water 10, no. 12: 1839. https://doi.org/10.3390/w10121839
APA StyleShin, M.-J., & Choi, Y. S. (2018). Sensitivity Analysis to Investigate the Reliability of the Grid-Based Rainfall-Runoff Model. Water, 10(12), 1839. https://doi.org/10.3390/w10121839





