Flow Velocity Distribution Towards Flowmeter Accuracy: CFD, UDV, and Field Tests
Abstract
1. Introduction
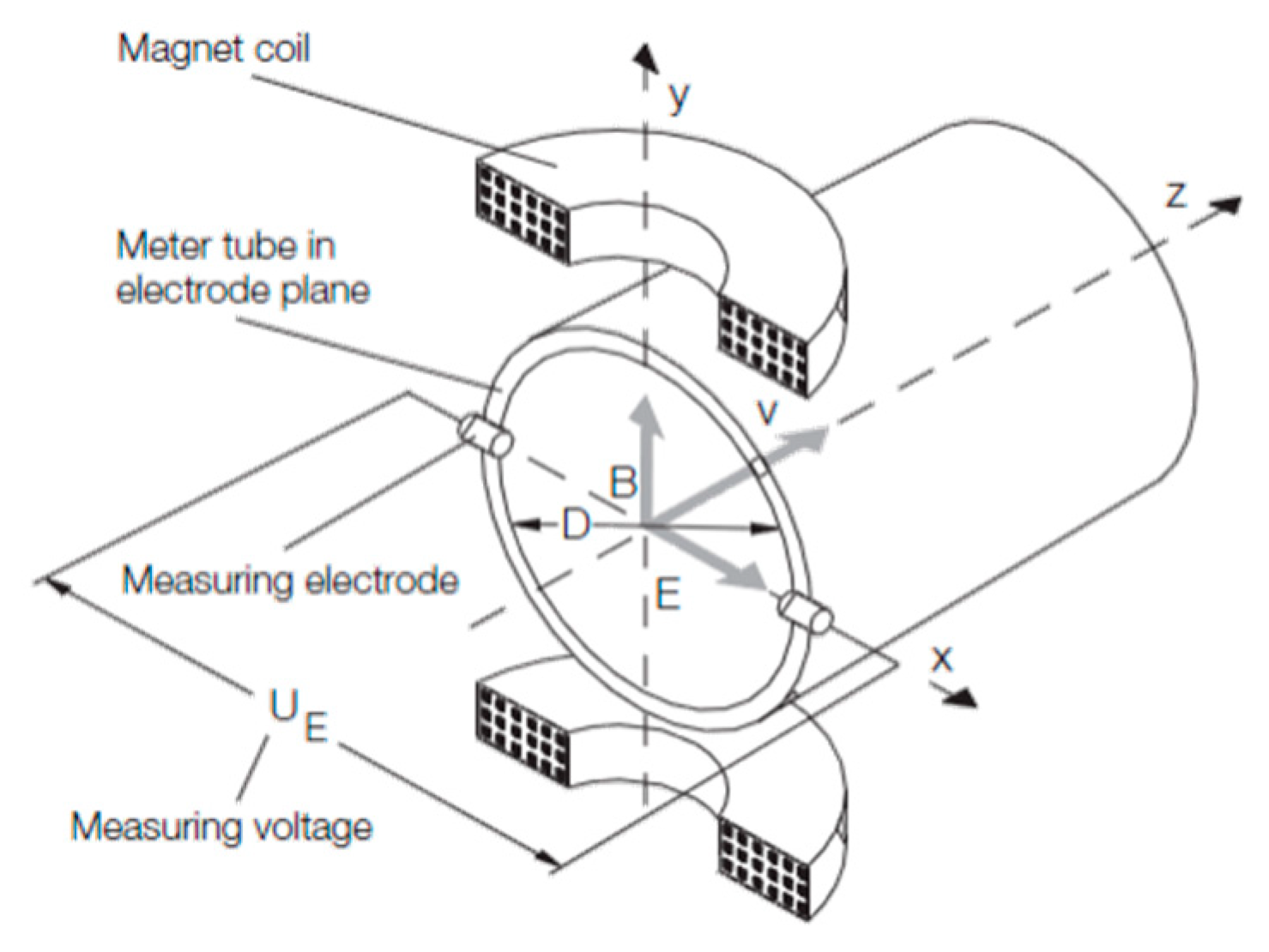
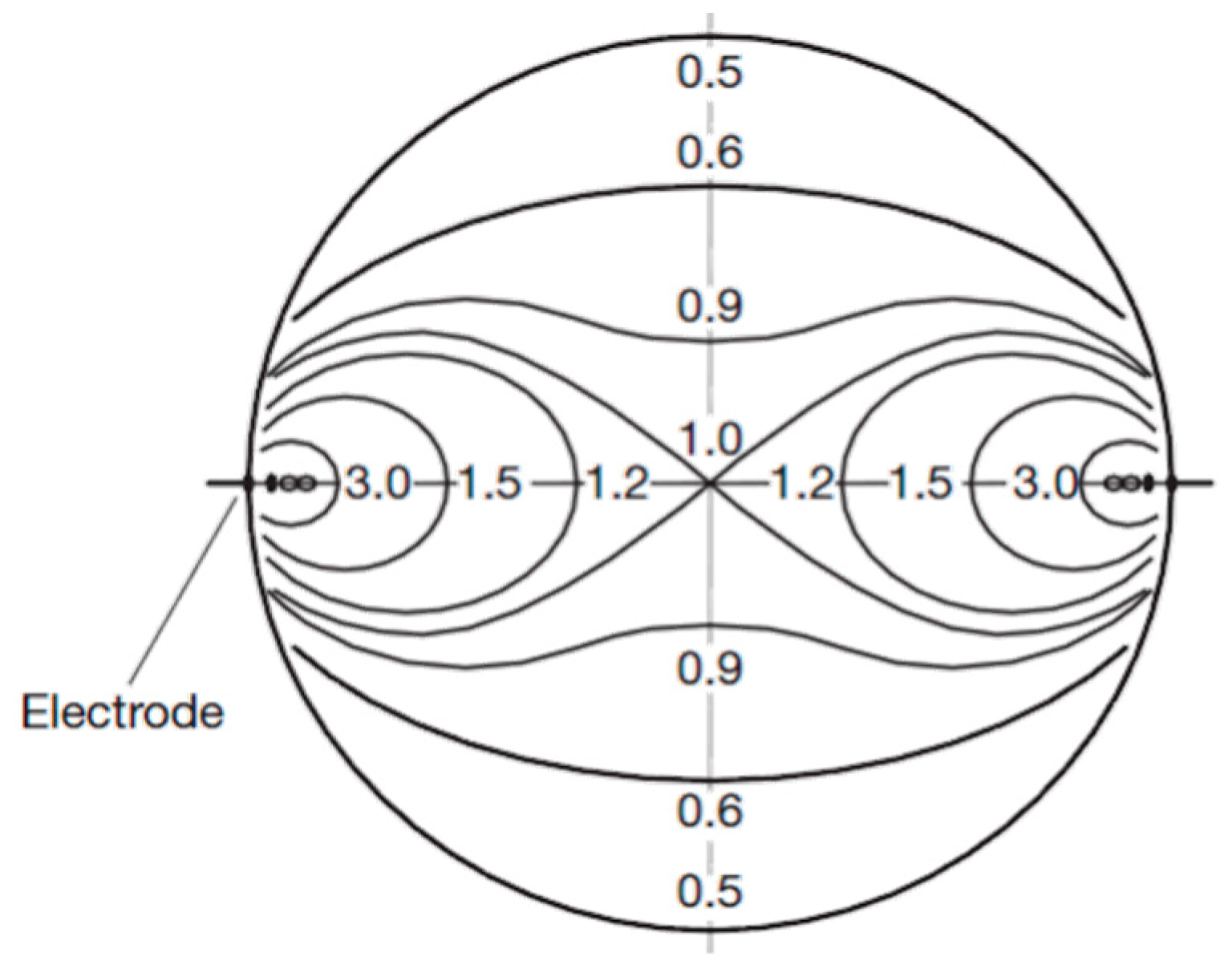
2. Electromagnetic Flowmeters
3. Equipment and Layout
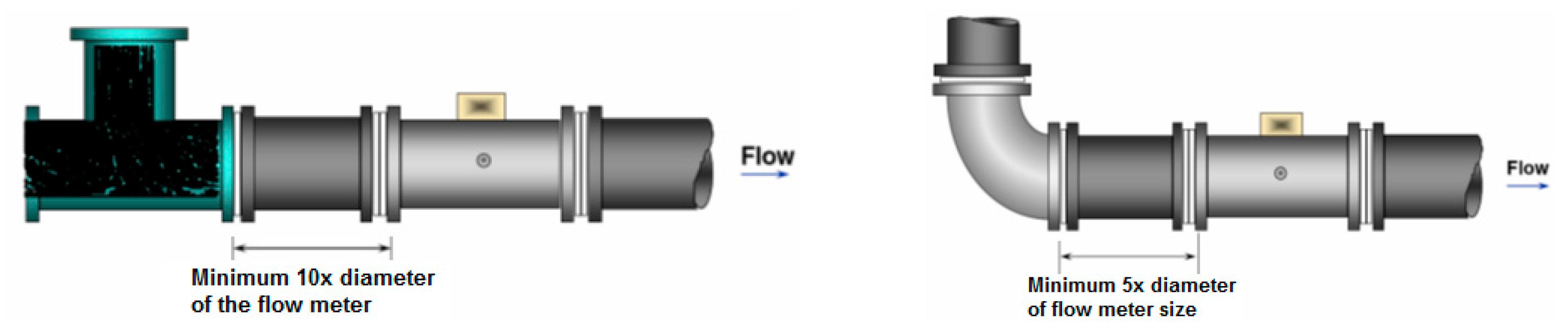
3.1. Flow Meter Installation
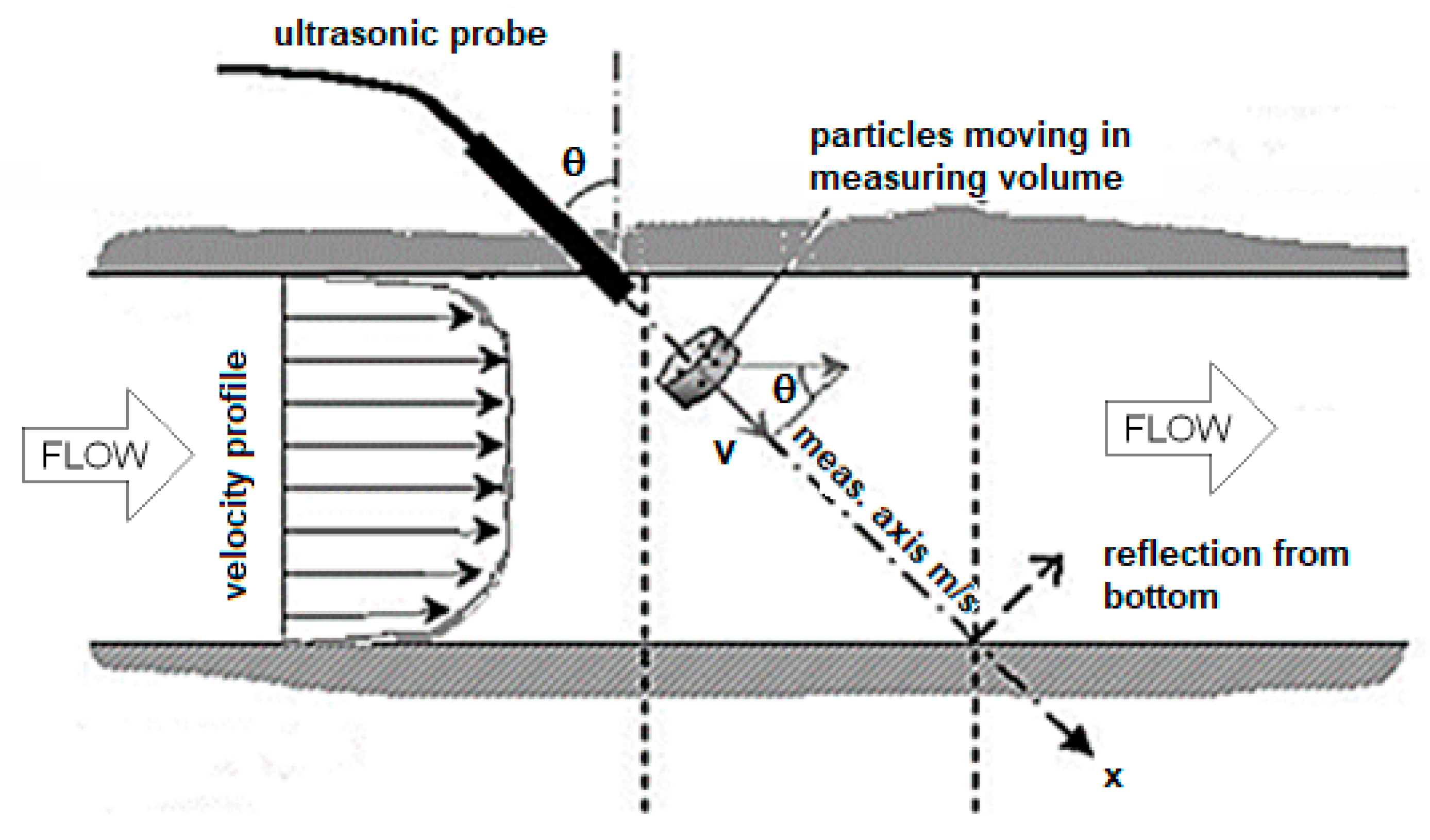
3.2. UDV Installation
3.3. Experimental Facility
4. CFD Model
4.1. Governing Equations
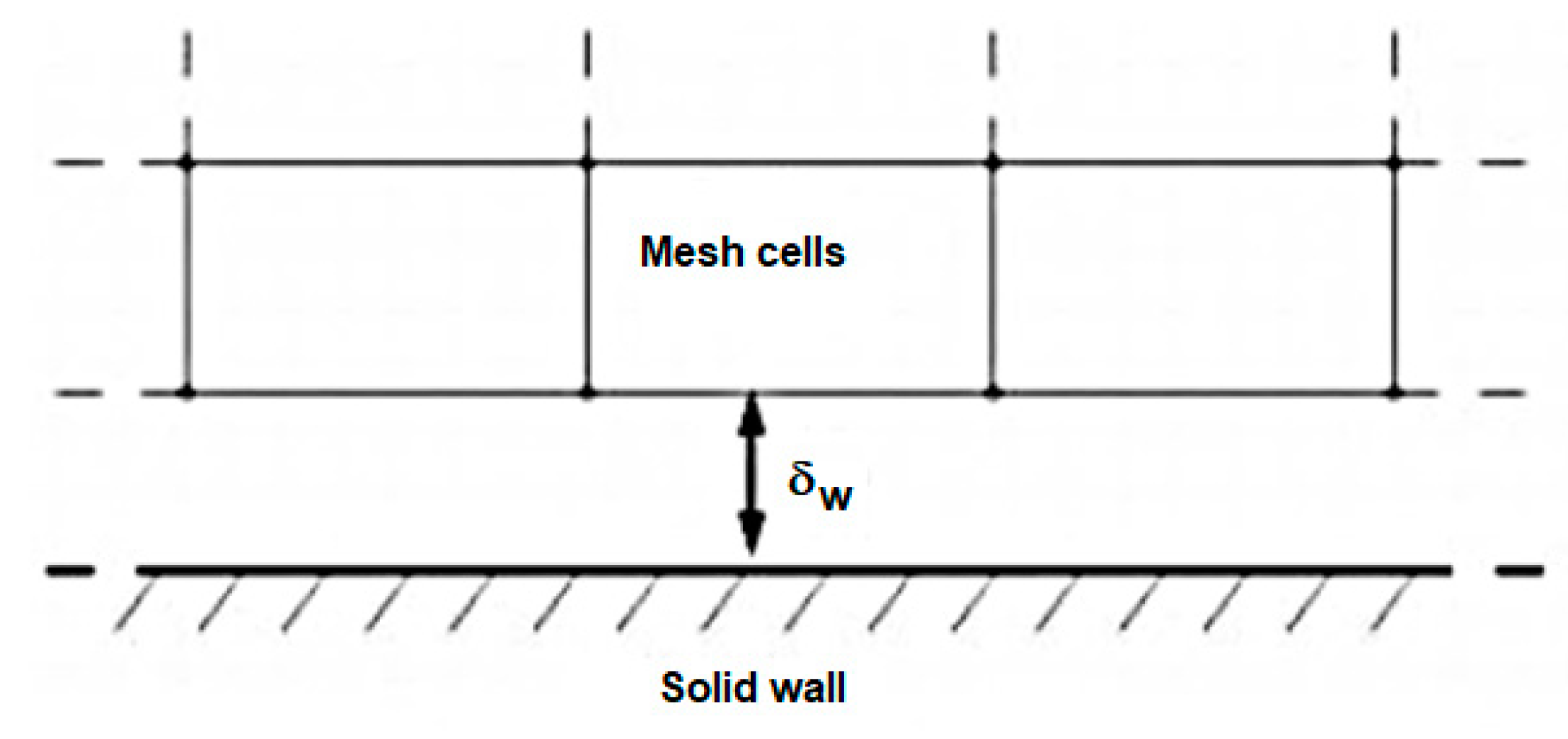
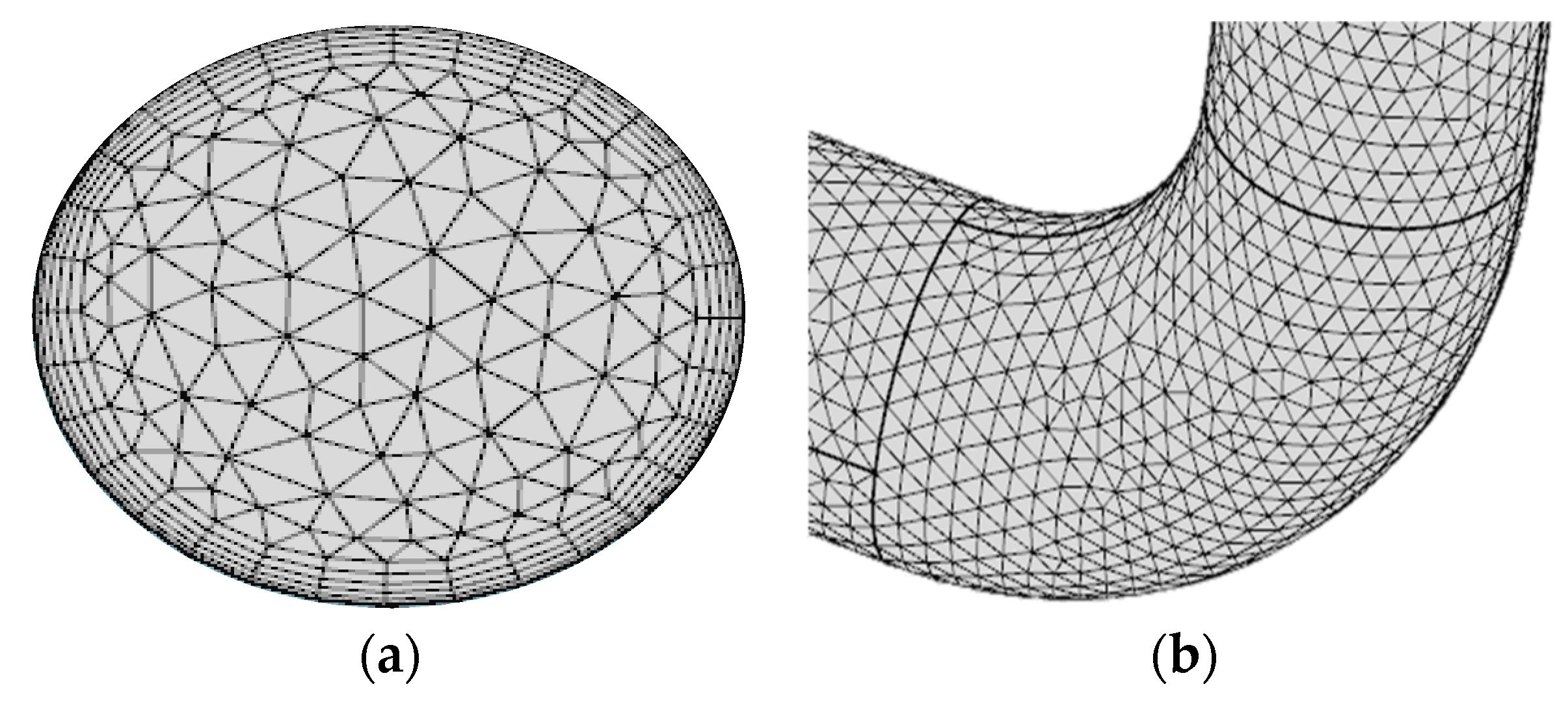
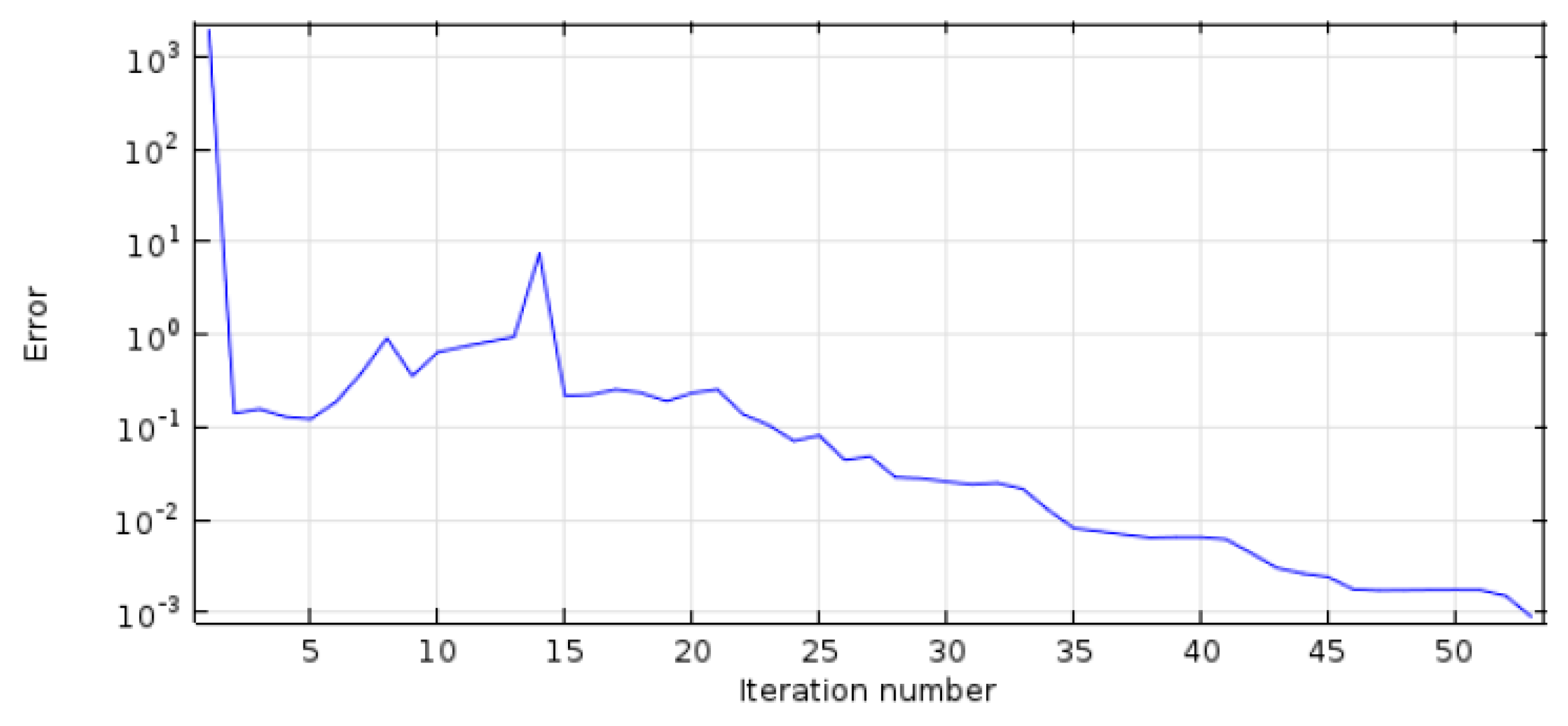
4.2. Mesh Definition and Solution Convergence
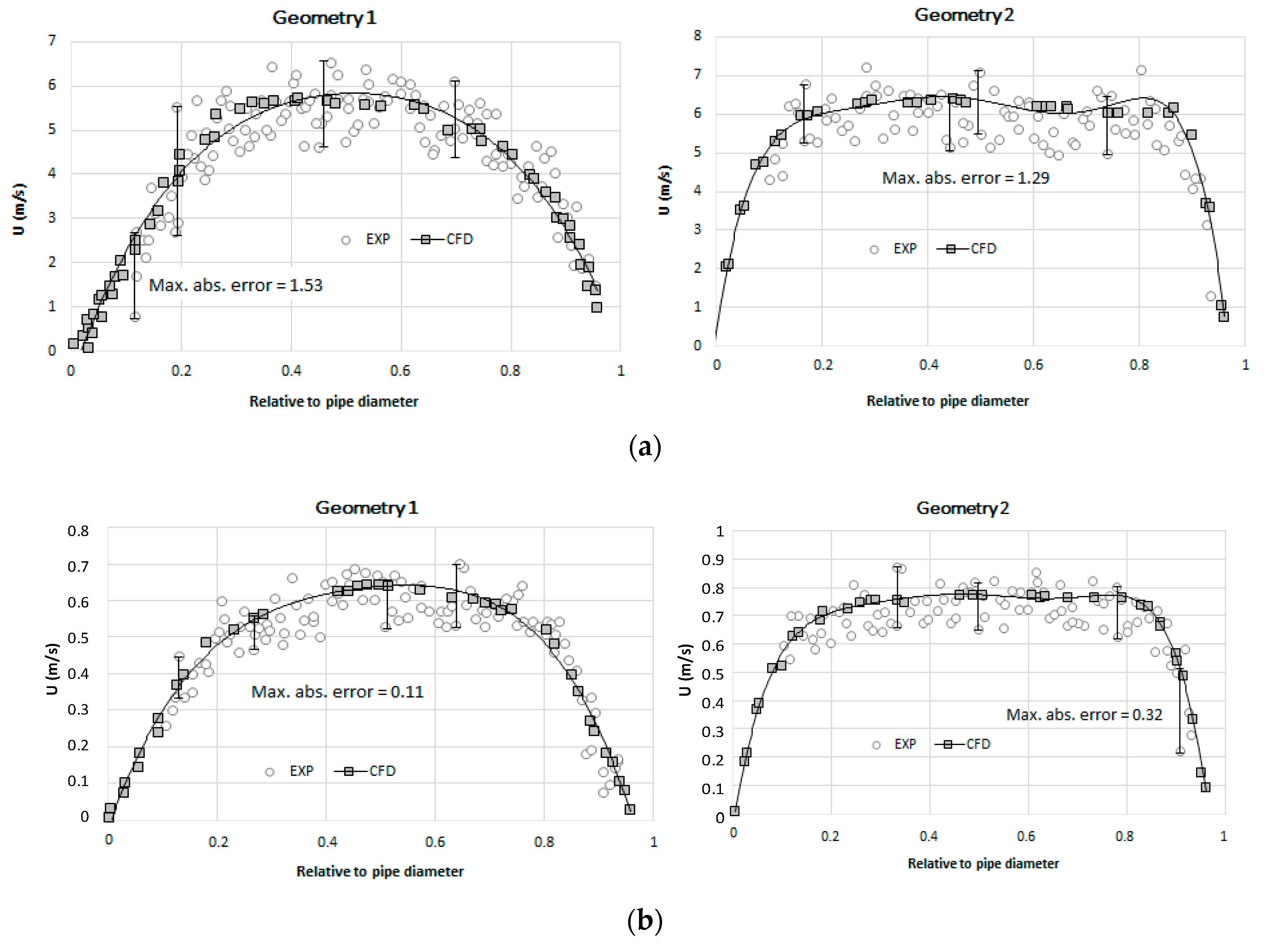
4.3. Calibration and Validation
5. Case Study
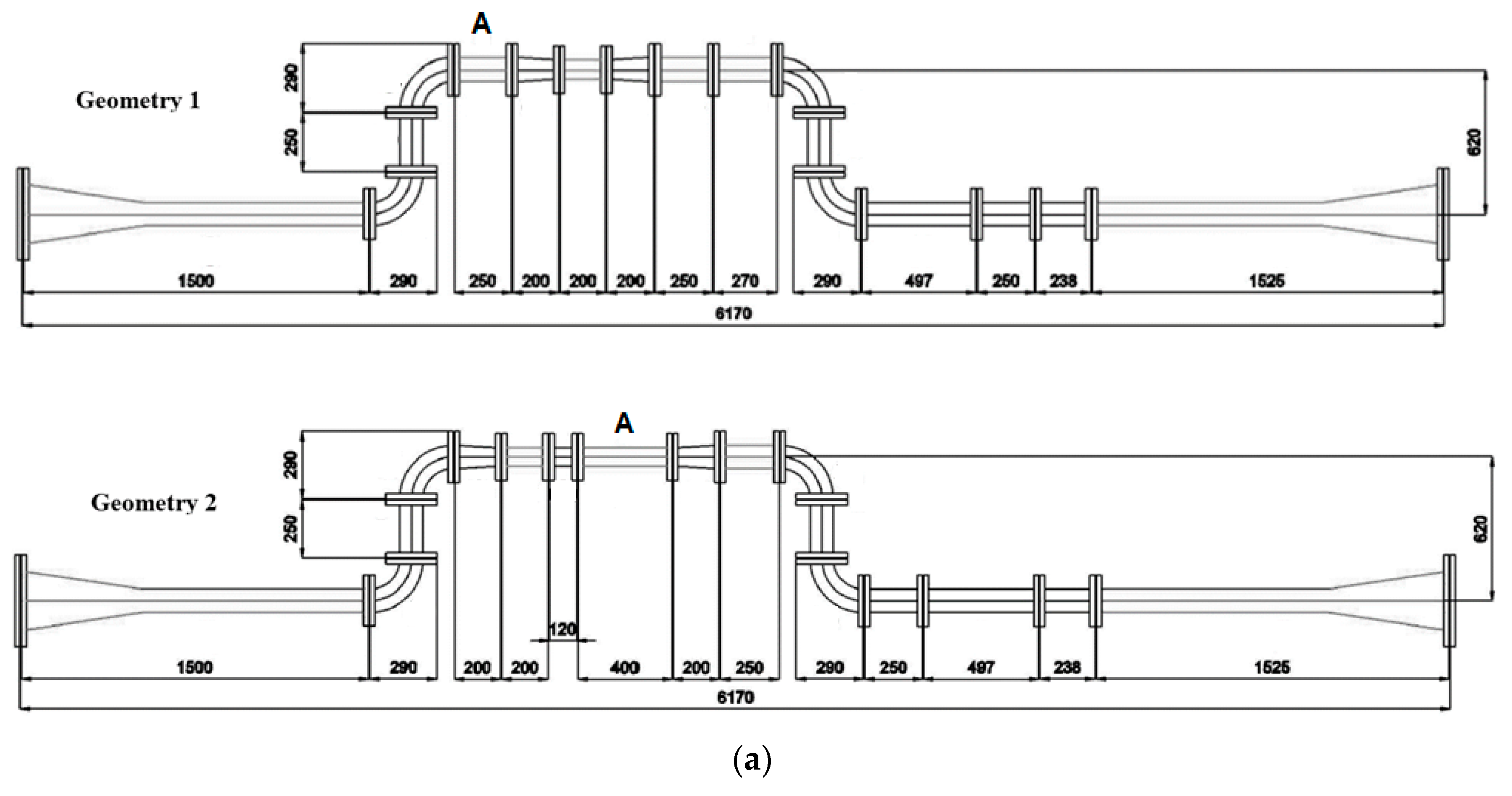
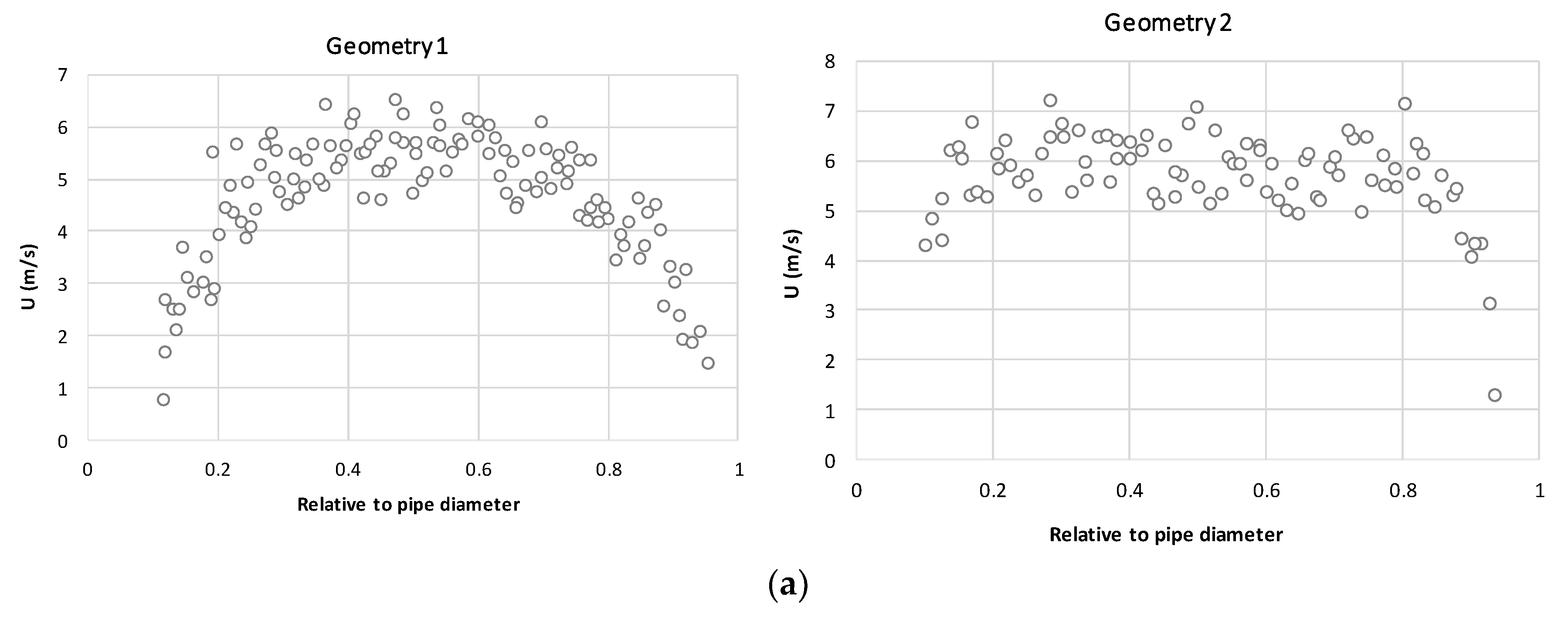
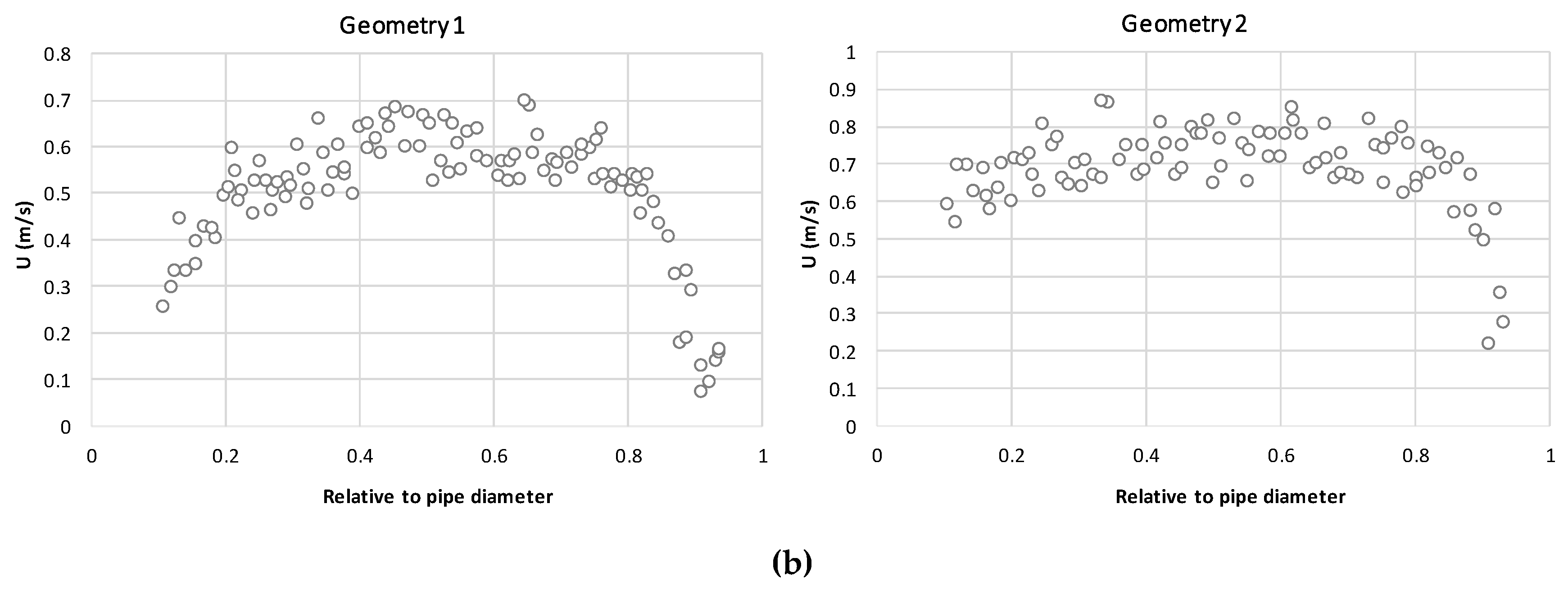
5.1. Geometry Layout
5.2. Simulations
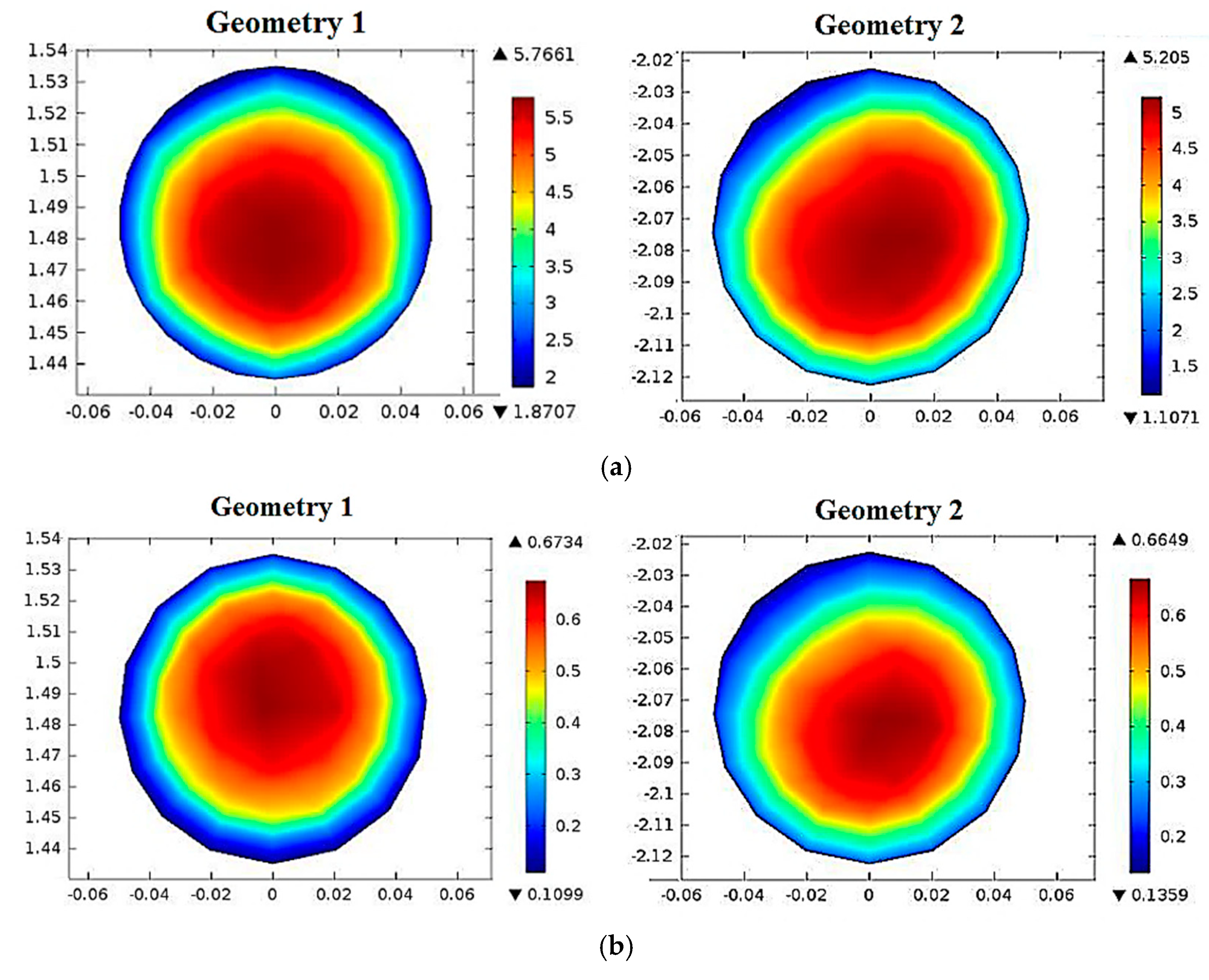
5.3. Solution
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Frenzel, F.; Grothey, H.; Habersetzer, C.; Hiatt, M.; Hogrefe, W.; Kirchner, M.; Lütkepohl, G.; Marchewka, W.; Mecke, U.; Ohm, M.; et al. Industrial Flow Measurement Basics and Practice; ABB Automation Products GmbH: Gottingen, Germany, 2011. [Google Scholar]
- Sheng, H.; Lihui, P.; Nakazato, H. Computational fluid dynamics based sound path optimization for ultrasonic flow meter. Chin. J. Sci. Instrum. 2009, 30, 852–856. [Google Scholar]
- Cardoso, A.H. Hidráulica Geral I—Apontamentos Complementares das Aulas Teóricas; IST: Lisboa, Portugal, 2009. [Google Scholar]
- Lysak, P.D.; Jenkins, D.M.; Capone, D.E.; Brown, W.L. Analytical model of an ultrasonic cross-correlation flow meter, part 1: Stochastic modeling of turbulence. Flow Meas. Instrum. 2008, 19, 41–46. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Quintela, A.C. Hidráulica; Fundação Calouste Gulbenkian: Lisboa, Portugal, 2002. [Google Scholar]
- Matas, R.; Cibera, V.; Syka, T. Modelling of flow in pipes and ultrasonic flowmeter bodies. EPJ Web Conf. 2014, 67, 02073. [Google Scholar] [CrossRef]
- EN 14154-2. Water Meters—Part 2: Installation and Conditions of Use; NSAI: Dublin, Ireland, 2005. [Google Scholar]
- EN 14154-3. Water Meters—Part 3: Test Methods and Equipment; NSAI: Dublin, Ireland, 2005. [Google Scholar]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics; Springer: Berlin, Germany, 1991. [Google Scholar]
- Brunone, B.; Berni, A. Wall shear stress in transient turbulent pipe flow by local velocity measurement. J. Hydraul. Eng. ASCE 2010, 136, 716–726. [Google Scholar] [CrossRef]
- UVP Monitor –User’s Guide” Model UVP-DUO with Software Version 3, Met-Flow. 2014.
- Hammoudia, M.; Legrand, J.; Si-Ahmeda, E.K.; Salem, A. Flow analysis by pulsed ultrasonic velocimetry technique in Sulzer SMX static mixer. Chem. Eng. J. 2008, 139, 562–574. [Google Scholar] [CrossRef]
- Haavisto, S.; Syrjnen, J.; Koponen, A.; Mannien, M. UDV Measurements and CFD Simulation of Two-Phase Flow in a Stirred Vessel. In Proceedings of the 6th International Conference on CFD in Oil & Gas, Metallurgical and Process Industries, Trondheim, Norway, 10–12 June 2008. [Google Scholar]
- Georgescu, A.; Bernad, S.; Georgescu, S.-C.; CoSoiu, I. COMSOL Multiphysics versus FLUENT: 2D numerical simulation of the stationary flow arround a blade of the achard turbine. In Proceedings of the 3rd Workshop on Vortex Dominated Flows, Timisoara, Romania, 1–2 June 2007. [Google Scholar]
- COMSOL 4.3. COMSOL Multiphysics Reference Guide; COMSOL AB: Stockholm, Sweden, 2012. [Google Scholar]
- Speziale, C.G. On nonlinear k-l and k-ε models of turbulence. J. Fluid Mech. 1987, 178, 459–475. [Google Scholar] [CrossRef]
- Simão, M. Fluid-Structure Interaction in Pressurized Systems. Ph.D. Thesis, Insituto Superior Técnico, Universidade de Lisboa, Lisboa, Portugal, 2017. [Google Scholar]
- Gresho, P.M. Incompressible Fluid Dynamics: Some Fundamental Formulation Issues. Ann. Rev. Fluid Mech. 1991, 23, 413–453. [Google Scholar] [CrossRef]
- Prandtl, L. Guide à Traves de la Méchanique dês Fluides; Dunod: Paris, France, 1952. [Google Scholar]
- Lumley, J.L. Computational modelling of turbulent flows. Adv. Appl. Mech. 1978, 18, 123–176. [Google Scholar]
- Lumley, J.L. Some comments on turbulence. Phys. Fluids A 1992, 4, 203–211. [Google Scholar] [CrossRef]
- COMSOL 4.3. COMSOL Multiphysics User’s Guide; COMSOL AB: Stockholm, Sweden, 2012. [Google Scholar]
- Bakewell, H.P.; Lumley, J.L. Viscous sublayer and adjacent wall region in the turbulent pipe flow. Phys. Fluids 1967, 10, 1880–1889. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education Limited: London, UK, 2007. [Google Scholar]
- Çengel, Y.A.; Cimbala, J.M. Fluid Mechanics—Fundamentals and Applications; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Abbott, M.B.; Basco, D.R. Computational Fluid Dynamics—An Introduction of Engineers; Longman Scientific & Technical: Harlow, UK, 1989. [Google Scholar]
- Wosnik, M.; Castillo, L.; George, W.K. A theory for turbulent pipe and channel flows. J. Fluid Mech. 2000, 421, 115–145. [Google Scholar] [CrossRef]
- Braga, F.; Fernandes, M. Analise de Eventuais Perdas na rede de Adução da EPAL: Casos de Estudo; EPAL: Lisboa, Portugal, 2009. [Google Scholar]





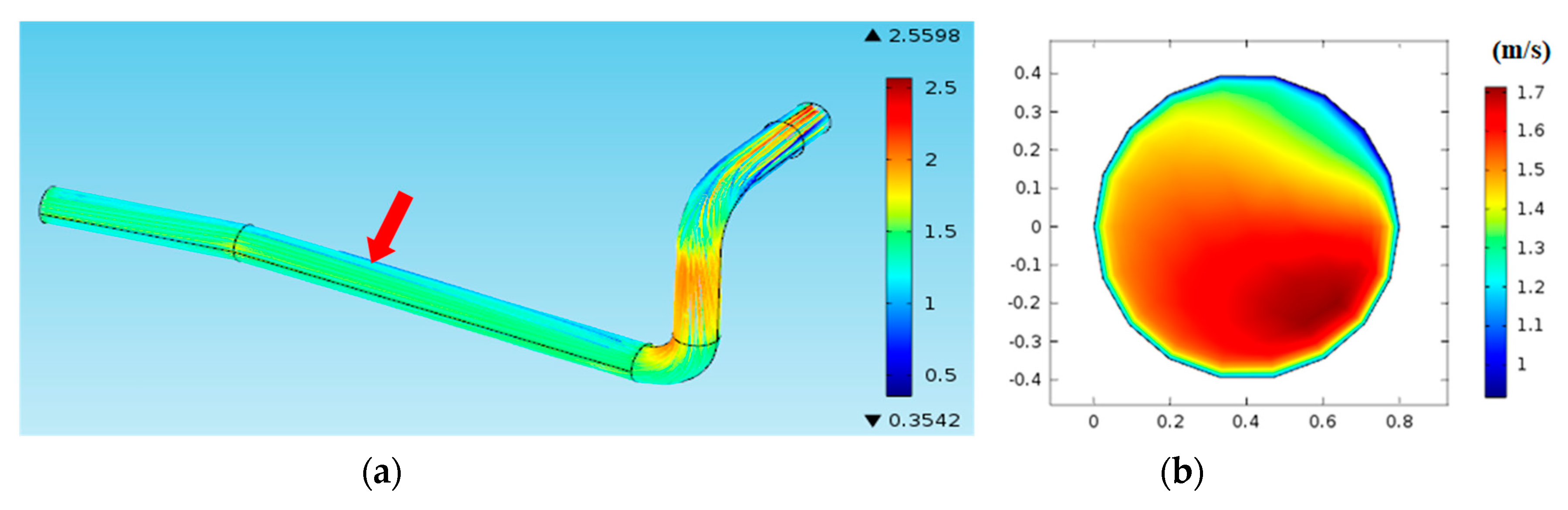
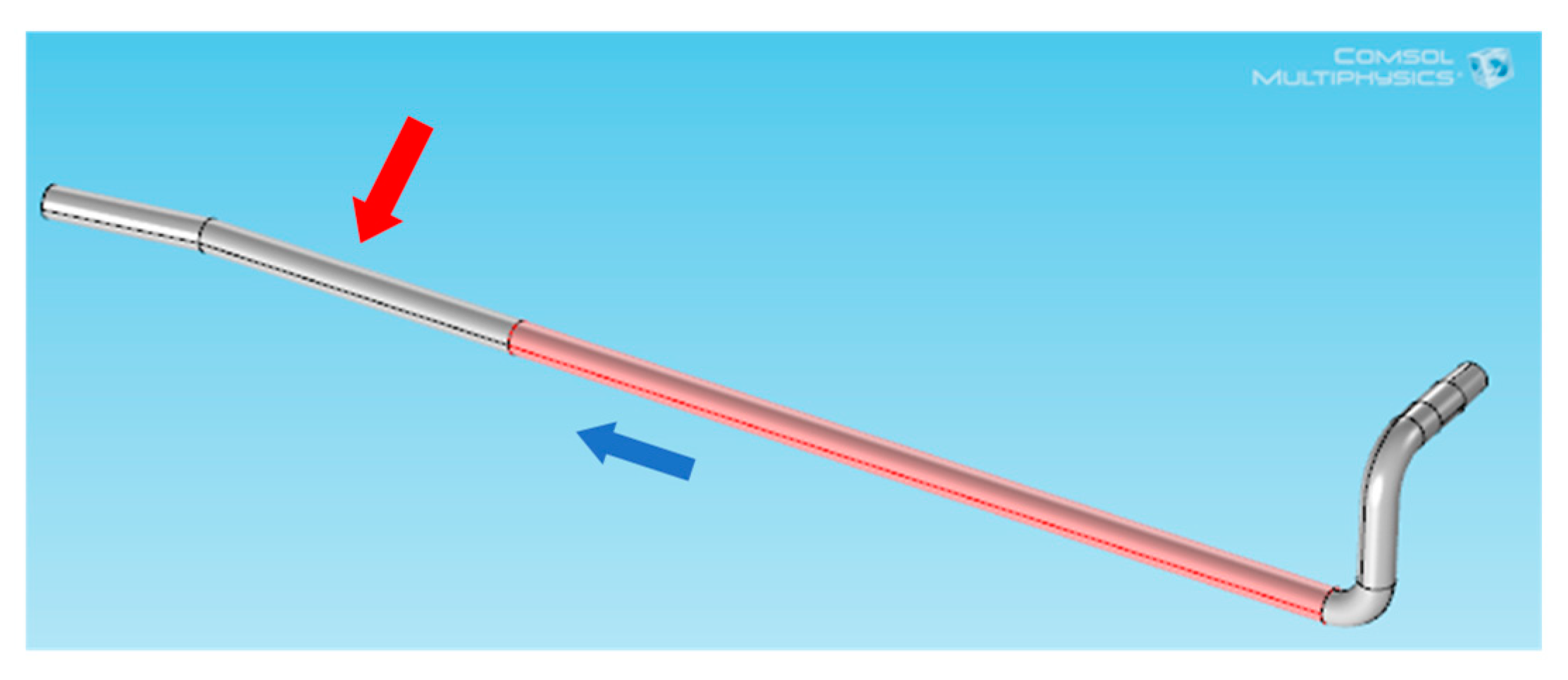

| Geometry | Qtheoretical (m³/h) | Tests Results | Error | |||||
|---|---|---|---|---|---|---|---|---|
| VND100 (L) | Vreference (L) | ttheoretical (s) | treal (s) | Qreference (m3/h) | ND100 (%) | Re (-) | ||
| 1 | 100 | 4980 | 5000 | 180 | 173 | 104 | −0.40% | 365,631 |
| 12 | 1006 | 1018 | 305 | 285 | 13 | −1.18% | 45,704 | |
| 2 | 100 | 5026 | 5000 | 180 | 172 | 105 | 0.52% | 369,147 |
| 12 | 1035 | 1020 | 306 | 295 | 12 | 1.47% | 42,188 | |
| Characteristics | 100 m3/h | 12 m3/h |
|---|---|---|
| Inlet | 5.6 bar | 5.8 bar |
| Outlet | 0.59 m/s | 0.07 m/s |
| Wall | No-slip | |
| Mesh | Physics-controlled | |
| Flow conditions | Steady state | |
| Geometry | Q = 100 m3/h | Q = 12 m3/h | ||
|---|---|---|---|---|
| Error | Error | |||
| Experimental | Model | Experimental | Model | |
| 1 | −0.40% | −0.48% | −1.18% | −1.27% |
| 2 | 0.52% | 1.11% | 1.47% | 1.61% |
| Material | Steel |
|---|---|
| Expansion | ND700 to ND800 |
| Remaining pipes | ND800 |
| Flowmeter | ND800 |
| Inlet | 9.5 bar |
|---|---|
| Outlet | 1.5 m/s |
| Wall | No-slip |
| Mesh | Physics-controlled |
| Flow conditions | Steady state |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simão, M.; Besharat, M.; Carravetta, A.; Ramos, H.M. Flow Velocity Distribution Towards Flowmeter Accuracy: CFD, UDV, and Field Tests. Water 2018, 10, 1807. https://doi.org/10.3390/w10121807
Simão M, Besharat M, Carravetta A, Ramos HM. Flow Velocity Distribution Towards Flowmeter Accuracy: CFD, UDV, and Field Tests. Water. 2018; 10(12):1807. https://doi.org/10.3390/w10121807
Chicago/Turabian StyleSimão, Mariana, Mohsen Besharat, Armando Carravetta, and Helena M. Ramos. 2018. "Flow Velocity Distribution Towards Flowmeter Accuracy: CFD, UDV, and Field Tests" Water 10, no. 12: 1807. https://doi.org/10.3390/w10121807
APA StyleSimão, M., Besharat, M., Carravetta, A., & Ramos, H. M. (2018). Flow Velocity Distribution Towards Flowmeter Accuracy: CFD, UDV, and Field Tests. Water, 10(12), 1807. https://doi.org/10.3390/w10121807








