Numerical Simulation of Liquid Sloshing with Different Filling Levels Using OpenFOAM and Experimental Validation
Abstract
1. Introduction
2. Numerical Model
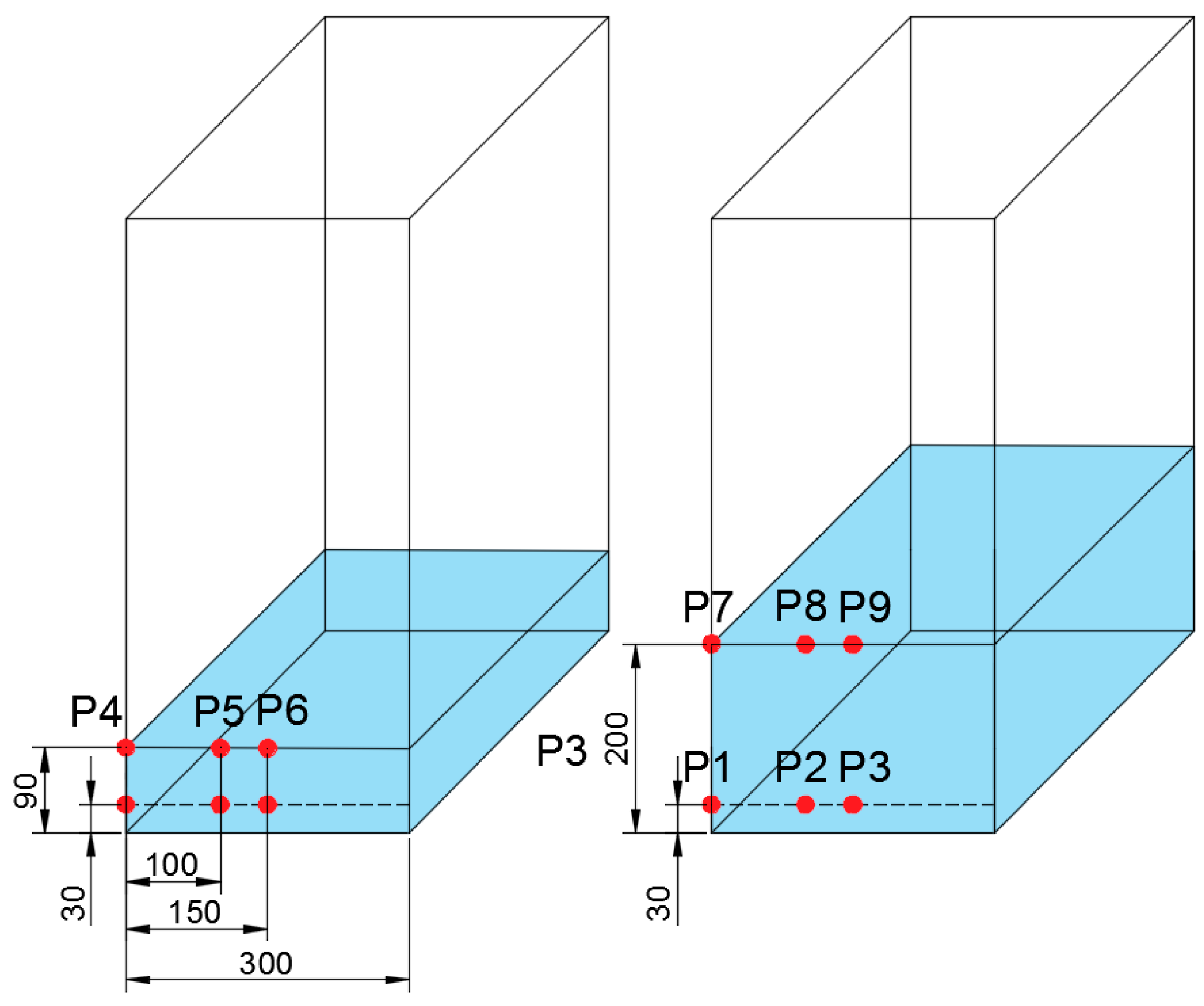
3. Experimental Setup
4. Model Validation
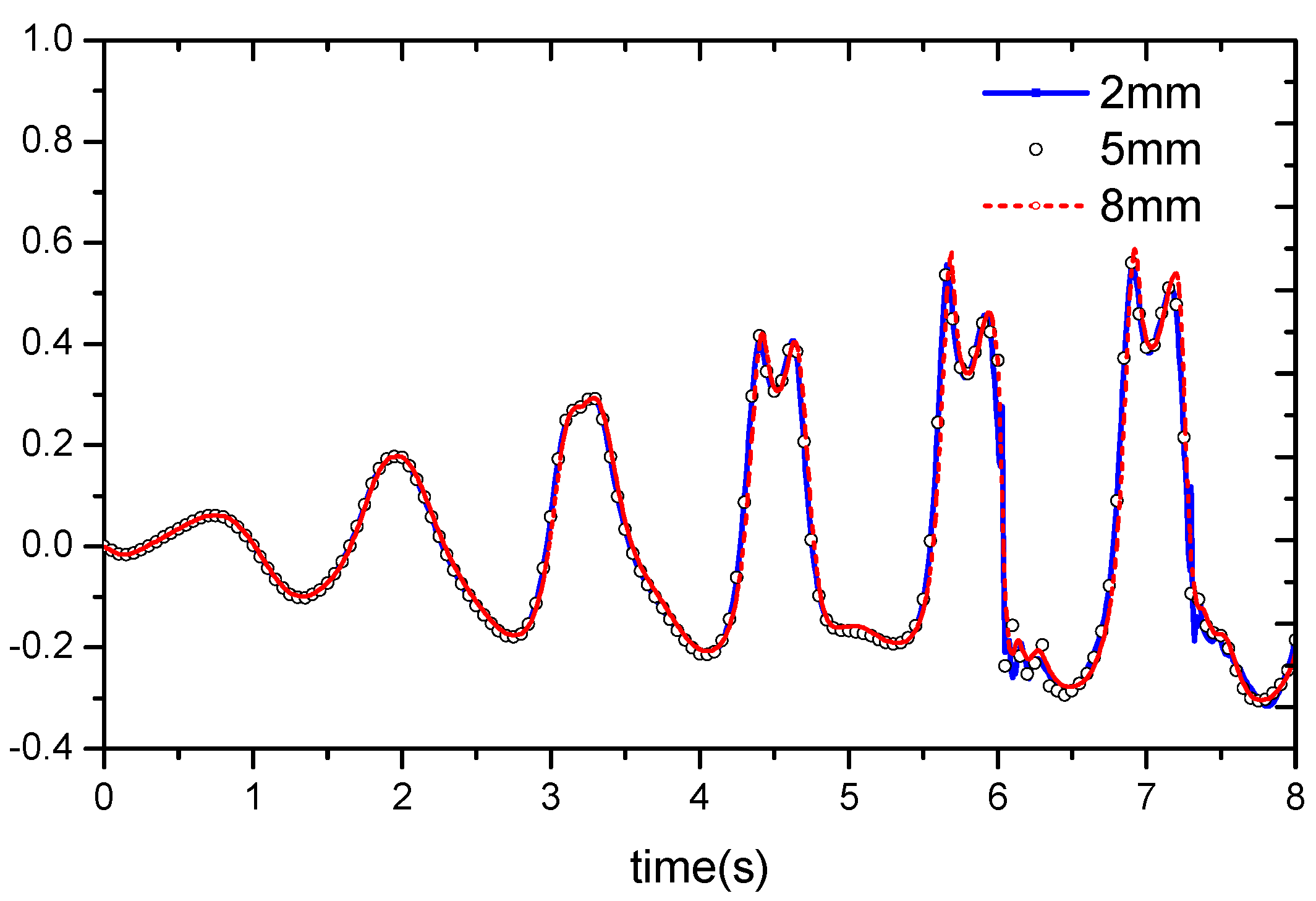
4.1. Mesh Convergence Test
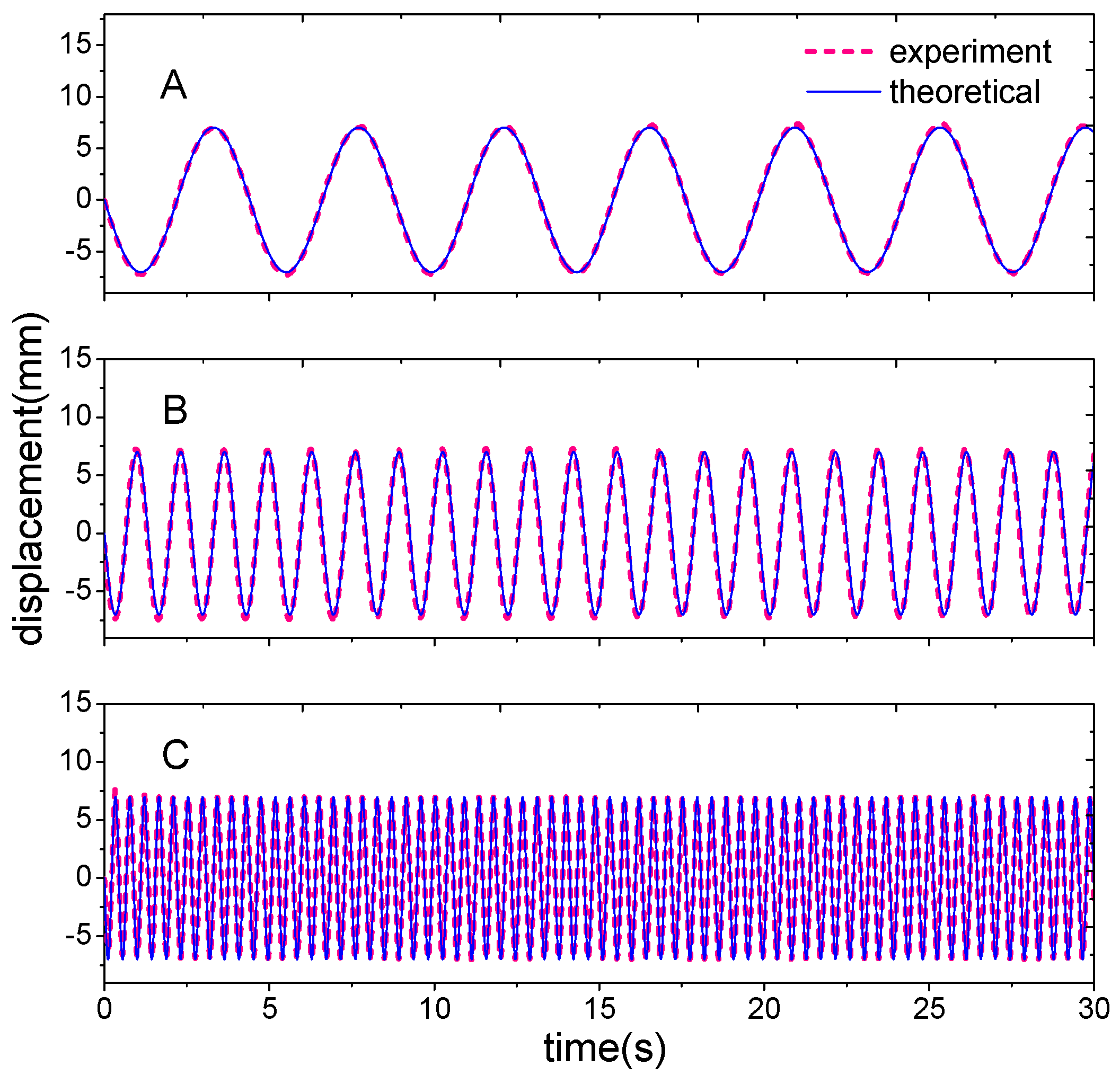
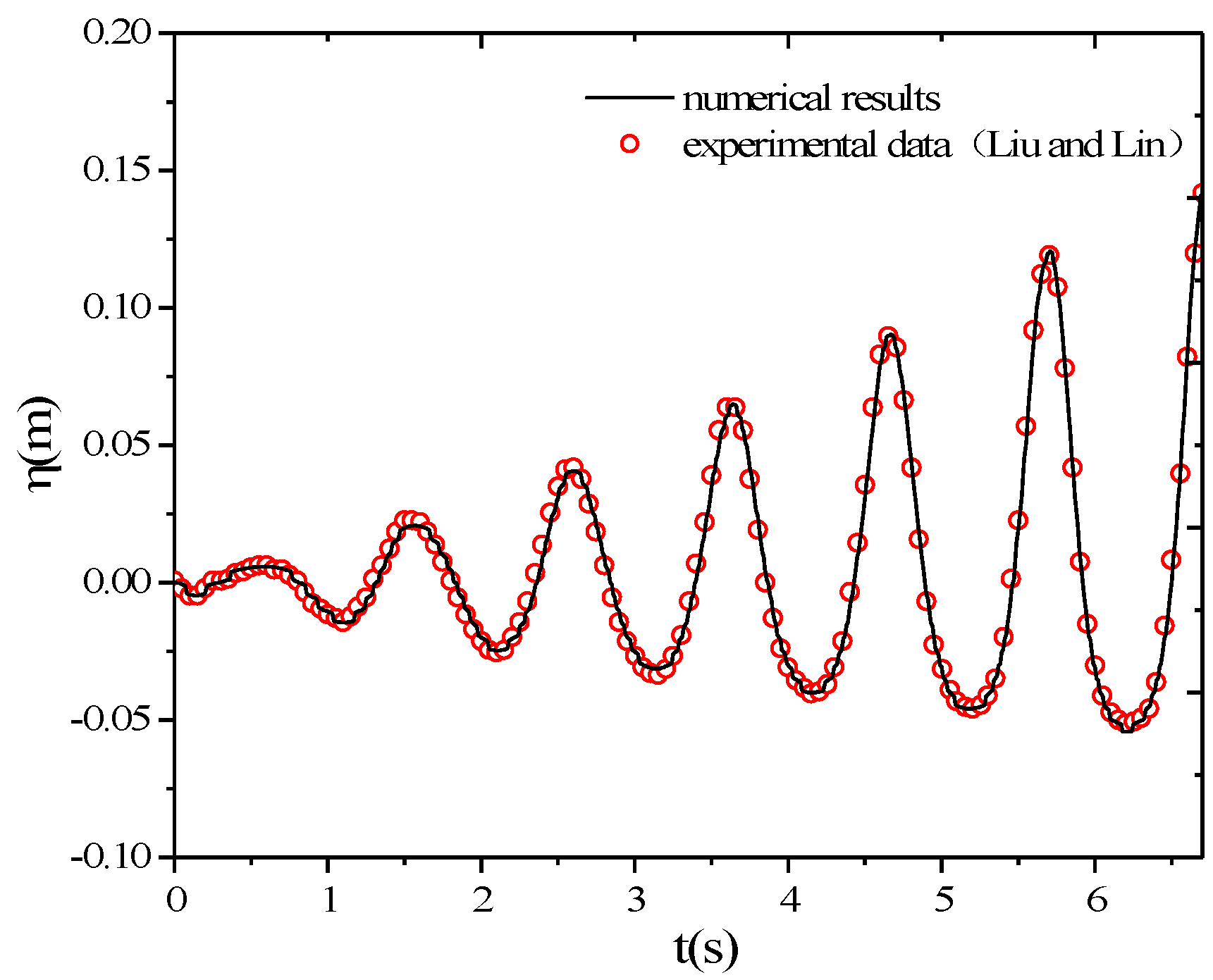
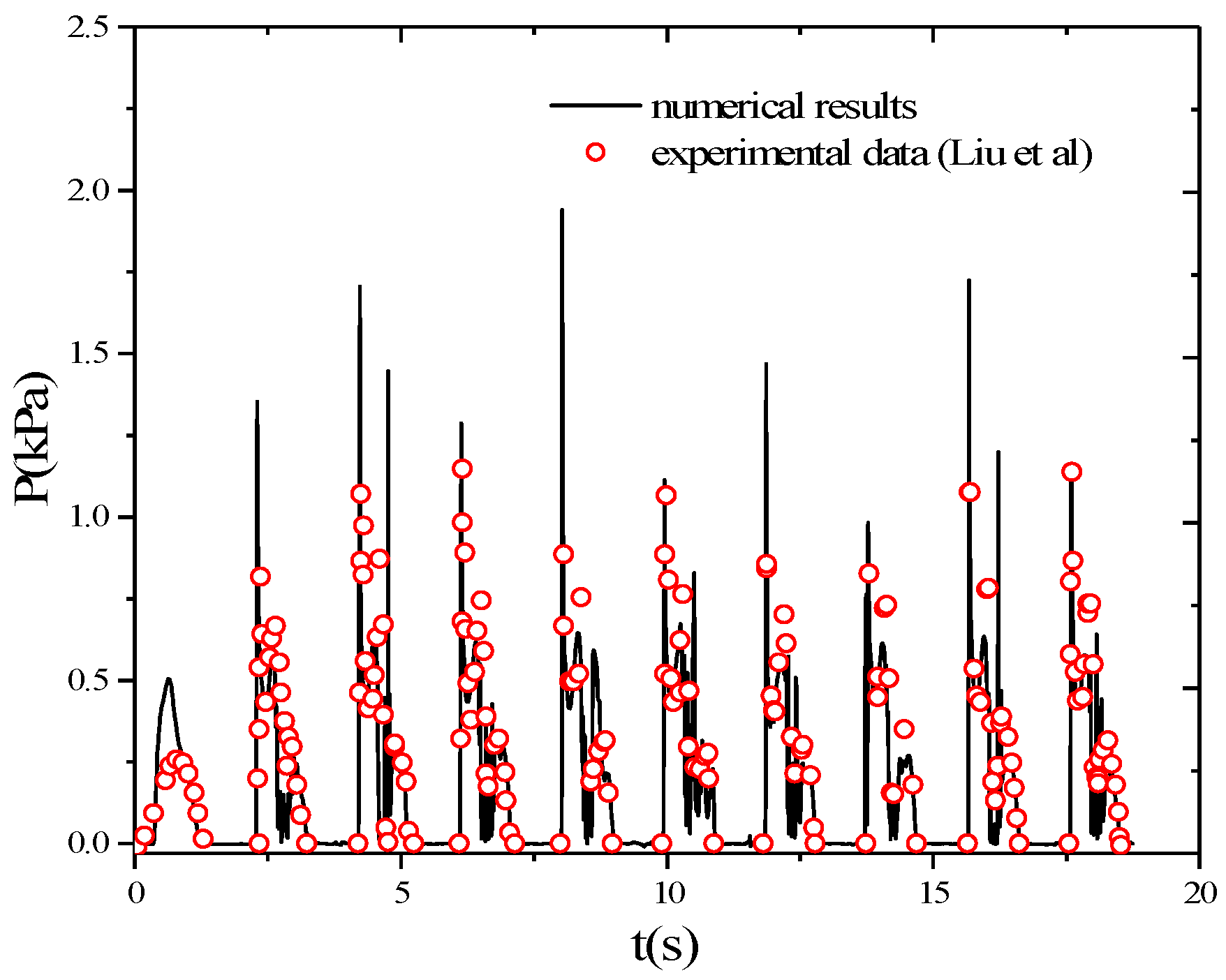
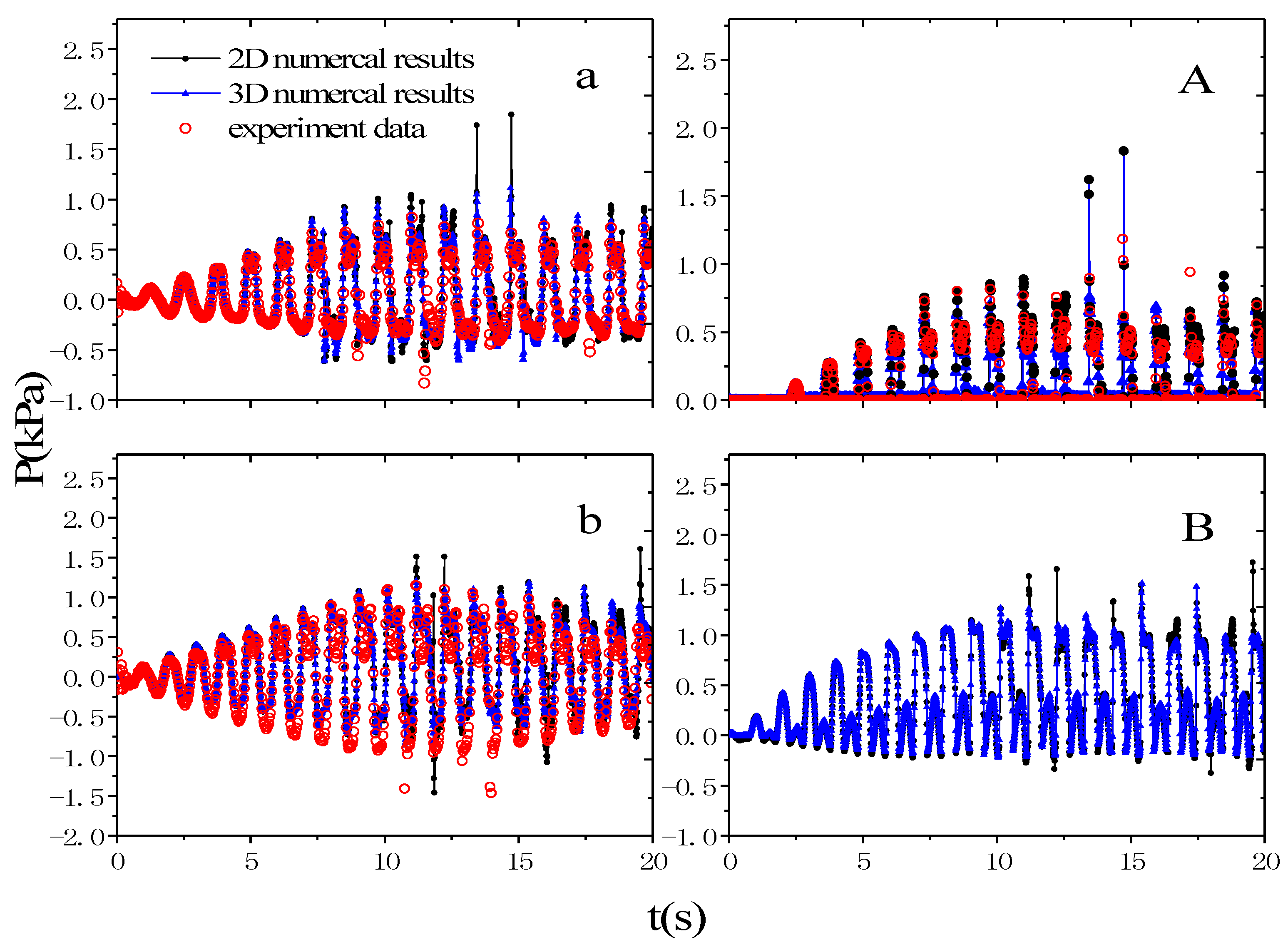
4.2. Experimental Validation
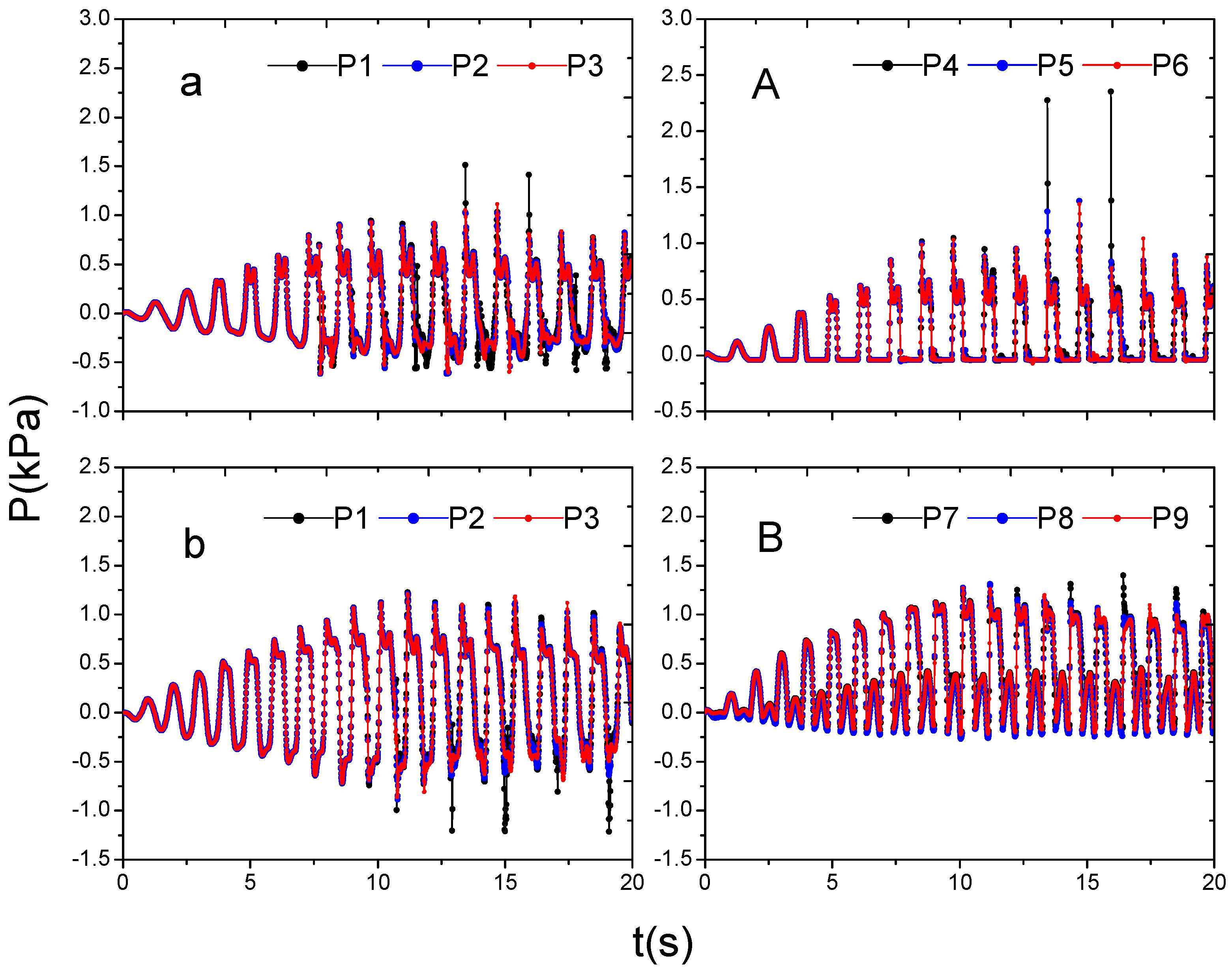
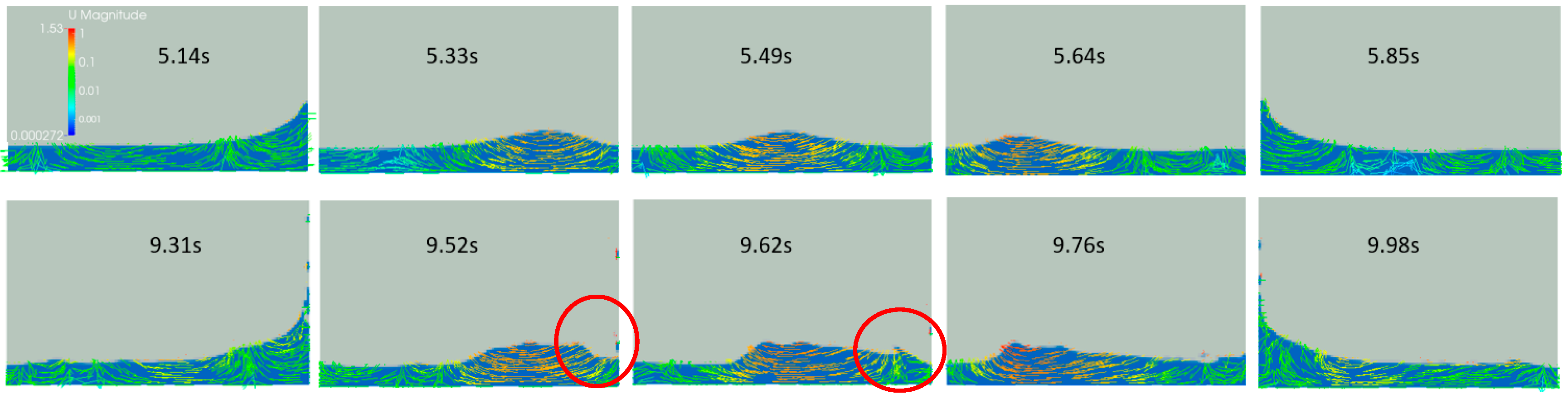
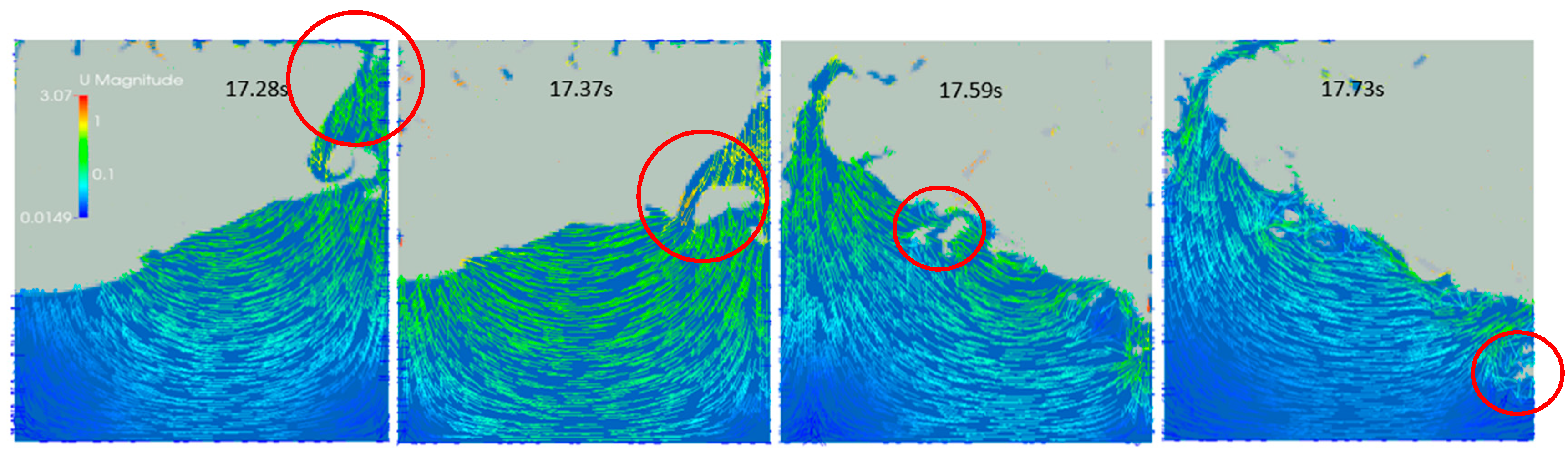
4.3. Three-Dimensional Results
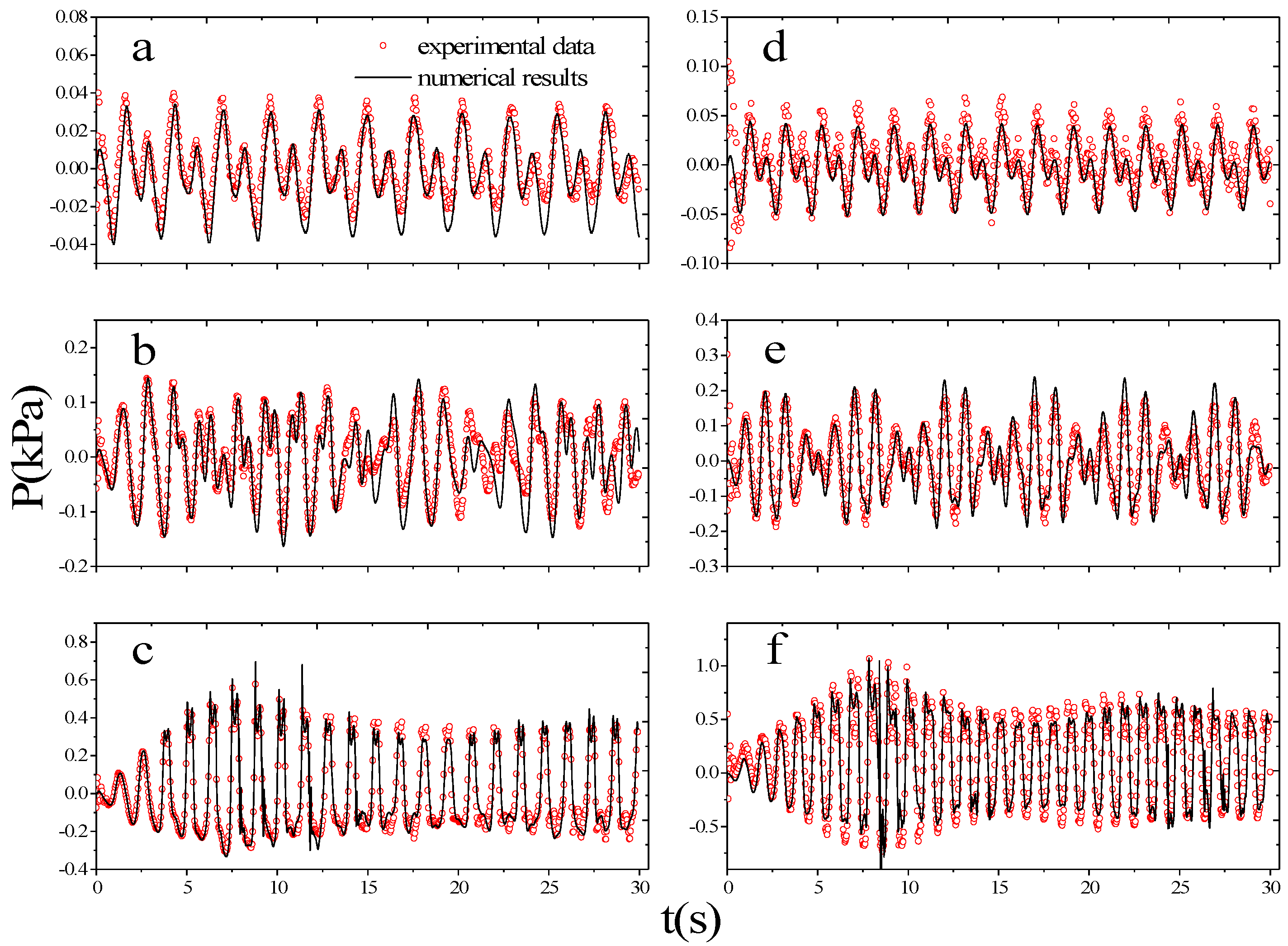
5. Results and Discussions
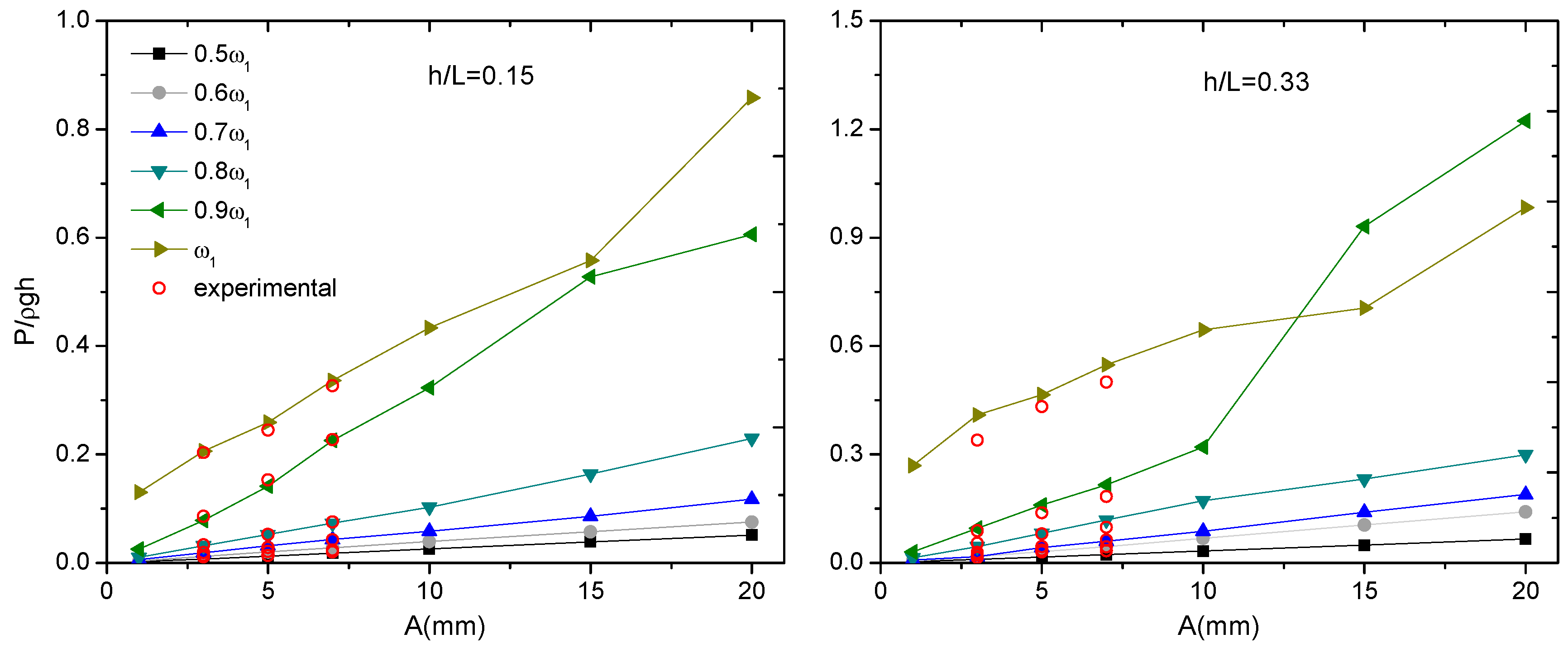
5.1. Effects of External Excitation Amplitudes
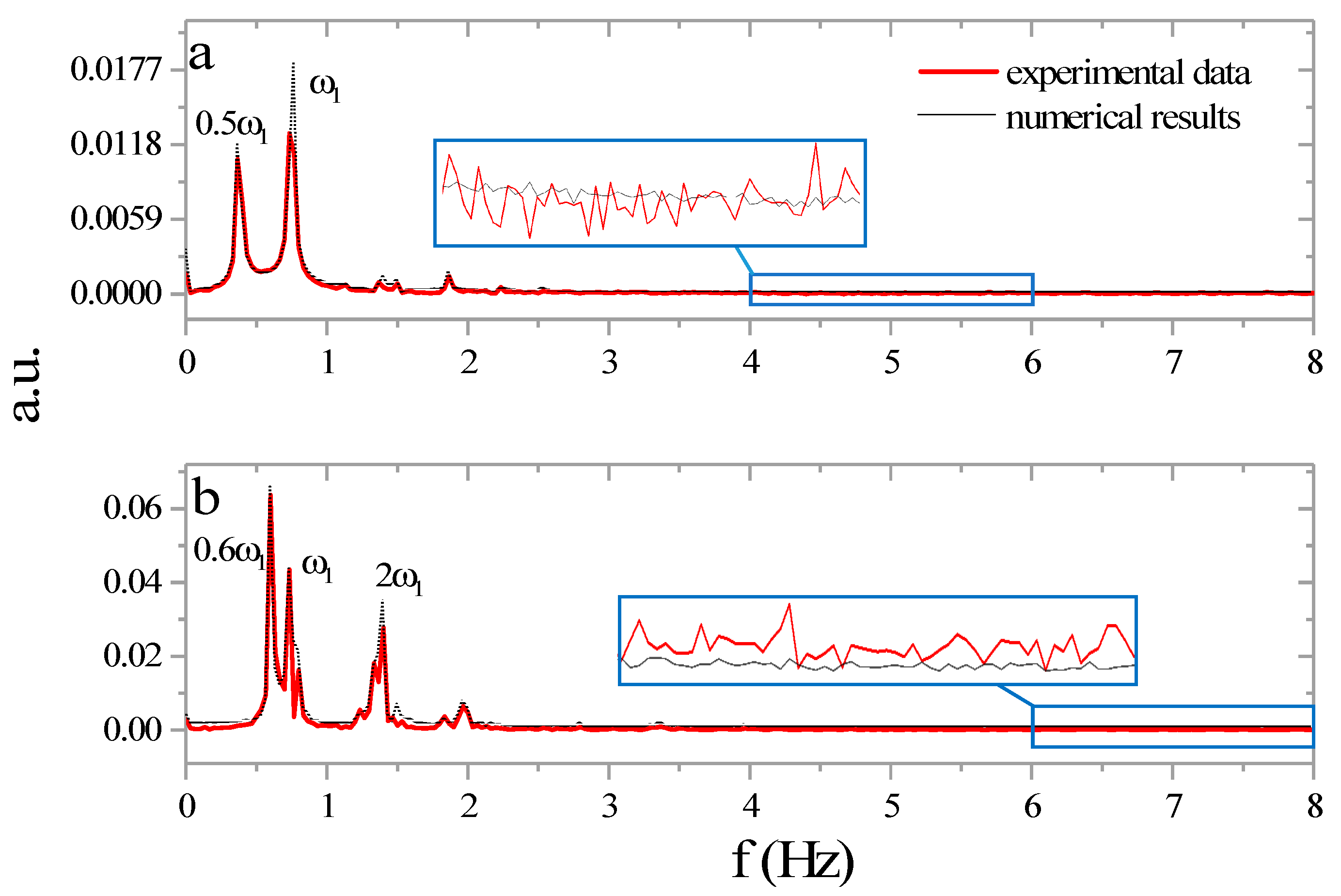
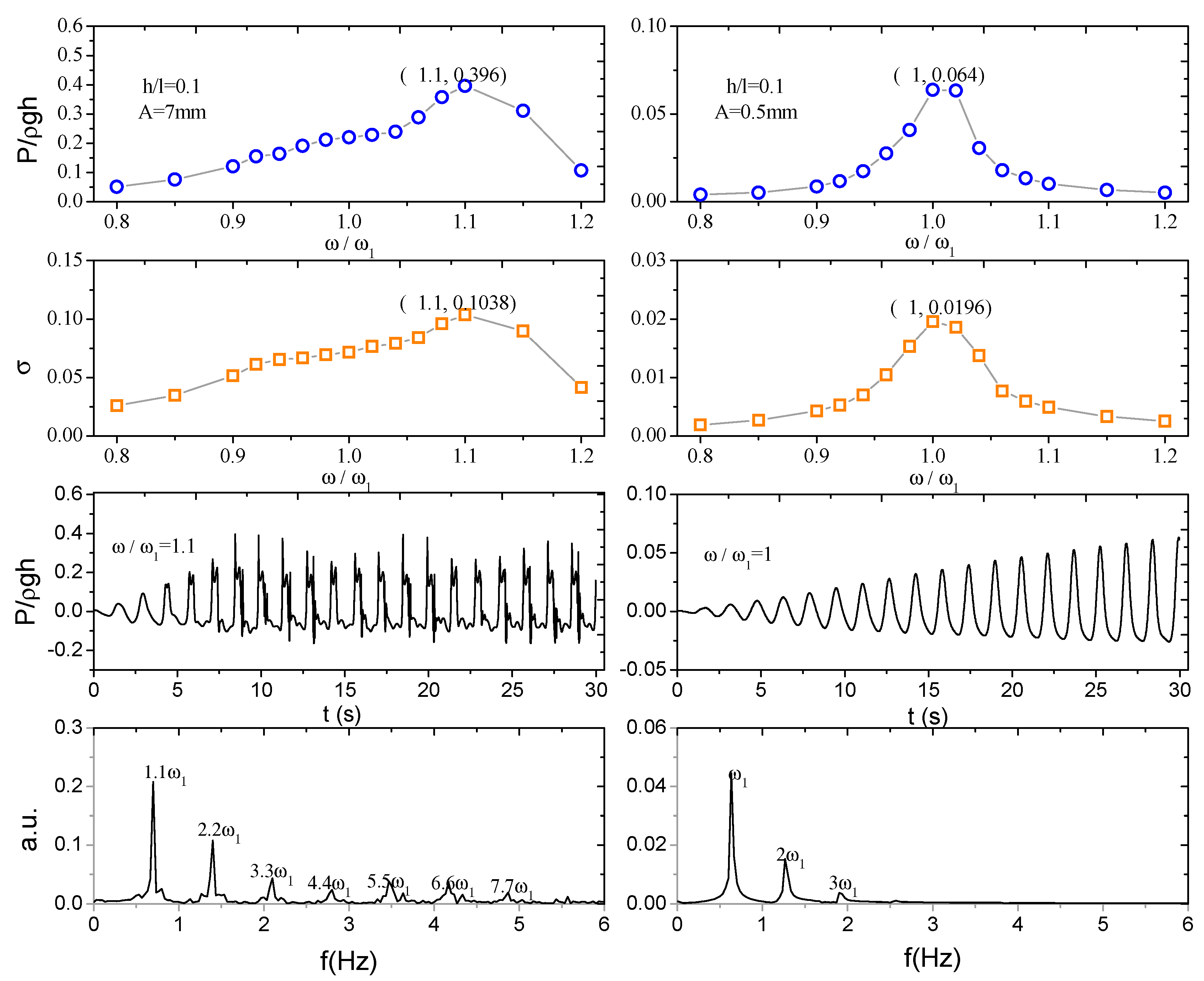
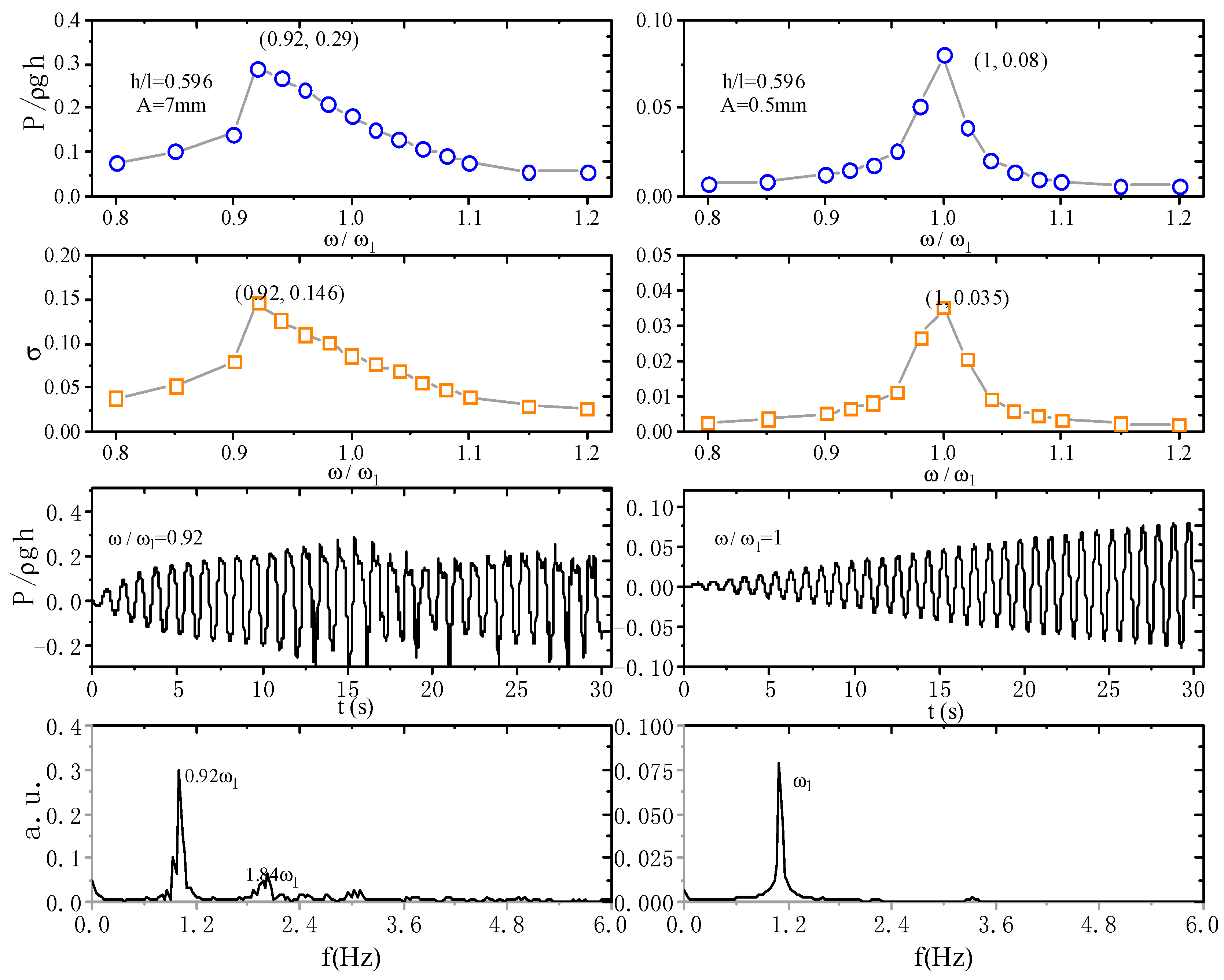
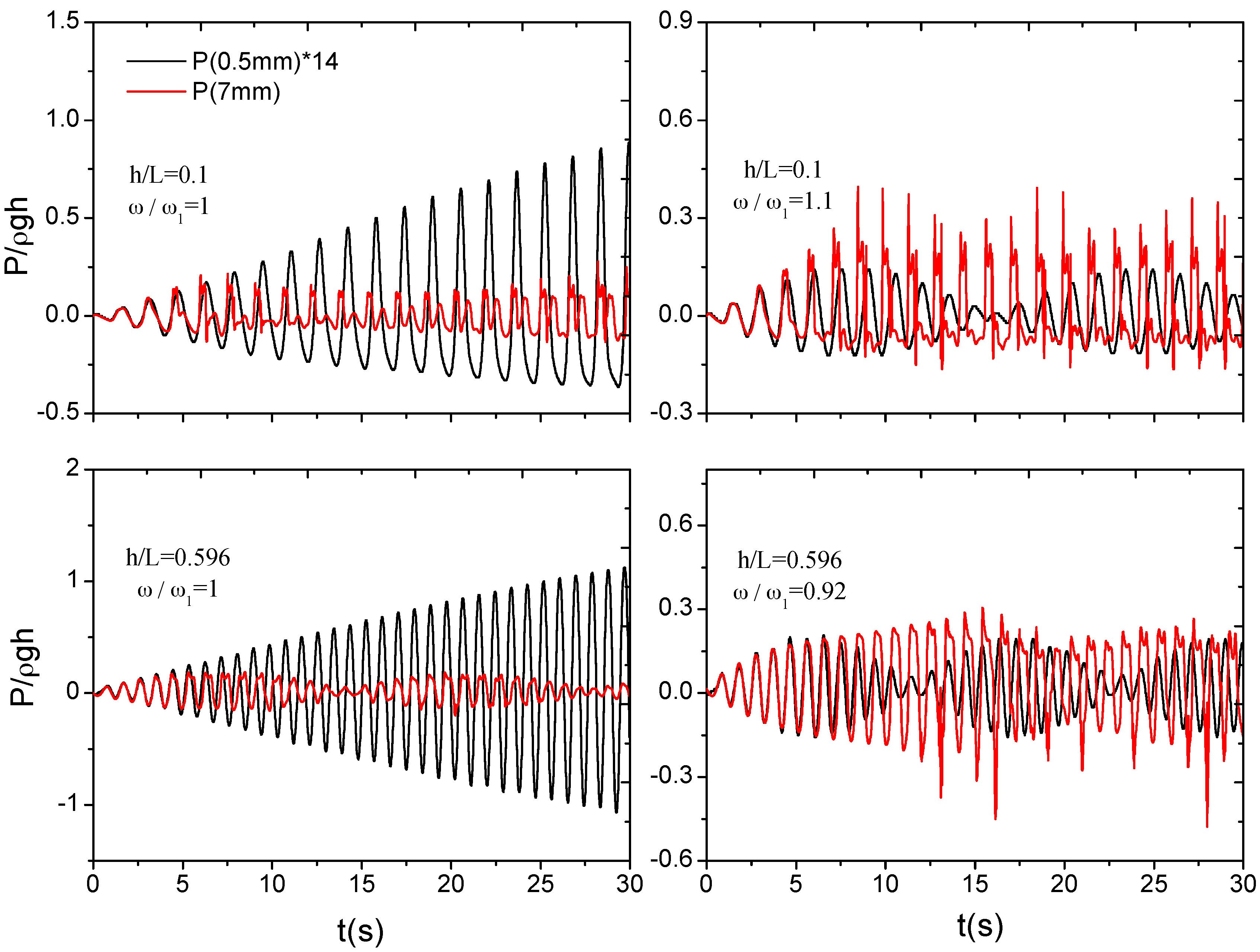
5.2. Resonant Hysteresis and Resonance in Advance
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moiseev, N.N. On the theory of nonlinear vibrations of a liquid of finite volume. J. Appl. Math. Mech. 1958, 22, 860–872. [Google Scholar] [CrossRef]
- Faltinsen, O.M. A nonlinear theory of sloshing in rectangular tanks. J. Ship Res. 1974, 18, 224–241. [Google Scholar]
- Faltinsen, O.M.; Rognebakke, O.F.; Lukovsky, I.A.; Timokha, A.N. Multidimensional modal analysis of nonlinear sloshing in a rectangular tank with finite water depth. J. Fluid Mech. 2000, 407, 201–234. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Timokha, A.N. An adaptive multimodal approach to nonlinear sloshing in a rectangular tank. J. Fluid Mech. 2001, 432, 167–200. [Google Scholar]
- Ikeda, T.; Nakagawa, N. Non-linear vibrations of a structure caused by water sloshing in a rectangular tank. J. Sound Vib. 1997, 201, 23–41. [Google Scholar] [CrossRef]
- Pistani, F.; Thiagarajan, K. Experimental measurements and data analysis of the impact pressures in a sloshing experiment. Ocean Eng. 2012, 52, 60–74. [Google Scholar] [CrossRef]
- Xue, M.-A.; Zheng, J.; Lin, P.; Yuan, X. Experimental study on vertical baffles of different configurations in suppressing sloshing pressure. Ocean Eng. 2017, 136, 178–189. [Google Scholar] [CrossRef]
- Kalinichenko, V.A.; Sekerzh-Zen’kovich, S.Y. Experimental investigation of Faraday waves of maximum height. Fluid Dyn. 2007, 42, 959–965. [Google Scholar] [CrossRef]
- Xue, M.-A.; Lin, P.; Zheng, J.H.; Ma, Y.; Yuan, X.; Nguyen, V.T. Effects of perforated baffle on reducing sloshing in rectangular tank: experimental and numerical study. China Ocean Eng. 2013, 27, 615–628. [Google Scholar] [CrossRef]
- Cai, Z.H.; Wang, D.Y.; Li, Z. Influence of excitation frequency on slosh-induced impact pressures of liquefied natural gas tanks. J. Shanghai Jiaotong Univ. 2011, 16, 124–128. [Google Scholar] [CrossRef]
- Xue, M.-A.; Zheng, J.H.; Lin, P.; Xiao, Z. Violent transient sloshing-wave interaction with a baffle in a three-dimensional numerical tank. J. Ocean Univ. China 2017, 16, 661–673. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P. A numerical study of three-dimensional liquid sloshing in tanks. J. Comput. Phys. 2008, 227, 3921–3939. [Google Scholar] [CrossRef]
- Buldakov, E. Lagrangian modelling of fluid sloshing in moving tanks. J. Fluids Struct. 2014, 45, 1–14. [Google Scholar] [CrossRef]
- Xue, M.-A.; Zheng, J.H.; Lin, P. Numerical simulation of sloshing phenomena in cubic tank with multiple baffles. J. Appl. Math. 2012, 2012, 1–21. [Google Scholar] [CrossRef]
- Kim, Y. Numerical simulation of sloshing flows with impact load. Appl. Ocean Res. 2001, 23, 53–62. [Google Scholar] [CrossRef]
- Ramaswamy, B.; Kawahara, M.; Nakayama, T. Lagrangian finite element method for the analysis of two-dimensional sloshing problems. Int. J. Numer. Methods Fluids 1986, 6, 659–670. [Google Scholar] [CrossRef]
- Oxtoby, O.F.; Malan, A.G.; Heyns, J.A. A computationally efficient 3D finite-volume scheme for violent liquid–gas sloshing. Int. J. Numer. Methods Fluids 2015, 79, 306–321. [Google Scholar] [CrossRef]
- Kishev, Z.R.; Hu, C.; Kashiwagi, M. Numerical simulation of violent sloshing by a CIP-based method. J. Mar. Sci. Technol. 2006, 11, 111–122. [Google Scholar] [CrossRef]
- Chen, Z.; Zong, Z.; Li, H.T.; Li, J. An investigation into the pressure on solid walls in 2D sloshing using SPH method. Ocean Eng. 2013, 59, 129–141. [Google Scholar] [CrossRef]
- Xue, M.-A.; Lin, P. Numerical study of ring baffle effects on reducing violent liquid sloshing. Comput. Fluids. 2011, 52, 116–129. [Google Scholar] [CrossRef]
- Kim, Y. Experimental and numerical analyses of sloshing flows. J. Eng. Math. 2007, 58, 191–210. [Google Scholar] [CrossRef]
- Jin, X.; Lin, P.Z. Viscous effects on liquid sloshing under external excitations. Ocean Eng. 2018, in press. [Google Scholar] [CrossRef]
- Ma, Z.H.; Causon, D.M.; Qian, L.; Mingham, C.G.; Martinez, F.P. Numerical investigation of air enclosed wave impacts in a depressurised tank. Ocean Eng. 2016, 123, 15–27. [Google Scholar] [CrossRef]
- Jiang, S.C.; Teng, B.; Bai, W.; Ying, G. Numerical simulation of coupling effect between ship motion and liquid sloshing under wave action. Ocean Eng. 2015, 108, 140–154. [Google Scholar] [CrossRef]
- Wang, Y.-S.; Politano, M.; Laughery, R. Towards full predictions of temperature dynamics in McNary Dam forebay using OpenFOAM. Water Sci. Eng. 2013, 6, 317–330. [Google Scholar]
- Faltinsen, O.M.; Timokha, A.N. Sloshing; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Liu, D.; Tang, W.; Wang, J.; Xue, H.; Wang, K. Comparison of laminar model, RANS, LES and VLES for simulation of liquid sloshing. Appl. Ocean Res. 2016, 59, 638–649. [Google Scholar] [CrossRef]
- Waterhouse, D.D. Resonant sloshing near a critical depth. J. Fluid Mech. 2006, 281, 313–318. [Google Scholar] [CrossRef]
- Kobine, J.J. Nonlinear resonant characteristics of shallow fluid layers. Philos. Trans. 2008, 366, 1331–1346. [Google Scholar] [CrossRef] [PubMed]






| Two-dimensional Model | Three-dimensional Model | |
|---|---|---|
| Mesh Size | 5 × 5 mm | 5 × 5 × 5 mm |
| Mesh Number | 15,600 | 936,000 |
| Computing | CPU:AMD Ryzen 7 1700X Eight-Core Processor 3.40 GHz no parallel | |
| Times | 1962 s | 394,971 s |
| Analysis of Result | In agreement with the experimental data; Sometimes there are large pressure peaks. | Match well with the experimental value |
| Case | h/L | ω1 (rad/s) | ω/ω1 | ω | A(m) |
|---|---|---|---|---|---|
| Case 1 | 0.15 | 4.749 | 0.5 | 2.3745 | 0.001 0.003 0.005 0.007 0.01 0.02 |
| Case 2 | 0.6 | 2.8494 | |||
| Case 3 | 0.7 | 3.3243 | |||
| Case 4 | 0.8 | 3.7992 | |||
| Case 5 | 0.9 | 4.2741 | |||
| Case 6 | 1 | 4.749 | |||
| Case 7 | 0.33 | 6.333 | 0.5 | 3.1665 | |
| Case 8 | 0.6 | 3.7998 | |||
| Case 9 | 0.7 | 4.4331 | |||
| Case 10 | 0.8 | 5.0664 | |||
| Case 11 | 0.9 | 5.6997 | |||
| Case 12 | 1 | 6.333 |
| Case | h/L | L(m) | h(m) | A(m) | ω1 (rad/s) | ω (rad/s) |
|---|---|---|---|---|---|---|
| Case 13 | 0.054 | 0.6 | 0.0324 | 0.007 | 2.942 | 0.8 ω1–1.2 ω1 |
| Case 14 | 0.1 | 0.06 | 3.953 | |||
| Case 15 | 0.15 | 0.09 | 4.749 | |||
| Case 16 | 0.217 | 0.1302 | 5.514 | |||
| Case 17 | 0.25 | 0.15 | 5.804 | |||
| Case 18 | 0.28 | 0.168 | 6.023 | |||
| Case 19 | 0.3 | 0.18 | 6.15 | |||
| Case 20 | 0.33 | 0.198 | 6.316 | |||
| Case 21 | 0.433 | 0.2598 | 6.711 | |||
| Case 22 | 0.596 | 0.3576 | 6.999 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Xue, M.-A. Numerical Simulation of Liquid Sloshing with Different Filling Levels Using OpenFOAM and Experimental Validation. Water 2018, 10, 1752. https://doi.org/10.3390/w10121752
Chen Y, Xue M-A. Numerical Simulation of Liquid Sloshing with Different Filling Levels Using OpenFOAM and Experimental Validation. Water. 2018; 10(12):1752. https://doi.org/10.3390/w10121752
Chicago/Turabian StyleChen, Yichao, and Mi-An Xue. 2018. "Numerical Simulation of Liquid Sloshing with Different Filling Levels Using OpenFOAM and Experimental Validation" Water 10, no. 12: 1752. https://doi.org/10.3390/w10121752
APA StyleChen, Y., & Xue, M.-A. (2018). Numerical Simulation of Liquid Sloshing with Different Filling Levels Using OpenFOAM and Experimental Validation. Water, 10(12), 1752. https://doi.org/10.3390/w10121752






