4.1. Preliminary Screening of Models
A widely used approach for the preliminary discrimination of most consistent distributions to describe the understudy variable is the so-called “moment-ratio diagrams.” This type of analysis has been widely applied in the probabilistic study of hydrological variables especially in cases where a large number of records are examined since it provides a quick and direct evaluation of the suitability of several distributions from a statistical point-of-view by using just a single graphical instrument [
38,
41,
42,
45]. In the present work, we first transfer this framework in the analysis of large datasets of water demand records.
The moment-ratio diagrams provide a graphical comparison between the sample statistics, calculated from the records, and the theoretical ones as they are given by the formulas of the candidate parametric distributions. The proximity of the sample statistics to the theoretical locus (i.e., point, curve, or area) of a particular distribution provides an indication of the appropriateness of this distribution to describe the understudy records, which implies whether a specific set of a distribution parameter exists so as to reproduce the understudy moments. In such diagrams, a coefficient of variation
vs. a coefficient of skewness or a coefficient of skewness
vs. a coefficient of kurtosis are typically depicted while any pair of standardized moments could be also used. A comprehensive review of the conventional product moment-ratio diagrams summarizing 37 theoretical probabilistic models can be found in Vargo and Leemis [
46].
During the last decades, the L-moments ratio diagrams, which were first introduced by Hosking [
40], have gained popularity against conventional ones and have been widely used in many hydrological applications due to the better statistical properties of L-moments [
42]. L-variation
vs. L-skewness and L-skewness
vs. L-kurtosis pairs are mostly used while the latter is more popular since L-variation is not well defined for distributions with a mean value equals zero or is negative. The theoretical locus of a distribution in L-ratio diagrams as well as in conventional moments diagrams can be a point, a curve, or an area depending on the number of parameters of the distribution. In L-skewness
vs. L-kurtosis diagram, the type of the locus depends on the number of shape parameters, i.e., distributions without a shape parameter form a point (e.g., Normal distribution) with one shape parameter forming a curve (e.g., Gamma distribution) and with two shape parameters forming an area (e.g., Burr Type XII). On the contrary, the theoretical locus of distributions in an L-variation
vs. an L-skewness diagram depends also on the location and scale parameters (if they are adjusted to take any value) and, subsequently, the number of distributions whose locus is a point and is lower. The present analysis was based on the L-variation
vs. L-skewness diagram for positive random variables such as nonzero water demand is well defined and more robust than L-kurtosis [
38].
The special characteristics of the 15-minute and an hourly nonzero demand process, as derived from the above analysis, determine the initial set of candidate probabilistic models that are going to be examined as more suitable to describe the understudy variables. First, the studied distributions should be defined in the real positive axis. Additionally, the high L-skewness and L-variation coefficients along with the great variability of those shape characteristics from household-to-household and hour-to-hour imply the use of distributions whose shape parameters support a range of values for those statistics. Further to that, we took into account the probabilistic models that are used by the simulation schemes to model water demand at super-fine time scales (e.g., the Exponential [
1,
19,
20,
21,
22], Weibull [
5], Lognormal [
15,
17,
47], and Normal [
14]) as well as in the simulation of hydrological variables with similar characteristics.
Having said that, as candidate models to describe the understudy variables, we selected the Gamma (G) distribution, the Generalized Logistic (GL) bounded at zero from below, the Generalized Pareto (GP) bounded at zero from below, the Generalized Extreme Value (GEV) distribution bounded at zero from below, the Lognormal (LN) distribution and the Weibull (W) distribution. The Normal (N) and Exponential (EXP) distribution were also included in the analysis since they are very popular and widely used models. As we see in the L-variation
vs. L-skewness diagrams of
Figure 6, the locus of all understudy distributions is a curve except from that of the Exponential distribution, which is controlled via just one scale parameter and subsequently it has constant L-variation (τ
3 = 0.50) and L-skewness (τ
3 = 1/3). Normal distribution is symmetric about the mean, i.e., τ
3 = 0, and their theoretical locus is a horizontal line since L-variation can be adjusted to take any value by controlling the location and scale parameters.
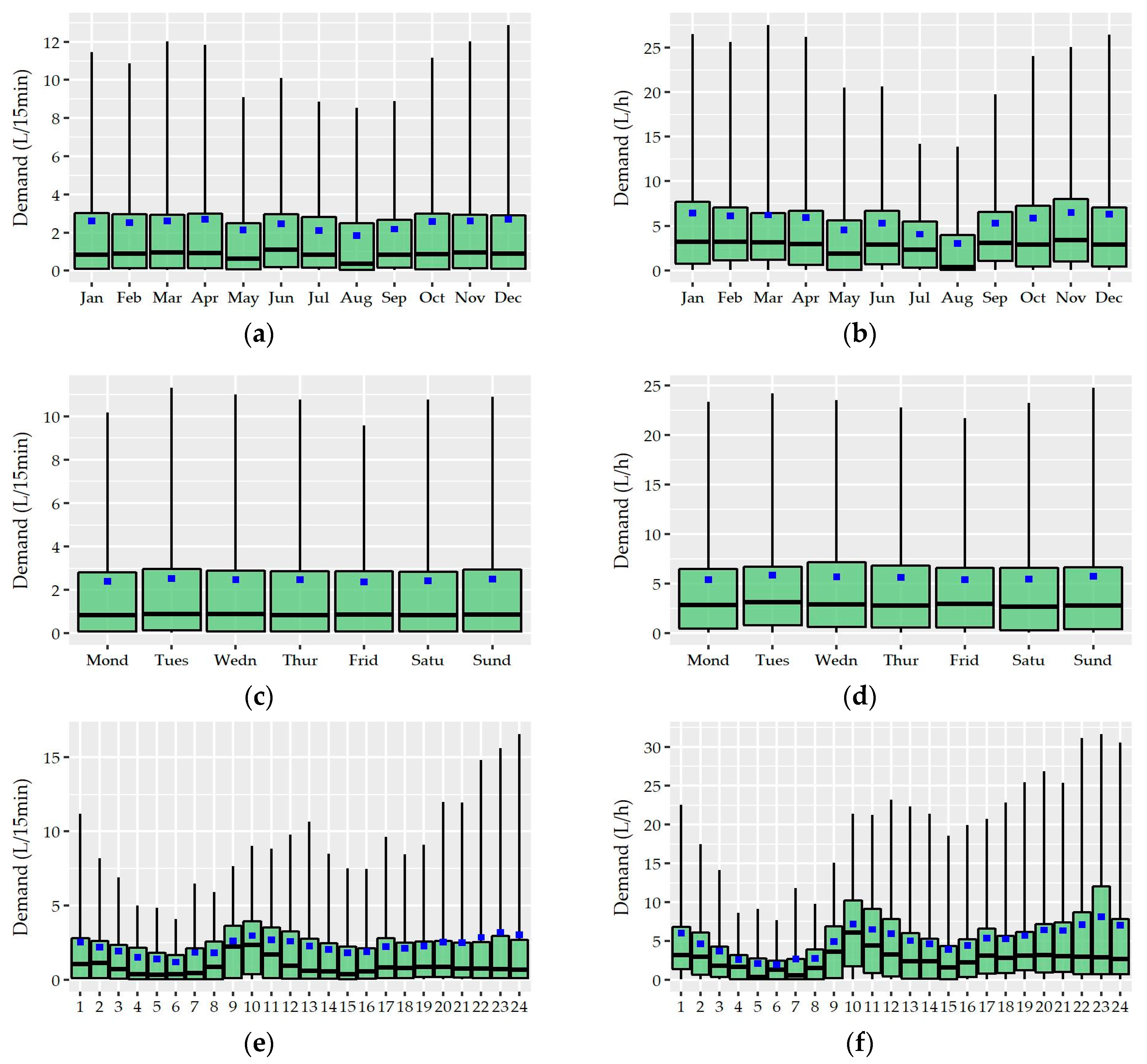
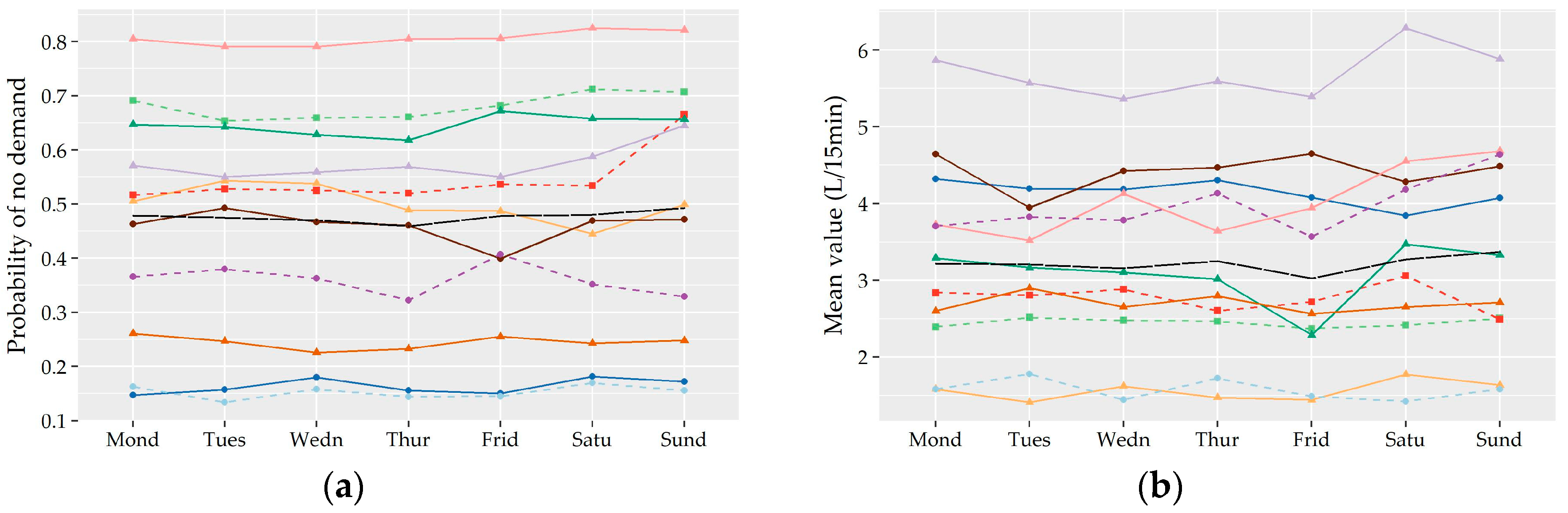
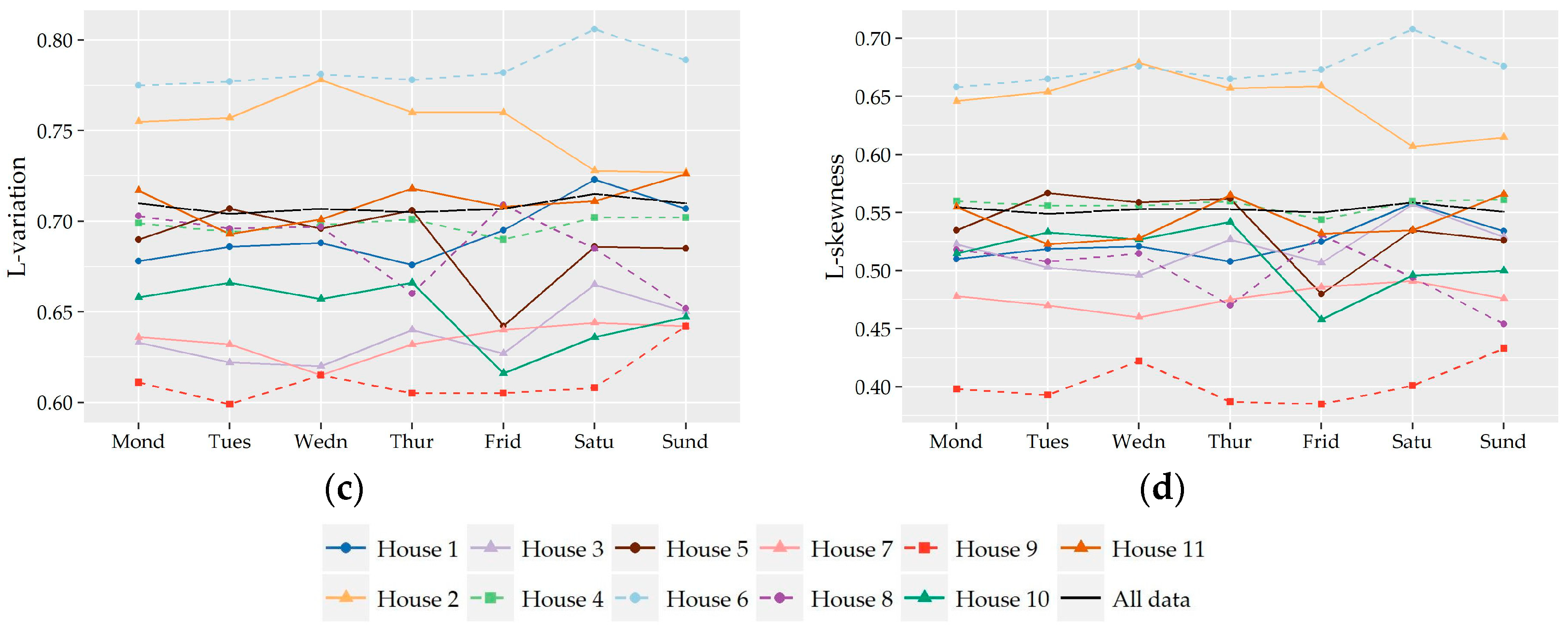
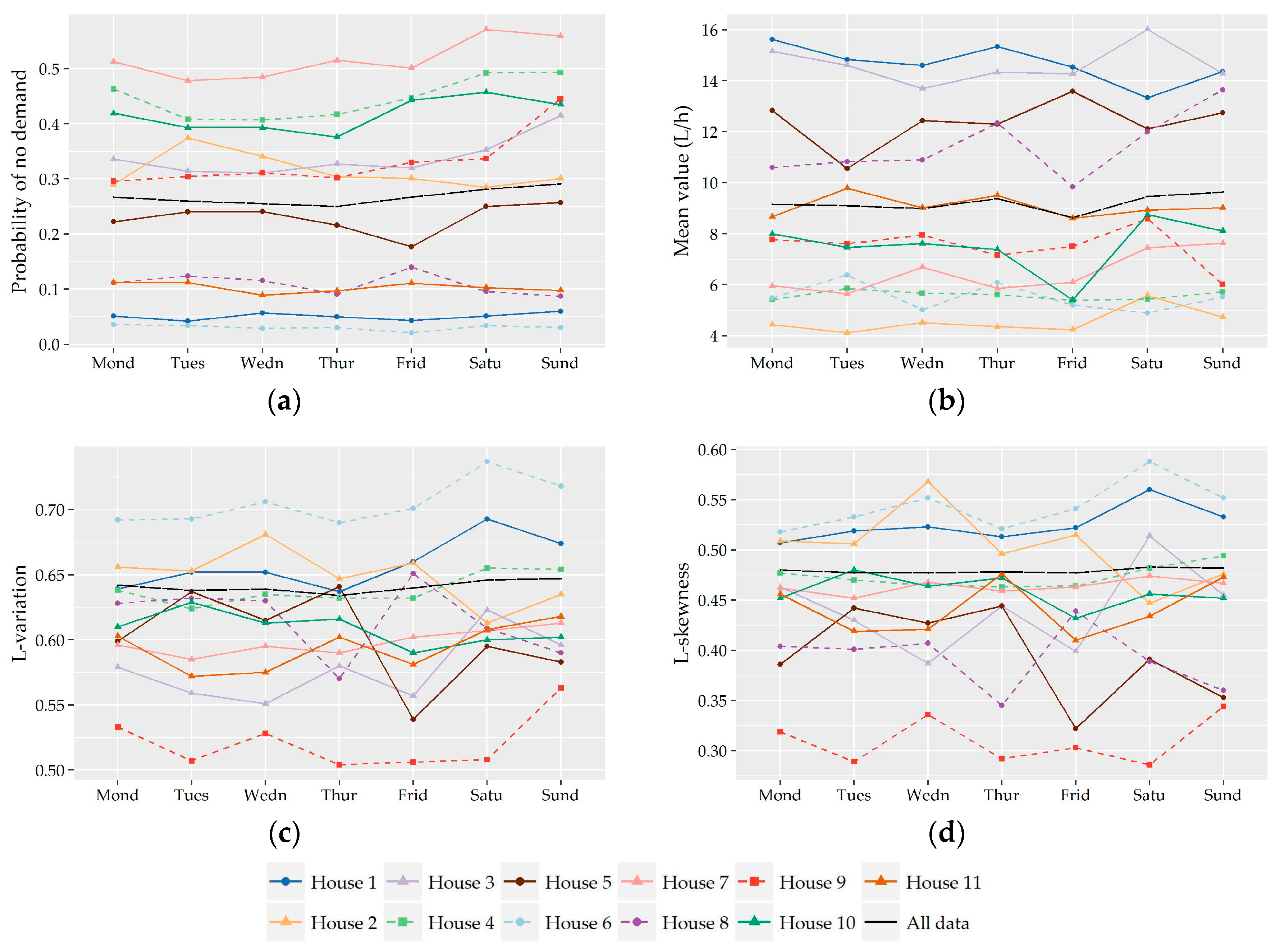
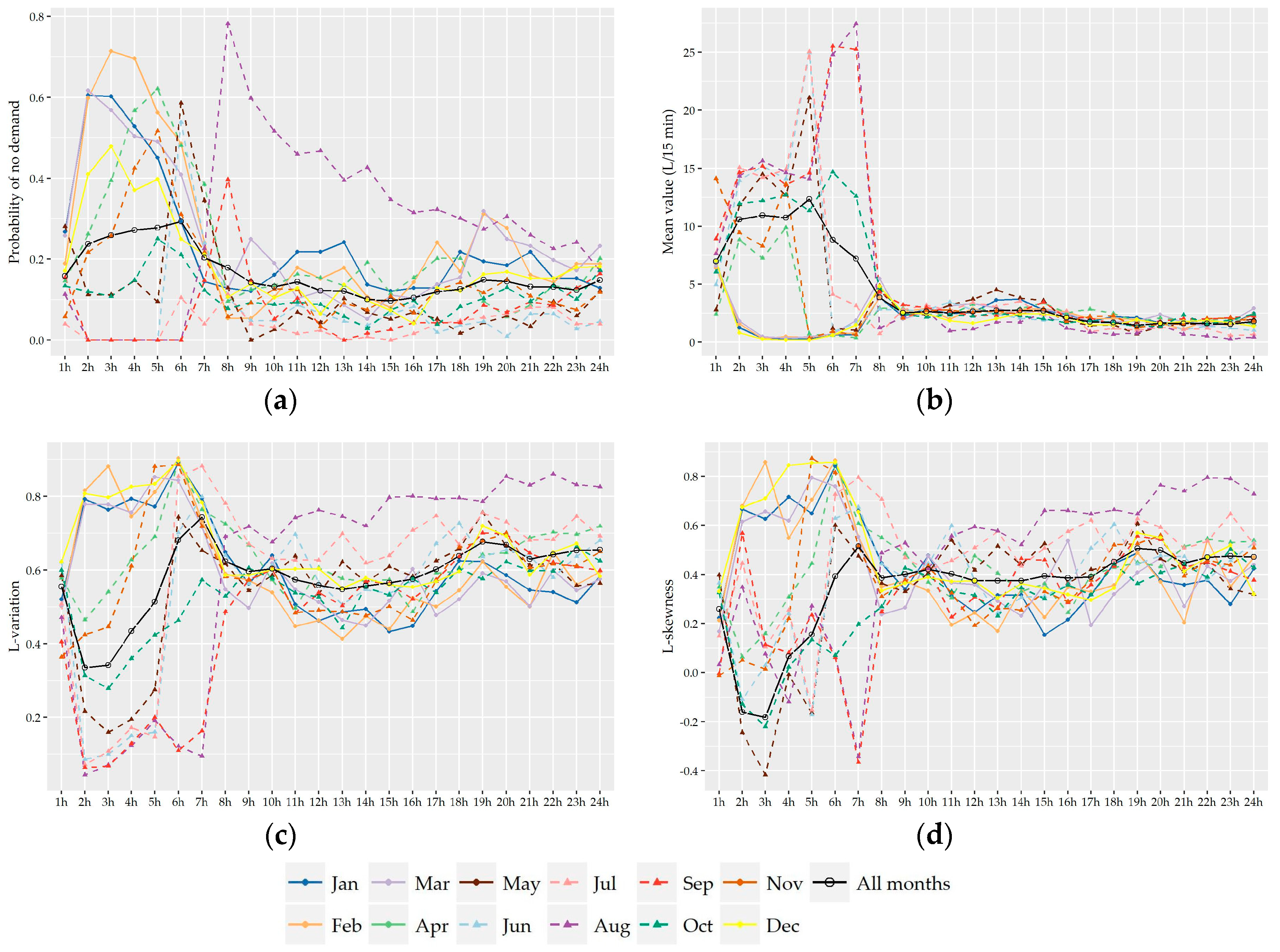
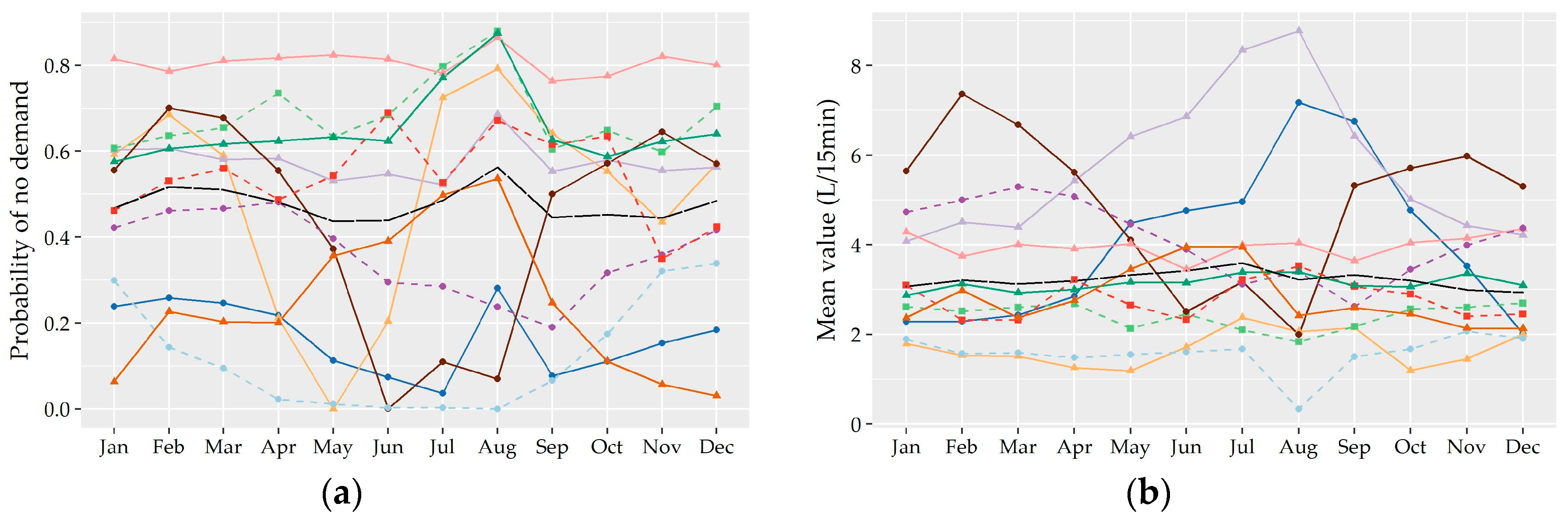
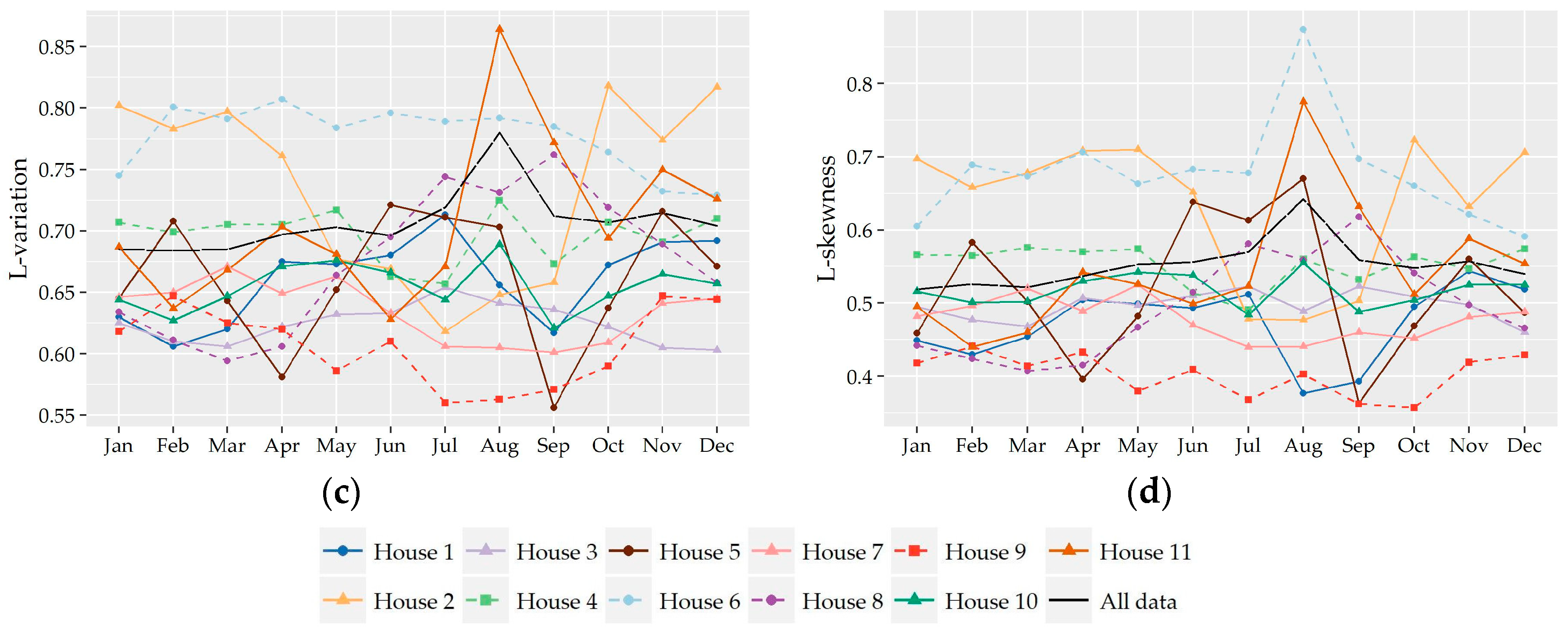
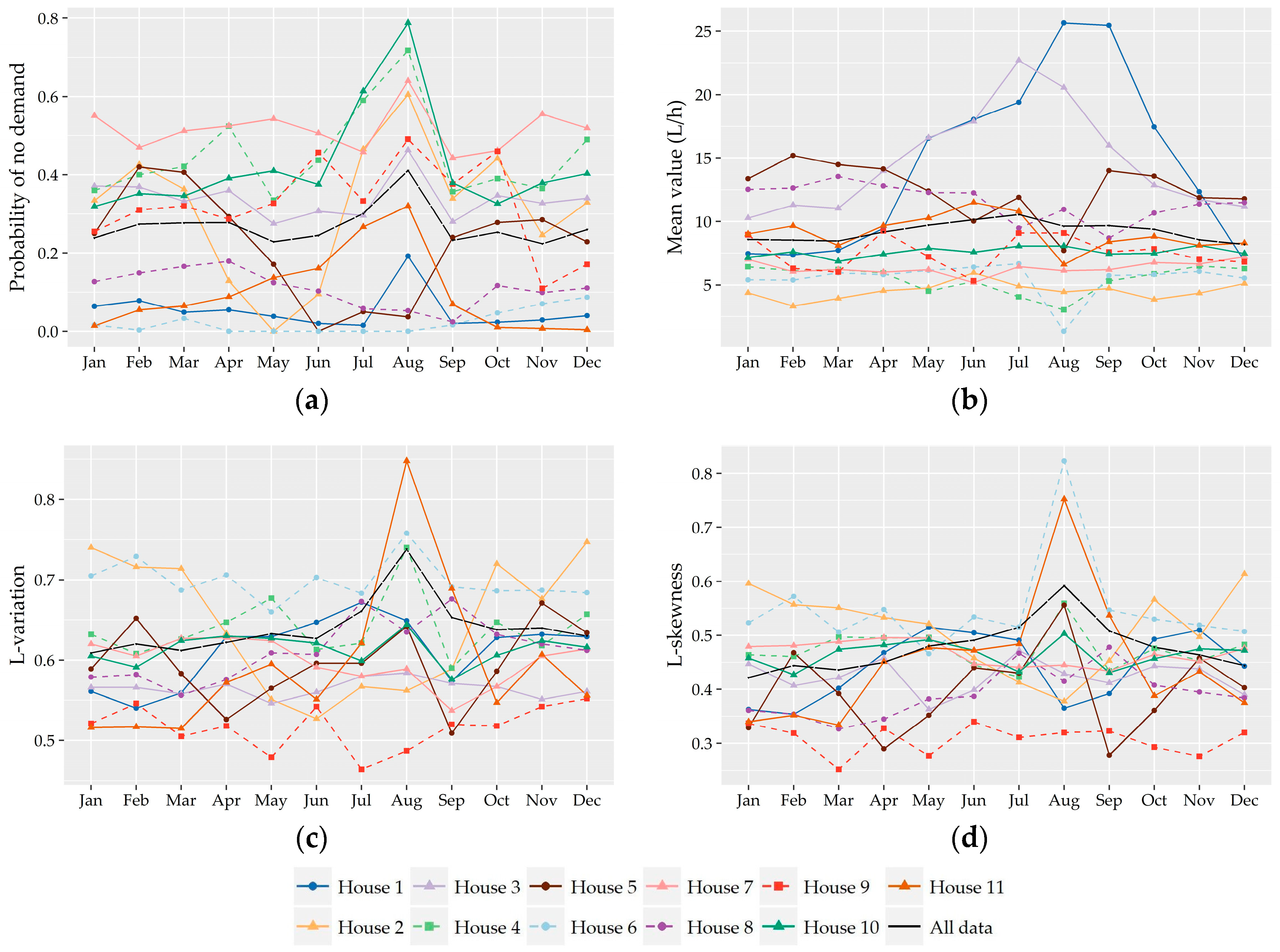
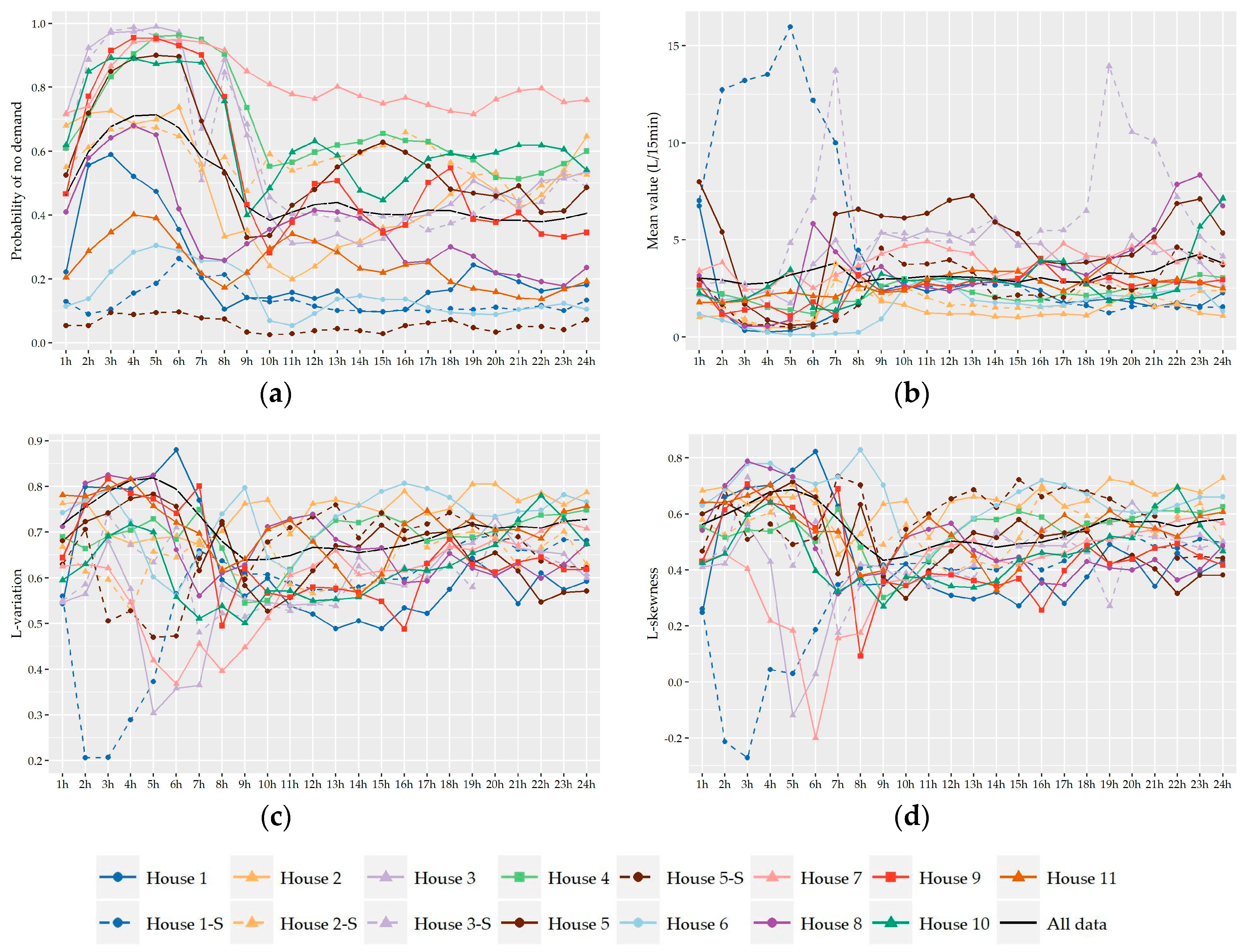
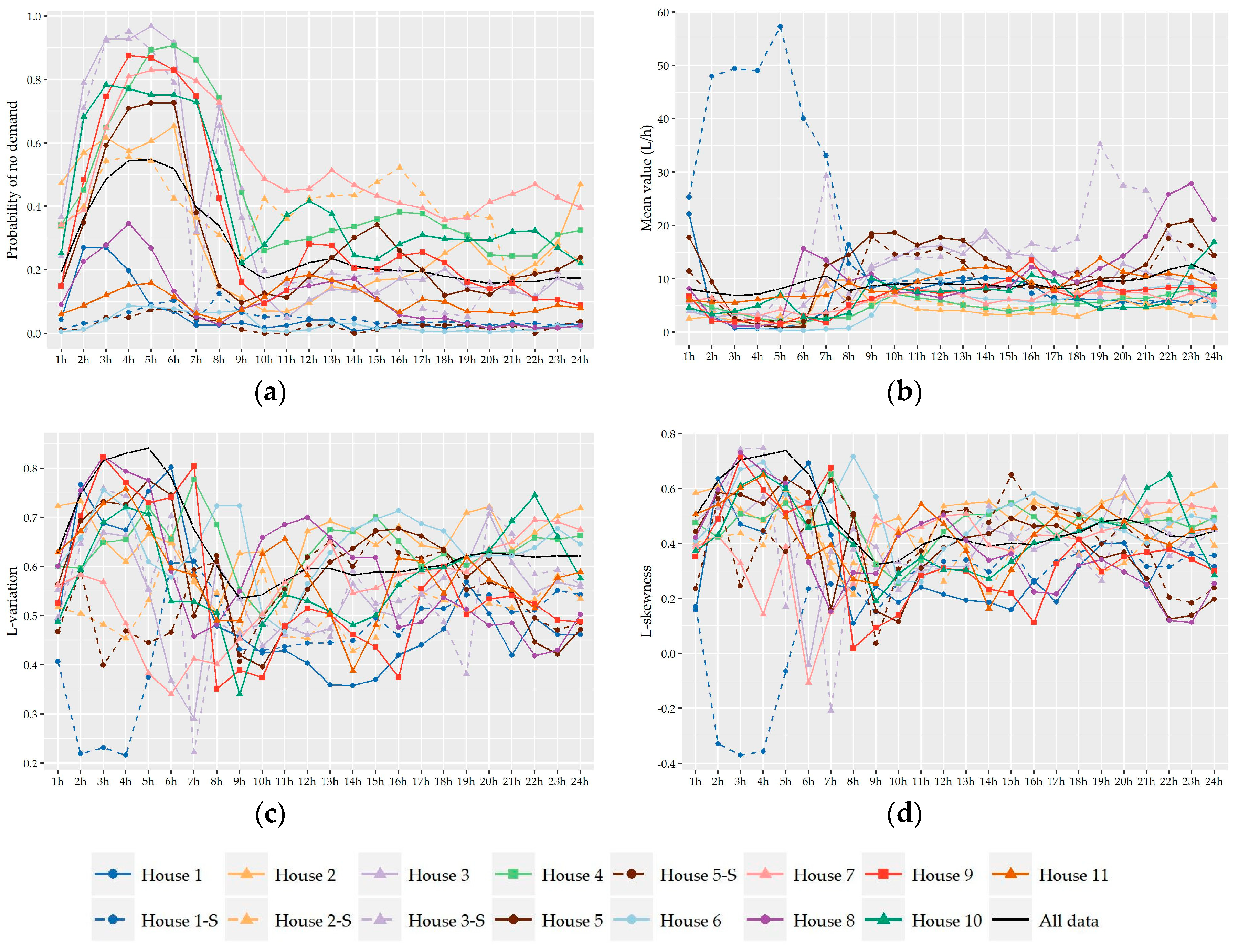
Following the analysis of the variation of the two shape characteristics of the nonzero water demand at different temporal levels of analysis (i.e., monthly, daily, hourly), the preliminary identification of most suitable probabilistic models as well as their fitting and further performance evaluation was conducted on the records used in the hour-to-hour analysis, i.e., 24 individual records for the seven households without significant monthly variation and a different set of individual records for the winter and summer period for the remaining four households (i.e., 24 × 7 + 24 × 2 × 4 = 360 records). Since L-variation and L-skewness do not exhibit significant variation from hour-to-hour especially among successive hours, the following analysis could be conducted for forming larger individual records composed of 15-minute and hourly data of more than one hour intervals (e.g., assuming a variation between night and daily hours). However, we chose to keep the seasonal discretization of the previous section in order to study a larger cluster of L-points.
Subsequently, the evaluation of the suitability of various distributions was not conducted on the basis of 11 series of households but on the basis of 360 individual records.
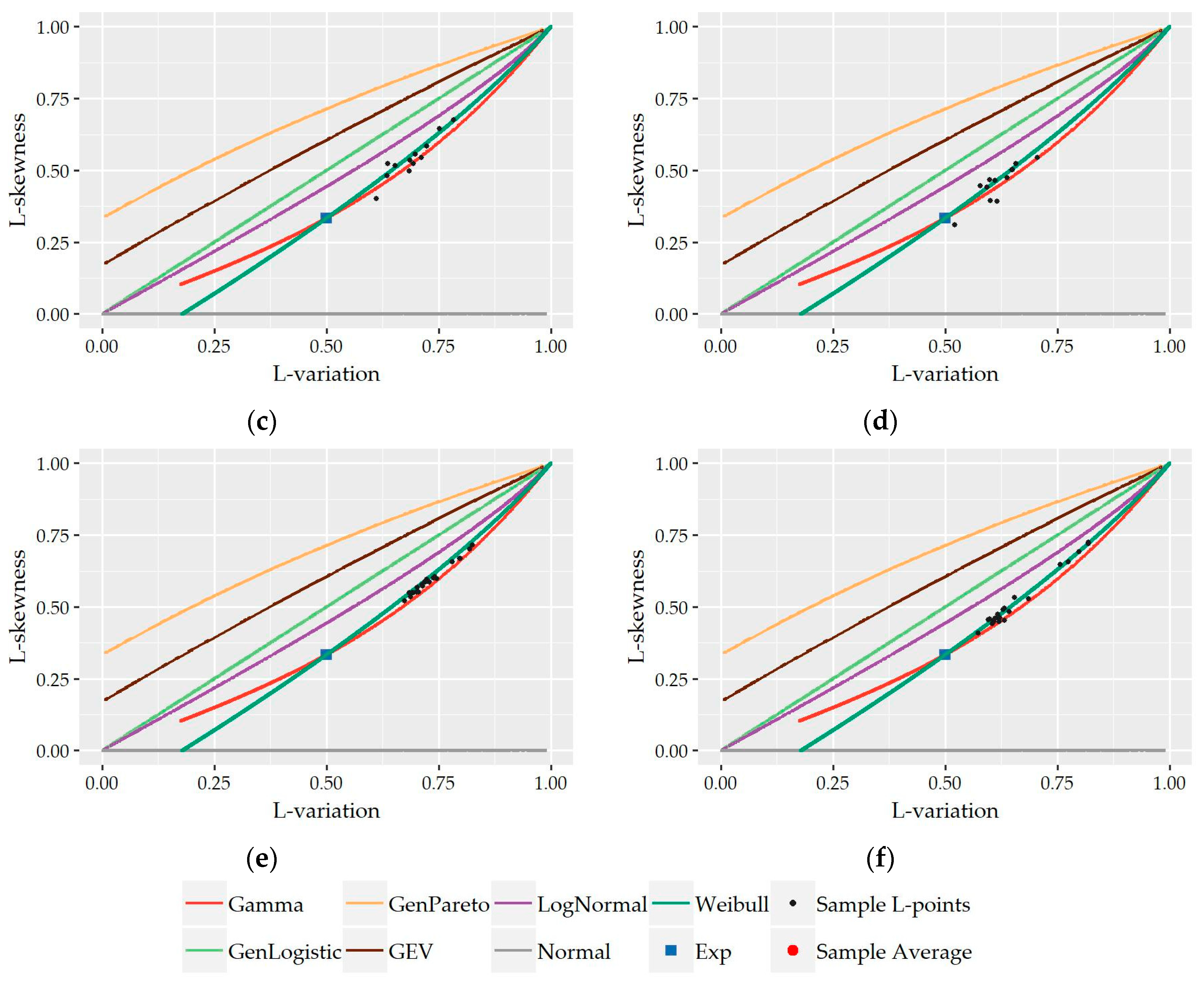
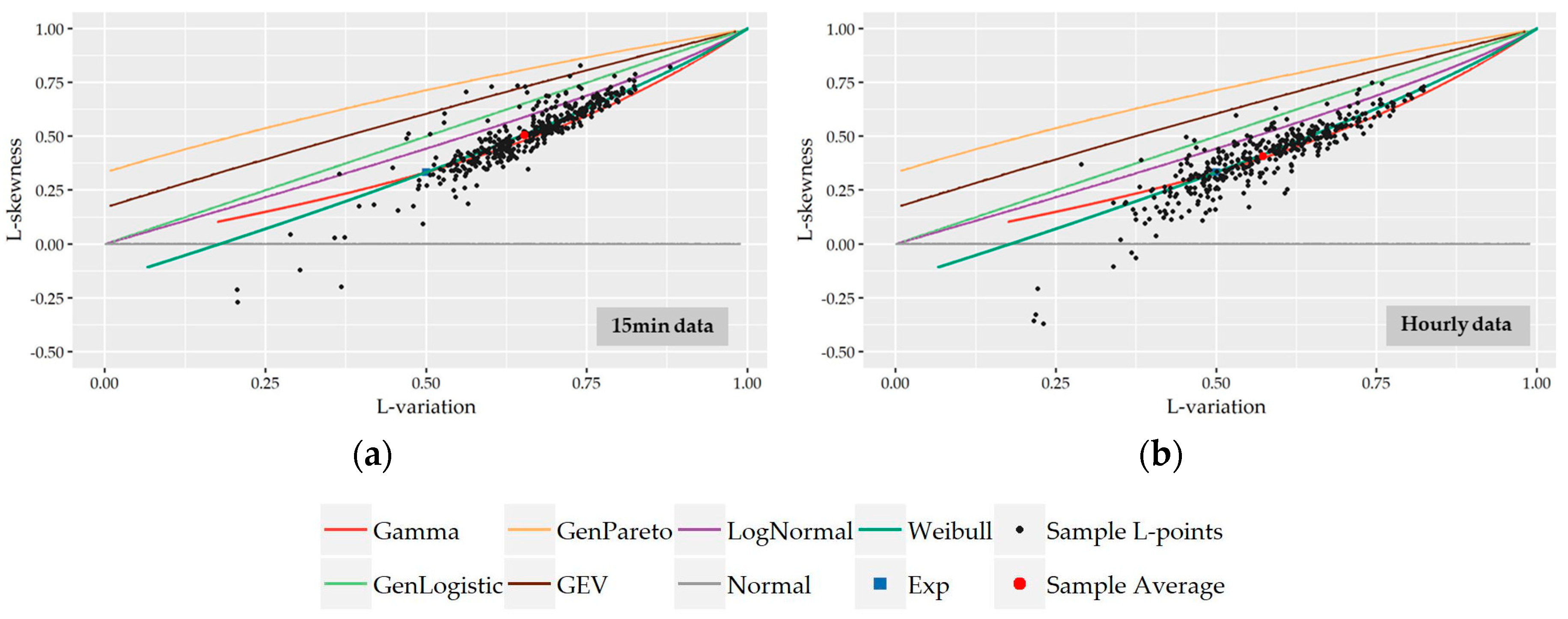
The observed L-points (τ
2,τ
3) of the understudy nonzero 15-minute and hourly water demand records along with the theoretical locus of the examined distributions are presented in
Figure 6. Visually, it is apparent that Gamma and Weibull distribution provide the best approximation to the great majority of observed L-points at both time scales while a smaller cluster of points is concentrated closer to the Lognormal distribution especially at an hourly scale. As we see, the average position of the sample 15-minute L-points (0.63,0.50) lies upon the theoretical curve of Weibull distribution while, at the hourly scale, the average point (0.58,0.40) is among the curves of Gamma and Weibull distributions close to the point of their interception. It is worth noting that the sample L-points, which are out of the main body of the cluster (i.e., τ
2 ≤ 0.50 and τ
3 ≤ 0.30) and away to the curves of the above distributions, correspond to the records of night hours, i.e., 12:00 to 8:00 am, where the probability of zero demand is high and the sample size of nonzero records is smaller. Since the variability of statistics is closely associated with sample size, it is expected that these points would be closer to the main scatter of L-points and closer to the distributions if a greater number of records was available.
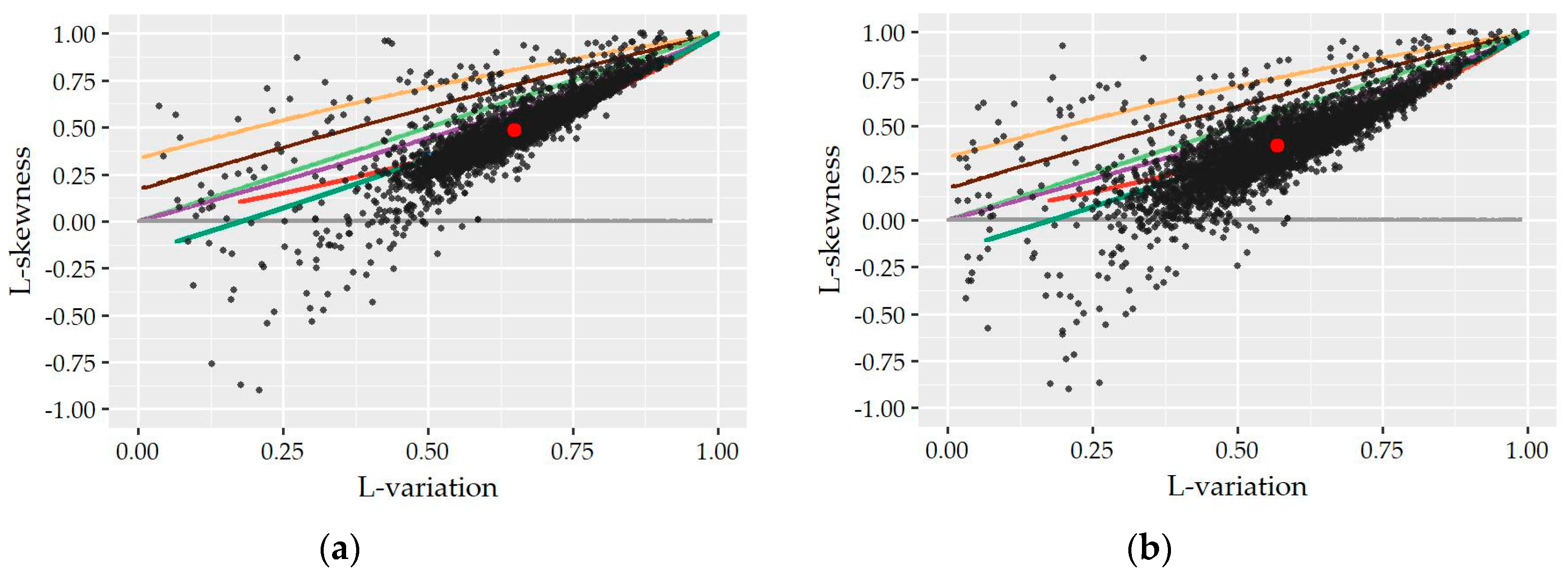
The preliminary selection of the three above discussed distributions (i.e., Gamma, Weibull, and Lognormal) as more suitable to describe nonzero demand is further supported by the complementary L-variation vs. L-skewness diagrams provided in the
Appendix B.
Figure A5a,b present the sample L-points (τ
2,τ
3) of the individual records of each hour assuming also monthly separation (i.e., 12 × 24 = 288 points for each household), at a 15-minute and hourly scale, respectively. As shown, the sample L-plots are mostly concentrated around the three above mentioned distributions while the average L-point lies upon the curve of Weibull distribution. Additionally,
Figure A5c,d present the L-points (τ
2,τ
3) of the entire nonzero record of each household (12 points) without assuming seasonal discrimination at 15-minute and hourly time scales, respectively, while
Figure A5e,f contain the L-points of the records of each hour of the day including the records of all households at 15-minute and hourly scale, respectively (24 points). In all cases, the sample L-points are very close to the curve of either Gamma or Weibull distribution.
4.2. Evaluation of the Models
The preliminary evaluation from the previous section showed that Gamma and Weibull distribution seem to be the most suitable probabilistic models to describe at least in terms of the first three L-moments. The great majority of the nonzero 15-minute and hourly water demand records of all households and all hours of the day. At the same time, it seems that a smaller percentage of records is better captured by the Lognormal distribution. The performance of the three distributions is further evaluated and compared after their actual fitting to the above described records. In this section, we present the evaluation of the three models on the basis of fitting error measures while the fitting procedure along with the analysis of the values of distribution parameters are presented in the next section.
The three probabilistic models, which are examined, have two parameters and more specifically one scale and one shape parameter with the latter controlling the asymptotic behavior of the distribution tail. The two-parameter Gamma distribution is one of the most commonly used probabilistic models in hydrological applications due to its special characteristics, i.e., it is defined only for non-negative values of the variable and is positively skewed. Its pdf is given by the equation below.
where
β > 0 is the scale parameter and
γ > 0 is the shape parameter. For
γ < 1, the pdf is J-shaped with an infinite ordinate at
x = 0 and its right tail decreases slightly faster than the exponential tail. For
γ = 1 the distribution is identical with exponential whereas, for
γ > 1, the pdf is bell-shaped and it has a tail that decreases slightly slower than the exponential one. For large values of shape parameters (
γ > 15) Gamma distribution approaches the normal.
The Weibull distribution is another popular probabilistic model and its pdf is given by the equation below.
where
β > 0 is the scale parameter and
γ > 0 is the shape parameter. Like Gamma, Weibull distribution is positively skewed and defined for non-negative values of the variable while the value of shape parameter controls the form of the pdf. For
γ < 1, the pdf is J-shaped with an infinite ordinate at
x = 0 while, for
γ = 1, the pdf tends to 1/
γ as
x approaches 0 and then decreases exponentially. For
γ > 1, the pdf tends to 0 at
x = 0 from above, increases until the mode, and decreases after the mode. Regarding the asymptotic behavior of the tail, for
γ < 1, the Weibull distribution has a heavier tail (i.e., tending to zero less rapidly) than the exponential one while, for
γ > 1, the tail decreases faster than the exponential.
Lastly, the pdf of Lognormal distribution is given by the equation below.
where
β > 0 is the scale parameter and
γ > 0 is the shape parameter. A random variable
x is lognormally distributed if random variable
is normally distributed. Due to this transformation, Lognormal distribution is defined for non-negative values of the variable, is positively skewed, and has a bell-shaped pdf. It is worth noting that the Lognormal distribution is commonly parameterized by using the mean and standard deviation of the distribution on the log scale. In the present work, we use the shape and scale parameterization concept to facilitate the direct comparison with the other two understudy distributions. Regarding extremes, Lognormal distribution is considered a heavy-tailed distribution.
The three probabilistic models are characterized by different tail behaviors, which have been have been extensively assessed and compared in the reproduction of extremes of different hydrometeorological variables such as rainfall and runoff (e.g., see Reference [
48] and the literature herein). Summarizing the above, further to the Lognormal distribution that is considered heavy-tailed distribution, Weibull can be both heavy-tailed and light-tailed depending on the shape parameter while Gamma is considered essentially as an exponential tail distribution. The ordering of these distributions from a heavier to a lighter tail is Lognormal, Weibull with
γ < 1, Gamma and Weibull distribution with
γ > 1.
It is worth noting that the three above described distributions as well as exponential distributions are special cases of the Generalized Gamma distribution [
49]. This distribution is very flexible but more complicated. It is comprised of one scale and two shape parameters that govern the form of the pdf and the behavior of the left and right tail. Although this model can be clearly regarded as a “universal model” for the 15-minute and hourly nonzero water demand, we prefer in this scenario to focus our study on two parameter models for the sake of parsimony and simplicity. Furthermore, the estimation of three parameters instead of two is a more uncertain, sensitive, and complicated procedure, requiring very long records of data. The appropriate reproduction of extremes is also of high importance in the sufficient modeling of residential water demand since the correct estimation of peak flow demand plays a crucial role in the efficient design, planning, and management of urban water systems [
6,
50]. Subsequently, a naïve selection of the probabilistic model may result in the overestimation or underestimation of maximum water demand magnitudes. In this respect, further to the standardized mean square error (MSE) that was used as the main “goodness-of-fit” measure to evaluate the overall fitting performance of the above three distributions, two additional error measures that indicate the performance in terms of extreme values were employed. A similar set of measures were employed by Papalexiou and Koutsoyiannis [
38] to evaluate the distributions’ performance on daily precipitation.
The MSE considers the relative error between the empirical and the theoretical quantile values.
where
is the value predicted by the theoretical quantile function of the distribution where
u equals the empirical probability
of
(the
i indicates the position of the
ith element in the sample of length
n, ranked in ascending order), according to the Weibull plotting position, i.e.,
. In this case, taking into account the observations on the form of empirical pdf of nonzero water demand records, we preferred to use a standardized measure instead of the classical MSE in order to avoid the dominance of large values in the estimation of the error. The fitted distribution with the smallest
value is considered as better.
Complementary to the MSE, the first measure, focused on the extremes, considers the relative error between the
m largest sample values and the corresponding theoretical values.
In the present work,
was estimated on the 10 largest values for each of the understudy record and distribution while the better fitted distribution is that with the smallest
value. The second measure assesses the percentage difference between the maximum sample value and the predicted maximum value.
The negative or positive percentage difference in implies, respectively, underestimation or overestimation of the maximum value by the fitted distribution. This error measure along with provides a clear indication on which type of tail behavior of the three understudy probabilistic is in better agreement with the observed water demand extremes.
The three distributions were fitted on the individual records described in the previous section as well as on the entire record of each household (i.e., 11 series) and each hour of the day (i.e., data from all households for each hour of the day, 24 series) for 15-minute and hourly time scale. Since all three distributions that are studied here are positively skewed, it was not possible to obtain a set of parameters for the individual records with negative or zero L-skewness. As discussed in
Section 3.2., this is the case for seven 15-minute records and 10-h records, which correspond mainly to night hours (02:00–07:00 am) during the summer period. These records were excluded from the below evaluation of fitting, which is flagged as “NA” (i.e., Not Available) in
Table A1 and
Table A2 in
Appendix B that present the best fitted distribution on the understudy 15-minute and hourly nonzero water demand records, respectively, according to
measures.
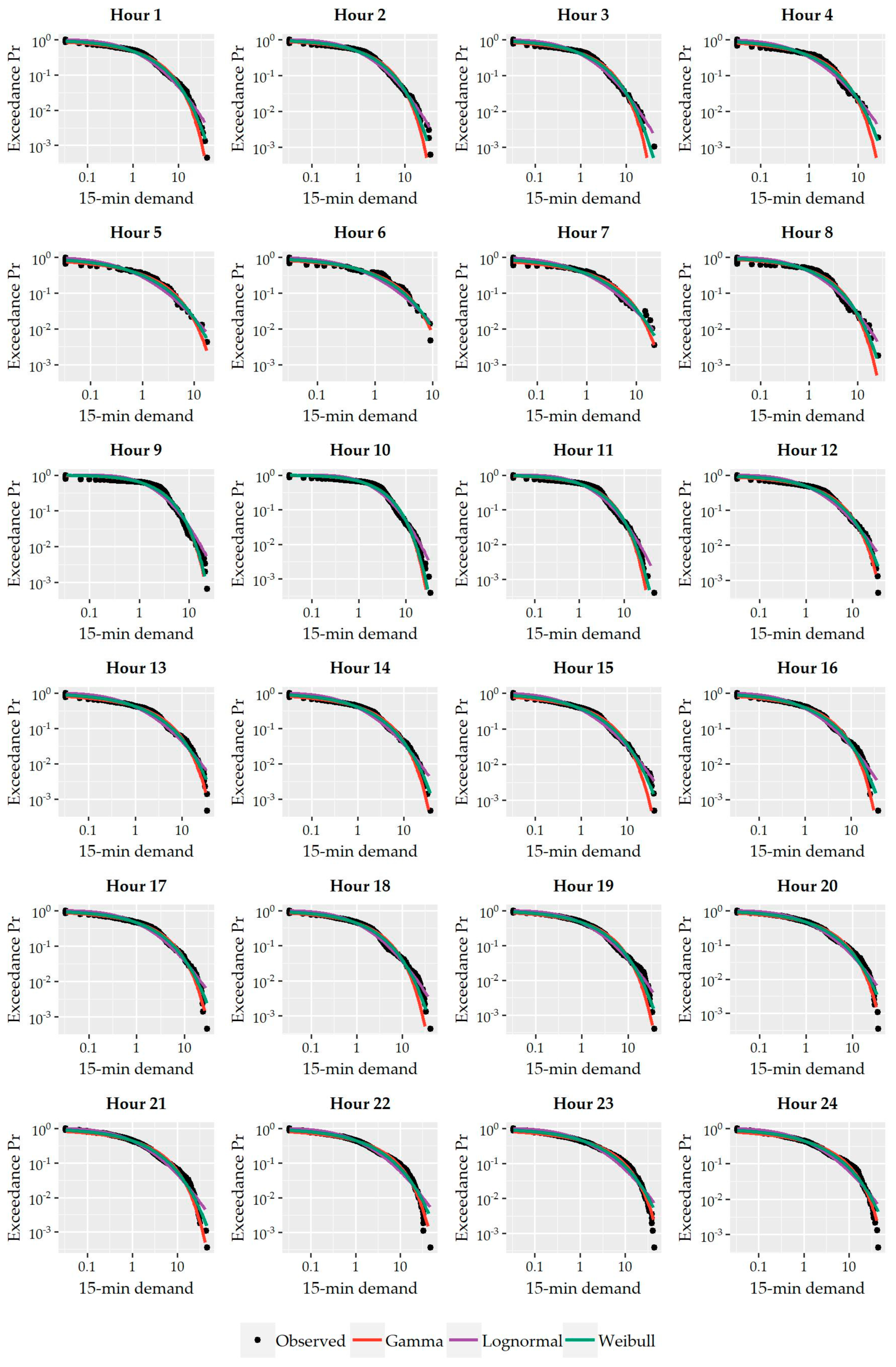
Figure 7 presents, indicatively, the empirical probability plots per hour of the three fitted distributions to the nonzero 15-minute water demand values of House #4. All three distributions fit well the sample data while the different right tail behavior of each distribution is clearly illustrated with a Lognormal distribution having a heavier tail than the other two. Similar behavior was observed on the plots of the remaining households at both time scales.
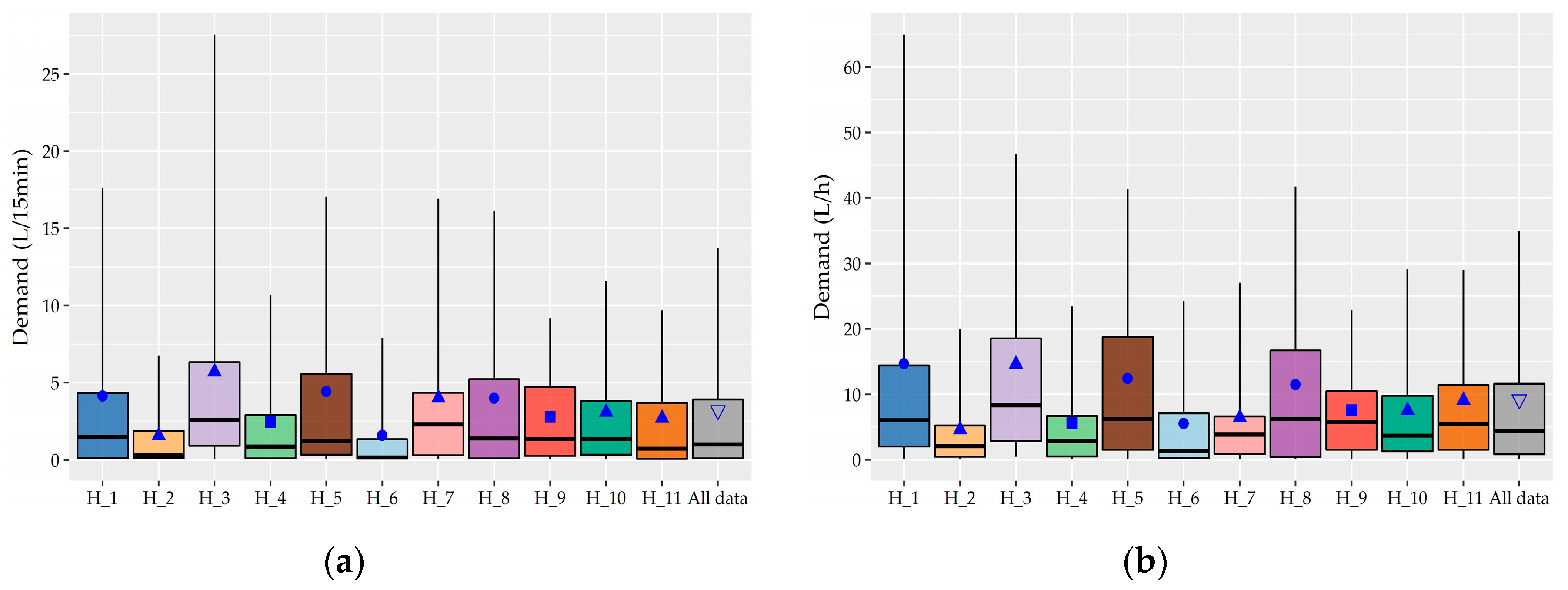
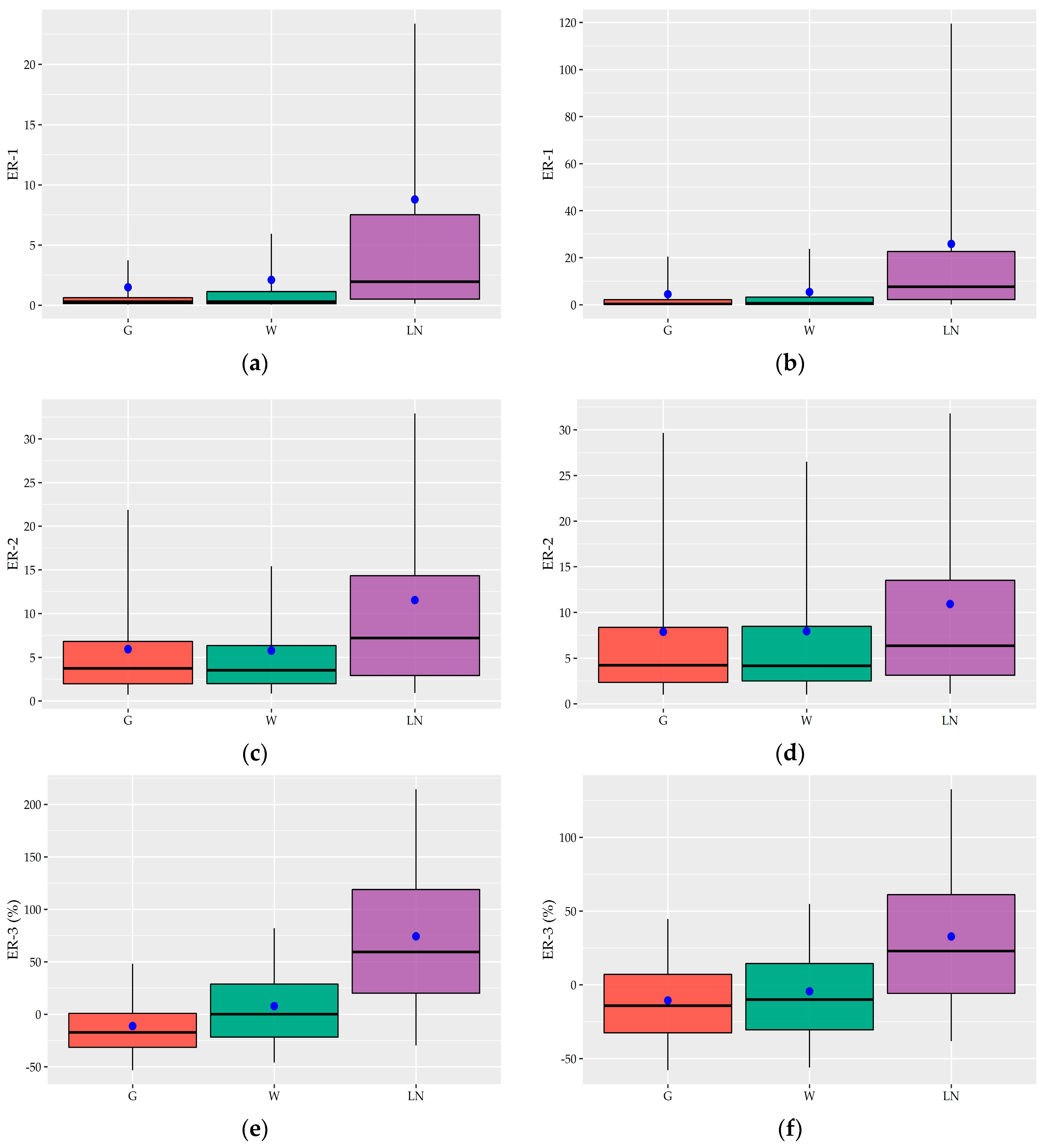
The fitting performance of G, W, and LN distribution on the individual records are graphically illustrated in terms of box plots (
Figure 8) while
Table A3 in
Appendix B summarizes the main statistical characteristics of the three error measures along with the percentage of records in which each distribution exhibits a better performance.
Figure 8 and
Table A3 show that G and W distributions perform much better than the LN. According to the
measure that assesses the overall fitting, the former two distributions achieve a very good fit to the great majority of individual 15-minute and hourly records (i.e., 85% of 15-minute records and 95% of hourly records) while the analysis of individual values revealed that they fitted equally well with the LN distribution in the records in which the latter is appears to be superior (i.e., mainly in the records of House #5 and #2). As we see in
Figure 8a,b, the LN distribution is characterized by very high mean
values, i.e., 8.78 and 25.81 in 15-minute and hourly records, respectively, along with much wider 90% ECI. In
Table A1 and
Table A2, it becomes evident that the three study distributions do not dominate in specific time intervals or households in terms of the
measure since G and W distributions are the best fitted models in the records of all households.
Focusing on the fitting measures regarding extremes, G and W distributions perform equally well with mean
equal to 5.92 and 5.77, respectively, in 15-minute records, and 7.85 and 7.93, respectively, in hourly records. On the contrary, the LN distribution has higher mean values such as 11.53 and 10.6 at 15-minute and hourly scale, respectively, and wider 90% ECI. However, its performance seems to be improved in the hourly records. In terms of
measure that evaluates the difference between the predicted and observed maximum value, LN distribution, which is considered a heavy-tailed model, tends to overestimate the maximum on average 74.31 and 32.76 at 15-minute and hourly scale, respectively, which have very wide 90% ECI, ranging from −29.73% to 214.49% and from −38.26% to 132.62, respectively. In contrast, both G and W distributions are able to produce maximum values that are in closer agreement with the observed one with mean
equals to −11.27 and 7.72, respectively, in 15-minute records and −10.65 and −4.45, respectively, in hourly records while the 90% ECI range of variation is much narrower than the corresponding LN distribution.
Figure 8e shows that G distribution tends to underestimate the predicted maximum value of 15-minute records while the
values of W distribution have a uniform dispersion around the median that is very close to zero. Regarding hourly records, as
Figure 8 presents, the two distributions show similar performance, underestimating the maximum. Taking into account the strictness of the last assessment criterion that examines values with exceedance probability very close to 0 along with the results of the
measure, the general performance of G and W distribution in terms of extremes can be characterized as exceptionally good at both time scales.
Further to individual records, the three distributions were also fitted and evaluated on the entire record of each household as well as on the data of the “parent household” (i.e., 12 series).
Table A4 in the
Appendix B reveals that G and W distributions outperform LN in terms of all error measures in all cases and achieve an equally good fitting to the observed data. Focusing especially on
and
measures, it is evident that the fitting of LN distribution to the sample tail is poor, overestimating the maximum value. Since the entire records of each household are much larger than the individual one allowing a more accurate estimation of parameters, this can be regarded as an additional important indication of the non-suitability of this heavy-tailed distribution to model the nonzero 15-minute and hourly demand values.
The above analysis provided insights in the two of the questions posed in the beginning of this sections, i.e., which are the most suitable models to simulate the understudy variables and whether there is one or a set of models that prevail the others. As shown G, W and LN distributions are able to describe the great majority of nonzero water demand records, while the more thorough evaluation of the three models revealed the superiority of the two former models compared to the LN distribution. At the same time, G and W distributions show an almost equally good performance, at least on the basis of three error measures.
However, it is of high importance to investigate whether G and W distributions are complementary in the sense that one model achieves a good fitting on the records in which the other model has poor performance and vice versa or the two models have similar performance in the same records. This directly answers the third question posed in the beginning of
Section 4, i.e., whether we can use just one probabilistic model to reproduce the characteristics of nonzero water demand records of all households and all hours of the day, indicating if there is just one distribution that should be the first choice in the modeling of nonzero water demand at these time scales.
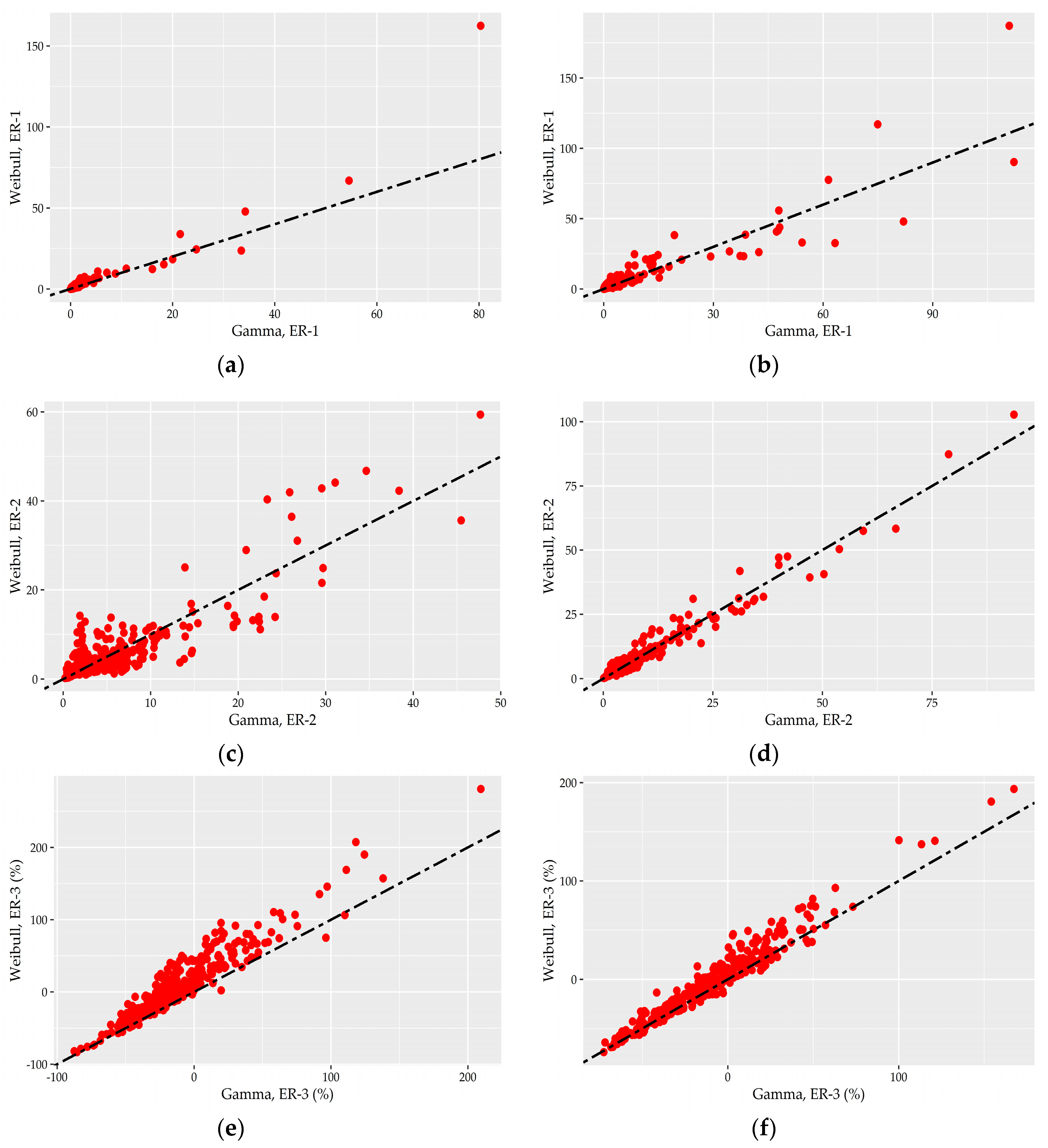
A direct comparison of the G and W distribution is provided in the scatter plots of
Figure 9 that depict the error measures of the fitting of the two models on individual records. In the plots corresponding to
and
measures, a point above the diagonal black dashed line implies better performance for G distribution for this record while the points below the line corresponds to records in which W distribution achieved a better fit. In the plots depicting
values, the points with both coordinates greater than zero imply an overestimation of the maximum from the two models and can be interpreted as the plots of the other two error measures while the opposite stands for the points with both coordinates lower than zero.
As is apparent in all box plots, the performance of G and W distributions follows a similar pattern in the sense that they exhibit a poor fit in the same few records, which correspond to the nigh hours of summer and winter period of House #1 while an almost identical good fitting was achieved for the remaining records. Similar scatter plots presenting the points of the LN distribution show that the fitting error for the “poor-fitted” points is even higher. Furthermore, we can see that especially the and points at the hourly scale are dispersed closely around the diagonal line, which implies an almost identical fitting performance.
The above observations provide strong evidence that the G and W distributions cannot be regarded as complementary models but as essentially equally good models. However, if there was a necessity for the discrimination of just one model, then Weibull distribution should be the first choice to represent the nonzero water demand data both at 15-minute and hourly time scales due to its ability to better reproduce the observed extremes.
4.3. Fitting and Parameters of the Models
In the present section, we describe the fitting procedure of the G, W, and LN distributions to the nonzero records water demand records, providing the actual values of their scale and shape parameters. From a practical point-of-view, the derive sets of parameters consist of valuable prior information, e.g., for instance, using the mean values of the parameter as the initial estimation especially in cases where no recorded data is available for a household or the sample size is small and, subsequently, the sufficient fitting of a model is highly uncertain.
To fit the three models, the method of L-moments was followed by using the analytical formulas for the first three L-moments for each distribution. This method is analogous to the usual method of moments, according to which the parameter estimates are obtained by equating the first
p sample L-moments to the corresponding distribution moments. Then, by solving the system of equations, we obtain the shape and scale parameters of the distribution. The first three L-moments for the three understudy distribution (e.g., [
40]) as a function of scale parameter
β and shape parameter
γ are provided in
Table A5 in
Appendix B. The method of L-moments were implemented in the R programming environment [
51] with the use of the “lmom” package [
52]. Scale and shape parameters were obtained for the nonzero 15-minute and hourly time scales and the individual records described in the previous section as well as on the entire record of each household (i.e., 11 series) including each hour of the day (i.e., data from all households for each hour of the day, 24 series). As explained in the previous section, the records with negative or zero skewness on which it was not possible to fit the three distributions were excluded from the analysis. The scale and shape parameters for 15-minute and hourly individual records are presented in the form of box plots in
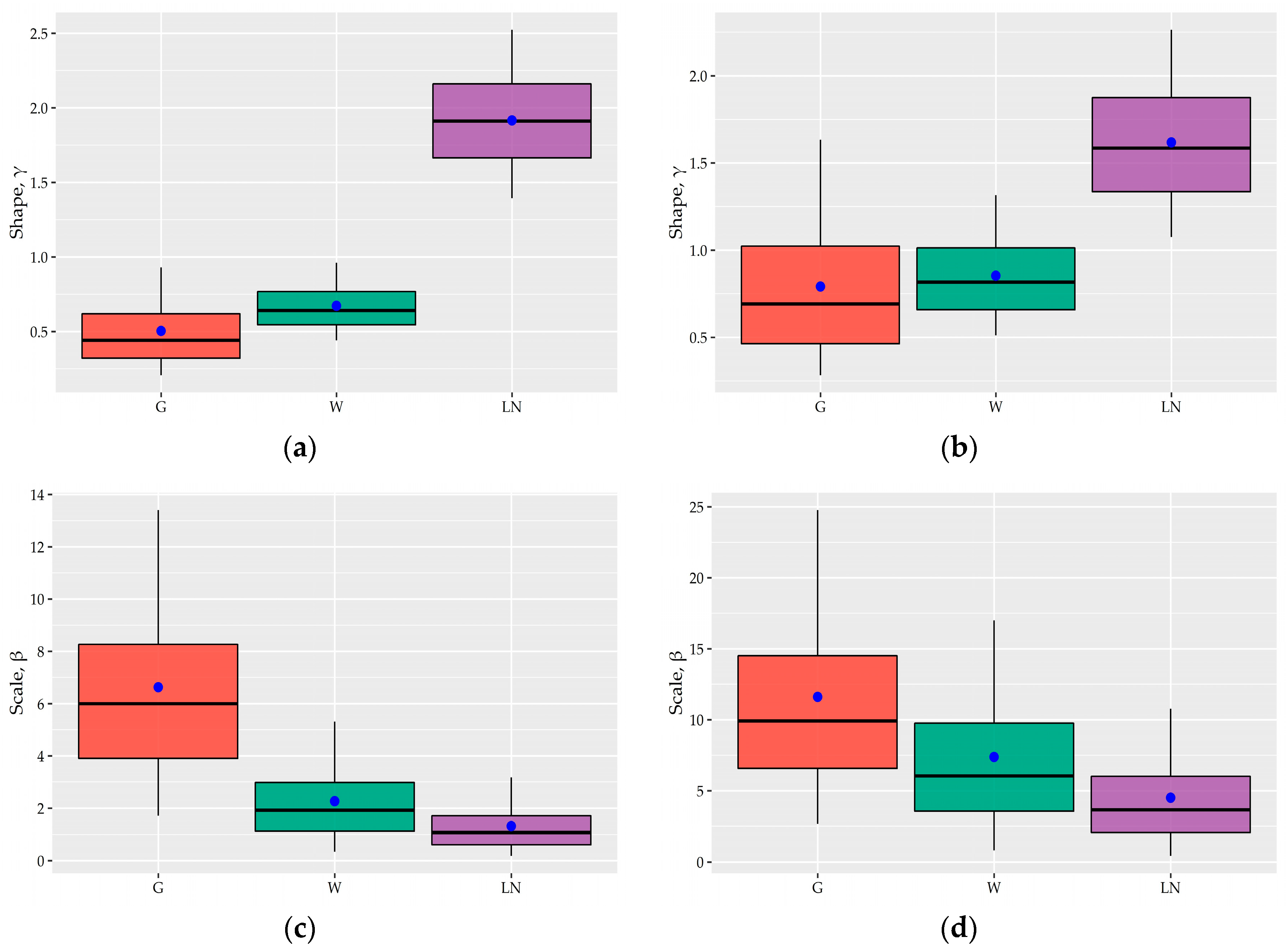
Figure 10 while their summary statistics are given in
Table A6 in
Appendix B. With regard to G and W distributions, we also included in the present analysis the shape and scale parameters for the LN distribution.
As evident in
Figure 10, the shape parameters of the two former models and especially those of W distributions vary in a very narrow range at both time scales (i.e., consider that the theoretical range of this parameter is (0,∞)). The values of shape parameters for both W and G distribution is lower than 1 for the great majority of 15-minute records, i.e., the 90% ECI is (0.44,0.96) and (0.21,0.93), which indicates J-shaped density functions. Regarding the hourly records, a greater number of records results in bell-shaped densities with
γ > 1 since the 90% ECI of
γ for W and G distribution is (0.51,1.32) and (0.28,1.63), respectively. As is also apparent in
Table A7, the variability of the shape parameter of the fitted distributions to the entire records of each household is even lower with all values being significantly less than 1.
As expected, the scale parameters vary in a wider range since this type of parameter depends on the unit of measurement and the values of a variable. The effect of the scale parameter is to stretch out the pdf of the distribution. As we can see in general, the scale parameters of hourly records are greater than the corresponding 15-minute records while, for both time scales, the empirical 90% ECI of the β parameter of Weibull distribution, i.e., (0.34,5.31) and (0.81,16.99) for 15-minute and hourly records, respectively, is much narrower than that of Gamma distribution, i.e., (1.71,13.41) and (2.67,24.77) for 15-minute and hourly records, respectively.