Analysis of Flood Risk of Urban Agglomeration Polders Using Multivariate Copula
Abstract
:1. Introduction
2. Materials and Methods
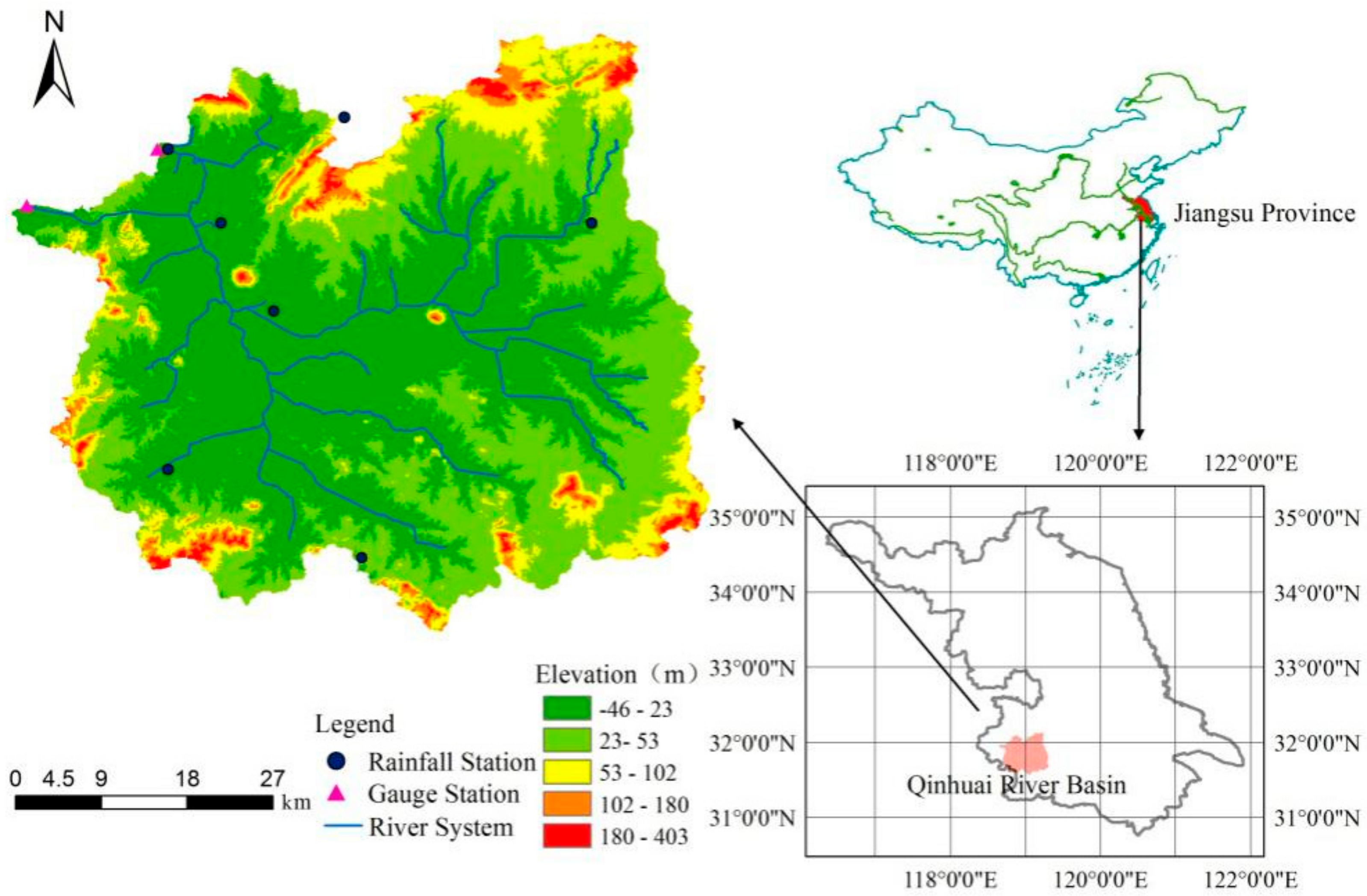
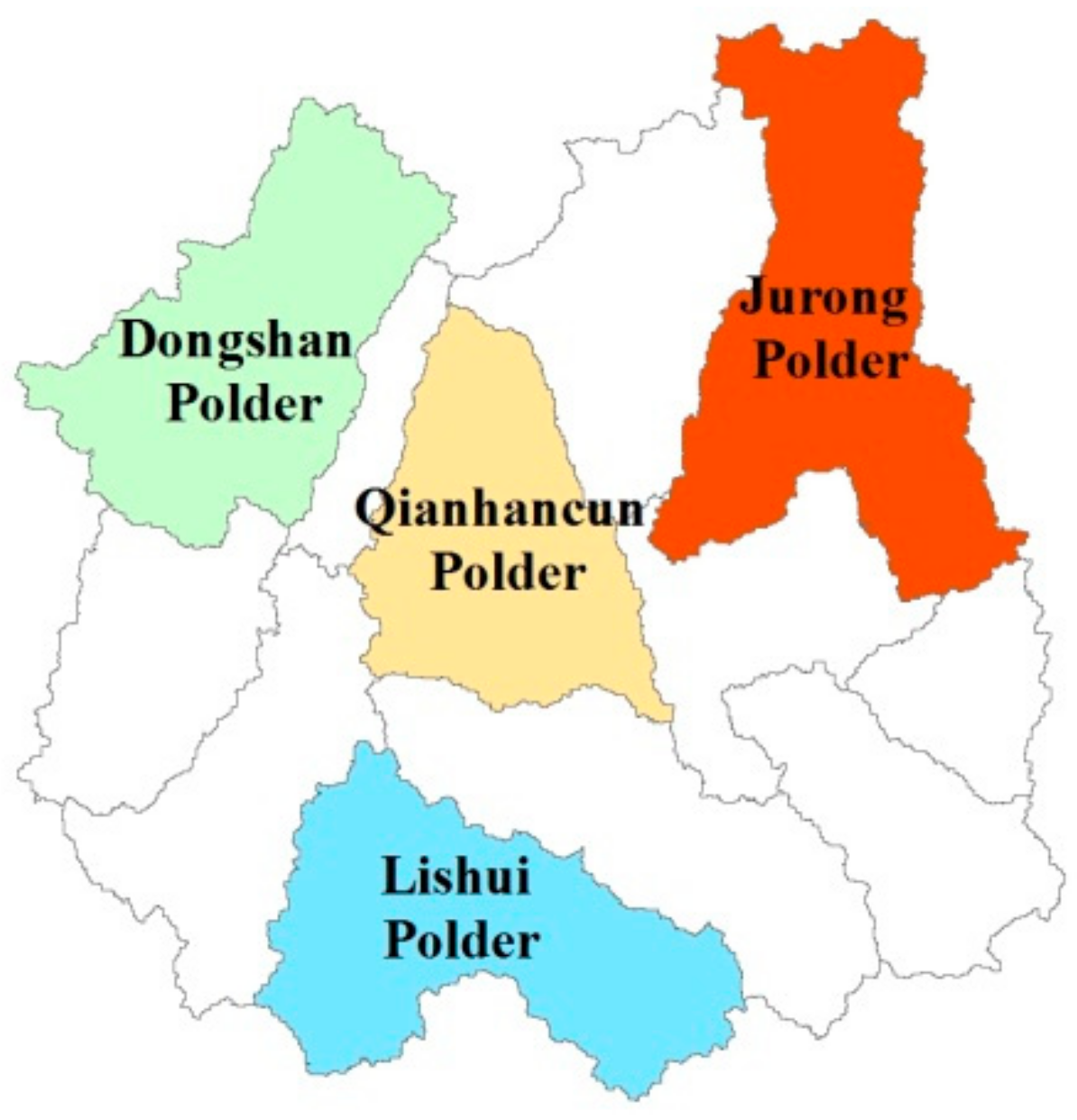
2.1. Study Area and Data
2.2. Methodology
2.2.1. Archimedean Copula
2.2.2. Dependence and Ranks
- Chi-plot
- K-plot
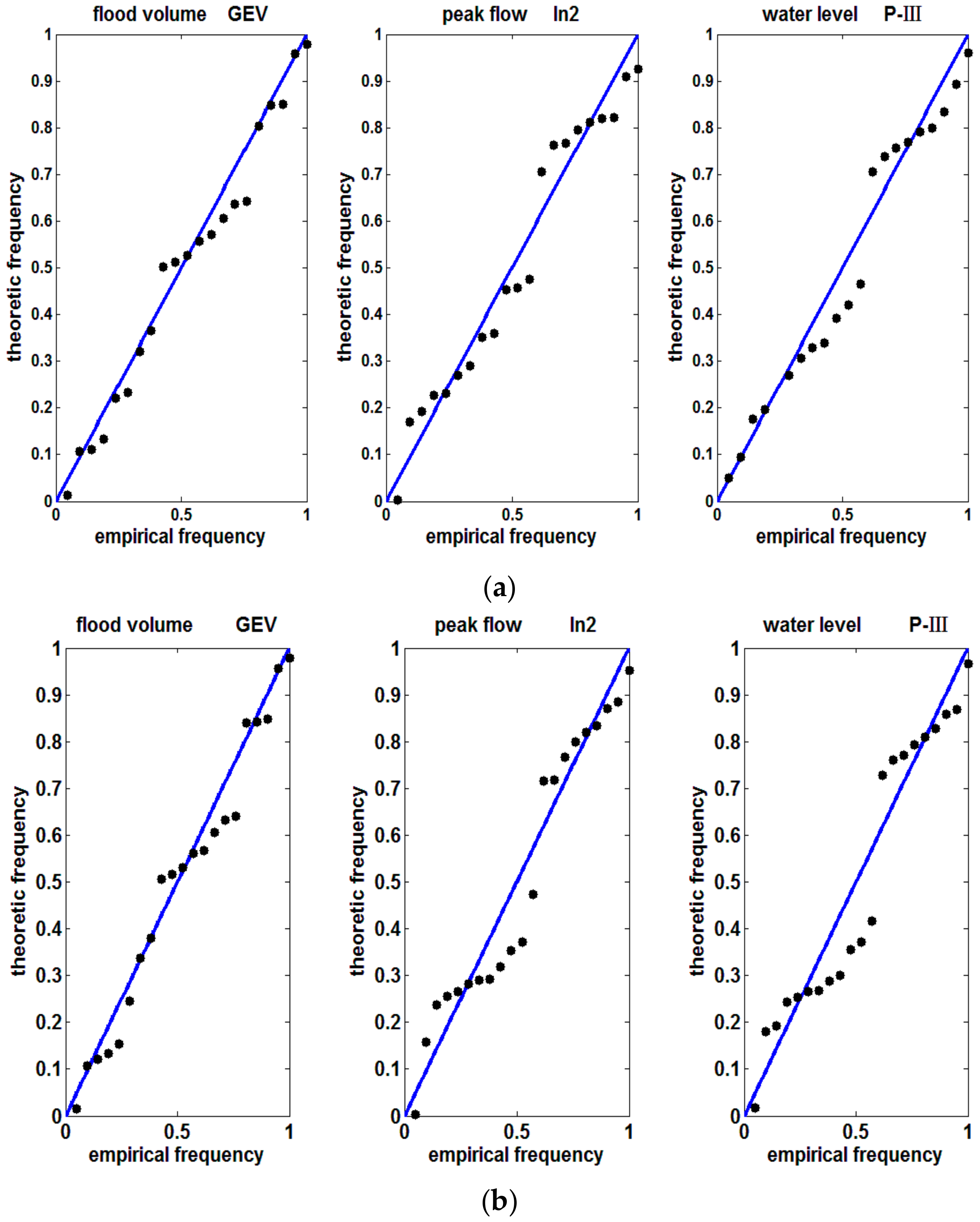
2.2.3. Goodness of Fit
3. Results
3.1. Dependence of Flood Characteristics
3.2. Marginal Distribution
3.3. Joint Distribution
4. Discussion
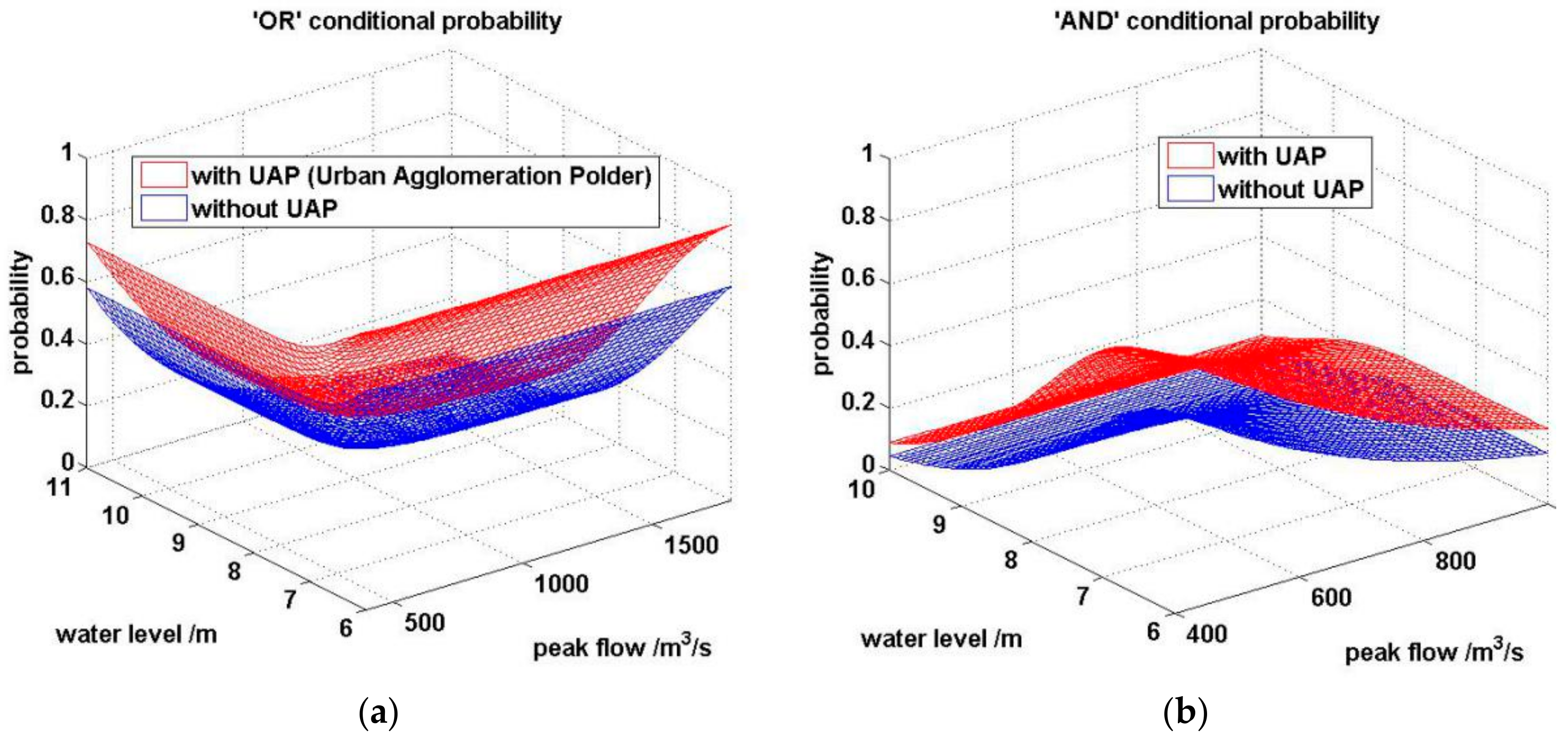
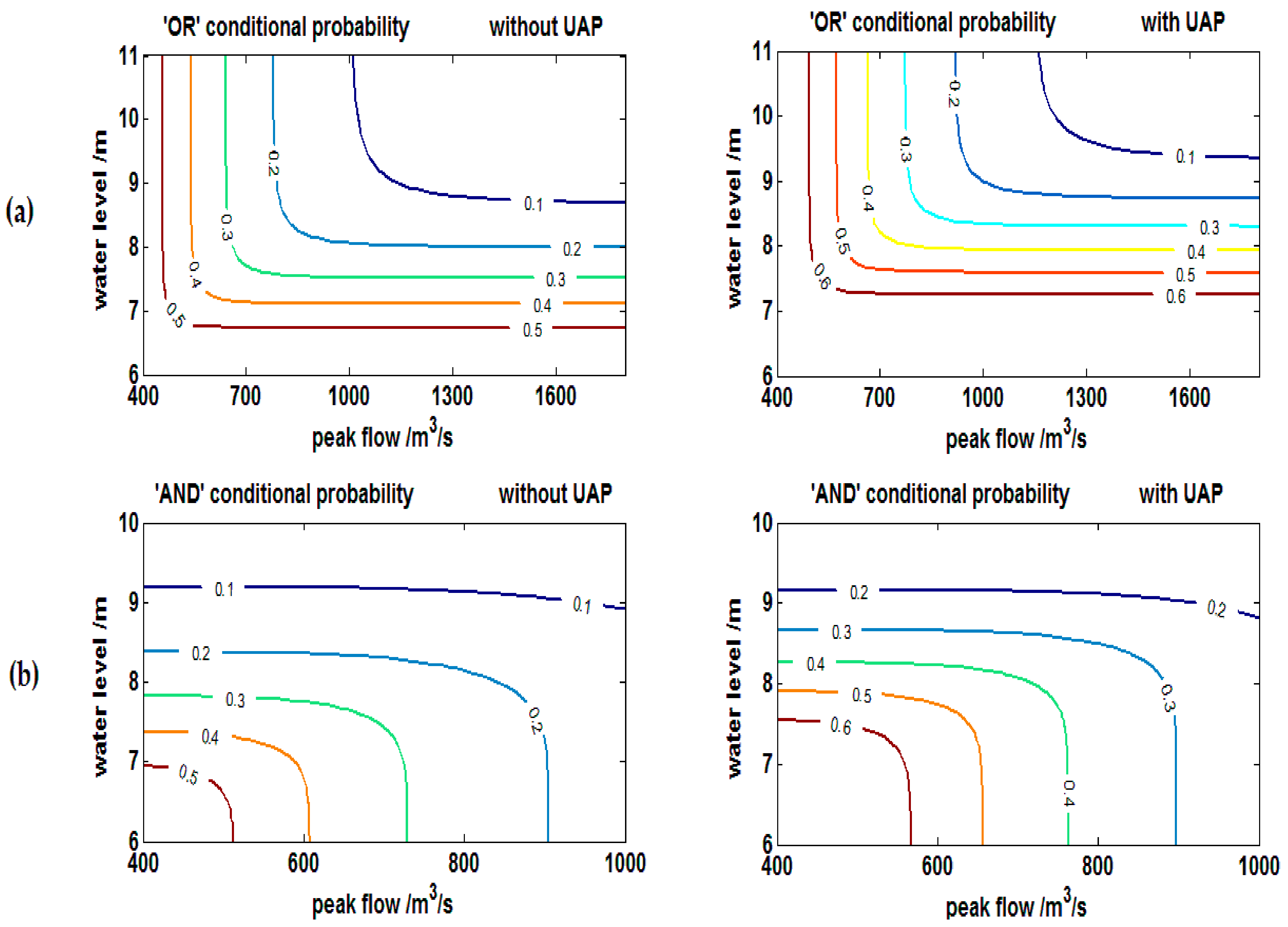
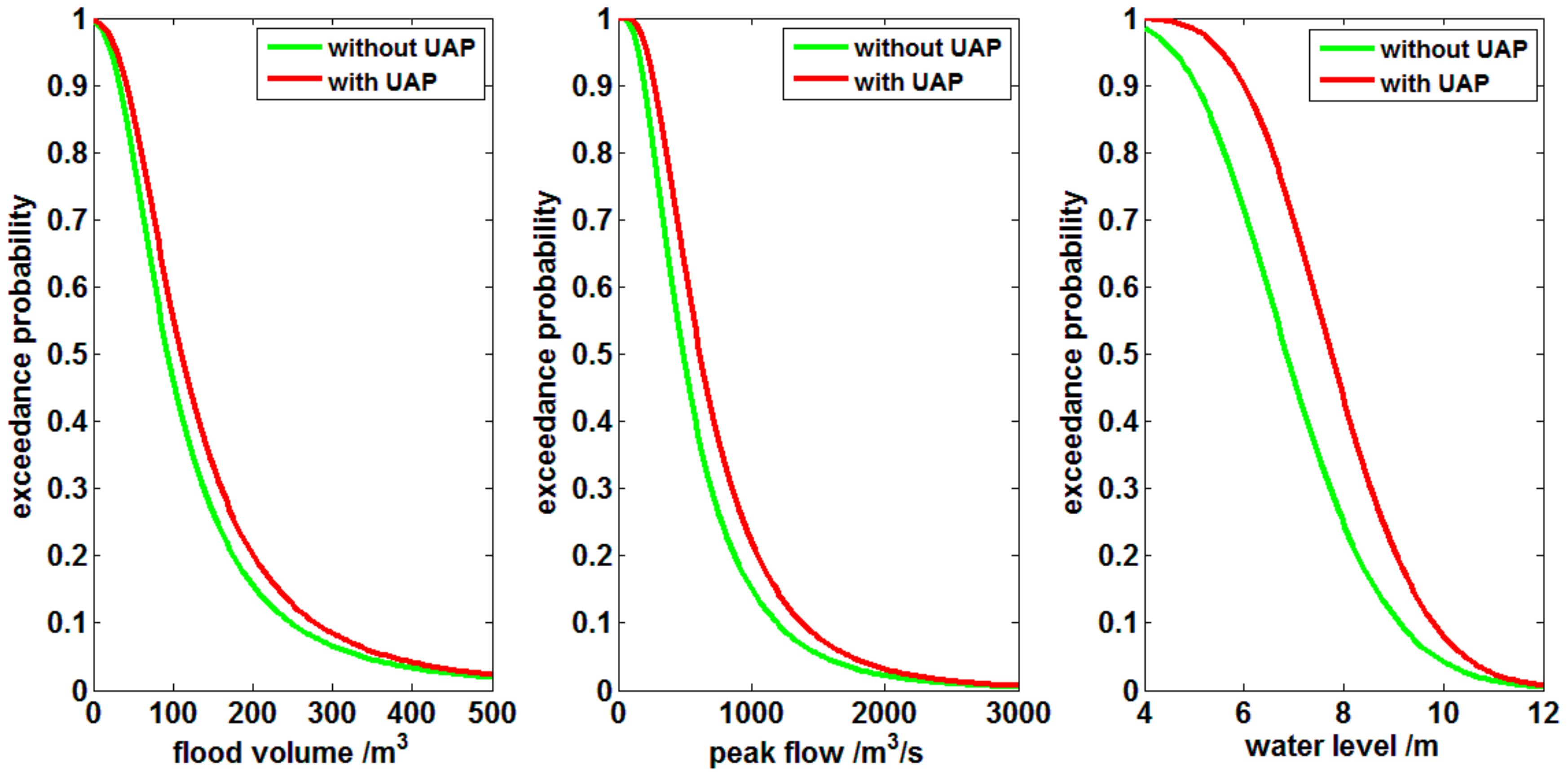
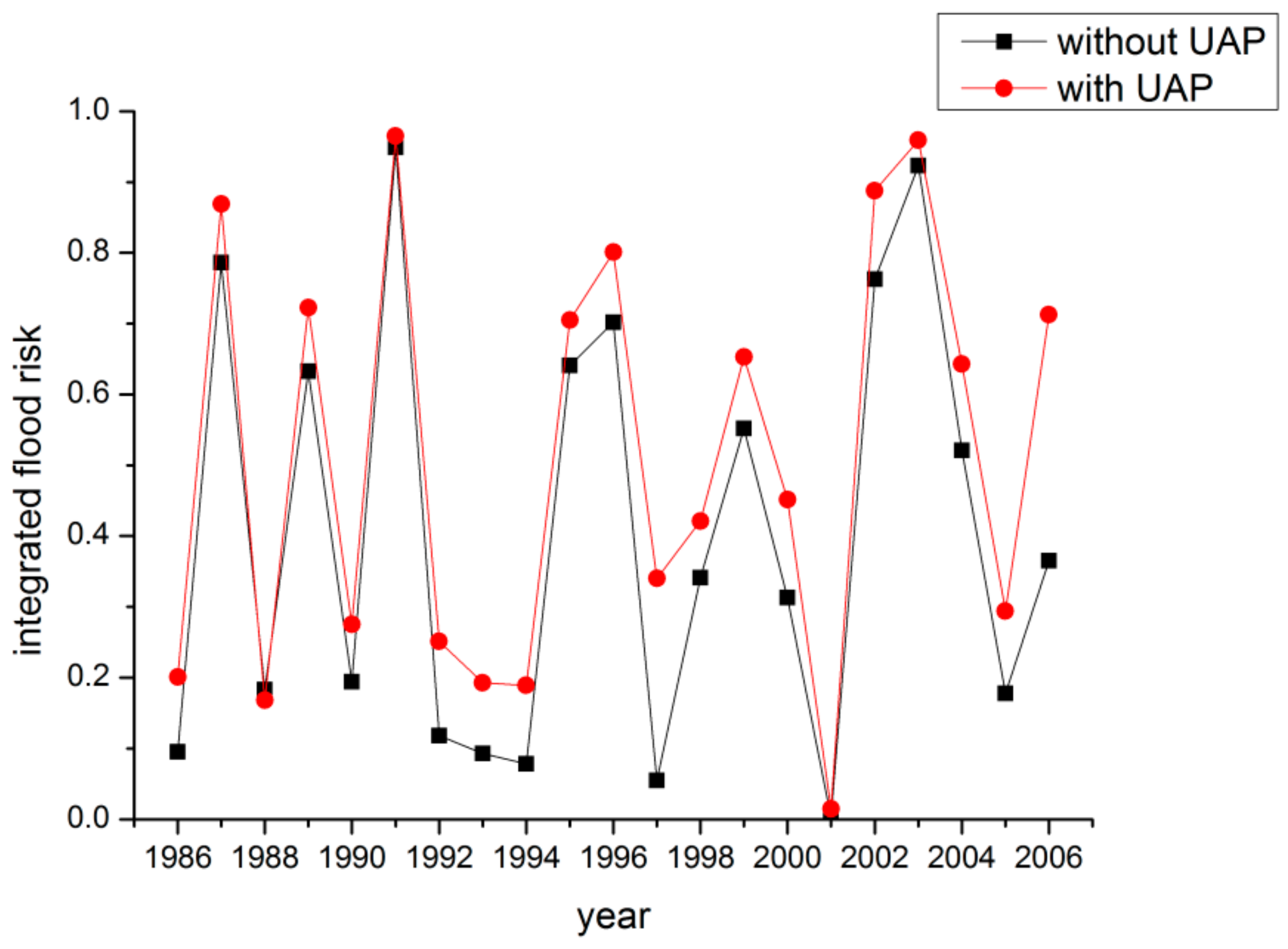
4.1. Impacts on Flood Risks of Polders
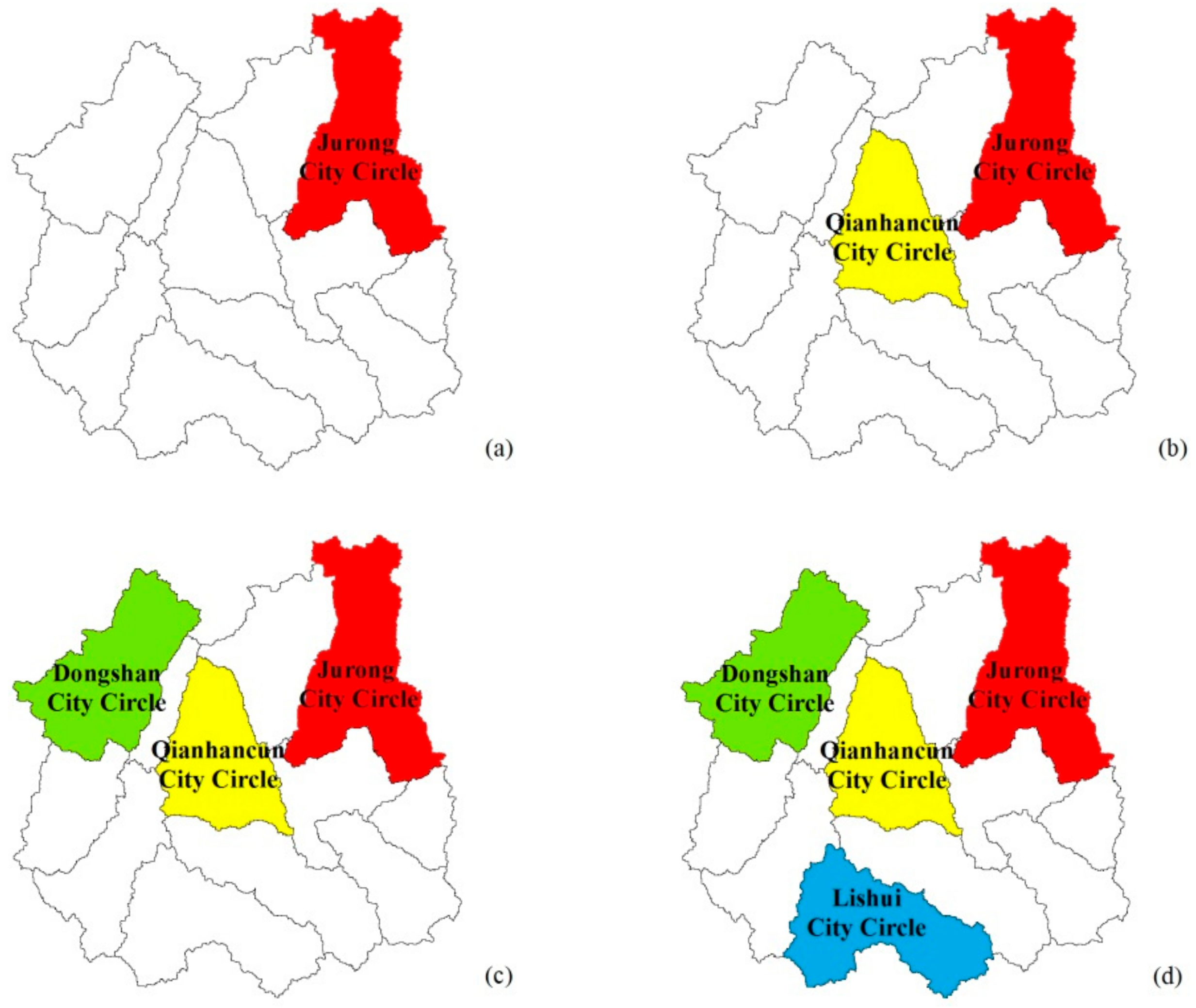
4.2. Impacts on Flood Risks of Polder Area
- (a)
- Jurong City Circle only;
- (b)
- Jurong, Qianhancun City Circle combined;
- (c)
- Jurong, Qianhancun, Dongshan City Circle combined; and
- (d)
- Jurong, Qianshancun, Dongshan, Lishui City Circle combined.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Variable | With UAP | Without UAP | ||
|---|---|---|---|---|
| Spearman | Kendall | Spearman | Kendall | |
| V&P | 0.921(4.5 × 10−6) | 0.762(5.8 × 10−8) | 0.877(9.5 × 10−7) | 0.686(2.4 × 10−6) |
| V&Z | 0.893(5.1 × 10−8) | 0.73(4.4 × 10−6) | 0.821(3.4 × 10−6) | 0.619(3.2 × 10−5) |
| P&Z | 0.974(1.2 × 10−13) | 0.921(6.6 × 10−9) | 0.926(4.7 × 10−6) | 0.8(6.0 × 10−9) |
| Statistics | Without UAP | With UAP | ||||
|---|---|---|---|---|---|---|
| V | P | Z | V | P | Z | |
| Mean | 126.03 | 591.21 | 6.99 | 143.99 | 729.01 | 7.84 |
| Std. | 112.81 | 350.50 | 1.45 | 118.17 | 419.10 | 1.41 |
| Skewness | 1.90 | 0.59 | 0.30 | 1.73 | 0.74 | 0.18 |
| Kurtosis | 6.20 | 2.32 | 2.20 | 5.64 | 2.72 | 2.32 |
References
- Luo, P.P.; Zhou, M.M.; Deng, H.Z.; Lyu, J.; Cao, W.Q.; Takara, K.; Nover, D.; Schladow, S.G. Impact of forest maintenance on water shortages: Hydrologic modeling and effects of climate change. Sci. Total Environ. 2018, 615, 1355–1363. [Google Scholar] [CrossRef] [PubMed]
- Luo, P.P.; He, B.; Duan, W.; Takara, K.; Nover, D. Impact assessment of rainfall scenarios and land-use change on hydrologic response using synthetic Area IDF curves. J. Flood Risk Manag. 2018, 11, S84–S97. [Google Scholar] [CrossRef]
- Luo, P.P.; Mu, D.R.; Xue, H.; Ngo-Duc, T.; Dang-Dinh, K.; Takara, K.; Nover, D.; Schladow, G. Flood inundation assessment for the Hanoi Central Area, Vietnam under historical and extreme rainfall conditions. Sci. Rep. Nat. 2018, 8, 12623. [Google Scholar] [CrossRef] [PubMed]
- Jiao, T. Influence of construction in low-lying region on aquatic environment of city and countermeasures. Jiangsu Environ. Sci. Technol. 2006, S2, 121–123. [Google Scholar]
- Luo, P.P.; He, B.; Takara, K.; Xiong, Y.E.; Nover, D.; Duan, W.L.; Fukushi, K. Historical assessment of Chinese and Janpanese flood management policies and implications for managing future floods. Environ. Sci. Policy 2015, 48, 265–277. [Google Scholar] [CrossRef]
- Van Manen, S.E.; Brinkhuis, M. Quantitative flood risk assessment for Polders. Reliab. Eng. Syst. Saf. 2005, 90, 229–237. [Google Scholar] [CrossRef]
- Gao, Y.Q.; Yuan, Y.; Wang, H.Z.; Schmidt, A.R.; Wang, K.X.; Ye, L. Examining the effects of urban agglomeration polders on flood events in Qinhuai River basin, China with HEC-HMS model. Water Sci. Technol. 2017, 75, 2130–2138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, Y.Q.; Yuan, Y.; Wang, H.Z.; Zhang, Z.X.; Ye, L. Analysis of impacts of polders on flood processes in Qinhuai River Basin, China, using the HEC-RAS model. Water Sci. Technol. Water Supply 2018, 18, 1852–1860. [Google Scholar] [CrossRef]
- Xing, W.B.; Xu, W.Y.; Wang, K.; Yan, X. Risk analysis of hydrological failures of levees in external Qinhuai River. J. Hohai Univ. Nat. Sci. 2006, 3, 262–266. [Google Scholar]
- Xu, J.X.; Yao, S.P. A method to determine the mode of wipe off waterlogging on dyke. J. Agric. Mech. Res. 2008, 6, 61–63. [Google Scholar]
- Zhao, G.F.; Jiang, Z.R.; Ding, Y.; Liang, G.Q. Assessment on risk analysis and risk evaluation of levees. China Water Transp. (Second Semimonthly) 2010, 11, 182–184. [Google Scholar]
- Zhang, G.F. Polder construction and its ecological and social effects—An investigation of joint river embankment in Taihu Drainage Area (1950s–1970s). J. Minzu Univ. China (Philos. Soc. Sci. Edit.) 2012, 4, 36–41. [Google Scholar]
- Xu, H.; Yang, S.J. Exploring the evolution of river networks in plain polders of Taihu Lake basin. Adv. Water Sci. 2013, 3, 366–371. [Google Scholar]
- Yuan, Y.; Gao, Y.Q.; Wu, X. Flood simulation of flood control model for polder type based on HEC-HMS Hydrological Model in Qinhuai River Basin. J. China Three Gorges Univ. (Nat. Sci.) 2015, 5, 34–39. [Google Scholar]
- Chen, H.R.; Wang, S.L.; Han, S.J. Assessment of field waterlogging risk in Lixiahe Plain Lake Region, Jiangsu Province: Case study from Yundong Plain in Gaoyou. J. Drain. Irrig. Mach. Eng. 2017, 10, 887–896. [Google Scholar]
- Reddy, M.J.; Ganguli, P. Bivariate Flood Frequency Analysis of Upper Godavari River Flows Using Archimedean Copulas. Water Resour. Manag. 2012, 26, 3995–4018. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Probabilistic assessment of flood risks using trivariate copulas. Theor. Appl. Climatol. 2013, 111, 341–360. [Google Scholar] [CrossRef]
- Clayton, D.G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Frank, M.J. On the simultaneous associativity of F(x, y) and x + y − F(x, y). Aequationes Math 1979, 19, 194–226. [Google Scholar] [CrossRef]
- Genest, C. Frank’s family of bivariate distributions. Biometrika 1987, 74, 549–555. [Google Scholar] [CrossRef]
- Chowdhary, H.; Escobar, L.A.; Singh, V.P. Identification of suitable copulas for bivariate frequency analysis of flood peak and flood volume data. Hydrol. Res. 2011, 42, 193. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A. Everything you always wanted to know about copula modeling but were afraid to ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Klein, B.; Pahlow, M.; Hundecha, Y.; Schumann, A. Probability analysis of hydrological loads for the design of flood control systems using copulas. J. Hydrol. Eng. 2010, 15, 360–369. [Google Scholar] [CrossRef]
- Fisher, N.I.; Switzer, P. Graphical assessment of dependence: Is a picture worth 100 tests? Am. Stat. 2001, 55, 233–239. [Google Scholar] [CrossRef]
- Genest, C.; Boies, J.C. Detecting dependence with Kendall plots. Am. Stat. 2003, 57, 275–284. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel inference—Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 22, 261–304. [Google Scholar] [CrossRef]
- Suriya, S.; Mudgal, B.V. Impact of urbanization on flooding: The Thirusoolam sub watershed—A case study. J. Hydrol. 2012, 412, 210–219. [Google Scholar] [CrossRef]
- Nanjing Urban Flood Control Planning Report. Available online: http://max.book118.com/html/2017/1105/139066558.shtm (accessed on 10 1 2018).

| Copula | Trivariate Coupla Function |
|---|---|
| GH | |
| Clayton | |
| Frank |
| Without UAPs (Urban Agglomeration Polders) | With UAPs (Urban Agglomeration Polders) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Location | Scale | Shape | KS | P | Location | Scale | Shape | KS | P | ||
| V | P-Ш | 28.38 | 0.004 | 0.44 | 0.23 | 0.20 | 14.40 | 0.006 | 0.83 | 0.20 | 0.34 |
| GEV | 72.60 | 53.86 | 0.31 | 0.12 | 0.88 | 87.17 | 61.07 | 0.28 | 0.12 | 0.86 | |
| LN | 4.51 | 0.87 | - | 0.14 | 0.79 | 4.68 | 0.80 | - | 0.14 | 0.79 | |
| P | P-Ш | −247.93 | 0.006 | 4.63 | 0.15 | 0.71 | 32.16 | 0.003 | 2.16 | 0.16 | 0.56 |
| GEV | 424.66 | 263.84 | 0.05 | 0.16 | 0.61 | 526.58 | 301.26 | 0.09 | 0.19 | 0.39 | |
| LN | 6.18 | 0.70 | - | 0.14 | 0.73 | 6.42 | 0.63 | - | 0.15 | 0.66 | |
| Z | P-Ш | 0.56 | 2.49 | 16.00 | 0.14 | 0.79 | −0.21 | 3.63 | 29.22 | 0.16 | 0.63 |
| GEV | 6.42 | 1.29 | −0.17 | 0.16 | 0.63 | 7.33 | 1.33 | −0.24 | 0.17 | 0.49 | |
| LN | 1.92 | 0.21 | - | 0.16 | 0.63 | 2.04 | 0.18 | - | 0.17 | 0.54 | |
| Copula | Without UAPs | With UAPs | ||||
|---|---|---|---|---|---|---|
| Theta | RMSE | AIC | Theta | RMSE | AIC | |
| GH | 3.680 | 0.015 | −111.45 | 3.149 | 0.015 | −111.42 |
| Clayton | 2.773 | 0.022 | −94.58 | 2.463 | 0.018 | −102.31 |
| Frank | 15.905 | 0.013 | −117.43 | 14.040 | 0.014 | −113.36 |
| JRP (/a) | Without UAPs | With UAPs | ||||
|---|---|---|---|---|---|---|
| V (m3) | P (m3/s) | Z (m) | V (m3) | P (m3/s) | Z (m) | |
| 10 | 331.03 | 1514.57 | 9.80 | 370.81 | 1738.81 | 10.40 |
| 20 | 473.94 | 2010.97 | 10.63 | 514.92 | 2232.61 | 11.13 |
| 50 | 702.69 | 2683.57 | 11.51 | 738.23 | 2884.44 | 11.89 |
| 100 | 914.87 | 3216.57 | 12.05 | 940.25 | 3392.11 | 12.35 |
| 200 | 1172.74 | 3783.76 | 12.55 | 1180.64 | 3925.00 | 12.74 |
| Flood Volume Return Period | ‘OR’ Exceedance Probability | ‘AND’ Exceedance Probability | ||||
|---|---|---|---|---|---|---|
| No UAPs | UAPs | Δ (%) | No UAPs | UAPs | Δ (%) | |
| 10 | 0.0224 | 0.0425 | 89.91 | 0.0113 | 0.0234 | 28.67 |
| 20 | 0.0401 | 0.0667 | 66.27 | 0.0107 | 0.0222 | 17.31 |
| 50 | 0.0545 | 0.0842 | 54.36 | 0.0103 | 0.0215 | 13.29 |
| 100 | 0.0600 | 0.0904 | 50.83 | 0.0102 | 0.0213 | 12.25 |
| 200 | 0.0628 | 0.0936 | 49.14 | 0.0102 | 0.0212 | 11.77 |
| Average | - | - | 62.10 | - | - | 16.66 |
| Flood No. | Scenario (a) | Scenario (b) | ||||||
| Flood Volume (m3) | Peak Flow (m3/s) | Water Level (m) | Integrated Risk | Flood Volume (m3) | Peak Flow (m3/s) | Water Level (m) | Integrated Risk | |
| 1989 | 0.6636 | 0.8256 | 0.8077 | 0.6510 | 0.6796 | 0.8492 | 0.8140 | 0.6682 |
| 1987 | 0.8582 | 0.8372 | 0.8405 | 0.7934 | 0.8642 | 0.8449 | 0.8664 | 0.8102 |
| 1991 | 0.9603 | 0.9773 | 0.9731 | 0.9565 | 0.9644 | 0.9807 | 0.9828 | 0.9626 |
| Flood No. | Scenario (c) | Scenario (d) | ||||||
| Flood Volume (m3) | Peak Flow (m3/s) | Water Level (m) | Integrated Risk | Flood Volume (m3) | Peak Flow (m3/s) | Water Level (m) | Integrated Risk | |
| 1989 | 06990 | 0.8662 | 0.8652 | 0.6933 | 0.7140 | 0.8910 | 0.9515 | 0.7123 |
| 1987 | 0.8715 | 0.8579 | 0.8937 | 0.8290 | 0.8773 | 0.8743 | 0.9081 | 0.8446 |
| 1991 | 0.9632 | 0.9847 | 0.9838 | 0.9622 | 0.9645 | 0.9877 | 0.9937 | 0.9642 |
| Scenario | (1) Ratio of Area Protected by Polders | (2) Integrated Risk | (1) × (2) | ||||
|---|---|---|---|---|---|---|---|
| 1989 | 1987 | 1991 | 1989 | 1987 | 1991 | ||
| a | 0.13 | 0.651 | 0.7934 | 0.9565 | 0.56 | 0.69 | 0.83 |
| b | 0.23 | 0.6682 | 0.8102 | 0.9626 | 0.52 | 0.63 | 0.74 |
| c | 0.34 | 0.6933 | 0.829 | 0.9622 | 0.46 | 0.55 | 0.64 |
| d | 0.45 | 0.7123 | 0.8446 | 0.9642 | 0.39 | 0.47 | 0.53 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Wang, D.; Zhang, Z.; Ma, Z.; Guo, Z.; Ye, L. Analysis of Flood Risk of Urban Agglomeration Polders Using Multivariate Copula. Water 2018, 10, 1470. https://doi.org/10.3390/w10101470
Gao Y, Wang D, Zhang Z, Ma Z, Guo Z, Ye L. Analysis of Flood Risk of Urban Agglomeration Polders Using Multivariate Copula. Water. 2018; 10(10):1470. https://doi.org/10.3390/w10101470
Chicago/Turabian StyleGao, Yuqin, Dongdong Wang, Zhenxing Zhang, Zhenzhen Ma, Zichen Guo, and Liu Ye. 2018. "Analysis of Flood Risk of Urban Agglomeration Polders Using Multivariate Copula" Water 10, no. 10: 1470. https://doi.org/10.3390/w10101470
APA StyleGao, Y., Wang, D., Zhang, Z., Ma, Z., Guo, Z., & Ye, L. (2018). Analysis of Flood Risk of Urban Agglomeration Polders Using Multivariate Copula. Water, 10(10), 1470. https://doi.org/10.3390/w10101470




