Experimental Optimization of Gate-Opening Modes to Minimize Near-Field Vibrations in Hydropower Stations

Abstract

Multi-Horizontal-Submerged Jets are successfully applied to dissipate energy within a large-scale hydropower station. However, notable near-field vibrations are generated when releasing high discharges through the gates, which is generally typical in a flooding case scenario. Under these conditions, the magnitude of the vibrations varies when applying different gate-opening modes. To investigate and find optimized gate-opening modes to reduce the near-field vibration, multiple combinations were tested by varying gate-opening modes and hydraulic conditions. For each of the tests conducted, fluctuating pressures acting on side-walls and bottoms of a stilling basin were measured. The collected datasets were used to determine the maximum and minimum fluctuating pressure values associated with the correspondent gate-opening mode and a detailed comparison between each of the gate-opening modes was completed. The paper presents the quantitative analysis of the discharge ratio’s effect on fluctuating pressures. It also investigates the influence of different gate-opening modes by including side to middle spillways and upper to lower spillways configurations. The flow pattern evolutions triggered by each different gate-opening mode are discussed and optimal configurations that minimize near-field vibrations at high discharges are recommended to support both the design of new systems and assessment of the performance of existing ones.

1. Introduction

Since 2000, over 300 hydropower projects have been completed or are under construction in China [1]. Flood discharge and energy dissipation are crucial to maintaining the safety of these hydropower installations. Furthermore, lessons must be drawn from the past dam disasters, e.g., Vajont Dam [2,3] and Banqiao Dam [4]. Decades ago, hydropower stations were not constructed in proximity to residential areas, and as a result, research at that time mainly focused on the stability and the functionality of the hydraulic structures. However, in recent years, due to increasing urbanization [5], some large hydropower stations had to be located in the proximity of residential areas. Moreover, due to the climatic scenario [6], it is likely that in the future there will be numerous and more frequent intense rainfall events, and consequently large volumes of water may need to be released from dam reservoirs. Therefore, it is essential to provide solutions to a need for increasing the stability of these hydraulic structures and surrounding areas, minimizing environmental impacts due to extreme flow discharges [7].

The purpose of this work is to optimize a recently developed novel technique for energy dissipation, Multi-Horizontal-Submerged Jets (simplified as MHSJ). MHSJ have been studied and improved by many researchers in recent years [8,9,10,11,12,13,14,15,16,17]. It has been demonstrated that MSHJ possesses three main advantages when compared with the hydraulic jump, which is the traditional energy dissipater: (1) lower atomization; (2) a higher rate of energy dissipation; (3) more flexibility of gate-opening modes [12,13,14]. Thus, it seems feasible to implement MHSJ to tackle the problem of energy dissipation within large hydropower stations that are typically characterized by higher water heads and larger flowrates. The adoption of MHSJ was tested by Deng et al. [12] and successfully applied as energy dissipation in large-scale hydropower stations [14].

However, despite positive progress on solving energy dissipation and erosion problems, there is still a lack of studies on the considerable flow-induced vibrations that occur in this kind of structure and propagate towards the near-field when releasing the greater flowrates. These near-field vibrations can be considered a serious threat for the stability of the structure, and hence this phenomenon needs to be further investigated. Yin and Zhang [18] and Yin et al. [19] studied the relationship between the discharge flow and the induced vibrations and simulated the results with a finite element method. Yin et al. [19] found that at higher flowrates during flooding situations, the flow is complex and unsteady, and this is the main cause of near-field vibrations. Therefore, if the vibrations are caused by releasing higher flowrates, optimizing gate-opening modes could reduce this effect and near-field vibrations could decrease correspondingly. To date, this issue has not been investigated in detail and to address this gap, this paper presents an experimental study to explore the relationship between complex flow scenarios and gate-opening modes in order to recommend an optimal solution to minimize the formation of vibrations.

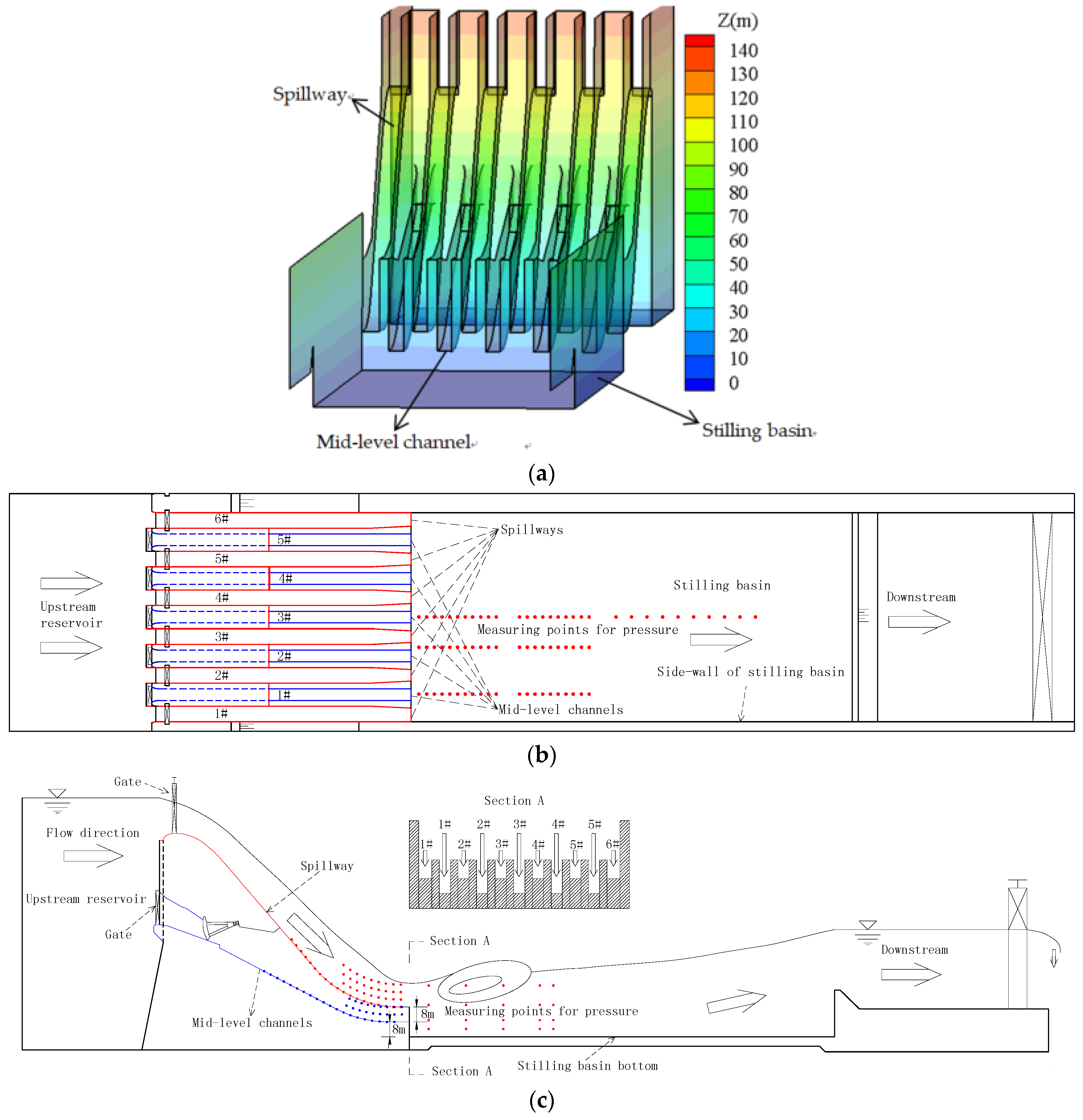
2. Methods

The experimental facility, shown in Figure 1, was constructed based on a large-scale hydropower station (Xiangjiaba hydropower station. It sits on the Jinsha River, a tributary of the Yangtze River in Yunnan Province and Sichuan Province, Southwest China). The experimental facility follows Froude similarity, i.e., the ratio between inertial and gravitational forces remains constant, with the scale of 1:80. The experimental model is composed of the upper and lower reaches of the river, a dam, mid-level channels, spillways and two stilling basins with identical layout (the difference between two stilling basins is the their location on the dam, being parallels). The single stilling basin includes 5 mid-level channels and 6 spillways. Both of mid-level channels and spillways were arranged alternately and division piers were located between them.

In the model, the outlets of spillways are horizontal with symmetrical contraction of 1 m and width of 8 m. Also, the mid-level channels’ outlets are horizontal, without any contraction, and their width is 6 m. The division piers are 3 m wide. The offset of mid-level channels, spillways, and division piers from the bottom of the stilling basin are 8 m, 16 m, 26 m, respectively. The test section (L = 15 m, W = 2 m and H = 1 m) is made of plexiglass. The modelled stilling basin is 3 m long and a gate is adopted to control tail-water level downstream of the model. To measure the fluctuating pressure within the system, 135 measurement taps for pressure transducers are located in the right-side wall and bottom of the stilling basin, as well as in the right-side wall and bottom of spillway (1# spillway in Figure 1) and mid-level channel (1# mid-level channel in Figure 1). For each test, the fluctuating pressure was measured synchronously by sensors for pressure transducers at each measurement point. The accuracy of the pressure sensors utilized in this study is 0.1%, with a 0–50 kPa working range and a frequency response of 100 Hz.

Multiple experimental flooding scenarios were completed within the experimental facility, varying flowrate and changing gate-opening modes. The area under investigation includes the: (i) stilling basin bottom (BB); (ii) stilling basin side-wall (BS); and (iii) piers, spillways and mid-level channels (PSO). Discharges considered varied gradually between 800 and 24,500 m³/s. The downstream water elevation was measured within the model for each test.

3. Results and Discussion

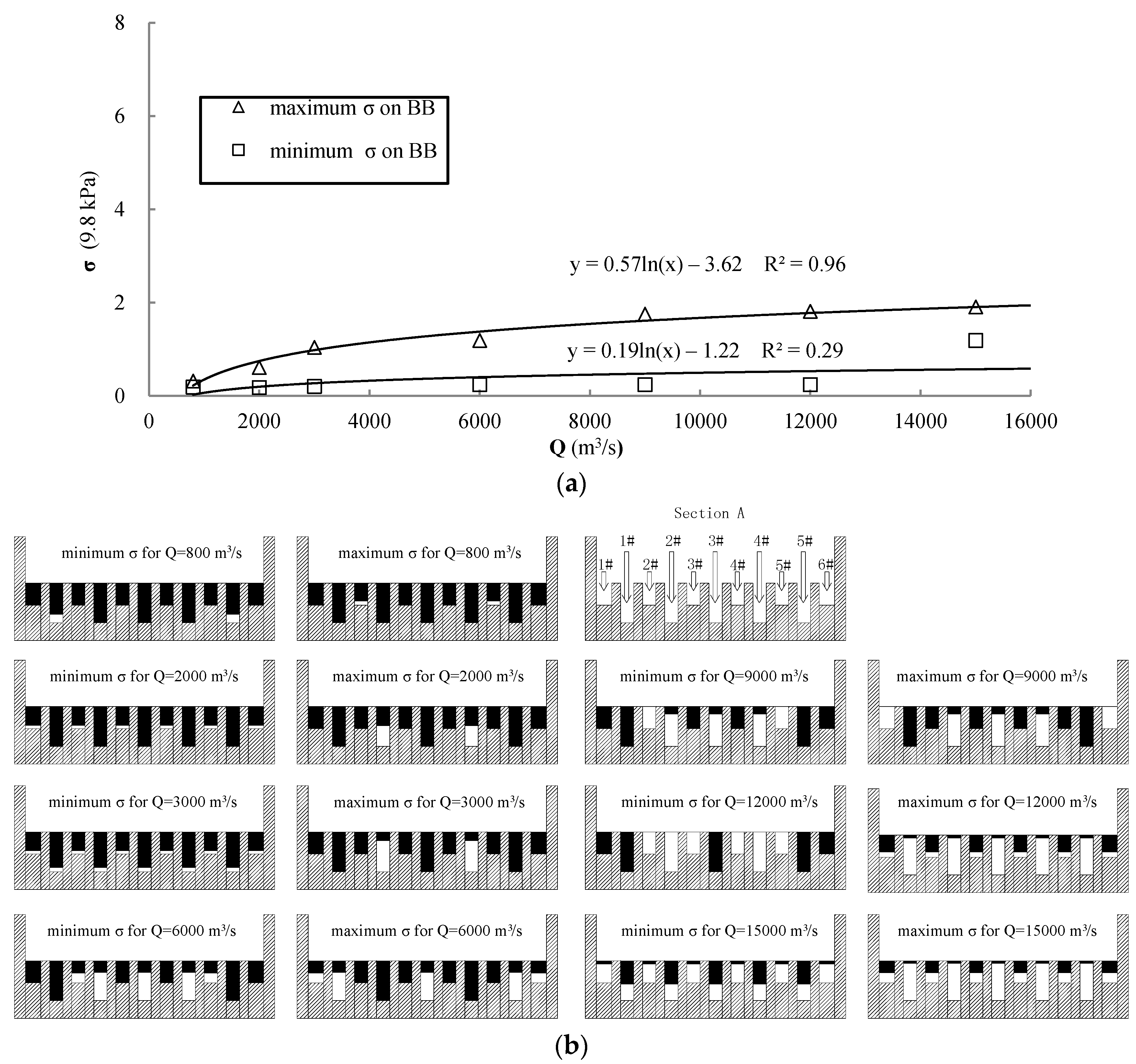
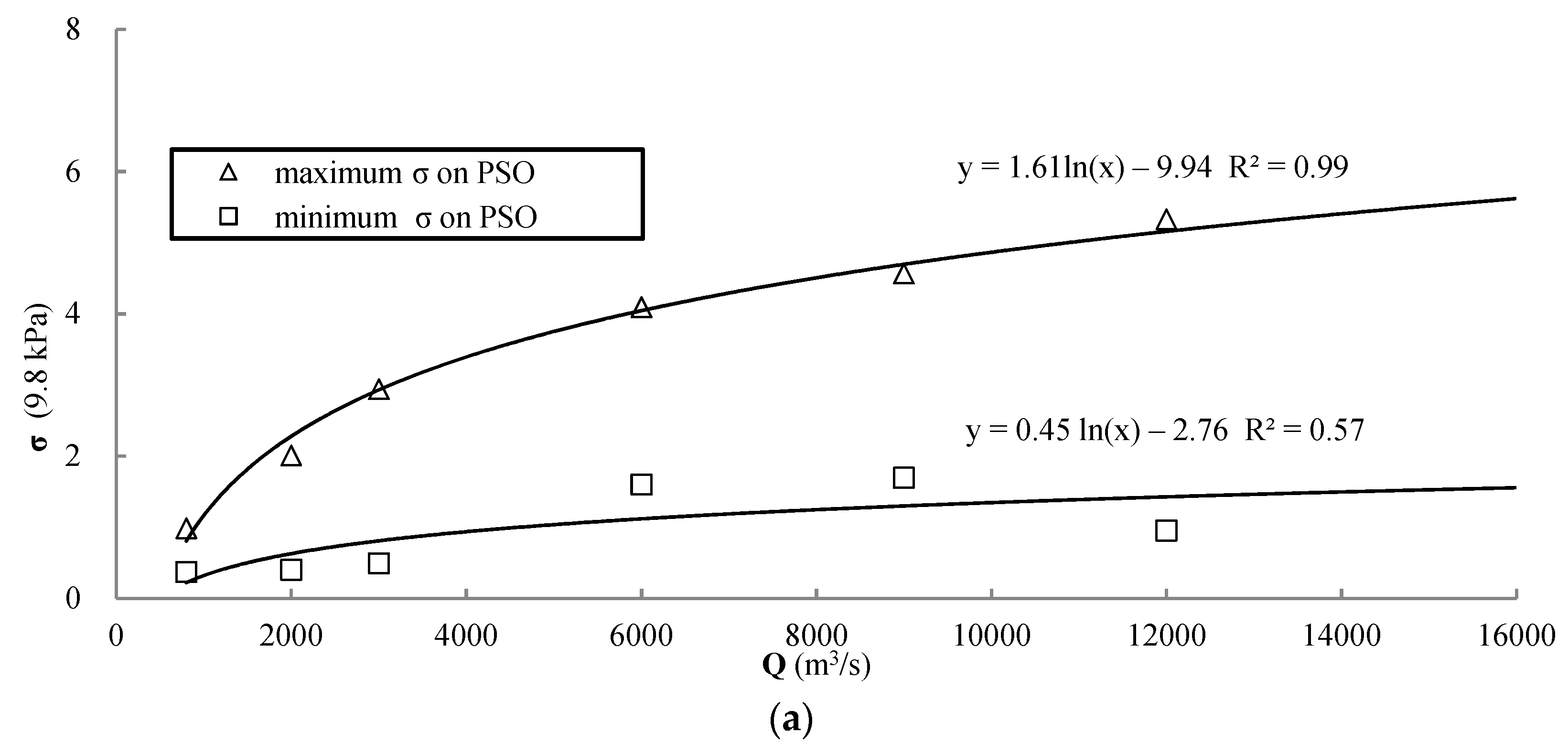
3.1. Relation between Fluctuating Pressure and Flood Discharge

After calculating the root-mean-square (RMS) of the fluctuating pressure measured for each hydraulic condition tested, the arithmetic mean of RMS values obtained for every part of the BB, BS and PSO were calculated individually and these final values are used in the following sections.

Figure 2 shows (a) the maximum and minimum RMS of fluctuating pressure on BB against the flood discharge scenario and (b) the gate-opening modes considered. In Figure 2a, the best fitting line and its correspondent equation are displayed. The configuration of gate-opening modes has a significant impact on the magnitude of the fluctuating load acting on the BB during the release of flows in the range of 2000 to 12,000 m³/s. This is a clear indicator that the fluctuating load can be reduced effectively by optimizing gate-opening modes. As a consequence, the near-field vibrations induced by releasing higher flow associated with flooding scenario can also be reduced. However, this cannot be confirmed when the flood discharge increases to 15,000 m³/s into a single stilling basin (as shown in Figure 2a) due to the limited adjustment of the gate-opening modes available within this experimental facility. Additionally, Figure 2b highlights that the use of side spillways seems favorable to reduce fluctuating pressure on the BB.

Figure 3 displays the maximum and minimum RMS of fluctuating pressure on the BS during flood discharge scenarios, similar to Figure 2. Outcomes displayed in Figure 3 are clear indicators that it is beneficial to reduce pressure values in the BS by reducing the discharge associated with the side spillways as they are directly connected with BS, and hence cause a higher impact. For example, the maximum is more than 7 times higher than the minimum on BS, with Q of 12,000 m³/s.

Figure 4 indicates maximum and minimum RMS of fluctuating pressure on the PSO and corresponding gate opening modes. Although fluctuating pressure on the PSO is larger than those on the BB and BS, the main sources of near-field vibration are the BB and BS. The effect of PSO is relatively small according to Yin and Zhang [18] and Yin et al. [19].

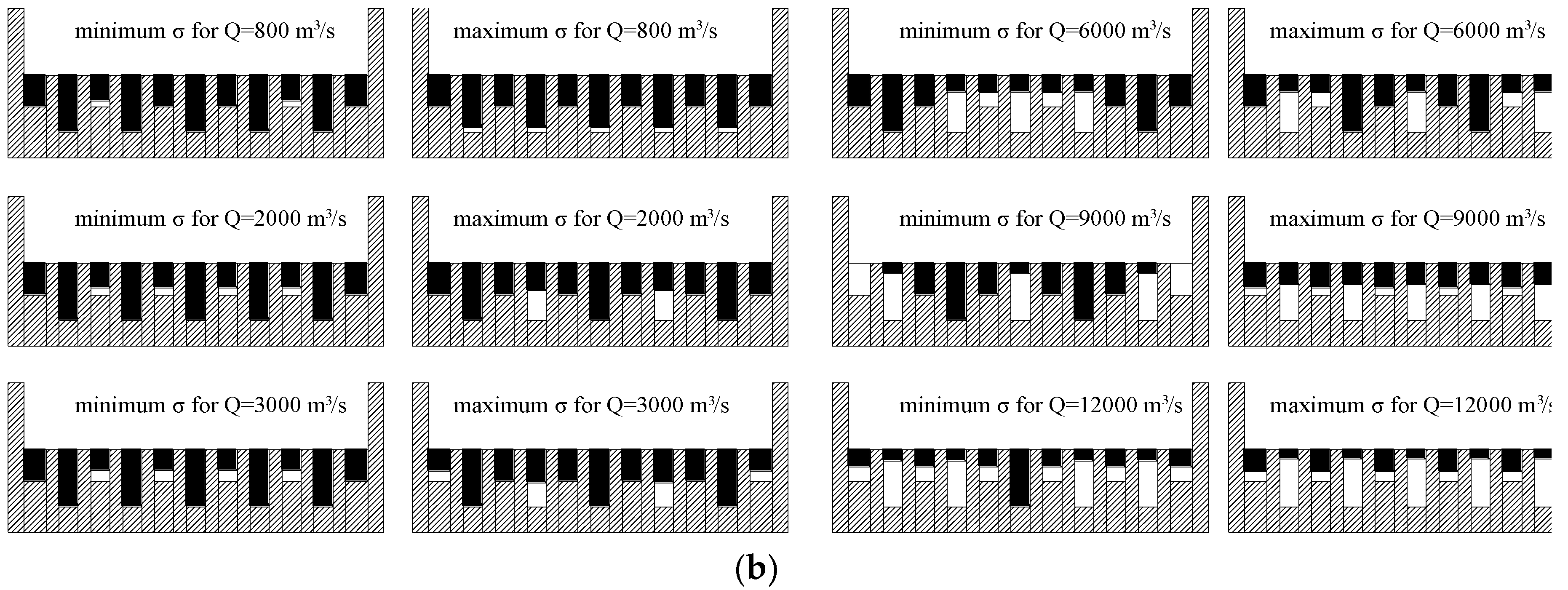
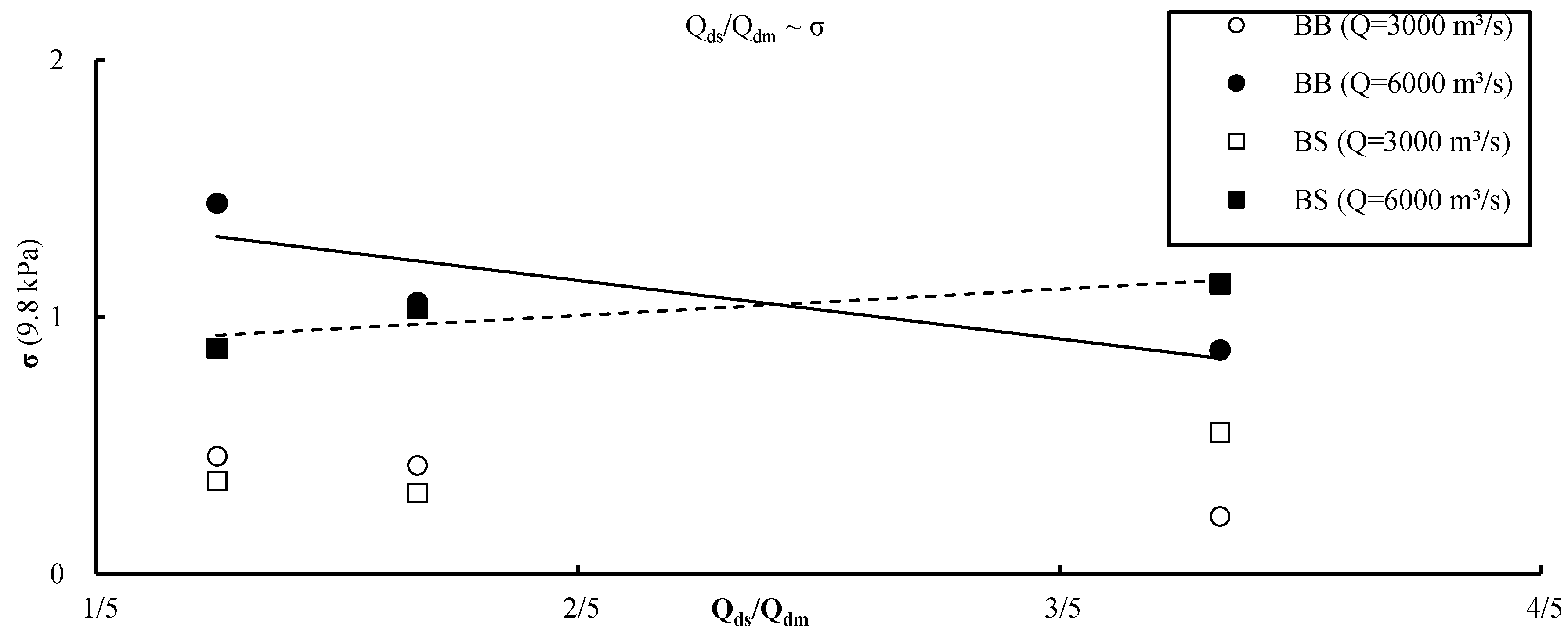
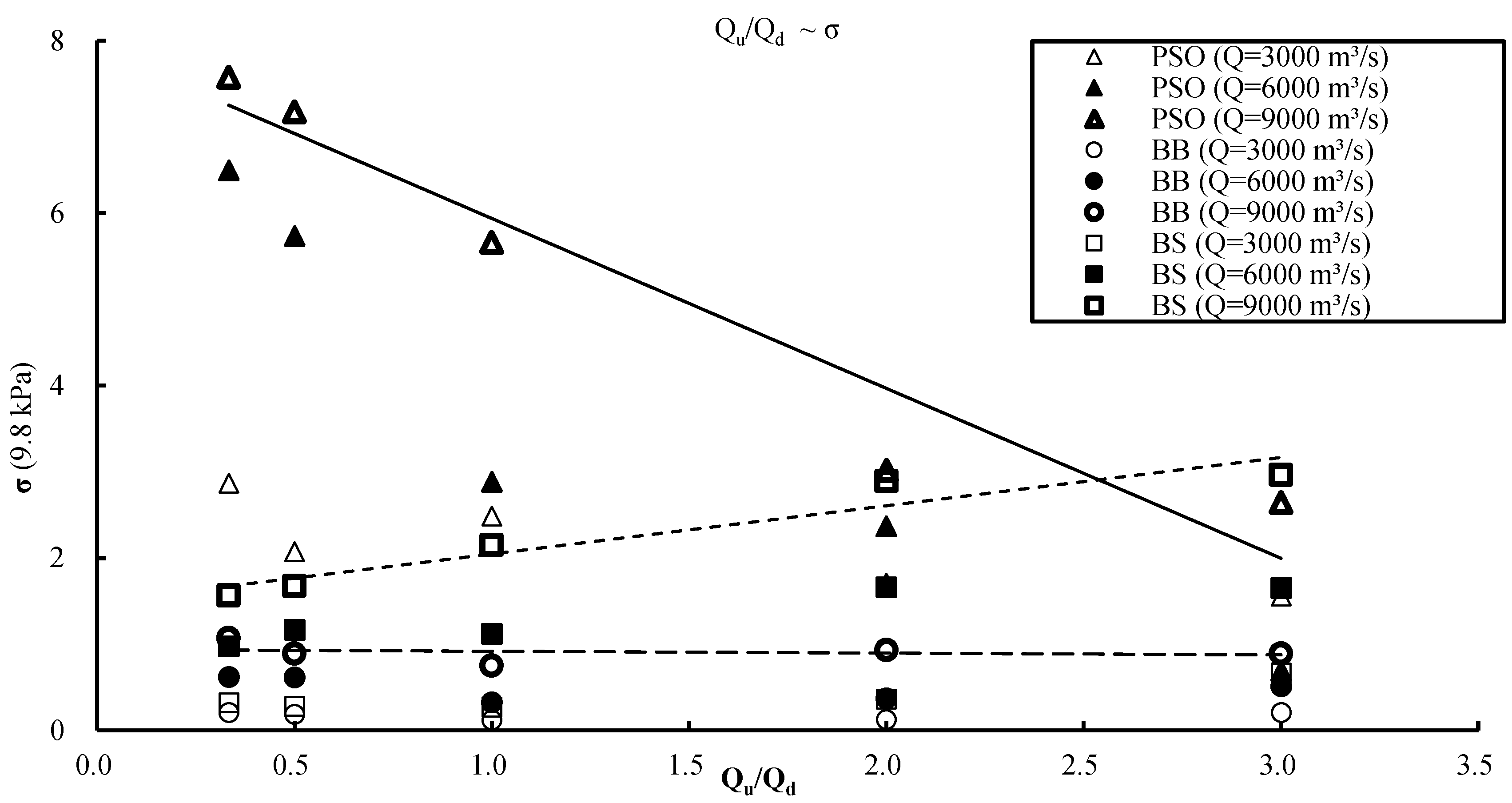
3.2. Effect of Flow Discharge Ratio and Configuration Adopted to Release the Flow on Fluctuating Pressure

To quantitatively study the effect of different flowrates, more experiments were carried out. Specifically, three kinds of gate-opening modes were tested at higher flowrates typical of flooding scenarios: (i) mid-level channels separately, (ii) spillways separately, and (iii) combining both previous cases (i) and (ii). Based on measured fluctuating pressure and flow pattern evolution of these three different configurations, recommended gate-opening modes are proposed for various flood discharge rates.

The following notations are used to simplify the understanding of outcomes described in the upcoming sections: Q is total flood discharge for single stilling basin (m³/s); Q_u and Q_d are the total discharge of spillways and mid-level channels, respectively (m³/s); Q_ds and Q_dm are the total discharge of two side mid-level channels (1# and 5# as shown in Figure 1) and three middle ones (2–4#), respectively (m³/s); Q_us and Q_um are total flood discharge of two side spillways (1# and 6#) (m³/s) and four middle ones (2–5#) (m³/s).

Figure 5 illustrates the effect of the ratio Q_ds/Q_dm on fluctuating pressure on the BB and BS. It indicates that fluctuating pressure tends to increase on the BS and to reduce on the BB as Q_ds increases slightly if the mid-level channels are used separately. This result suggests that mid-level channels should be opened uniformly to avoid this disruption.

Figure 6 shows the effect of the ratio Q_us/Q_um on fluctuating pressure on BB and BS. By slightly increasing Q_us, if spillways are used separately, Figure 6 shows that the corresponding fluctuating pressure generated increases on the BS and reduces on the BB. This effect is consistent if applied to the mid-level channels configuration. Therefore, the same as the mid-level channels, spillways should be opened uniformly to reduce the magnitude of pressure on the BB.

Figure 7 displays the effect of the ratio Q_u/Q_d on fluctuating pressure on the PSO, BB, and BS. When combination of the spillways and mid-level channels is adopted, fluctuating pressure increases on the BS and reduces on the BB and PSO as Q_u increases maintaining constant Q. Additionally, by applying this configuration, fluctuating load varies more rapidly on the PSO, and this effect is clearer as Q increases. When the ratio Q_u/Q_d is between 2 and 3, values of fluctuating pressure in all of three areas of study are relatively small.

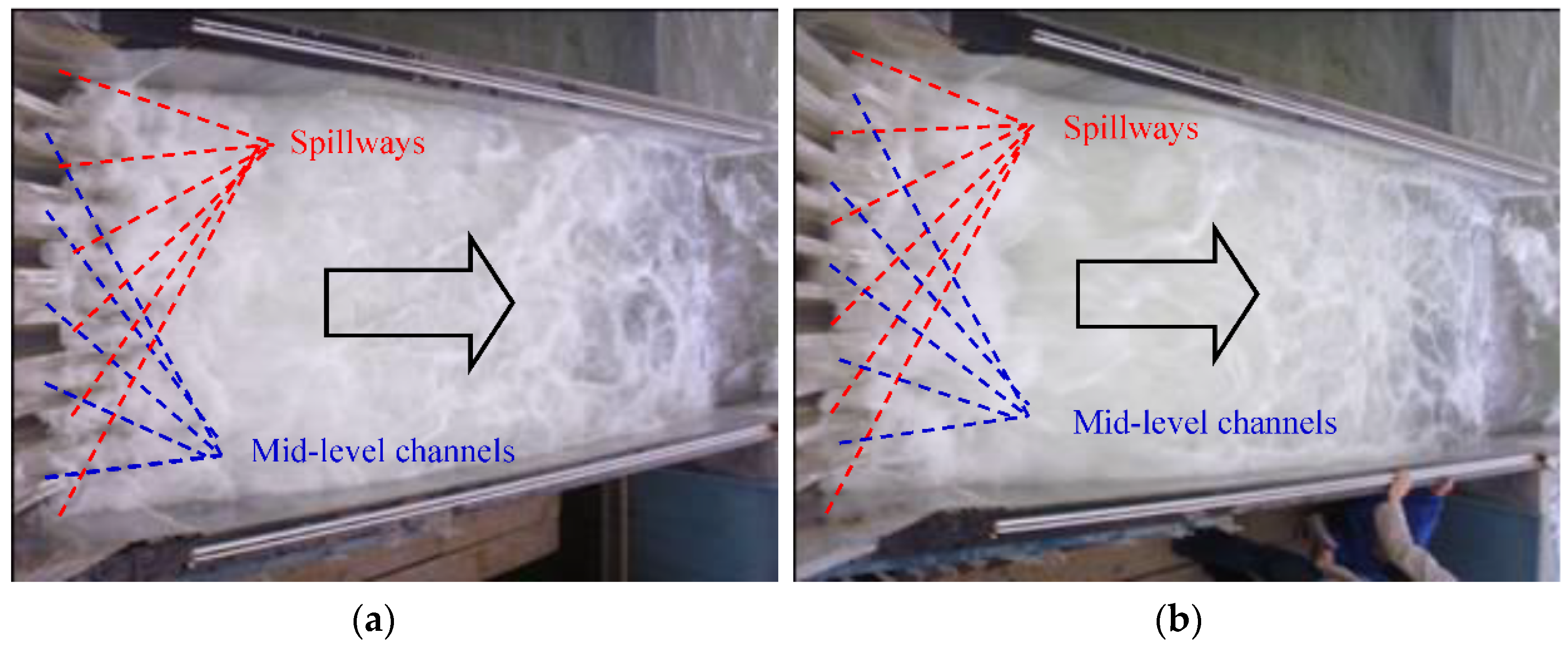
3.3. Effect of Flow Discharge Ratio and Configuration Adopted to Release the Flow on Flow Patterns in the Stilling Basin

In this section, the flow patterns in the stilling basin generated by the different hydraulic conditions and gate-opening configurations tested are discussed. As observed by previous studies [10], there is a correlation between the flow fluctuations and the flow patterns in the stilling basin. This explains why there is a significant difference, considering the same discharge flowrate, between fluctuating pressure on the PSO, on BB, and on BS. Figure 8 displays some examples of flow patterns observed in the stilling basin when the mid-level channels were used separately for diverse discharge flowrates. This is an indicator that various jets tend to quickly merge together and are likely to swing in the stilling basin if two or three of the middle mid-level channels are opened symmetrically. The formation of these flow patterns generates an increase in fluctuating pressure on the side-walls of the stilling basin. This phenomenon is mainly due to the outlet’ width of each mid-level channel that is much smaller than the width of the stilling basin. When replicating this hydraulic condition of using mid-level channels separately, a backflow characterized by an “S” shape emerges in the stilling basin. The flow stability is relative good in the case of combination of 1#, 3#, 5# orifices (Figure 8c), or 1#, 2#, 4#, 5# orifices (Figure 8d), but the flow is not stable when all 1–5# orifices (Figure 8f) are fully open. This result suggests that mid-level channels can only be used individually for small flowrates during flooding events, and mid-level channels should only be opened symmetrically.

Figure 9 displays flow patterns that tend to develop when spillways are opened separately. It shows that the flow pattern is stable when the spillways are uniformly opened and separately regardless of the gate-opening height. Moreover, flow patterns are still stable if the middle spillways are opened symmetrically by closing side spillways. Finally, Figure 10 shows flow patterns generated when combining discharging orifices and spillways. In this case, flows discharged and flow in the stilling basin fully mix, and the flow patterns produced confirm the stability of the flow in the stilling basin. This stability continues until the outlet section of the stilling basin.

To summarize, flow patterns are stable in the stilling basin when combinations of mid-level channels and spillways are applied. The lack of clear and repeatable flow patterns in the stilling basin generated under different scenarios when mid-level channels are opened separately suggest that such a scenario should be avoided. Despite this, there is a consistent good agreement between the flow patterns and the measured fluctuating pressure values acting on the overflow walls.

4. Conclusions

According to the experimental results, the relationship between gate-opening modes and fluctuating pressure on the overflowing walls was explored and optimal gate-opening modes were recommended. Based on the above study, the following conclusions can be stated:

(1)

Gate-opening modes are very flexible for MHSJ. Moreover, proper and strategical adjustment of gate-opening modes can be very effective in reducing fluctuating loads on overflow walls (e.g., fluctuating pressure can be reduced by nearly 50% for the same flood discharge by optimizing the opening mode of the gates).

(2)

To improve the overall performance and stability of the hydraulic structure, both spillways and mid-level channels should be opened uniformly, but side spillways should be opened slightly less to reduce fluctuating pressure on the side-wall of the stilling basin. The discharge ratio Q_u/Q_d (the ratio of spillway discharge to mid-level channel discharge) should be kept between 2–3 when side spillways and mid-level channels are used together.

(3)

The flow patterns in the stilling basin show remarkable differences depending on gate-opening modes. No repeatable shape was observed when trying different configurations. It is recommended to open the mid-level channels partially and uniformly when discharging orifices are used separately. The flow patterns are always stable when spillways are used separately regardless of full or partial opening. The flow patterns are relatively stable in the stilling basin when a combination of spillways and mid-level channels are used to release a high flowrate typical of flooding scenarios.

(4)

It is proposed to use spillways and mid-level channels separately for middle orifices and small flowrates released. The combination of mid-level channels and spillways can be used for large discharge.