Multiperiod Optimisation of Irrigated Crops under Different Conditions of Water Availability
Abstract
1. Introduction
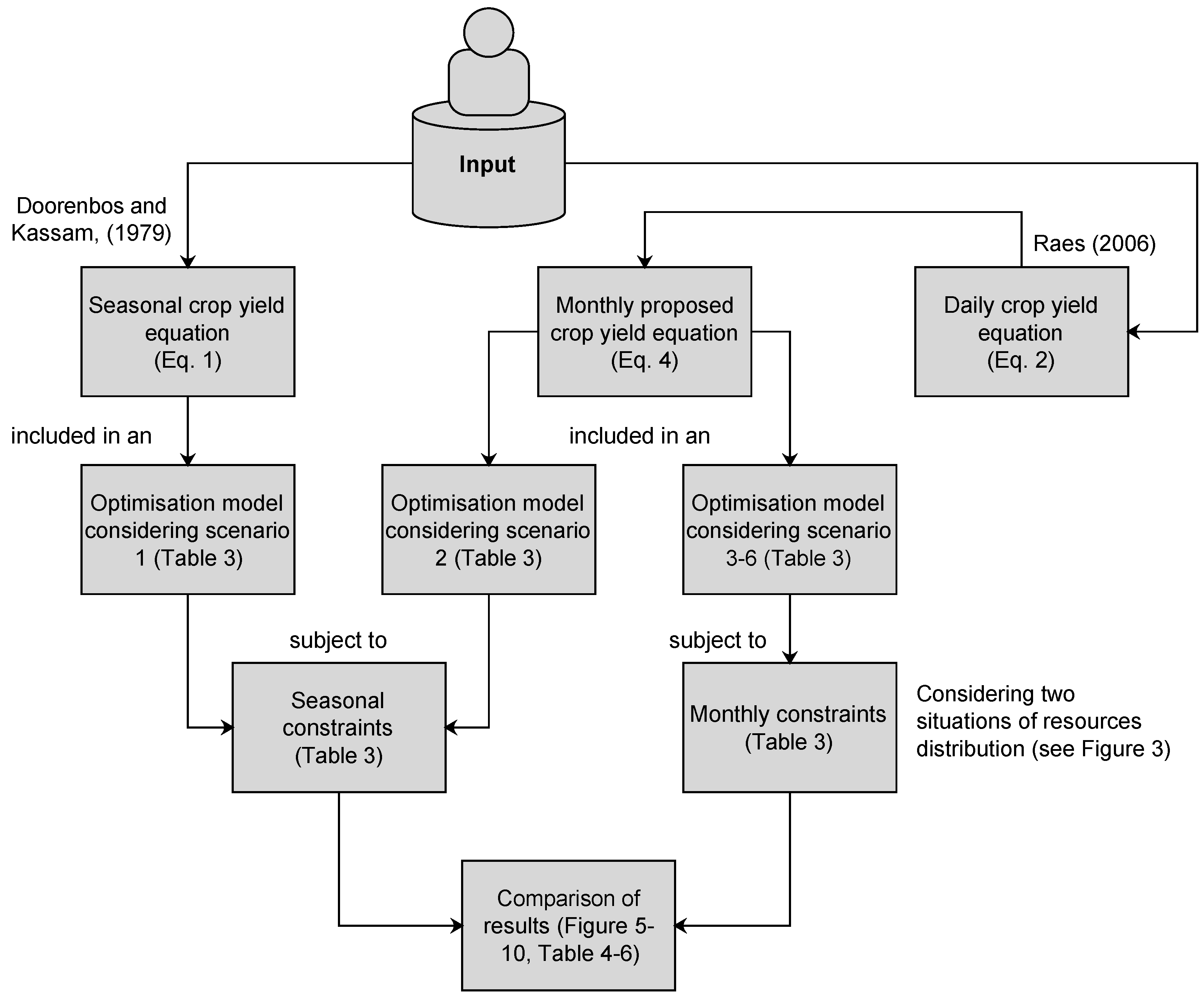
2. Methodology
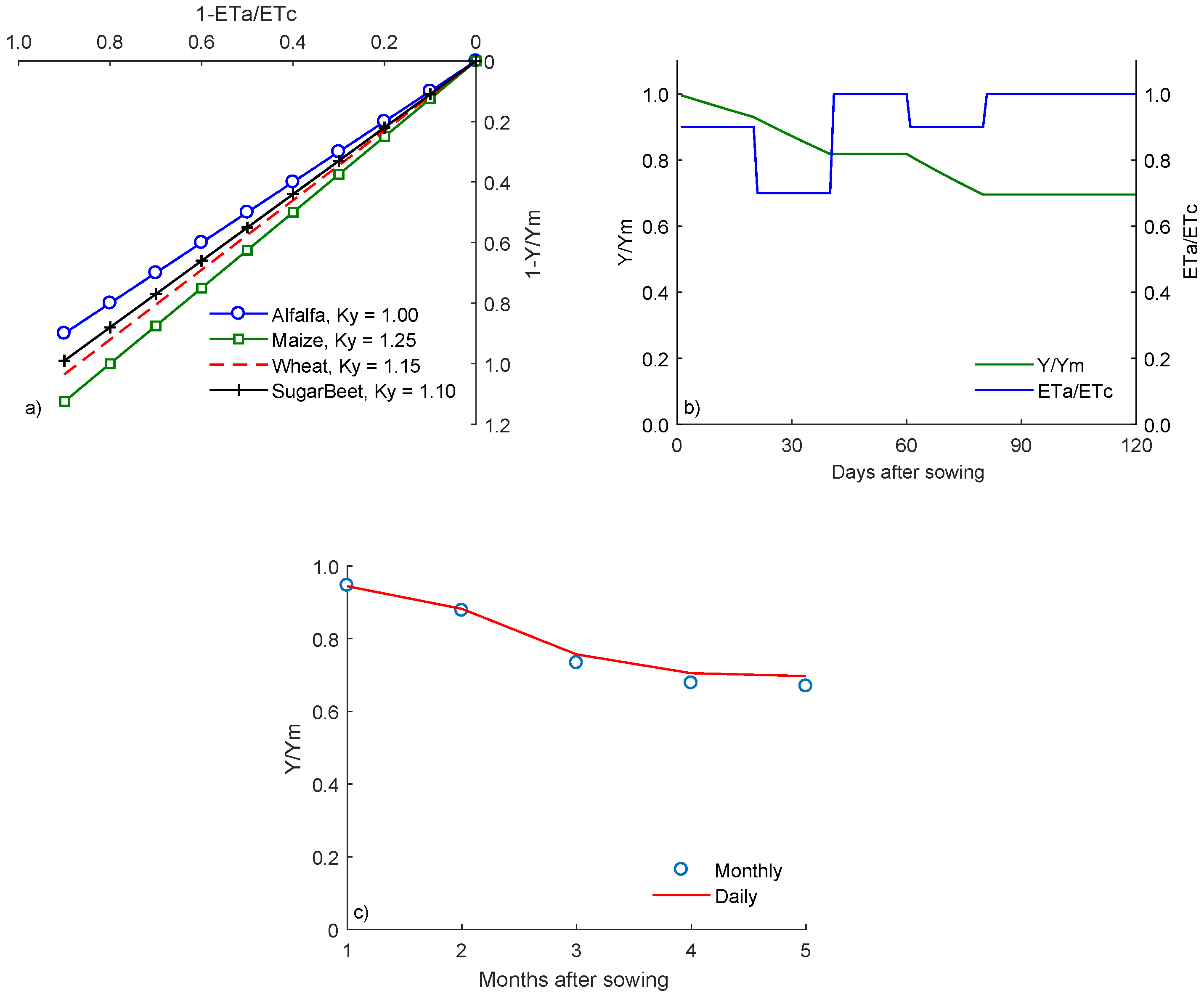
2.1. Multiperiod Crop Yield Function
2.2. Optimisation of Irrigated Crops
- Water availability: Assuming that the farmer has the infrastructure to store water at monthly scale ( m3 of capacity), available water is defined as:where is the application efficiency of the irrigation system for crop i. It is important to mention that refers to the water contained in the soil after applied an initial volume of water , where there are losses due to irrigation system efficiency. This variable is multiplied by 10 for conversion to m3 per hectare.
- Land availability: This constraint defines the area to be cultivated.where is the land availability (in ha).
- Labour availability: Assuming that the labour availability can change for each month, this constraint is defined as:where is the labour availability at month k (in person-d month−1).
- Capital availability: Assuming that farmers can save money if it is not spent, the monthly capital availability is considered as:where is the economic capital availability at month (in US$ month−1).
- Crop area considerations: It is necessary to consider agricultural, market and productive diversity management criteria to restrict the maximum or minimum crop areas. This is due to marketing situations, rotations, or other agricultural limitations. These constraints are expressed as:where and are the minimum and maximum areas assigned to farm with crop i, respectively.
- Complementary considerations: To force the crop water requirement to be zero when the cultivated area is also zero, the constraint is expressed as:where is a positive constant ( = 10,000 mm ha−1). In order to not apply more water than required by the crop, the following constraint is also considered:Finally, there are non-negativity constraints expressed as:
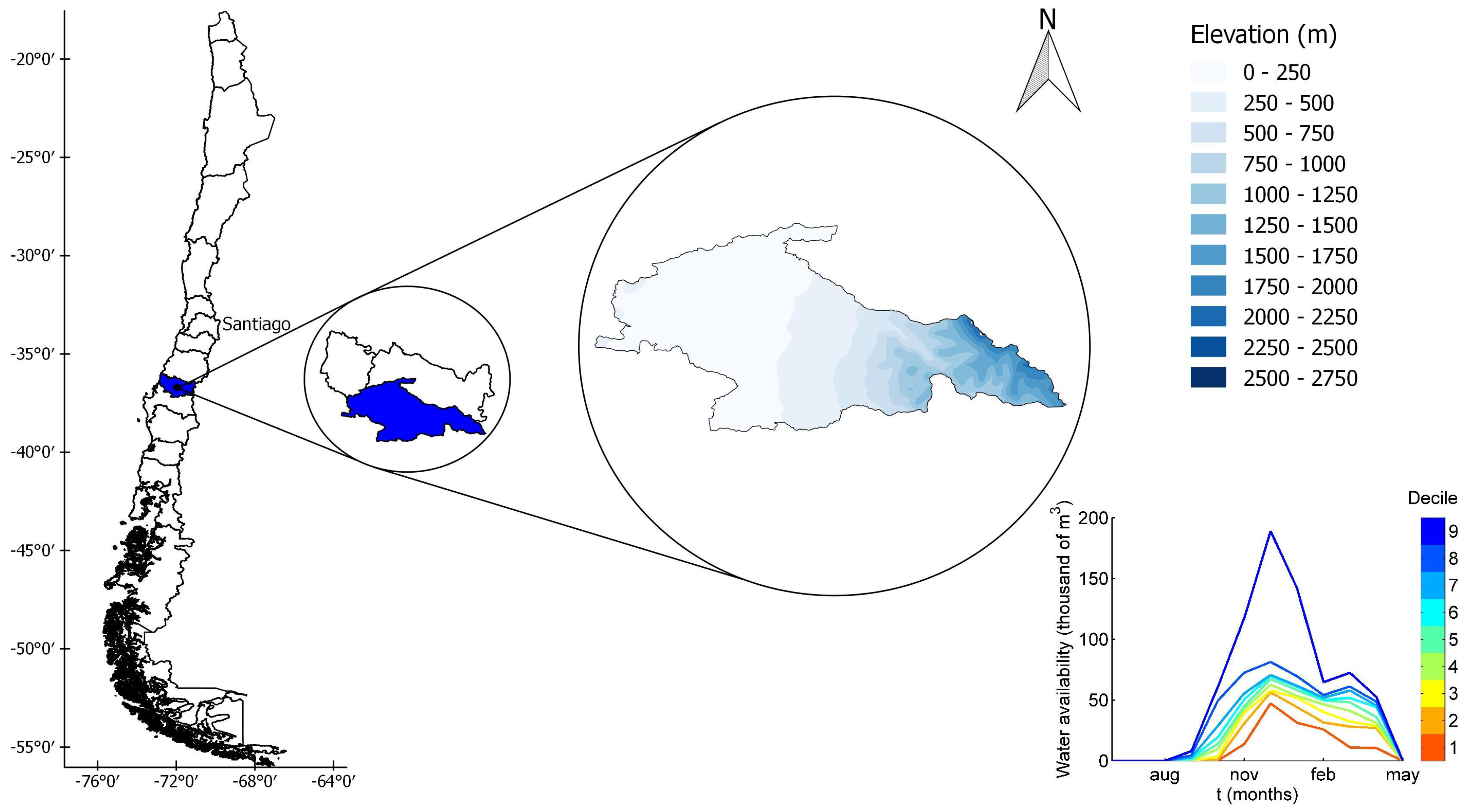
2.3. Case Study
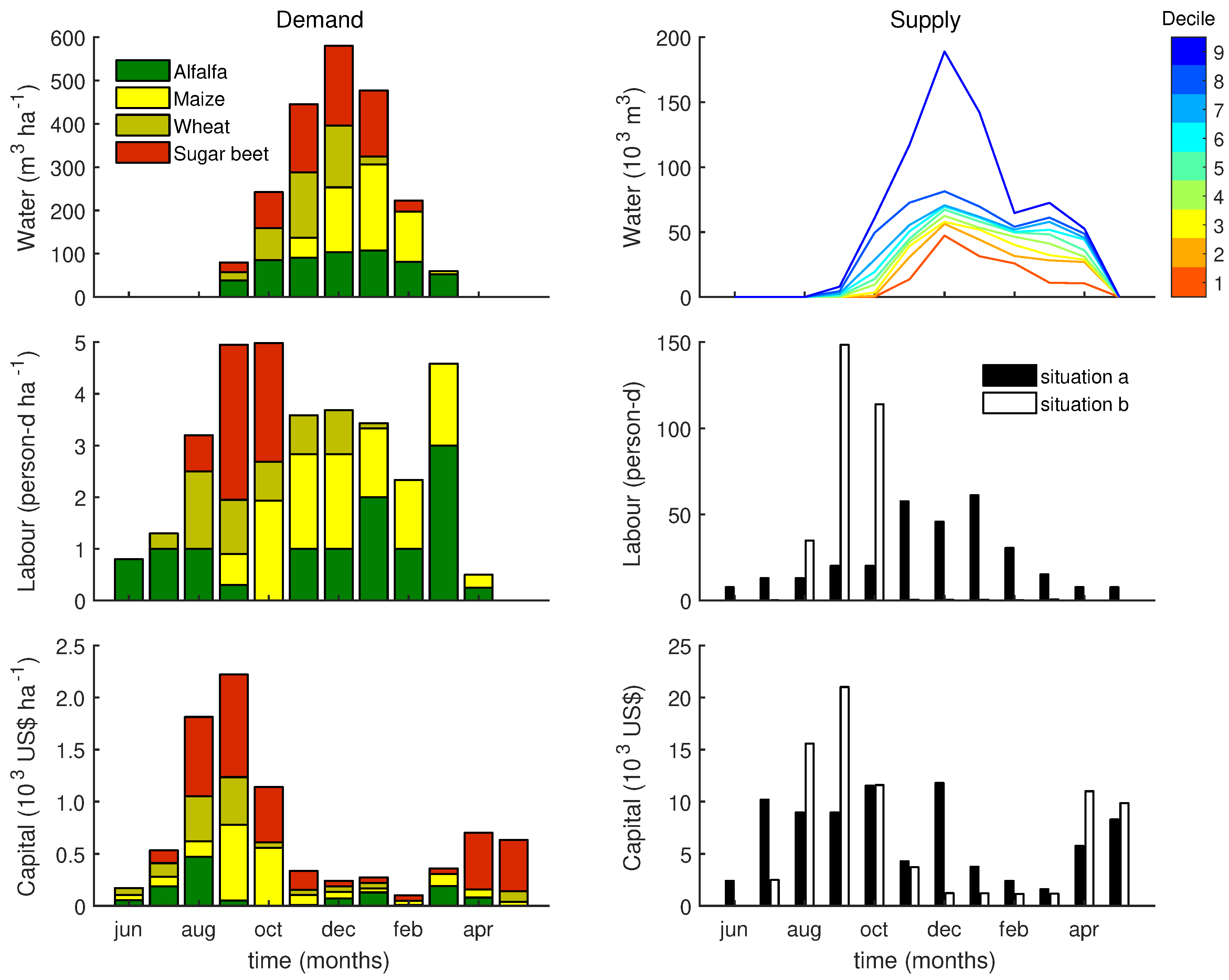
2.3.1. Model Inputs
2.3.2. Model Application
- Scenario 1: Optimisation subject to seasonal constraints. This scenario assumes that resources are available for the season, but does not consider intraseasonal variability. In this scenario, for the whole growing period, only one value of and for each crop i was considered. Water storage and water transactions were not considered.
- Scenario 2: Optimisation subject to seasonal constraints. For the whole growing period, monthly values of and for each crop i were considered. In this scenario, water storage and water transactions were not considered.
- Scenario 3: Optimisation subject to monthly constraints, i.e., water and other resources availability at a monthly scale are considered. In this scenario, water storage and water transactions were not considered.
- Scenario 4: Optimisation subject to monthly constraints with water transactions.
- Scenario 5: Optimisation subject to monthly constraints with water storage.
- Scenario 6: Optimisation subject to monthly constraints with water storage and transactions. This scenario is the most complete, considering all possible factors involved in the process.
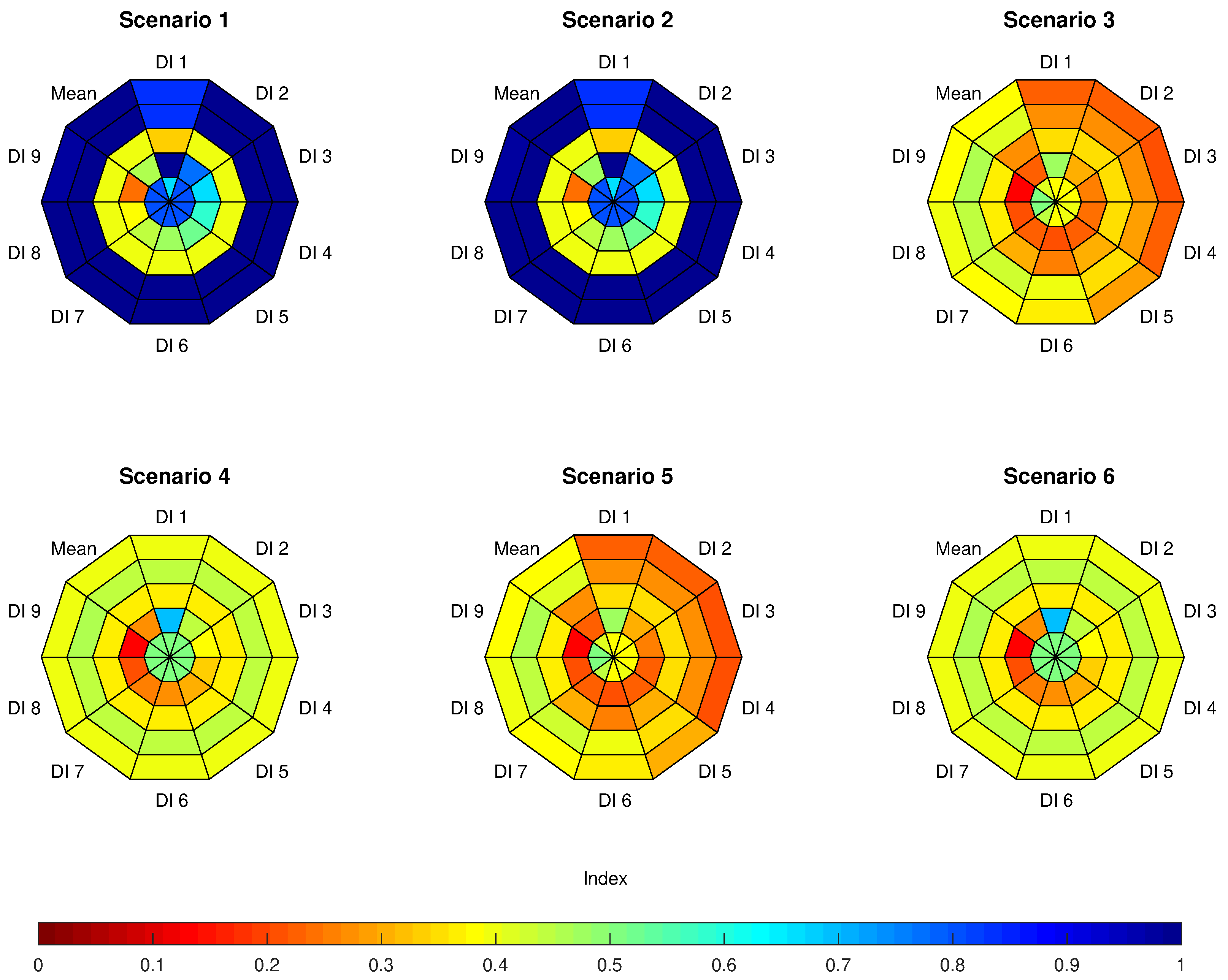
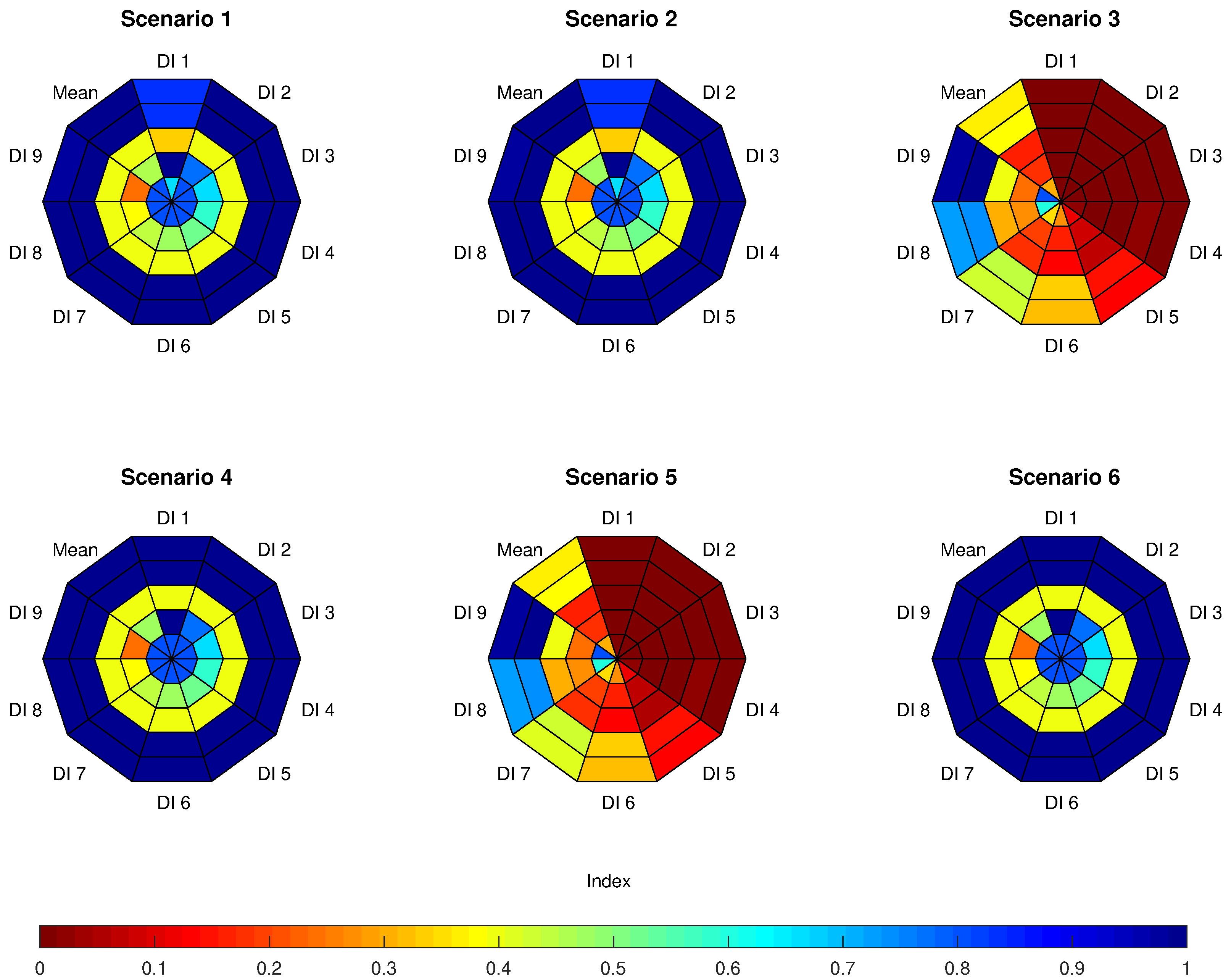
3. Results and Discussion
3.1. Seasonal Use of Resources and Profits
3.1.1. Situation a
3.1.2. Situation b
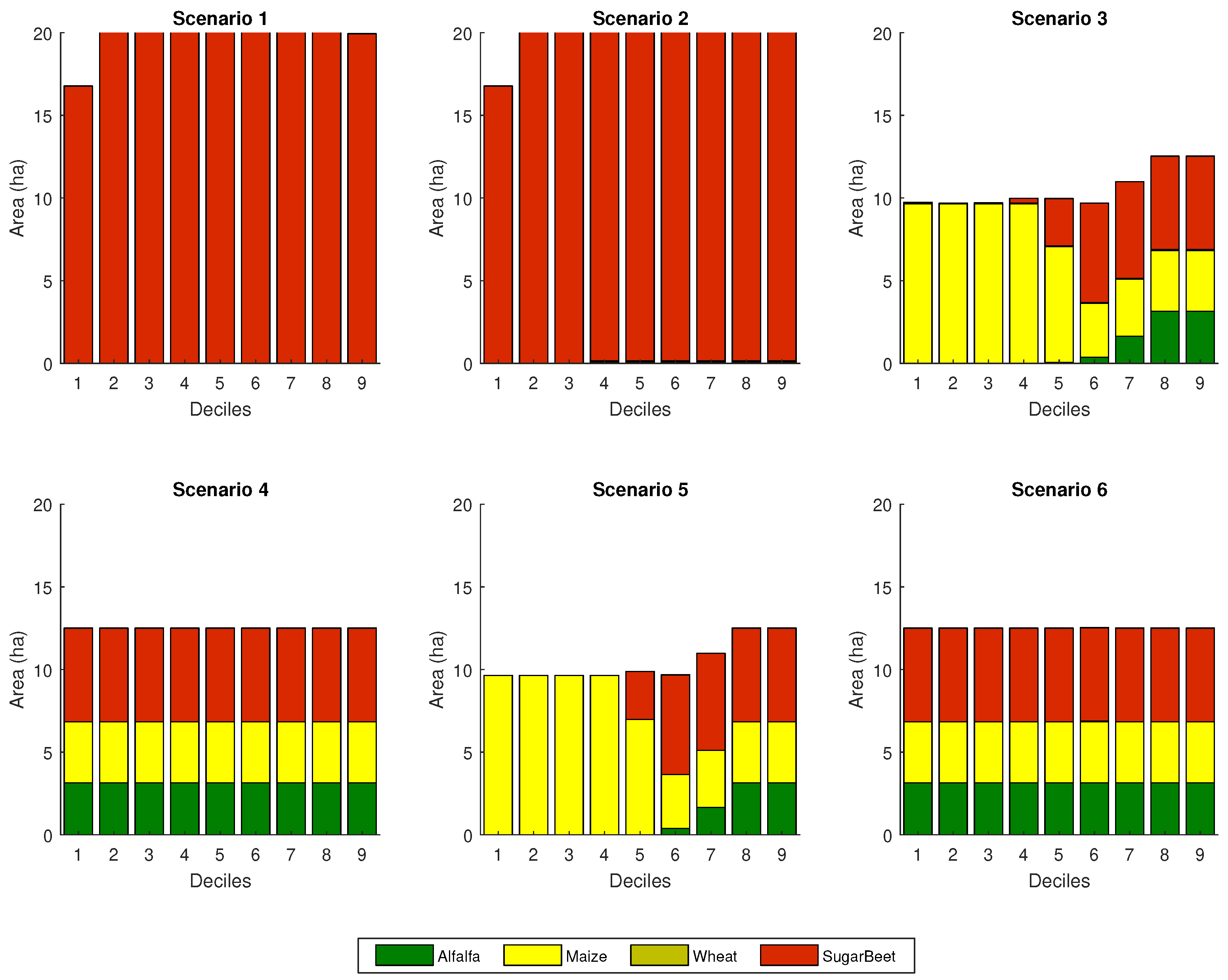
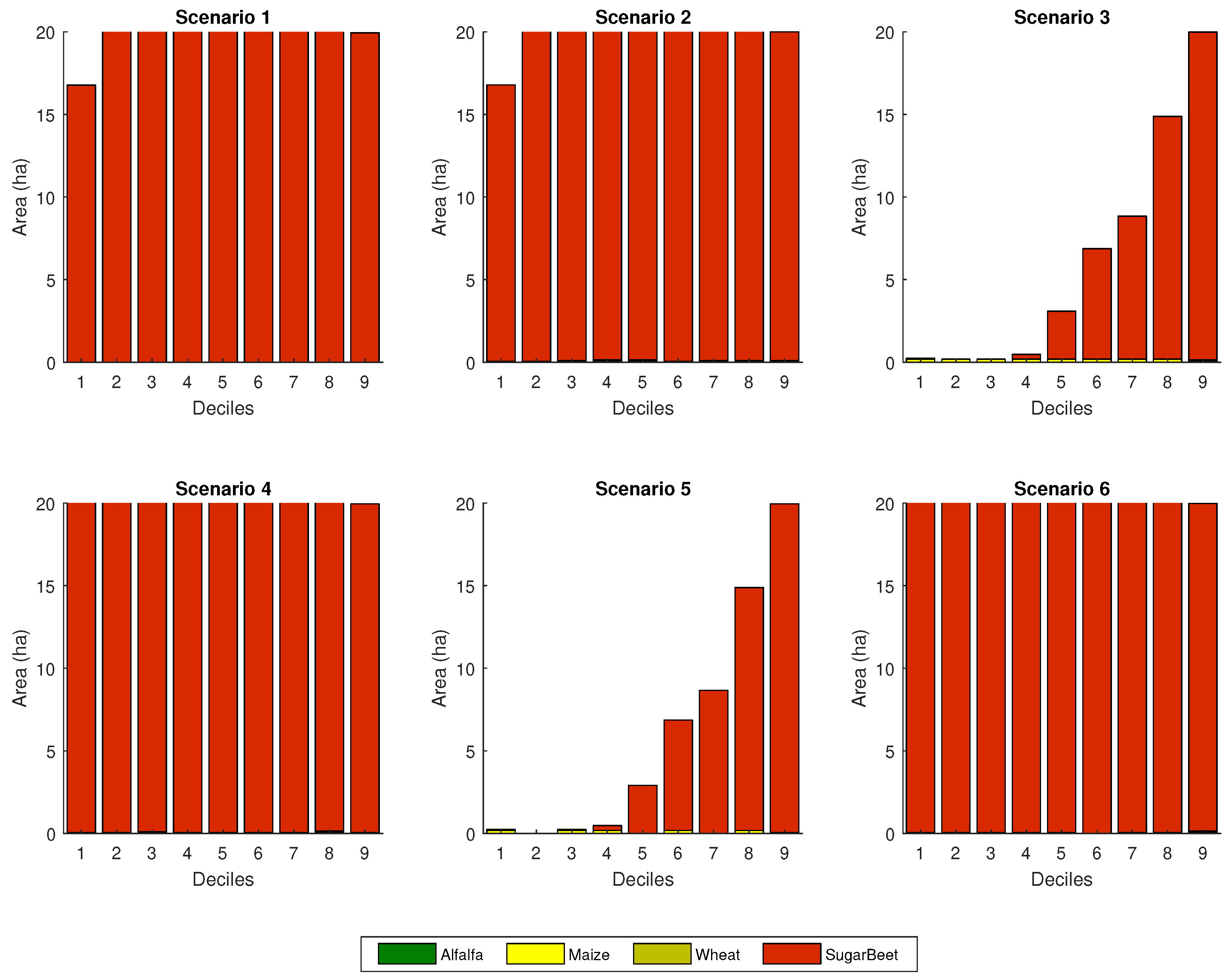
3.2. Crop Allocation
3.2.1. Situation a
3.2.2. Situation b
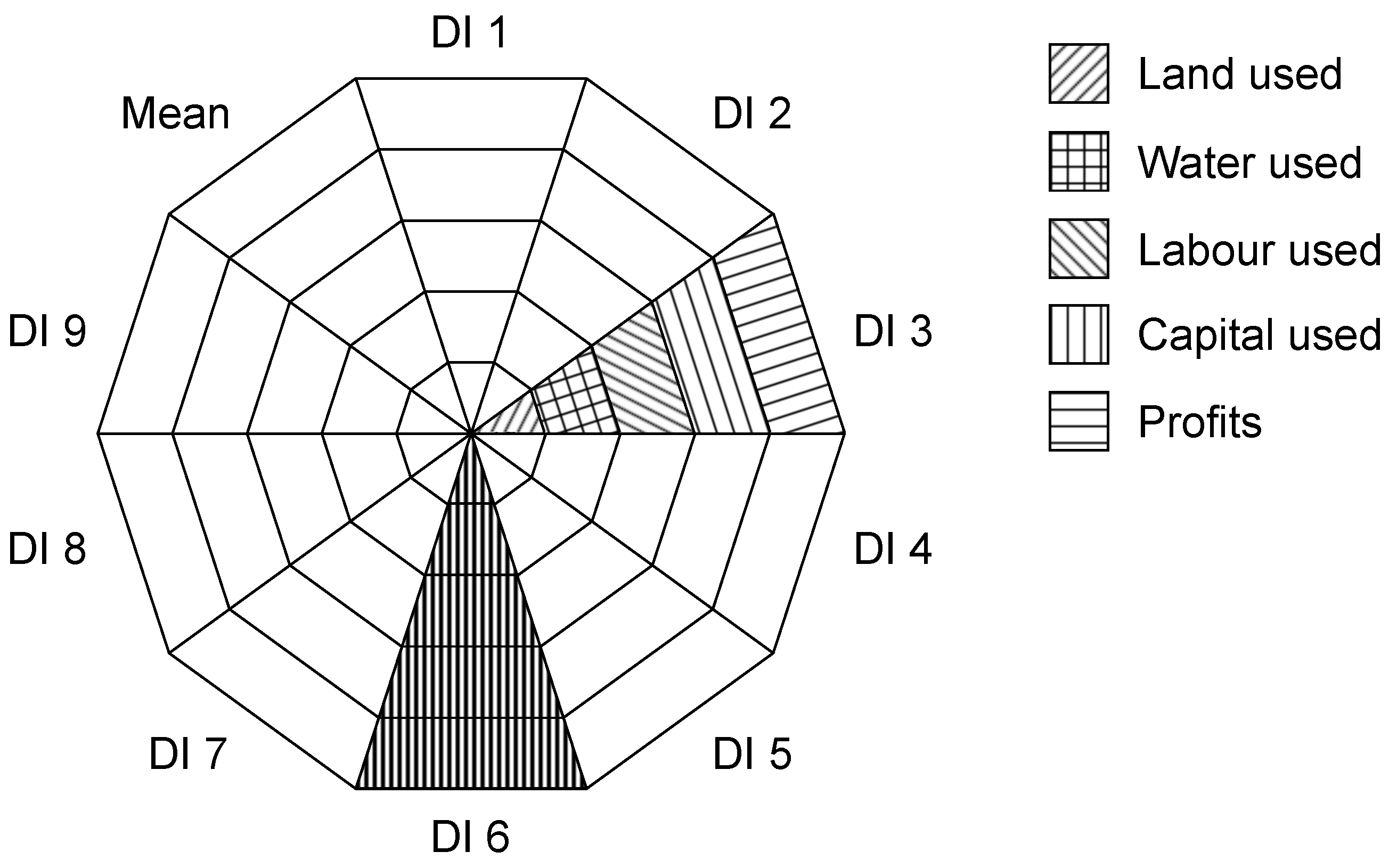
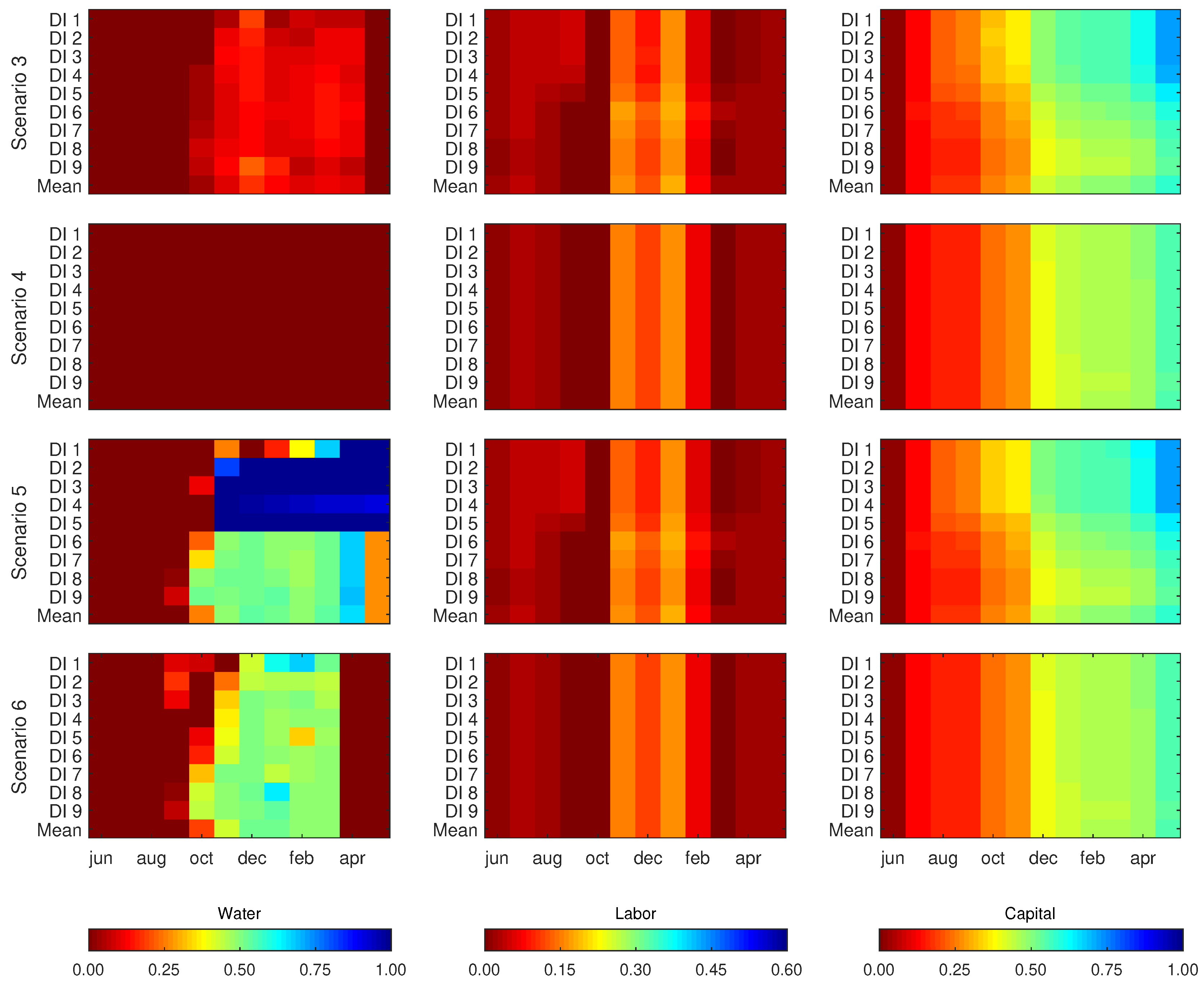
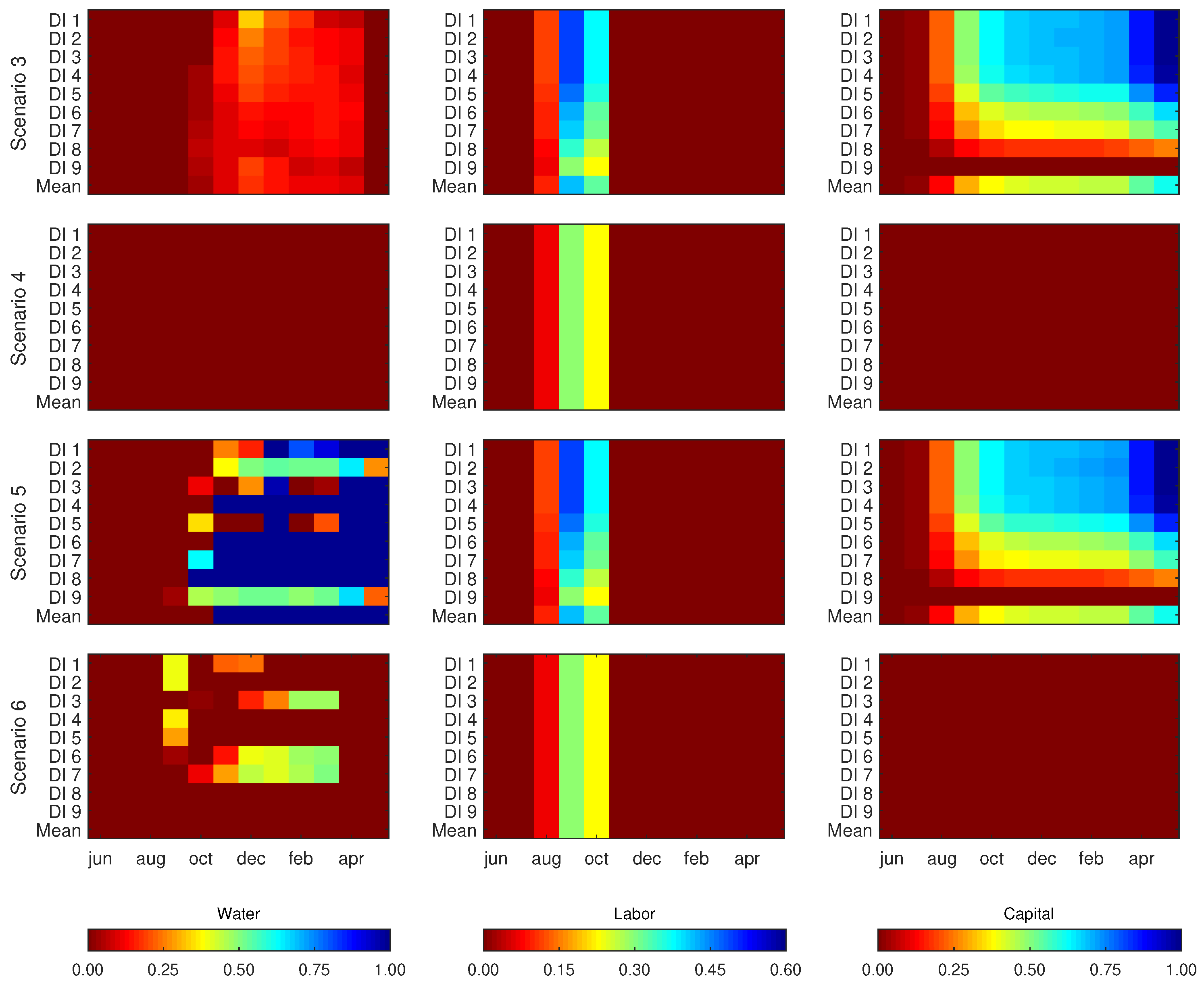
3.3. Monthly Limiting Resource
3.3.1. Situation a
3.3.2. Situation b
3.4. Sensitivity Analysis
3.4.1. Scenario 1
3.4.2. Scenario 6, Situation a
3.4.3. Scenario 6, Situation b
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Al-Ansari, T.; Korre, A.; Shah, N. Integrated modelling of the energy, water and food nexus to enhance the environmental performance of food production systems. In Proceedings of the 9th International Conference on Life Cycle Assessment in the Agri-Food Sector (LCA Food 2014), San Francisco, CA, USA, 8–10 October 2014; pp. 1–10. [Google Scholar]
- FAO; IFAD; WFP. The State of Food Insecurity in the World 2015. Meeting the 2015 International Hunger Targets: Taking Stock of Uneven Progress; FAO: Rome, Italy, 2015. [Google Scholar]
- McMichael, A.J.; Powles, J.W.; Butler, C.D.; Uauy, R. Food, livestock production, energy, climate change and health. Lancet 2007, 370, 1253–1263. [Google Scholar] [CrossRef]
- Gohari, A.; Mirchi, A.; Madani, K. System dynamics evaluation of climate change adaption strategies for water resources management in central Iran. Water Resour. Manag. 2017, 31, 1413–1434. [Google Scholar] [CrossRef]
- Assouline, S.; Russo, D.; Silber, A.; Or, D. Balancing water scarcity and quality for sustainable irrigated agriculture. Water Resour. Res. 2015, 51, 3419–3436. [Google Scholar] [CrossRef]
- Harmancioglu, N. Overview of water policy developments pre- and post- 2015 development agenda. Water Resour. Manag. 2017, 31, 3001–3021. [Google Scholar] [CrossRef]
- Garrick, D.; Siebentritt, M.; Aylward, B.; Bauer, C.; Purkey, A. Water markets and freshwater ecosystem services: Policy reform and implementation in the Columbia and Murray-Darling Basins. Ecol. Econ. 2009, 69, 366–379. [Google Scholar] [CrossRef]
- Erfani, T.; Binions, O.; Harou, J.J. Simulating water markets with transaction costs. Water Resour. Res. 2014, 50, 4726–4745. [Google Scholar] [CrossRef] [PubMed]
- Cosgrove, W.J.; Loucks, D.P. Water management: Current and future challenges and research directions. Water Resour. Res. 2015, 51, 4823–4839. [Google Scholar] [CrossRef]
- Iglesias, A.; Sánchez, B.; Garrote, L.; López, I. Towards adaptation to climate change: Water for rice in the coastal wetlands of Doñana, souther Spain. Water Resour. Manag. 2017, 31, 629–653. [Google Scholar] [CrossRef]
- Maneta, M.P.; Torres, M.O.; Wallender, W.W.; Vosti, S.; Howitt, R.; Rodrigues, L.; Bassoi, L.H.; Panday, S. A spatially distributed hydroeconomic model to assess the effects of drought on land use, farm profits, and agricultural employment. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Liu, D.; Chen, X.; Lou, Z. A Model for the Optimal Allocation of Water Resources in a Saltwater Intrusion Area: A Case Study in Pearl River Delta in China. Water Resour. Manag. 2010, 24, 63–81. [Google Scholar] [CrossRef]
- Homayounfar, M.; Lai, S.; Zomorodian, M.; Sepaskhah, A.; Ganji, A. Optimal crop water allocation in case of drought occurrence, imposing deficit irrigation with proportional cutback constraint. Water Resour. Manag. 2014, 28, 3207–3225. [Google Scholar] [CrossRef]
- Zhu, T.; Marques, G.F.; Lund, J.R. Hydroeconomic optimization of integrated water management and transfers under stochastic surface water supply. Water Resour. Res. 2015, 51, 3568–3587. [Google Scholar] [CrossRef]
- Hillier, F.; Lieberman, G. Introduction to Operations Research; McGraw Hill: New York, NY, USA, 2001. [Google Scholar]
- Sethi, L.; Kumar, D.; Panda, S.; Mal, B. Optimal crop planning and conjuctive use of water resources in a Coastal river basin. Water Resour. Manag. 2002, 16, 145–169. [Google Scholar] [CrossRef]
- Mishra, A.; Adhikary, A.; Panda, S. Optimal size of auxiliary storage reservoir for rainwater harvesting and better crop planning in a minor irrigation project. Water Resour. Manag. 2009, 23, 265–288. [Google Scholar] [CrossRef]
- Fasakhodi, A.; Nouri, S.; Amini, M. Water resources sustainability and optimal cropping pattern in farming systems: A multi-objective fractional goal programming approach. Water Resour. Manag. 2010, 24, 4639–4657. [Google Scholar] [CrossRef]
- Ponce, R.; Blanco, M.; Giupponi, C. The economic impacts of climate change on the chilean agricultural sector: A non-linear agricultural supply model. Chil. J. Agric. Res. 2014, 74, 404–412. [Google Scholar] [CrossRef]
- Su, X.; Li, J.; Singh, V. Optimal Allocation of Agricultural Water Resources Based on Virtual Water Subdivision in Shiyang River Basin. Water Resour. Manag. 2014, 28, 2243–2257. [Google Scholar] [CrossRef]
- Das, B.; Singh, A.; Panda, S.; Yasuda, H. Optimal land and water resources allocation policies for sustainable irrigated agriculture. Land Use Policy 2015, 42, 527–537. [Google Scholar] [CrossRef]
- Tan, Q.; Zhang, S.; Li, R. Optimal use of agricultural water and land resources through reconfiguring crop planting structure under socioeconomic and ecological objectives. Water 2017, 9, 488. [Google Scholar] [CrossRef]
- Varade, S.; Patel, J. Determination of Optimum Cropping Pattern Using Advanced Optimization Algorithms. J. Hydrol. Eng. 2018, 23, 05018010. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.; Fereres, E.; Raes, D. Crop Yield Response to Water. FAO Irrigation and Drainage Paper 66; Food and Agriculture Organization of the United Nations: Rome, Italy, 2012; p. 503. [Google Scholar]
- Doorenbos, J.; Kassam, A. Yield Response to Water; FAO: Rome, Italy, 1979. [Google Scholar]
- Mainuddin, M.; Das Gupta, A.; Raj Onta, P. Optimal crop planning model for an existing groundwater irrigation project in Thailand. Agric. Water Manag. 1997, 33, 43–62. [Google Scholar] [CrossRef]
- Prasad, A.S.; Umamahesh, N.V.; Viswanath, G.K. Optimal irrigation planning under water scarcity. J. Irrig. Drain. Eng. 2006, 132, 228–237. [Google Scholar] [CrossRef]
- Banihabib, M.; Zahraei, A.; Eslamian, S. Dynamic programming model for the system of a non-uniform deficit irrigation and reservoir. Irrig. Drain. 2017, 66, 71–81. [Google Scholar] [CrossRef]
- Carvallo, H.; Holzapfel, E.; López, M.; Mariño, M. Irrigated cropping optimization. J. Irrig. Drain. Eng. 1998, 124, 67–72. [Google Scholar] [CrossRef]
- Singh, A. Optimal Allocation of Resources for the Maximization of Net Agricultural Return. J. Irrig. Drain. Eng. 2012, 138, 830–836. [Google Scholar] [CrossRef]
- Raes, D.; Geerts, S.; Kipkorir, E.; Wellens, J.; Sahli, A. Simulation of yield decline as a result of water stress with a robust soil water balance model. Agric. Water Manag. 2006, 81, 335–357. [Google Scholar] [CrossRef]
- Karamouz, M.; Zahraie, B.; Kerachian, R.; Eslami, A. Crop pattern and conjuctive use management: A case study. Irrig. Drain. 2010, 59, 161–173. [Google Scholar] [CrossRef]
- Moghaddasi, M.; Araghinejad, S.; Morid, S. Long-term operation of irrigation dams considering variable demands: case study of Zayandeh-rud reservoir, Iran. J. Irrig. Drain. Eng. 2010, 136, 309–316. [Google Scholar] [CrossRef]
- Garg, K.; Dadhich, S. Integrated non-linear model for optimal cropping pattern and irrigation scheduling under deficit irrigation. Agric. Water Manag. 2014, 140, 1–13. [Google Scholar] [CrossRef]
- Jensen, M. Water consumption by agricultural plants. In Water Deficits in Plant Growth; Academic, P., Kozlowski, T., Eds.; Academic Press: New York, NY, USA, 1968; Chapter 1; pp. 1–22. [Google Scholar]
- Kipkorir, E.; Sahli, A.; Raes, D. MIOS: A decision tool for determination of optimal irrigated cropping pattern of a multicrop system under water scarcity constraints. Irrig. Drain. 2002, 51, 155–166. [Google Scholar] [CrossRef]
- Sadati, S.; Speelman, S.; Sabouhi, M.; Gitizadeh, M.; Ghahraman, B. Optimal irrigation water allocation using a genetic algorithm under various weather conditions. Water 2014, 6, 3068–3084. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, P. Integrated agriculture water management optimization model for water saving potential analysis. Agric. Water Manag. 2016, 170, 5–19. [Google Scholar] [CrossRef]
- DGA. Diagnóstico y Clasificación de los Cursos y Cuerpos de agua Según Objetivo y Calidad; Cuenca del río Itata.: Santiago, Chile, 2004. [Google Scholar]
- ODEPA. Región del Biobío: Información Regional 2018; Technical Report; Oficina de Estudios y Políticas Agrarias (ODEPA): Santiago, Chile, 2018.
- FAO. “CROPWAT 8.0” Databases and Software; FAO: Rome, Italy, 2017. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998; Volume 300. [Google Scholar]
- Faiguenbaum, H. Labranza, Siembra y Producción de los Principales Cultivos de Chile; Vivaldi y Asociados: Santiago, Chile, 2003; p. 760. [Google Scholar]
- Allen, R.G.; Walter, I.A.; Elliott, R.; Itenfisu, D.; Brown, P.; Jensen, M.E.; Mecham, B.; Howell, T.A.; Snyder, R.; Eching, S.; Spofford, T. Task Committee on Standardization of Reference Evapotranspiration; ASCE: Reston, VA, USA, 2005. [Google Scholar]
- INIA. Antecedentes Económicos de la Producción de Forrajes en Suelos Regados de la VIII Región; Technical Report; Instituto de Investigaciones Agropecuarias (INIA): Santiago, Chile, 2005. [Google Scholar]
- ODEPA. Boletin de Cereales; Technical Report; Oficina de Estudios y Políticas Agrarias (ODEPA): Santiago, Chile, 2017.
- ODEPA. Estudio: Identificación y Análisis del Impacto Económico del uso de Variedades y/o Híbridos Transgénicos de Maíz (Zea mays), Raps (Brassica Napus) y Remolacha (Beta Vulgaris), para los Agricultores en Chile: Informe Final; Technical report; Oficina de Estudios y Políticas Agrarias (ODEPA): Santiago, Chile, 2011.
- Brooke, A.; Kendrick, D.; Meeraus, A.; Raman, R. GAMS User’s Guide; The Scientific Press: Washington, DC, USA, 2014. [Google Scholar]
- Arnell, N. Climate change and global water resources: Sres emissions and socio-economics scenarios. Glob. Environ. Chang. 2004, 14, 31–52. [Google Scholar] [CrossRef]
- De Vries, T.; Weatherhead, E. Adapting to irrigation water scarcity due to climate changes in eastern England. Impacts of global climate change. In World Water and Environmental Resources Congress; ASCE: Reston, VA, USA, 2005; pp. 1–6. [Google Scholar]
- Luo, B.; Maqsood, I.; Gong, Y. Modeling climate change impacts on water trading. Sci. Total Environ. 2010, 408, 2034–2041. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Zheng, H.; Liu, Y.; Wang, Z. Assessment of the water market in the Xiying irrigation district, Shiyang River Basin, China. Water Resour. Plan. Manag. 2016, 142, 04016021. [Google Scholar] [CrossRef]
- Singh, A. Land and water management planning for increasing farm income in irrigated dry areas. Land Use Policy 2015, 42, 244–250. [Google Scholar] [CrossRef]
| Crop | Parameter | Month | Sowing | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sep | Oct | Nov | Dec | Jan | Feb | Mar | |||
| Alfalfa | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 01-Sep | |
| 30.0 | 31.0 | 30.0 | 31.0 | 31.0 | 28.0 | 15.0 | |||
| 49.0 | 49.0 | 49.0 | 49.0 | 49.0 | 49.0 | 49.0 | |||
| Maize | - | - | 0.5 | 0.7 | 1.2 | 0.5 | 0.1 | 01-Nov | |
| - | - | 30.0 | 31.0 | 31.0 | 28.0 | 5.0 | |||
| - | - | 28.4 | 35.1 | 35.6 | 34.3 | 33.4 | |||
| Wheat | 0.4 | 0.6 | 0.7 | 0.5 | 0.1 | - | - | 01-Sep | |
| 30.0 | 31.0 | 30.0 | 31.0 | 8.0 | - | - | |||
| 30.0 | 30.9 | 32.5 | 32.6 | 8.5 | - | - | |||
| Sugar beet | 0.6 | 0.8 | 1.0 | 1.0 | 0.9 | 0.6 | - | 01-Sep | |
| 30.0 | 31.0 | 30.0 | 31.0 | 31.0 | 7.0 | - | |||
| 29.5 | 31.5 | 35.2 | 37.3 | 38.8 | 38.4 | - | |||
| Crop | Price | Maximum Yield | Source | ||
|---|---|---|---|---|---|
| Value | Units | Value | Units | ||
| Alfalfa | 5.1 | US$ bale−1 | 400 | bales ha−1 | INIA [45] |
| Maize | 22.3 | US$ qqm−1 | 150 | qqm ha−1 | ODEPA [46] |
| Wheat | 22.5 | US$ qqm−1 | 70 | qqm ha−1 | ODEPA [46] |
| Sugar beet | 62.7 | US$ ton−1 | 100 | ton ha−1 | ODEPA [47] |
| Function or Constraint | Equation | Scenarios |
|---|---|---|
| Objective | 1 | |
| 2, 3, 5 | ||
| 4, 6 | ||
| Capital | 1, 2 | |
| 3–6 | ||
| Water | 1 | |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
| Crop Allocation | Use of Resources | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Alfalfa | Maize | Wheat | Sugar Beet | Land | Water | Labor | Capital | Profits | |
| (ha) | (ha) | (m3) | (Person-d) | (US$) | (US$) | ||||
| 1. Optimum cropping pattern | 0 | 0 | 0 | 20 | 20 | 167,477 | 120 | 80,000 | 45,917 |
| 2. Export prices | |||||||||
| 2.1 Decrease in 50% for sugar beet | 0 | 25 | 0 | 0 | 25 | 172,417 | 267 | 57,114 | 26,671 |
| 2.2 Decrease in 50% for maize | 0 | 0 | 0 | 20 | 20 | 167,477 | 120 | 80,000 | 45,917 |
| 2.3 Increase in 50% for alfalfa | 8 | 0 | 0 | 17 | 25 | 201,623 | 192 | 80,000 | 51,708 |
| 2.4 Increase in 50% for wheat | 0 | 0 | 0 | 20 | 20 | 167,477 | 120 | 80,000 | 45,917 |
| 3. Agronomic management | |||||||||
| 3.1 Minimum area to be sowed corresponds to 3 ha | 3 | 3 | 3 | 16 | 25 | 196,754 | 178 | 79,578 | 41,695 |
| 4. Application efficiency of the irrigation system | |||||||||
| 4.1 Sugar beet is irrigated by furrow () and | |||||||||
| wheat by sprinkler () | 0 | 0 | 0 | 20 | 20 | 209,346 | 120 | 80,000 | 45,917 |
| 5. Water costs | |||||||||
| 5.1 Costs of water rights increase to 0.05 US$/m3 | 0 | 0 | 0 | 16 | 16 | 131,010 | 94 | 80,000 | 18,500 |
| 6. Labour | |||||||||
| 6.1 Costs increase to 30 US$/person-d | 0 | 0 | 0 | 20 | 20 | 164,974 | 119 | 80,000 | 44,036 |
| 6.2 Availability decreases to 100 person-d | 0 | 0 | 0 | 17 | 17 | 139,015 | 100 | 66,502 | 38,017 |
| 7. Other costs | |||||||||
| 7.1 Increase in 50% for sugar beet | 0 | 25 | 0 | 0 | 25 | 172,417 | 267 | 57,114 | 26,671 |
| 7.2 Increase in 50% for maize | 0 | 0 | 0 | 20 | 20 | 167,477 | 120 | 80,000 | 45,917 |
| 7.3 Decrease in 50% for alfalfa | 6 | 0 | 0 | 19 | 25 | 203,014 | 184 | 80,000 | 50,321 |
| 7.4 Decrease in 50% for wheat | 0 | 0 | 6 | 19 | 25 | 198,643 | 146 | 80,000 | 47,781 |
| 8. Capital | |||||||||
| 8.1 Availability decreases to 50% | 0 | 0 | 0 | 10 | 10 | 83,136 | 60 | 40,000 | 22,506 |
| Crop Allocation | Use of Resources | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Alfalfa | Maize | Wheat | Sugar Beet | Land | Water | Labor | Capital | Profits | |
| (ha) | (ha) | (m3) | (Person-d) | (US$) | (US$) | ||||
| 1. Optimum cropping pattern | 3 | 4 | 0 | 6 | 13 | 96,212 | 109 | 36,000 | 18,754 |
| 2. Export prices | |||||||||
| 2.1 Decrease in 50% for sugar beet | 5 | 0 | 0 | 0 | 5 | 37,995 | 58 | 8098 | 2805 |
| 2.2 Decrease in 50% for maize | 5 | 0 | 0 | 6 | 11 | 89,835 | 95 | 32,687 | 17,122 |
| 2.3 Increase in 50% for alfalfa | 5 | 0 | 0 | 6 | 11 | 89,835 | 95 | 32,687 | 22,349 |
| 2.4 Increase in 50% for wheat | 3 | 4 | 5 | 4 | 16 | 114,625 | 125 | 36,687 | 19,046 |
| 3. Agronomic management | |||||||||
| 3.1 Minimum area to be sowed corresponds to 3 ha | 3 | 4 | 3 | 5 | 14 | 107,854 | 119 | 36,434 | 16,578 |
| 4. Application efficiency of the irrigation system | |||||||||
| 4.1 Sugar beet is irrigated by furrow () and | |||||||||
| wheat by sprinkler () | 3 | 4 | 0 | 6 | 13 | 108,040 | 109 | 36,000 | 18,737 |
| 5. Water costs | |||||||||
| 5.1 Costs of water rights increase to 0.05 US$/m3 | 3 | 4 | 0 | 6 | 13 | 96,212 | 109 | 53,350 | 12,505 |
| 6. Labour | |||||||||
| 6.1 Costs increase to 30 US$/person-d | 3 | 4 | 0 | 6 | 13 | 96,212 | 109 | 37,091 | 17,662 |
| 6.2 Availability decreases to 100 person-d | 1 | 1 | 0 | 2 | 4 | 32,071 | 36 | 12,380 | 6204 |
| 7. Other costs | |||||||||
| 7.1 Increase in 50% for sugar beet | 0 | 10 | 2 | 0 | 12 | 81,744 | 115 | 25,683 | 10,416 |
| 7.2 Increase in 50% for maize | 5 | 0 | 0 | 6 | 11 | 89,835 | 95 | 32,687 | 17,122 |
| 7.3 Decrease in 50% for alfalfa | 3 | 4 | 0 | 6 | 13 | 96,212 | 109 | 34,032 | 20,722 |
| 7.4 Decrease in 50% for wheat | 3 | 4 | 0 | 6 | 13 | 96,212 | 109 | 36,000 | 18,754 |
| 8. Capital | |||||||||
| 8.1 Availability decreases to 50% | 3 | 0 | 0 | 6 | 10 | 79,035 | 78 | 30,922 | 16,577 |
| Crop Allocation | Use of Resources | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Alfalfa | Maize | Wheat | Sugar Beet | Land | Water | Labor | Capital | Profits | |
| (ha) | (ha) | (m3) | (Person-d) | (US$) | (US$) | ||||
| 1. Optimum cropping pattern | 0 | 0 | 0 | 20 | 20 | 167,460 | 120 | 80,000 | 46,177 |
| 2. Export prices | |||||||||
| 2.1 Decrease in 50% for sugar beet | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 572 | −71 |
| 2.2 Decrease in 50% for maize | 0 | 0 | 0 | 20 | 20 | 167,460 | 120 | 80,000 | 46,177 |
| 2.3 Increase in 50% for alfalfa | 0 | 0 | 0 | 20 | 20 | 167,739 | 121 | 80,000 | 46,224 |
| 2.4 Increase in 50% for wheat | 0 | 0 | 0 | 20 | 20 | 167,760 | 121 | 79,958 | 46,135 |
| 3. Agronomic management | |||||||||
| 3.1 Minimum area to be sowed corresponds to 3 ha | 3 | 3 | 3 | 5 | 14 | 101,803 | 113 | 36,395 | 7464 |
| 4. Application efficiency of the irrigation system | |||||||||
| 4.1 Sugar beet is irrigated by furrow () and | |||||||||
| wheat by sprinkler () | 0 | 0 | 0 | 20 | 20 | 209,292 | 120 | 80,000 | 46,108 |
| 5. Water costs | |||||||||
| 5.1 Costs of water rights increase to 0.05 US$/m3 | 0 | 0 | 0 | 17 | 17 | 143,133 | 103 | 77,493 | 32,014 |
| 6. Labour | |||||||||
| 6.1 Costs increase to 30 US$/person-d | 0 | 0 | 0 | 20 | 20 | 163,870 | 118 | 79,363 | 43,920 |
| 6.2 Availability decreases to 100 person-d | 0 | 0 | 0 | 16 | 16 | 137,558 | 99 | 65,815 | 37,919 |
| 7. Other costs | |||||||||
| 7.1 Increase in 50% for sugar beet | 0 | 0 | 0 | 13 | 14 | 112,451 | 82 | 79,277 | 5221 |
| 7.2 Increase in 50% for maize | 0 | 0 | 0 | 20 | 20 | 167,433 | 121 | 79,988 | 46,074 |
| 7.3 Decrease in 50% for alfalfa | 0 | 0 | 0 | 20 | 20 | 168,256 | 122 | 79,980 | 46,268 |
| 7.4 Decrease in 50% for wheat | 0 | 0 | 0 | 20 | 20 | 168,256 | 122 | 79,980 | 46,268 |
| 8. Capital | |||||||||
| 8.1 Availability decreases to 50% | 0 | 0 | 0 | 10 | 10 | 83,074 | 60 | 39,972 | 22,872 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuschel-Otárola, M.; Rivera, D.; Holzapfel, E.; Palma, C.D.; Godoy-Faúndez, A. Multiperiod Optimisation of Irrigated Crops under Different Conditions of Water Availability. Water 2018, 10, 1434. https://doi.org/10.3390/w10101434
Kuschel-Otárola M, Rivera D, Holzapfel E, Palma CD, Godoy-Faúndez A. Multiperiod Optimisation of Irrigated Crops under Different Conditions of Water Availability. Water. 2018; 10(10):1434. https://doi.org/10.3390/w10101434
Chicago/Turabian StyleKuschel-Otárola, Mathias, Diego Rivera, Eduardo Holzapfel, Cristian D. Palma, and Alex Godoy-Faúndez. 2018. "Multiperiod Optimisation of Irrigated Crops under Different Conditions of Water Availability" Water 10, no. 10: 1434. https://doi.org/10.3390/w10101434
APA StyleKuschel-Otárola, M., Rivera, D., Holzapfel, E., Palma, C. D., & Godoy-Faúndez, A. (2018). Multiperiod Optimisation of Irrigated Crops under Different Conditions of Water Availability. Water, 10(10), 1434. https://doi.org/10.3390/w10101434









