Study of Cavitation Bubble Collapse near a Wall by the Modified Lattice Boltzmann Method
Abstract
:1. Introduction
2. Basic Principle of the LBM
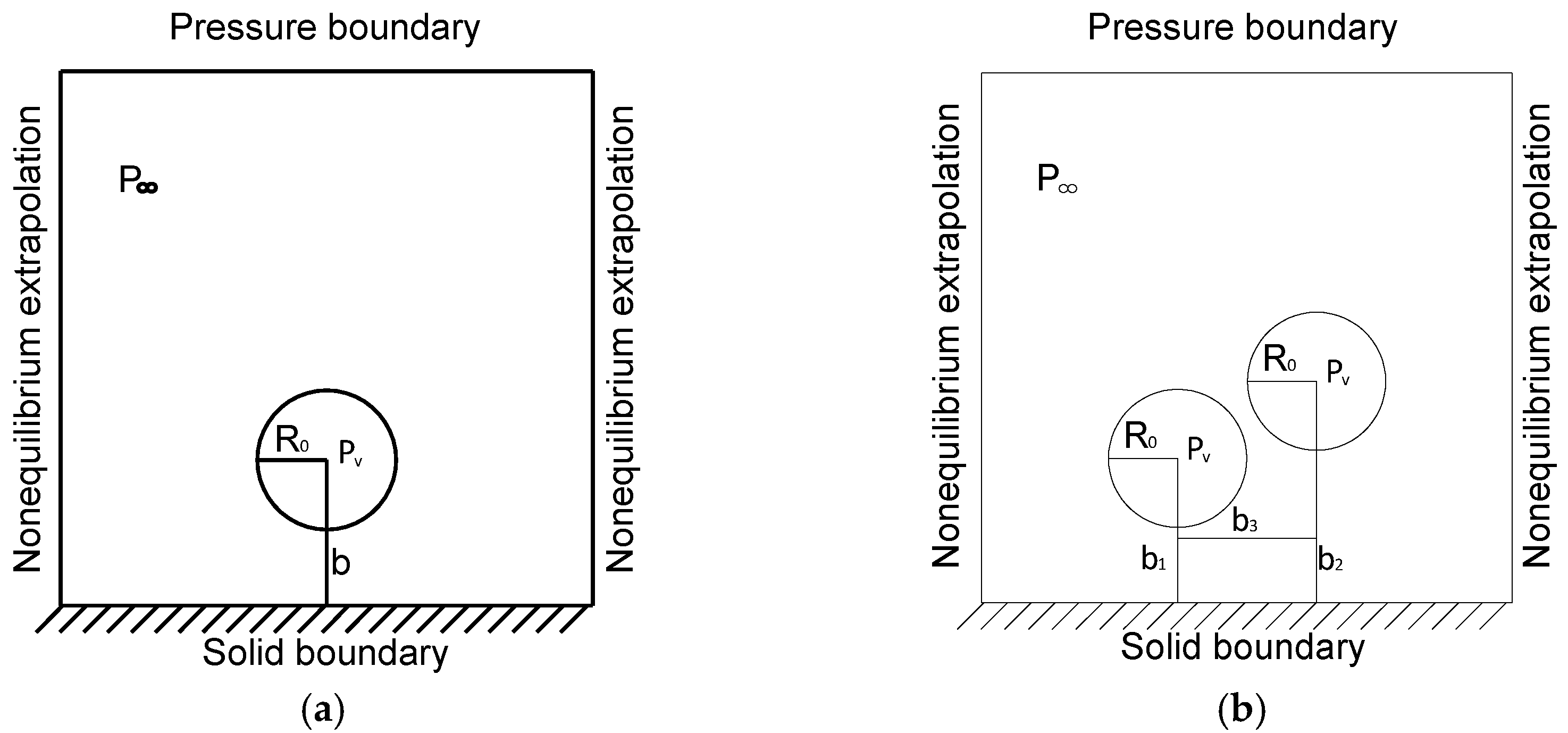
3. Physical Model
4. Simulation Content and Parameter Initialization Settings
5. Study of the Evolution of a Single Cavitation Bubble
6. Study of the Evolution of a Double Cavitation Bubble
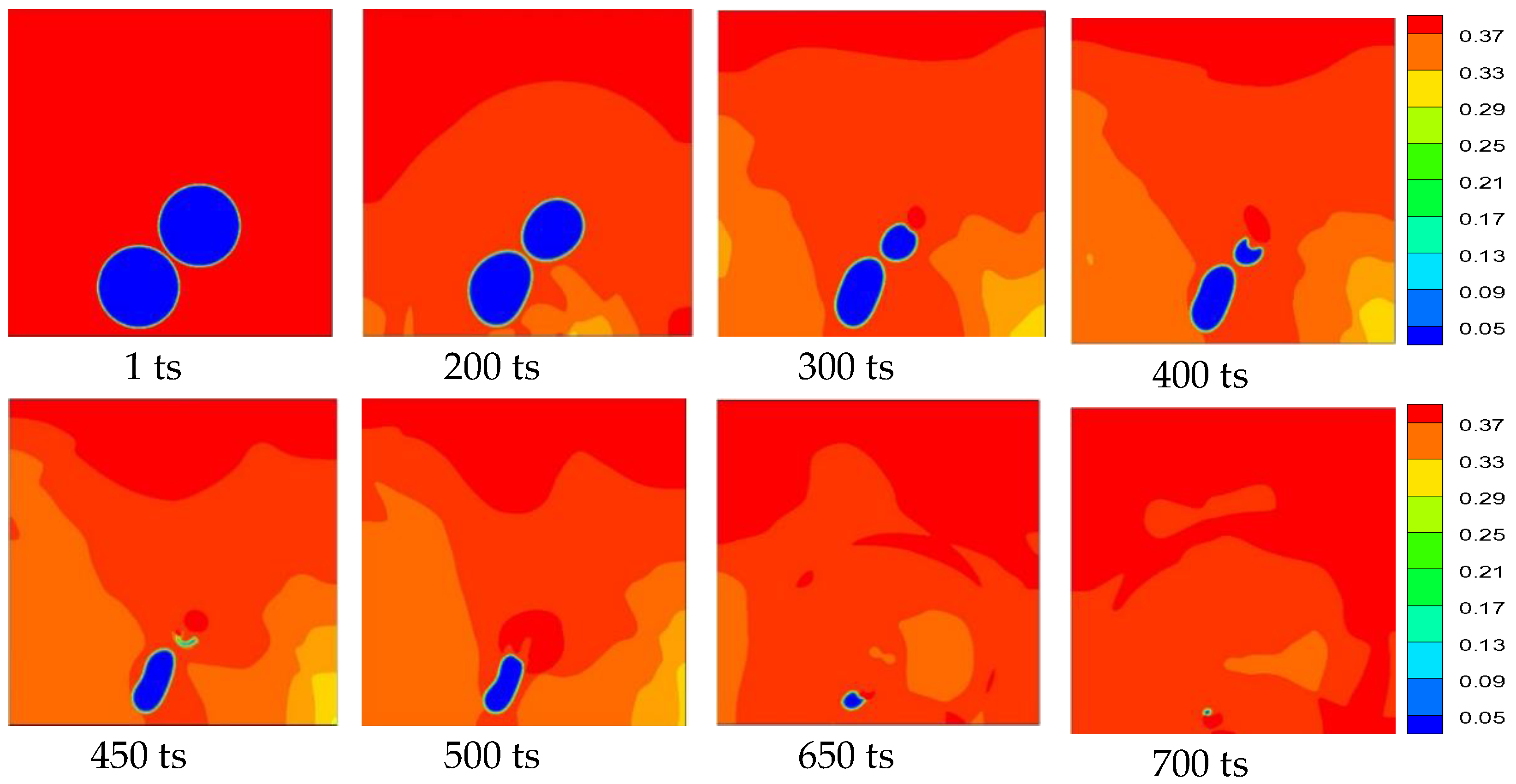
6.1. Case 1: Numerical Simulation of Tilt Distribution Cavitation with Two Cavitation Bubbles
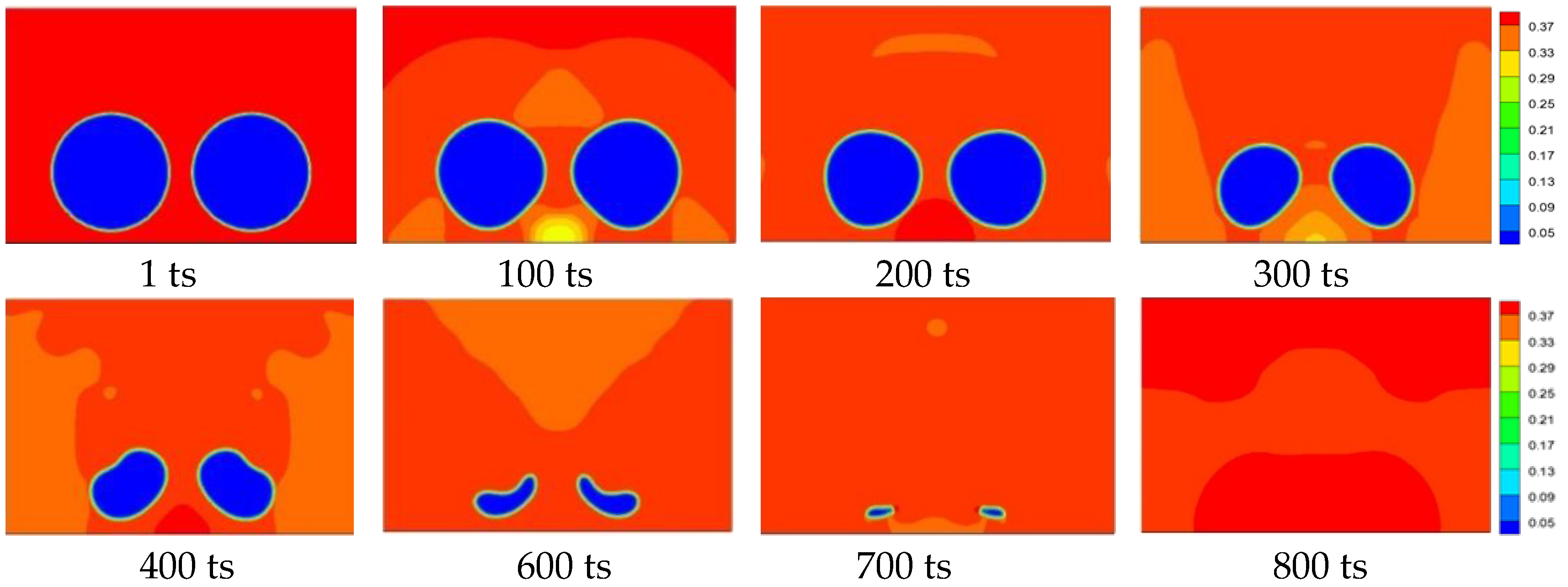
6.2. Case 2: Numerical Simulation of Two Parallel Cavitation Bubbles
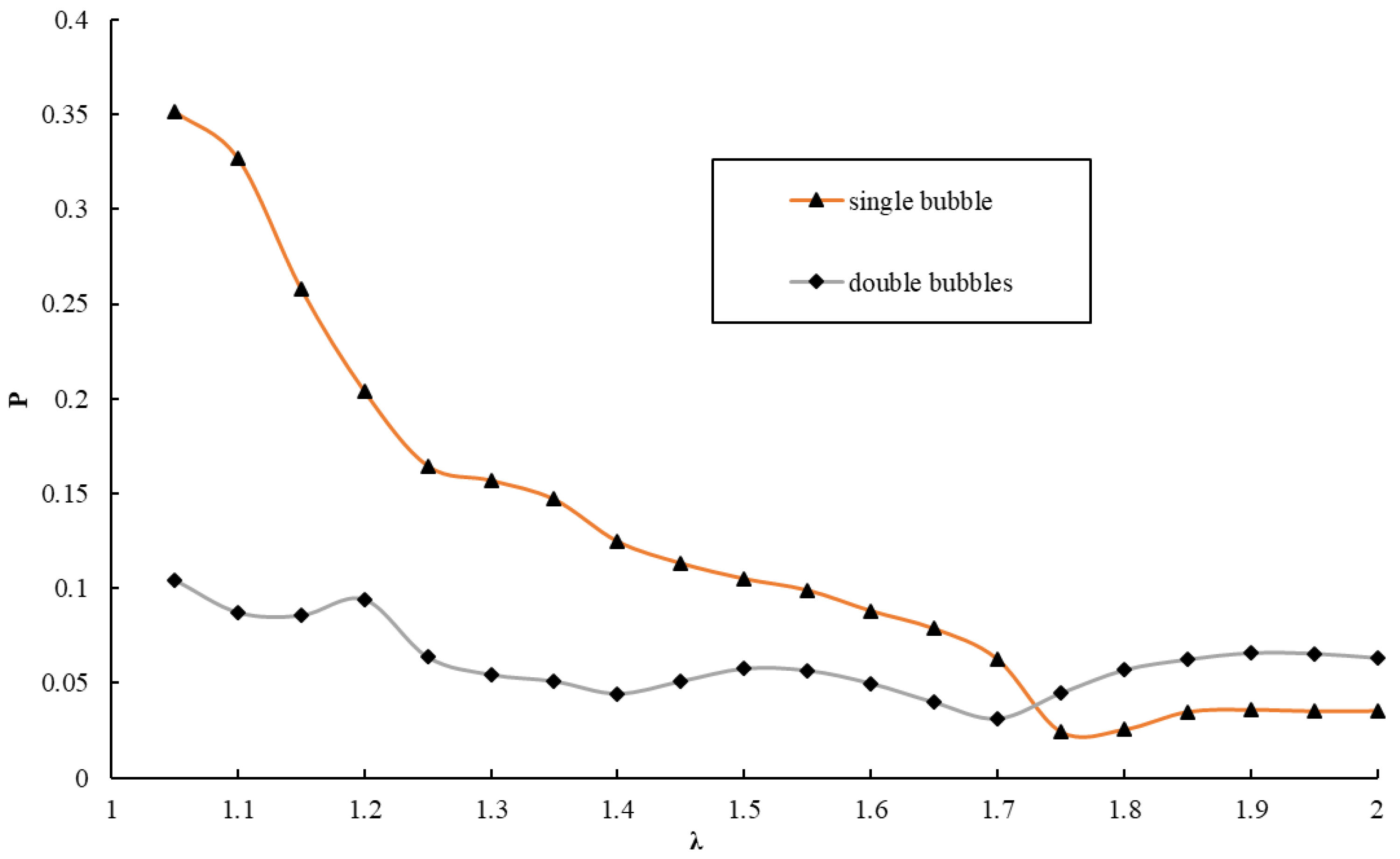
7. Maximum Wall Pressure
- The maximum wall pressure generated by the collapse of a single cavitation bubble in the near-wall region decreases with increasing distance from the wall surface, and it first drops sharply, then slowly decreases and finally becomes relatively stable. This is because the closer to the wall, the smaller the thickness of the fluid that the micro shock wave generated by cavitation passes to the wall and the smaller the blockage effect of the flow field, the greater the wall pressure generated.
- It is complex for the case where a double parallel cavitation bubble collapses in the near-wall region because the maximum wall pressure produces a different position under different initial conditions. When λ = 1.05–1.10, the wall below the cavitation bubble is subjected to the maximum wall pressure, because the cavitation bubble is closer to the wall surface, and the generated micro-shock is transmitted to the wall surface almost unimpeded and the cavitation bubble of the pressure change region is not fully developed, which is not enough to generate create a huge pressure with the lifting force to bubble. When λ = 1.15–1.25, the maximum wall pressure occurs in the pressure change zone where new cavitation bubbles are generated and collapse rapidly, resulting in a large wall pressure exceeding the maximum wall pressure at other locations. When λ = 1.40–2.0, the area where the maximum wall pressure is generated is the pressure change zone, but the pressure generation at this time is not when the new cavitation bubble collapses but the pressure after the collapse of the two cavitation bubbles overlaps each other on the wall. The change in wall pressure depends mainly on the size of the new cavitation bubble induced and the pressure generated by the collapse and the lifting force of the bubbles.
- When λ < 1.7, the wall pressure generated by the collapse of a single cavitation bubble is relatively large. This is because, for the case where the double cavitation bubble collapses in the near-wall region, the pressure generated by the collapse of the new cavitation bubble induced in the pressure change region has an effect of lifting force on the cavitation bubble. Thereby, the bottom pressure of the cavitation bubble collapse is increased, and the blockage effect of the wall surface is weakened, which is equivalent to an increase of λ, and the resulting wall pressure is relatively small. When λ > 1.7, the wall pressure of the pressure change zone is formed by the superposition of pressure generated by the collapse of two cavitation bubbles, so the generated wall pressure is greater than the pressure generated by the collapse of a single cavitation bubble.
8. Conclusions
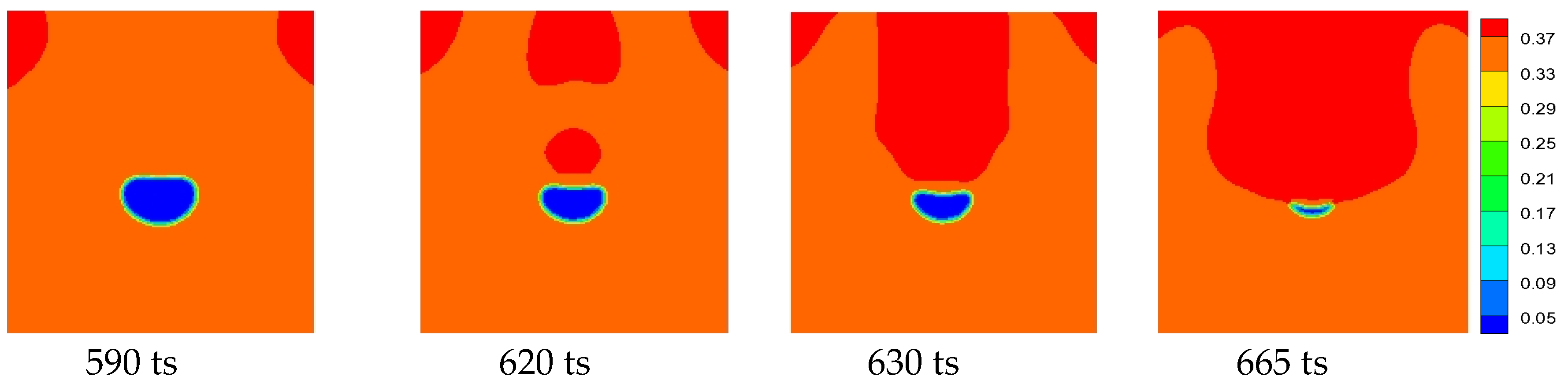
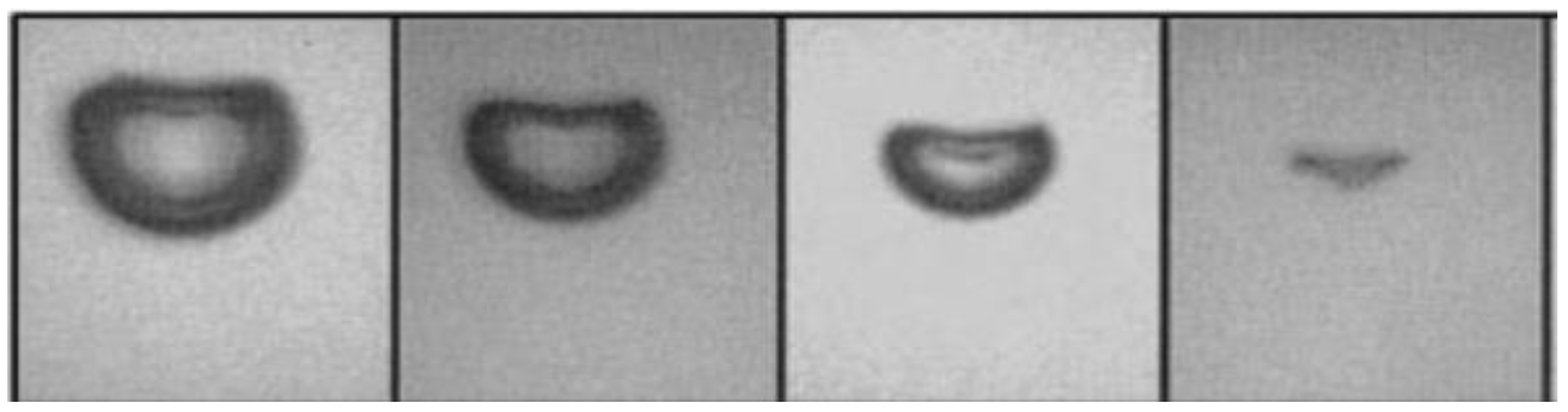
- For the case where a single cavitation bubble collapses in the near-wall region, when λ = 1.6, a crescent-shaped bubble is formed that is broken down to form two bubbles, and a micro-shock is generated; when λ = 2.5, the bubbles are crushed to form crescent-shaped bubbles, but the bubbles do not break in the middle but rather ultimately collapse in the form of a small bubble. The shape of the cavitation bubble is related to the distance of the cavitation bubble from the rigid wall.
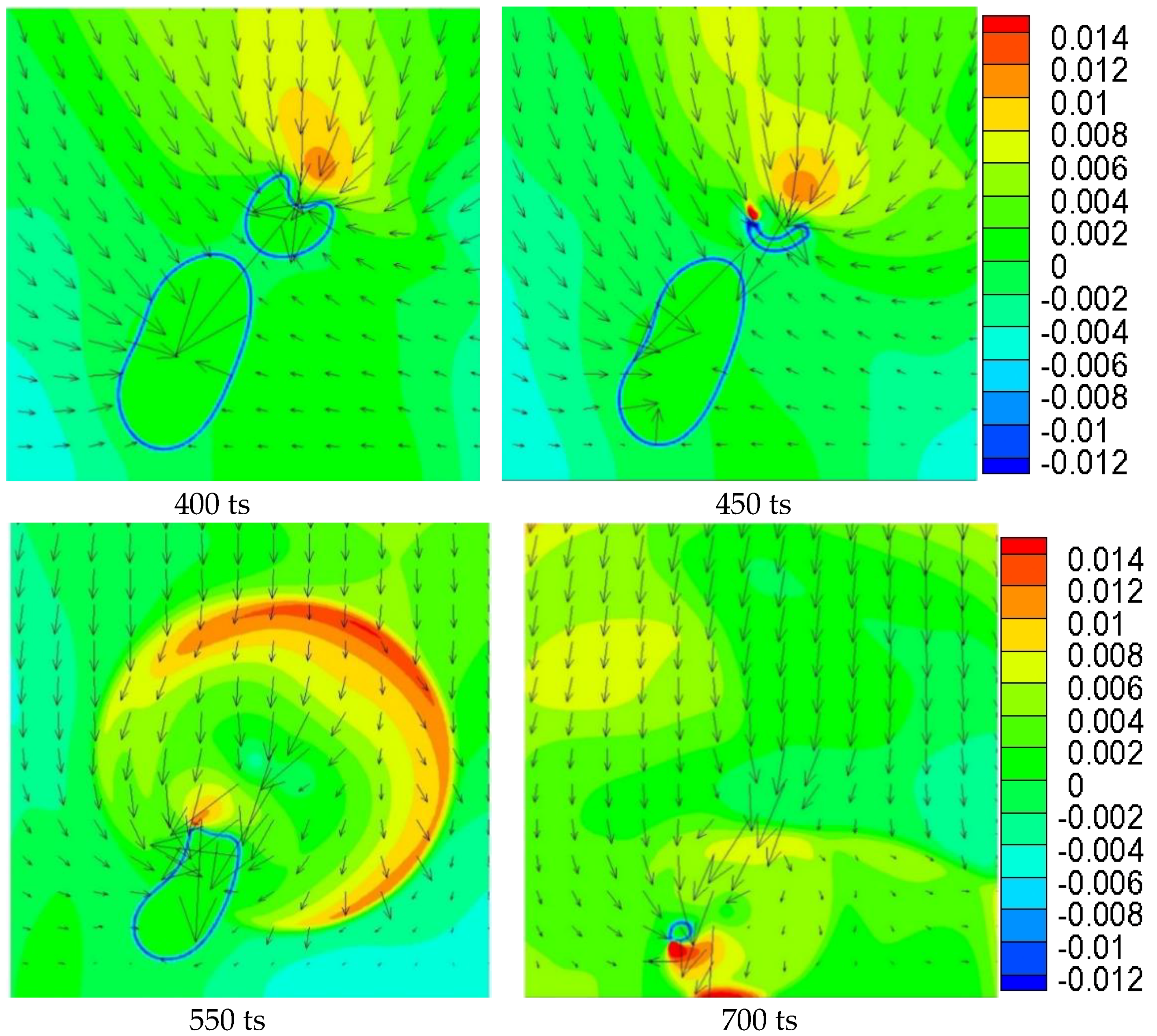
- For the numerical simulation of tilted distribution cavitation with two cavitation bubbles, in the early stage of simulation, the collapse behaviour is similar to that of the single-bubble case. Subsequently, the e6 direction of RB has a concave deformation, which is very important in the collapse of the two bubbles. The velocity field indicates that the maximum velocity appears in the depression of RB. The tremendous pressure generated by this velocity directly penetrates the bubble; thereafter, the bubble is crescent-shaped until collapsing completely. Due to the asymmetry of the collapse, the flow field becomes complex after RB collapses and particularly so after LB collapses, and vortices appear in the flow field.
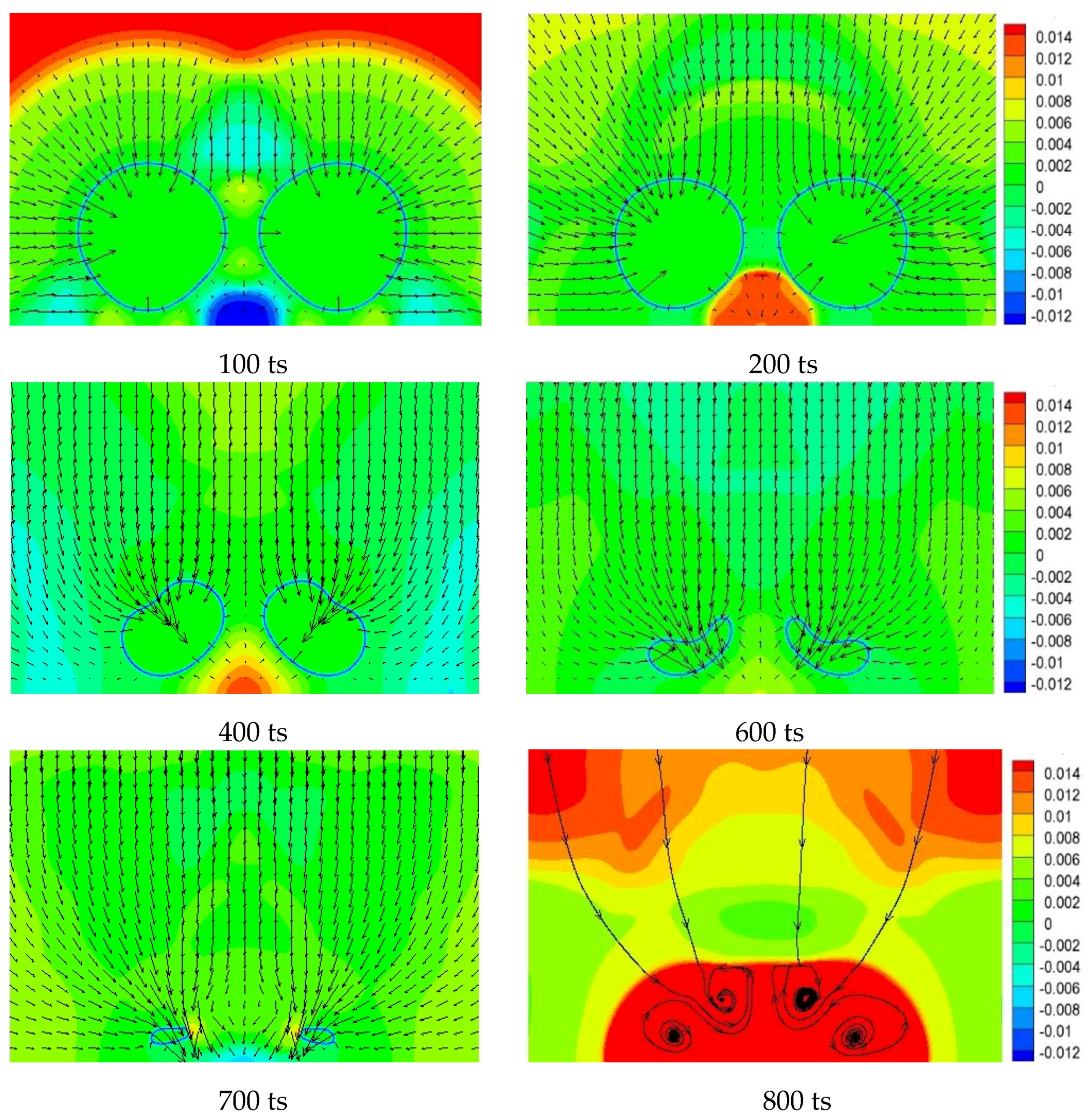
- For the numerical simulation of parallel distribution cavitation of two bubbles, the bubble collapses under the blocking effect of the rigid wall and the attraction of the two bubbles, and the two bubbles collapse simultaneously. Therefore, the mutual influence during the collapse process is smaller than that of Case 1; in addition, the erosion effect of the bubble collapse on the wall surface is the result of superimposing the pressure fields formed by the collapse of the two bubbles. However, for each bubble, since the collapse does not occur instantaneously but is collapsed from the upper part of the closest position of the two cavitation bubbles, a complex vortex phenomenon occurs in the flow field.
- By comparing the maximum wall pressure generated by cavitation under different initial conditions, the factors affecting the maximum wall pressure are obtained. For a single cavitation bubble, the distance from the wall is the most important factor. For two cavitation bubbles, the lifting effect of the new induced cavitation bubble collapse is the most important factor.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Single Particle Density Distribution Function | |
|---|---|
| equilibrium particle distribution function | |
| relaxation time | |
| kinematic viscosity | |
| grid velocity | |
| grid step | |
| time step | |
| lattice sound velocity | |
| weighting factor | |
| u | fluid velocity |
| interaction force | |
| interaction potential | |
| critical temperature | |
| critical pressure | |
| F | total interaction force |
| Pv | pressure of the cavitation bubble |
| P∞ | the pressure outside the cavitation bubble |
| R0 | radius of the cavitation bubble |
| b (,) | distance between corresponding points |
| T | lattice temperature |
| a (in Equation (11)) | parameter of the C-S state of equation |
| b (in Equation (11)) | parameter of the C-S state of equation |
| R (in Equation (11)) | parameter of the C-S state of equation |
| the equilibrium gas pressure | |
| the equilibrium liquid pressure | |
| λ() | dimensionless value that characterizes the distance |
References
- Kling, C.L.; Hammitt, F.G. A photographic study of spark-induced cavitation bubble collapse. J. Basic Eng. 1972, 94, 825–832. [Google Scholar] [CrossRef]
- Lauterborn, W. High-speed photography of laser-induced breakdown in liquids. Appl. Phys. Lett. 1977, 31, 663–664. [Google Scholar] [CrossRef]
- Lauterborn, W.; Bolle, H. Experimental investigations of cavitation-bubble collapse in the neighbourhood of a solid boundary. J. Fluid Mech. 1975, 72, 391–399. [Google Scholar] [CrossRef]
- Reuter, F. Electrochemical wall shear rate microscopy of collapsing bubbles. Phys. Rev. Fluids 2018, 3, 063601. [Google Scholar] [CrossRef]
- Watanabe, R.; Yanagisawa, K.; Yamagata, T.; Fujisawa, N. Simultaneous shadowgraph imaging and acceleration pulse measurement of cavitating jet. Wear 2016, 358–359, 72–79. [Google Scholar] [CrossRef]
- Reuter, F.; Cairos, C.; Mettin, R. Vortex dynamics of collapsing bubbles: Impact on the boundary layer measured by chronoamperometry. Ultrason. Sonochem. 2016, 33, 170–181. [Google Scholar] [CrossRef] [PubMed]
- Cui, P.; Zhang, A.M.; Wang, S.P.; Khoo, B.C. Ice breaking by a collapsing bubble. J. Fluid Mech. 2018, 841, 287–309. [Google Scholar] [CrossRef]
- Rossello, J.M.; Urteaga, R.; Bonetto, F.J. A novel water hammer device designed to produce controlled bubble collapses. Exp. Therm. Fluid Sci. 2018, 92, 46–55. [Google Scholar] [CrossRef]
- Pal, A.; Joseph, E.; Vadakkumbatt, V.; Yadav, N.; Srinivasan, V.; Maris, H.J.; Ghosh, A. Collapse of Vapor-Filled Bubbles in Liquid Helium. J. Low Temp. Phys. 2017, 188, 101–111. [Google Scholar] [CrossRef]
- Daou, M.M.; Igualada, E.; Dutilleul, H.; Citerne, J.-M.; Rodriguez-Rodriguez, J.; Zaleski, S.; Fuster, D. Investigation of the collapse of bubbles after the impact of a piston on a liquid free surface. AIChE J. 2017, 63, 2483–2495. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.J.; Huang, B.A.; Zhao, X.; Wang, Y.; Chang, Q.; Qui, S.; Fu, X.; Wang, G. Comparisons of spark-charge bubble dynamics near the elastic and rigid boundaries. Ultrason. Sonochem. 2018, 43, 80–90. [Google Scholar] [CrossRef] [PubMed]
- Gong, S.W.; Ohl, S.W.; Klaseboer, E.; Khoo, B.C. Interaction of a spark-generated bubble with a two-layered composite beam. J. Fluids Struct. 2018, 76, 336–348. [Google Scholar] [CrossRef]
- Oh, J.; Yoo, Y.; Seung, S.; Kwak, H.-Y. Laser-induced bubble formation on a micro gold particle levitated in water under ultrasonic field. Exp. Therm. Fluid Sci. 2018, 93, 285–291. [Google Scholar] [CrossRef]
- Sukop, M.C.; Or, D. Lattice Boltzmann method for homogeneous and heterogeneous cavitation. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.P.; Zhong, C.W.; Yuan, X.L. Lattice Boltzmann simulation of cavitating bubble growth with large density ratio. Comput. Math. Appli. 2012, 61, 3577–3584. [Google Scholar] [CrossRef]
- Shan, M.L.; Zhu, C.P.; Zhou, X.; Yin, C.; Han, Q.B. Investigation of cavitation bubble collapse near rigid boundary by lattice Boltzmann method. J. Hydrodyn. 2016, 28, 442–450. [Google Scholar] [CrossRef]
- Zhou, X.; Shan, M.L.; Zhu, C.P.; Chen, B.Y.; Yin, C.; Ren, Q.G.; Han, Q.B.; Tang, Y.B. Simulation of Acoustic Cavitation Bubble Motion by Lattice Boltzmann Method. Appl. Mech. Mater. 2014, 580–583, 3098–3105. [Google Scholar] [CrossRef]
- Kucera, A.; Blake, J.R. Approximate methods for modeling cavitation bubbles near boundaries. Bull. Austral. Math. Soc. 1990, 41, 1–44. [Google Scholar] [CrossRef]
- Li, B.B.; Zhang, H.C.; Han, B.; Chen, J.; Ni, X.W.; Lu, J. Investigation of the collapse of laser-induced bubble near a cone boundary. Acta Phys. Sin. 2012, 61, 21. [Google Scholar]
- Zhang, X.M.; Zhou, C.Y.; Islam, S.; Liu, J.Q. Three-dimensional cavitation simulation using lattice Boltzmann method. Acta Phys. Sin. 2009, 58, 8406–8414. [Google Scholar]
- Mishra, S.K.; Deymier, P.A.; Muralidharan, K.; Frantziskonis, G.; Pannala, S.; Simunovic, S. Modeling the coupling of reaction kinetics and hydrodynamics in a collapsing cavity. Ultrason. Sonochem. 2010, 17, 258–265. [Google Scholar] [CrossRef] [PubMed]
- Schanz, D.; Metten, B.; Kurz, T.; Lauterborn, W. Molecular dynamics simulations of cavitation bubble collapse and sonoluminescence. New J. Phys. 2012, 14. [Google Scholar] [CrossRef]
- Du, T.; Wang, Y.; Huang, C.; Liao, L. A numerical model for cloud cavitation based on bubble cluster. Theor. Appl. Mech. Lett. 2017, 7, 231–234. [Google Scholar] [CrossRef]
- Wang, Q.; Yao, W.; Quan, X.; Cheng, P. Validation of a dynamic model for vapor bubble growth and collapse under microgravity conditions. Int. Commun. Heat Mass Transf. 2018, 95, 63–73. [Google Scholar] [CrossRef]
- Ogloblina, D.; Schmidt, S.J.; Adams, N.A. Simulation and analysis of collapsing vapor-bubble clusters with special emphasis on potentially erosive impact loads at walls. EPJ Web Conf. 2018, 180, 9. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, C.J.; Chen, X.; Li, J.; Gong, Z.X. Numerical investigation of the time-resolved bubble cluster dynamics by using the interface capturing method of multiphase flow approach. J. Hydrodynam. 2017, 29, 485–494. [Google Scholar] [CrossRef]
- Ming, L.; Zhi, N.; Chunhua, S. Numerical Simulation of Cavitation Bubble Collapse within a Droplet. Comput. Fluids 2017, 152, 157–163. [Google Scholar] [CrossRef]
- Peng, K.; Tian, S.; Li, G.; Huang, Z.; Yang, R.; Guo, Z. Bubble dynamics characteristics and influencing factors on the cavitation collapse intensity for self-resonating cavitating jets. Petrol. Explor. Dev. 2018, 45, 343–350. [Google Scholar] [CrossRef]
- Xue, H.H.; Shan, F.; Guo, X.S.; Tu, J.; Zhang, D. Cavitation Bubble Collapse near a Curved Wall by the Multiple-Relaxation-Time Shan-Chen Lattice Boltzmann Model. Chin. Phys. Lett. 2017, 34, 83–87. [Google Scholar] [CrossRef]
- Tagawa, Y.; Peters, I.R. Bubble Collapse and Jet Formation in Corner Geometries. Phys. Rev. Fluids 2018, 2. [Google Scholar] [CrossRef]
- Goncalves, E.; Zeidan, D. Numerical study of bubble collapse near a wall. AIP Conf. Proc. 2018, 1978. [Google Scholar] [CrossRef]
- Peng, Y.; Mao, Y.F.; Wang, B. Study on C–S and P–R EOS in pseudo-potential lattice Boltzmann model for two-phase flows. Int. J. Mod. Phys. C 2017, 28. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, B.; Mao, Y. Study on Force Schemes in Pseudopotential Lattice Boltzmann Model for Two-Phase Flows. Math. Probl. Eng. 2018. [Google Scholar] [CrossRef]
- Yuan, P.; Schaefer, L. Equations of state in a lattice Boltzmann model. Phys. Fluids 2006, 18. [Google Scholar] [CrossRef]
- Philipp, A.; Lauterborn, W. Cavitation erosion by single laser-produced bubbles. J. Fluid Mech. 2000, 361, 75–116. [Google Scholar] [CrossRef]
- Plesset, M.S.; Chapman, R.B. Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary. J. Fluid Mech. 1970, 47, 283–290. [Google Scholar] [CrossRef]
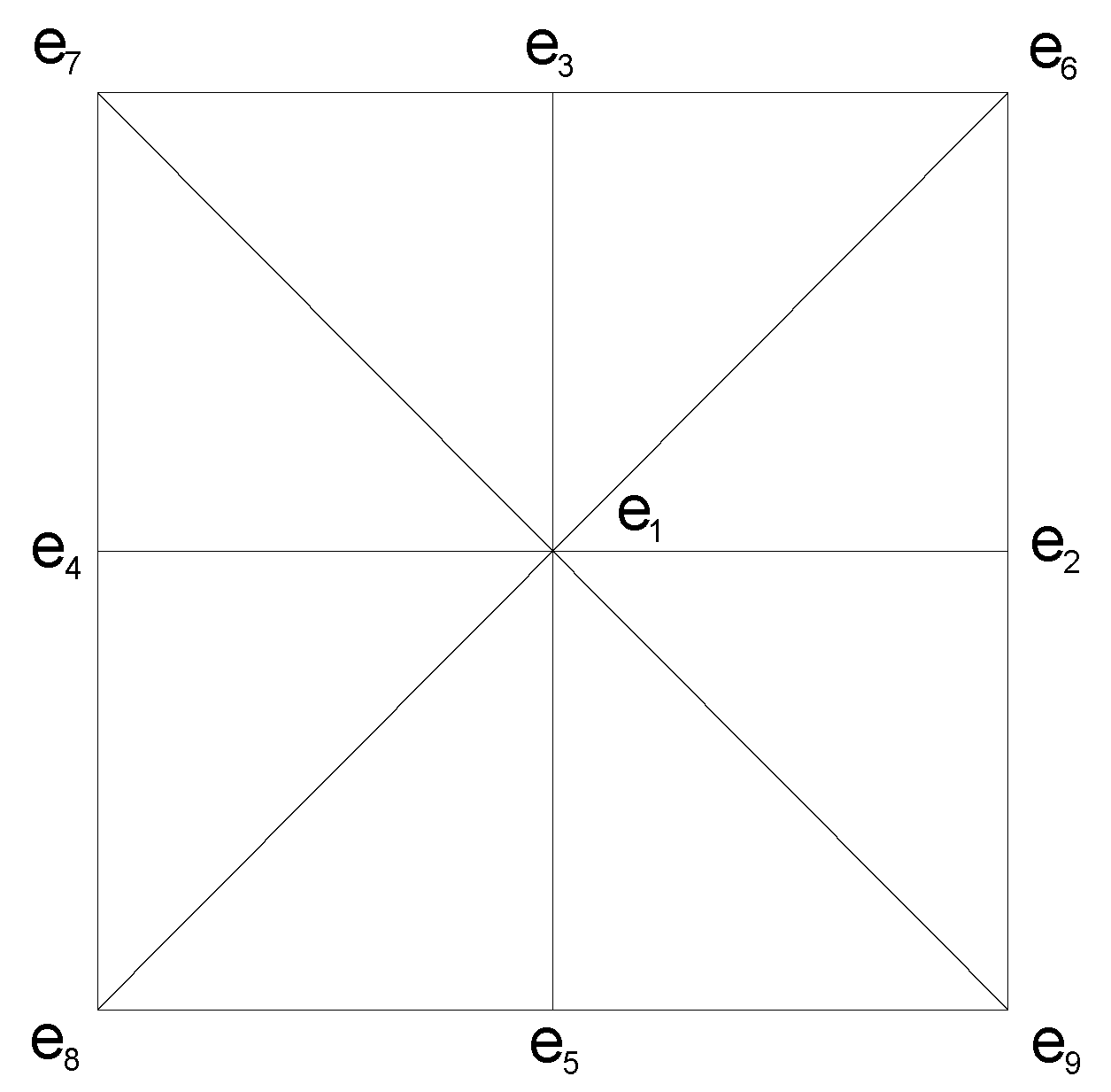


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, Y.; Peng, Y.; Zhang, J. Study of Cavitation Bubble Collapse near a Wall by the Modified Lattice Boltzmann Method. Water 2018, 10, 1439. https://doi.org/10.3390/w10101439
Mao Y, Peng Y, Zhang J. Study of Cavitation Bubble Collapse near a Wall by the Modified Lattice Boltzmann Method. Water. 2018; 10(10):1439. https://doi.org/10.3390/w10101439
Chicago/Turabian StyleMao, Yunfei, Yong Peng, and Jianmin Zhang. 2018. "Study of Cavitation Bubble Collapse near a Wall by the Modified Lattice Boltzmann Method" Water 10, no. 10: 1439. https://doi.org/10.3390/w10101439
APA StyleMao, Y., Peng, Y., & Zhang, J. (2018). Study of Cavitation Bubble Collapse near a Wall by the Modified Lattice Boltzmann Method. Water, 10(10), 1439. https://doi.org/10.3390/w10101439






