Computationally Efficient Multivariate Calibration and Validation of a Grid-Based Hydrologic Model in Sparsely Gauged West African River Basins
Abstract
:1. Introduction
2. Materials and Methods
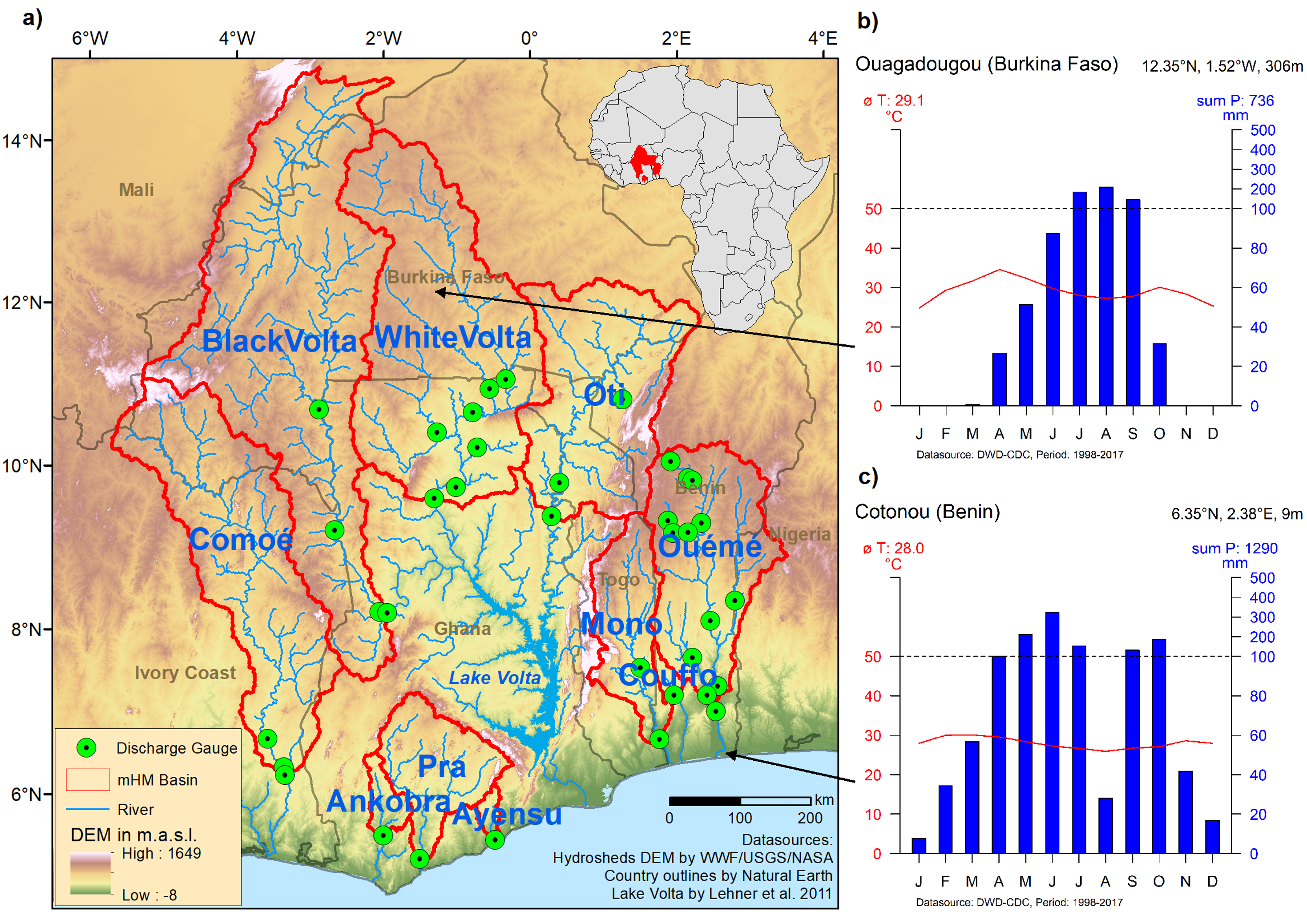
2.1. Study Area
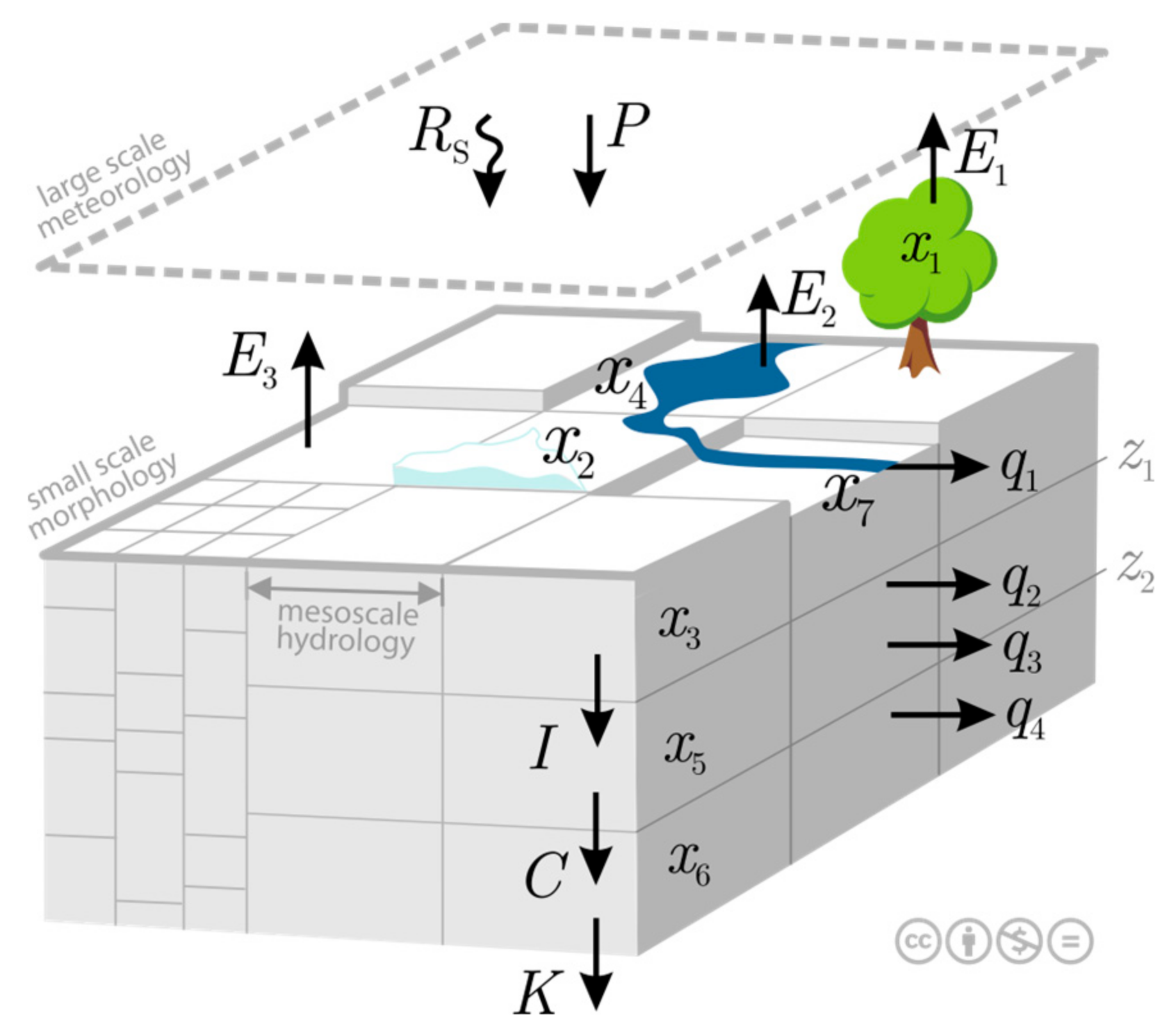
2.2. The Mesoscale Hydrologic Model (mHM)
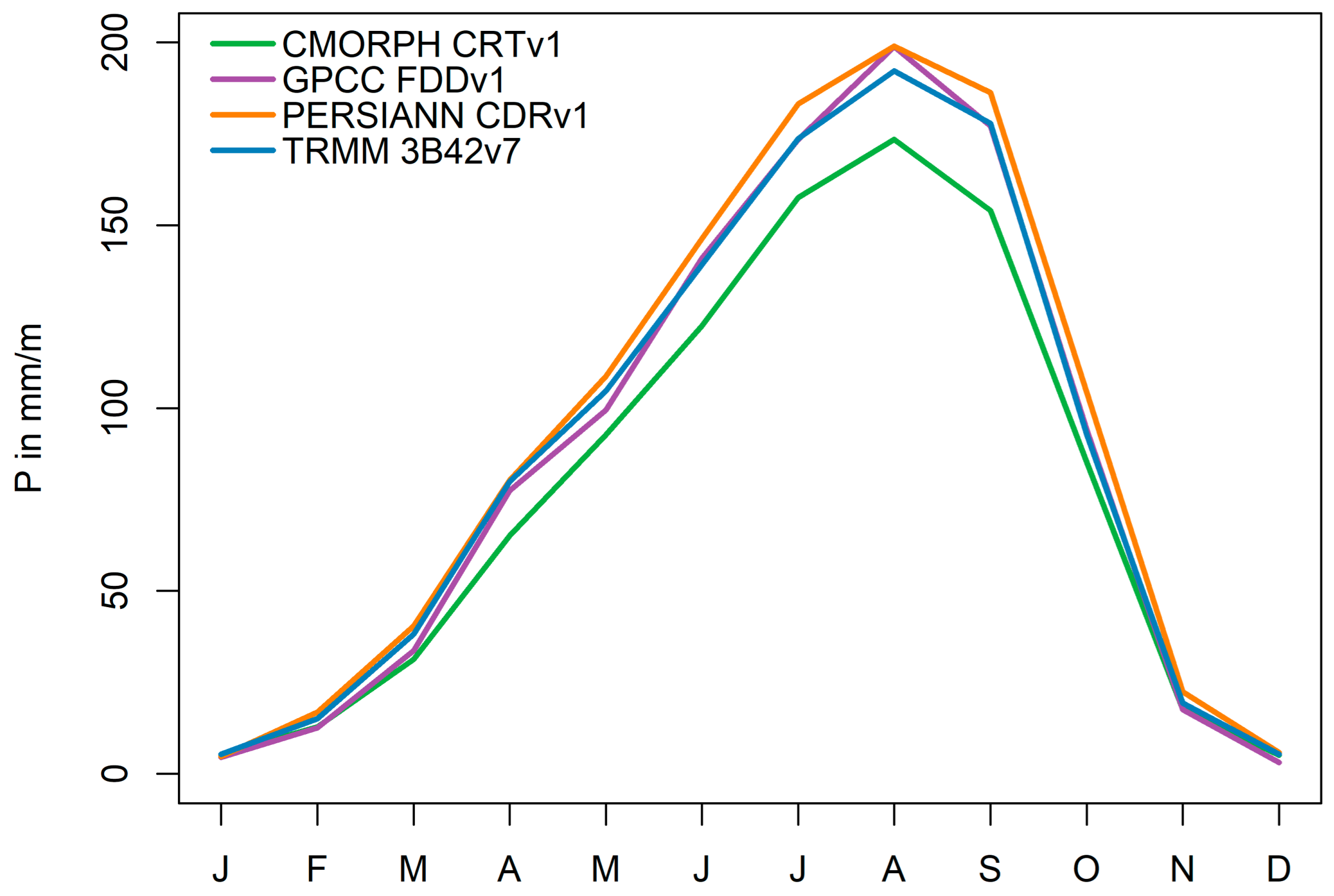
2.3. Input Data
2.3.1. Morphological Inputs
2.3.2. Soil Inputs
2.3.3. Land Use Inputs
2.3.4. Meteorological Inputs
2.3.5. Discharge Inputs
2.3.6. Validation Data
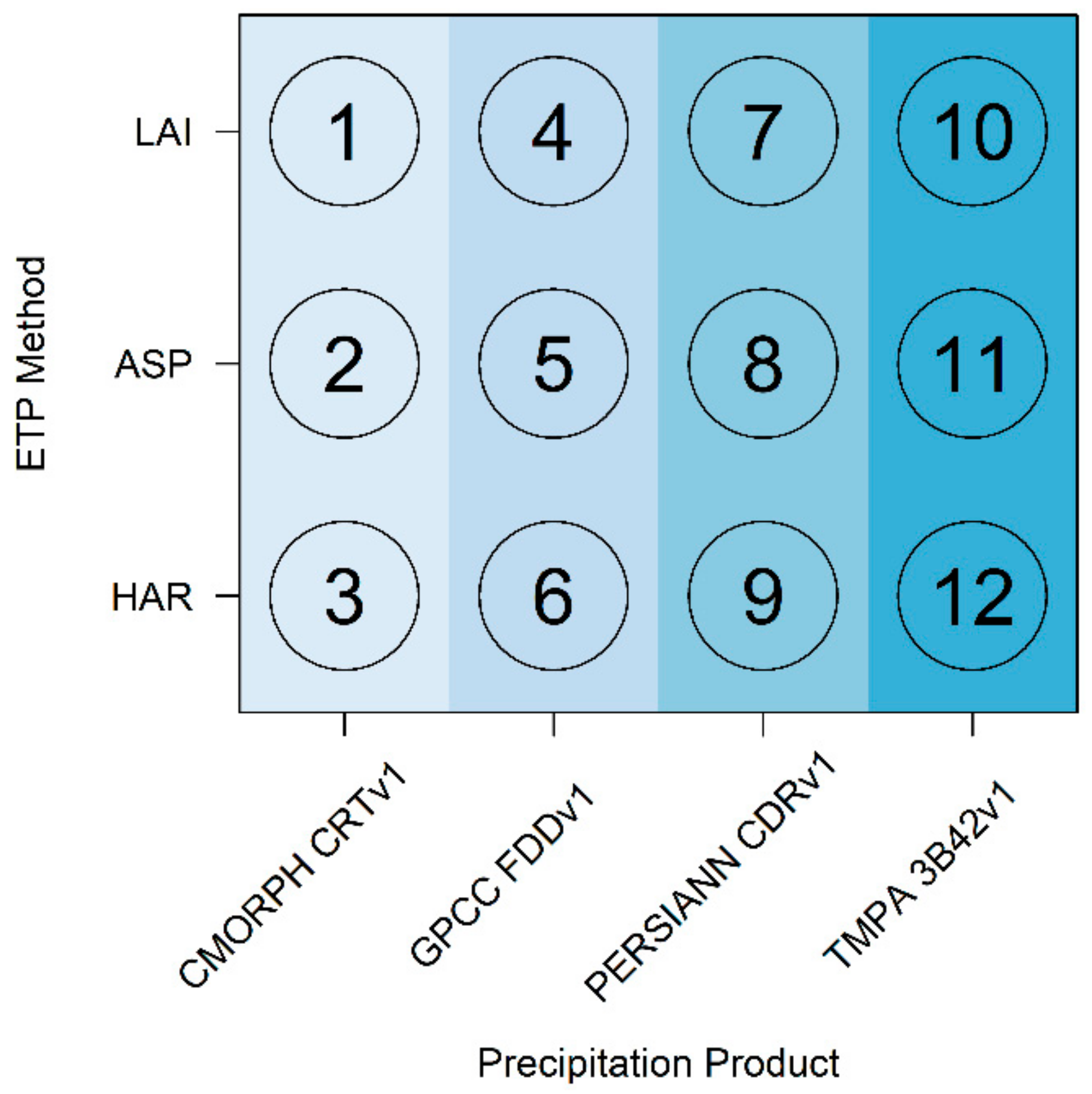
2.4 Framework of the Modeling Experiment
3. Results
3.1. Initial Model Setup Results
3.2. Calibration and Discharge Validation Results
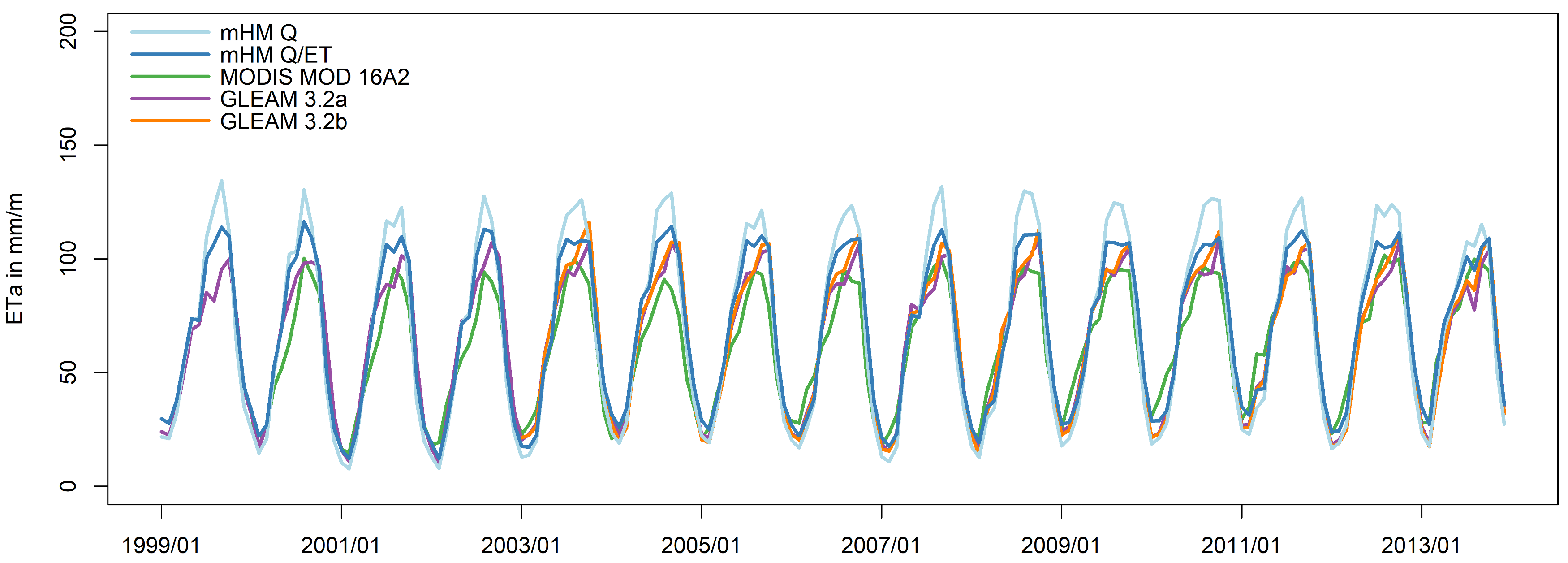
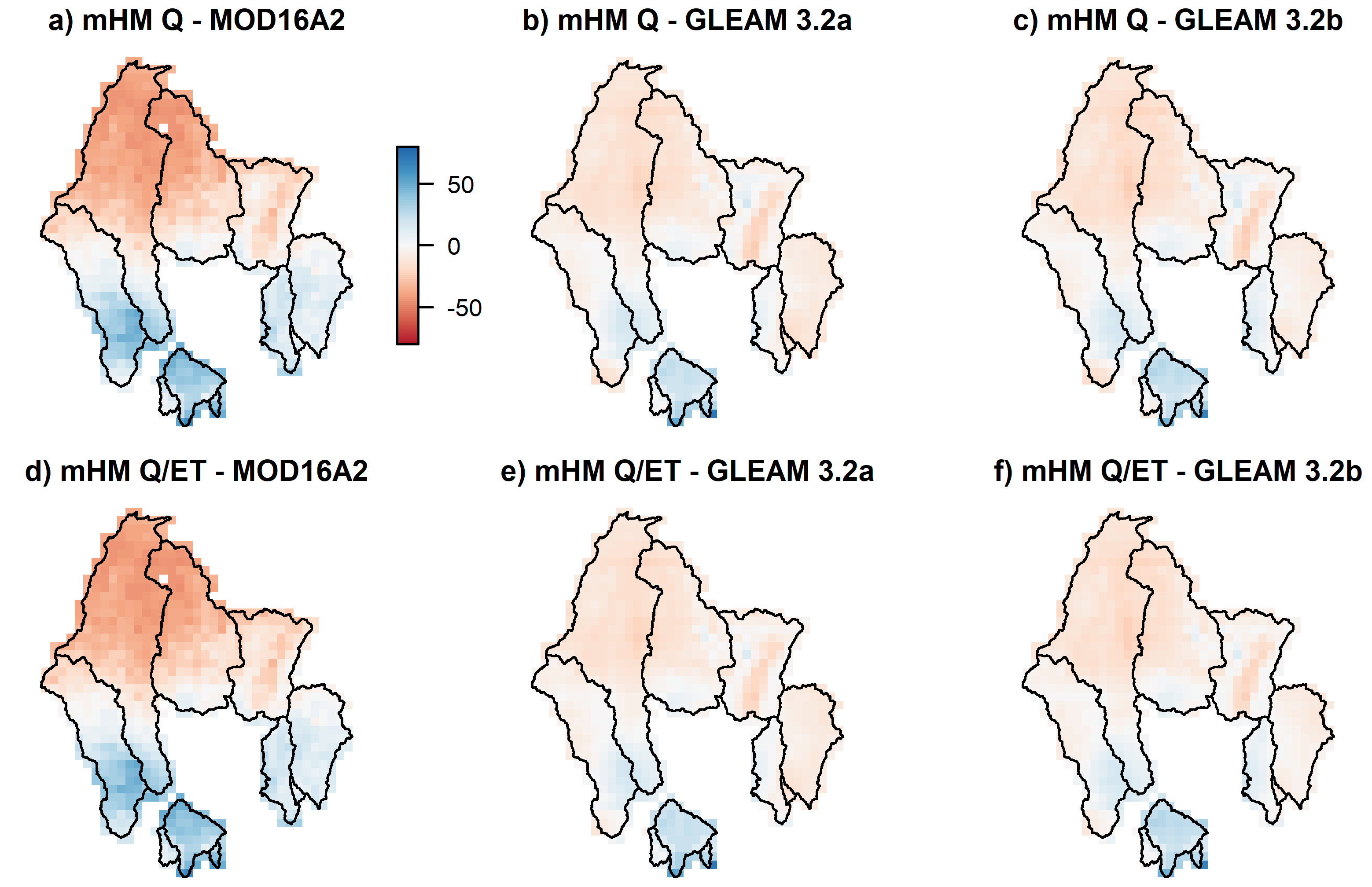
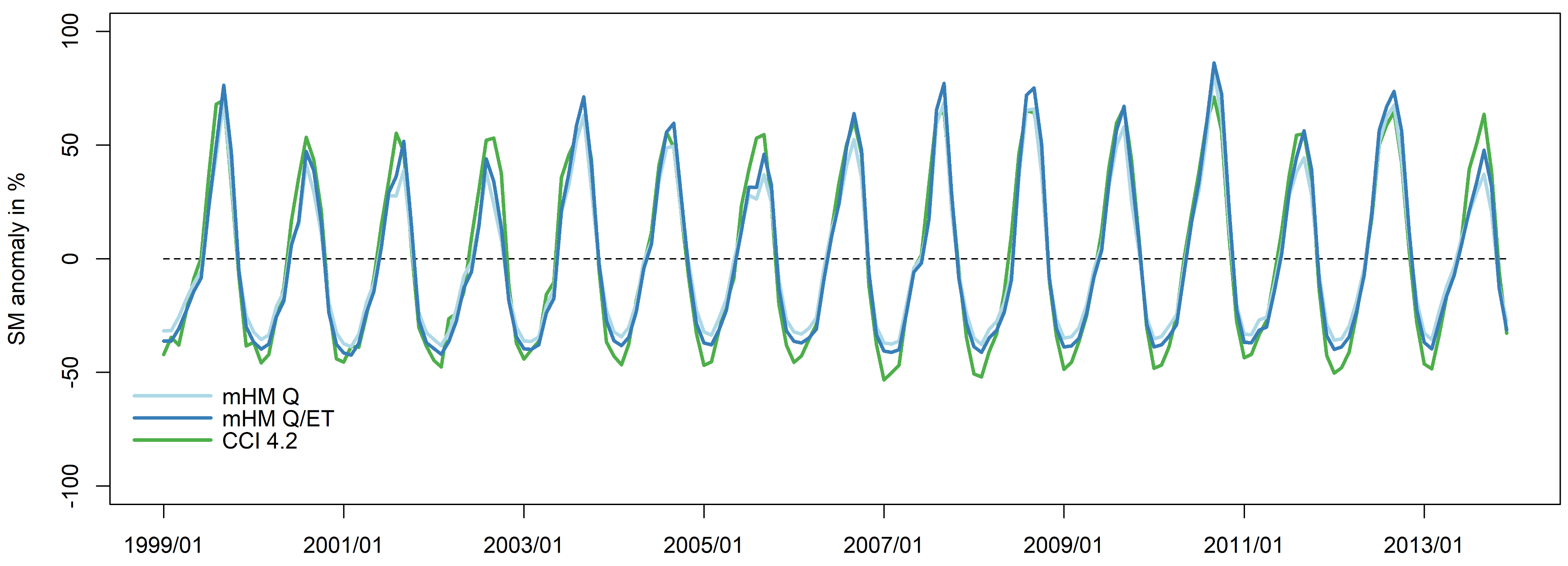
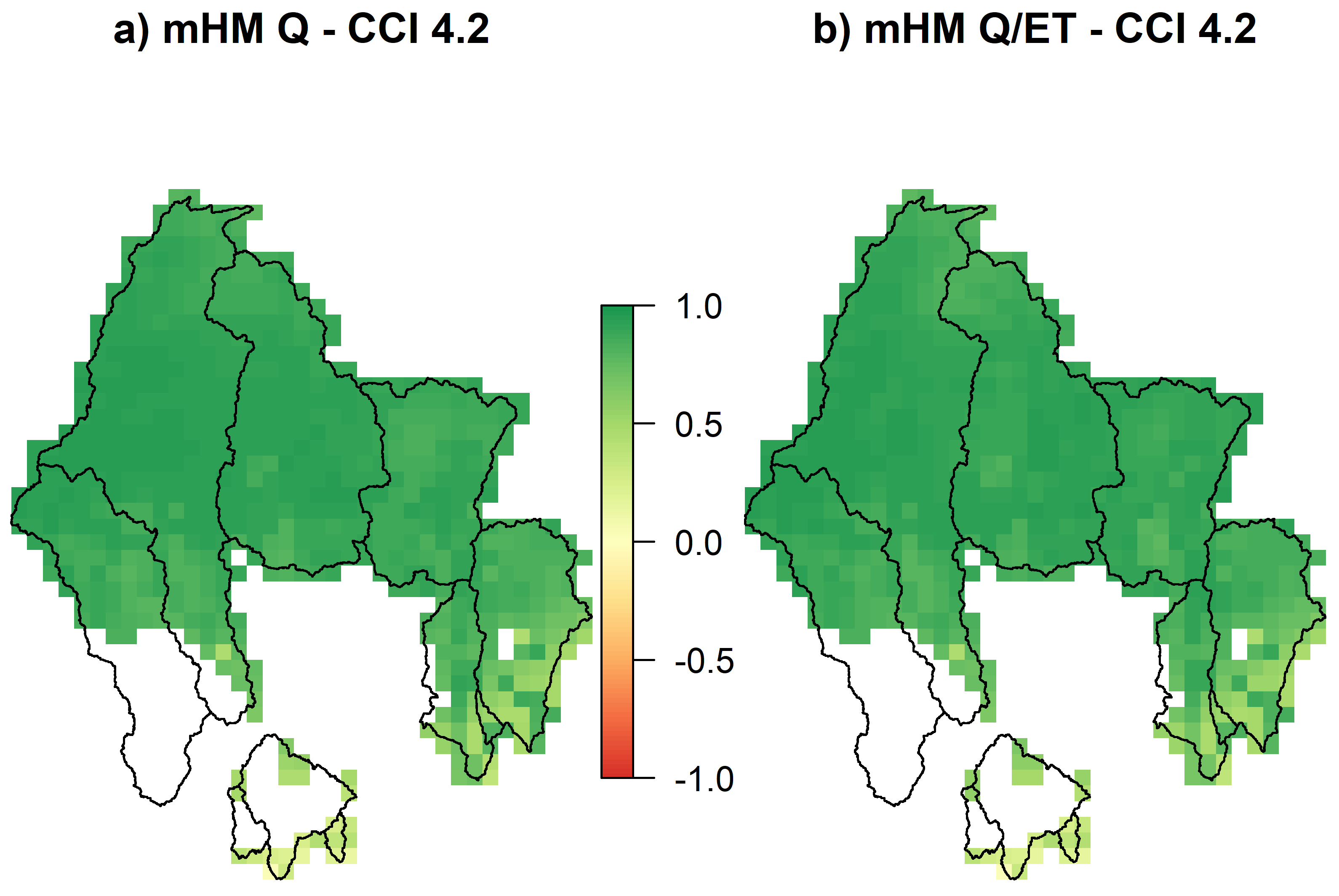
3.3. Multivariate Validation Results
3.4. Evaluation of mHM-MPR for Transferability across Scales
4. Discussion
4.1. Initial Model Runs and Discharge Calibration and Validation
4.2. Multivariate Validation and Scale Transferability of the mHM-MPR Scheme
5. Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. mHM Parameters
| Parameter | Lower Threshold | Upper Threshold |
|---|---|---|
| Interception | ||
| canopyInterceptionFactor | 0.15 | 0.4 |
| Soil Moisture | ||
| orgMatterContent_forest | 0 | 20 |
| orgMatterContent_impervious | 0 | 1 |
| orgMatterContent_pervious | 0 | 4 |
| PTF_lower66_5_constant | 0.6462 | 0.9506 |
| PTF_lower66_5_clay | 0.0001 | 0.0029 |
| PTF_lower66_5_Db | −0.3727 | −0.1871 |
| PTF_higher66_5_constant | 0.5358 | 1.1232 |
| PTF_higher66_5_clay | −0.0055 | 0.0049 |
| PTF_higher66_5_Db | −0.5513 | −0.0913 |
| PTF_Ks_constant | −1.2 | −0.285 |
| PTF_Ks_sand | 0.006 | 0.026 |
| PTF_Ks_clay | 0.003 | 0.013 |
| rootFractionCoefficient_forest | 0.9 | 0.999 |
| rootFractionCoefficient_impervious | 0.9 | 0.95 |
| rootFractionCoefficient_pervious | 0.001 | 0.09 |
| infiltrationShapeFactor | 1 | 4 |
| Direct Sealed Area Runoff | ||
| imperviousStorageCapacity | 0 | 5 |
| Potential Evapotranspiration | ||
| minCorrectionFactorPET | 0.7 (0.9) | 1.3 (0.96) |
| maxCorrectionFactorPET | 0 (0.17) | 0.2 |
| aspectTresholdPET | 160 | 200 |
| HargreavesSamaniCoeff | 0.0016 (0.0021) | 0.003 (0.0027) |
| Interflow | ||
| interflowStorageCapacityFactor | 75 | 200 |
| interflowRecession_slope | 0 | 10 |
| fastInterflowRecession_forest | 1 | 3 |
| slowInterflowRecession_Ks | 1 | 30 |
| exponentSlowInterflow | 0.05 | 0.3 |
| Percolation | ||
| rechargeCoefficient | 0 | 50 (200) |
| Geological Parameter | ||
| GeoParam(1) | 1 | 1000 (1500) |
References
- Hollinger, F.; Staatz, J.M. Agricultural Growth in West Africa: Market and Policy Drivers; Hollinger, F., Staatz, J.M., Eds.; African Development Bank/Food and Agriculture Organization of the United Nations: Rome, Italy, 2015; ISBN 9789251087008. [Google Scholar]
- Jalloh, A.; Faye, M.D.; Roy-Macauley, H.; Sérémé, P.; Zougmoré, R.; Thomas, T.S.; Nelson, G.C. Overview. In West African Agriculture and Climate Change; Jalloh, A., Nelson, G.C., Thomas, T.S., Zougmoré, R., Roy-Macauley, H., Eds.; International Food Policy Research Institute: Washington, DC, USA, 2013. [Google Scholar]
- African Development Bank. West Africa Economic Outlook 2018; African Development Bank Group: Abidjan, Côte d’Ivoire, 2018; ISBN 9789938882667. [Google Scholar]
- Schuol, J.; Abbaspour, K.C.; Srinivasan, R.; Yang, H. Estimation of freshwater availability in the West African sub-continent using the SWAT hydrologic model. J. Hydrol. 2008, 352, 30–49. [Google Scholar] [CrossRef]
- Bormann, H. Regional hydrological modelling in Benin (West Africa): Uncertainty issues versus scenarios of expected future environmental change. Phys. Chem. Earth 2005, 30, 472–484. [Google Scholar] [CrossRef]
- Wagner, S.; Kunstmann, H.; Bárdossy, A.; Conrad, C.; Colditz, R.R. Water balance estimation of a poorly gauged catchment in West Africa using dynamically downscaled meteorological fields and remote sensing information. Phys. Chem. Earth 2009, 34, 225–235. [Google Scholar] [CrossRef]
- Fujihara, Y.; Yamamoto, Y.; Tsujimoto, Y.; Sakagami, J. Discharge Simulation in a Data-Scarce Basin Using Reanalysis and Global Precipitation Data: A Case Study of the White Volta Basin. J. Water Resour. Prot. 2014, 6, 1316–1325. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C. Calibration and uncertainty issues of a hydrological model (SWAT) applied to West Africa. Adv. Geosci. 2006, 9, 137–143. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C.; Yang, H.; Srinivasan, R.; Zehnder, A.J.B. Modeling blue and green water availability in Africa. Water Resour. Res. 2008, 44, 1–18. [Google Scholar] [CrossRef]
- Xie, H.; Longuevergne, L.; Ringler, C.; Scanlon, B.R. Calibration and evaluation of a semi-distributed watershed model of Sub-Saharan Africa using GRACE data. Hydrol. Earth Syst. Sci. 2012, 16, 3083–3099. [Google Scholar] [CrossRef] [Green Version]
- Poméon, T.; Diekkrüger, B.; Springer, A.; Kusche, J.; Eicker, A. Multi-Objective Validation of SWAT for Sparsely-Gauged West African River Basins—A Remote Sensing Approach. Water 2018, 10, 451. [Google Scholar] [CrossRef]
- Adjei, K.A.; Ren, L.; Appiah-Adjei, E.K.; Kankam-Yeboah, K.; Agyapong, A.A. Validation of TRMM Data in the Black Volta Basin of Ghana. J. Hydrol. Eng. 2012, 17, 647–654. [Google Scholar] [CrossRef]
- Hughes, D.A. Comparison of satellite rainfall data with observations from gauging station networks. J. Hydrol. 2006, 327, 399–410. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; VanLiew, M.W.; et al. Swat: Model Use, Calibration, and Validation. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment Part 1: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Srinivasan, R.; Ramanarayanan, T.S.; Arnold, J.G.; Bednarz, S.T. Large area hydrologic modeling and assessment part II: Model application. J. Am. Water Resour. Assoc. 1998, 34, 91–101. [Google Scholar] [CrossRef]
- Beven, K. Rainfall-Runoff Modelling: The Primer, 2nd ed.; Wiley-Blackwell: Chichester, UK, 2012; ISBN 9781119951001. [Google Scholar]
- Samaniego, L.; Kumar, R.; Attinger, S. Multiscale parameter regionalization of a grid-based hydrologic model at the mesoscale. Water Resour. Res. 2010, 46, 1–25. [Google Scholar] [CrossRef]
- Schulla, J.; Jasper, K. Model Description WaSiM-ETH (Water Balance Simulation Model ETH); ETH Zurich: Zurich, Switzerland, 2007; Volume 41. [Google Scholar]
- Beven, K. How far can we go in distributed hydrological modelling? Hydrol. Earth Syst. Sci. 2001, 5, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Samaniego, L.; Attinger, S. Implications of distributed hydrologic model parameterization on water fluxes at multiple scales and locations. Water Resour. Res. 2013, 49, 360–379. [Google Scholar] [CrossRef]
- Orth, R.; Staudinger, M.; Seneviratne, S.I.; Seibert, J.; Zappa, M. Does model performance improve with complexity? A case study with three hydrological models. J. Hydrol. 2015, 523, 147–159. [Google Scholar] [CrossRef] [Green Version]
- Pokhrel, P.; Gupta, H.V.; Wagener, T. A spatial regularization approach to parameter estimation for a distributed watershed model. Water Resour. Res. 2008, 44, 1–16. [Google Scholar] [CrossRef]
- Beven, K.J. Prophecy, reality and uncertainty in distributed hydrological modelling. Adv. Water Resour. 1993, 16, 41–51. [Google Scholar] [CrossRef]
- Becker, A.; Braun, P. Disaggregation, aggregation and spatial scaling in hydrological modelling. J. Hydrol. 1999, 217, 239–252. [Google Scholar] [CrossRef]
- Kumar, R.; Samaniego, L.; Attinger, S. The effects of spatial discretization and model parameterization on the prediction of extreme runoff characteristics. J. Hydrol. 2010, 392, 54–69. [Google Scholar] [CrossRef]
- Kumar, R.; Livneh, B.; Samaniego, L. Toward computationally efficient large-scale hydrologic predictions with a multiscale regionalization scheme. Water Resour. Res. 2013, 49, 5700–5714. [Google Scholar] [CrossRef] [Green Version]
- Rakovec, O.; Kumar, R.; Mai, J.; Cuntz, M.; Thober, S.; Zink, M.; Attinger, S.; Schäfer, D.; Schrön, M.; Samaniego, L. Multiscale and Multivariate Evaluation of Water Fluxes and States over European River Basins. J. Hydrometeorol. 2016, 17, 287–307. [Google Scholar] [CrossRef]
- Rakovec, O.; Kumar, R.; Attinger, S.; Samaniego, L. Improving the realism of hydrologic model functioning through multivariate parameter estimation. Water Resour. Res. 2016, 52, 7779–7792. [Google Scholar] [CrossRef]
- Zink, M.; Kumar, R.; Cuntz, M.; Samaniego, L. A high-resolution dataset of water fluxes and states for Germany accounting for parametric uncertainty. Hydrol. Earth Syst. Sci. 2017, 21, 1769–1790. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Zink, M. Implications of Parameter Uncertainty on Soil Moisture Drought Analysis in Germany. J. Hydrometeorol. 2013, 14, 47–68. [Google Scholar] [CrossRef]
- Thober, S.; Kumar, R.; Sheffield, J.; Mai, J.; Schäfer, D.; Samaniego, L. Seasonal Soil Moisture Drought Prediction over Europe Using the North American Multi-Model Ensemble (NMME). J. Hydrometeorol. 2015, 16, 2329–2344. [Google Scholar] [CrossRef]
- Kauffeldt, A.; Wetterhall, F.; Pappenberger, F.; Salamon, P.; Thielen, J. Technical review of large-scale hydrological models for implementation in operational flood forecasting schemes on continental level. Environ. Model. Softw. 2016, 75, 68–76. [Google Scholar] [CrossRef]
- Hattermann, F.; Krysanova, V.; Gosling, S.N.; Dankers, R.; Daggupati, P.; Donnelly, C.; Flörke, M.; Huang, S.; Motovilov, Y.; Buda, S.; et al. Cross-scale intercomparison of climate change impacts simulated by regional and global hydrological models in eleven large river basins. Clim. Chang. 2017, 141, 561–576. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Breuer, L.; Chamorro, A.; Flörke, M.; Pechlivanidis, I.G.; Schäfer, D.; Shah, H.; Vetter, T.; Wortmann, M.; et al. Propagation of forcing and model uncertainties on to hydrological drought characteristics in a multi-model century-long experiment in large river basins. Clim. Chang. 2017, 141, 435–449. [Google Scholar] [CrossRef]
- Krysanova, V.; Vetter, T.; Eisner, S.; Huang, S.; Pechlivanidis, I.; Strauch, M.; Gelfan, A.; Kumar, R.; Aich, V.; Arheimer, B.; et al. Intercomparison of regional-scale hydrological models and climate change impacts projected for 12 large river basins worldwide—A synthesis. Environ. Res. Lett. 2017, 12, 105002. [Google Scholar] [CrossRef]
- Huang, S.; Kumar, R.; Flörke, M.; Yang, T.; Hundecha, Y.; Kraft, P.; Gao, C.; Gelfan, A.; Liersch, S.; Lobanova, A.; et al. Erratum to: Evaluation of an ensemble of regional hydrological models in 12 large-scale river basins worldwide (Climatic Change, 10.1007/s10584-016-1841-8). Clim. Chang. 2017, 141, 399–400. [Google Scholar] [CrossRef]
- Zink, M.; Samaniego, L.; Kumar, R.; Thober, S.; Mai, J.; Schäfer, D.; Marx, A. The German drought monitor. Environ. Res. Lett. 2016, 11, 074002. [Google Scholar] [CrossRef] [Green Version]
- Samaniego, L.; Kumar, R.; Jackisch, C. Predictions in a data-sparse region using a regionalized grid-based hydrologic model driven by remotely sensed data. Hydrol. Res. 2011, 42, 338–355. [Google Scholar] [CrossRef]
- Zink, M.; Mai, J.; Cuntz, M.; Samaniego, L. Conditioning a Hydrologic Model Using Patterns of Remotely Sensed Land Surface Temperature. Water Resour. Res. 2018, 54, 2976–2998. [Google Scholar] [CrossRef]
- Poméon, T.; Jackisch, D.; Diekkrüger, B. Evaluating the performance of remotely sensed and reanalysed precipitation data over West Africa using HBV light. J. Hydrol. 2017, 547, 222–235. [Google Scholar] [CrossRef]
- CILSS. Landscapes of West Africa—A Window on a Changing World; U.S. Geological Survey EROS: Garretson, SD, USA, 2016.
- Lehner, B.; Verdin, K.; Jarvis, A. HydroSHEDS Technical Documentation Version 1.2; World Wildlife Fund US: Washington, DC, USA, 2013. [Google Scholar]
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Fink, A.H.; Christoph, M.; Born, K.; Bruecher, T.; Piecha, K.; Pohle, S.; Schulz, O.; Ermert, V. Climate. In Impacts of Global Change on the Hydrological Cycle in West and Northwest Africa; Speth, P., Christoph, M., Diekkrüger, B., Eds.; Springer: Heidelberg, Germany, 2010; pp. 54–58. [Google Scholar]
- Sebastian, K. Agro-Ecological Zones of Africa; International Food Policy Research Institute (Datasets): Washington, DC, USA, 2009. [Google Scholar]
- Gessner, U.; Niklaus, M.; Kuenzer, C.; Dech, S. Intercomparison of Leaf Area Index Products for a Gradient of Sub-Humid to Arid Environments in West Africa. Remote Sens. 2013, 5, 1235–1257. [Google Scholar] [CrossRef] [Green Version]
- Bergström, S. Global Perspectives on Loss of Human Life Caused by Floods; Swedish Meteorological and Hydrological Institute: Norrköping, Sweden, 1976. [Google Scholar]
- Bergström, S. The HBV Model—Its Structure and Applications; Swedish Meteorological and Hydrological Institute: Norrköping, Sweden, 1992; ISBN 0-918334-91-8. [Google Scholar]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Samaniego, L.; Brenner, J.; Cuntz, M.; Demirel, C.M.; Kaluza, M.; Kumar, R.; Langenberg, B.; Mai, J.; Rokovec, O.; Schäfer, D.; et al. The Mesoscale Hydrologic Model—Documentation for Verion 5.8; Helmholtz Centre for Environmental Research—UFZ: Leipzig, Germany, 2017. [Google Scholar]
- Livneh, B.; Kumar, R.; Samaniego, L. Influence of soil textural properties on hydrologic fluxes in the Mississippi river basin. Hydrol. Process. 2015, 29, 4638–4655. [Google Scholar] [CrossRef]
- Tolson, B.A.; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007, 43, 1–16. [Google Scholar] [CrossRef]
- Behrangi, A.; Khakbaz, B.; Vrugt, J.A.; Duan, Q.; Sorooshian, S. Comment on “Dynamically dimensioned search algorithm for computationally efficient watershed model calibration” by Bryan, A. Tolson and Christine, A. Shoemaker. Water Resour. Res. 2008, 44, 2–4. [Google Scholar] [CrossRef]
- FAO/IIASA/ISRIC/ISS-CAS/JRC. Harmonized World Soil Database (Version 1.2); FAO: Rome, Italy; IIASA: Laxenburg, Austria, 2012. [Google Scholar]
- Bontemps, S.; Defourny, P.; Van Bogaert, E.; Arino, O.; Kalogirou, V.; Perez, J. GLOBCOVER 2009 Products Description and Validation Report; Université catholique de Louvain, European Space Agency: Louvain, Paris, 2011. [Google Scholar]
- Myneni, R.; Knyazikhin, Y.; Park, T. MCD15A2 MODIS/Combined Terra+Aqua Leaf Area Index/FPAR Daily L4 Global 1 km SIN Grid. Available online: https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/products/lai-and-fpar/MCD15A2/ (accessed on 1 August 2018).
- Knyazikhin, Y.; Glassy, J.; Privette, J.L.; Tian, Y.; Lotsch, A.; Zhang, Y.; Wang, Y.; Morisette, J.T.; Votava, P.; Myneni, R.B.; et al. MODIS Leaf Area Index (LAI) and Fraction of Photosynthetically Active Radiation Absorbed by Vegetation (FPAR) Product (MOD15) Algorithm Theoretical Basis Document. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod15.pdf (accessed on 1 August 2018).
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Xie, P.; Yoo, S.; Joyce, R.; Yarosh, Y. Bias-Corrected CMORPH: A 13-Year Analysis of High-Resolution Global Precipitation. Available online: http://ftp.cpc.ncep.noaa.gov/precip/CMORPH_V1.0/REF/EGU_1104_Xie_bias-CMORPH.pdf (accessed on 13 March 2018).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Schamm, K.; Ziese, M.; Raykova, K.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Schneider, U. GPCC Full Data Daily Version 1.0 at 1.0°: Daily Land-Surface Precipitation from Rain-Gauges Built on GTS-Based and Historic Data. Available online: ftp://ftp.dwd.de/pub/data/gpcc/html/fulldata-daily_v1_doi_download.html (accessed on 7 June 2016).
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Lucchesi, R.; Suarez, M. MERRA-2: File Specification. GMAO Office Note No. 9 (Version 1.1); NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2016.
- Martens, B.; Miralles, D.G.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model. Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Dorigo, W.A.; Parinussa, R.M.; De Jeu, R.A.M.; Wagner, W.; McCabe, M.F.; Evans, J.P.; Van Dijk, A.I.J.M. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sens. Environ. 2012, 123, 280–297. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Parinussa, R.M.; Dorigo, W.A.; De Jeu, R.A.M.; Wagner, W.; Van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef] [Green Version]
- Wagner, W.; Dorigo, W.; de Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fusion of Active and Passive Microwave Observations To Create an Essential Climate Variable Data Record on Soil Moisture. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 7, 315–321. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.A.; Crow, W.; Wagner, W. Triple Collocation-Based Merging of Satellite Soil Moisture Retrievals. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6780–6792. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Mayer-Gürr, T.; Behzadpour, S.; Ellmer, M.; Kvas, A.; Klinger, B.; Zehentner, N. ITSG-Grace2016—Monthly and Daily Gravity Field Solutions from GRACE; TU Graz—Institute of Geodesy: Graz, Austria, 2016. [Google Scholar]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- López, P.L.; Sutanudjaja, E.H.; Schellekens, J.; Sterk, G.; Bierkens, M.F.P. Calibration of a large-scale hydrological model using satellite-based soil moisture and evapotranspiration products. Hydrol. Earth Syst. Sci. 2017, 21, 3125–3144. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Gavilán, P.; Lorite, I.J.; Tornero, S.; Berengena, J. Regional calibration of Hargreaves equation for estimating reference et in a semiarid environment. Agric. Water Manag. 2006, 81, 257–281. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Qi, W.; Zhang, C.; Fu, G.; Sweetapple, C.; Zhou, H. Evaluation of global fine-resolution precipitation products and their uncertainty quantification in ensemble discharge simulations. Hydrol. Earth Syst. Sci. 2016, 20, 903–920. [Google Scholar] [CrossRef] [Green Version]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; De Roo, A. Hydrological evaluation of satellite-based rainfall estimates over the Volta and Baro-Akobo Basin. J. Hydrol. 2013, 499, 324–338. [Google Scholar] [CrossRef]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High-resolution mapping of the world’s reservoirs and dams for sustainable river-flow management. Front. Ecol. Environ. 2011, 9, 494–520. [Google Scholar] [CrossRef]
- Jovanovic, N.; Mu, Q.; Bugan, R.D.H.; Zhao, M. Dynamics of MODIS evapotranspiration in South Africa. Water SA 2015, 41, 79–91. [Google Scholar] [CrossRef]
- Sun, Z.; Gebremichael, M.; Ardö, J.; Nickless, A.; Caquet, B.; Merboldh, L.; Kutschi, W. Estimation of daily evapotranspiration over Africa using MODIS/Terra and SEVIRI/MSG data. Atmos. Res. 2012, 112, 35–44. [Google Scholar] [CrossRef]
- Grippa, M.; Kergoat, L.; Frappart, F.; Araud, Q.; Boone, A.; De Rosnay, P.; Lemoine, J.M.; Gascoin, S.; Balsamo, G.; Ottlé, C.; et al. Land water storage variability over West Africa estimated by Gravity Recovery and Climate Experiment (GRACE) and land surface models. Water Resour. Res. 2011, 47, 1–18. [Google Scholar] [CrossRef]
- Ndehedehe, C.; Awange, J.; Agutu, N.; Kuhn, M.; Heck, B. Understanding Changes in Terrestrial Water Storage over West Africa between 2002 and 2014. Adv. Water Resour. 2016, 88, 211–230. [Google Scholar] [CrossRef]
- Boone, A.; Decharme, B.; Guichard, F.; de Rosnay, P.; Balsamo, G.; Beljaars, A.; Chopin, F.; Orgeval, T.; Polcher, J.; Delire, C.; et al. The AMMA Land Surface Model Intercomparison Project (ALMIP). Bull. Am. Meteorol. Soc. 2009, 90, 1865–1880. [Google Scholar] [CrossRef] [Green Version]
- Forootan, E.; Kusche, J.; Loth, I.; Schuh, W.D.; Eicker, A.; Awange, J.; Longuevergne, L.; Diekkrüger, B.; Schmidt, M.; Shum, C.K. Multivariate Prediction of Total Water Storage Changes Over West Africa from Multi-Satellite Data. Surv. Geophys. 2014, 35, 913–940. [Google Scholar] [CrossRef] [Green Version]
- Rateb, A.; Kuo, C.-Y.; Imani, M.; Tseng, K.-H.; Lan, W.-H.; Ching, K.-E.; Tseng, T.-P. Terrestrial Water Storage in African Hydrological Regimes Derived from GRACE Mission Data: Intercomparison of Spherical Harmonics, Mass Concentration, and Scalar Slepian Methods. Sensors 2017, 17, 566. [Google Scholar] [CrossRef] [PubMed]
- Hassan, A.; Jin, S. Water storage changes and balances in Africa observed by GRACE and hydrologic models. Geod. Geodyn. 2016, 7, 39–49. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Awange, J.L.; Kuhn, M.; Agutu, N.O.; Fukuda, Y. Analysis of hydrological variability over the Volta river basin using in-situ data and satellite observations. J. Hydrol. Reg. Stud. 2017, 12, 88–110. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, X.; Corbari, C.; Mancini, M.; Niu, G.; Zeng, W. Improving the Xin’anjiang hydrological model based on mass—Energy balance. Hydrol. Earth Syst. Sci. 2017, 21, 3359–3375. [Google Scholar] [CrossRef]
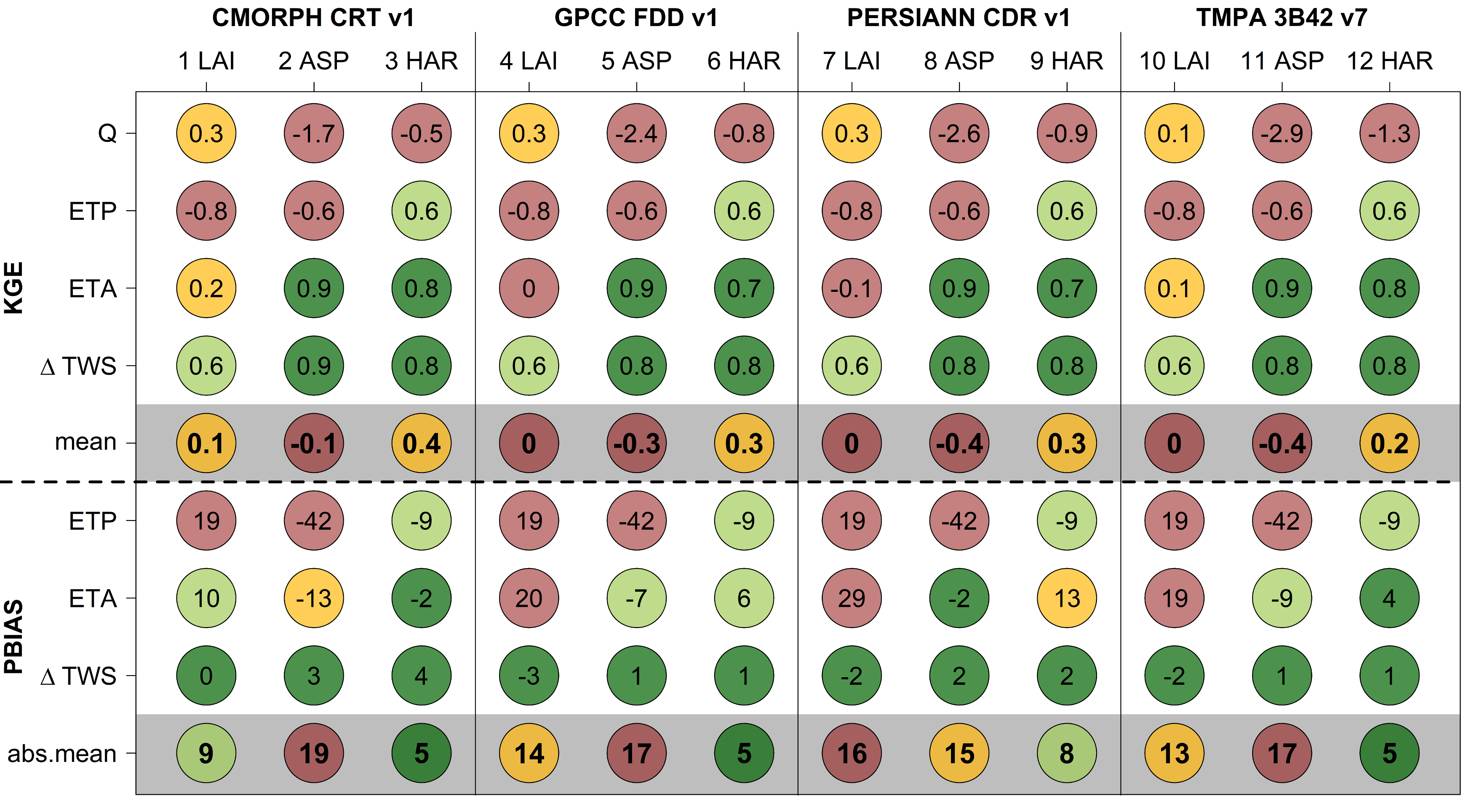
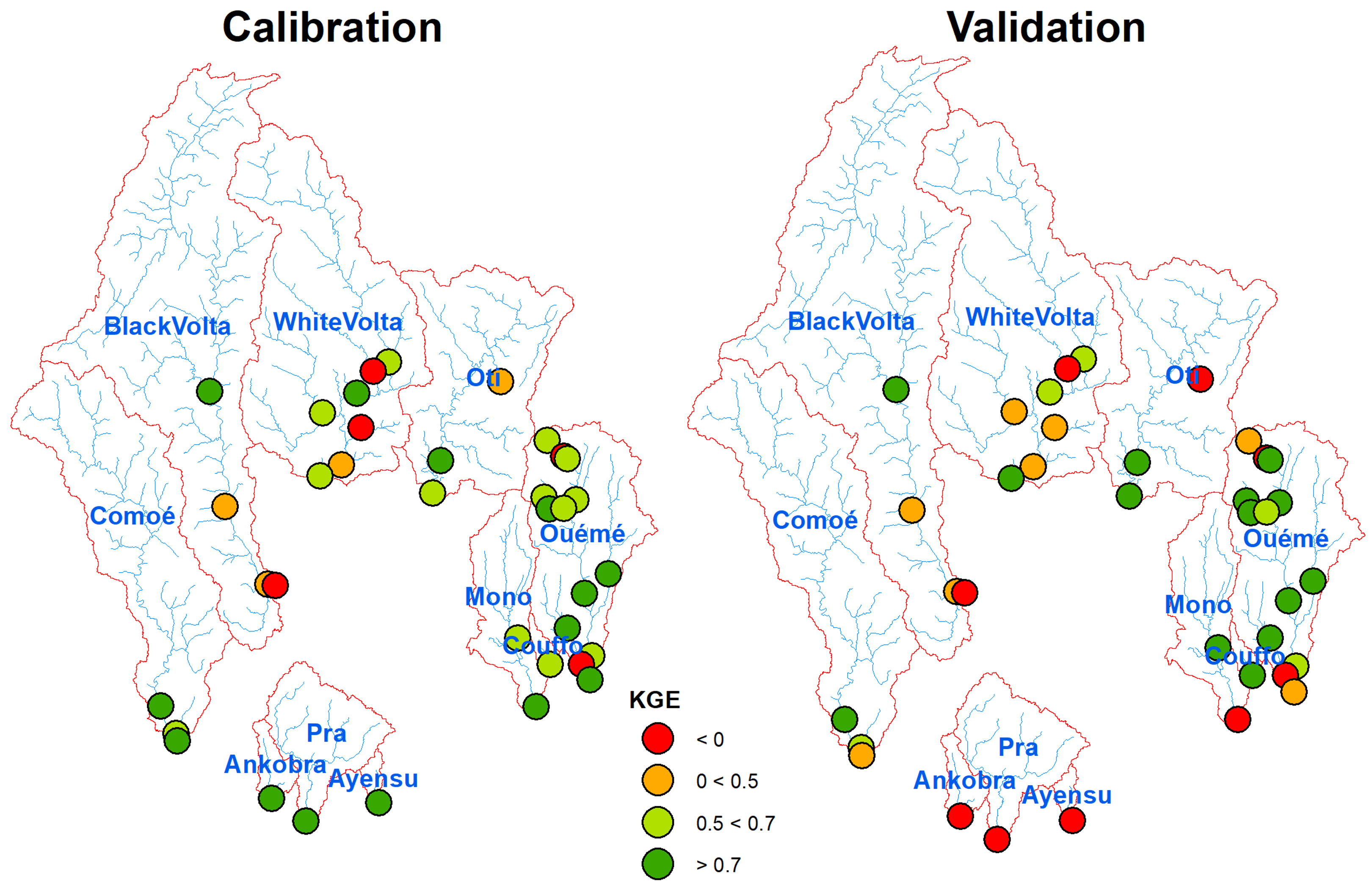
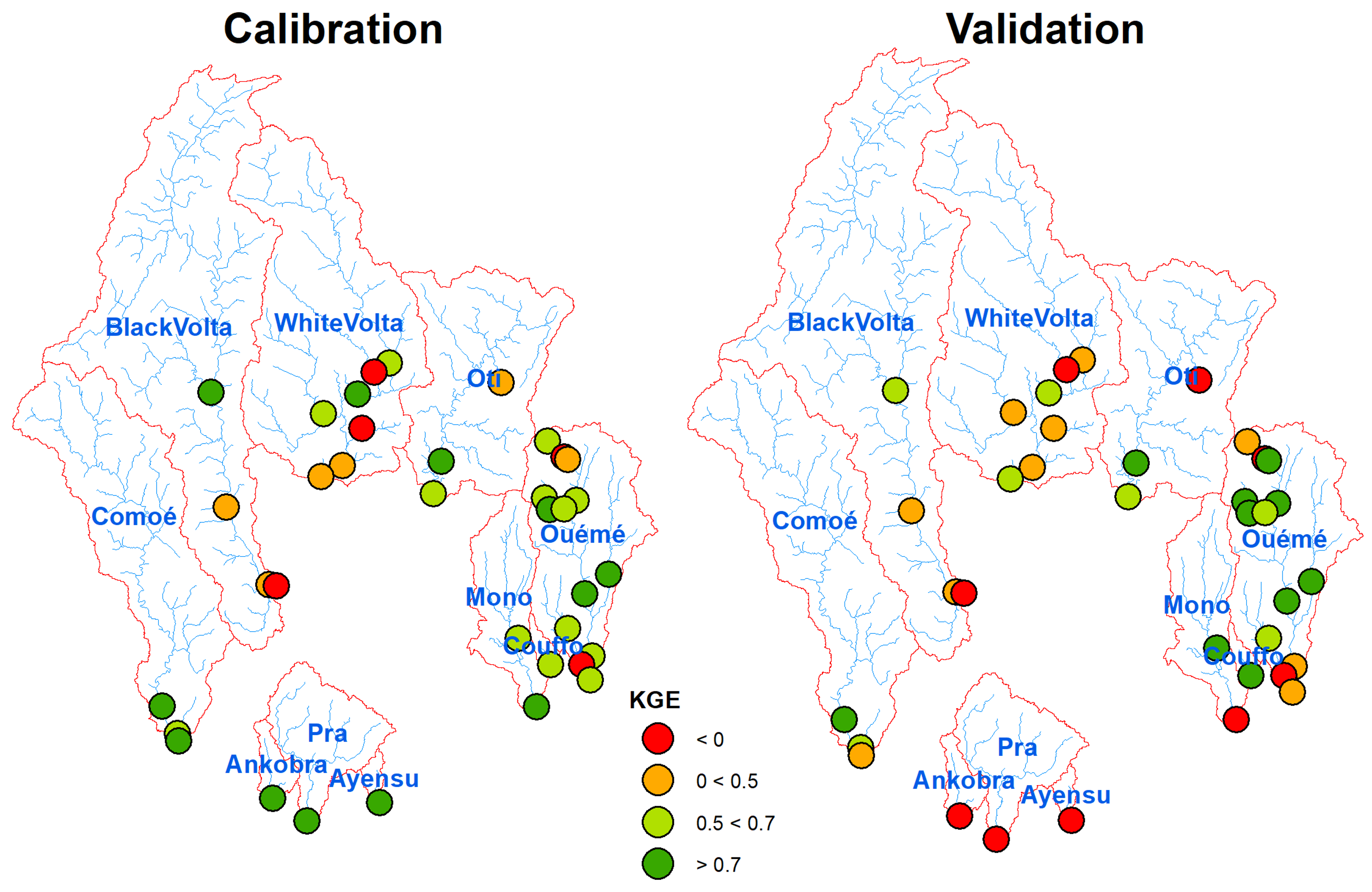
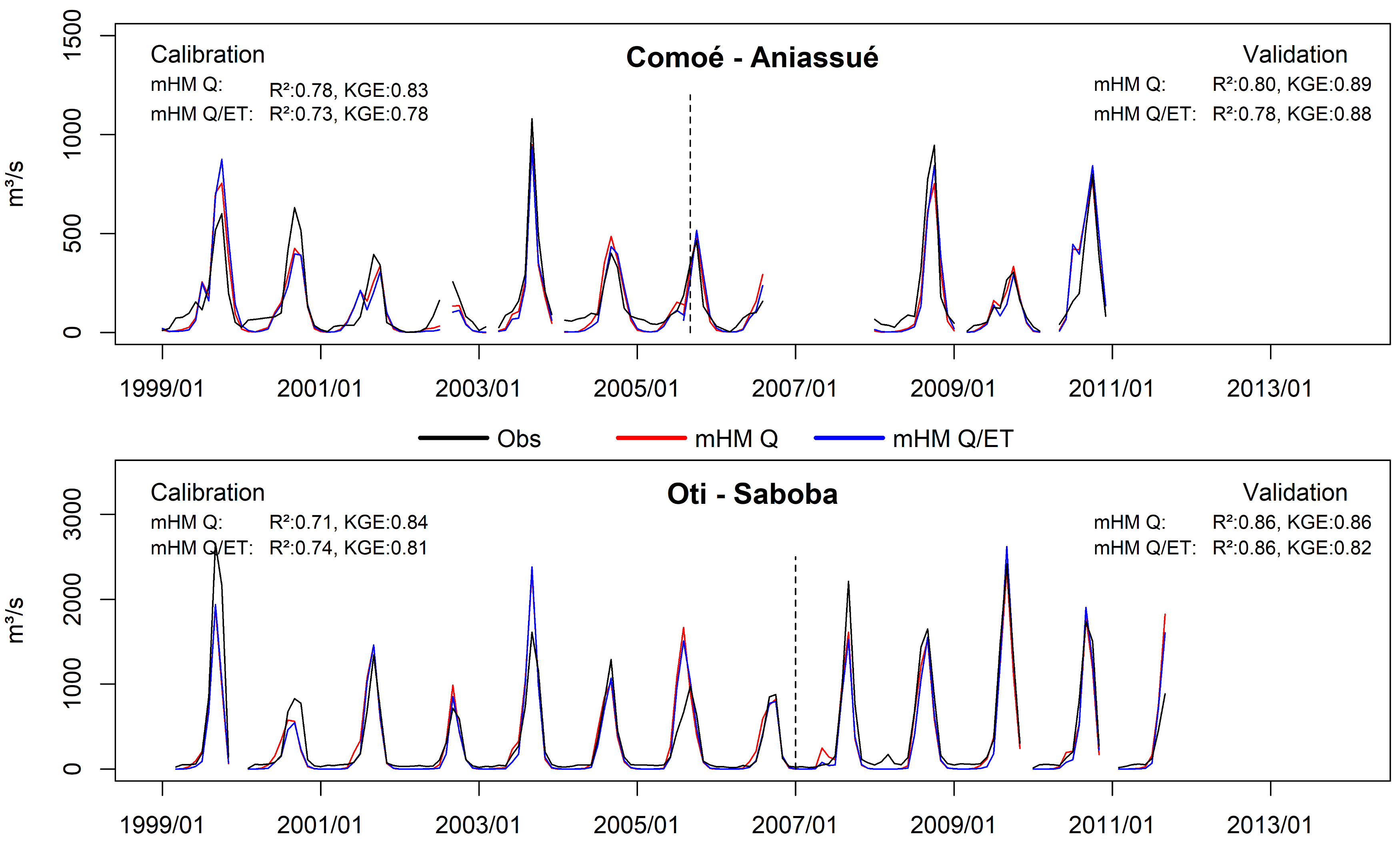
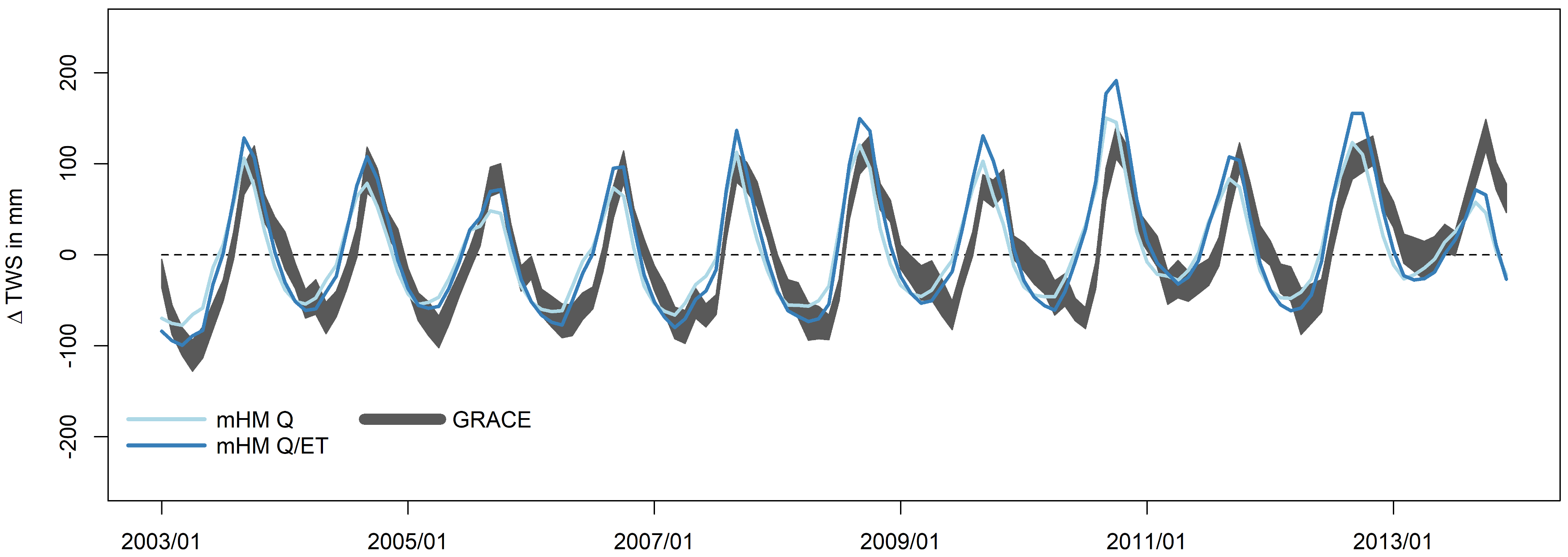
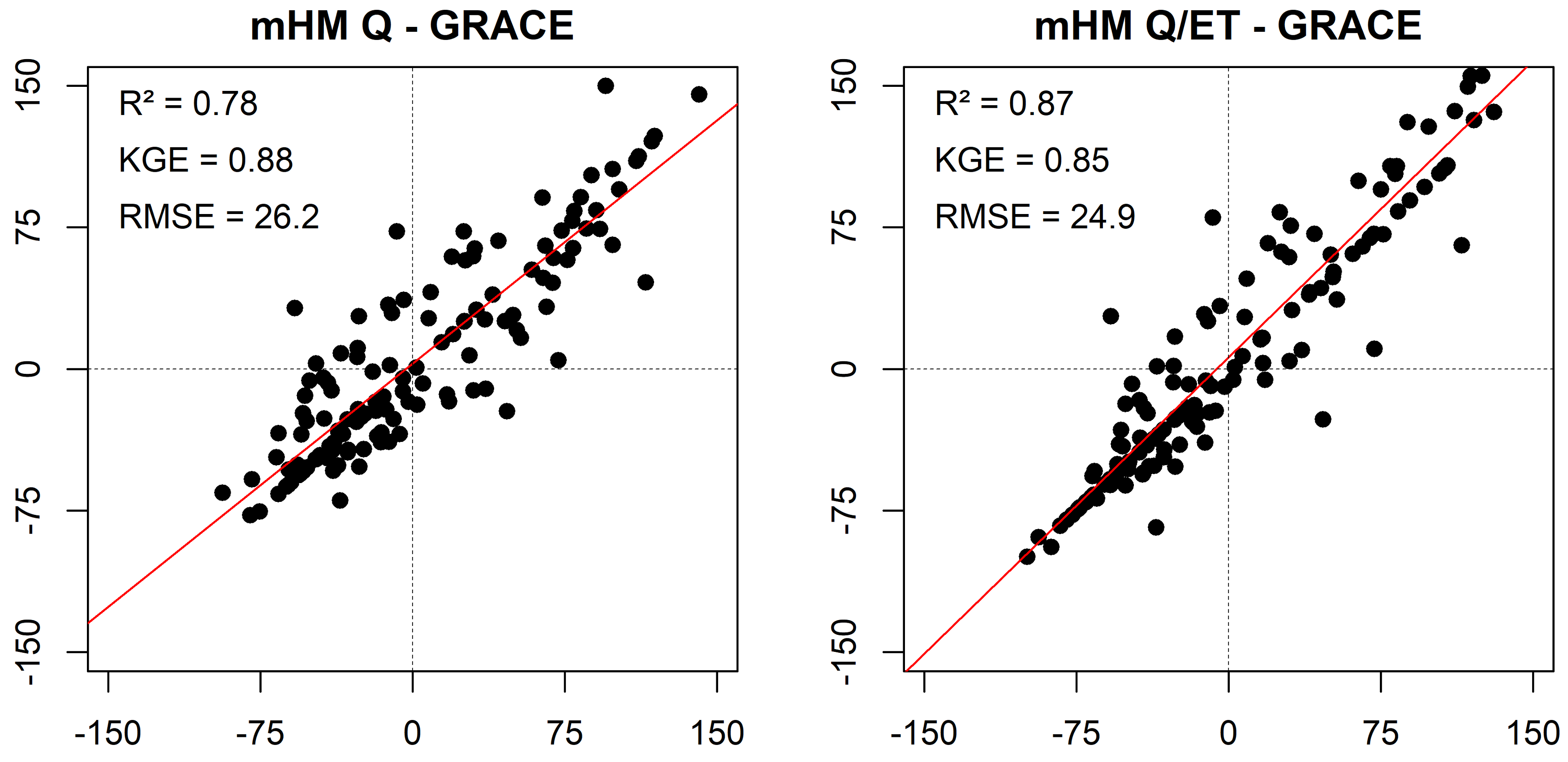
| Objective Function | Discharge Stations | ||||||
|---|---|---|---|---|---|---|---|
| R2 | sig. | PBIAS | KGE | R2 ≥ 0.5 | KGE ≥ 0.5 | KGE ≥ 0.7 | |
| Q Calibration | |||||||
| Calibration | 0.61 | <0.001 | −8.8 | 0.53 | 83% | 75% | 39% |
| Validation | 0.65 | <0.001 | 12.9 | 0.23 | 75% | 53% | 39% |
| Average | 0.63 | 2.0 | 0.38 | 79% | 64% | 39% | |
| Q/ET Calibration | |||||||
| Calibration | 0.56 | <0.001 | −8.1 | 0.49 | 72% | 69% | 33% |
| Validation | 0.62 | <0.001 | 25.2 | 0.13 | 75% | 47% | 28% |
| Average | 0.59 | 8.5 | 0.31 | 74% | 58% | 31% | |
| Dataset | Objective Function | ||||
|---|---|---|---|---|---|
| R2 | sig. | PBIAS | KGE | RMSE | |
| Q Calibration | |||||
| MOD 16A2 | 0.93 | <0.001 | 11.3 | 0.44 | 17.9 |
| GLEAM 3.2a | 0.93 | <0.001 | 8.1 | 0.64 | 14.8 |
| GLEAM 3.2b | 0.93 | <0.001 | 6.6 | 0.73 | 13.1 |
| Average | 0.93 | 8.7 | 0.60 | 15.3 | |
| Q/ET Calibration | |||||
| MOD 16A2 | 0.92 | <0.001 | 10.7 | 0.72 | 12.3 |
| GLEAM 3.2a | 0.97 | <0.001 | 7.4 | 0.88 | 7.9 |
| GLEAM 3.2b | 0.97 | <0.001 | 5.9 | 0.93 | 6.9 |
| Average | 0.95 | 8.0 | 0.84 | 9.0 | |
| Spatial Resolution | |||
|---|---|---|---|
| 26 km | 13 km | 6.5 km | |
| Ø KGE Discharge | |||
| Calibration − Q | 0.53 | 0.53 | 0.53 |
| Calibration − Q/ET | 0.49 | 0.49 | 0.49 |
| Validation − Q | 0.23 | 0.26 | 0.28 |
| Validation Q/ET | 0.13 | 0.15 | 0.17 |
| Model Domain | |||
| Pixel Count | 830 | 3320 | 13,280 |
| Pixel Area | 676 km2 | 169 km2 | 42.3 km2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poméon, T.; Diekkrüger, B.; Kumar, R. Computationally Efficient Multivariate Calibration and Validation of a Grid-Based Hydrologic Model in Sparsely Gauged West African River Basins. Water 2018, 10, 1418. https://doi.org/10.3390/w10101418
Poméon T, Diekkrüger B, Kumar R. Computationally Efficient Multivariate Calibration and Validation of a Grid-Based Hydrologic Model in Sparsely Gauged West African River Basins. Water. 2018; 10(10):1418. https://doi.org/10.3390/w10101418
Chicago/Turabian StylePoméon, Thomas, Bernd Diekkrüger, and Rohini Kumar. 2018. "Computationally Efficient Multivariate Calibration and Validation of a Grid-Based Hydrologic Model in Sparsely Gauged West African River Basins" Water 10, no. 10: 1418. https://doi.org/10.3390/w10101418






