Rainfall-Runoff Modelling Considerations to Predict Streamflow Characteristics in Ungauged Catchments and under Climate Change
Abstract
1. Introduction
- Do we need a different calibration objective function or criteria to target each specific streamflow characteristic or signature? or
- Is there a general calibration criteria that can adequately reproduce most streamflow characteristics? (Hence allowing for a consistent simulation of streamflow time series and the different streamflow characteristics using one single set of parameter values); or
- Do we need a couple of calibration criteria for groups of similar types of streamflow characteristics? and
- What are the implications when the calibrated model is then used to predict changes in the different flow characteristics under climate change?
2. Data and Methods
2.1. Model Simulation in Single Catchments
2.2. Prediction in Ungauged Catchments
2.3. Modelling Climate Change Impact on Streamflow Characteristics
3. Results
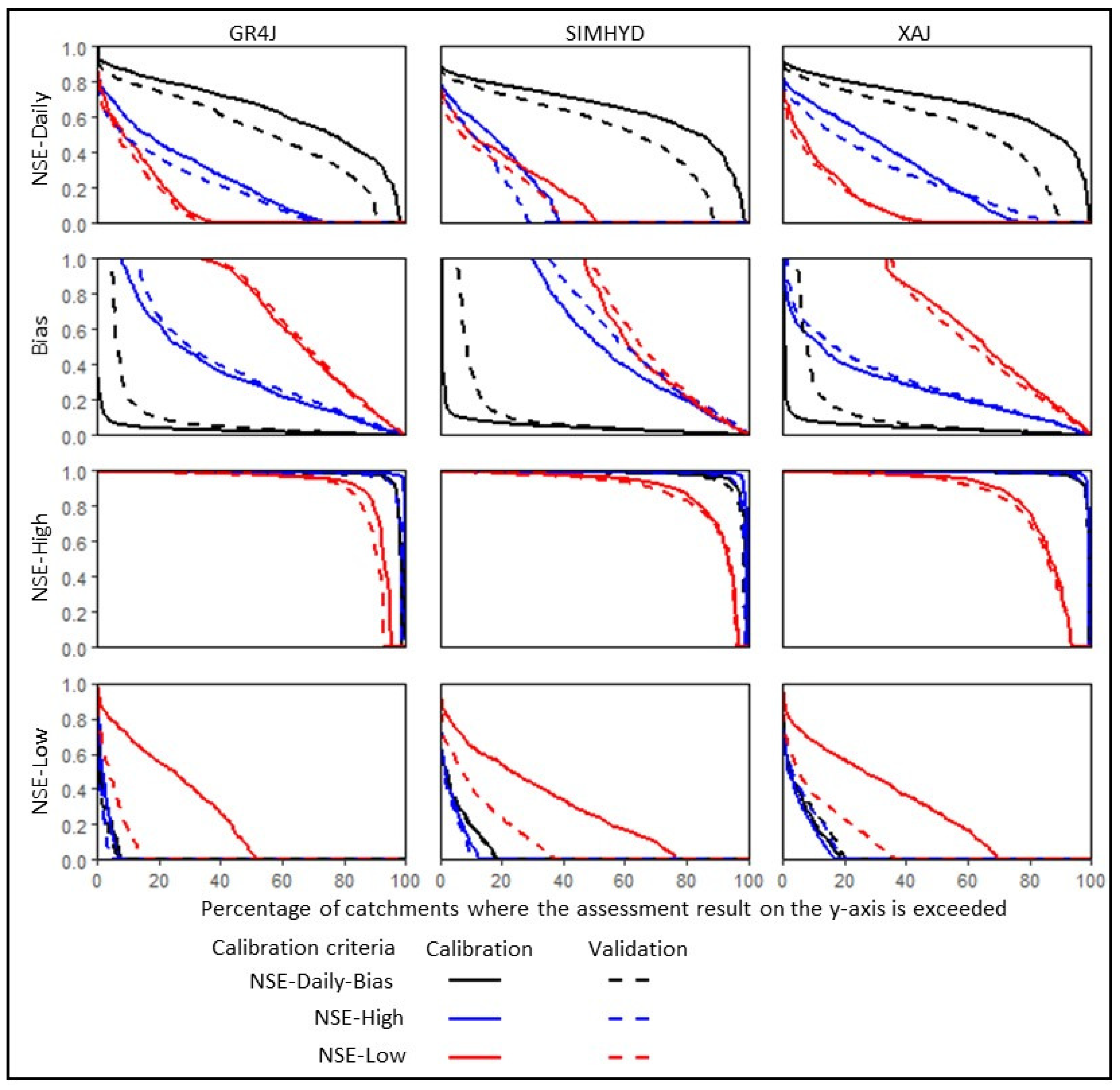
3.1. Model Simulation in Single Catchments
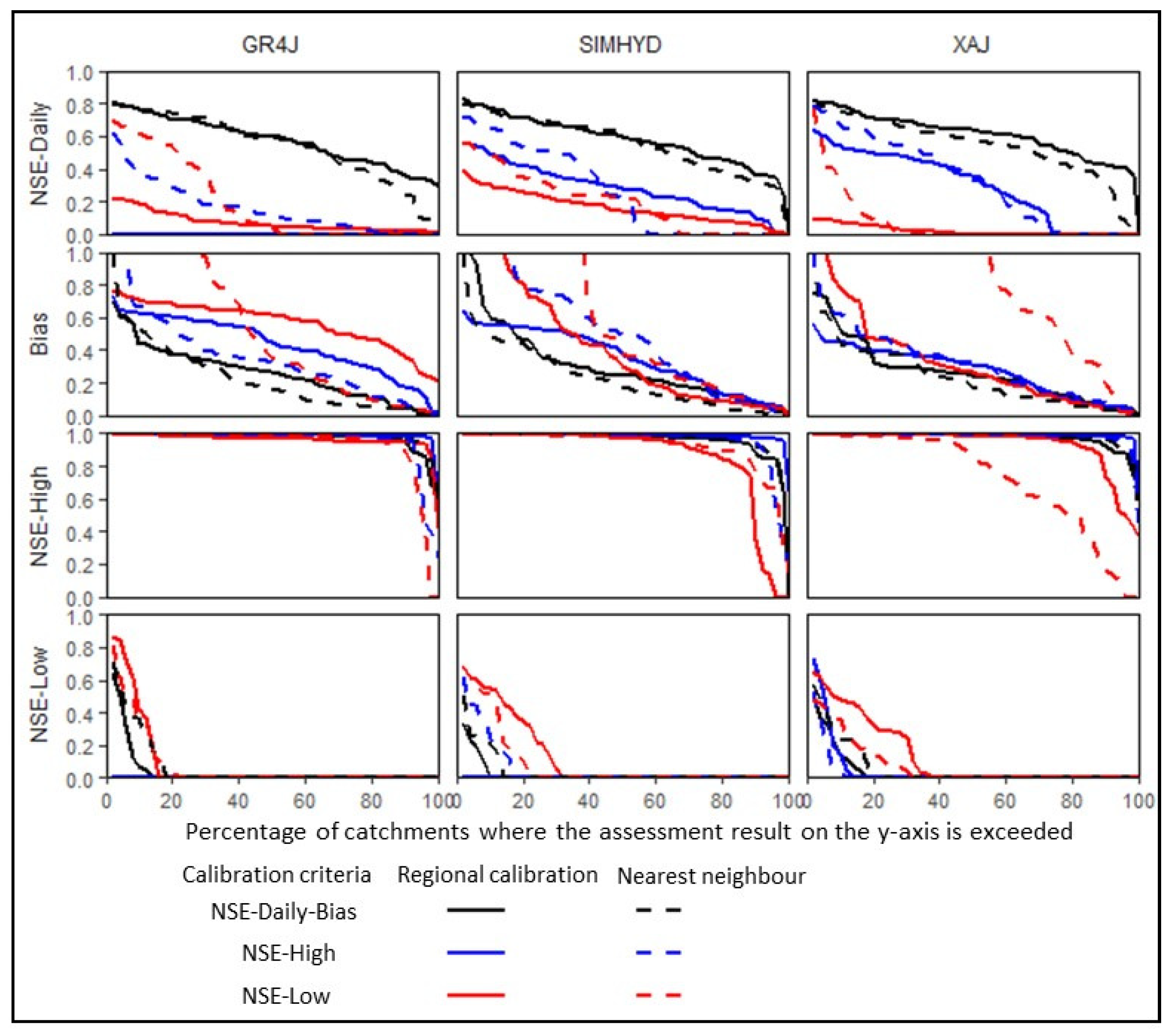
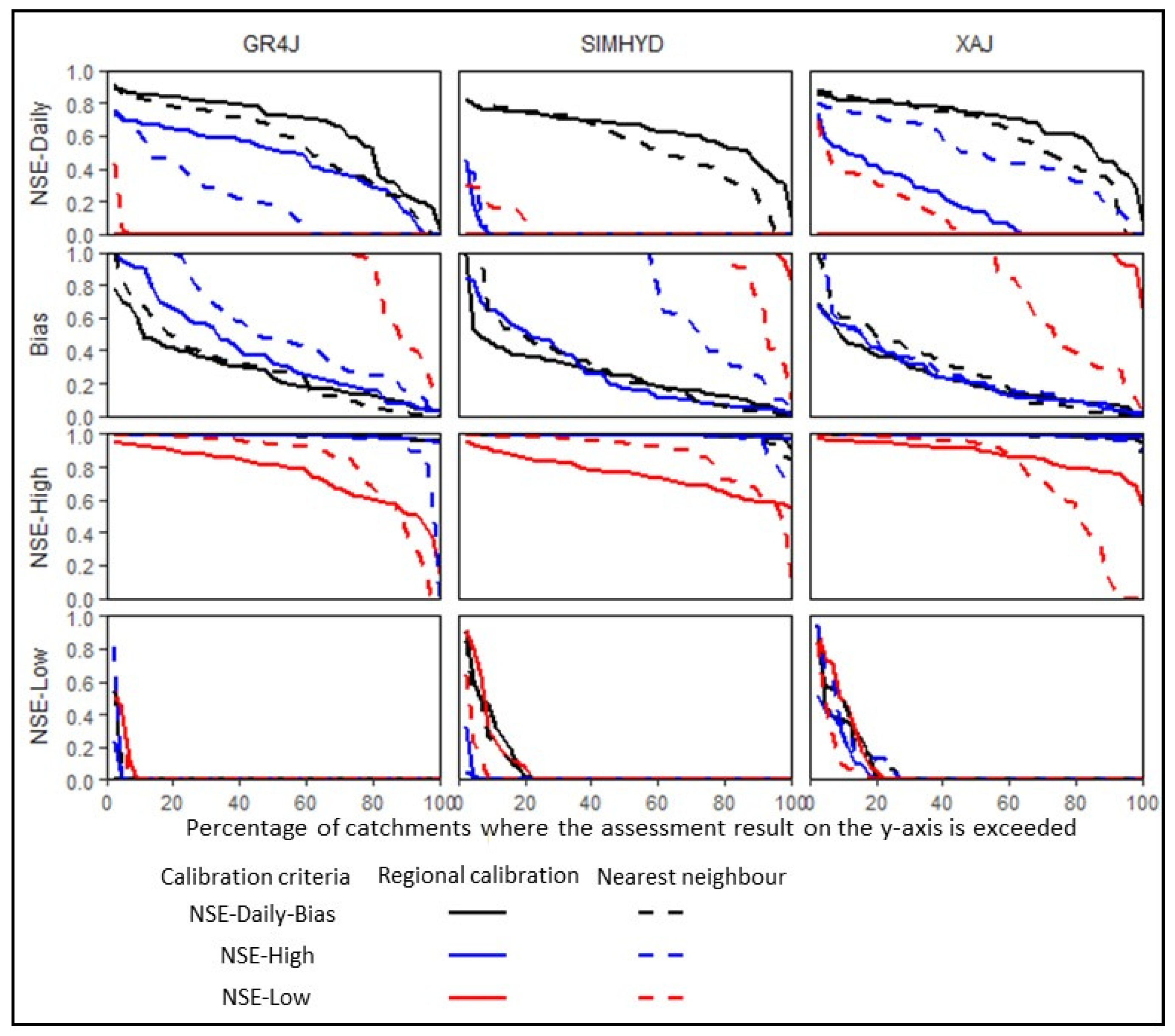
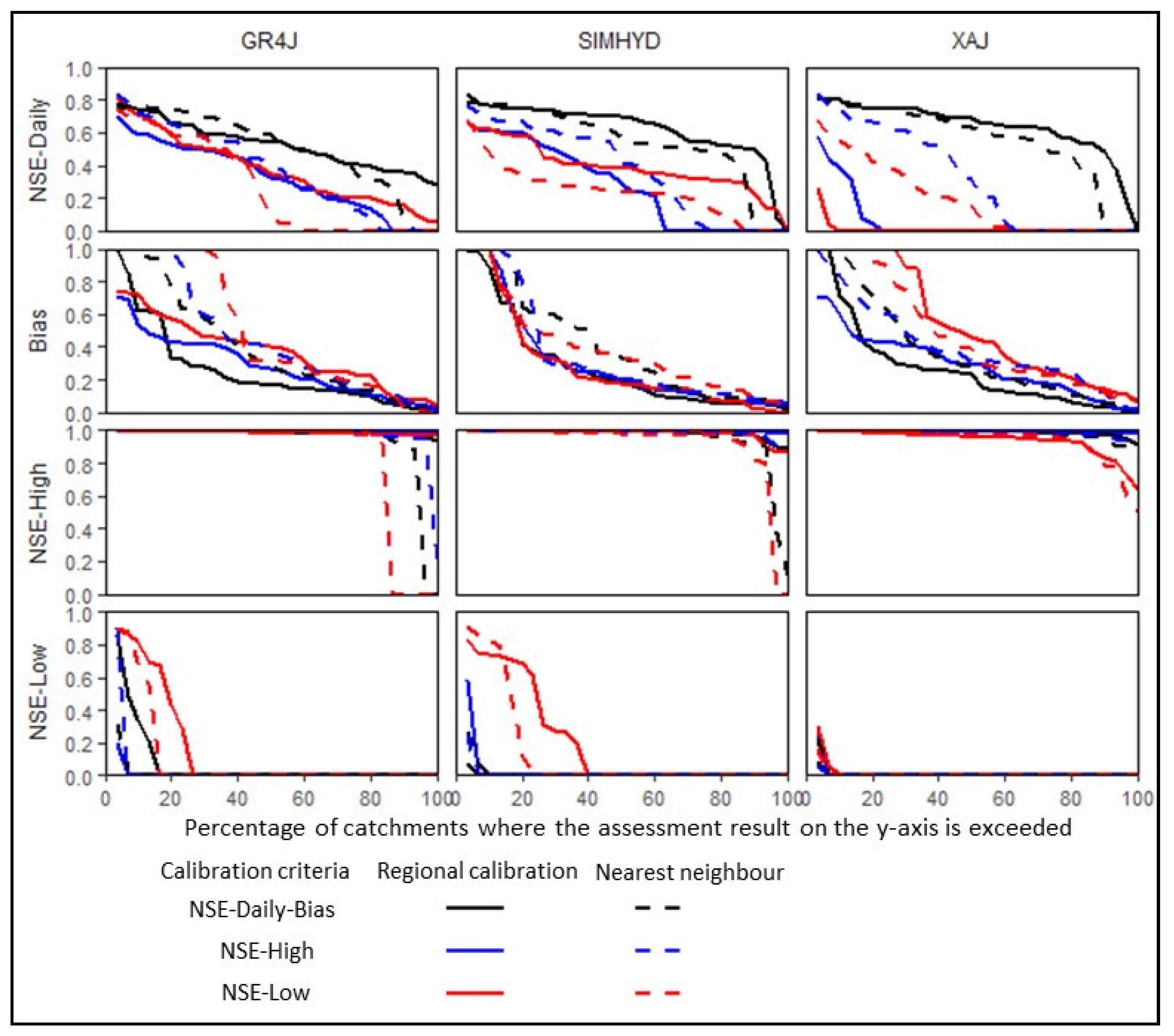
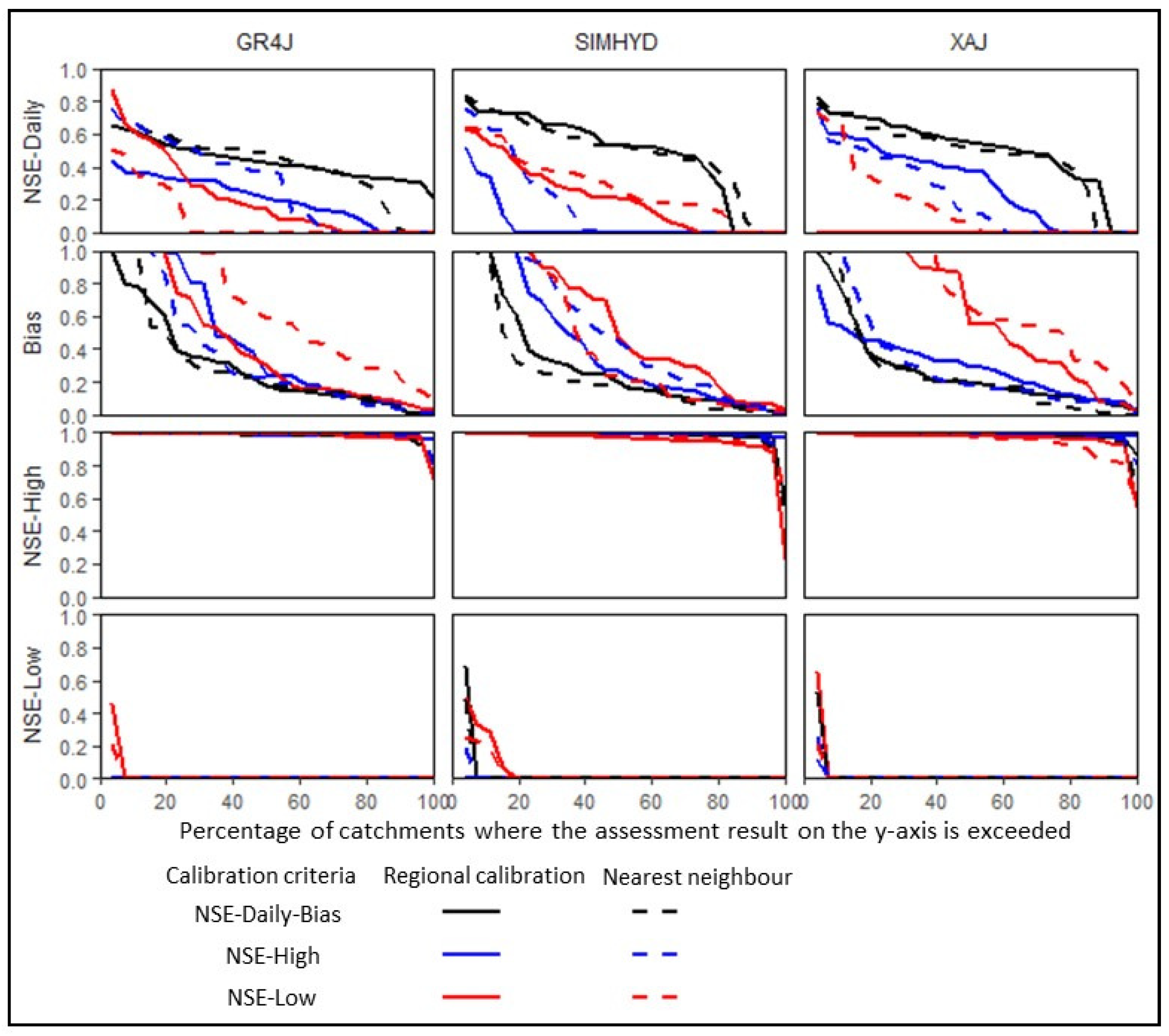
3.2. Prediction in Ungauged Catchments
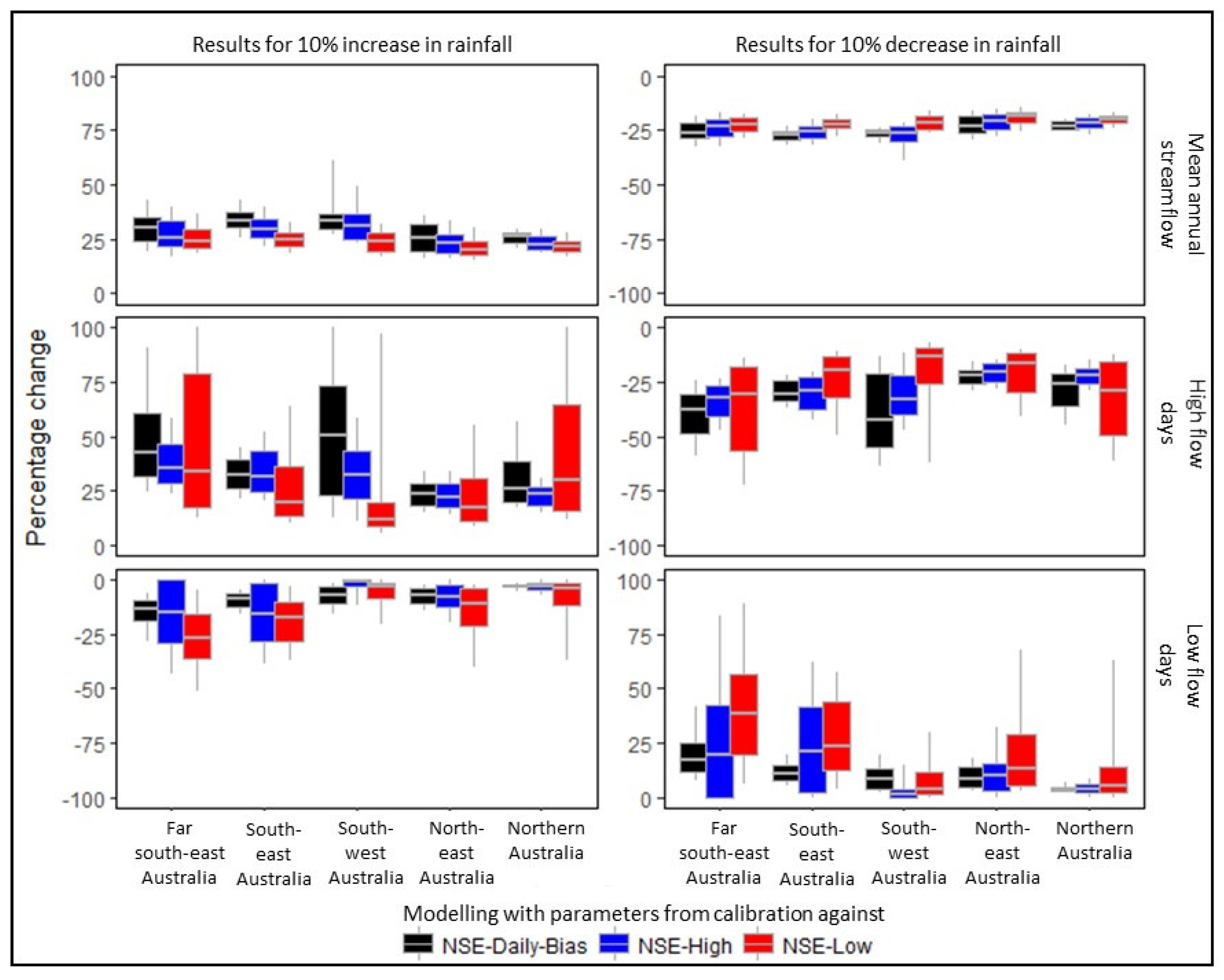
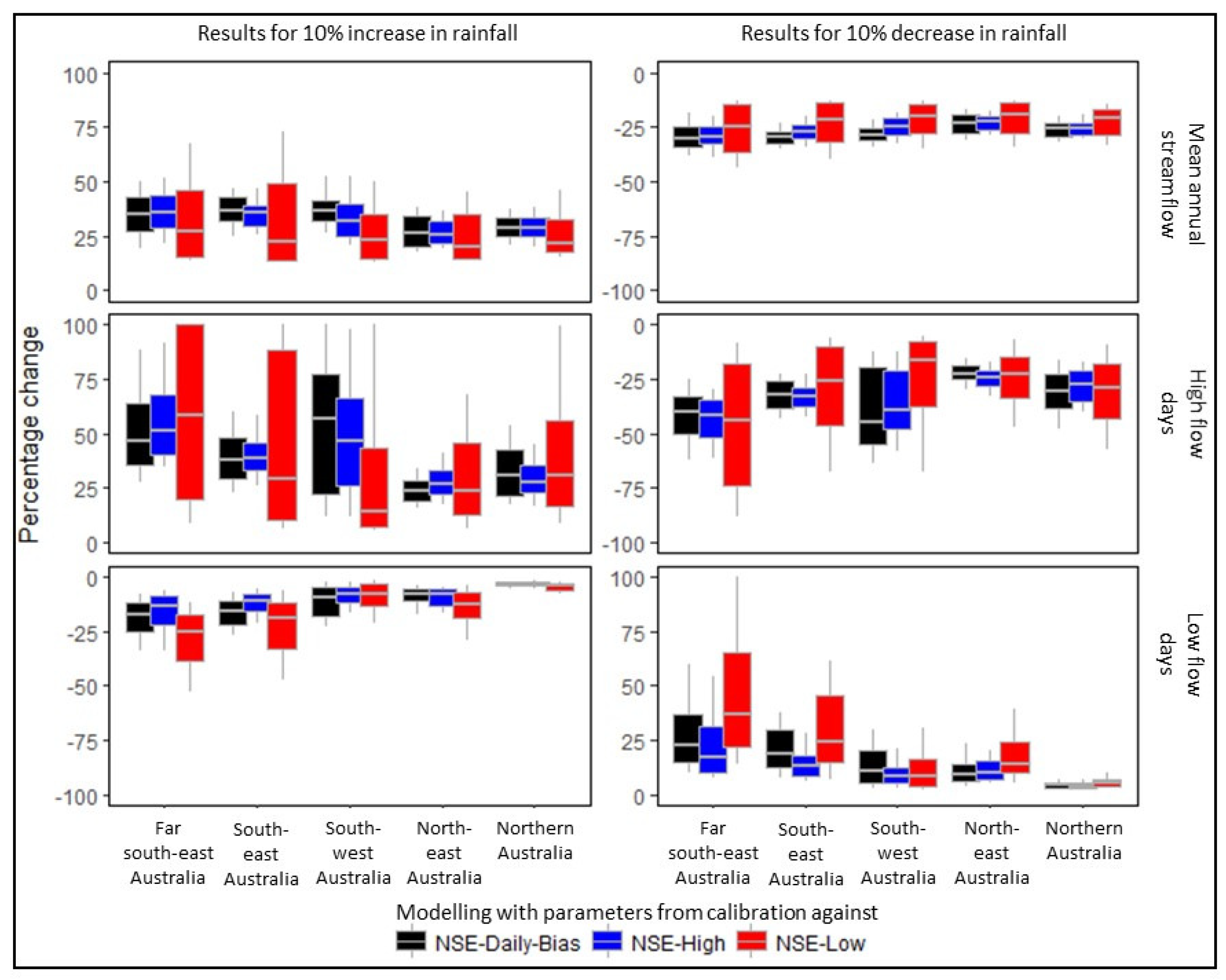
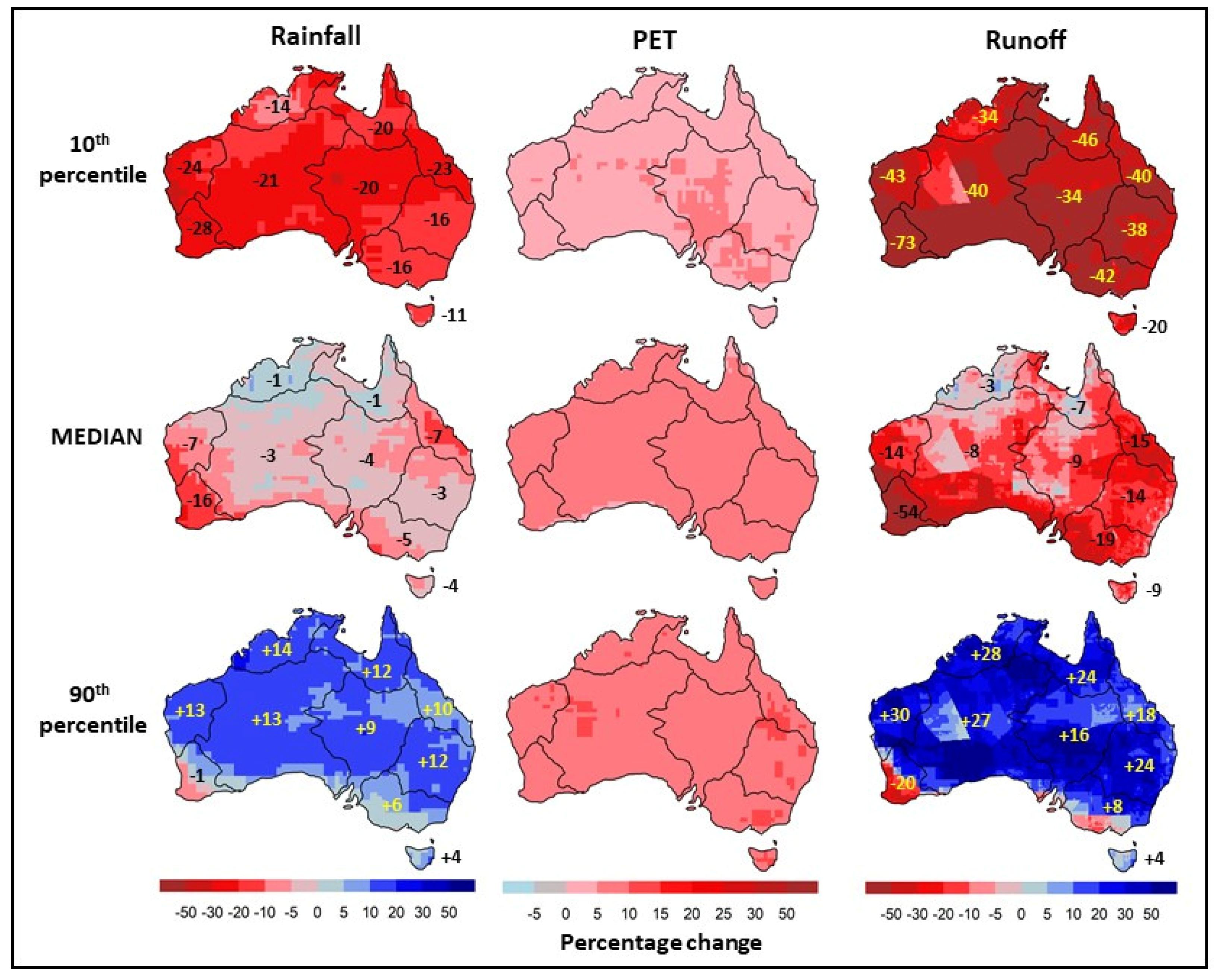
3.3. Modelling Climate Change Impact on Streamflow Characteristics
4. Discussion
4.1. Hydrological Prediction in Ungauged Catchments
4.2. Hydrological Prediction under Climate Change
5. Summary and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Beven, K.J. Rainfall-Runoff Modelling—The Primer; Wiley: West Sussex, UK, 2001; 360p. [Google Scholar]
- Bloschl, G.; Sivapalan, M.; Wagener, T.; Viglione, A.; Savenije, H. Runoff Prediction in Ungauged Basins—Synthesis across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013; 465p. [Google Scholar]
- Chiew, F.H.S.; Teng, J.; Vaze, J.; Post, D.A.; Perraud, J.-M.; Kirono, D.G.C.; Viney, N.R. Estimating climate change impact on runoff across south-east Australia: Method, results and implications of modelling method. Water Resour. Res. 2009, 45, W10414. [Google Scholar] [CrossRef]
- Chiew, F.H.S. Lumped conceptual rainfall-runoff models and simple water balance methods: Overview and applications in ungauged and data limited regions. Geogr. Compass 2010, 4, 206–225. [Google Scholar] [CrossRef]
- Parajka, J.; Bloschl, G. The value of MODIS snow cover data in validating and calibrating conceptual hydrological models. J. Hydrol. 2008, 358, 240–258. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Chiew, F.H.S.; Zhang, L.; Li, H.X. Use of remotely sensed actual evapotranspiration to improve rainfall-runoff modelling in southeast Australia. J. Hydrometeorol. 2009, 10, 969–980. [Google Scholar] [CrossRef]
- Oudin, L.; Andreassian, V.; Perrin, C.; Michel, C.; Le Moine, N. Spatial proximity, physical similarity, regression and ungauged catchments: A comparison of regionalisation approaches based on 913 French catchments. Water Resour. Res. 2008, 44, W03413. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Chiew, F.H.S. Relative merits of different methods for runoff predictions in ungauged catchments. Water Resour. Res. 2009, 45, W07412. [Google Scholar] [CrossRef]
- Parajka, J.; Bloschl, G.; Merz, R. Regional calibration of catchment models: Potential for ungauged catchments. Water Resour. Res. 2007, 43, W06406. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Laaha, G.; Demuth, S.; Hisdal, H.; Kroll, C.N.; van Lanen, H.A.J.; Nester, T.; Rogger, M.; Sanquet, E.; Tallaksen, L.M.; Woods, R.A.; et al. Prediction of low flows in ungauged basins. In Runoff Prediction in Ungauged Basins; Bloschl, G., Sivapalan, M., Wagener, T., Viglione, A., Savinije, H., Eds.; Cambridge University Press: Cambridge, UK, 2009; pp. 163–188. [Google Scholar]
- Rosbjerg, D.; Bloschl, G.; Burn, D.H.; Castellarin, A.; Croke, B.; Di Baldassarre, G.; Iacobellis, V.; Kjeldsen, T.R.; Kuczera, G.; Merz, R.; et al. Prediction of floods in ungauged basins. In Runoff Prediction in Ungauged Basins; Bloschl, G., Sivapalan, M., Wagener, T., Viglione, A., Savinije, H., Eds.; Cambridge University Press: Cambridge, UK, 2009; pp. 189–226. [Google Scholar]
- Tan, K.S.; Chiew, F.H.S.; Grayson, R.B.; Scanlon, P.J.; Siriwardena, L. Calibration of a daily rainfall-runoff model to estimate high daily flows. In Proceedings of the MODSIM 2005 International Congress on Modelling and Simulation, Melbourne, Australia, 12–15 December 2005; pp. 2960–2966. [Google Scholar]
- Perrin, C.; Michel, C.; Andreassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Peel, M.C.; Western, A.W. Application and testing of the simple rainfall-runoff model SIMHYD. In Mathematical Models of Small Watershed Hydrology and Applications; Singh, V.P., Frevert, D.K., Eds.; Water Resources Publication: Littleton, CO, USA, 2002; pp. 335–367. [Google Scholar]
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Jeffrey, S.J.; Carter, J.O.; Moodie, K.B.; Beswick, A.R. Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environ. Model. Softw. 2001, 16, 309–330. [Google Scholar] [CrossRef]
- Morton, F.I. Operational estimates of areal evapotranspiration and their significance to the science and practice of hydrology. J. Hydrol. 1983, 66, 1–76. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; McMahon, T.A. The applicability of Morton’s and Penman’s evapotranspiration estimates in rainfall-runoff modelling. Water Resour. Bull. 1991, 27, 611–620. [Google Scholar] [CrossRef]
- Vaze, J.; Chiew, F.H.S.; Perraud, J.-M.; Viney, N.; Post, D.; Teng, J.; Wang, B.; Lerat, J.; Goswomi, M. Rainfall-runoff modelling across southeast Australia: Datasets, models and results. Australas. J. Water Resour. 2011, 14, 101–116. [Google Scholar] [CrossRef]
- Viney, N.R.; Perraud, J.; Vaze, J.; Chiew, F.H.S.; Post, D.A.; Yang, A. The usefulness of bias constraints in model calibration for regionalisation to ungauged catchments. In Proceedings of the MODSIM2009 International Congress on Modelling and Simulation, Cairns, Australia, 13–17 July 2009; pp. 3421–3427. [Google Scholar]
- Poff, N.L.; Richter, B.D.; Arthington, A.H.; Bunn, S.E.; Naiman, R.J.; Kendy, E.; Acreman, M.; Apse, C.; Bledsoe, B.P.; Freeman, M.C. The ecological limits of hydrologic alteration (ELOHA): A new framework for developing regional environmental flow standards. Freshw. Biol. 2010, 55, 147–170. [Google Scholar] [CrossRef]
- Rolls, R.J.; Leigh, C.; Sheldon, F. Mechanistic effects of low-flow hydrology on riverine ecosystems: Ecological principles and consequences of alteration. Freshw. Sci. 2012, 31, 1163–1186. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Potter, N.J.; Vaze, J.; Petheram, C.; Zhang, L.; Teng, J.; Post, D.A. Observed hydrologic non-stationarity in far south-eastern Australia: Implications and future modelling predictions. Stoch. Environ. Res. Risk Assess. 2014, 28, 3–15. [Google Scholar] [CrossRef]
- Vaze, J.; Post, D.A.; Chiew, F.H.S.; Perraud, J.-M.; Viney, N.; Teng, J. Climate non-stationarity—Validity of calibrated rainfall-runoff models for use in climate change studies. J. Hydrol. 2010, 394, 447–457. [Google Scholar] [CrossRef]
- Merz, R.; Bloschl, G. Regionalisation of catchment model parameters. J. Hydrol. 2004, 287, 95–123. [Google Scholar] [CrossRef]
- Viney, N.; Vaze, J.; Crosbie, R.; Wang, B.; Dawes, W.; Frost, A. AWRA-L v5.0: Technical Description of Model Algorithms and Inputs; Commonwealth Scientific and Industrial Research Organisation: Canberra, Australia, 2015; 76p.
- Chiew, F.H.S. Estimation of rainfall elasticity of streamflow in Australia. Hydrol. Sci. J. 2006, 51, 613–625. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Vaze, J.; Chiew, F.H.S.; Teng, J.; Li, M. Predicting hydrological signatures in ungauged catchments using spatial interpolation, index model and rainfall-runoff modelling. J. Hydrol. 2014, 517, 936–948. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Zheng, H.; Potter, N.J.; Ekstrom, M.; Grose, R.; Kirono, D.G.C.; Zhang, L.; Vaze, J. Future runoff projections for Australia and science challenges in producing next generation projections. In Proceedings of the MODSIM2017 International Congress on Modelling and Simulation, Hobart, Australia, 3–8 December 2017; pp. 1745–1751. [Google Scholar]
- Potter, N.J.; Chiew, F.H.S. An investigation into changes in climate characteristics causing the recent very low runoff in the southern Murray-Darling Basin using rainfall-runoff models. Water Resour. Res. 2011, 47, W00G10. [Google Scholar] [CrossRef]
- Teng, J.; Vaze, J.; Chiew, F.H.S.; Wang, B.; Perraud, J.-M. Estimating the relative uncertainties sourced from GCMs and hydrological models in modelling climate change impact on runoff. J. Hydrometeorol. 2012, 13, 122–139. [Google Scholar] [CrossRef]
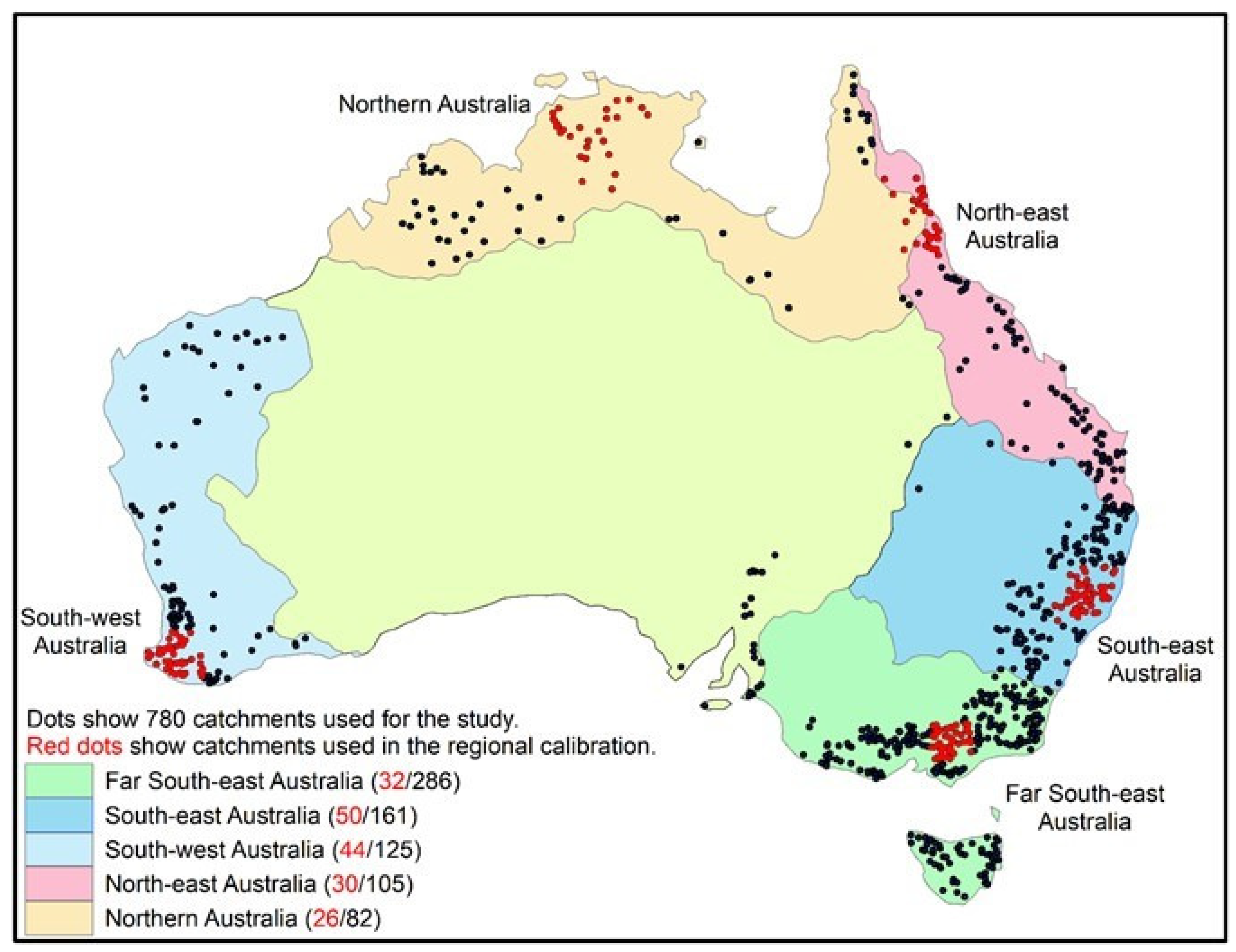


| Entire Dataset | Far South-East Australia | South-East Australia | South-West Australia | North-East Australia | Northern Australia | |
|---|---|---|---|---|---|---|
| Number of Catchments | 780 | 286 | 161 | 125 | 82 | 105 |
| Catchment Area (km2) | 373 * (85–3415) * | 258 (83–909) | 387 (89–2532) | 474 (72–6442) | 469 (102–2303) | 1658 (265–11143) |
| Mean Annual Rainfall (mm) | 867 (557–1420) | 913 (633–1382) | 847 (671–1350) | 698 (326–981) | 1040 (707–2020) | 1087 (644–1544) |
| Mean Annual Streamflow (mm) | 124 (21–534) | 172 (38–566) | 99 (24–385) | 37 (5–160) | 216 (34–1021) | 192 (72–560) |
| Mean Annual Streamflow (×106 m3) (GL) | 46 (7–437) | 39 (9–236) | 42 (10–211) | 20 (3–99) | 103 (248–544) | 380 (64–2054) |
| Runoff Coefficient | 0.14 (0.04–0.38) | 0.18 (0.06–0.42) | 0.12 (0.04–0.29) | 0.06 (0.01–0.16) | 0.19 (0.05–0.55) | 0.21 (0.10–0.39) |
| 95th Percentile Daily Streamflow (mm) | 1.20 (0.14–5.50) | 1.59 (0.41–5.50) | 0.87 (0.16–3.32) | 0.43 (0.02–1.94) | 1.64 (0.20–10.49) | 2.74 (0.70–7.80) |
| 95th Percentile Daily Streamflow (×103 m3) (ML) | 419 (64–4313) | 394 (85–2115) | 347 (68–1816) | 169 (14–1189) | 697 (144–4511) | 4936 (637–30070) |
| 5th Percentile Daily Streamflow (×103 m3) (ML) # | 0.61 (0.04–35) | 2.70 (0.10–65) | 0.67 (0.04–18) | 0.16 (0.01–3.7) | 0.10 (0.04–26) | 0.63 (0.04–60) |
| Number of Zero Days per Year | 10 (0–178) | 1 (0–98) | 11 (0–126) | 89 (0–286) | 19 (0–107) | 37 (0–177) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiew, F.H.S.; Zheng, H.; Potter, N.J. Rainfall-Runoff Modelling Considerations to Predict Streamflow Characteristics in Ungauged Catchments and under Climate Change. Water 2018, 10, 1319. https://doi.org/10.3390/w10101319
Chiew FHS, Zheng H, Potter NJ. Rainfall-Runoff Modelling Considerations to Predict Streamflow Characteristics in Ungauged Catchments and under Climate Change. Water. 2018; 10(10):1319. https://doi.org/10.3390/w10101319
Chicago/Turabian StyleChiew, Francis H.S., Hongxing Zheng, and Nicholas J. Potter. 2018. "Rainfall-Runoff Modelling Considerations to Predict Streamflow Characteristics in Ungauged Catchments and under Climate Change" Water 10, no. 10: 1319. https://doi.org/10.3390/w10101319
APA StyleChiew, F. H. S., Zheng, H., & Potter, N. J. (2018). Rainfall-Runoff Modelling Considerations to Predict Streamflow Characteristics in Ungauged Catchments and under Climate Change. Water, 10(10), 1319. https://doi.org/10.3390/w10101319






