Estimation of Conservative Contaminant Travel Time through Vadose Zone Based on Transient and Steady Flow Approaches
Abstract
:1. Introduction
2. Materials and Methods
2.1. Vadose Zone Profiles
2.2. Numerical Modeling
2.3. Analytical Equations for Vertical Travel Time
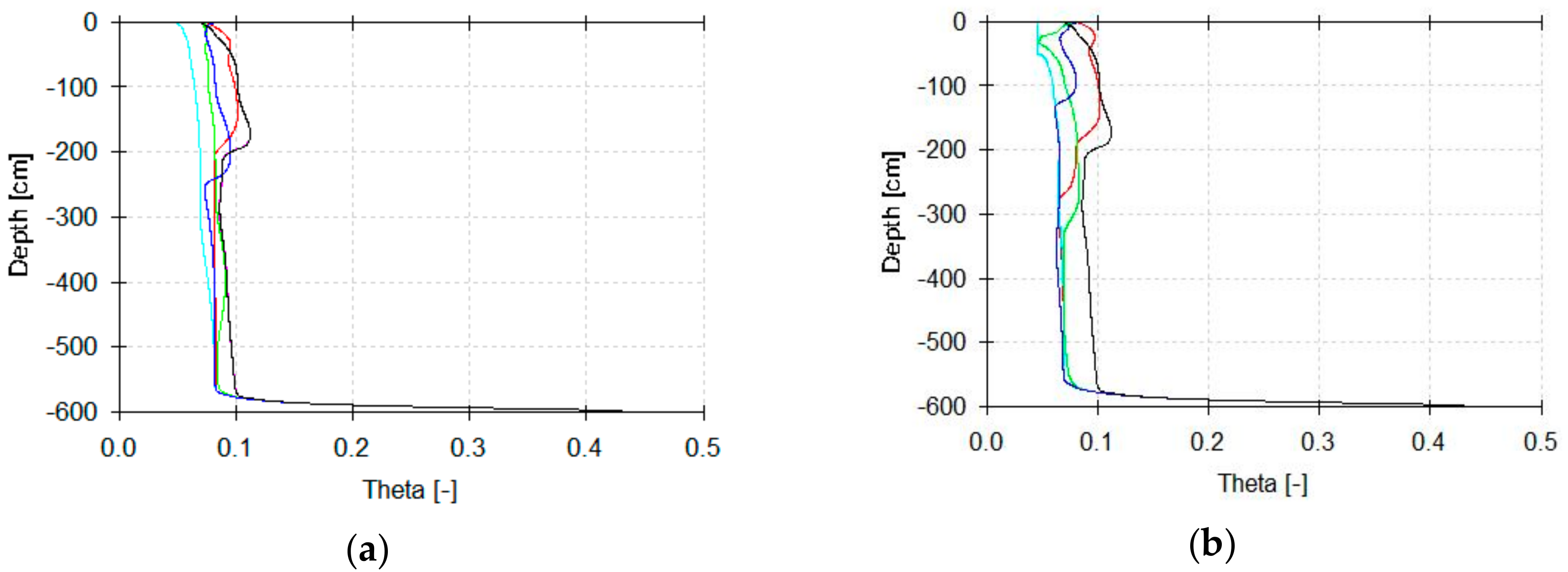
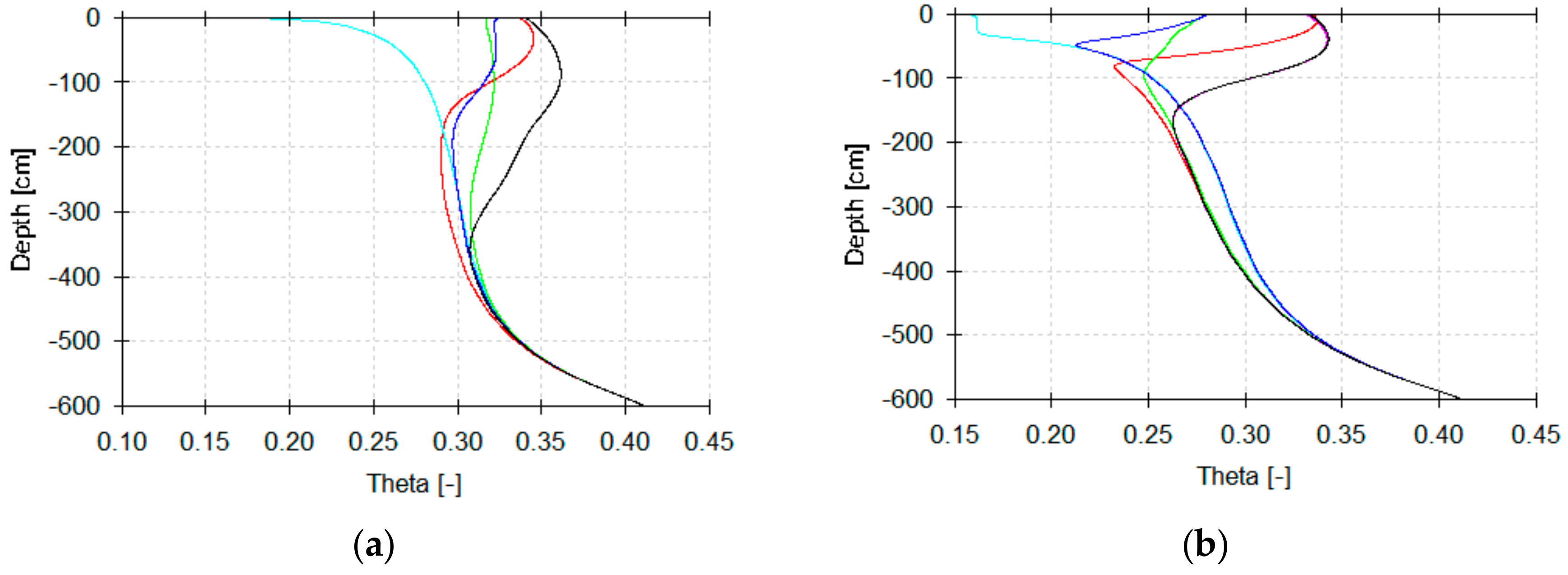
3. Results
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fenton, O.; Schulte, R.P.; Jordan, P.; Lalor, S.T.; Richards, K.G. Time lag: A methodology for the estimation of vertical and horizontal travel and flushing timescales to nitrate threshold concentrations in Irish aquifers. Environ. Sci. Policy 2011, 14, 419–431. [Google Scholar] [CrossRef] [Green Version]
- Rossman, N.R.; Zlotnik, V.A.; Rowe, C.M.; Szilagyi, J. Vadose zone lag time and potential 21st century climate change effects on spatially distributed groundwater recharge in the semi-arid Nebraska Sand Hills. J. Hydrol. 2014, 519, 656–669. [Google Scholar] [CrossRef] [Green Version]
- Wachniew, P.; Żurek, A.J.; Stumpp, C.; Gemitzi, A.; Gargini, A.; Filippini, M.; Różański, K.; Meeks, J.; Kværner, J.; Witczak, S. Toward operational methods for the assessment of intrinsic groundwater vulnerability: A review. Crit. Rev. Environ. Sci. Technol. 2016, 46, 827–884. [Google Scholar] [CrossRef]
- Witkowski, A.J.; Rubin, K.; Kowalczyk, A.; Różkowski, A.; Wróbel, J. Groundwater vulnerability map of the Chrzanów karst-fissured Triassic aquifer (Poland). Environ. Geol. 2003, 44, 59–67. [Google Scholar] [CrossRef]
- Krogulec, E.; Trzeciak, J. Drastic assessment of groundwater vulnerability to pollution in the Vistula floodplain in central Poland. Hydrol. Res. 2017, 48, 1088–1099. [Google Scholar] [CrossRef]
- Miglietta, P.P.; Toma, P.; Fanizzi, F.P.; De Donno, A.; Coluccia, B.; Migoni, D.; Bagordo, F.; Serio, F.A. Grey water footprint assessment of groundwater chemical pollution: Case study in Salento (southern Italy). Sustainability 2017, 9, 799. [Google Scholar] [CrossRef]
- Serio, F.; Miglietta, P.P.; Lamastra, L.; Ficocelli, S.; Intini, F.; De Leo, F.; De Donno, A. Groundwater nitrate contamination and agricultural land use: A grey water footprint perspective in Southern Apulia Region (Italy). Sci. Total Environ. 2018, 645, 1425–1431. [Google Scholar] [CrossRef] [PubMed]
- Bachmat, Y.; Collin, M. Mapping to assess groundwater vulnerability to pollution. In Vulnerability of Soil and Groundwater to Pollutants; van Duijvenbooden, W., van Waegeningh, H.G., Eds.; TNO Committee on Hydrological Research: The Hague, The Netherlands, 1987; pp. 297–307. ISBN 90-6743-109-5. [Google Scholar]
- Charbeneau, R.J.; Daniel, D.E. Contaminant transport in unsaturated flow. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Szestakow, W.S.; Witczak, S. Podstawy fizyczno-matematycznego opisu migracji substancji zanieczyszczających [Fundamentals of physical-mathematical description of pollutants]. In Ochrona Wód Podziemnych [Groundwater Protection]; Kleczkowski, A.S., Ed.; Wydawnictwa Geologiczne: Warszawa, Poland, 1984. (In Polish) [Google Scholar]
- Witczak, S.; Żurek, A. Wykorzystanie map glebowo-rolniczych wocenie ochronnej roli gleb dla wód podziemnych [Use of soil-agricultural maps in the evolution of protective role of soil for groundwater]. In Metodyczne Podstawy Ochrony Wód Podziemnych [Methodical Principles of Groundwater Protection]; Kleczkowski, A., Ed.; Akademia Górniczo-Hutnicza: Kraków, Poland, 1994. (In Polish) [Google Scholar]
- Macioszczyk, T. Czas przesączania pionowego wody jako wskaźnik stopnia ekranowania warstw wodonośnych [Time of vertical seepage as an indicator of the degree of aquifer insulation]. Przegląd Geologiczny 1999, 47, 731–736. (In Polish) [Google Scholar]
- De Vries, J.J.; Simmers, I. Groundwater recharge: An overview of processes and challenges. Hydrogeol. J. 2002, 10, 5–17. [Google Scholar] [CrossRef]
- Potrykus, D.; Gumuła-Kawęcka, A.; Jaworska-Szulc, B.; Pruszkowska-Caceres, M.; Szymkiewicz, A. Assessing groundwater vulnerability to pollution in the Puck region (denudation moraine upland) using vertical seepage method. E3S Web. Conf. 2018, 44, 00147. [Google Scholar] [CrossRef]
- Sousa, M.R.; Jones, J.; Frind, E.O.; Rudolph, D.L. A simple method to assess unsaturated zone time lag in the travel time from ground surface to receptor. J. Contam. Hydrol. 2013, 144, 138–151. [Google Scholar] [CrossRef] [PubMed]
- Vero, S.E.; Ibrahim, T.G.; Creamer, R.E.; Grant, J.; Healy, M.G.; Henry, T.; Kramers, G.; Richards, K.G.; Fenton, O. Consequences of varied soil hydraulic and meteorological complexity on unsaturated zone time lag estimates. J. Contam. Hydrol. 2014, 170, 53–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Batalha, M.S.; Barbosa, M.C.; Faybishenko, B.; van Genuchten, M.T. Effect of temporal averaging of meteorological data on predictions of groundwater recharge. J. Hydrol. Hydromech. 2018, 66, 143–152. [Google Scholar] [CrossRef] [Green Version]
- Szymkiewicz, A.; Gumuła-Kawęcka, A.; Šimůnek, J.; Leterme, B.; Beegum, S.; Jaworska-Szulc, B.; Pruszkowska-Cacers, M.; Gorczewska-Langner, W.; Jacques, D. Simulations of freshwater lens recharge and salt/freshwater interfaces using the HYDRUS and SWI2 packages for MODFLOW. J. Hydrol. Hydromech. 2018, 66, 246–256. [Google Scholar] [CrossRef] [Green Version]
- Vero, S.E.; Healy, M.G.; Henry, T.; Creamer, R.E.; Ibrahim, T.G.; Richards, K.G.; Mellander, P.-E.; McDonald, N.T.; Fenton, O. A framework for determining unsaturated zone water quality time lags at catchment scale. Agric. Ecosyst. Environ. 2017, 236, 234–242. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, Version 4.0; HYDRUS Software Series 3; University of California: Riverside, CA, USA, 2008. [Google Scholar]
- Yu, C.; Yao, Y.; Hayes, G.; Zhang, B.; Zheng, C. Quantitative assessment of groundwater vulnerability using index system and transport simulation, Huangshuihe catchment, China. Sci. Total Environ. 2010, 408, 6108–6116. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Jin, M.; van Genuchten, M.Th.; Wang, B. Groundwater recharge at five representative sites in the Hebei Plain, China. Groundwater 2011, 49, 286–294. [Google Scholar] [CrossRef] [PubMed]
- Fenton, O.; Vero, S.; Ibrahim, T.G.; Murphy, P.N.C.; Sherriff, S.C.; Ó hUallacháin, D. Consequences of using different soil texture determination methodologies for soil physical quality and unsaturated zone time lag estimates. J. Contam. Hydrol. 2015, 182, 16–24. [Google Scholar] [CrossRef] [PubMed]
- Van Genuchten, M.Th. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Bittelli, M.; Campbell, G.S.; Tomei, F. Soil Physics with Python: Transport in the Soil-Plant-Atmosphere System; OUP Oxford: Oxford, UK, 2015; ISBN 0191505587. [Google Scholar]
- Peters, A. Simple consistent models for water retention and hydraulic conductivity in the complete moisture range. Water Resour. Res. 2013, 49, 6765–6780. [Google Scholar] [CrossRef] [Green Version]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Clothier, B.E.; Green, S.R.; Deurer, M. Preferential flow and transport in soil: Progress and prognosis. Eur. J. Soil Sci. 2008, 59, 2–13. [Google Scholar] [CrossRef]
- Allen, R.G. A Penman for all seasons. J. Irrig. Drain. Eng. 1986, 112, 348–368. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; John Wiley & Sons: New York, NY, USA, 1978; ISBN 0470264632. [Google Scholar]
- Meyer, P.D.; Rockhold, M.L.; Gee, G.W. Uncertainty Analyses of Infiltration and Subsurface Flow and Transport for SDMP Sites; Nuclear Regulatory Commission: Washington, DC, USA, 1997. [Google Scholar]
- Hillel, D. Environmental Soil Physics: Fundamentals, Applications, and Environmental Considerations; Elsevier: Amsterdam, The Netherlands, 1998; ISBN 0080544150. [Google Scholar]
- Charbeneau, R.J. Groundwater Hydraulics and Pollutant Transport; Waveland Press: Long Grove, IL, USA, 2006; ISBN 1478608315. [Google Scholar]
- Duda, R.; Winid, B.; Zdechlik, R.; Stępień, M. Metodyka Wyboru Optymalnej Metody Wyznaczania Zasięgu Stref Ochronnych Ujęć Zwykłych Wód Podziemnych Z Uwzględnieniem Warunków Hydrogeologicznych Obszaru Rzgw W Krakowie [Methodology of Selecting the Optimal Method of the Wellhead Protection Area Delineation Taking into Account the Hydrogeological Conditions in Areas Administered by the Regional Water Management Board in Cracow]; Akademia Górniczo-Hutnicza: Kraków, Poland, 2013; ISBN 9788388927294. (In Polish) [Google Scholar]
- Stephens, D.B.; Hsu, K.C.; Prieksat, M.A.; Ankeny, M.D.; Blandford, N.; Roth, T.L.; Kelsey, J.A.; Whitworth, J.R. A comparison of estimated and calculated effective porosity. Hydrogeol. J. 1998, 6, 156–165. [Google Scholar] [CrossRef]
- Dyck, S.; Chardabellas, P. WegezurErmittlung der nutzbarenGrundwasserreserven [Methods to estimate usable groundwater resources]. Ber. Geol. Ges. DDR 1963, 8, 245–262. (In German) [Google Scholar]
- Hölting, B.; Coldewey, W. Hydrogeologie: Einführung in die Allgemeine und Angewandte Hydrogeologie [Hydrogeology: Introduction to General and Applied Hydrogeology]; Springer-Verlag: Heidelberg, Germany, 2013; ISBN 3827423546. (In German) [Google Scholar]
- Beegum, S.; Šimůnek, J.; Szymkiewicz, A.; Sudheer, K.P.; Nambi, I.M. Implementation of solute transport in the vadose zone into the ‘HYDRUS package for MODFLOW’. Groundwater 2018. [Google Scholar] [CrossRef] [PubMed]
- Beegum, S.; Šimůnek, J.; Szymkiewicz, A.; Sudheer, K.P.; Nambi, I.M. Updating the coupling algorithm between HYDRUS and MODFLOW in the ‘HYDRUS Package for MODFLOW’. Vadose Zone J. 2018, 17. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T. Modeling nonequilibrium flow and transport processes using HYDRUS. Vadose Zone J. 2008, 7, 782–797. [Google Scholar] [CrossRef]
| Soil Type | θr (-) | θs (-) | α (cm−1) | ng (-) | ks (m day−1) |
|---|---|---|---|---|---|
| Sand | 0.045 | 0.430 | 0.145 | 2.68 | 7.13 |
| Clay Loam | 0.095 | 0.410 | 0.019 | 1.31 | 0.06 |
| Quantity | Bare Sand | Sand with Grass Cover | Bare Clay Loam | Clay Loam with Grass Cover |
|---|---|---|---|---|
| Mean annual recharge (mm/year) | 336 | 154 | 121 | 31 |
| Recharge/precipitation ratio (-) | 0.61 | 0.28 | 0.22 | 0.06 |
| Parameters | Bare Sand | Sand with Grass Cover | Bare Clay Loam | Clay Loam with Grass Cover |
|---|---|---|---|---|
| αL = 0.60 m, c = 0.01 mg/cm3 | 81 | 102 | 1060 | 3898 |
| αL = 0.60 m, c = 0.99 mg/cm3 | 620 | 803 | 3362 | 8419 |
| αL = 0.06 m, c = 0.01 mg/cm3 | 398 | 801 | 2669 | 7864 |
| αL = 0.06 m, c = 0.99 mg/cm3 | 628 | 846 | 3918 | 11329 |
| Profile | Bare Sand | Sand with Grass Cover | Bare Clay Loam | Clay Loam with Grass Cover |
|---|---|---|---|---|
| steady flow | 590 | 1184 | 5850 | 21584 |
| hydrostatic | 357 | 779 | 5237 | 20441 |
| Equation | Bare Sand | Sand with Grass Cover | Bare Clay Loam | Clay Loam with Grass Cover |
|---|---|---|---|---|
| (6), (Witczak and Żurek 1994) | 455–649 | 899–1285 | 4360–5813 | 16841–22455 |
| (9), (Charbeneau and Daniel 1993) | 589 | 1176 | 5011 | 17675 |
| (10), (Bindemann, cited in Szestakow and Witczak 1984) | 66–127 | 112–214 | 319–999 | 784–2461 |
| (11) (Macioszczyk 1999) | 23–33 | 35–50 | 827–1182 | 1849–2642 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szymkiewicz, A.; Gumuła-Kawęcka, A.; Potrykus, D.; Jaworska-Szulc, B.; Pruszkowska-Caceres, M.; Gorczewska-Langner, W. Estimation of Conservative Contaminant Travel Time through Vadose Zone Based on Transient and Steady Flow Approaches. Water 2018, 10, 1417. https://doi.org/10.3390/w10101417
Szymkiewicz A, Gumuła-Kawęcka A, Potrykus D, Jaworska-Szulc B, Pruszkowska-Caceres M, Gorczewska-Langner W. Estimation of Conservative Contaminant Travel Time through Vadose Zone Based on Transient and Steady Flow Approaches. Water. 2018; 10(10):1417. https://doi.org/10.3390/w10101417
Chicago/Turabian StyleSzymkiewicz, Adam, Anna Gumuła-Kawęcka, Dawid Potrykus, Beata Jaworska-Szulc, Małgorzata Pruszkowska-Caceres, and Wioletta Gorczewska-Langner. 2018. "Estimation of Conservative Contaminant Travel Time through Vadose Zone Based on Transient and Steady Flow Approaches" Water 10, no. 10: 1417. https://doi.org/10.3390/w10101417
APA StyleSzymkiewicz, A., Gumuła-Kawęcka, A., Potrykus, D., Jaworska-Szulc, B., Pruszkowska-Caceres, M., & Gorczewska-Langner, W. (2018). Estimation of Conservative Contaminant Travel Time through Vadose Zone Based on Transient and Steady Flow Approaches. Water, 10(10), 1417. https://doi.org/10.3390/w10101417




