1. Introduction
In recent years, with the in-depth development of information technology and the overall promotion of water conservancy, China’s water conservancy information construction has gradually deepened. Water conservancy informatization is to make full use of information technology to improve the application level and development and sharing of information resources through the collection, transmission, storage, processing, and use of water conservancy data [
1].
With efficient computing facilities, hydrological data has grown exponentially and flooded into hydrological real-time databases. Mining more practical and valuable information from big data is getting more and more attention with the rapid growth of hydrological data. In the big data mining of massive hydrological data, the accuracy and credibility of experiments and applications can be guaranteed only when the data quality problems such as missing and abnormal data are in the controllable range. However, the monitoring level of hydrological stations in China is in the transition from manual recording and semi-automatic to fully automated monitoring. During this period, there will be uncertainties such as installation and the upgrade of the automatic station acquisition system, monitoring sensor interference with measurement accuracy, abnormal jump of instruments caused by extreme weather, and so on. These factors cause anomalies as well as lacks and errors in hydrological data of many monitoring stations. Such erroneous and abnormal data records sometimes mislead disaster management judgment and lead to property losses. Therefore, how to ensure the normalization and accuracy of incoming data is a key issue in the field of hydrology.
Many scholars have proposed some schemes for the control, management, and evaluation of data quality in recent years. Sciuto et al. [
2] relied on the consistency of temperature data, set the sliding window of 11 to use the Fourier transform to smooth the average and mean square error of the data in the window, and establish the maximum and minimum temperature confidence intervals to find the abnormal values in the data. Steinacker et al. [
3] expounded the error types and introduced some basic data quality control methods (such as extremum detection, consistency detection, Bayesian quality control, and complex artificial auxiliary control). On this basis, he proposed a method to find the weights between stations by establishing topological structure of the station space position for the direction of artificial auxiliary control. Sciuto and Abbot [
4,
5] used the rainfall data of the surrounding stations to establish the neural network prediction model and set the confidence interval of the data and regarded the rainfall data outside the confidence interval as the outlier. Fangjing Fu and Xi Luo [
6] respectively investigated and detected the hydrological data stored in the warehouse from the aspects of rationality, completeness, and consistency of the data including detecting the extreme range of data records and the consistency between the internal factors. Yu Yufeng [
7] used Benford’s rule to analyze the distribution law of data in the hydrological database and to test the rationality of the hydrological dataset as a whole. On the basis of research, the established hydrological data quality model proposed a hydrological data quality improvement scheme combining automatic cleaning and manual cleaning [
8] and expounded the basic data quality processing methods from five aspects: missing data processing, logical error detection, repeated data processing, abnormal data detection, and inconsistent data processing, which provide some ideas for hydrological data quality control.
However, there are still many problems in the quality control of hydrological data. For example, the hydrological data quality control methods in China are more in the theoretical research and modeling stage, lack of complete data quality control algorithms, and models for real-time control of hydrological data. Many papers [
3,
4,
5,
6,
7,
8] mention that basic data quality control methods such as logic checking, extremum checking, internal consistency checking, time consistency checking, and spatial consistency checking can detect the data with quality problems but do not give a reliable value or an effective method to replace the problem data. For hydrological data that is short-term missing due to machine failure, linear quality control interpolation methods such as the average method, the weighting method, or the spatial interpolation method are generally used for filling. However, the filling values vary according to the density of the data collected and the credibility of the filling data lacks the measurement scale.
To solve these problems, this paper proposes a data-driven quality control method for hydrological data. According to the continuity of data in time, the hydrological data is divided into two types: continuous type and discrete type. The corresponding control models are established for different types of data to detect and control the real-time monitored data and to analyze and identify problem data such as abnormalities, errors, and redundancy from the point of view of data and expert knowledge to ensure the quality of hydrological data and to provide data support for hydrologists to conduct data mining analysis and decision-making. This article works as follows:
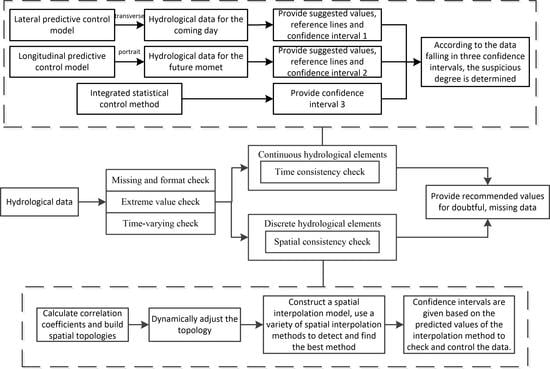
For continuous data, two stable predictive control models, i.e. the horizontal optimized integrated predictive control model and the longitudinal predictive control model, are constructed from the horizontal and vertical perspectives. The model provides two predictive values and confidence intervals for suspicious data and it is up to the staff to decide whether to manually fill, recommend replacement, or retain the original value. The latest data is used as a sample set for periodic training and model adjustment, so that the model parameters can be dynamically updated with time. The predicted values of the two models are used to set the control interval at the center to detect and control the quality of continuous hydrological data. Establish the statistical data quality control interval from the perspective of statistics, combine horizontal and vertical predictive control models, and propose the continuous hydrological data control model. The hourly hydrological real-time data is detected from the perspective of time consistency and the number of monitoring data violating the control interval is taken as its suspicion.
For discrete hydrological data with a large spatial difference and poor temporal continuity (such as rainfall), a discrete hydrological data control scheme is proposed. Centered on the measured stations, a topological map of similarity weights between neighboring stations is established and adjusted with seasonal variation. The spatial interpolation model of daily precipitation is constructed by using the monitoring data of stations with a large correlation around and the missing precipitation data in the short term are attempted to be filled.
Set the online real-time adjustment strategy, according to the seasonal variation characteristics of hydrology, and dynamically adjust the parameters of the basic QC parameters, thresholds, and parameters of the predictive control model when establishing the control interval.
The structure of this paper is as follows:
Section 2 introduces the research status and related theories,
Section 3 describes the control model schemes for different types of data,
Section 4 carries out experimental analysis of different model schemes, and
Section 5 summarizes the conclusions.
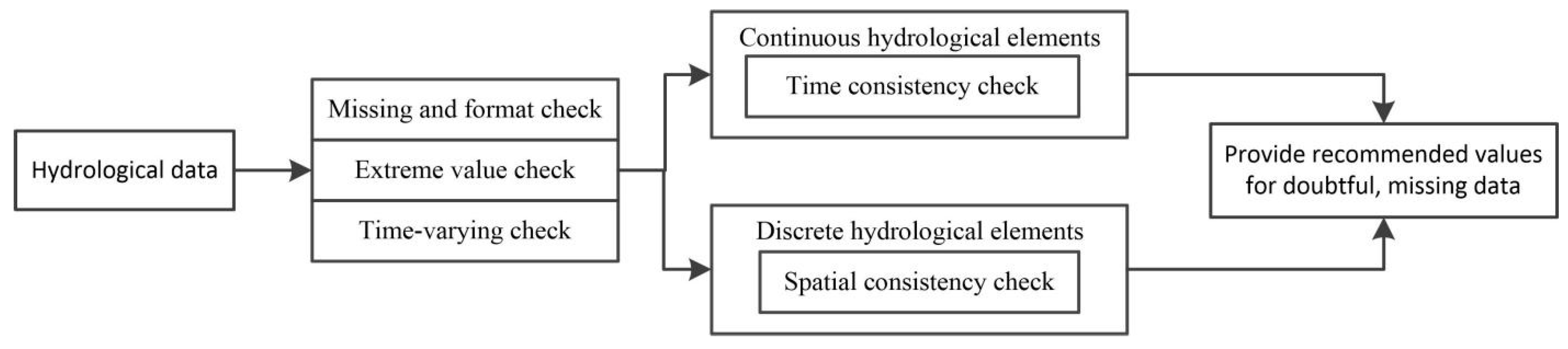
3. Continuous Hydrological Data Control Model
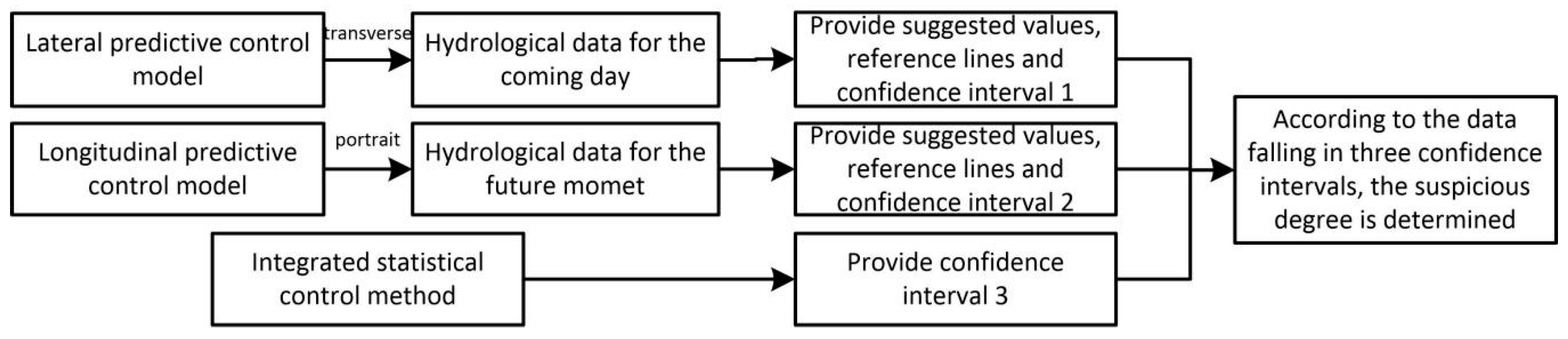
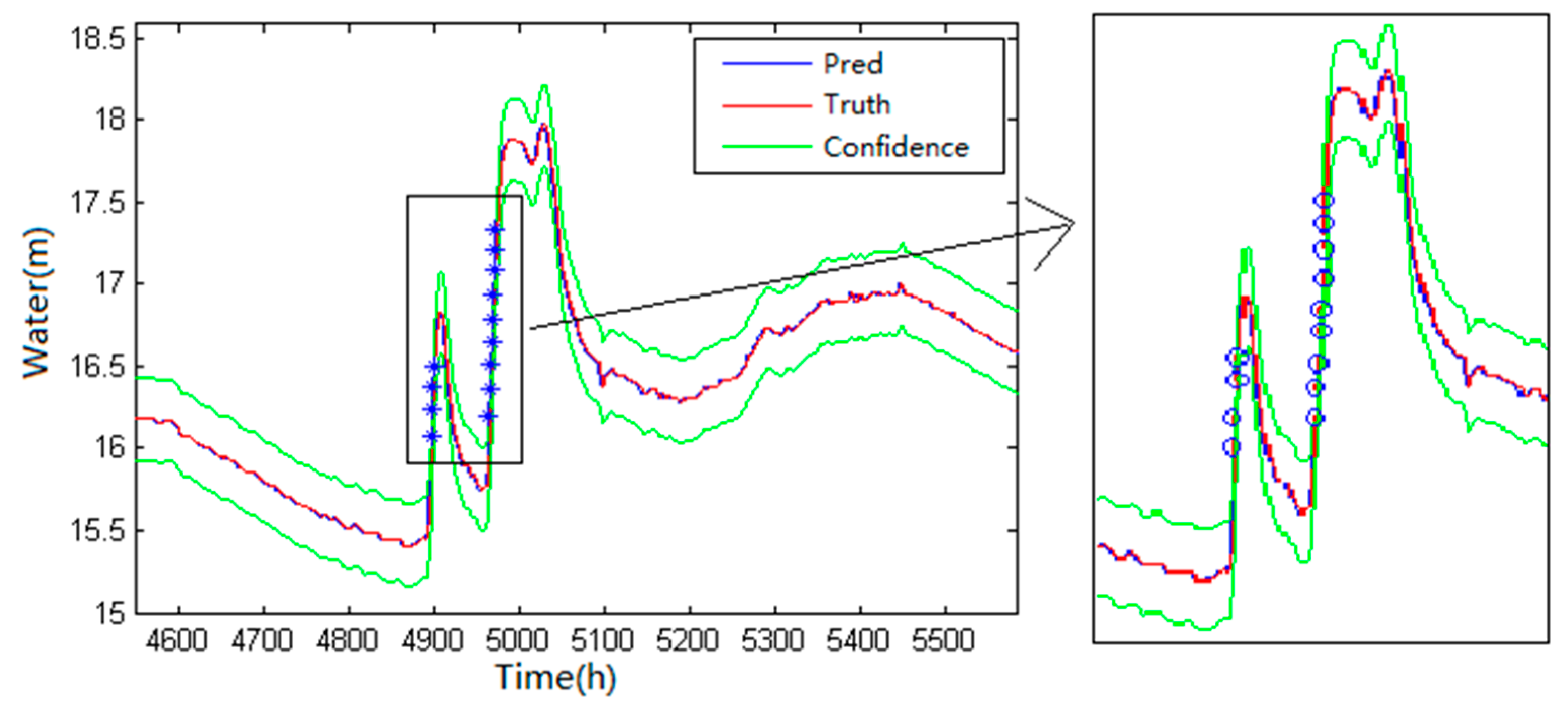
For the quality control of continuous hydrological time series, an integrated quality control scheme combining predictive control and statistical control is proposed in this paper. It includes the horizontal predictive control model, the longitudinal predictive control model, and the statistical control method based on wavelet analysis. The first two methods provide predictive reference lines and set predictive control intervals, according to predictive errors. The statistical method sets confidence intervals for real-time data, according to data consistency. If the data points are located in three control intervals, it is normal data. Otherwise, the number of control intervals violated will judge the suspicious data and the wrong data and a more credible alternative value will be provided for hydrologists instead of the suspicious and wrong data. The continuous hydrological data control method is shown in the following
Figure 2.
3.1. Horizontal Predictive Control Model
Continuous hydrological time series data (such as water level and flow) have continuity and periodicity in a certain period. For continuous hydrological data, the data at the same times in adjacent two days are changed in a certain range generally. It is feasible to predict the hydrological condition of the same time in the future by using the data of the same time in history.
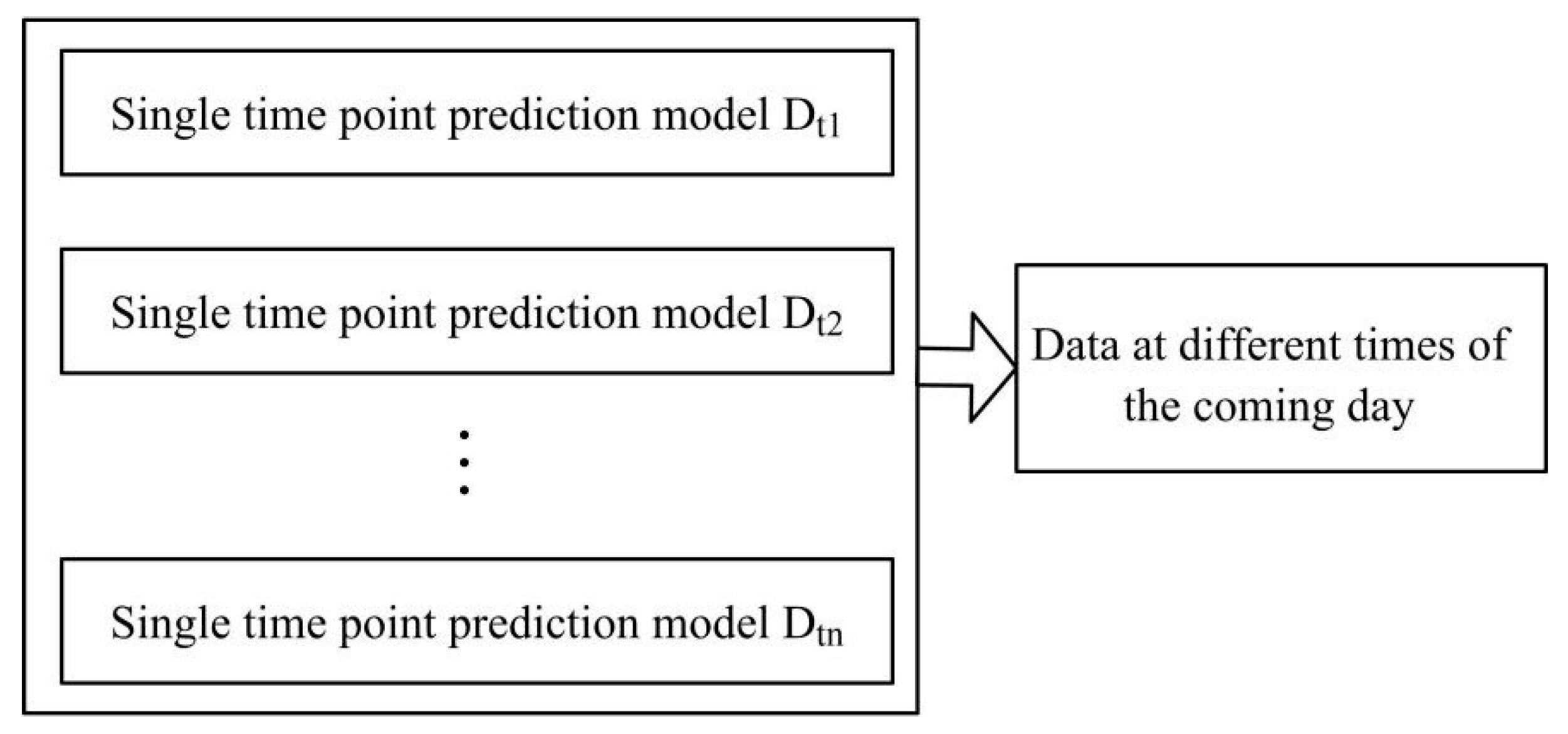
The hydrological real-time data is divided into hourly and minute levels, according to the reported time interval. The horizontal predictive control model is based on the real-time data per hour. It uses the real-time data at the same historical time to establish 24 unit control models for the next 24 h. That is, hydrologists can have a full understanding of the data changes in the coming day, according to the integrated control model (
Figure 3).
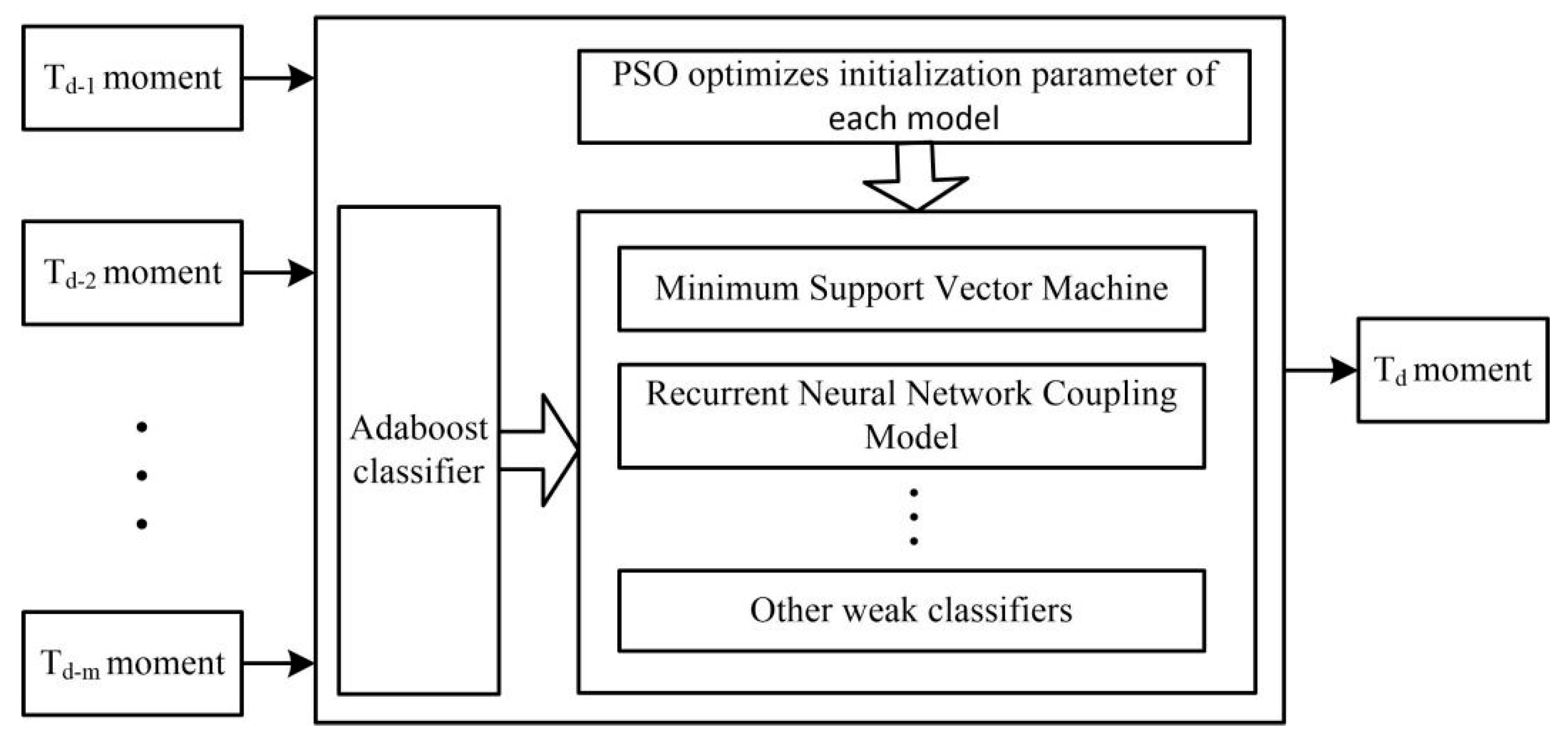
The horizontal predictive control model adopts the prediction model based on particle swarm optimization as the weak predictor and then combines several excellent weak predictors by the Adaboost algorithm to form a strong predictor. Compared with the single prediction model, the integrated predictive model has higher stability and robustness.
Particle swarm optimization (PSO) and the genetic algorithm (GA) belong to the global optimization evolutionary algorithm and both algorithms are widely used. The GA algorithm needs to adjust more parameters and is difficult to adjust. Compared with the PSO algorithm, which can solve complex nonlinear problems, the PSO algorithm needs to adjust fewer parameters and is easy to implement. Moreover, some studies [
24,
25,
26,
27] verify that the improved PSO is better than GA in optimizing the prediction model. Both recurrent neural networks (RNN) and support vector machines (SVM) are excellent predictive models and are all based on the selection of good initial parameters and high quality data. RNN is a popular learning method in the field of deep learning in recent years. Compared with the independent characteristics of the calculation results of ordinary neural networks, RNN can use its internal memory to process the input sequence of arbitrary time series, which has stronger dynamic behavior and computational ability. SVM transfers the inseparable problem in low-dimensional space to high-dimensional space to make the problem solvable. It is based on the Vapnik-Chervonenkis Dimension theory of statistical learning theory and the principle of structural risk minimization. Therefore, it can effectively avoid local minima and over-learning. If the two models are applied to the real-time control of hydrological data of automatic stations, the optimization algorithm is needed to optimize the initial parameters and select the appropriate model parameters. Using PSO to optimize the two models and select the global optimal parameters as the initial parameters of the prediction model can improve the prediction accuracy. Therefore, the real-time monitoring of the automatic station can be trained and applied without a manual selection of parameters.
The weak predictor in the Adaboost algorithm is an unstable predictive model (such as a neural network) or a variety of different predictive models. RNN is an unstable prediction model because the weights of each training network are different. Compared with the neural network, the generalization ability of SVM is stronger and the training results for the same data are stable. Selecting the single support vector machine and multiple recurrent neural networks as Adaboost weak predictors can complement the shortcomings between the algorithms and improve their generalization ability through the weighted combination of weak predictors. The SVM with larger generalization ability will be given larger weight.
An integrated predictive control model (as shown in
Figure 4) is constructed for the same time in the future by using the strong predictor combined with the Adaboost algorithm. The confidence interval is established between the predicted value of the predictor and the weighted value of the mean square error to detect the reliability of the real-time data.
The horizontal predictive control model algorithm process is described below.
Select data and normalize it to make data between (−1, 1).
The initial parameters of SVM and RNN are optimized by PSO. The optimal SVM weak prediction model and WNN weak prediction model are established.
Select m RNN and the best SVM. Then the m + 1 excellent models are selected as the weak predictor of Adaboost and establish the strong predictor of Adaboost.
Referring to the predicted value and mean square error of the prediction model, the confidence interval of quality control is established with the predicted value as the center. Then the interval is connected and the upper and lower confidence intervals are smoothed by a wavelet transformation (More algorithm details can be found in the
Supplementary Materials).
For the sample data, it is necessary to normalize the data so that the data is distributed between (−1, 1), which makes the sample data evenly distributed and reduces the possibility of early saturation of the weak predictor of RNN. The formula is as follows: , is the mean of all sample data and is the standard deviation of all sample data.
For the test sample data, we need to select the historical data of the same period to test and get the error standard of the strong predictor. The error of the strong predictor is related to the quality control range of real-time data. Because the hydrological data have annual periodicity, it is necessary to test the generalization ability of the strong predictor by using the hydrological data of the same historical period to make the control interval meaningful. In this way, the quality control interval of real-time data will change constantly, according to the time. For example, when the winter data changes slowly and the error is low, then the winter confidence interval will become smaller. The summer data fluctuations are larger and, therefore, its confidence interval will become larger. This dynamic adjustment of the confidence interval can improve the practicability of the control model.
The Adaboost algorithm is used to form a strong predictor to predict the real-time data simultaneously in the future and the predicted value
yc and the mean square error
mse are used to form a confidence interval
where
is a weighted value, and
[
27]. The confidence interval becomes
when
. The horizontal predictive control model is established to predict and control the data in the coming day. If the confidence interval is obtained,
,
. In the 24 models, there may be some abnormal predictive situations, which make some values of the confidence interval of predictive control abnormal. Common deionizing methods are easy to use to remove useful signals. Compared with common methods, wavelet analysis can use different soft and hard thresholds for the scale wave and every detail wave and maintain useful signals effectively. Therefore, the upper and lower bounds of the confidence interval are smoothed by wavelet analysis to make the adjacent control interval more consistent with the characteristics of the hour hydrological data.
3.2. Longitudinal Predictive Control Model
The hydrological real-time control station uploads m data every day with real-time characteristics. The offline training single predictive control model may cause the prediction error to increase because of the imperfect training, which makes the data predictive control deviation. However, the accuracy of the data needs real-time detection and control.
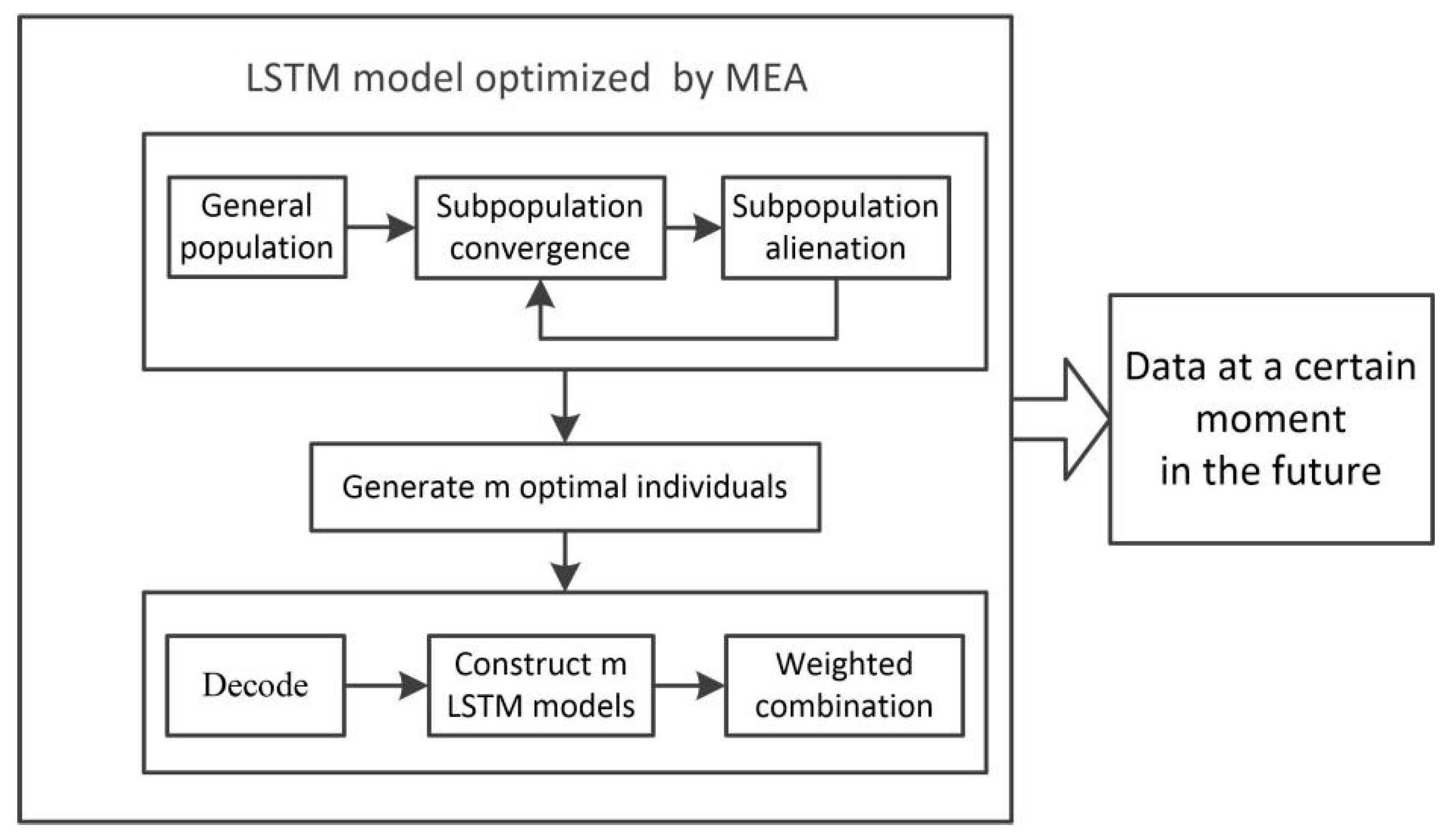
Based on the convergence and alienation of thought evolutionary algorithms and the idea of posting excellent individuals on the bulletin board, this paper improves the long-term and short-term memory network prediction model and proposes a longitudinal predictive control model. The model establishes a weighted combined control model to increase the robustness of the predictive control by selecting the first m excellent parameters on the bulletin board as the initial parameters of the network. It mainly trains the temporary model on the bulletin board after a period by using real-time historical data as the data set. If the best model in the temporary model is better than the worst model in the combined control model, it will be replaced in time. Lastly, it will be re-weighted to form the predictive control model, according to the predictive error (
Figure 5).
The longitudinal predictive control model uses the temporary model to replace the worst model. In the case of ensuring that the stability of the combined model is small, the old network is replaced by a new excellent network. This method can continuously adjust the timeliness of the control model. According to the idea of MEA, the longitudinal predictive control model is constructed. The specific algorithm process is as follows.
Training set / test set generation: Select data and normalize it to make data between (−1, 1). Then organize the data and predict the hydrological situation in the future by using the data of the previous N hours. Lastly, we randomly disrupt the sequence and select 80% of the data as the training set and the rest as the test set.
Population generation: The initial population is randomly generated and ranked according to the mean square error from small to large. The first m individuals were selected as the center of the superior subpopulation, the first m + 1 to m + k individuals were selected as the center of the temporary subpopulation, and then m new subpopulations were generated, which surround the m centers within limits.
Sub-population convergence operation: Convergence operation is to change the central point of the subpopulation by iteration and then randomly generate multiple points around the center to form a new subpopulation until the central point position does not change any more and the average error of the prediction model is minimized (that is, the highest score). Then the subpopulation reaches maturity. Lastly, the score of the center position is taken as the score of this sub-population.
Subpopulation alienation operation: The scores of the mature subpopulations are ranked from large to small and the superior subgroups are replaced by the temporary subgroups with high scores. The temporary subgroups are supplemented to ensure the quantity is unchanged.
Output the current iterative best individual and score: Find the highest scored individual from the winner subgroup as the best individual and score currently obtained and save it in the temporary array temp_best
Select excellent individuals: The loop iteratively performs the convergence and dissimilation operations of the sub-populations until the loop stop condition is satisfied, that is, the optimal individual position does not change or the number of loop iterations is reached. Sort the array temp_best from large to small and select the top m as excellent individuals.
Establish LSTM model: Decode m excellent individuals generated in 6, establish m LSTM models, assign the optimized initial weights and thresholds to different network models, and train the sample sets again to construct m LSTM models.
Establish longitudinal predictive control model: use the test set to simulate the m model and then weigh the combination of m models according to the test mean square error to establish the longitudinal predictive control model.
After the above eight steps, the longitudinal predictive control model is established. Then, at intervals, m excellent individuals are selected from temp_best and k individuals randomly generated are added to form the center of the initial population and m + k populations are generated. Then perform steps 3 to 6. Lastly, the newly generated optimal individual in step 6 is selected, the optimal initialization parameter is assigned to the new LSTM model, the network is trained, and the mean square error of the new test set is obtained. If the error of the new network is smaller than the network in the combined model, use it to replace the largest error in the combined model and rebuild the combined model. Otherwise, the original combined model is not changed.
According to the data at different times, a time series curve is drawn. The predicted value at each moment on the prediction curve plus the positive and negative error values of the 95% confidence interval demarcation point of the single model prediction error is used as the upper and lower bounds of the point data control. Lastly, the control boundary is smoothed by the wavelet transformation and the part between the two smooth curves is used as the confidence interval.
3.3. Statistical Data Quality Control Model
The traditional data quality control method mainly relies on statistical methods to consistently detect and mark abnormal data and erroneous data. The test results are for expert reference.
The hydrological time series statistical data quality control method draws on the Fourier transform-based control method of Sciuto et al. [
28] to establish a confidence interval by setting a fixed-size sliding window. In order to overcome the defects of the Fourier transformation, this paper uses the multi-scale refinement wavelet analysis of finite-width basis function to smooth the data of the sliding window and then the weighted mean and mean square error are obtained based on the method of giving high weights to adjacent values. The weighted mean and δ-fold mean square error are used to form a time series confidence interval to control the data quality in real time. The process flow is shown in
Figure 6.
The statistical data quality control method (SDQC) is to establish a statistical confidence interval by weighted combination of horizontal and vertical statistical control methods. The algorithm steps are as follows:
Parameter setting: Set the size of the horizontal and vertical sliding windows to n and m, respectively. The wavelet base of the wavelet analysis is the bior and the decomposition scale is k. The smoothing time span is d and the dynamic weight is and .
Time series smoothing: The wavelet analysis is used to decompose and reconstruct the hydrological data and the smoothing sequence is obtained to reduce the short-term fluctuation and noise of the hydrological data.
Confidence interval of hydrological time series: Taking hour real-time data as an example, the weighted mean value and the mean square error of sliding window length n at each time are obtained. Set as the confidence interval at the same time for the next day. The upper and lower bounds of confidence intervals are connected to form two upper and lower bound sequences and then the two sequences are smoothed by wavelet analysis to eliminate possible mutation points. If the interval change rate is large, the range of the error rate is limited to reduce the interval cell variation rate.
Confidence interval of longitudinal time series: The monitoring data of the first m times are smoothed by wavelet analysis and the weighted mean value and mean square error are obtained. In addition, set as the confidence interval of real-time data at the next time, which needs to be constantly adjusted.
Comprehensive confidence interval: The weighted control interval is obtained by using the confidence interval of the vertical time series and the horizontal time series at the same time.
3.4. Continuous Hydrological Data Quality Control Method
The continuous hydrological data quality control method combines the above two consistency check prediction control models and adds regular QC methods in meteorological fields such as the format check, lack of test, the extreme value check, and the time-varying check to carry out comprehensive quality control for hydrological data.
The continuous hydrological data quality control method consists of four parts: missing inspection, format inspection, extreme value inspection, and consistency inspection. The missing inspection is to detect data points that cannot be uploaded due to instrument failure. The format inspection is to check the date of the real time uploading system and whether the format of the station code conforms to the specification. Climate extreme value inspection is to detect the quality of real-time data uploaded from stations. Climate extreme value depends on the extreme value of regional historical data. If the real time data is greater than the extreme value, it is labeled as the wrong data. The consistency check is divided into two consistency checks: time and space. The temporal consistency includes the time-varying checking of the detection elements and the changing relationship between the multi-elements of the same station (such as the relationship between the water level and the discharge of the station). The spatial consistency is checking and controlling the consistency by using the correlation of the elements between the regional stations.
Continuous hydrological data quality control method establishes three confidence intervals with two predictive control methods and statistical data quality control methods on the premise of basic QC inspection. If the hydrological real-time data is in three confidence intervals, the data is considered to be correct. Otherwise, it is considered suspicious. According to the number of confidence intervals of data violation, the suspicious degree is formulated into three grades. In addition, there are six grades in all.
Level 1: Data is outside a confidence interval.
Level 2: Data is outside two confidence intervals.
Level 3: Data is outside all confidence intervals.
Level 4: Data is larger than the time varying rate.
Level 5: Data is outside the maximum and minimum value.
Level 6: The missing and malformed data.
As the number of intervals in which the detected data is violated increases, the suspiciousness of the data increases. All suspicious data, the erroneous data, and the missing data of the basic control detection are recorded in the system log and the recommended value of the real-time data modification and its credibility are given by the predictive control model, which can be referred by the water supply staff.
In the quality control process, if the data is missing, the horizontal predictive control model is used to give a suggested value and the input of the longitudinal predictive control model is replaced by the former recommended value. The statistical confidence interval is the horizontal time series confidence interval. This ensures that, in the event of an instrumental failure, it can still supply hydrological staff the three confidence intervals and recommended values of the real-time data for reference. If the lack of measurement time is long, the hydrological data of the adjacent station is required to help fill the measurement time.
4. Discrete Hydrological Data Control Model
The discrete hydrological data control model is aimed at hydrological data with large spatial and temporal differences such as rainfall. It uses spatial correlation of adjacent stations to establish network weight topology and dynamically adjusts network weight value according to real-time data correlation between stations in order to provide reference for hydrological workers to fill in the data. The data of automatic measurement stations with larger weights around the stations are selected for spatial interpolation. The advantages and disadvantages of the spatial interpolation method are analyzed by fitting error and the suitable method is found to detect and control the discrete data. The flow chart is shown below (
Figure 7).
4.1. Hydrological Spatial Topological Structure
Among the hydrological data elements, the rainfall is not easy to control and test the data due to the large spatial anisotropy and poor time continuity. The method of controlling and checking the data of the rain gauge station through single station consistency does not work and spatial consistency data quality control between multiple stations is required. It makes use of the spatial distribution characteristics of hydrological elements and the distance, altitude, and topography between the regional hydrological automatic stations as well as the correlation degree between the elements and space affect the control effect.
In order to let hydrologists understand the relationship between an automatic station and other stations around it, this paper establishes a weight map of the station relationship based on the location and rainfall data of the automatic station so that hydrologists can understand the relationship between the stations in the whole basin or region. The construction of a regional topology network requires the following steps.
Screening stations: Taking the measured stations as the center, the peripheral stations with radius distance S as the candidate set n are selected and marked, and then the station m with sufficient hydrological data are selected from the candidate stations.
Constructing time series: Extracting the station data set in the specified time from the compiled historical hydrological database and counting the monthly factor values and constructing the m monthly time series.
Correlation analysis: Analyze the correlation coefficient between the station under test and the m surrounding stations and obtain the correlation coefficient set between m + 1 stations where . The correlation coefficient set of the station under test is sorted from large to small and the stations with large correlations are selected (the general coefficient is above 0.6).
Preserving the correlation coefficient: The station code and the coefficient, which have the bigger correlation coefficient with the station under test, are saved in the station relation table st-relation. In addition, for the other m stations, the stations with correlation coefficients greater than 0.6 are selected and stored in the table st-relation.
Constructing regional networks: Looping steps 1 to 4 and constructing relational networks. The difference is that only unmarked peripheral stations are selected in step 1, which can greatly reduce the construction time of the regional station network.
First, in the construction of the station network, choosing the historical hydrological data as the data set of the model can reduce the influence of a large number of abnormal or erroneous data and make the network model coincide with the actual relationship. Second, for the hydrological elements with poor continuity such as precipitation, the time series composed of monthly precipitation with a large grain size is selected to calculate and construct the relationship network between stations. Because the time series consisting of daily, hourly, or minute precipitation has a small particle size, the missing or abnormal data have a great influence on the time series. For example, the correlation coefficients of monthly grain size of Shangli rainfall station with Chishan and Pingxiang rainfall stations on Xiangjiang River in Jiangxi Province are 0.85 and 0.77, respectively, while those of daily grain sizes are 0.78 and 0.73, respectively, and those of hourly grain sizes are 0.72 and 0.68, respectively. Lastly, the markup method is used to avoid repeated modeling and reduce the time of establishing the whole network.
Taking the radius S of the measured stations as a reference, the closeness of the stations is defined by the correlation coefficient between the data of the hydrological stations and the correlation network of the regional hydrological stations under the specified factors is constructed. Hydrologists can refer to the similarity coefficients between the measured stations and the surrounding stations and rely on the hydrological conditions of the surrounding stations to fill in missing or suspicious data in order to provide a basis for filling and replacing the hydrological data.
4.2. Dynamic Adjustment of the Topological Structure
For the correlation between hydrological stations considered as a whole above, the correlation of data between regional stations varies when applied to a particular season or month (as shown in
Table 1).
It can be seen from the table that the overall correlation coefficients of Shangli with Chishan, Pingxiang, and Zongli rainfall stations on the Xiangjiang River in Jiangxi Province are 0.85, 0.77, and 0.56, respectively, while the correlation coefficients of spring, summer, autumn, and winter have some changes with the overall coefficient. For example, the correlation coefficient between Laoguan and Shangli in the spring is small while the other three seasons are relatively large. The correlation coefficient between Zongli and Shangli in the autumn and the winter is small and the correlation coefficient between the four stations and Shangli in the summertime is relatively low. Then, if only the overall correlation coefficient is used as a reference, it will result in an inability to accurately reflect the true correlation in different periods.
The correlation coefficients of the factors between stations will change with time and the correlation coefficients are directly related to the reliability of the data. Therefore, reducing errors and suspicious data can increase the confidence of the correlation coefficients. The variation of hydrological station elements is seasonal and periodic and the dynamic adjustment of the topological structure of the elements will provide a better basis for the hydrological workers to fill in the missing data and replace the suspicious data.
4.3. Spatial Interpolation Model
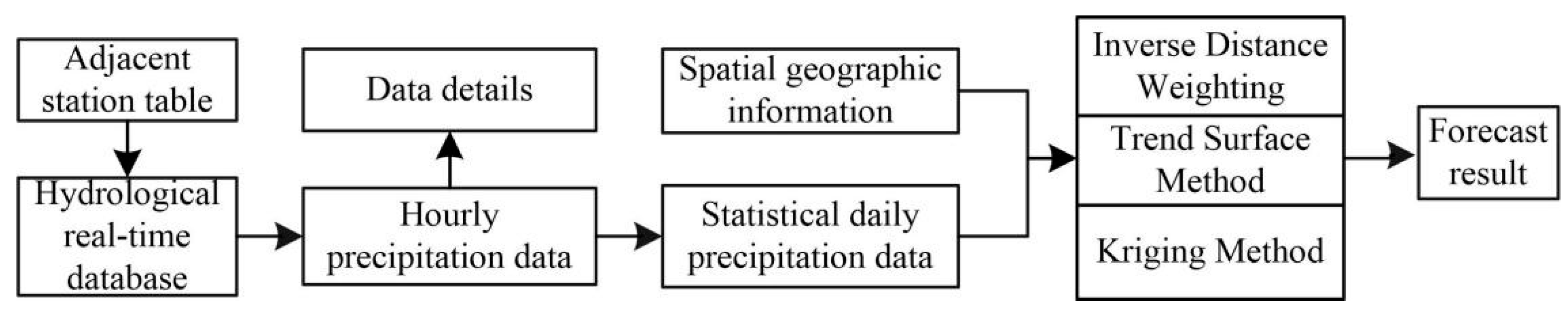
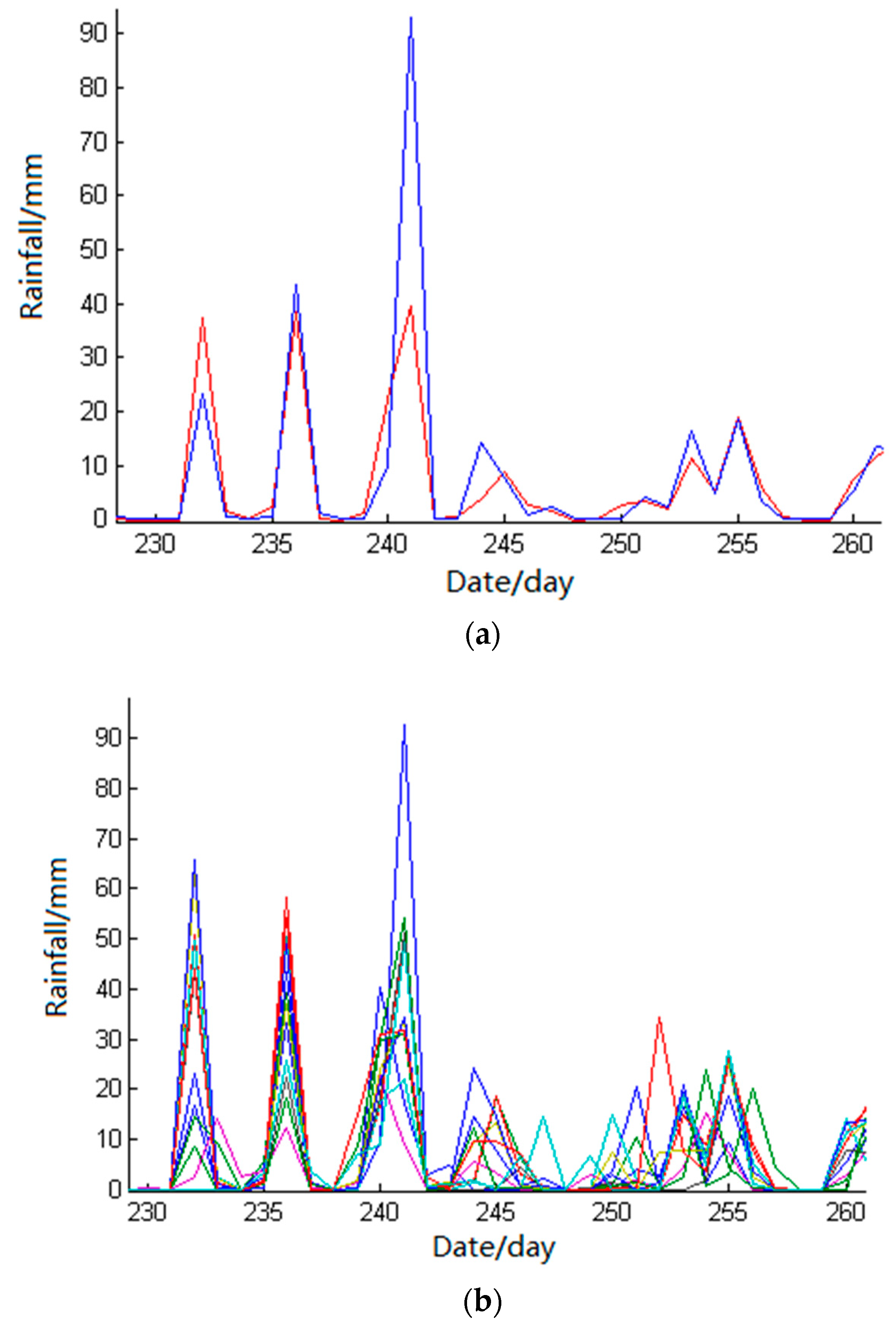
Influenced by the range and density of precipitation, the precipitation will form different rainfall grading lines in space. The spatial difference makes the area and direction of each precipitation process different, which will make the real-time rainfall difficult to control. Therefore, the basic QC detection method (time-varying rate test) is used to detect and control the hourly or minute rainfall while the spatial interpolation method is used to check the statistical daily rainfall data and the coarse-grained control of the quality of rainfall data is reliable.
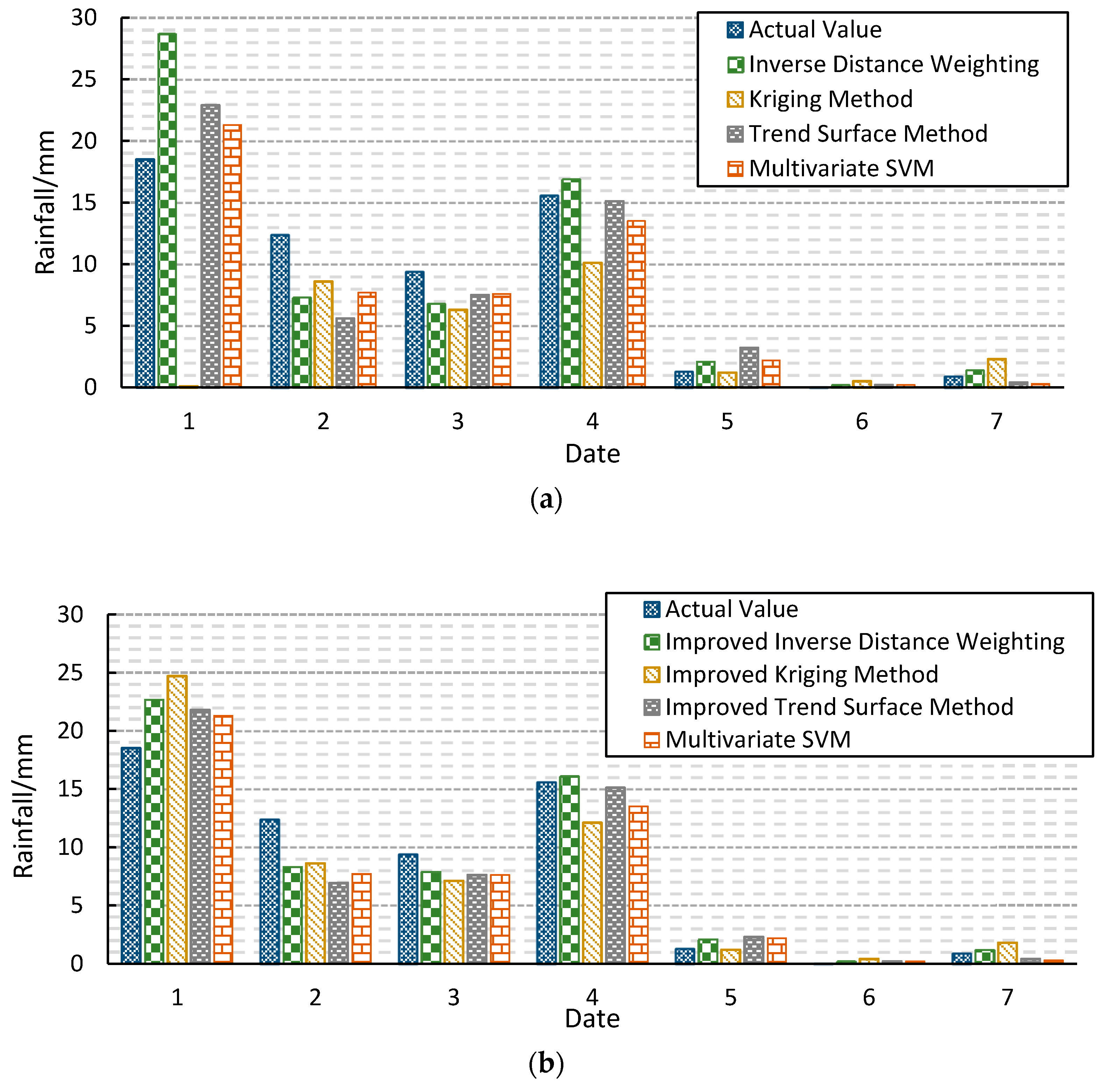
Based on the correlation coefficients of the stations under test, a variety of spatial interpolation methods (such as Inverse Distance Weight, the Trend Surface Method, and the Kriging Method) can be constructed quickly. The multivariate SVM model and the commonly used spatial interpolation methods are constructed to compare. The input terms of various spatial interpolation methods and multivariate SVM models are the regional station data with the same elements at the same time as the station being measured and the outputs are the values of the measured stations at the same time.
The specific process is shown in
Figure 8.
The construction of the spatial quality control model is divided into the following steps:
Referring to the table information of adjacent stations, the hourly real-time rainfall data of selected adjacent stations are extracted from the hydrological real-time database.
View the data details and count the daily precipitation data without missing stations on the day.
Using spatial geographic information (such as longitude and latitude or elevation) and daily precipitation data to construct three spatial interpolation methods, these three spatial interpolation methods have nothing to do with historical data. The model parameters are changed with the changes of regional data.
Establish a three-dimensional space model and obtain predicted results based on the geographic information of the stations.
In order to improve the prediction accuracy of the spatial interpolation method, the spatial interpolation method is constructed by using the stations with large correlation coefficients in the same period (quarterly).
The final form of constructing the model by spatial interpolation is to assign a weight value to the stations around the region, which belongs to linear interpolation. In view of the uncertainty of rainfall data, the method of establishing the spatial prediction model only by using rainfall data of peripheral stations with coordinates is a little inadequate. Therefore, the suspicious data detected by the spatial interpolation method needs to be further checked and confirmed by manual intervention.
4.4. Discrete Hydrological Data Quality Control Method
The discrete hydrological data quality control method is mainly for the quality detection and manual replacement of hydrological elements (such as rainfall) with large spatial, temporal differences and strong spatial correlation. The steps are shown below.
Calculate the correlation between the station under test and the surrounding stations based on the spatial geography and data association of hydrological elements and construct a spatial topology.
The correlation will change with the change of seasons. It is necessary to dynamically adjust the topology to fill the reference data and suspicious data for hydrological workers.
Construct a spatial interpolation model, use a variety of spatial interpolation methods to detect spatial consistency, compare various linear spatial interpolation methods with nonlinear multivariate SVM methods, and analyze their advantages and disadvantages.
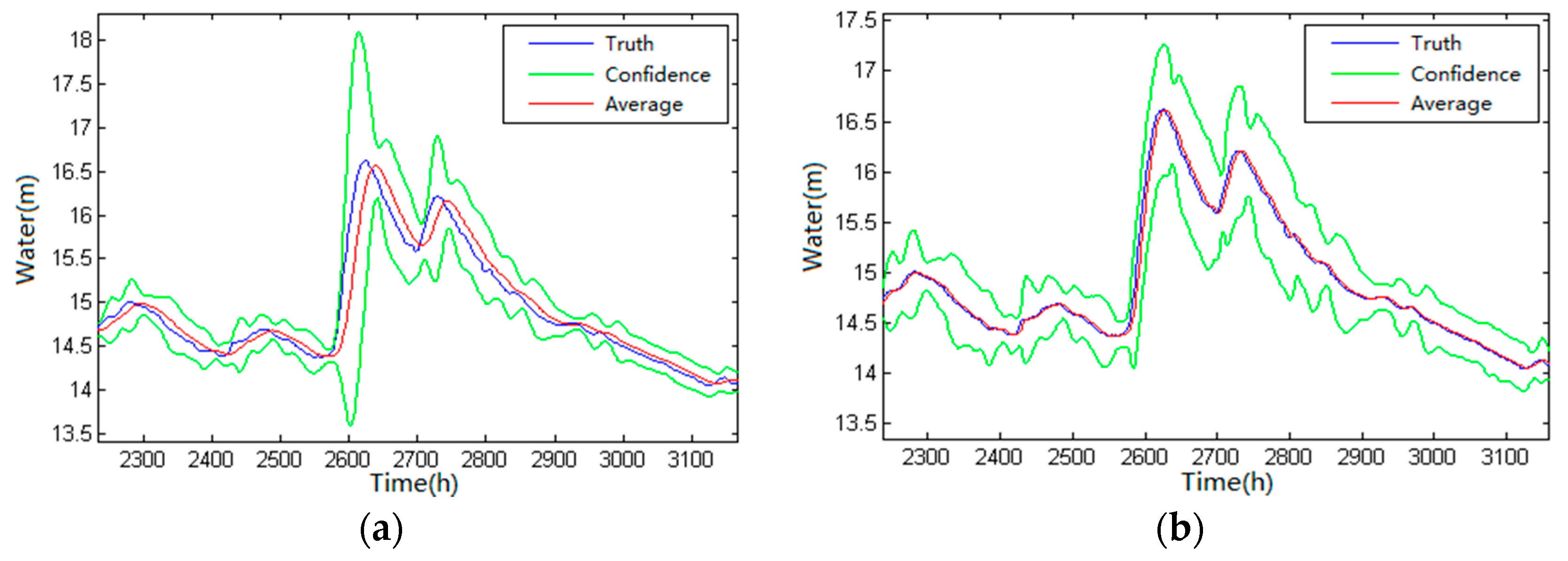
Based on the predicted value of best-improved inverse distance spatial interpolation method, the confidence interval is given to check and control the daily precipitation data.
6. Conclusions
According to the characteristics of hydrological data and combined with the idea of predictive control, this paper studies the methods of data quality control and data consistency and puts forward the hydrological data quality control method based on data-driven methods.
For continuous hydrological data, the method is established from the perspective of time consistency. Two combined predictive control models, one statistical control model and the corresponding control interval are constructed to detect and control the hydrological factors such as water level and discharge with good continuity from the horizontal, vertical, and statistical perspectives and the suspicion degree is set by the number of data violating the control interval. For the suspicious data and the short-term missing data, the model provides the recommended value and confidence interval.
For discrete hydrological data, the method is established from the point of view of spatial consistency. Aimed at the disadvantage that rainfall data is difficult to control, this paper constructs the topological relation diagram of correlation coefficients centered on the measured stations, studies and analyzes the advantages and disadvantages of various spatial interpolation methods, points out that the prediction effect of ordinary spatial interpolation method is poor, and finds that the spatial interpolation method based on the station data with large correlation coefficients can improve the prediction effect.
Experiments show that the proposed method can detect and control the hydrological data more effectively and provide a highly reliable substitution value for the hydrological workstation as a reference. Yet, there are still many shortcomings in this paper. For example, the network topology established in the discrete hydrological data quality control model can consider more hydrological factors (such as slope, slope direction, and the location of the station away from the water). For hydrological elements with large spatial variability (such as precipitation), more factors (such as regional seasonal periods) can be considered as auxiliary factors to construct the spatial interpolation model.