Automated Floodway Determination Using Particle Swarm Optimization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Mathematical Representation of the Problem
2.3. Isolated-Speciation-Based Particle Swarm Optimization
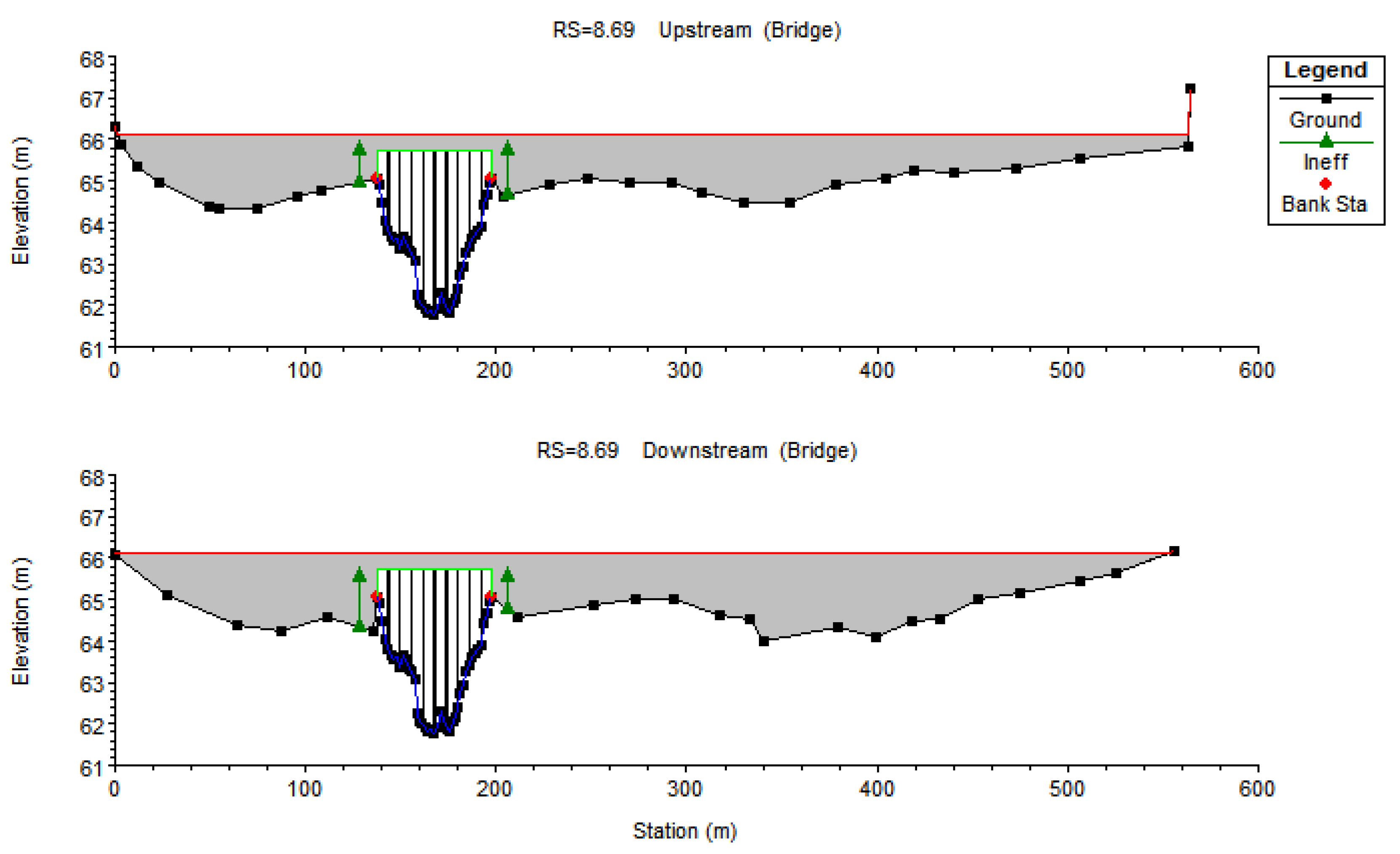
2.4. Automated Floodway Optimizer for HEC-RAS
| Algorithm 1 Pseudocode for automated floodway optimization for HEC-RAS. | |
| Require: itermax | ▹ Maximum number of iterations |
| Require:M(·) | ▹ HEC-RAS model with 100-year and floodway plans and profiles |
| Require: BC ∈ {None, DS, US, Both} | ▹ Boundary conditions for the encroachment limits |
| Extract cross section information from M(·) | |
| Number of cross sections | |
| Number of boundary conditions | |
| ▹ Problem dimension | |
| ▹ Swarm size | |
| Afw,min, Afw,max ← Minimum and maximum possible areas of the floodway | |
| X number of D-tuples randomly sampled from | ▹ Initial population |
| Let that maps particles to encroachment limits | |
| iter | |
| repeat | ▹ ISPSO loop |
| for do | |
| Xi ← Row i from X | ▹ trial encroachment limits or particle i in ISPSO |
| Simulate M(g(Xi)) using CLIRAS | ▹ Execute the HEC-RAS program |
| Evaluate f (M(g(Xi))) | ▹Equation (1) |
| if or f (M(g(Xi))) < f (M(g(Xbest))) then | ▹ If Xi is better than Xbest |
| Xbest ← Xi | ▹ Store the best encroachment limits from the current iteration |
| end if | |
| end for | |
| if iter = 1 or f (M(g(Xbest))) < f (M(g(xbest))) then | ▹ If Xbest is better than xbest |
| xbest ← Xbest | ▹ Store the best encroachment limits so far |
| end if | |
| Evolve X using ISPSO | ▹ Evolution of the swarm in ISPSO |
| iter ← iter + 1 | |
| until iter = itermax or other conditions are satisfied | |
| Optimized encroachment limits (xbest) | ▹ Found the best encroachment limits |
2.5. Numerical Experiments
3. Results and Discussion
3.1. Comparison of Different Approaches
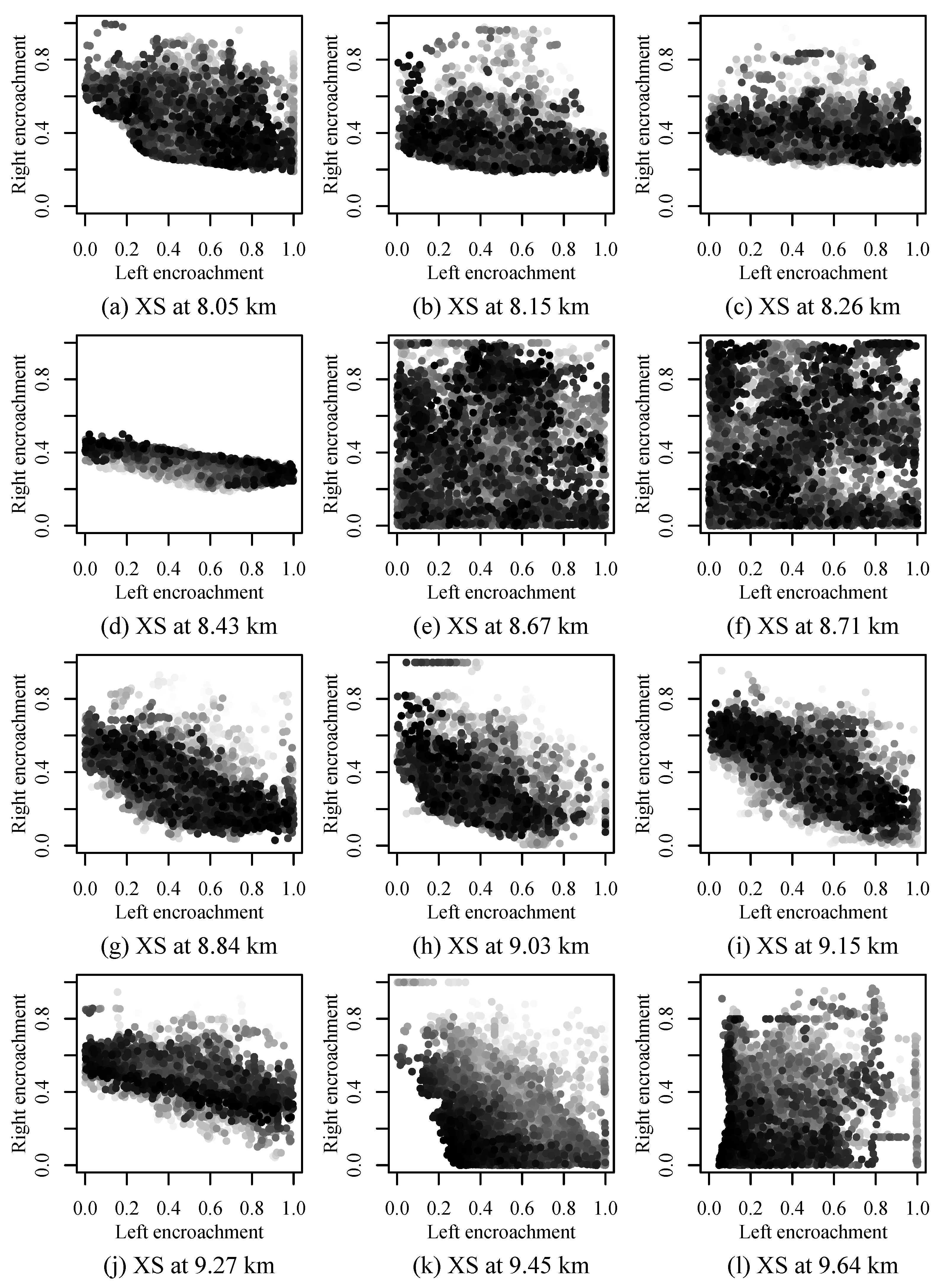
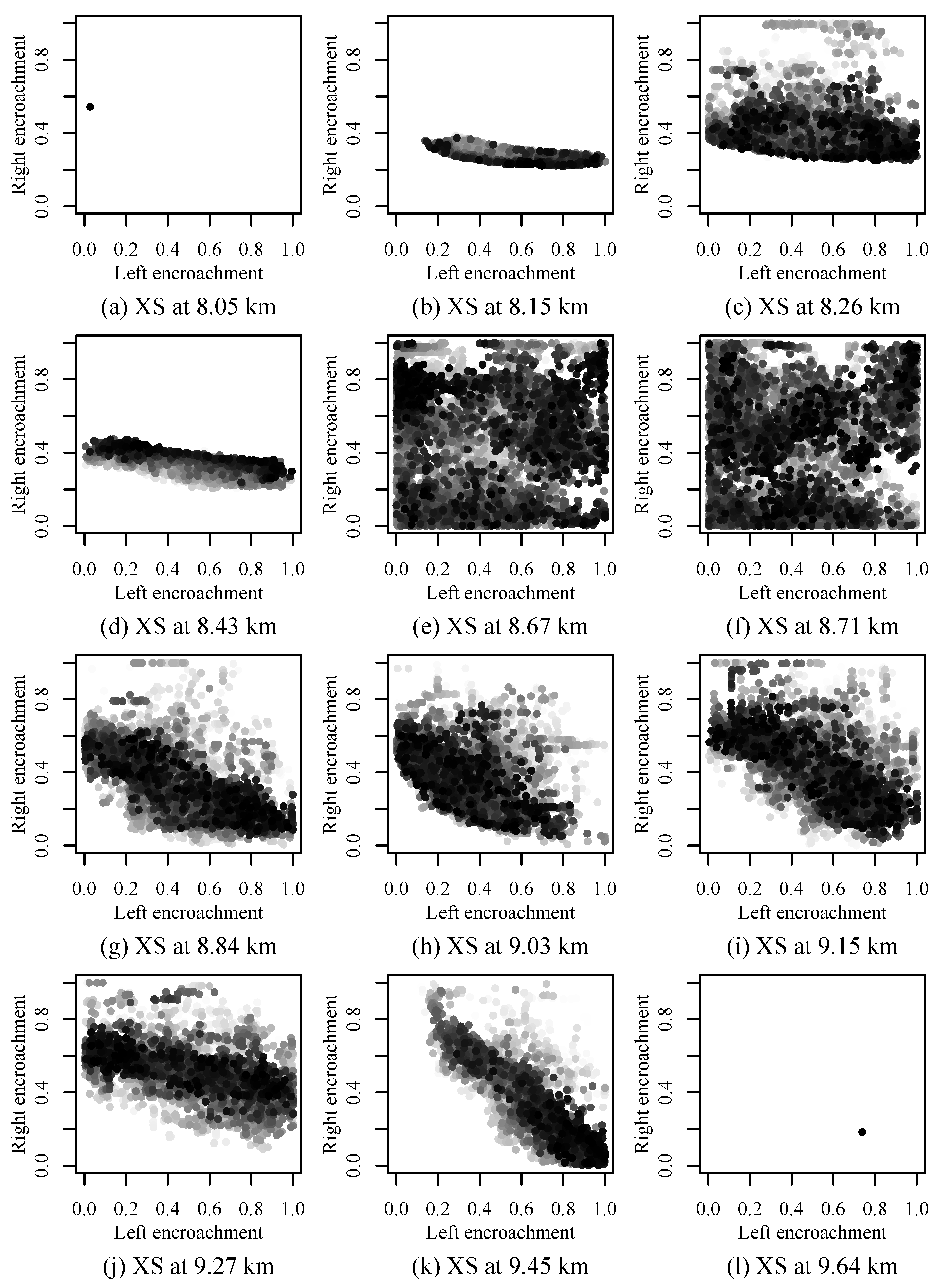
3.2. Sensitivity of Encroachment Limits to the Boundary Condition
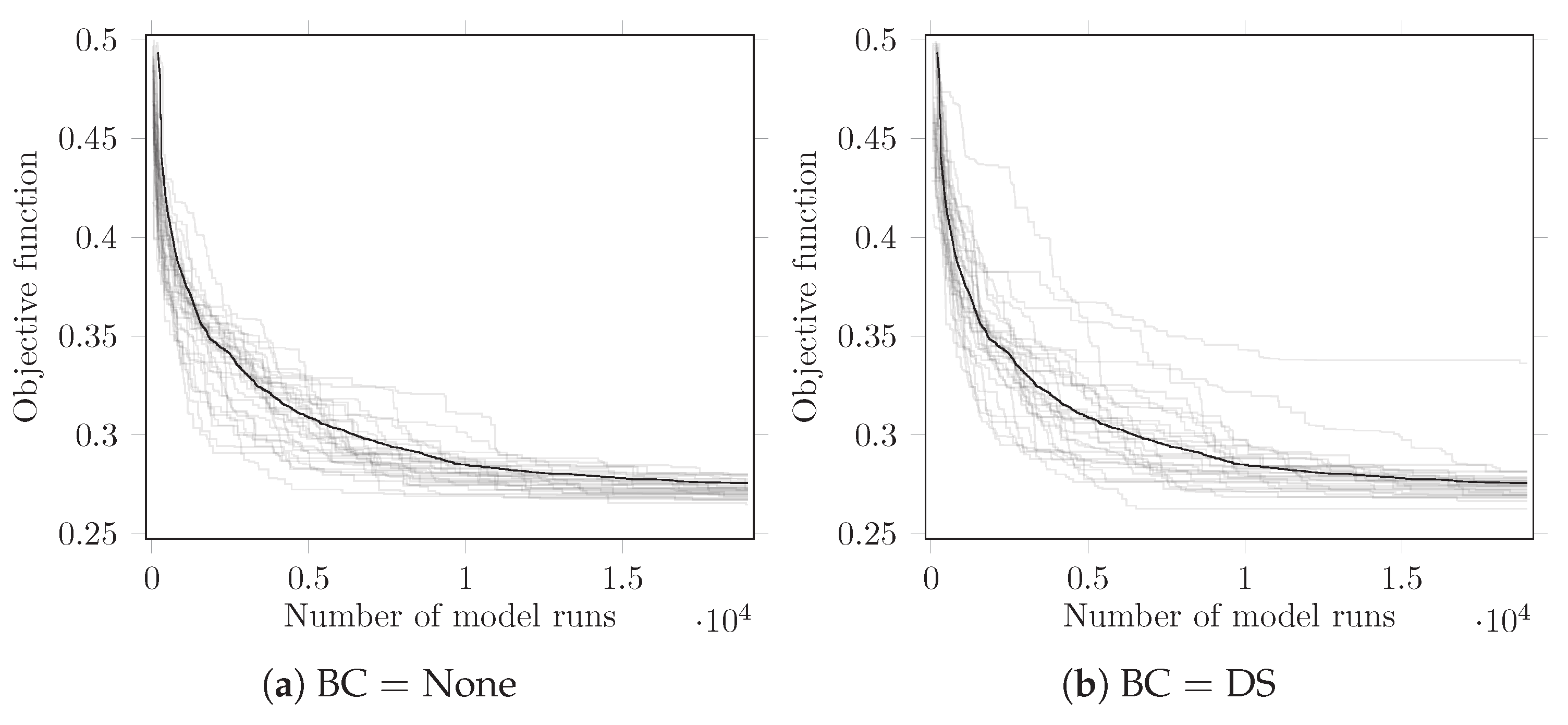
3.3. Optimization Performance
3.4. AFORAS as a Tool for Floodway Optimization
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- FEMA. Guidance for Flood Risk Analysis and Mapping: General Hydrologic Considerations. 2018. Available online: https://www.fema.gov/media-library-data/1525201756728-390e667d3d0958347b8374f6321bd488/General_Hydrologic_Guidance_Feb_2018.pdf (accessed on 18 April 2018).
- FEMA. Guidance for Flood Risk Analysis and Mapping: Hydraulics—One-Dimensional Analysis. 2016. Available online: https://www.fema.gov/media-library-data/1484864685338-42d21ccf2d87c2aac95ea1d7ab6798eb/Hydraulics_OneDimensionalAnalyses_Nov_2016.pdf (accessed on 28 December 2016).
- Brunner, G.W. HEC-RAS River Analysis System User’s Manual Version 4.1; US Army Corps of Engineers, Institute for Water Resources, Hydrologic Engineering Center: Davis, CA, USA, 2010. [Google Scholar]
- Rastislav, F.; Martina, Z. The HEC-RAS model of regulated stream for purposes of flood risk reduction. Sel. Sci. Pap. J. Civ. Eng. 2016, 11, 59–70. [Google Scholar] [CrossRef]
- ShahiriParsa, A.; Noori, M.; Heydari, M.; Rashidi, M. Floodplain zoning simulation by using HEC-RAS and CCHE2D models in the Sungai Maka River. Air Soil Water Res. 2016, 2016, 55–62. [Google Scholar] [CrossRef]
- Golshan, M.; Jahanshahi, A.; Afzali, A. Flood hazard zoning using HEC-RAS in GIS environment and impact of Manning roughness coefficient changes on flood zones in semi-arid climate. Desert 2016, 21, 25–34. [Google Scholar]
- Balogun, O.S.; Ganiyu, H.O. Development of inundation map for hypothetical Asa dam break using HEC-RAS and ArcGIS. Arid Zone J. Eng. Technol. Environ. 2017, 13, 831–839. [Google Scholar]
- Ben Khalfallah, C.; Saidi, S. Spatiotemporal floodplain mapping and prediction using HEC-RAS-GIS tools: Case of the Mejerda River, Tunisia. J. Afr. Earth Sci. 2018, 142, 44–51. [Google Scholar] [CrossRef]
- Goodell, C. Breaking the HEC-RAS Code: A User’s Guide to Automating HEC-RAS; h2ls: Portland, OR, USA, 2014. [Google Scholar]
- FEMA. Flood Insurance Study Guidelines and Specifications for Study Contractors. 2002. Available online: http://www.fema.gov/media-library-data/20130726-1546-20490-8681/frm_scg.doc (accessed on 24 December 2015).
- Franz, D.D.; Melching, C.S. Full Equations Utilities (FEQUTL) Model for the Approximation of Hydraulic Characteristics of Open Channels and Control Structures During Unsteady Flow; Technical Report Water-Resources Investigations Report 97–4037; U.S. Department of the Interior, U.S. Geological Survey: Reston, Virginia, USA, 1997.
- Howells, L.; McLuckie, D.; Collings, G.; Lawson, N. Defining the floodway—Can one size fit all? In Proceedings of the 44th Annual Floodplain Management Australia Conference, Coffs Harbour, Australia, 12–14 May 2004. [Google Scholar]
- Thomas, C.R.; Honour, W.; Golasweski, R. Procedures for floodway definition: Is there a uniform approach? In Proceedings of the 50th Annual Floodplain Management Australia Conference, Gosford, Australia, 23–26 February 2010. [Google Scholar]
- Selvanathan, S.; Dymond, R.L. FloodwayGIS: An ArcGIS visualization environment to remodel a floodway. Trans. GIS 2010, 14, 671–688. [Google Scholar] [CrossRef]
- Esri. ArcGIS Desktop: Release 10; Esri: Redlands, CA, USA, 2011. [Google Scholar]
- Rigby, T. Floodplain development manual (NSW) A document in need of review. In Proceedings of the 47th Annual Floodplain Management Australia Conference, Gunnedah, Australia, 27 February–1 March 2007. [Google Scholar]
- Thomas, C.R.; Golaszewski, R. Refinement of procedures for determining floodway extent. In Proceedings of the 52nd Annual Floodplain Management Australia Conference, Batemans Bay, Australia, 21–24 February 2012. [Google Scholar]
- Szemis, J.M.; Maier, H.R.; Dandy, G.C. A framework for using ant colony optimization to schedule environmental flow management alternatives for rivers, wetlands, and floodplains. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Bogárdi, I.; Balogh, E. Flood system operation along levee-protected rivers. J. Water Resour. Plan. Manag. 2013, 140, 04014014. [Google Scholar] [CrossRef]
- Luke, A.; Kaplan, B.; Neal, J.; Lant, J.; Sanders, B.; Bates, P.; Alsdorf, D. Hydraulic modeling of the 2011 New Madrid Floodway activation: A case study on floodway activation controls. Nat. Hazards 2015, 77, 1863–1887. [Google Scholar] [CrossRef]
- Lund, J.R. Floodplain planning with risk-based optimization. J. Water Resour. Plan. Manag. 2002, 128, 202–207. [Google Scholar] [CrossRef]
- Shafiei, M.; Bozorg-Haddad, O.; Afshar, A. GA in optimizing Ajichai flood levee’s encroachment. In Proceedings of the 6th World Scientific and Engineering Academy and Society International Conference on Evolutionary Computing, World Scientific and Engineering Academy and Society, Lisbon, Portugal, 16–18 June 2005. [Google Scholar]
- Mori, K.; Perrings, C. Optimal management of the flood risks of floodplain development. Sci. Total Environ. 2012, 431, 109–121. [Google Scholar] [CrossRef] [PubMed]
- Yazdi, J.; Neyshabouri, S.S. A simulation-based optimization model for flood management on a watershed scale. Water Resour. Manag. 2012, 26, 4569–4586. [Google Scholar] [CrossRef]
- Lu, H.W.; He, L.; Du, P.; Zhang, Y.M. An inexact sequential response planning approach for optimizing combinations of multiple floodplain management policies. Pol. J. Environ. Stud. 2014, 23, 1245–1253. [Google Scholar]
- Porse, E. Risk-based zoning for urban floodplains. Water Sci. Technol. 2014, 70, 1755–1763. [Google Scholar] [CrossRef] [PubMed]
- Woodward, M.; Gouldby, B.; Kapelan, Z.; Hames, D. Multiobjective optimization for improved management of flood risk. JW Resour. Plan. Manag. 2014, 140, 201–215. [Google Scholar] [CrossRef]
- Woodward, M.; Kapelan, Z.; Gouldby, B. Adaptive flood risk management under climate change uncertainty using real ooption and optimization. Risk Anal. 2014, 34, 75–92. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopez-Llompart, P.; Kondolf, G.M. Encroachments in floodways of the Mississippi River and Tributaries Project. Nat. Hazards 2016, 81, 513–542. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Lopez-Llompart, P. National-local land-use conflicts in floodways of the Mississippi River system. AIMS Environ. Sci. 2018, 5, 47–63. [Google Scholar] [CrossRef]
- Czigáni, S.; Pirkhoffer, E.; Halmai, A.; Lóczy, D. Application of MIKE 21 in a multi-purpose floodway zoning along the lower Hungarian Drava section. Revista de Geomorfologie 2016, 18, 5–18. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. The ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- DHI. MIKE 21 FlowModel FM. Parallelisation Using GPU. Benchmarking Report. 2014. Available online: http://www.mikebydhi.com/~/media/Microsite_MIKEbyDHI/Publications/PDF/GPU_Benchmarking.ashx (accessed on 28 September 2018).
- Yu, L. Using Genetic Algorithms to Calculate Floodway Stations with HEC-RAS. Master’s Thesis, University of Dayton, Dayton, OH, USA, 2015. [Google Scholar]
- Froehlich, D.C. A fair way to a floodway: Optimal delineation of floodplain encroachment limits. In Proceedings of the 1999 Water Resources Engineering Conference, Seattle, WA, USA, 8–12 August 1999. [Google Scholar]
- Cho, H.; Kim, D.; Olivera, F.; Guikema, S.D. Enhanced speciation in particle swarm optimization for multi-modal problems. Eur. J. Oper. Res. 2011, 213, 15–23. [Google Scholar] [CrossRef]
- Chanson, H. Development of the Bélanger equation and backwater equation by Jean-Baptiste Bélanger (1828). J. Hydraul. Eng. 2009, 135, 159–163. [Google Scholar] [CrossRef]
- FEMA. Guidance for Flood Risk Analysis and Mapping: Floodway Analysis and Mapping. 2016. Available online: https://www.fema.gov/media-library-data/1484864412580-de4aa11166f23a8f06e6121925a5b543/Floodway_Analysis_and_Mapping_Nov_2016.pdf (accessed on 28 December 2016).
- Kim, D.; Olivera, F.; Cho, H. Effect of the inter-annual variability of rainfall statistics on stochastically generated rainfall time series: Part 1: Impact on peak and extreme rainfall values. Stoch. Environ. Res. Risk Assess. 2013, 27, 1601–1610. [Google Scholar] [CrossRef]
- Kim, D.; Olivera, F.; Cho, H.; Lee, S.O. Effect of the inter-annual variability of rainfall statistics on stochastically generated rainfall time series: Part 2: Impact on watershed response variables. Stoch. Environ. Res. Risk Assess. 2013, 27, 1611–1619. [Google Scholar] [CrossRef]
- Kim, D.; Olivera, F.; Cho, H.; Socolofsky, S. Regionalization of the modified Bartlett-Lewis rectangular pulse stochastic rainfall model. Terr. Atmos. Ocean. Sci. 2013, 24. [Google Scholar] [CrossRef]
- Kim, D.; Cho, H.; Onof, C.; Choi, M. Let-It-Rain: A web application for stochastic point rainfall generation at ungaged basins and its applicability in runoff and flood modeling. Stoch. Environ. Res. Risk Assess. 2016, 31, 1023–1043. [Google Scholar] [CrossRef]
- Cho, H.; Kim, D.; Lee, K.; Lee, J.; Lee, D. Development and application of a storm identification algorithm that conceptualizes storms by elliptical shape. J. Korean Soc. Hazard Mitig. 2013, 13, 325–335. [Google Scholar] [CrossRef]
- Cho, H.; Olivera, F. Application of multimodal optimization for uncertainty estimation of computationally expensive hydrologic models. J. Water Resour. Plan. Manag. 2014, 140, 313–321. [Google Scholar] [CrossRef]
- Cho, H.; Kim, D.; Lee, K. Efficient uncertainty analysis of TOPMODEL using particle swarm optimization. J. Korean Water Resour. Assoc. 2014, 47, 285–295. [Google Scholar] [CrossRef]
- Heo, J.; Yu, J.; Giardino, J.R.; Cho, H. Impacts of climate and land-cover changes on water resources in a humid subtropical watershed: A case study from East Texas, USA. Water Environ. J. 2015, 29, 51–60. [Google Scholar] [CrossRef]
- Heo, J.; Yu, J.; Giardino, J.R.; Cho, H. Water resources response to climate and land-cover changes in a semi-arid watershed, New Mexico, USA. Terr. Atmos. Ocean. Sci. 2015, 26. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2006; ISBN 3-900051-07-0. Available online: http://www.r-project.org (accessed on 9 November 2015).
- Clerc, M. Standard Particle Swarm Optimization. 2012. Available online: http://clerc.maurice.free.fr/pso/SPSO_descriptions.pdf (accessed on 24 December 2013).

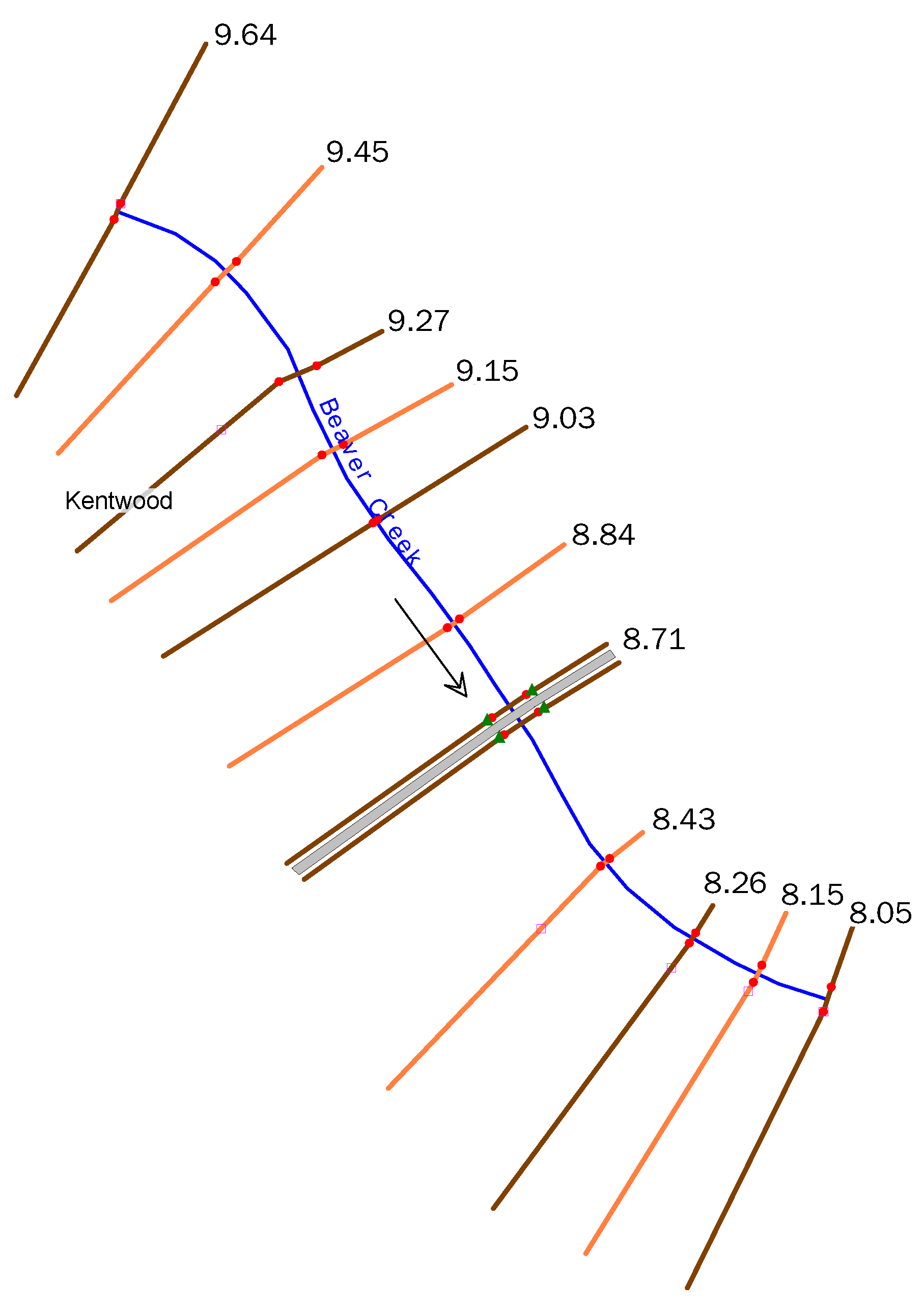

 Straightened river,
Straightened river,  Automated Floodway Optimizer for HEC-RAS (AFORAS) floodway,
Automated Floodway Optimizer for HEC-RAS (AFORAS) floodway,  Manual floodway, and
Manual floodway, and  Hydrologic Engineering Center’s River Analysis System (HEC-RAS) floodway.
Hydrologic Engineering Center’s River Analysis System (HEC-RAS) floodway.
 Straightened river,
Straightened river,  Automated Floodway Optimizer for HEC-RAS (AFORAS) floodway,
Automated Floodway Optimizer for HEC-RAS (AFORAS) floodway,  Manual floodway, and
Manual floodway, and  Hydrologic Engineering Center’s River Analysis System (HEC-RAS) floodway.
Hydrologic Engineering Center’s River Analysis System (HEC-RAS) floodway.

| Trial | (m) | (m) | Violations | Equation (1) | Equation (2) | |||
|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 0.366 | 0.397 | 1.1 | 1.2 | 4 | 1.80 | 0.50 |
| 2 | 60 | 0.336 | 0.366 | 1.0 | 0.8 | 3 | 1.30 | 0.30 |
| 3 | 70 | 0.310 | 0.320 | 1.1 | 0.9 | 1 | 1.17 | 0.07 |
| 4 | 80 | 0.295 | 0.295 | 0.9 | 0.7 | 0 | 0.60 | 0.07 |
| 5 | 90 | 0.244 | 0.214 | 0.8 | 0.6 | 0 | 0.80 | 0.50 |
| 6 | 100 | 0.305 | 0.305 | 0.9 | 0.8 | 0 | 1.00 | 0.00 |
| BC | Problem Dimension | AFORAS | Manual | HEC-RAS |
|---|---|---|---|---|
| None | 24 | 0.270 | 0.348 (29%) | 0.379 (40%) |
| DS | 22 | 0.278 | 0.345 (24%) | 0.379 (36%) |
| US | 22 | 0.333 | 0.347 (4%) | 0.379 (14%) |
| Both | 20 | 0.338 | 0.342 (1%) | 0.379 (12%) |
| BC | XS 8.05 km | XS 8.15 km | XS 8.26 km–9.27 km | XS 9.45 km | XS 9.64 km |
|---|---|---|---|---|---|
| None | 5a | 5b | 5c–5j | 5k | 5l |
| DS | 6a | ∼6b | ∼5c–5j | ∼5k | ∼5l |
| US | ∼5a | ∼5b | ∼5c–5j | ∼6k | 6l |
| Both | 6a | 6b | 6c–6j | 6k | 6l |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, H.; Yee, T.M.; Heo, J. Automated Floodway Determination Using Particle Swarm Optimization. Water 2018, 10, 1420. https://doi.org/10.3390/w10101420
Cho H, Yee TM, Heo J. Automated Floodway Determination Using Particle Swarm Optimization. Water. 2018; 10(10):1420. https://doi.org/10.3390/w10101420
Chicago/Turabian StyleCho, Huidae, Tien M. Yee, and Joonghyeok Heo. 2018. "Automated Floodway Determination Using Particle Swarm Optimization" Water 10, no. 10: 1420. https://doi.org/10.3390/w10101420
APA StyleCho, H., Yee, T. M., & Heo, J. (2018). Automated Floodway Determination Using Particle Swarm Optimization. Water, 10(10), 1420. https://doi.org/10.3390/w10101420







