Numerical Simulation of Hydraulic Characteristics in A Vortex Drop Shaft
Abstract
:1. Introduction
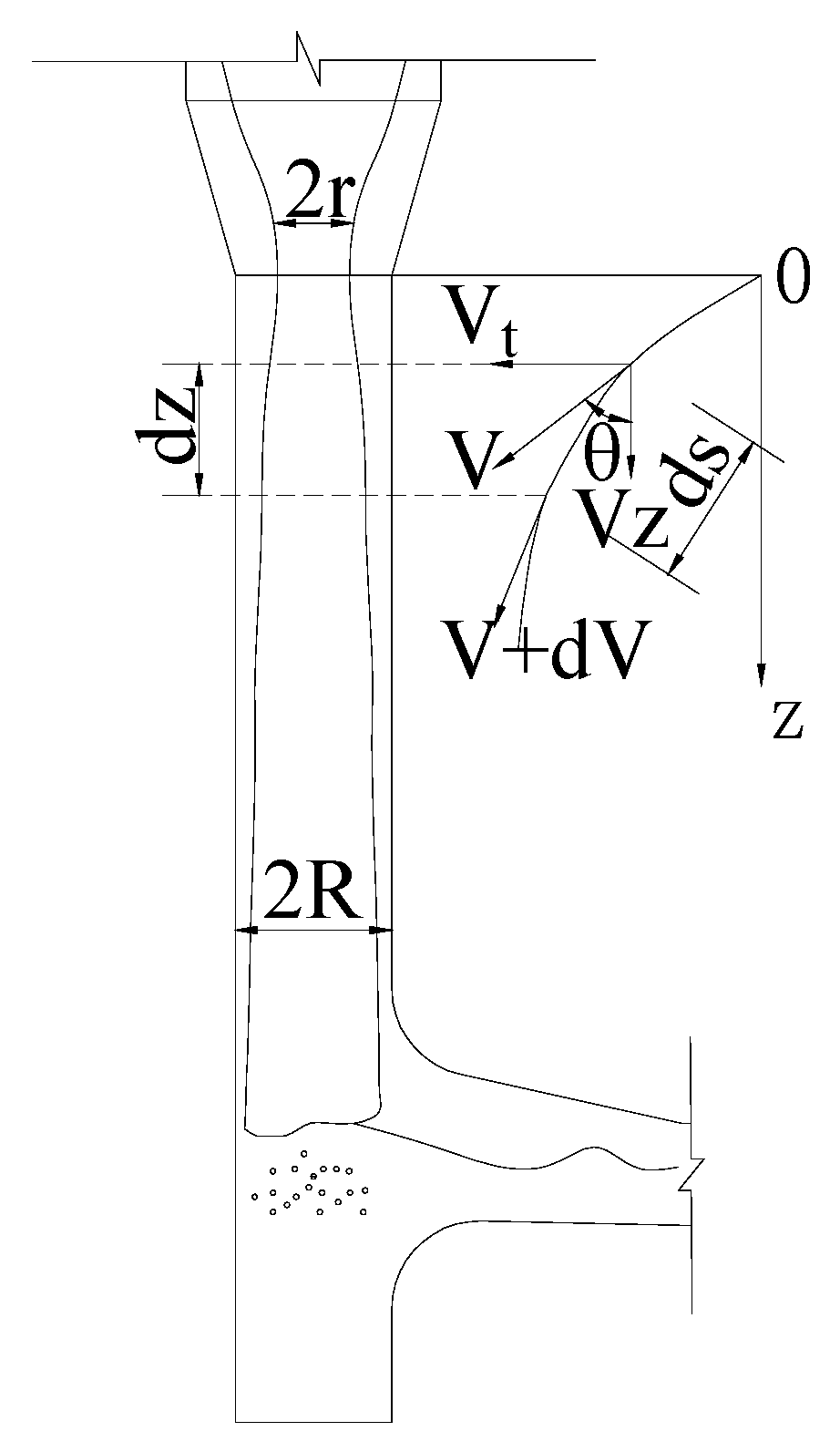
2. Physical Model
3. Numerical Simulation
3.1. Turbulence Model
3.2. Air Entrainment Model
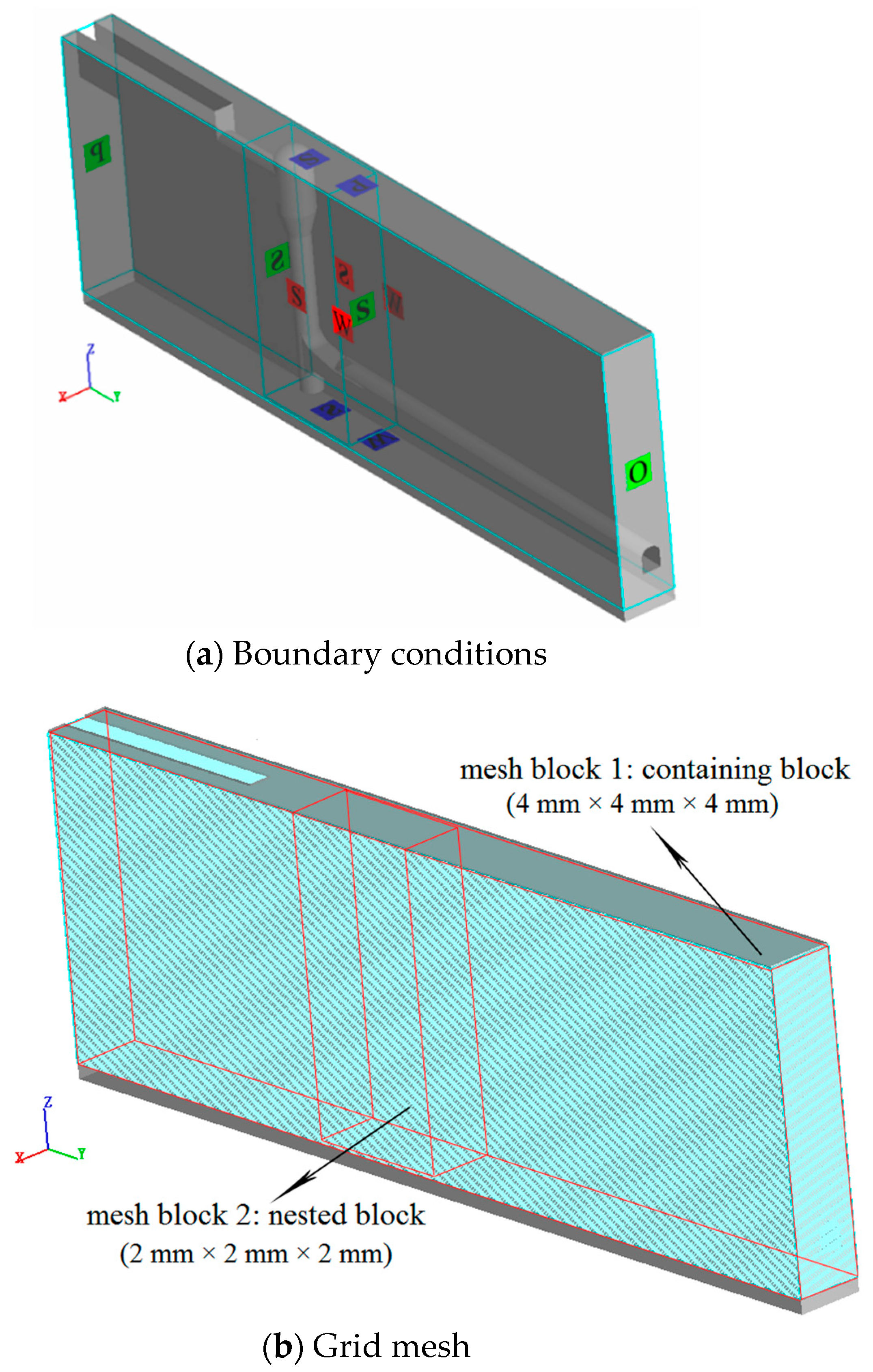
3.3. Computational Grid and Boundary Conditions
4. Results and Discussion
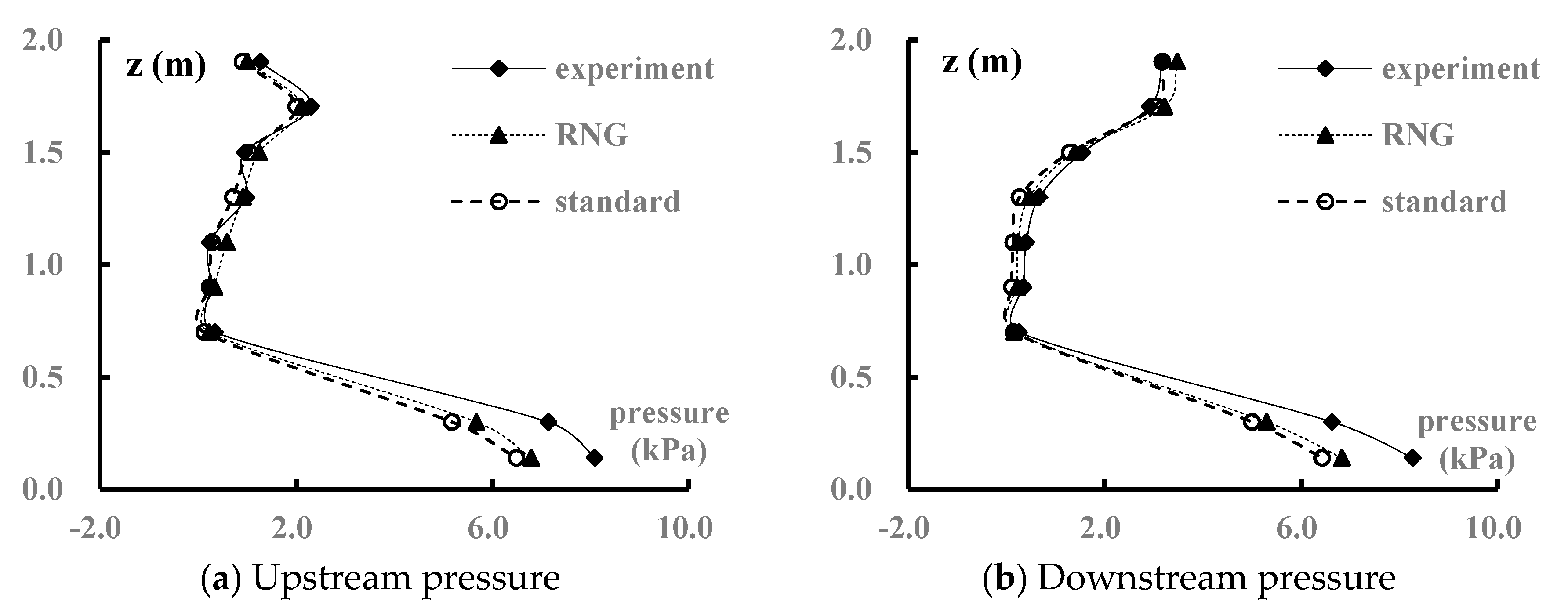
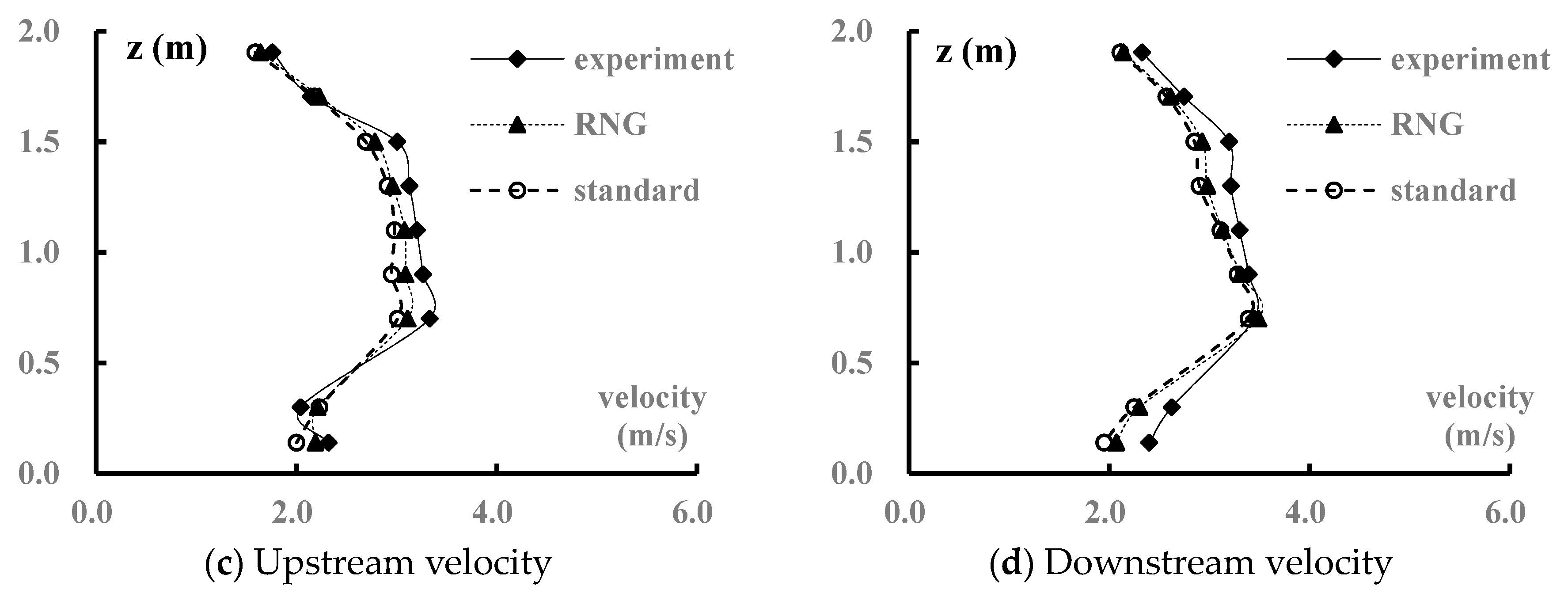
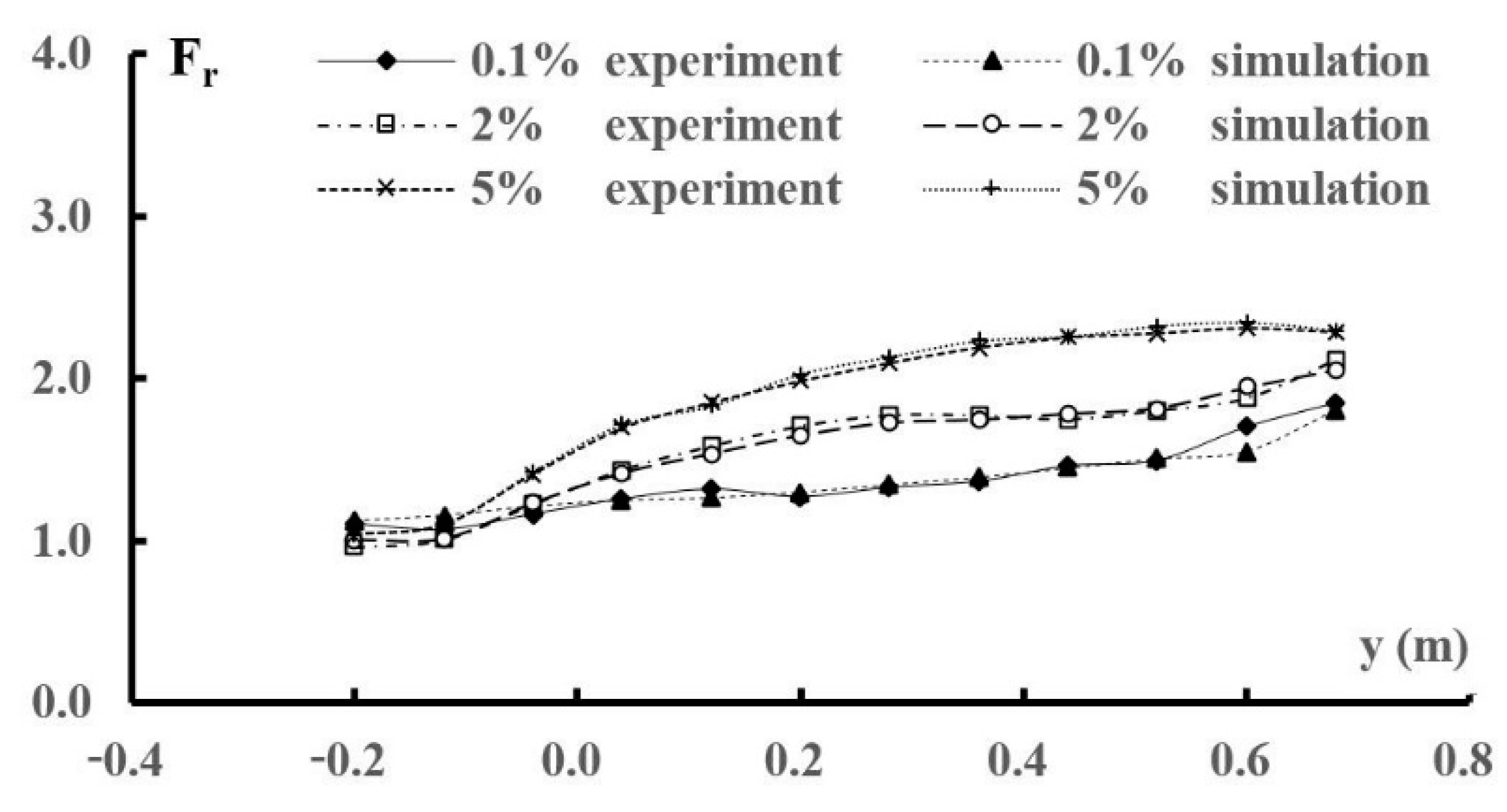
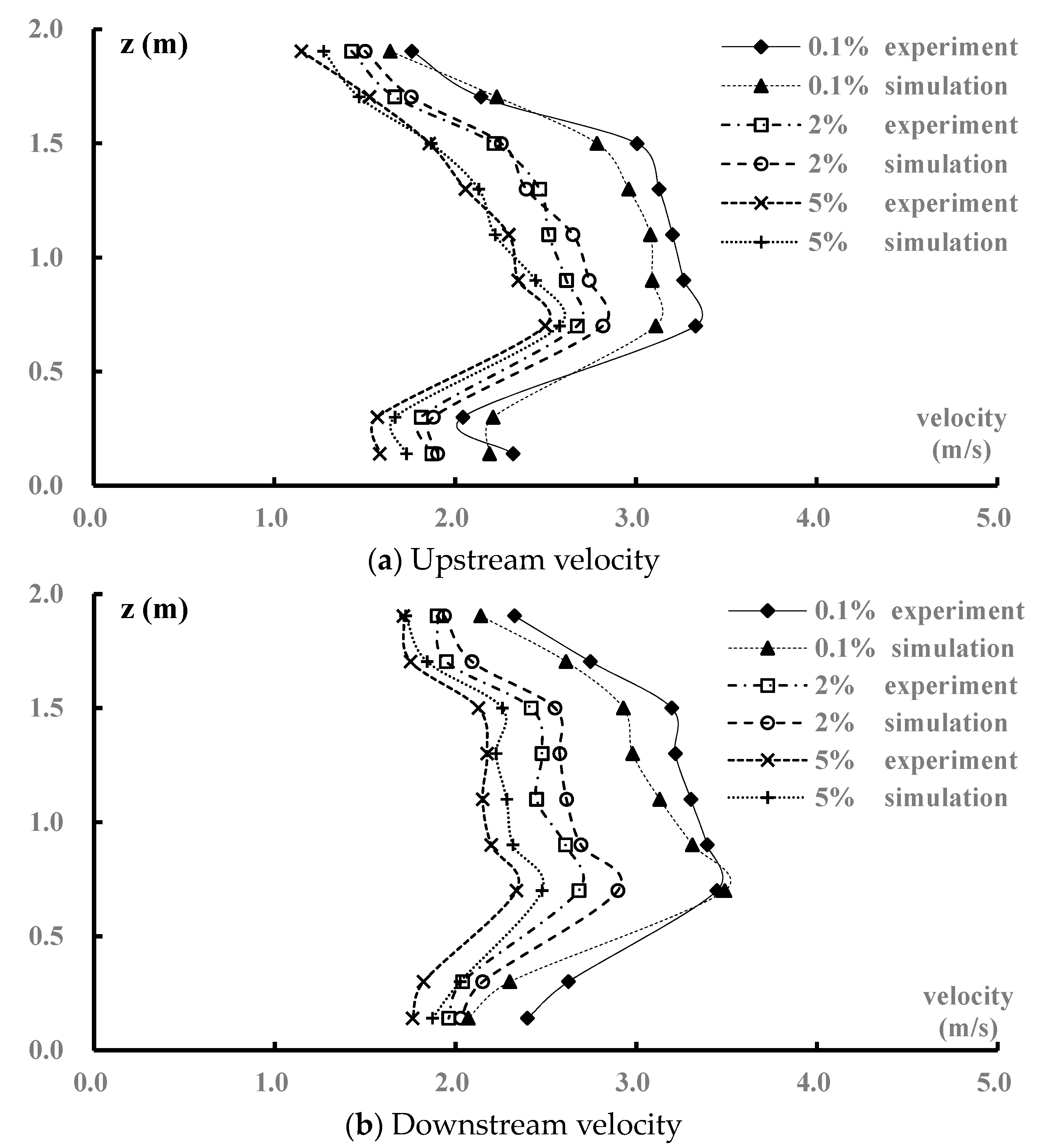
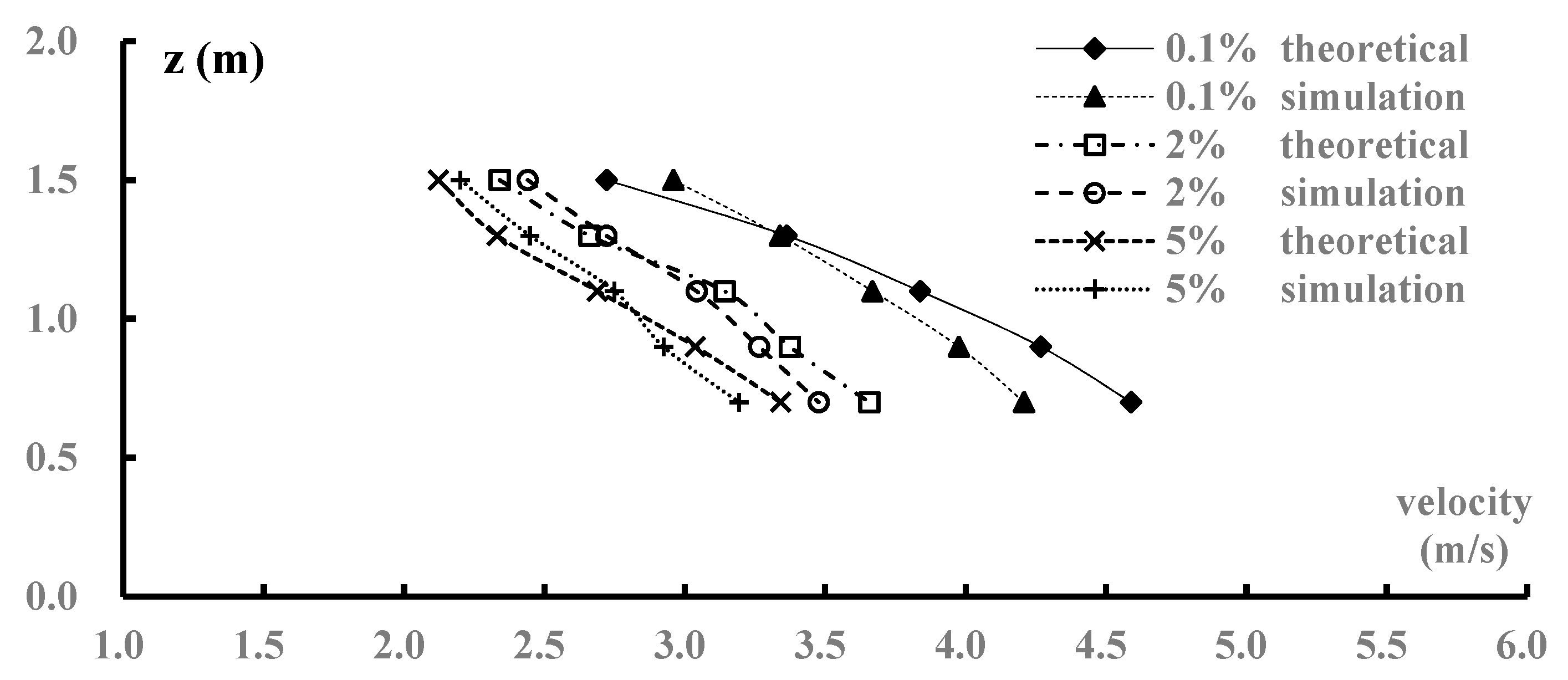
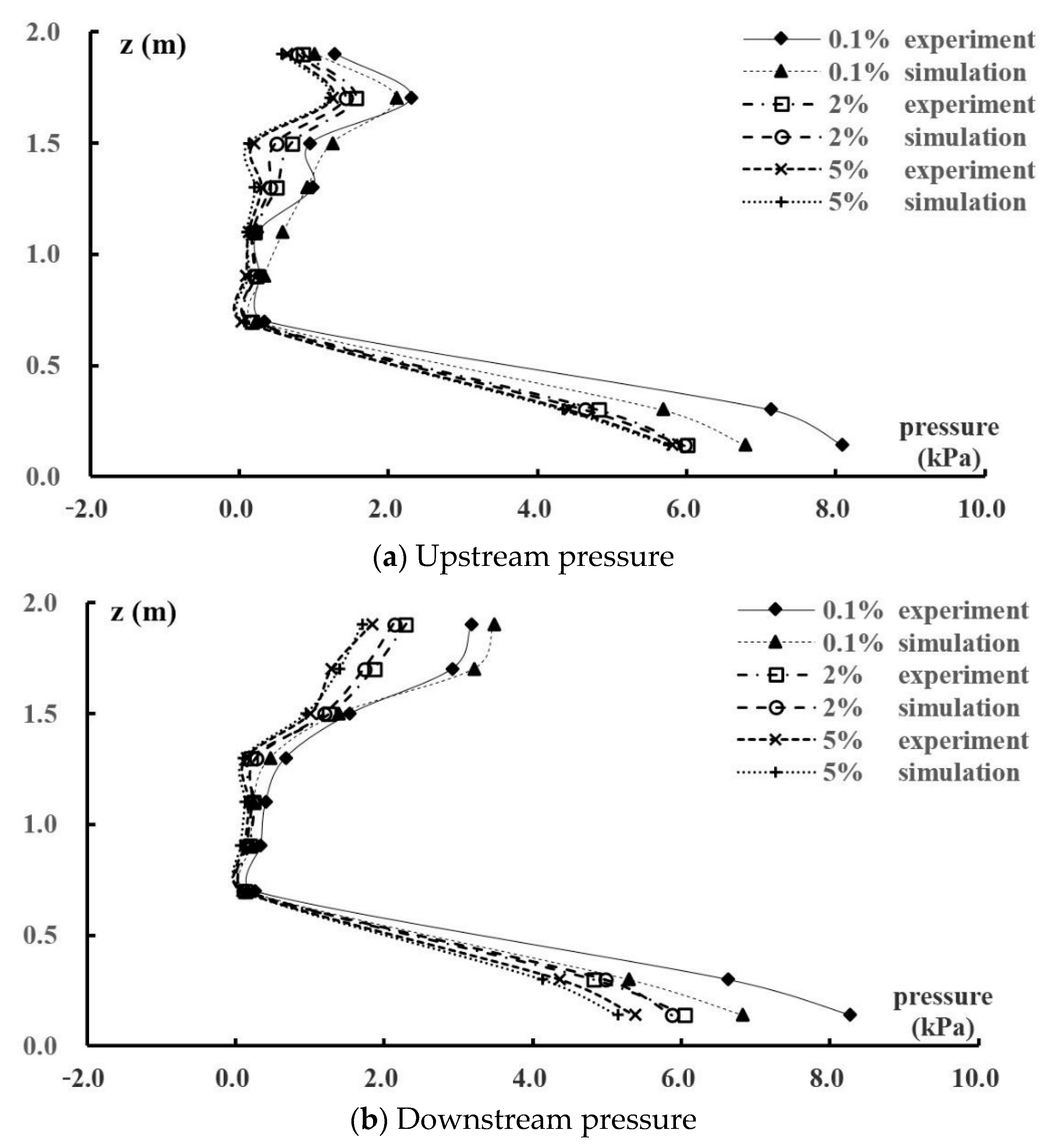
4.1. Model Verification
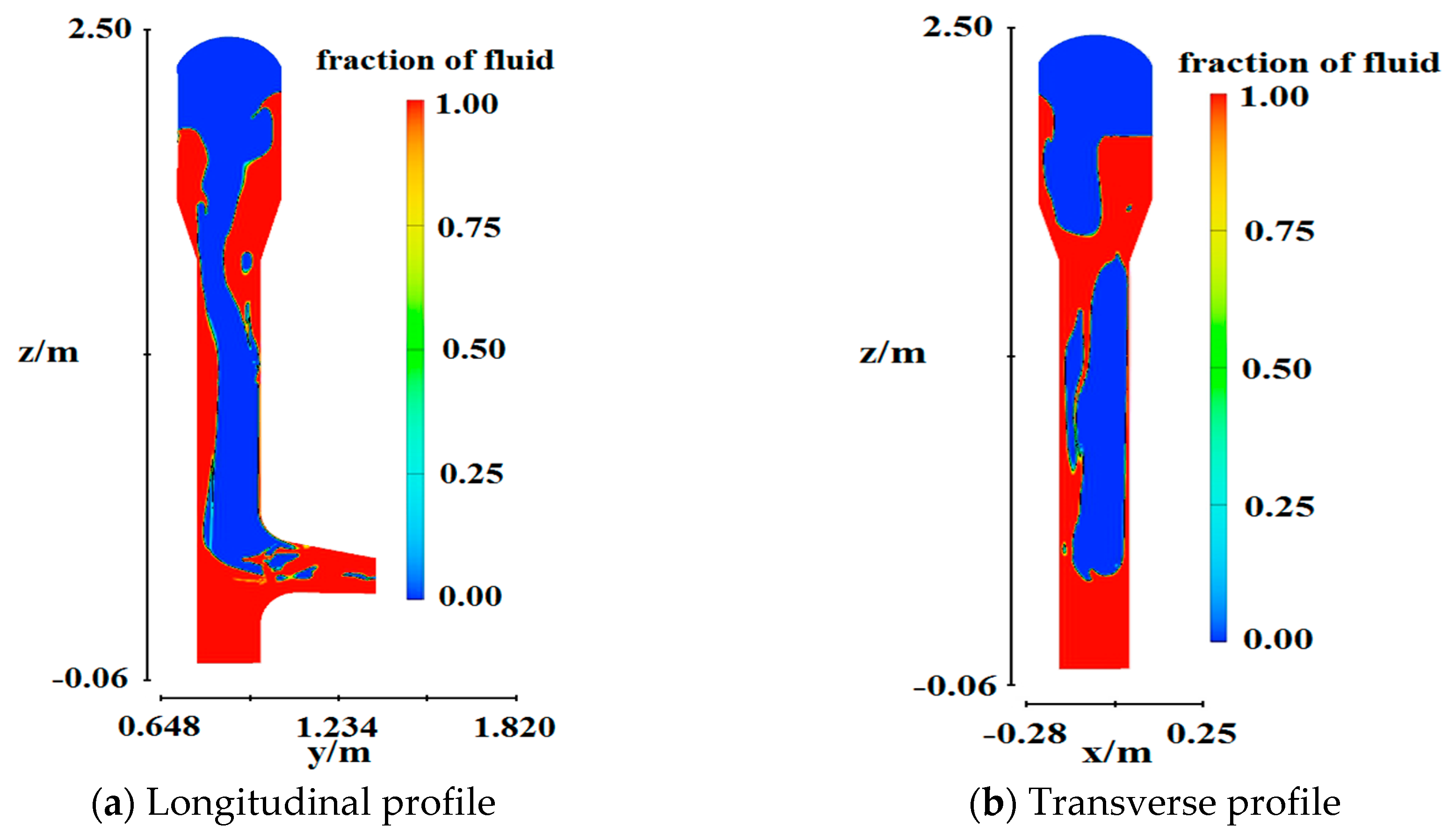
4.2. Flow Regime
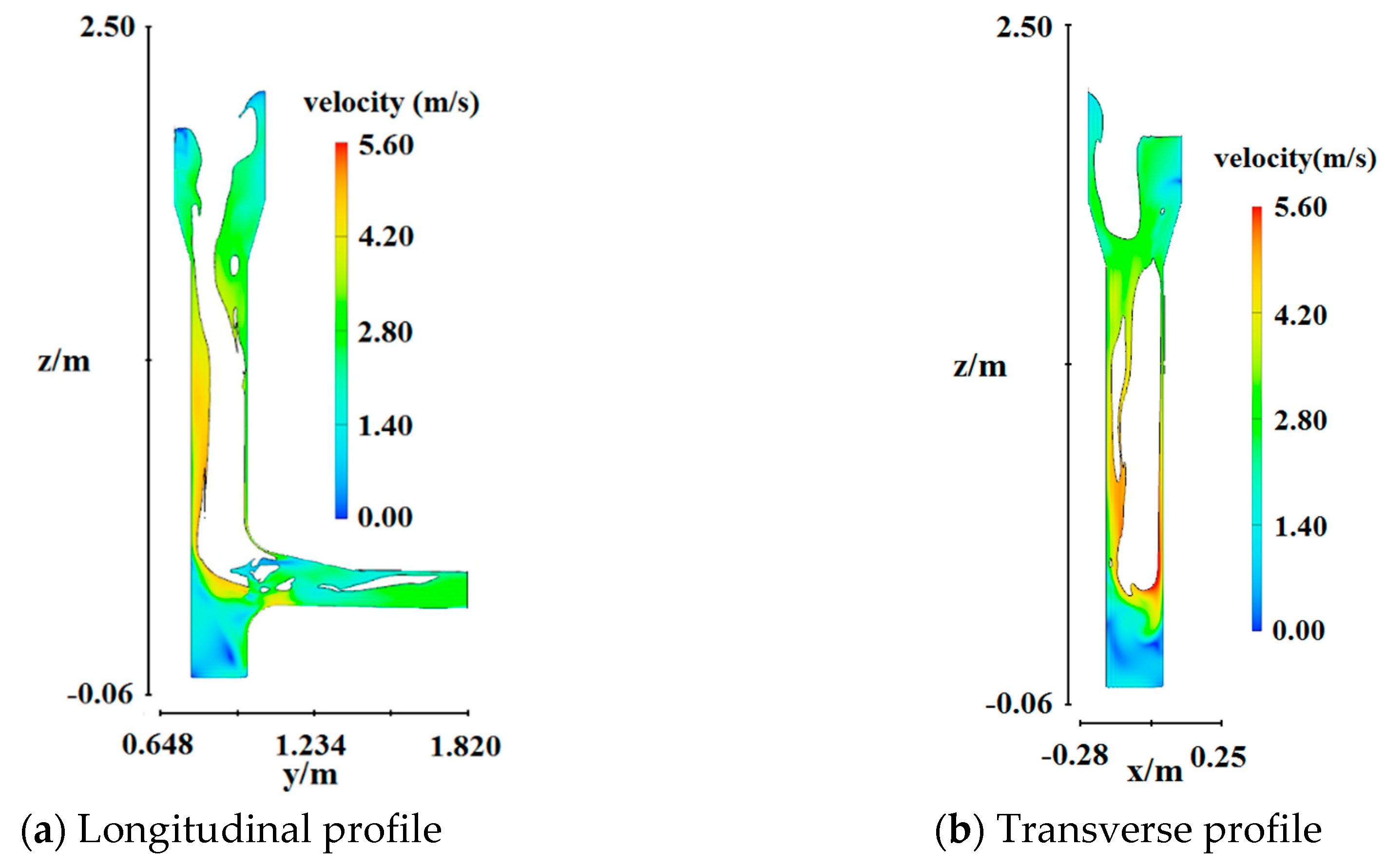
4.3. Velocity Distribution
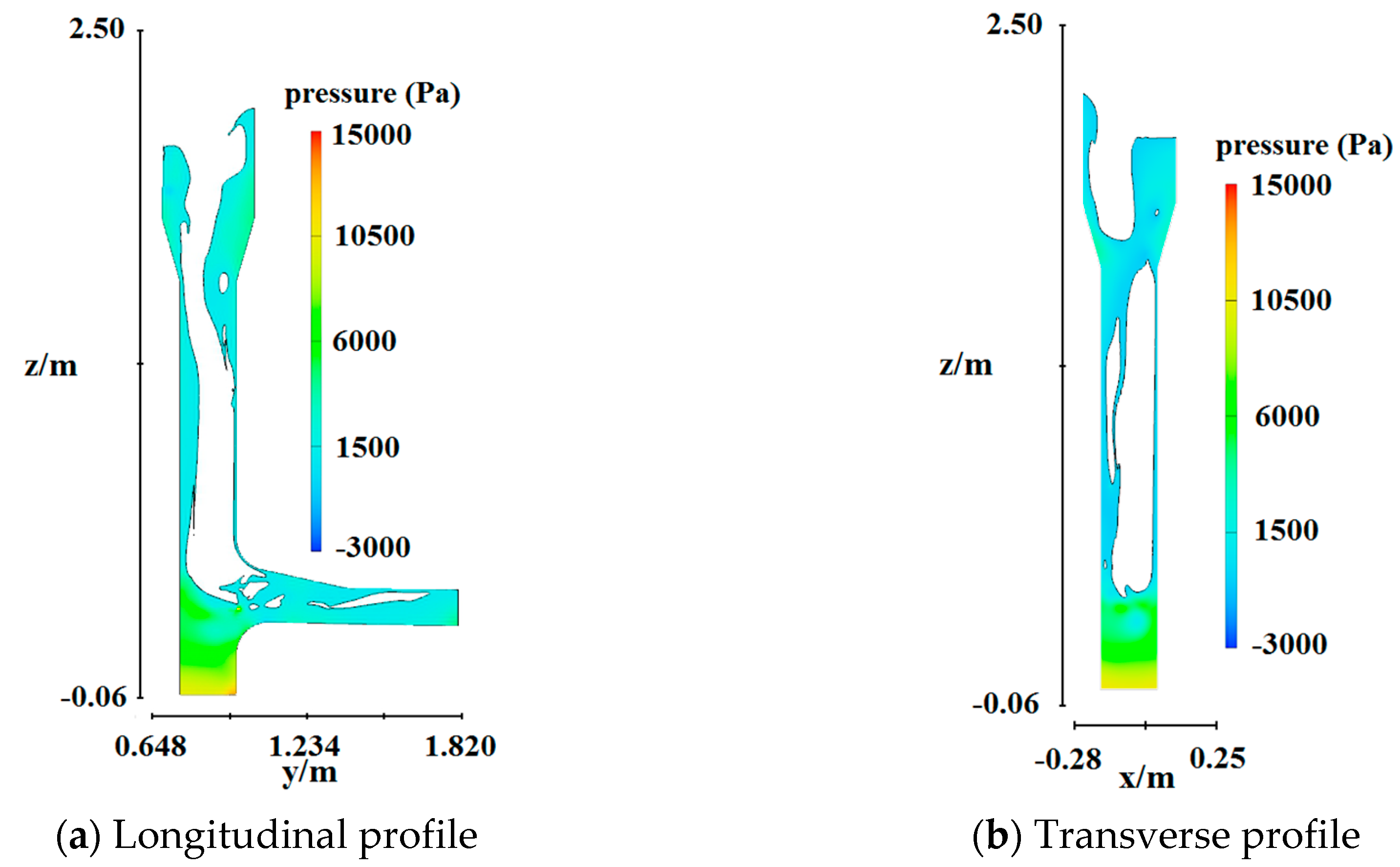
4.4. Pressure Distribution
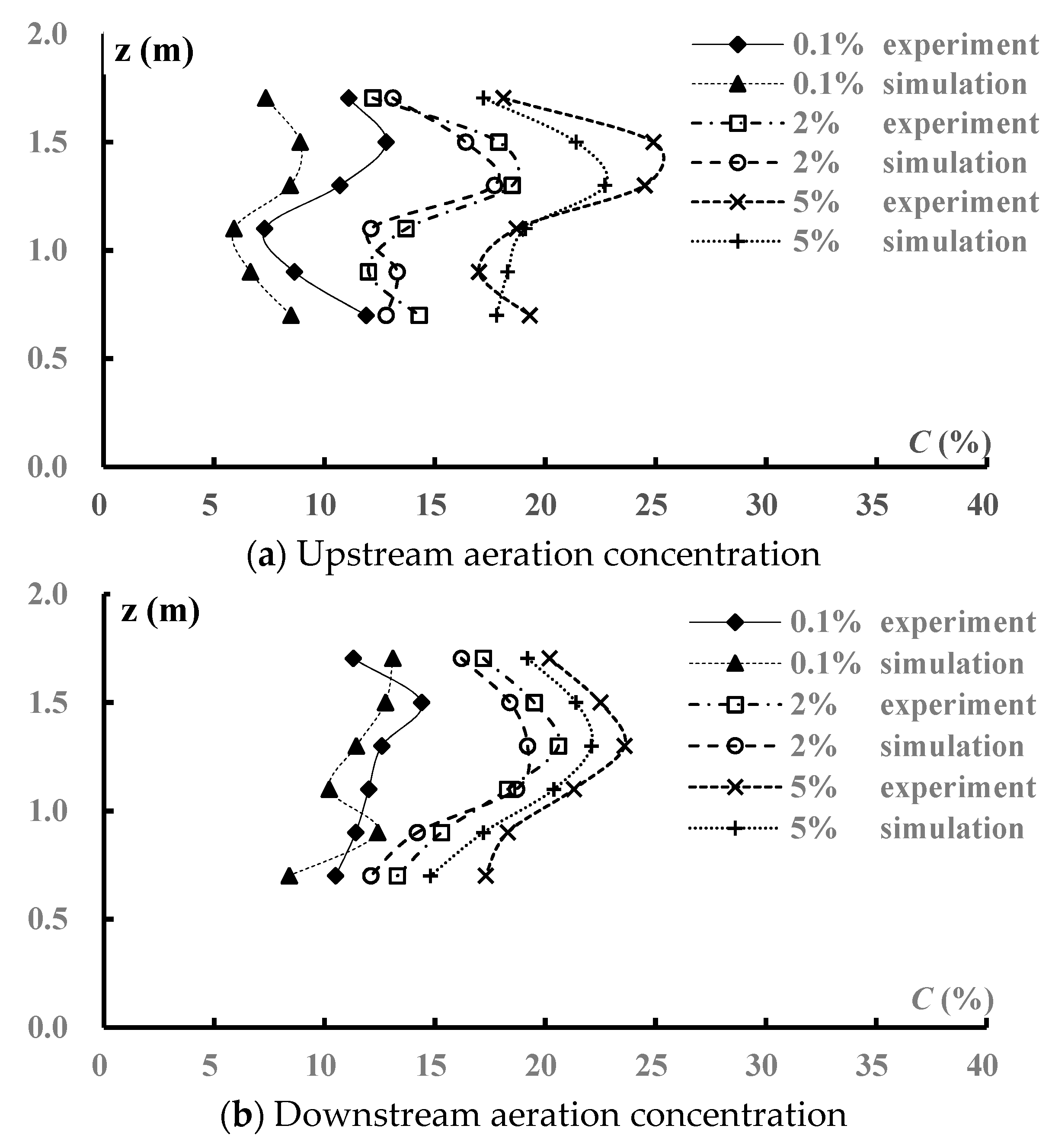
4.5. Aeration Concentration
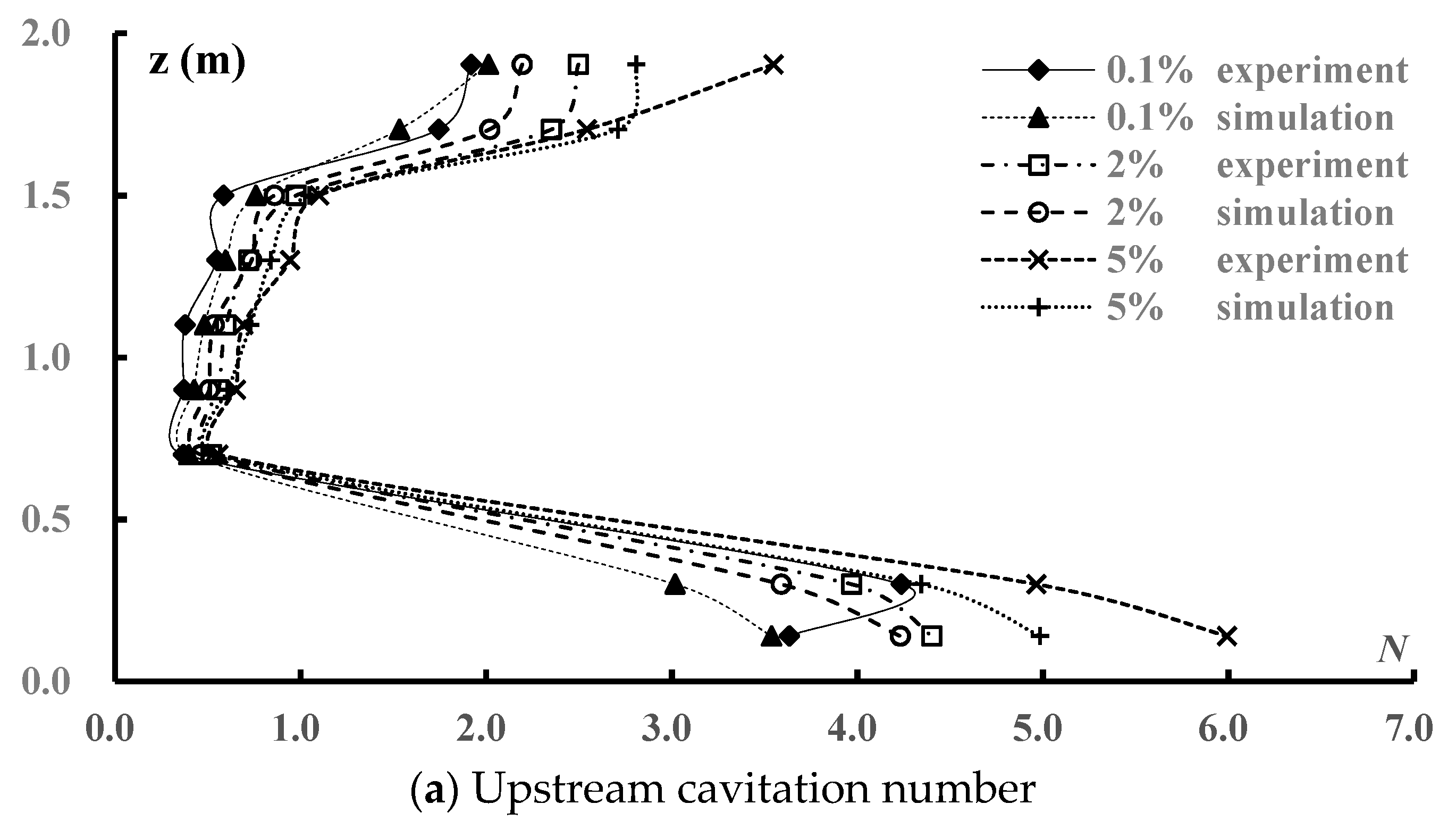
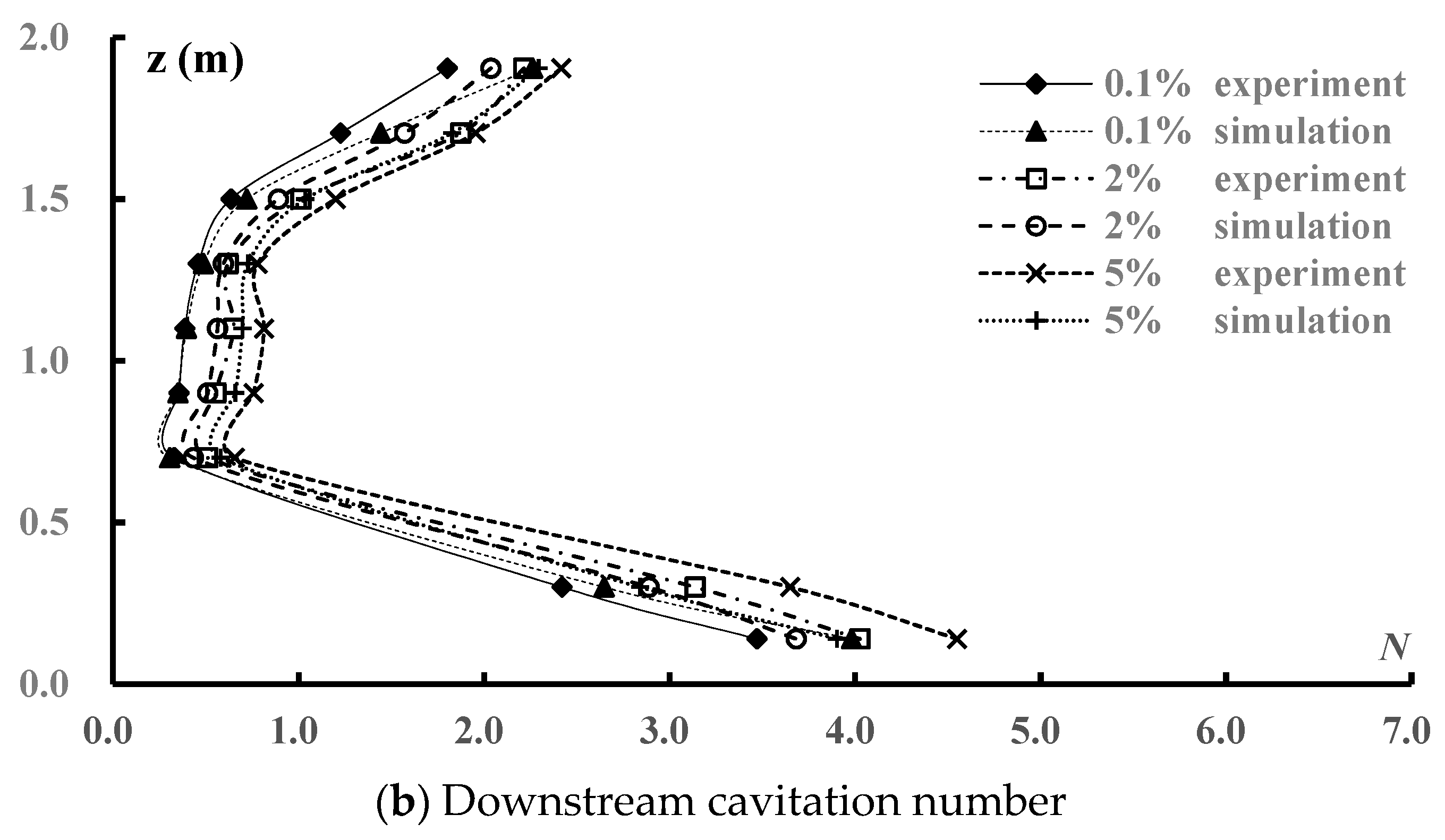
4.6. Cavitation Number
4.7. Energy Dissipation Rate
5. Conclusions
- The RNG k-ε turbulence model effectively simulated the flow characteristics of the vortex drop shaft. The hydraulic parameters, including the velocity and pressure, agreed well with the experimental data and showed the same trends. Thus, similar swirling problems can be simulated by the RNG k-ε turbulence model.
- The flow regime in the vertical shaft was stable, but the flow in the dissipation well was swirling and turbulent. The energy dissipation rate exceeded 70% from the gradient section to the outlet tunnel, indicating the occurrence of sufficient energy dissipation. The velocity was small at the top and bottom but large in the middle, and the pressure was large at the top and bottom but small in the middle. Small negative pressure areas were observed.
- By increasing the clearance height of the intake tunnel and changing the flow conditions, the water flowed into the vertical shaft with a large amount of air. There was a clear phenomenon of aeration and the aeration concentration could provide some reference for engineering design. Additionally, the cavitation number was larger than the critical value, which indicated a low probability of cavitation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notations
| surface area (m2) | |
| aeration concentration | |
| coefficient of proportionality | |
| turbulent dissipation rate m2·s−3 | |
| volume of fluid (VOF) function | |
| Froude number | |
| gravity component (m·s−2) | |
| gravity acceleration (m·s−2) | |
| component of gravity normal to the free surface (m·s−2) | |
| generation of turbulent energy caused by the average velocity gradient | |
| water depth (m) | |
| elevation head (m) | |
| slope | |
| turbulent kinetic energy (kg·m2·s−2) | |
| turbulence length scale (m) | |
| cavitation number | |
| flood frequency | |
| disturbance energy per unit volume (N·m−2) | |
| stabilising forces per unit volume (N·m−2) | |
| gauge pressure (Pa) | |
| absolute pressure (Pa) | |
| vapor pressure (Pa) | |
| density of water (kg·m−3) | |
| discharge (L·s−1) | |
| radius of the cavity (m) | |
| specific weight of water (N·m−3) | |
| radius of vertical shaft (m) | |
| hydraulic radius (m) | |
| water trajectory (m) | |
| time (s) | |
| velocity component (m/s) | |
| coefficient of dynamic viscosity (kg·m−1·s−1) | |
| revisionary coefficient of dynamic viscosity (kg·m−1·s−1) | |
| coefficient of kinematic viscosity (m2·s−1) | |
| resultant velocity (m·s−1) | |
| tangential velocity (m·s−1) | |
| vertical velocity (m·s−1) | |
| volume of air entrained per unit time m3 | |
| coefficient of surface tension (N·m−1) | |
| angle between the velocity direction and the vertical direction | |
| factor of friction loss | |
| coordinate component |
References
- Lian, J.J.; Yan, M. Hydrodynamics for High Dam; China Water & Power Press: Beijing, China, 2008. [Google Scholar]
- Zhao, C.H.; Zhu, D.Z.; Sun, S.K.; Liu, Z.P. Experimental study of flow in a vortex drop shaft. J. Hydraul. Eng. 2006, 132, 61–68. [Google Scholar] [CrossRef]
- Niu, Z.M.; Nan, J.H.; Hong, D. An experimental study on hydraulic characteristics of a novel aerator. Adv. Water Sci. 2013, 24, 372–378. [Google Scholar]
- Guo, L. Experimental Study on Bodily Form Optimization of the Vertical Shaft Spillway; Xi’an University of Technology: Xi’an, China, 2007. [Google Scholar]
- Dong, X.L.; Guo, J.; Xiao, B.Y.; Zhou, Z. Design principle of high head and large discharge vortex drop spillway. J. Hydraul. Eng. 2000, 31, 27–33. [Google Scholar]
- Dong, X.L. Spillway with Swirling Flow; The Yellow River Water Conservancy Press: Zhengzhou, China, 2011. [Google Scholar]
- Chen, X.W.; Zhang, Z.X.; Chong, L.; Xin, B. Experimental study on pressure of shaft spillway with different depth of stilling well. Chin. J. Appl. Mech. 2016, 33, 826–831. [Google Scholar]
- Yu, D.Y.; Lee, J.H.W. Hydraulics of tangential vortex intake for urban drainage. J. Hydraul. Eng. 2009, 135, 164–174. [Google Scholar] [CrossRef]
- Jain, S.C. Tangential vortex-inlet. J. Hydraul. Eng. ASCE 1984, 110, 1693–1699. [Google Scholar] [CrossRef]
- Del Giudice, G.; Gisonni, C. Vortex dropshaft retrofitting: Case of Naples city (Italy). J. Hydraul. Res. 2011, 49, 804–808. [Google Scholar] [CrossRef]
- Guo, Y. The hydraulic characteristics of shaft tunnel in vortex flow intake shaft spillway. J. Hydrodyn 1995, 2, 146–154. [Google Scholar]
- Nan, J.H.; Niu, Z.M.; Zhang, D.; Hong, D. Pressure characteristics of a cavity gyrating flow in gyrating discharge tunnel. J. Basic Sci. Eng. 2016, 24, 272–281. [Google Scholar]
- Niu, Z.M.; Zhang, M.Y. Basic hydrodynamics characteristics of cavity spiral flow in a large size level pipe. J. Hydrodyn. 2005, 17, 503–513. [Google Scholar]
- Cao, S.L.; Niu, Z.M.; Yang, J.; Lu, H.B. Velocity and pressure distributions in discharge tunnel of rotary-obstruction composite inner energy dissipation. Sci. Chin. Technol. Sci. 2011, 54, 111–117. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, F.X.; Deng, J.; Xu, W.L. Calculation of the cavity length of annular aerator in the vortex drop shaft spillway. J. Sichuan Univ. 2011, 43, 28–33. [Google Scholar]
- Dong, Z.X.; Ping, L.Z.; Zhang, G.J.; Song, W.X. 3-D numerical simulation of flow in shaft spillway with whirling current. J. Hydraul. Eng. 2003, 34, 58–63. [Google Scholar]
- Gao, X.P.; Zhang, H.; Liu, J.J.; Sun, B.; Tian, Y. Numerical investigation of flow in a vertical pipe inlet/outlet with a horizontal anti-vortex plate: Effect of diversion orifices height and divergence angle. Eng. Appl. Comput. Fluid Mech. 2018, 12, 182–194. [Google Scholar] [CrossRef]
- Guo, X.L.; Xia, Q.F.; Fu, H.; Yang, K.L.; Li, S.J. Numerical study on flow of newly vortex drop shaft spillway. J. Hydraul. Eng. 2016, 47, 733–741. [Google Scholar]
- Liu, Z.P.; Guo, X.L.; Xia, Q.F.; Fu, H.; Wang, T.; Dong, X.L. Experimental and numerical investigation of flow in a newly developed vortex drop shaft spillway. J. Hydraul. Eng. 2018, 144. [Google Scholar] [CrossRef]
- Gao, J.Z.; Dong, X.L.; Liu, J.G. Research and application of eco-friendly energy dissipation technology-internal energy dissipation. J. Hydraul. Eng. 2008, 39, 1176–1182. [Google Scholar]
- Yakhot, V.; Orzag, S.A. Renormalization group analysis of turbulence. I. Basic Theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.G.; Zhang, J.M.; Xu, W.L.; Wang, Y.R. Scale effects of air-water flows in stilling basin of multi-horizontal submerged jets. J. Hydrodyn. 2010, 22, 788–795. [Google Scholar] [CrossRef]
- Fuchs, H.; Hager, W.H.; Asce, F. Scale effects of impulse wave run-up and run-over. J. Waterw. Port Coast. Ocean Eng. 2012, 138, 303–311. [Google Scholar] [CrossRef]
- Pfister, M.; Chanson, H. Scale effects in modelling two-phase air-water flows. In Proceedings of the 35th IAHR World Congress, Cheng Du, China, 8–13 September 2013; pp. 1–10. [Google Scholar]
- Chanson, H. Turbulent air–water flows in hydraulic structures: Dynamic similarity and scale effects. Environ. Fluid Mech. 2009, 9, 125–142. [Google Scholar] [CrossRef] [Green Version]
- Chanson, H.; Chachereau, Y. Scale effects affecting two-phase flow properties in hydraulic jump with small inflow Froude number. Exp. Therm. Fluid Sci. 2013, 45, 234–242. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.Y.; Xu, W.L.; Deng, J.; Niu, Z.P.; Liu, S.J.; Wang, W. Theoretical and experimental studies of hydraulic characteristics of discharge tunnel with vortex drop. J. Hydrodyn. 2010, 22, 582–589. [Google Scholar] [CrossRef]
- Taghavi, M.; Ghodousi, H. A comparison on discharge coefficients of side and normal weirs with suspended flow load using Flow3D. Indian J. Sci. Technol. 2016, 9, 1–11. [Google Scholar] [CrossRef]
- Sarkardeh, H.; Zarrati, A.R.; Jabbari, E.; Marosi, M. Numerical simulation and analysis of flow in a reservoir in the presence of vortex. Eng. Appl. Comput. Fluid Mech. 2014, 8, 598–608. [Google Scholar] [CrossRef]
- Dong, Z.S.; Wang, J.X.; Zhang, W.C.; Da, J.R. Study on dissipation characteristics of incomplete flaring gate pier with low Froude number. J. Sichuan Univ. 2016, 48, 9–15. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Model of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Hirt, C.W. Modeling turbulent entrainment of air at a free surface. Flow Sci. 2004. [Google Scholar] [CrossRef]
- Meireles, I.C.; Bombardelli, F.A.; Matos, J. Air entrainment onset in skimming flows on steep stepped spillways: An analysis. J. Hydraul. Res. 2014, 52, 375–385. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Bakhsh, M.S.; Dadvand, A. Numerical study of the effect of wall injection on the cavitation phenomenon in diesel injector. Eng. Appl. Comput. Fluid Mech. 2014, 8, 562–573. [Google Scholar] [CrossRef]
- Liu, C.; Yang, Y.Q. Study on air entrainment to alleviate cavitations at the end of anti-arc in spillway tunnel. J. Hydrodyn. 2004, 3, 375–382. [Google Scholar]
- Peterka, A.J. The Effect of Entrained Air on Cavitation Pitting. In Proceedings of the Minnesota International Hydraulic Convention, Minneapolis, MN, USA, 1–4 September 1953; pp. 507–518. [Google Scholar]
- Šarc, A.; Stepišnik-Perdih, T.; Petkovšek, M.; Dular, M. The issue of cavitation number value in studies of water treatment by hydrodynamic cavitation. Ultrason. Sonochem. 2017, 34, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.J.; Wang, H.Y.; Dai, G.Q.; Yang, Q. Study on the hydraulic characteristics of chute section of high-head bank spillway. Water Power 2007, 33, 45–46. [Google Scholar]
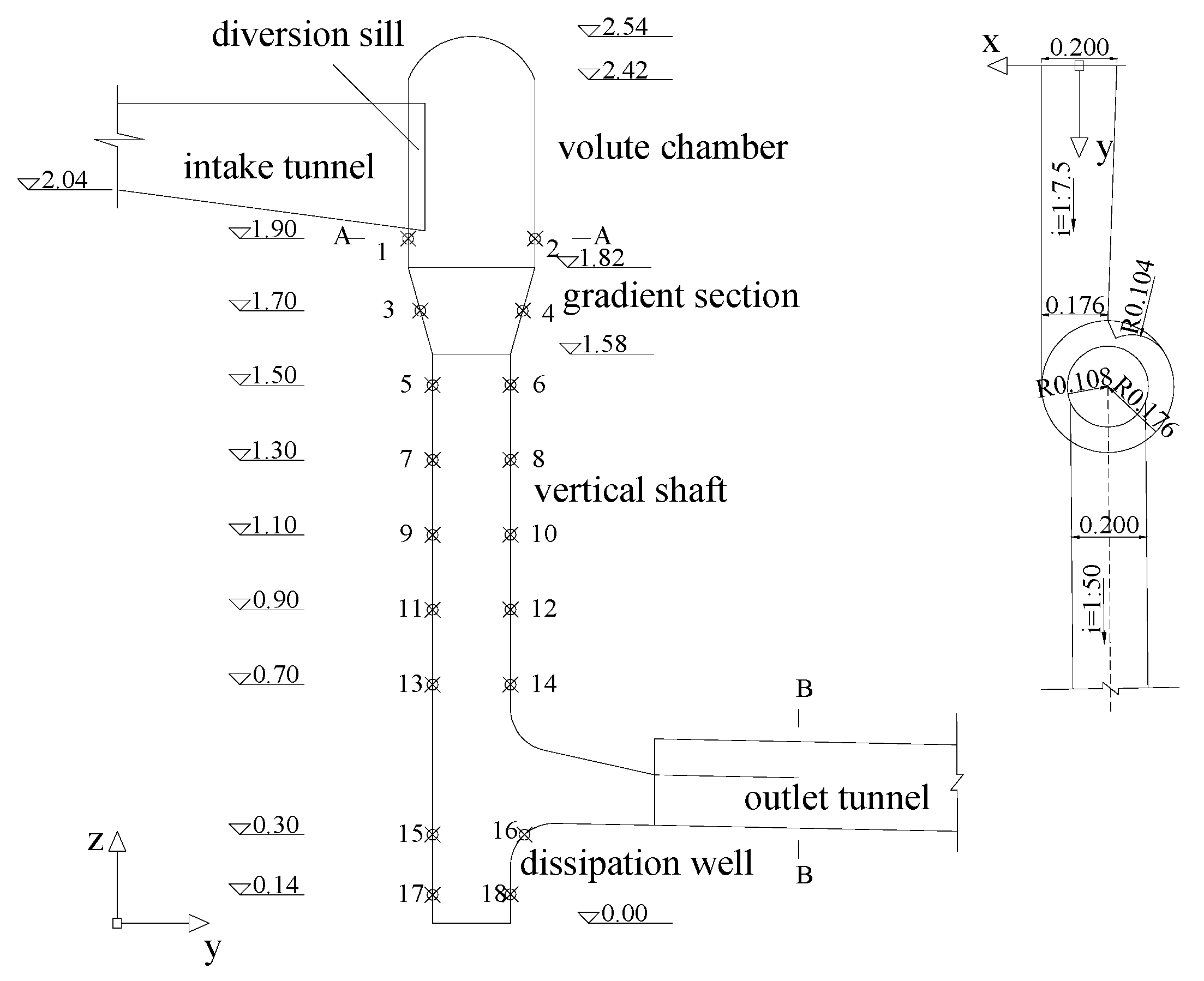


| Grid | Description | Size (X × Y × Z) | Discharge (L/s) |
|---|---|---|---|
| 1 | containing block | 15 mm × 15 mm × 15 mm | 54.47 |
| nested block | 10 mm × 10 mm × 10 mm | ||
| 2 | containing block | 10 mm × 10 mm × 10 mm | 58.25 |
| nested block | 5 mm × 5 mm × 5 mm | ||
| 3 | containing block | 5 mm × 5 mm × 5 mm | 60.28 |
| nested block | 3 mm × 3 mm × 3 mm | ||
| 4 | containing block | 4 mm × 4 mm × 4 mm | 60.96 |
| nested block | 2 mm × 2 mm × 2 mm |
| Flood Frequency | Discharge (L/s) | Deviation | |
|---|---|---|---|
| Experiment | Simulation | ||
| 5% | 30.45 | 29.92 | 1.74% |
| 2% | 38.21 | 38.01 | 0.52% |
| 0.1% | 62.29 | 60.96 | 2.14% |
| Condition | Section A-A | Section B-B | Energy Dissipation Rate (%) | |||
|---|---|---|---|---|---|---|
| 5% | Experiment | 0.16 | 1.65 | 0.19 | 0.29 | 73.48 |
| Simulation | 0.17 | 1.69 | 0.20 | 0.28 | 74.12 | |
| 2% | Experiment | 0.18 | 1.82 | 0.23 | 0.31 | 73.00 |
| Simulation | 0.19 | 1.81 | 0.24 | 0.33 | 71.66 | |
| 0.1% | Experiment | 0.21 | 2.12 | 0.24 | 0.39 | 72.95 |
| Simulation | 0.25 | 2.13 | 0.30 | 0.41 | 70.13 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Wang, J.; Zhou, C.; Dong, Z.; Zhou, Z. Numerical Simulation of Hydraulic Characteristics in A Vortex Drop Shaft. Water 2018, 10, 1393. https://doi.org/10.3390/w10101393
Zhang W, Wang J, Zhou C, Dong Z, Zhou Z. Numerical Simulation of Hydraulic Characteristics in A Vortex Drop Shaft. Water. 2018; 10(10):1393. https://doi.org/10.3390/w10101393
Chicago/Turabian StyleZhang, Wenchuan, Junxing Wang, Chuangbing Zhou, Zongshi Dong, and Zhao Zhou. 2018. "Numerical Simulation of Hydraulic Characteristics in A Vortex Drop Shaft" Water 10, no. 10: 1393. https://doi.org/10.3390/w10101393
APA StyleZhang, W., Wang, J., Zhou, C., Dong, Z., & Zhou, Z. (2018). Numerical Simulation of Hydraulic Characteristics in A Vortex Drop Shaft. Water, 10(10), 1393. https://doi.org/10.3390/w10101393





