Identifying the Sensitivity of Ensemble Streamflow Prediction by Artificial Intelligence
Abstract
:1. Introduction
2. Methodology
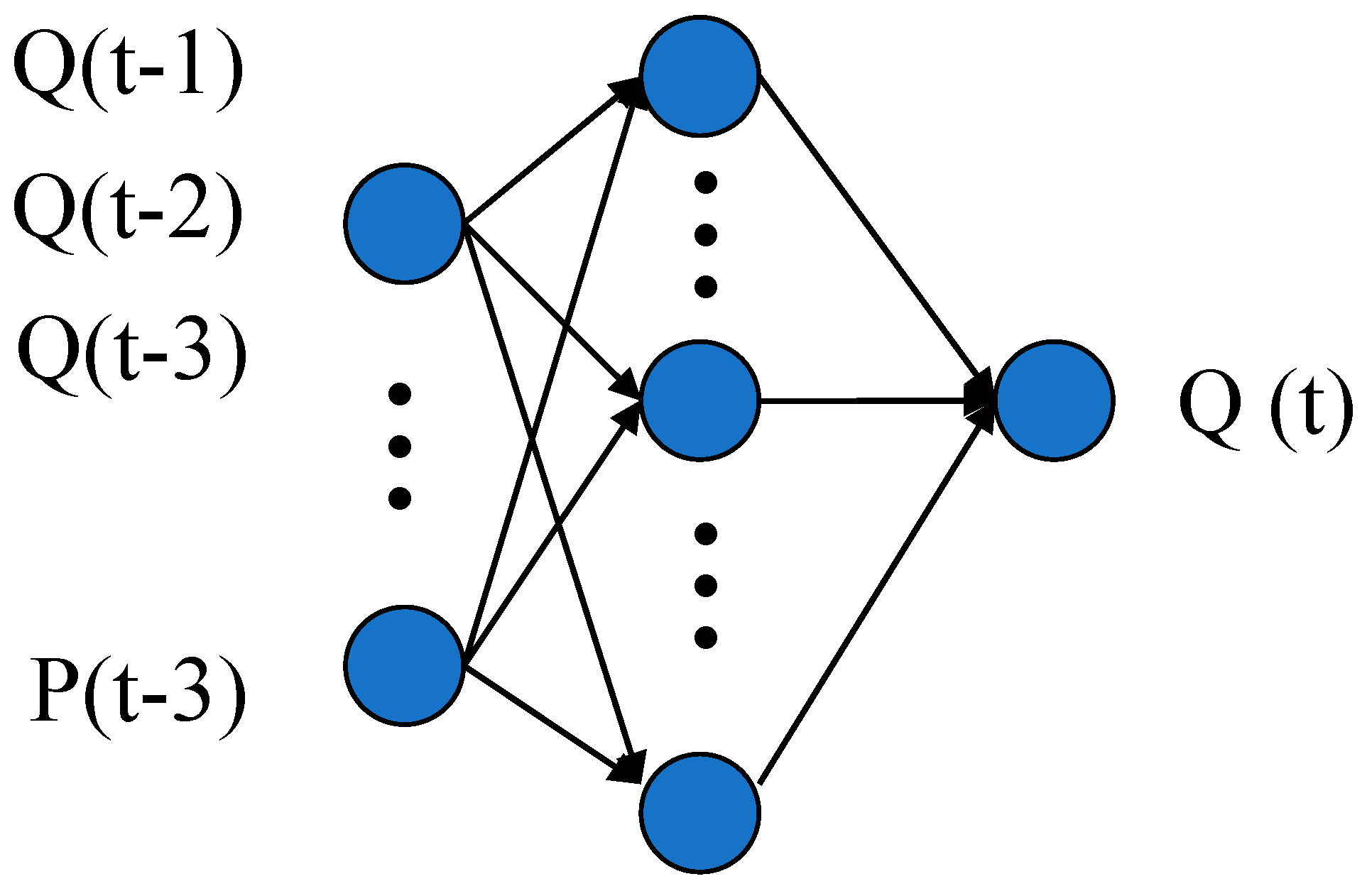
2.1. Back Propagation Neural Network
2.2. Ensemble Neural Network
2.3. Generating Ensemble Members
2.4. Integrating Ensemble Members
2.4.1. Arithmetic Averaging
2.4.2. Stack Averaging
2.4.3. Bayesian Model Average
3. Applications
3.1. Study Area and Data Description
3.2. Evaluation Criteria
- (i)
- Coefficient of Determination (R2)where and are the observed and predicted flow at time t + n, is the mean of the observed runoff, and N is the number of data points. The value of R2 varies between negative infinity and one. Values approaching one indicate higher accuracy in model performance.
- (ii)
- root mean square error (RMSE)The merits of models can be significantly reflected through RMSE values when assessing peak values of variables.
- (iii)
- Gbench index (Gbench)where represents the benchmark series of real observed runoff at time t. Gbench is negative if the model performance is poorer than the benchmark, zero if the model performs as well as the benchmark, and positive if the model is superior. Values closer to one indicate a perfect fit [34].
4. Results and Discussions
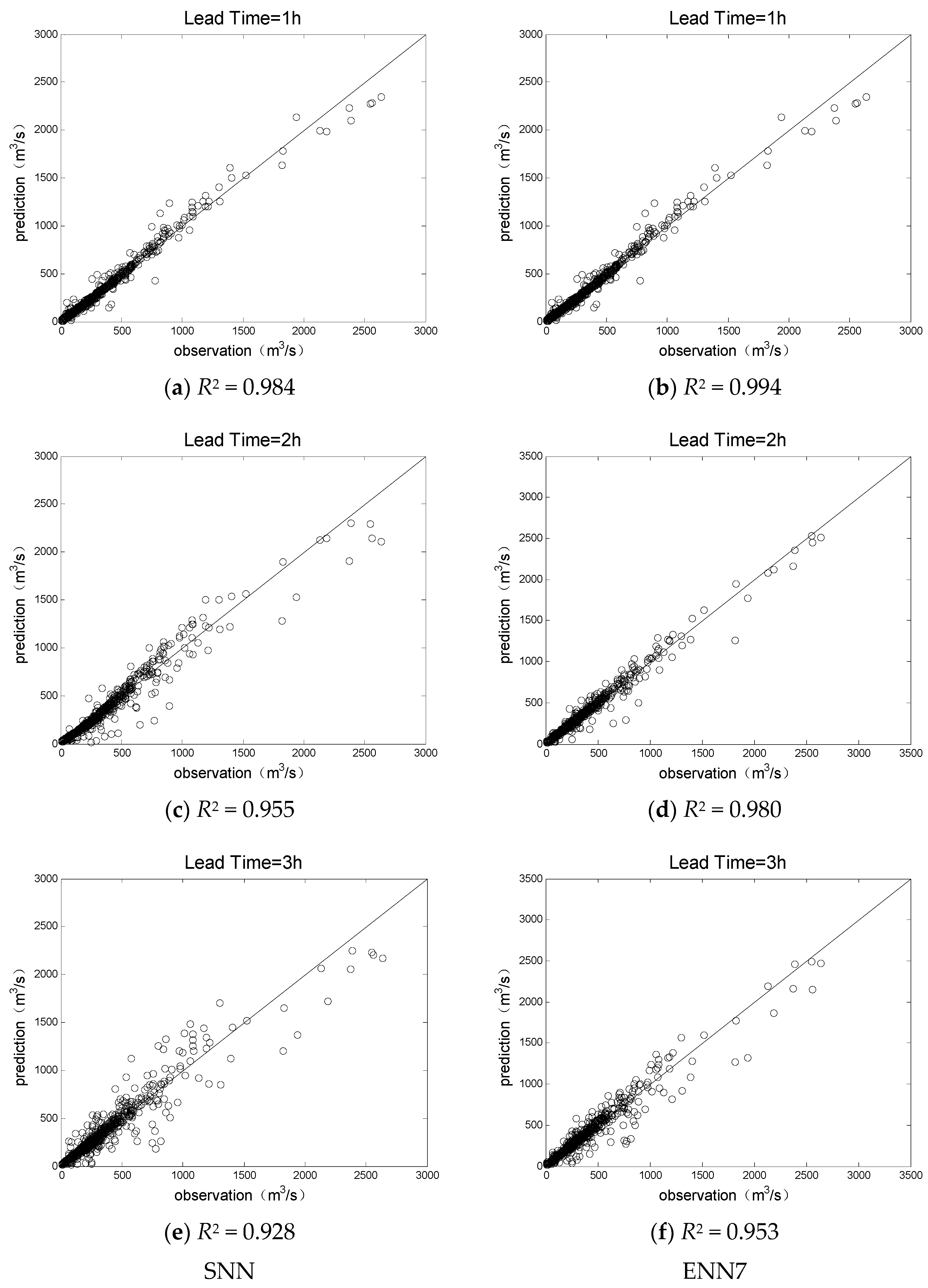
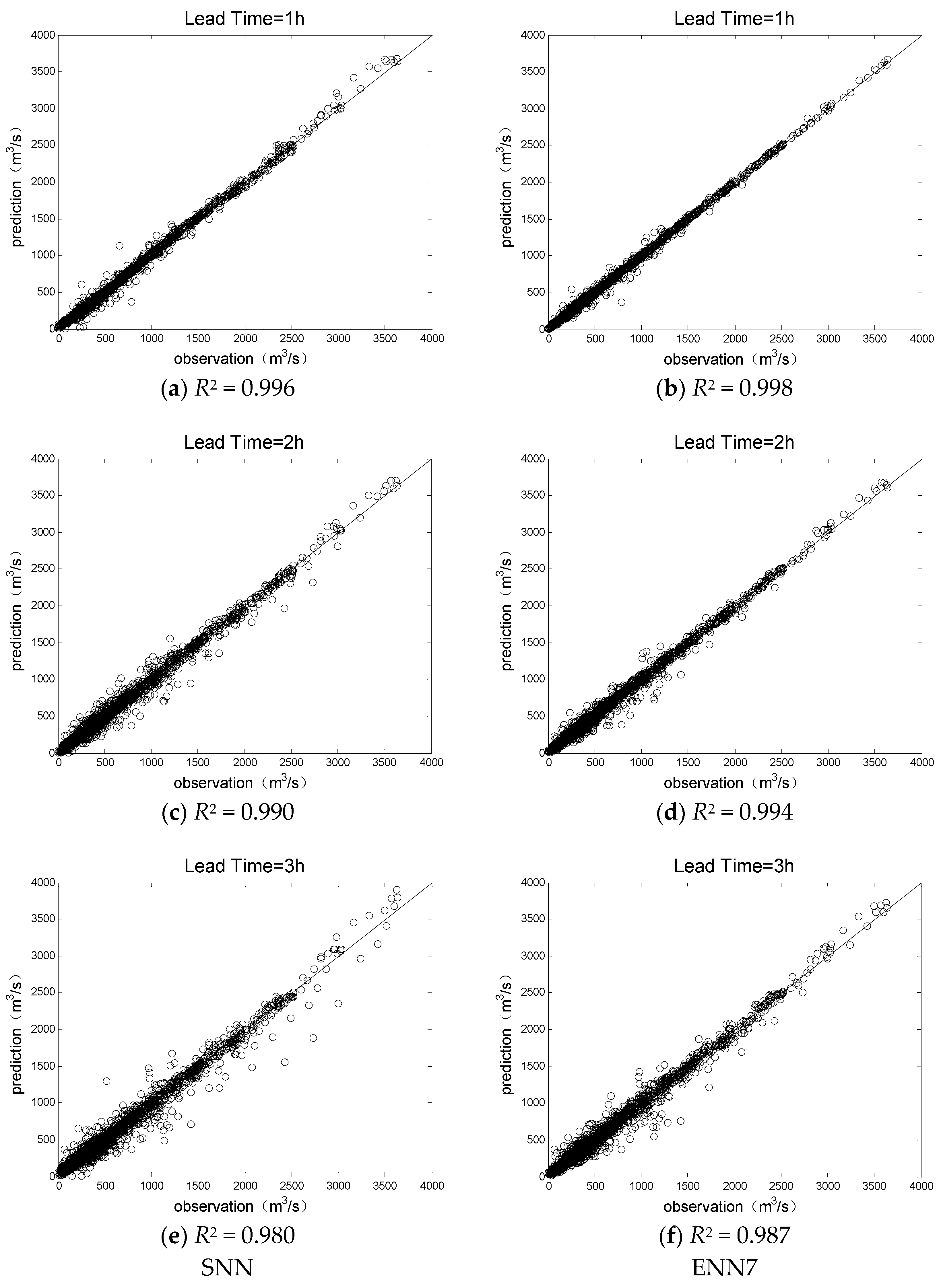
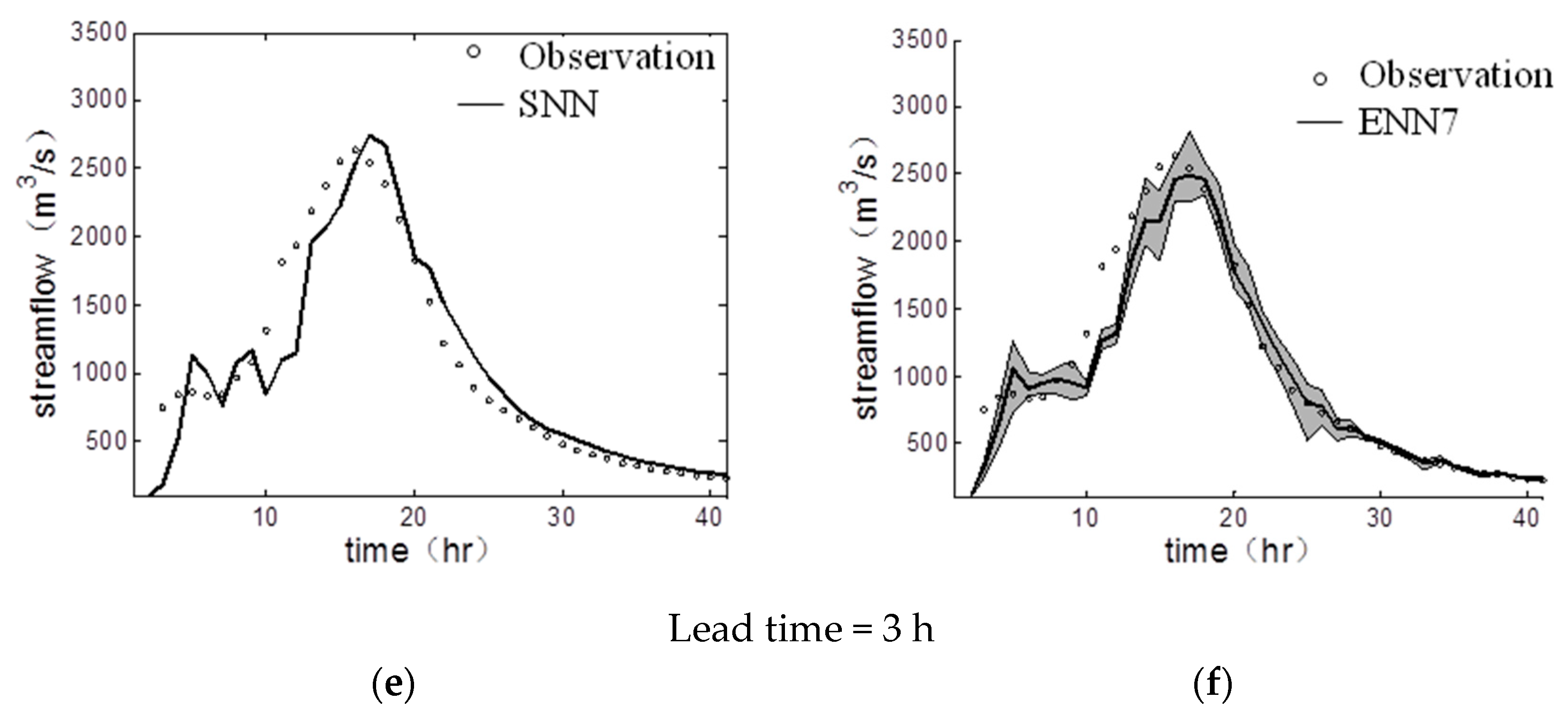
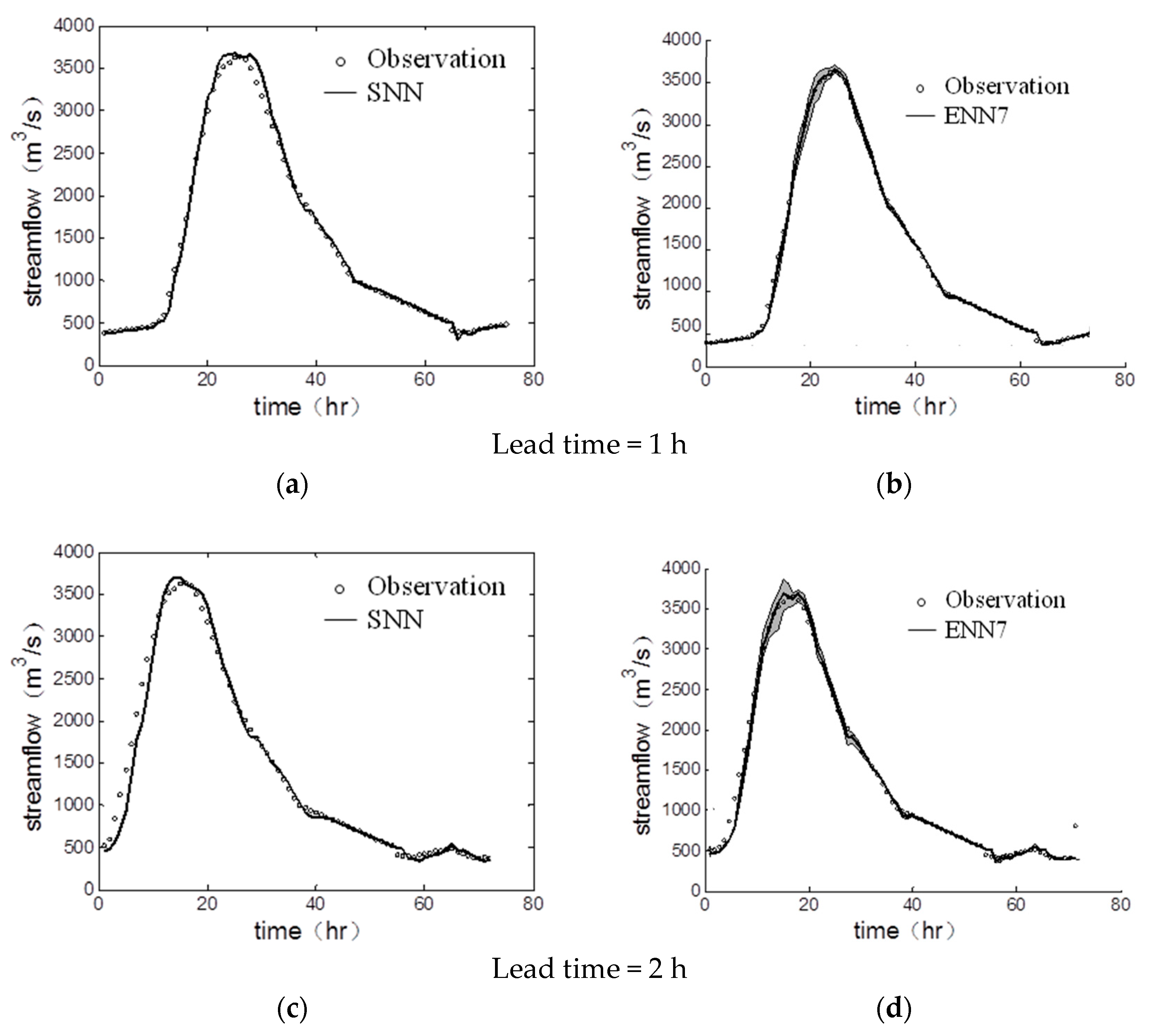
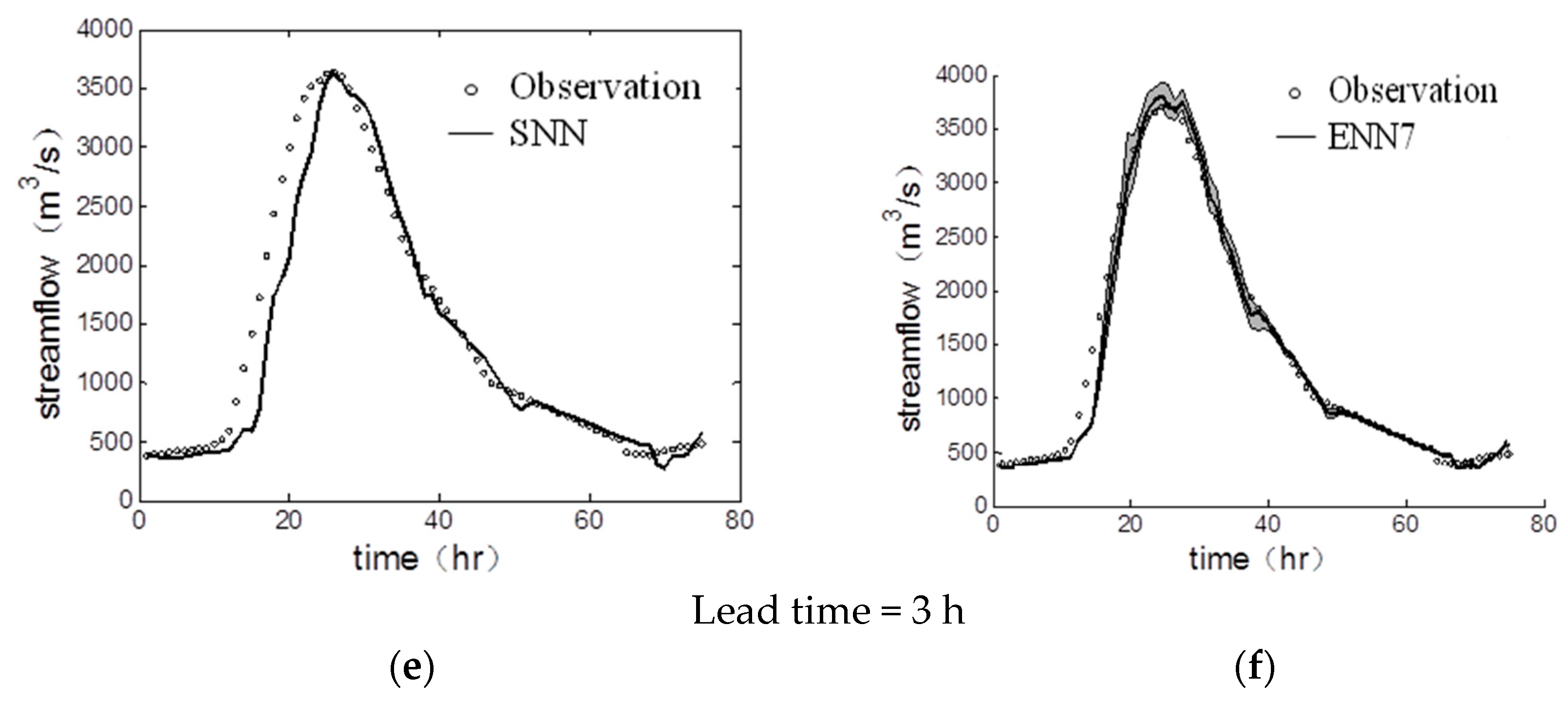
4.1. Comparison of a Single Neural Network and Ensemble Neural Network
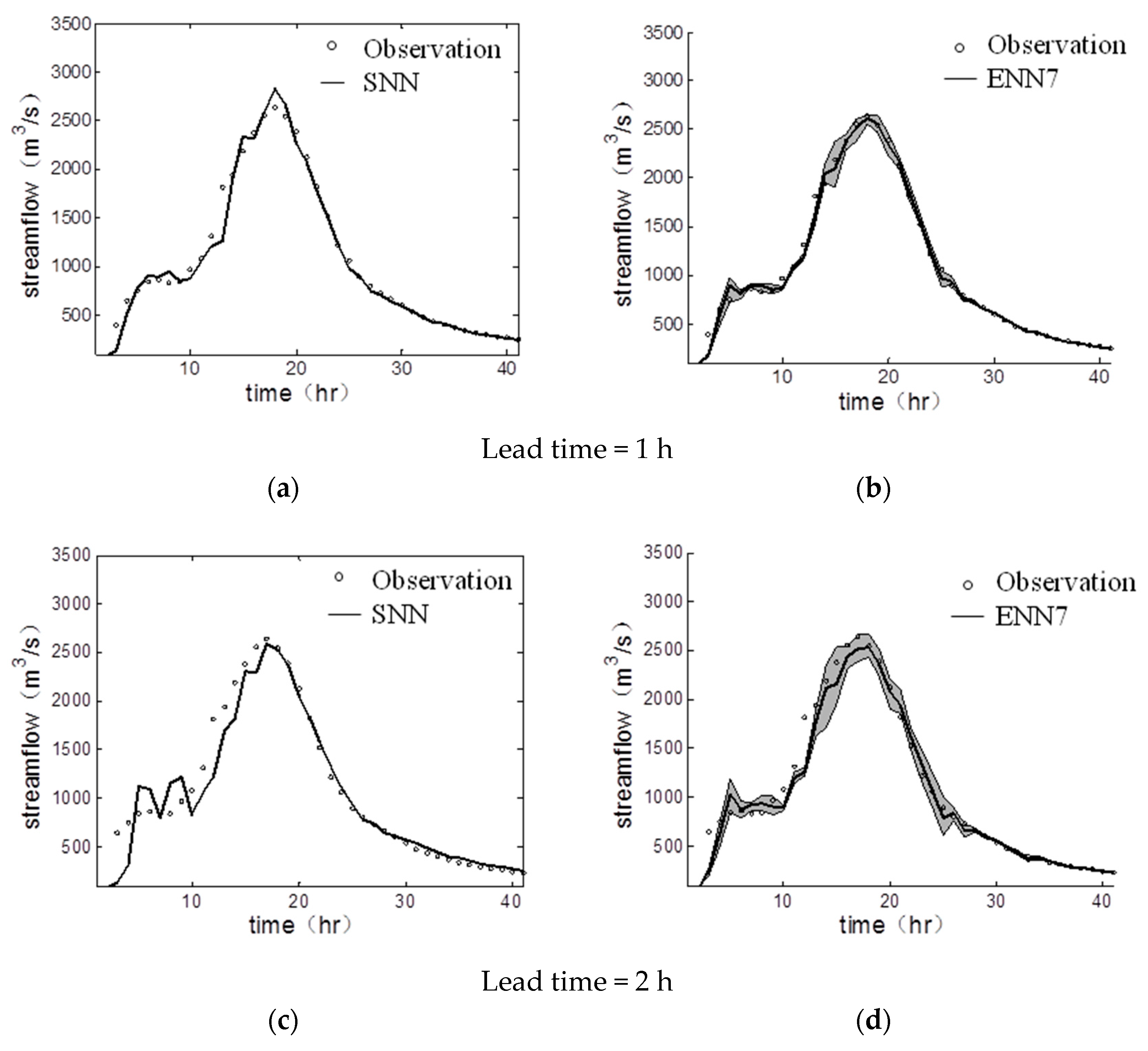
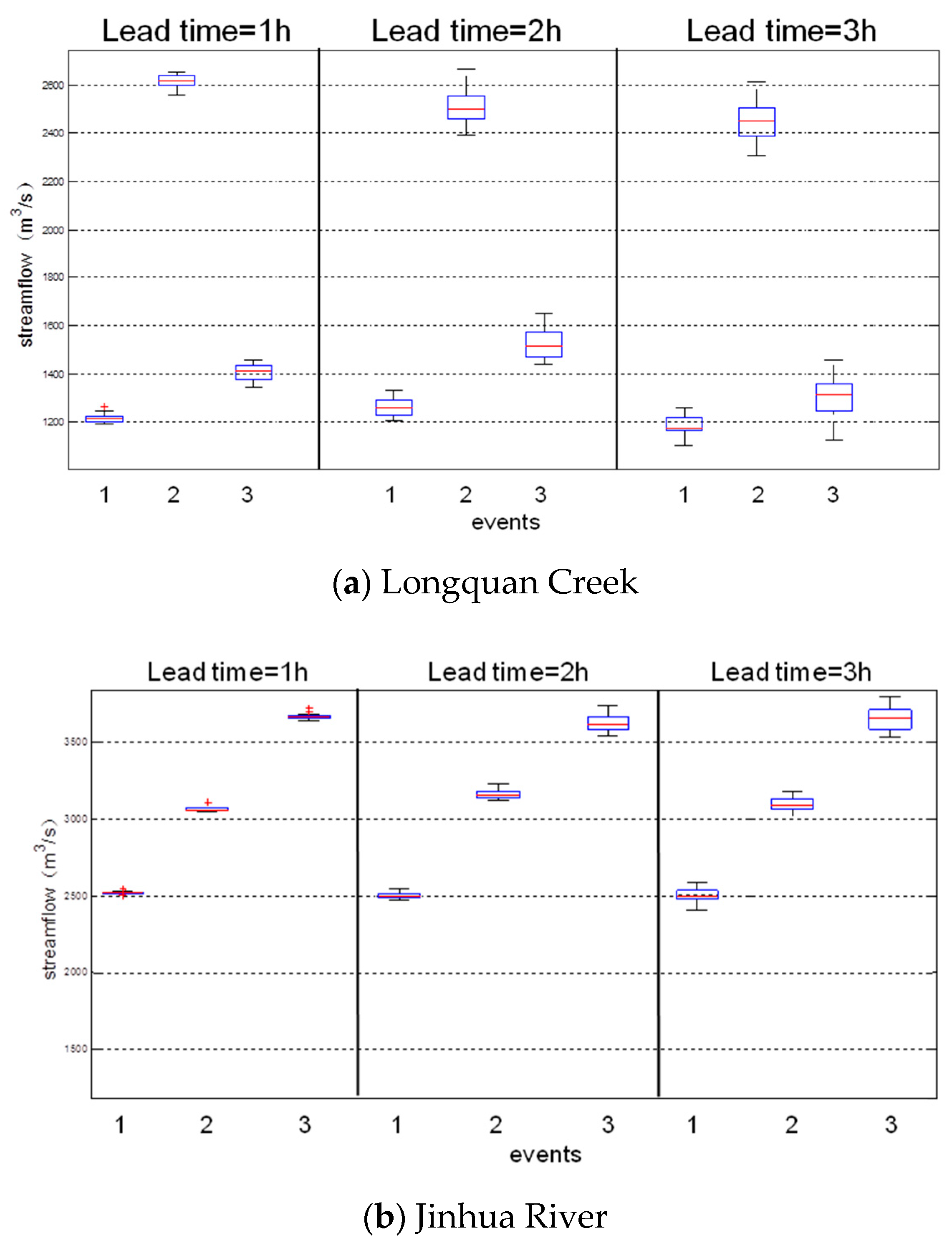
4.2. Peak Flow Prediction
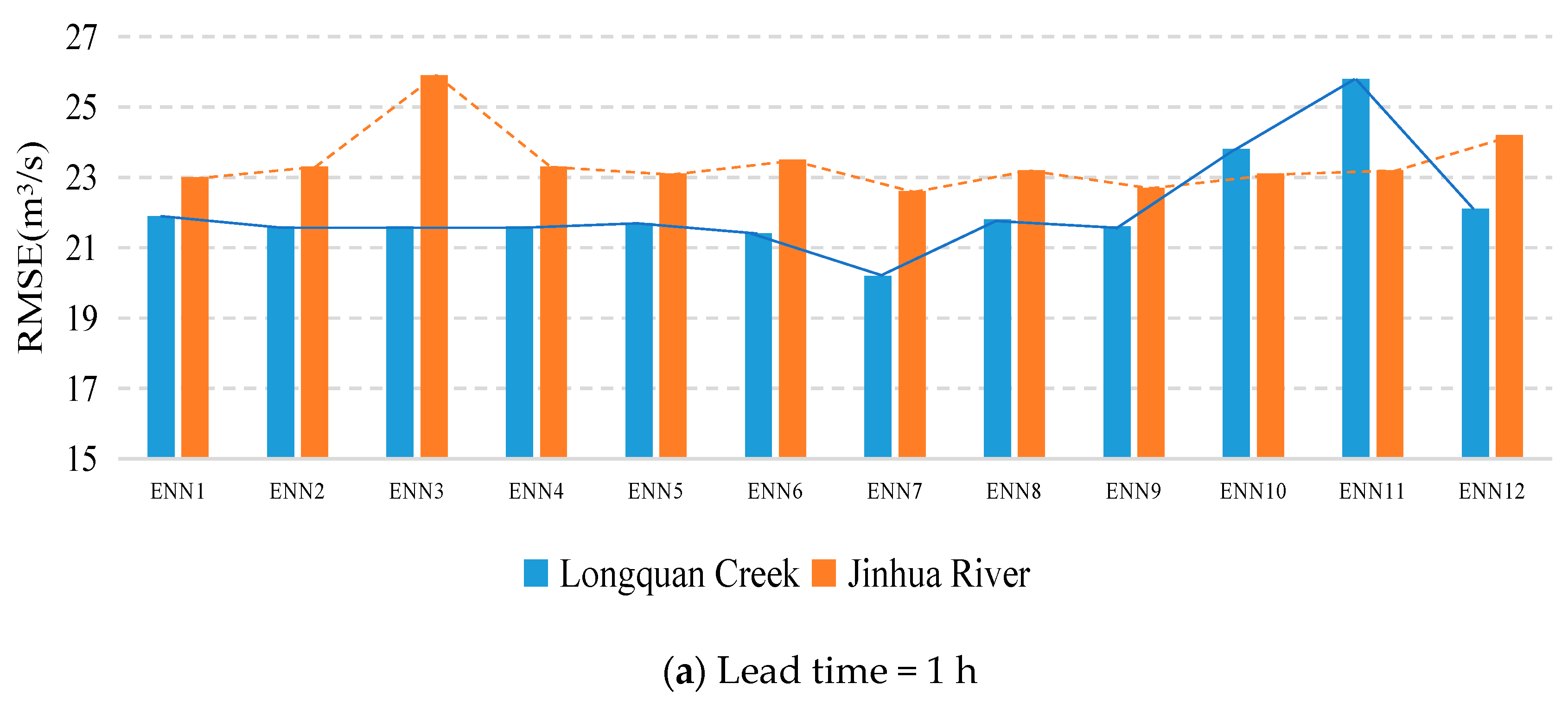
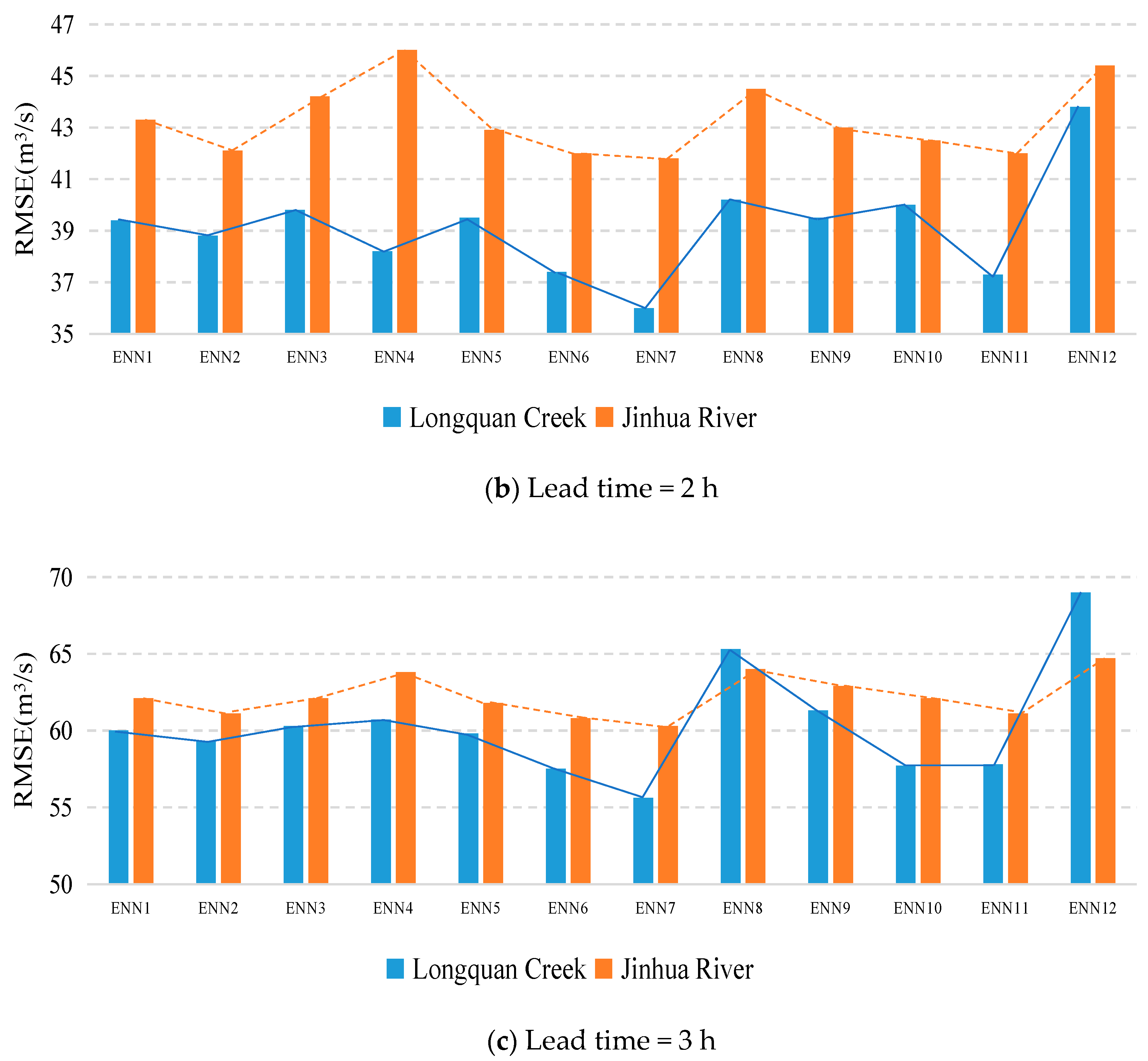
4.3. Sensitivity of Ensemble Neural Networks
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chang, F.J.; Tsai, M.J. A nonlinear spatio-temporal lumping of radar rainfall for modeling multi-step-ahead inflow forecasts by data-driven techniques. J. Hydrol. 2016, 535, 256–269. [Google Scholar] [CrossRef]
- Chokmani, K.; Ouarda, T.; Hamilton, S. Comparison of ice-affected streamflow estimates computed using artificial neural networks and multiple regression techniques. J. Hydrol. 2008, 349, 383–396. [Google Scholar] [CrossRef]
- Shu, C.; Ouarda, T.B.M.J. Flood frequency analysis at ungauged sites using artificial neural networks in canonical correlation analysis physiographic space. Water Resour. Res. 2007, 43, W07438. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, Y.; Lan, S.; Wang, H. A Comparative Study of Artificial Neural Networks, Support Vector Machines and Adaptive Neuro Fuzzy Inference System for Forecasting Groundwater Levels near Lake Okeechobee, Florida. Water Resour. Manag. 2016, 30, 375–391. [Google Scholar] [CrossRef]
- Maiti, S.; Tiwari, R.K. A comparative study of artificial neural networks, Bayesian neural networks and adaptive neuro-fuzzy inference system in groundwater level prediction. Environ. Earth Sci. 2014, 71, 3147–3160. [Google Scholar] [CrossRef]
- Sreekanth, J.; Datta, B. Stochastic and Robust Multi-Objective Optimal Management of Pumping from Coastal Aquifers Under Parameter Uncertainty. Water Resour. Manag. 2014, 28, 2005–2019. [Google Scholar] [CrossRef]
- Tsai, W.P.; Chiang, Y.M.; Huang, J.L.; Chang, F.J. Exploring the Mechanism of Surface and Ground Water through Data-Driven Techniques with Sensitivity Analysis for Water Resources Management. Water Resour. Manag. 2016, 30, 4789–4806. [Google Scholar] [CrossRef]
- Tsai, W.P.; Chang, F.J.; Chang, L.C.; Herricks, E.E. AI techniques for optimizing multi-objective reservoir operation upon human and riverine ecosystem demands. J. Hydrol. 2015, 530, 634–644. [Google Scholar] [CrossRef]
- Yin, X.A.; Yang, Z.F.; Petts, G.E.; Kondolf, G.M. A reservoir operating method for riverine ecosystem protection, reservoir sedimentation control and water supply. J. Hydrol. 2014, 512, 379–387. [Google Scholar] [CrossRef]
- Deolia, V.K.; Purwar, S.; Sharma, T.N. Stabilization of Unknown Nonlinear Discrete-Time Delay Systems Based on Neural Network. Intell. Control Autom. 2012, 3, 337–345. [Google Scholar] [CrossRef]
- Goyal, V.; Deolia, V.K.; Sharma, T.N. Neural network based sliding mode control for uncertain discrete-time nonlinear systems with time-varying delay. Int. J. Comput. Intell. Res. 2016, 12, 125–138. [Google Scholar]
- Dechant, C.M.; Moradkhani, H. Improving the characterization of initial condition for ensemble streamflow prediction using data assimilation. Hydrol. Earth Syst. Sci. 2011, 15, 3399–3410. [Google Scholar] [CrossRef] [Green Version]
- Faber, B.A.; Stedinger, J.R. Reservoir optimization using sampling SDP with ensemble streamflow prediction (ESP) forecasts. J. Hydrol. 2001, 249, 113–133. [Google Scholar] [CrossRef]
- Hao, Z.; Hao, F.; Singh, V.P. A general framework for multivariate multi-index drought prediction based on Multivariate Ensemble Streamflow Prediction (MESP). J. Hydrol. 2016, 539, 1–10. [Google Scholar] [CrossRef]
- Araghinejad, S.; Azmi, M.; Kholghi, M. Application of artificial neural network ensembles in probabilistic hydrological forecasting. J. Hydrol. 2011, 407, 94–104. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Chatterjee, C. Uncertainty assessment and ensemble flood forecasting using bootstrap based artificial neural networks (BANNs). J. Hydrol. 2010, 382, 20–33. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; Cibin, R.; Sudheer, K.P.; Chaubey, I. Constructing prediction interval for artificial neural network rainfall runoff models based on ensemble simulations. J. Hydrol. 2013, 499, 275–288. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Adamowski, J. Urban water demand forecasting and uncertainty assessment using ensemble wavelet-bootstrap-neural network models. Water Resour. Res. 2013, 49, 6486–6507. [Google Scholar] [CrossRef] [Green Version]
- El-Shafie, A.; Najah, A.; Alsulami, H.M.; Jahanbani, H. Optimized Neural Network Prediction Model for Potential Evapotranspiration Utilizing Ensemble Procedure. Water Resour. Manag. 2014, 28, 947–967. [Google Scholar] [CrossRef]
- Ohba, M.; Kadokura, S.; Yoshida, Y.; Nohara, D.; Toyoda, Y. Downscaling medium-range ensemble forecasts using a neural network approach. Proc. Int. Assoc. Hydrol. Sci. 2015, 369, 7–11. [Google Scholar] [CrossRef] [Green Version]
- Khalil, B.; Broda, S.; Adamowski, J.; Ozga-Zielinski, B.; Donohoe, A. Short-term forecasting of groundwater levels under conditions of mine-tailings recharge using wavelet ensemble neural network models. Hydrogeol. J. 2015, 23, 121–141. [Google Scholar] [CrossRef]
- Rumelhart, D.E. Learning Internal Representations by Error Propagation; MIT Press: Cambridge, MA, USA, 1986; ISBN 0-262-68053-X. [Google Scholar]
- Ouarda, T.B.M.J.; Shu, C. Regional low-flow frequency analysis using single and ensemble artificial neural networks. Water Resour. Res. 2009, 45, 114–122. [Google Scholar] [CrossRef]
- Chiang, Y.M.; Hao, R.N.; Ho, H.C.; Chang, T.J.; Xu, Y.P. Evaluating the contribution of multi-model combination to streamflow hindcasting by empirical and conceptual models. Hydrol. Sci. J. 2017, 62, 1456–1468. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm. In Proceedings of the Thirteenth International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef] [Green Version]
- Drucker, H. Improving Regressors using Boosting Techniques. In Proceedings of the Fourteenth International Conference on Machine Learning, Nashville, TN, USA, 8–12 July 1997; pp. 107–115. [Google Scholar]
- Breiman, L. Stacked regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Hoeting, J.A.; Madigan, D.M.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial (with discussion). Stat. Sci. 1999, 14, 382–401. [Google Scholar]
- Kass, R.E.; Raftery, A.E. Bayes factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Leamer, E.E. Specification Searches: Ad Hoc Inference with Nonexperimental Data; Wiley: New York, NY, USA, 1978; p. 370. ISBN 978-0471015208. [Google Scholar]
- Pearson, K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Seibert, J. On the need for benchmarks in hydrological modelling. Hydrol. Process. 2001, 15, 1063–1064. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, A.; van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Xiong, L.; Wan, M.; Wei, X.; O’Connor, K.M. Indices for assessing the prediction bounds of hydrological models and application by generalised likelihood uncertainty estimation. Hydrol. Sci. J. 2009, 54, 852–871. [Google Scholar] [CrossRef]

| Integrating Member | ||||
|---|---|---|---|---|
| Arithmetic Average | Bayesian Model Average | Stacking Average | ||
| Generating member | Disturbance of initial value | ENN1 | ENN5 | ENN9 |
| Bagging resampling skill | ENN2 | ENN6 | ENN10 | |
| Boosting resampling skill | ENN3 | ENN7 | ENN11 | |
| Alteration of model structure | ENN4 | ENN8 | ENN12 | |
| Statistic | Longquan Creek | Jinhua River | ||||
|---|---|---|---|---|---|---|
| Training | Validation | Testing | Training | Validation | Testing | |
| Max. | 3040 | 2430 | 2640 | 4200 | 3810 | 3640 |
| Min. | 13 | 7 | 11 | 2 | 6 | 3 |
| Mean | 248 | 216 | 202 | 514 | 575 | 510 |
| STD | 323 | 318 | 256 | 550 | 628 | 528 |
| Criteria | R2 | RMSE | Gbench | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Lead Time | 1 h | 2 h | 3 h | 1 h | 2 h | 3 h | 1 h | 2 h | 3 h |
| SNN | 0.984 | 0.955 | 0.928 | 32.2 | 54.3 | 69.0 | 0.375 | 0.489 | 0.587 |
| ENN1 | 0.993 | 0.976 | 0.945 | 21.9 | 39.4 | 60.0 | 0.712 | 0.731 | 0.688 |
| ENN2 | 0.993 | 0.977 | 0.947 | 21.6 | 38.8 | 59.3 | 0.720 | 0.740 | 0.696 |
| ENN3 | 0.993 | 0.976 | 0.945 | 21.6 | 39.8 | 60.3 | 0.720 | 0.726 | 0.685 |
| ENN4 | 0.993 | 0.978 | 0.944 | 21.6 | 38.2 | 60.7 | 0.720 | 0.746 | 0.680 |
| ENN5 | 0.993 | 0.976 | 0.946 | 21.7 | 39.5 | 59.8 | 0.718 | 0.730 | 0.690 |
| ENN6 | 0.993 | 0.979 | 0.950 | 21.4 | 37.4 | 57.5 | 0.726 | 0.757 | 0.713 |
| ENN7 | 0.994 | 0.980 | 0.953 | 20.2 | 36.0 | 55.6 | 0.754 | 0.775 | 0.732 |
| ENN8 | 0.993 | 0.975 | 0.936 | 21.8 | 40.2 | 65.3 | 0.715 | 0.719 | 0.631 |
| ENN9 | 0.993 | 0.976 | 0.943 | 21.6 | 39.5 | 61.3 | 0.720 | 0.730 | 0.674 |
| ENN10 | 0.991 | 0.976 | 0.950 | 23.8 | 40.0 | 57.7 | 0.659 | 0.723 | 0.711 |
| ENN11 | 0.990 | 0.979 | 0.949 | 25.8 | 37.3 | 57.8 | 0.600 | 0.759 | 0.711 |
| ENN12 | 0.993 | 0.971 | 0.928 | 22.1 | 43.8 | 69.0 | 0.706 | 0.668 | 0.587 |
| Criteria | R2 | RMSE | Gbench | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Lead Time | 1 h | 2 h | 3 h | 1 h | 2 h | 3 h | 1 h | 2 h | 3 h |
| SNN | 0.996 | 0.990 | 0.980 | 32.3 | 53.1 | 75.5 | 0.827 | 0.776 | 0.730 |
| ENN1 | 0.998 | 0.993 | 0.986 | 23.0 | 43.3 | 62.1 | 0.913 | 0.851 | 0.817 |
| ENN2 | 0.998 | 0.994 | 0.987 | 23.3 | 42.1 | 61.1 | 0.910 | 0.859 | 0.823 |
| ENN3 | 0.998 | 0.993 | 0.986 | 25.9 | 44.2 | 62.1 | 0.888 | 0.845 | 0.817 |
| ENN4 | 0.998 | 0.992 | 0.986 | 23.3 | 46.0 | 63.8 | 0.910 | 0.832 | 0.807 |
| ENN5 | 0.998 | 0.993 | 0.987 | 23.1 | 42.9 | 61.8 | 0.912 | 0.854 | 0.819 |
| ENN6 | 0.998 | 0.994 | 0.987 | 23.5 | 42.0 | 60.8 | 0.909 | 0.860 | 0.825 |
| ENN7 | 0.998 | 0.994 | 0.987 | 22.6 | 41.8 | 60.3 | 0.915 | 0.862 | 0.828 |
| ENN8 | 0.998 | 0.993 | 0.985 | 23.2 | 44.5 | 64.0 | 0.911 | 0.843 | 0.806 |
| ENN9 | 0.998 | 0.993 | 0.986 | 22.7 | 43.0 | 62.9 | 0.915 | 0.853 | 0.813 |
| ENN10 | 0.998 | 0.994 | 0.986 | 23.1 | 42.5 | 62.1 | 0.912 | 0.857 | 0.817 |
| ENN11 | 0.998 | 0.994 | 0.987 | 23.2 | 42.0 | 61.1 | 0.910 | 0.860 | 0.823 |
| ENN12 | 0.998 | 0.993 | 0.985 | 24.2 | 45.4 | 64.7 | 0.903 | 0.836 | 0.802 |
| ENN7 | Lead Time = 1 h | Lead Time = 2 h | Lead Time = 3 h | ||||
|---|---|---|---|---|---|---|---|
| Qp | Qp’ (m3/s) | Error (%) | Qp’ (m3/s) | Error (%) | Qp’ (m3/s) | Error (%) | |
| Longquan Creek Basin | |||||||
| Event 1 | 1191 | 1215 | 2 | 1261 | 6 | 1181 | −0.8 |
| Event 2 | 2640 | 2618 | −0.8 | 2510 | −5 | 2466 | −6.5 |
| Event 3 | 1410 | 1403 | −0.5 | 1524 | 8 | 1280 | −9 |
| Jinhua River Basin | |||||||
| Event 1 | 2520 | 2523 | 0.1 | 2507 | −0.5 | 2508 | −0.5 |
| Event 2 | 3040 | 3062 | 0.7 | 3045 | 0.2 | 3165 | 4.1 |
| Event 3 | 3640 | 3665 | 0.7 | 3611 | −0.8 | 3731 | 2.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiang, Y.-M.; Hao, R.-N.; Zhang, J.-Q.; Lin, Y.-T.; Tsai, W.-P. Identifying the Sensitivity of Ensemble Streamflow Prediction by Artificial Intelligence. Water 2018, 10, 1341. https://doi.org/10.3390/w10101341
Chiang Y-M, Hao R-N, Zhang J-Q, Lin Y-T, Tsai W-P. Identifying the Sensitivity of Ensemble Streamflow Prediction by Artificial Intelligence. Water. 2018; 10(10):1341. https://doi.org/10.3390/w10101341
Chicago/Turabian StyleChiang, Yen-Ming, Ruo-Nan Hao, Jian-Quan Zhang, Ying-Tien Lin, and Wen-Ping Tsai. 2018. "Identifying the Sensitivity of Ensemble Streamflow Prediction by Artificial Intelligence" Water 10, no. 10: 1341. https://doi.org/10.3390/w10101341
APA StyleChiang, Y.-M., Hao, R.-N., Zhang, J.-Q., Lin, Y.-T., & Tsai, W.-P. (2018). Identifying the Sensitivity of Ensemble Streamflow Prediction by Artificial Intelligence. Water, 10(10), 1341. https://doi.org/10.3390/w10101341







