Long Term Hydrodynamic Effects in a Semi-Arid Mediterranean Multilayer Aquifer: Campo de Cartagena in South-Eastern Spain

Abstract

The Mediterranean basin contains many semi-arid environments where aquifers are subject to intensive exploitation, generally to meet irrigation demands. The Campo de Cartagena aquifer is a clear example from such a semi-arid environment, and its hydrodynamic effects have aroused great scientific interest. The main objective of this study is to evaluate the hydrodynamic effects that have occurred in the last century of anthropogenic activity in this aquifer system. This aquifer is subject to intensive exploitation and shows clear deficits in times of drought, with recharge by irrigation playing an important role. This study’s methodology includes groundwater modelling to reconstruct the transient evolution of the aquifer system during the last century, to generate water balances and to illustrate how the evolution of irrigation has, in many ways, changed the aquifer’s groundwater flow pattern. The results delineate the hydraulic communication of the aquifer stratums through specific geological structures, as well as the flow transfer from the Quaternary layer to the Mar Menor and the Mediterranean Sea. The reconstruction of the entire system’s temporal evolution shows a fragile water balance that is supported by surface-water contributions.

1. Introduction

Anthropization is one of the main influences on groundwater hydrodynamics. These changes have an important impact on all water systems, with special repercussions for groundwater and for the hydrogeological processes associated with these systems. In the Mediterranean Sea’s basin, there are many cases of intensive aquifer exploitation, which have led to a need for sustainable environmental management and increased the fragility of the Mediterranean’s underground water resources [1]. Decades of strong agricultural development in these Mediterranean semi-arid zones have led to changes in groundwater systems and hydrogeological processes. A clear example of the pressure that anthropization has put on the Mediterranean environment is the area called Campo de Cartagena in south-eastern Spain, which has problems that are characteristic of semi-arid regions in developed countries. It is necessary to study areas such as this one to better understand the hydrogeological functioning of these aquifers and to create quantitative evaluations of internal water flows so as to improve the sustainable management of these water resources [2,3,4]. In these environments, intensive groundwater exploitation has affected numerous aquifers, with piezometric drops of up to 200 m across several decades [5].

The multilayer coastal aquifer at Campo de Cartagena in south-eastern Spain is an exceptional example of decades-long intensive exploitation and is a paradigmatic case for the Mediterranean region [6] due to the extreme anthropogenic activity and the fact that the aquifer system is in the semi-arid zone [7]. This anthropogenic activity has generated hydrogeological uncertainties that need to be resolved, including the hydrogeological geometry of the natural aquifer system; the hydrochemical conditions of the main multilayer aquifers; the recharge sources; the interconnectivity between surface aquifers and deeper, confined aquifers; the impact that existing wells have on the water system; and the quantification of groundwater discharge to the Mar Menor and the Mediterranean Sea. These uncertainties are challenges but are also opportunities to pursue research objectives. Important hydrological modifications in the Campo de Cartagena aquifer require research to improve the understanding of this water system’s evolution. This research has a clear scientific interest and important socioeconomic relevance due to the aquifer’s interrelations with agriculture and the presence of the Mar Menor coastal lagoon [7,8]. Since the 1979 initiation of the Tagus-Segura Water Transfer (TSWT)—which has a maximum endowment of 122 Mm³/yr—to provide surface water for irrigation in the area, the aquifer has tended toward decreasing piezometric levels in its deep layers and toward a recovery of piezometric levels in its shallow layers. This ambiguous effect is due to intensive use and irrigation returns, which modify the piezometric levels of the aquifer stratums differently depending on whether they are unconfined or confined. Thus, there is a clear scientific interest in this aquifer’s hydrogeological functioning.

Some researchers have provided preliminary models for this study, but in their works, they only studied the unconfined Quaternary layer, not the lower, confined aquifer layers [9,10]. These models of the Quaternary layer provide a preliminary prediction for a steady state, with uncertainties about recharge and pumping extractions. Some researchers have calculated the recharge of the study area, thus reducing the uncertainty associated with the calculations [7,10,11,12]. Other researchers have considered the evolution of agrarian demand in the area and the repercussions in terms of recharge. However, pumping extractions continue to be a source of uncertainty and require deeper study, as part of that uncertainty is transmitted to the results of future research.

Some scholars have conducted recent studies on alternative sources of water supply that could meet the existing demand, such as public seawater desalination plants and private groundwater desalination plants [13,14]. The reuse of purified wastewater has also been recognized as an adequate resource for water supply in arid and semi-arid zones. Recently, other scholars have developed studies on the overexploitation of aquifers in the Campo de Cartagena area and in the Segura basin [3], as well as on the transfer of contaminants through abandoned, leaky or poorly constructed boreholes and on cross-formational groundwater flow between unconfined (shallow) and confined (deep) aquifers [15,16,17,18,19].

Many authors have begun using current-flow models in groundwater research [20], and there are now a large number of works with flow modelling MODFLOW, which solves the flow equation using the finite-difference method [21]. There are still unresolved issues, including the hydrodynamic effect caused by the decades-long strong anthropization in the multilayered aquifers of semi-arid environments and the inversion of the hydraulic gradient (i.e., the dual effect of irrigation returns); these concerns mean that there is a need for new investigations that advance the hydrological and hydrogeological knowledge of this system. In these cases, the MODFLOW method of numerical modelling is a good way to obtain positive results despite the scarcity of existing data [22]. Researchers on both the anthropogenic impact and the dual effect of irrigation returns have concluded that the water system is most fragile in confined aquifers. Thus, there is a need for studies on this type of aquifer in semi-arid environments.

This study’s main objective is to evaluate the hydrodynamic effects that have occurred in the last century of intense anthropogenic activity in this multilayered coastal aquifer system. The main tool in this process is a new, multilayer mathematical model that evaluates the existing layers, both on the surface and below, using MODFLOW. This work includes a study of the water flows between the aquifer layers and a reconstruction of the temporary evolution in the transient regime from 1925 to 2015; this will allow for better understanding and quantification of the impact that human activities have had on the groundwater resources during that period. This study also includes the development of methods to evaluate vertical flow transfers due to abandoned and leaking boreholes, thus, creating a first approximation of the hydraulic communication between stratums. The interrelations of the water system with the coastal environment are also studied, with special attention given to the aquifer’s connections to the Mar Menor lagoon and the Mediterranean Sea. This allows for improved understanding of the Campo de Cartagena aquifer’s internal functioning and provides new tools for characterizing it and its relationships with the environment. Finally, this work includes a preliminary study on the influence that existing wells have on vertical hydraulic communication.

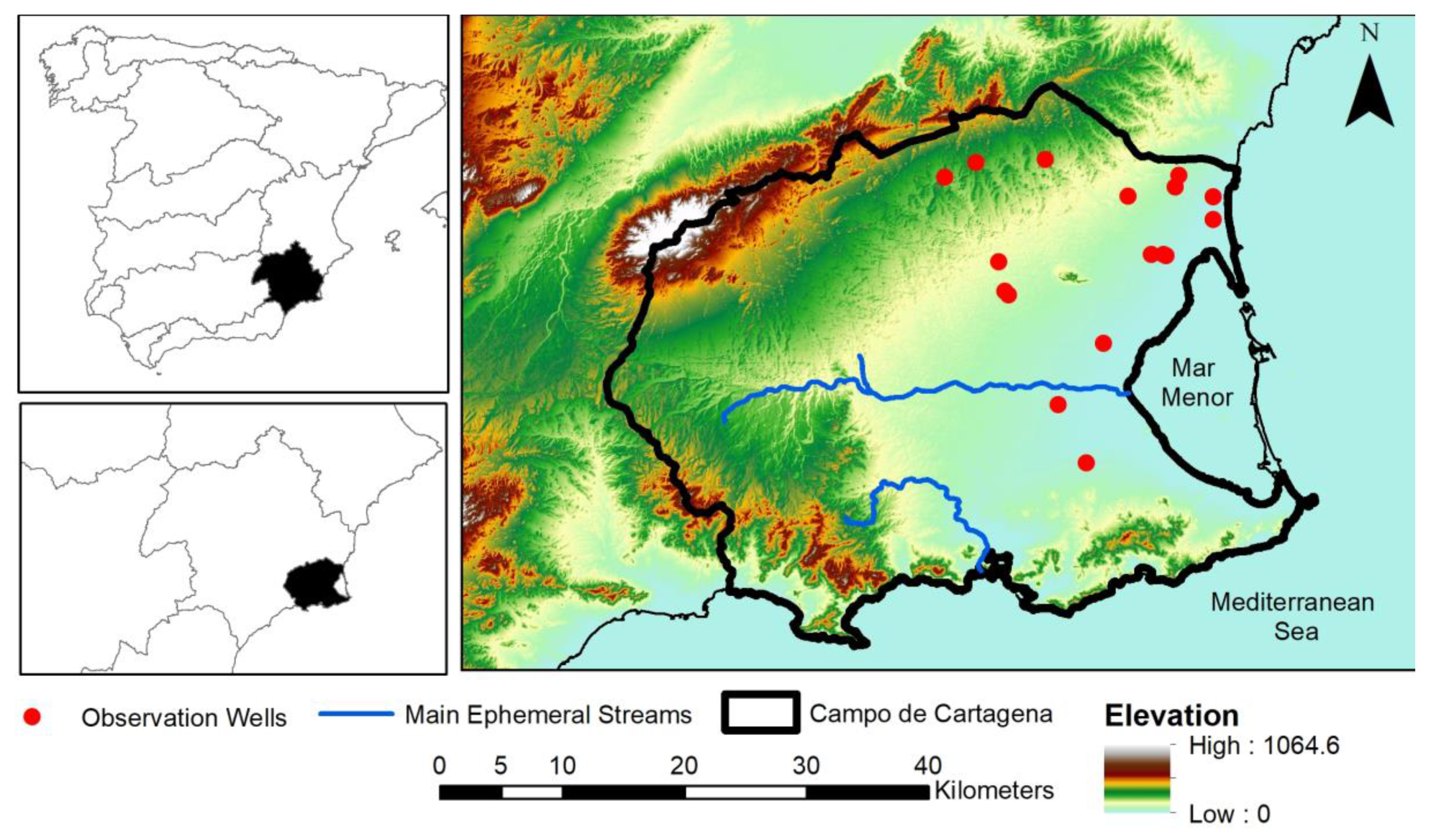
2. Case Study Area

The area called Campo de Cartagena is a large plain with a gentle slope toward the southeast; it has an approximate area of 1600 km², and is surrounded by mountainous terrain except in the east, where it borders the Mar Menor and the Mediterranean Sea (Figure 1). This area is characterized by a lack of permanent watercourses, as is the case in other semi-arid environments, as well as by the dry riverbeds (ramblas) with negligible slopes that form the peculiar morphology of south-eastern Spain [23]. These ephemeral streams collect surface runoff that travels short distances and ends up pouring into the Mar Menor lagoon or into the Mediterranean Sea [24].

This low basin or alluvial plain, which consists of unconstrained Quaternary detrital materials, currently includes an irrigated area around 43,000 ha [25]. The average annual precipitation in this area barely exceeds 315 mm—somewhat higher in the mountainous areas and somewhat lower in the coastal zones—according to data from several meteorological stations in the area [12]. The region’s scarce rainfall and high temperatures make its water needs significant. As a result, many aquifers have been overexploited to meet agricultural demand, causing significant reductions in piezometric levels and increased salinization (with a consequent degradation in water quality) [26].

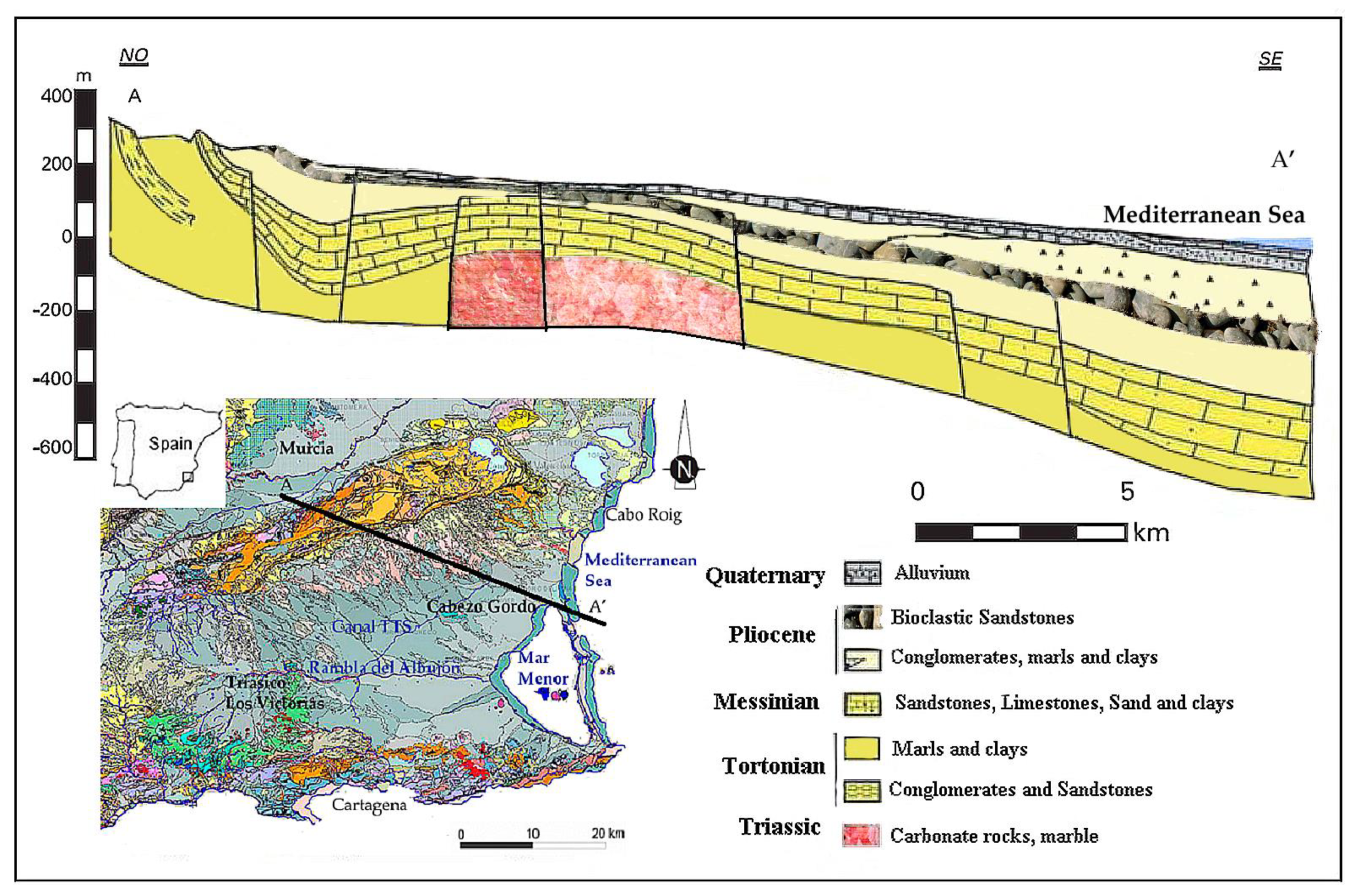
2.1. Geology

The neogenic coastal soil that forms this zone has a roughly 1000 m-thick Neogene-Quaternary filling from the Tertiary period on a bedrock of Triassic marble, and constitutes a post-orogenic depression of the Baetic Cordillera geological region. This region has a predominance of marl, alternating with sandstone and the conglomerates that form the Tortonian aquifer stratum; in the Messinian stratum, sandstone and bioclastic calcarenite alternate, giving shape to the upper Miocene. In the other stratums, the Pliocene aquifer layer is formed from sandstone and white marl. Within the Tertiary stretches is the Quaternary stratum, which consists of sand, silt, clay, conglomerates, caliche and sandstone (Figure 2). The various aquifers are geologically well-defined and are separated by thick aquitard layers [2]. Within this multilayered coastal aquifer, the Pliocene and Messinian stretches have special hydrogeological relevance due to their intensive exploitation.

The study area is stratified into permeable layers, which sometimes causes problems for the hydraulic continuity of the groundwater body. The tectonics of this zone, with its barriers and divisions, also affects the hydraulic continuity, giving rise to local hydrogeological independencies that cause general heterogeneity and that generate variability in the data obtained from nearby areas [10]—which is also incorporated into the developed model. In turn, more than 1200 private wells are officially registered, and many of them exploit several aquifers through internal communication, which allows for artificial connections between stretches of water [18].

2.2. Historical Evolution of Anthropogenic Activities

In the middle of the 19th century, several authors mentioned the existence of an artesian basin in the Campo de Cartagena, and in the early 20th century, several more commented on the drilling of artesian wells due to mining research [27]. In recent hydrogeological studies, researchers have addressed the groundwater problems of Campo de Cartagena from several perspectives, including sustainable management of groundwater based on sustainability indexes [28]; contamination between aquifers [18]; and recharge of the Campo de Cartagena aquifer [7,29].

The groundwater-irrigated surface area, plus the area irrigated by other sources, results in a net irrigated area of more than 43,000 ha, according to the Segura River Basin Agency (CHS) [25]. As can be seen in

Table 1. Temporal evolution of the irrigated area in Campo de Cartagena in terms of average irrigation endowments [25,30].

Description	1980	1991	1998	2004	2010	2015
Irrigated Area (ha)	14,521	23,911	34,328	39,254	42,253	43,071
Irrigated Demand (Mm3/yr)	94.39	155.42	223.14	223.75	270.50	258.40
Irrigated Rate (m3/ha/yr)	6500	6500	6500	5700	6500	6000

, in the 21th century, the increase in the irrigated area has slowed down and, in the last decade, it has even stabilized.

The groundwater of this aquifer system is of special importance to the entire region’s agrarian activity, as it has an extractive volume that varies from 70 to 125 Mm³/yr, in addition to contributions from TSWT (with a maximum annual allocation of 122 Mm³/yr), the Segura basin (4.2 Mm³/yr), the reuse of purified water (13.2 Mm³/yr) and the Mojón desalination plant (2.2 Mm³/yr) [25].

The irrigation demand and the average water supply for each agricultural demand unit and type of crop have evolved as more efficient irrigation systems have entered the market, thus enabling an optimization of resources and even reducing the gross endowments per hectare and per year; this has increased the surface area that is under localized irrigation to the current 98% [31]. The CHS calculates the gross demand for irrigated area [25], and the average endowment for Campo de Cartagena has shrunk from 6500 to 6000 m³/ha/yr. The actual consumption of water in the fields in some irrigation communities has decreased even further, with values close to 5700 m³/ha/yr (Table 1). The temporal evolution of the region’s gross irrigation demand has continuously grown over time, with a clearly increasing line and an important increase at the end of the 20th century and the beginning of the 21th century. However, it has stabilized in recent years, following patterns similar to the development of the irrigable surface in the agricultural demand units that compose Campo de Cartagena.

3. Materials and Methods

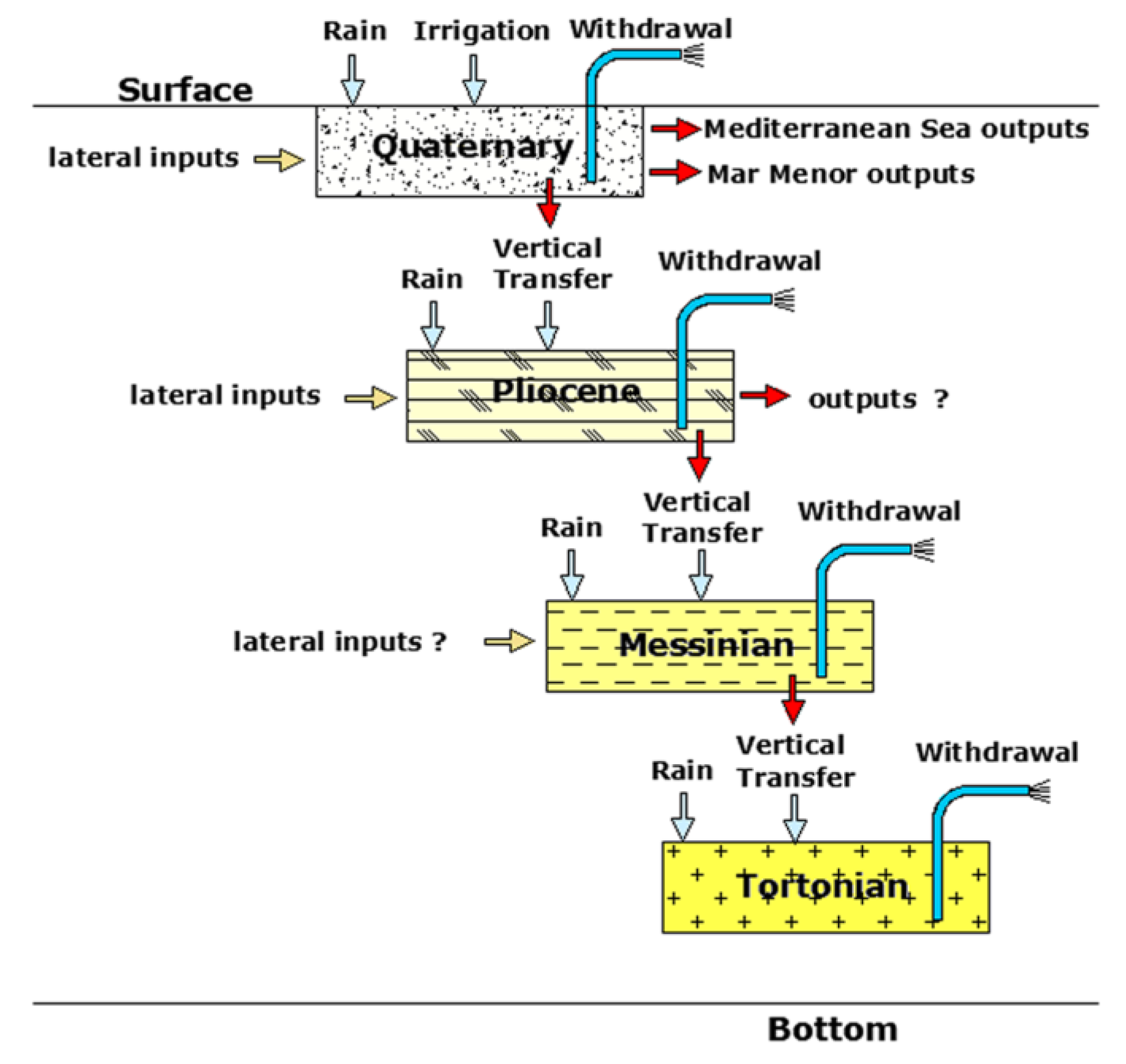
3.1. Numerical Model

Groundwater flow models, which provide adequate modelling for most hydrogeological problems from real situations, are a commonly used tool in hydrogeological research. Therefore, numerical modelling has become an important and valid method in groundwater research [20,32]. The method that is applied to the resolution of this study’s model is based on code that solves the equation for the underground flow using finite 3D differences. This method also discretizes the environment of block modelling [33], which is freely available and widely disseminated and which has multiple prior examples [22,34]; this gives the method a high degree of acceptance in the scientific research on groundwater, for which there is a lack of data. Researchers have used the Visual MODFLOW program, which simulates behavior under constant and transient regimes, as a processor in this method.

To realize complex numerical models at the regional level, it is necessary to simplify the model areas and to make certain assumptions [35]. This simplification of reality in this model is as follows. Although the stratums of the area are formed by rocks with fractures and faults, these stratums are treated in the model as a porous medium of constant density. The hydraulic conductivity is treated as anisotropic with respect to the vertical and horizontal directions and as heterogeneous according to the type of material (so as to apply Darcy’s law for groundwater). There is a slight uncertainty about the limit of the domain and about whether it coincides with the exact limit of the underground basin, so we decided to delimit the region of the model using a limit of zero flow, that is to say, that model boundary has no flow boundary condition.

Groundwater movement through porous materials of constant density can be described in three dimensions using the general groundwater-flow equation, which is based on Darcy’s law:

$$\nabla \left(K\nabla h\right)+W\left(x,y,z\right)=Ss\frac{\partial h}{\partial t}$$

(1)

where K is hydraulic conductivity (LT⁻¹), h is hydraulic head (L), W is volumetric flux per unit volume (representing sources and/or sinks), x and y are horizontal coordinates (L), z is vertical coordinate (L), Ss is specific storage and t is time (T).

When constructing a conceptual model, it is necessary to identify the domain boundaries and the stratums of the aquifer [35]. The flow models should include information on the geology and hydrogeology of the area under study; the well-log, pumping, piezometry and hydrogeological data; and the stratums’ geometry [36]. In this work, the data on water extractions via pumping and on recharging via rainfall and irrigation returns are required. To calculate the results, MODFLOW uses iterative methods and obtains the solution for the system of differential equations using the finite-difference method for each time step and several modelling phases.

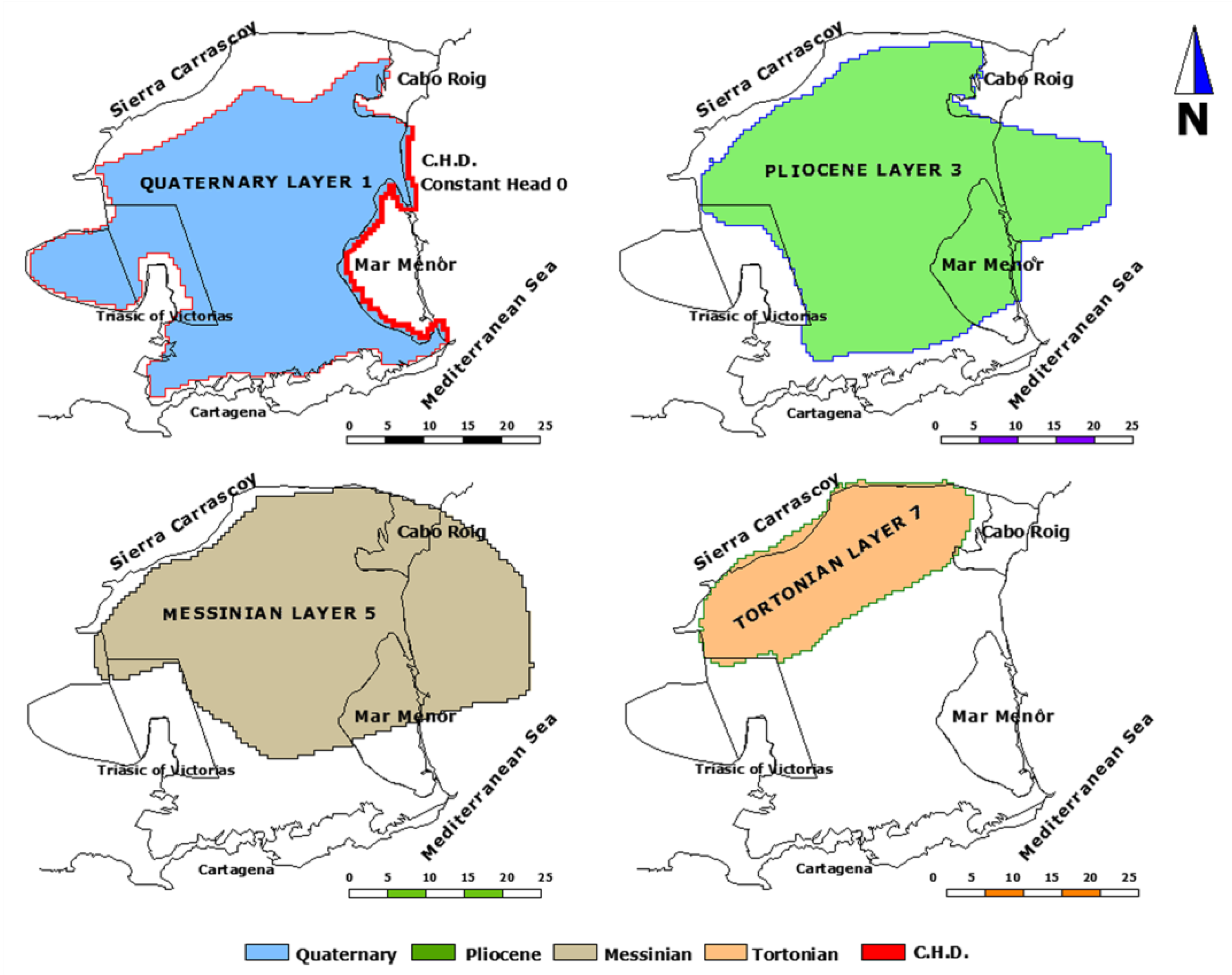
3.2. Model Setup and Geometry

The model layers’ geometry and the initial hydrogeological parameters were obtained from other studies that the Geological Survey of Spain (IGME) and other researchers have carried out [3,9,10,11,12]. A schematic representation of the conceptual model is shown in Figure 3. Values for the piezometric levels of the observation points were obtained from the CHS and the IGME, and the rainfall data were obtained from the State Meteorological Agency. For the preparation of the initial geometry, topography (0) was obtained from existing maps (National Geographic Institute) and then digitized using computer-aided design programs.

The model was framed using the Universal Transverse Mercator (UTM) coordinates (647,000, 4,155,000) and (720,000, 4,210,000). The study area was modelled using a finite-difference regular grid with grid cells spaced at 500 m × 500 m. The grid covered the whole area and contained 110 rows and 147 columns, for 16,170 total cells in each of the 9 layers and a total of 145,530 cells. The cells were of variable thickness, and the whole model’s catchment area was 4015 km².

Aquifer layer 1 represents the Quaternary aquifer layer in its full extension, between the outcrops of the Sierra Carrascoy and both the Mar Menor lagoon and Mediterranean Sea (Figure 4). Layers 2, 4, 6 and 8 are aquitards, which are generally composed of marl and clay, and the bottom later (Layer 8) is completed, according to the model, at −2500 m. The third (Pliocene) layer consists mainly of sandstone; the fifth (Messinian) layer is composed of conglomerates, with sand and marl intercalations and bioclastic limestone; and the seventh (Tortonian) layer consists of marl, sand and sandstone. This model has two types of boundary conditions: The flow limit and the constant head limit, which coincides with level 0 of the aquifer (at the Mar Menor lagoon and the Mediterranean Sea); this level includes all the cells bordering these two seas. The river and drainage conditions are not taken into account in this study because, in this area, the natural channels are dry all year round, except for some storms. The area’s geological structure is very complex; for instance, the Cabezo Gordo horst is an important structure in the bedrock, and there are also several deposits with thicknesses greater than 2000 m.

Previous researchers have studied a possible marine intrusion from the Mar Menor and the Mediterranean Sea into the Quaternary layer, but the results found very small values for such intrusion [9], so it was not introduced into the model. Other considerations include recharge by rain on the surfaces of the Quaternary layer and in the outcrops of the lower stratums, as well as the irrigation returns from the agricultural areas [2].

3.3. Hydrodynamic Parameters

After the conceptualization of the model (Figure 3), the values of the initial hydraulic head and the hydrogeological parameters (hydraulic conductivity, specific storage, and storage coefficient), hydraulic parameters (porosity) were introduced (

Table 2. Information introduced for numerical modelling of the Campo de Cartagena.

Layers	Type	Total Surface	Outcrops Surface	Elevation	Thickness	Hydraulic Conductivity	Specific Storage	Specific Yield	Effective Porosity
		(Inland Surface)		Top/Bottom	Average	Average	Average	Average	Average
		km2	km2	m	m	m/day	m−1
1	Unconfined	1187 (1135)	1135	0/−55	55	1.5 × 102	4.0 × 10−3	0.200	0.230
2	Confined	-	-	−55/−160	105	1.0 × 10−5	1.0 × 10−7	6.00 × 10−5	0.015
3	Confined	1265 (945)	110	−160/−225	65	5.5 × 102	4.2× 10−3	0.022	0.250
4	Confined	-	-	−225/−325	100	1.0 × 10−5	1.0 × 10−7	6.00 × 10−5	0.015
5	Confined	1309 (851)	63	−325/−470	145	4.0 × 102	1.0 × 10−5	0.020	0.250
6	Confined	-	-	−470/−610	140	1.0 × 10−5	1.0 × 10−7	6.00 × 10−5	0.015
7	Confined	460 (460)	46	−610/−725	115	2.0 × 102	3.5 × 10−5	0.035	0.230
8	Confined	-	-	−725/−2000	1275	1.0 × 10−6	1.0 × 10−7	6.00 × 10−5	0.015

), and each layer and cell were assigned values within the model. According to the recommendations of the MODFLOW user manual [33], the vertical hydraulic conductivity should be an order of magnitude lower than the horizontal hydraulic conductivity so as to introduce the anisotropy that usually exists in the underground water layers. To verify that the model’s geometry and its parameters are correct and that the model approaches the reality of the aquifers, it was necessary to compare the evolution of the levels calculated in MODFLOW with the existing piezometry.

3.4. Boundary Conditions and External Forcings

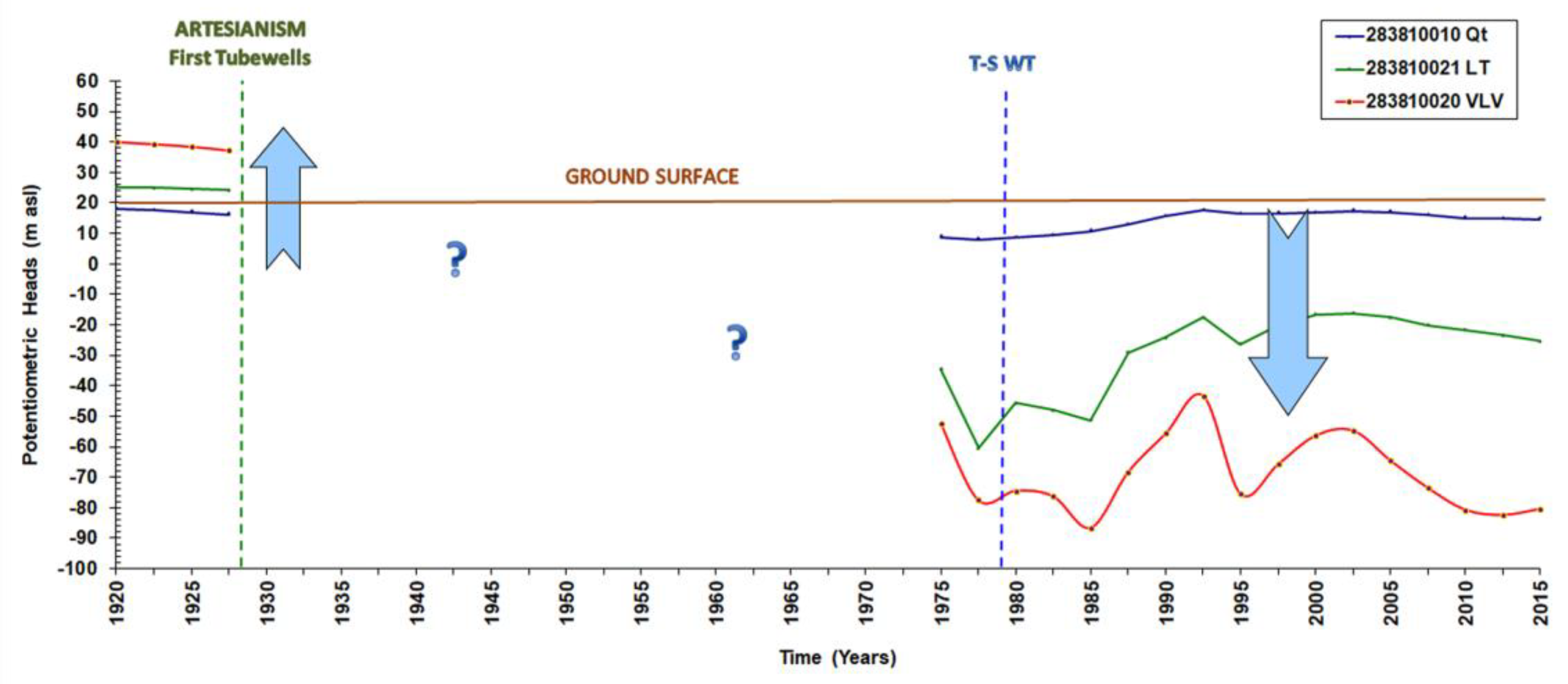
3.4.1. Piezometric Data

The piezometry was performed with well data from the CHS and IGME databases. IGME’s piezometric measurements, which began in the mid-1970s, show that current stability was preceded by a gradual recovery of groundwater, linked to the initiation of the TSWT as an external source of water at the beginning of 1979. The available historical data help to reveal the aquifer’s status before the IGME measurements began. At the initiation of water withdrawals in the 1920s, piezometric heads in the Pliocene and Messinian aquifer layers in the coastal area were respectively 25 m and 45 m above sea level (masl) (Figure 5). Such values are much higher than the ones provided by the IGME database and corroborate the description of artesian wells [37] by local newspapers at the beginning of the 20th century.

The data on the piezometric levels, which were obtained through the interpolation of non-linear functions between 1925 and 1975, as well as the IGME and CHS data for 1975 through to 2015, were evaluated and introduced into the model (in stress periods of 5 years) to determine the behavior of the system in both steady and transient states. The upper aquifers today have higher hydraulic heads than the deeper aquifers, which is the opposite of the situation a century ago (Figure 5).

An inversion occurred in the vertical hydraulic gradient between the layers, and the movement of the flow between the aquifer layers through the wells is now the opposite of what it was, corresponding to these two phases that occurred during this time. In the last 20 years of data (1995–2015), the groundwater levels were stable, with measurements of 10–15 masl for the Quaternary and 15–25 m below sea level (mbsl) for the Pliocene; however, there were irregular but decreasing levels of 55–80 mbsl for the Messinian. Despite the low heads of the confined levels, there is no evidence of seawater intrusion [7].

3.4.2. Recharge

To enter the recharge data in the model, zoning maps were created using agricultural demand units and type of crop. To calculate recharge, an average annual precipitation index value of 313 mm/yr was used [12]. According to other studies, average net infiltration varies between 17 mm/yr [7] and 50 mm/yr [30]. In this work, net infiltration was set to 35 mm/yr. Other researchers have estimated an average value of 210 mm/yr for the recharge of irrigation returns [2,11], and have related irrigation returns to the type of crop in a given area [10]. Where data are provided, the recharge rates from irrigation (Ir) are 397 mm/yr for horticultural crops, 201 mm/yr for perennial crops and 194 mm/yr for fruit trees. For the flow model, a recharge map based on various indices (according to the type of predominant crop) shows an average value of 160 mm/yr, except in the case of agricultural crops irrigated by rain, for which recharge occurs only through natural pluviometry.

For the applied value of a natural recharge of 35 mm/yr (Figure 6), the model showed an annual recharge volume of 47 Mm³/yr for rain. The gross demand in the study was 5800 m³/ha/yr for a net crop area of 43,071 ha. The volume of irrigation demand is 250 Mm³/yr, and the annual recharge volume is 116.2 Mm³/yr (for Ir = 102 mm/yr); these values are slightly higher than those provided in similar models (e.g., 84 mm/yr [9]) and using other methodologies (e.g., 80 mm/yr [38]).

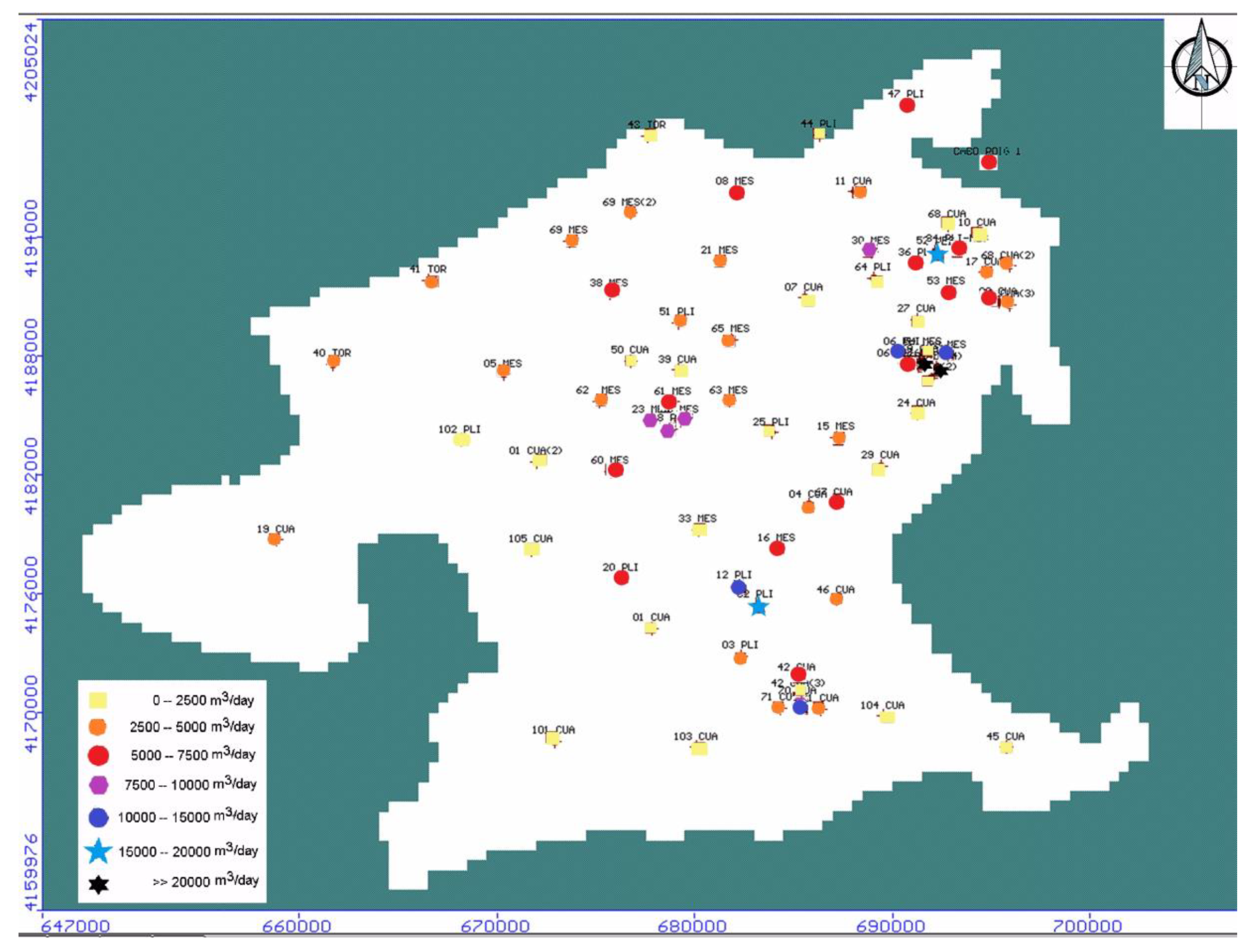
3.4.3. Withdrawals

We simplified the data for extractions through pumping wells due to the large number of existing wells (about 2000), using zones but preserving global flows; however, there is still some uncertainty about the quantity and location of real extractive flows. Among these pumping wells, some are old and/or inactive wells; they are generally deficiently constructed, and they generate hydraulic communication between the layers of the aquifer, sometimes causing water contamination from one aquifer to another [15,18]. The well data have been simplified to include 72 boreholes: A total of 17 located in their exact UTM positions and the rest located based on the concentration of existing wells in given areas (Figure 7). The withdrawal values were updated according to reference [25], with an estimated withdrawal of 88 Mm³/yr, but there is still some uncertainty about this parameter, as no more precise data are available. According to the available information, at the beginning of the TSWT in 1979, a volume of around 120 Mm³/yr was being pumped; withdrawal then declined in the following years, with increases in periods of droughts and withdrawal volumes of approximately 125 Mm³/yr. The flow model was calibrated with withdrawal volumes of 90.65 Mm³/yr, which is slightly higher than the values established in a prior study [25].

3.4.4. Intra-Borehole Aquifer Cross-Contamination

The transfer of contaminant flows between aquifers through poorly constructed, abandoned or leaking wells can have a great impact on the generation of contaminant flows between unconfined upper aquifers and confined deep aquifers [2,18]. This is due to contamination from agrochemicals in irrigation returns. The strong demand for irrigation water in certain periods has led to the installation of small desalination plants, usually using reverse osmosis, which in turn has caused brine discharges in the Quaternary layer that have deteriorated water quality [3].

A simulation was run using the model to quantify (approximately) which part of the flow is transmitted through faults, geological discontinuities and the Cabezo Gordo horst, as well as which part of the flow moves through poorly constructed, abandoned or leaking wells. Due to the enormous geographical dispersion of the existing wells (2000), simplification was necessary to reduce the number of wells in the model layers; a series of cells operates as concentration zones for wells in aquitards and in the layers of aquifers. In this way, a first approximation was made to quantify the flow through the wells by means of theories similar to those of Lacombe et al. (1995) [15] and IGME [30].

The model was run with the aquitards traversed only by the Cabezo Gordo horst; with a hydraulic conductivity of around 0.25 m/day; and with edge contacts in the Triassic of the Victories, which lies north of the Sierra de Cartagena-La Union and the outcrops of the Sierra de Carrascoy and which has a hydraulic conductivity of around 0.05 m/day. The effect of the abandoned pumping wells was estimated by means of cells in areas with a high density of wells, resulting in an average hydraulic conductivity of 2.3 m/day. A model execution was also carried out with the aquitards in their natural states, without taking into account the poorly constructed, abandoned or leaking wells. This was done to provide an order of magnitude of their impact on the vertical flow between the layers of the aquifer [39].

3.4.5. Lateral Groundwater Discharge

In the coastal area of Campo de Cartagena, where the Mar Menor lagoon and the Mediterranean Sea are located, only the Messinian, Pliocene and Quaternary aquifer layers are present; however, for stratigraphic and tectonic reasons, the hydraulic relationships between these seas take place mainly through the Quaternary layer. Due to the gradual increase in this aquifer’s piezometric levels in recent times, an increase in the discharge of groundwater to the Mar Menor lagoon is expected, with the possible consequent adverse effect of a greater entry of nitrates and other agrochemical elements from fertilization [8].

In the model, a constant head line 0 was introduced along the contact between the Quaternary layer and the seas. This border was divided into four parts: Three for the edge of the Mar Menor and one for the coast of San Pedro del Pinatar. The bidirectional flow between the land area and the maritime zone was then calculated. Finally, the various layers were introduced, up to the Messinian layer under the Mar Menor and the Mediterranean Sea, so as to determine whether there is a transfer of flow between the layers and the marine waters.

3.5. Model Evaluation Criteria

Model performance was assessed quantitatively using the coefficient of determination (R²), the root mean square error (RMSE) and the normalized root mean square error (NRMSE) and qualitatively using graphical time series plots. R², RMSE and NRMSE were calculated from the following equations:

$${\mathrm{R}}^2=\frac{{{\displaystyle \sum }}_{i=1}^n\left(h_m-\overline{h_m}\right)\times \left(h_s-\overline{h_s}\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(h_m-\overline{h_m}\right)}^2\times {\left(h_s-\overline{h_s}\right)}^2}}$$

(2)

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(h_m-h_s\right)}^2}{n}}$$

(3)

$$\mathrm{NRMSE}=\frac{\mathrm{RMSE}}{h_m^{max}-h_m^{min}}$$

(4)

where n is the total number of observations and $h_m$ and $h_s$ are the observed and simulated values of aquifer´s hydraulic head, respectively. $h_m^{max}-h_m^{min}$ is the maximum difference in the observed head values. If the value of R² is close to 1, it indicates a good correlation between simulated and observed head. The RMSE varies from the optimal value of 0 to a large positive value.

4. Results

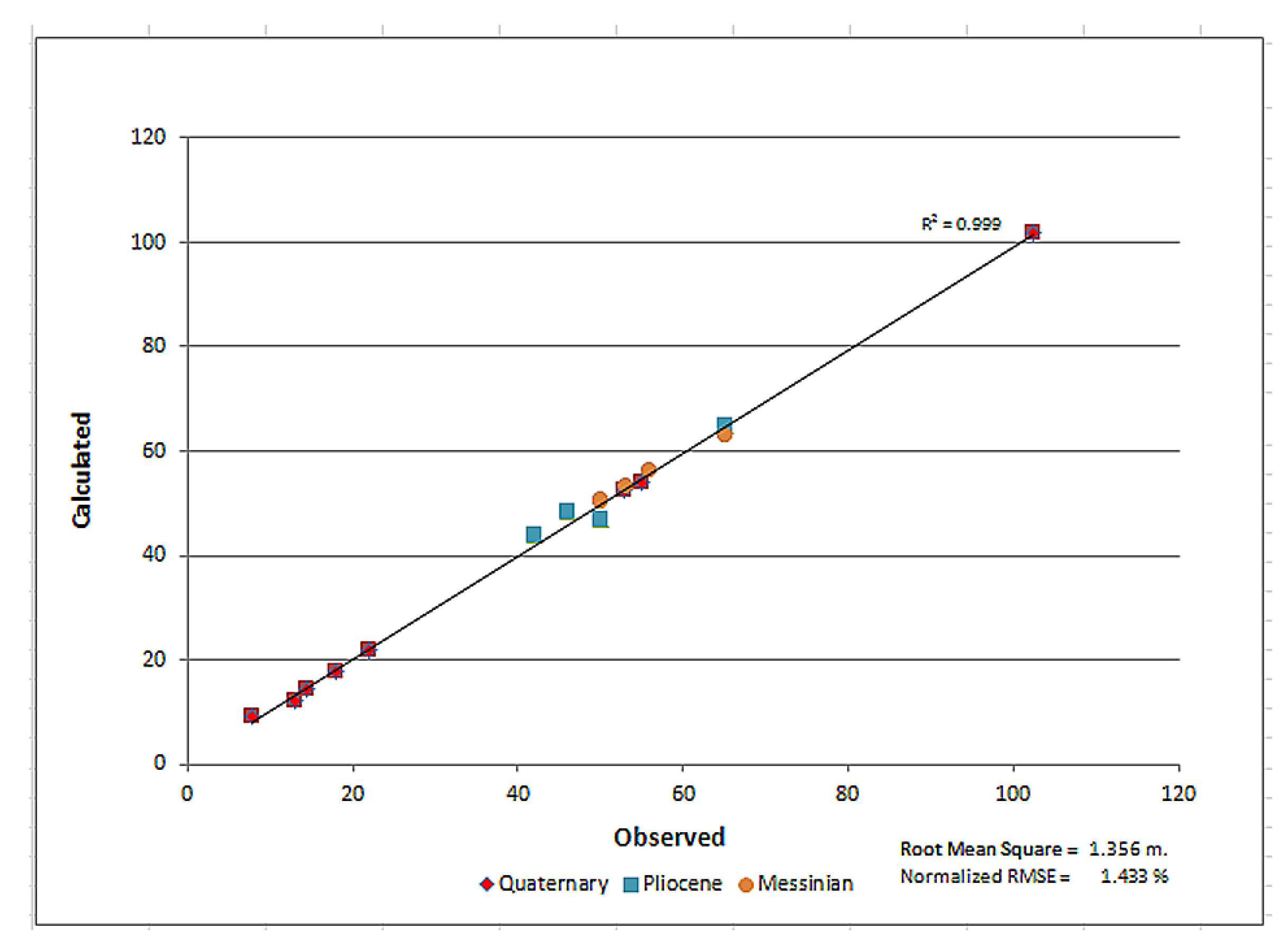
4.1. Calibration of the Model

Seventeen observation wells were used for the calibration, along with piezometric data obtained from the IGME and CHS databases (Figure 1). A simulation of the last 90 years, starting in 1925, was conducted. The steady-state simulation reflects the original state of the aquifers in 1925, prior to the anthropization of the zone due to extractive pumping. Model calibration is usually an iterative process in which values of hydrogeological parameters are adjusted so that the differences between the variables that the model calculates and the field measurements are as small as possible [40]. The method used in this study to calibrate the model was trial and error, and the most sensitive parameters were the recharge and the hydraulic conductivity.

4.1.1. Calibration of the Model in the Steady State

Equilibrium conditions for a steady state are achieved when the amount of water that recharges an aquifer is similar to the amount of discharge into other zones and when the hydraulic head is more or less constant over time [41]. The calibration for the steady-state regime in this study was thus achieved through the parameters of hydraulic conductivity and recharge. During the calibration process, the model’s main adjusted hydrogeological parameter was hydraulic conductivity; small adjustments were also made for recharge. The results show a good fit with the data obtained in 1925 in terms of the levels observed in the stratums of the aquifer and the levels that the model obtained (Figure 8). The coefficient of determination (R²) is 0.999 and the NRMSE is 1.433%. This validates the calibrated hydrogeological parameters and means that the developed model can be used for prediction.

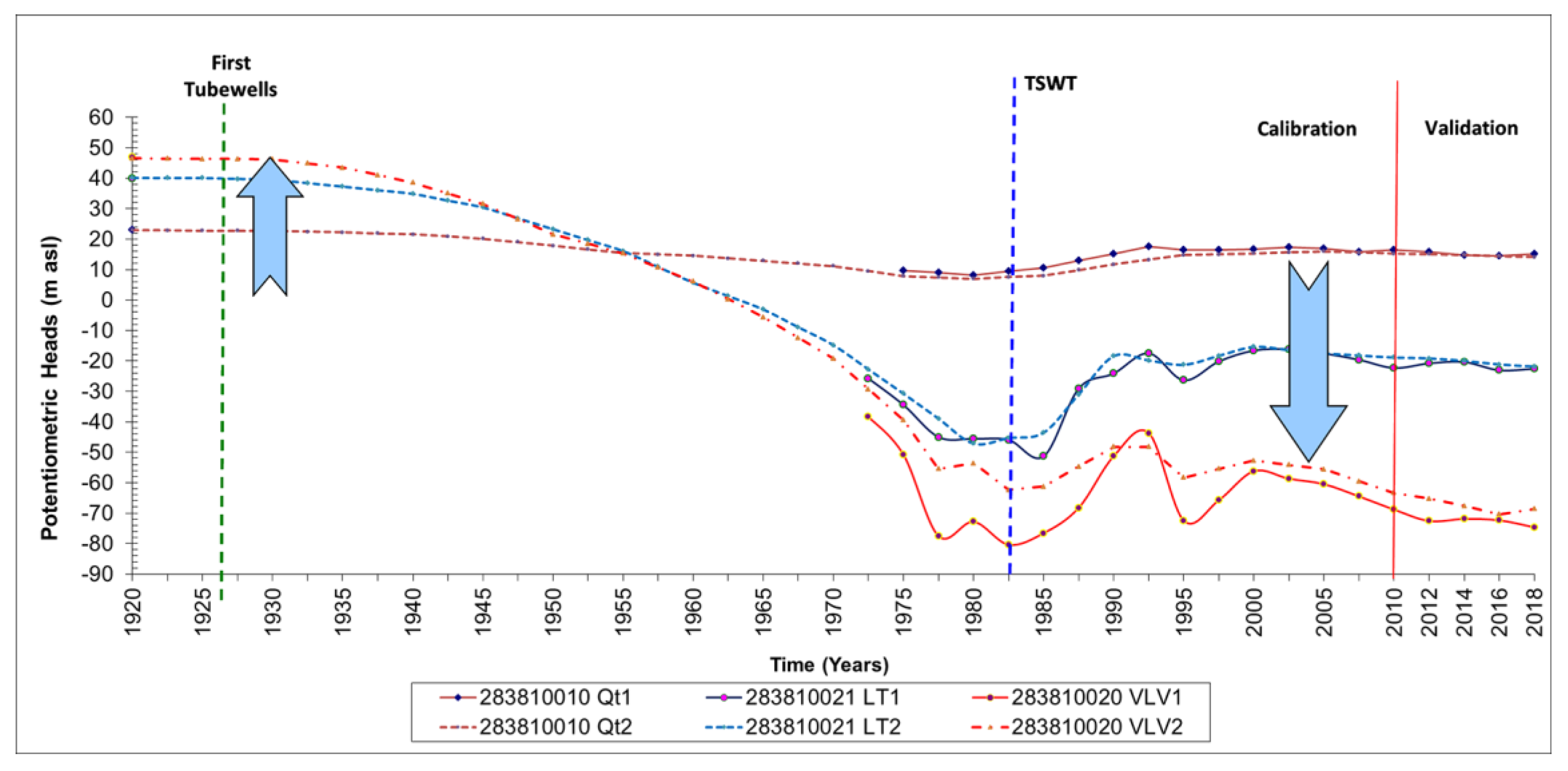
4.1.2. Calibration and Validation of the Model in Transient State

The model’s piezometric levels for the beginning of the transient state are equal to the levels at the steady state before the anthropization of the medium. Subsequently, this model was adjusted to a transient regime, and the data obtained for the aquifer exploitation were used. In the case of transient regimes, in addition to conductivity, the storage coefficient should be considered. In the period of the transitional state (from 1925 to 1980), there was a gradual growth in pumping extractions in Campo de Cartagena. This growth changed with the initiation of the TSWT, as the surface water from that project began to be used to supply agricultural demand.

As can be seen in Figure 9, the period from 1975 to 2010 was chosen for model calibration. For the transient state calibration, three parameters were used: Hydraulic conductivity (for some areas), the storage coefficient, and the rate of pumping extractions. This last parameter was very sensitive to calibration and is necessary to modify the values, including the spatial locations of the extraction points and these points’ allocations to each aquifer. The calibration adjustments were made by comparing the hydraulic head values from the available data with those that the model calculated.

Table 3. Calibrated parameters in the transient state.

Layers	K (m/day) (Min/Max)	Ss (1/m) (Min/Max)	P (Mm3/yr) (Average)
Quaternary	0.01/40	1.2 × 10−3/2.4 × 10−3	22.2
Pliocene	0.01/35	2.0 × 10−4/3.4 × 10−4	24.6
Messinian	0.01/4	2.0 × 10−4/2.4 × 10−4	42.1
Tortonian	0.01/3.5	3.2 × 10−4	3.1
Marls Aquitard	3 × 10−5	5 × 10−7

K: Hydraulic conductivity; Ss: Storage coefficient; P: Pumping extractions.

shows the calibrated value for each parameter. Previous authors such as IGME (1991) [30] and Baudron (2014) [7] used the wells shown in Figure 9 to evaluate the piezometric variations of this aquifer. The comparison between the observed hydraulic head and the calculated hydraulic head indicated a good fit between the contours and the maximum deviation, with values lower than 5 m. Therefore, the calibrated hydrogeological parameters are valid, so the developed model can be used for hydrogeological work and simulations. The model was considered calibrated when a good adjustment was reached for the 17 observation wells, with an average residual error of 0.299 m, a NRMSE of 1.277% and an R² of 0.999. The global adjustment is 0.94 for 322 points and 0.941 for 1496 points. After calibration, the model was validated using observed hydraulic head from 2010 to 2018. Based on the obtained R² (0.978) and RMSE (5.051%), the model produced acceptable results for both periods.

The model’s calibration generated slight variations from the initial data. The net volume of recharge for calibrated irrigation return is 73.05 Mm³/yr (Ir = 168 mm/yr, which is very close to the average value of 150 mm/yr reported in other studies). The total recharge volume is 120.05 Mm³/yr. The model’s rainfall recharge was 35.00 mm/yr, which represents 11.20% of the average rainfall in the region and is similar to the rainfall rates that other scholars have used for this type of semi-arid Mediterranean climate (e.g., 16% [9,10,30] or 6% [7]).

4.2. Results for the Steady State

A simulation of the steady-state system without anthropization was done for the year 1925. Piezometric levels between 30 masl and 50 masl were observed in the Messinian layer in the northwest part of the model and near the coast, and levels between 20 masl and 40 masl were observed in the Pliocene aquifer layer. These levels of hydraulic head were generated in the confined parts of the aquifer, indicating that, before the environment was anthropized, there were piezometric levels above sea level near the coast and even a few kilometers inland. The volume of lateral movement for the steady-state water flow is 11.20 Mm³/yr, and the vertical transfer rate is 20.60 Mm³/yr (

Table 4. Water-balance results for the Campo de Cartagena model in the steady state (1925) (Mm³/yr).

Layers	Inputs			Outputs
	R	V	L	MMD	MD	V	L
Quaternary	39.85	0	8.50	28.50	4.50	12.40	2.95
Pliocene	2.90	12.40	2.20	0	0	6.65	10.85
Messinian	2.65	6.65	0.50	0	0	1.55	8.25
Tortonian	1.60	1.55	0	0	0	0	3.15
Σ	47.00	20.60	11.20	28.50	4.50	20.60	25.20

R: From rainfall; V: From vertical transfer; L: From lateral aquifers and other sources; MMD: Discharge to the Mar Menor; MD: Discharge to the Mediterranean Sea.

).

4.3. Results for the Transient State

The most relevant data on the water balances that the model generated (

Table 5. Water-balance results for the Campo de Cartagena model in the transient state (2010–2015) (Mm³/yr).

Layers	Inputs				Outputs					Global Balance
	R	I	V	L	W	MMD	MD	L	V
Quaternary	39.85	73.05	0	3.30	22.67	34.80	5.50	1.00	44.53	+7.70
Pliocene	2.90	0	44.53	2.40	24.51	0	0	0.35	25.90	−0.93
Messinian	2.65	0	25.90	7.65	40.21	0	0	0	2.00	−6.01
Tortonian	1.60	0	2.00	0	3.07	0	0	0	0	+0.53
∑	47.00	73.05	72.43	12.25	90.46	34.80	5.50	1.35	72.43	+1.29

R: From rainfall; I: Irrigation; V: From vertical transfer; L: From lateral aquifers and other sources; W: Withdrawals; MMD: Discharge to the Mar Menor; MD: Discharge to the Mediterranean Sea.

) are the continuous increases in the system’s global balance since before the anthropization of the medium; the volume was 48.35 Mm³/yr in 1925 and 116.20 Mm³/yr in 2015. The extraction volume of the pumping wells in the model was 90.46 Mm³/yr, somewhat greater than the 88 Mm³/yr used in the recent CHS studies [25].

The water transfer volumes from the aquifer to the Mar Menor lagoon, according to the model, were 28.50 Mm³/yr in the steady state (1925; without anthropization) and 34.80 Mm³/yr in the transient state (2015); the volumes from the aquifer to the Mediterranean Sea were 4.50 and 5.50 Mm³/yr for the steady and transient states, respectively. The vertical flow transfers between aquifers in the transient state, according to the model, were 44.53 Mm³/yr between the Quaternary and the Pliocene layers, 25.90 Mm³/yr between the Pliocene and the Messinian, and 2.00 Mm³/yr between the Messinian and the Tortonian.

The global vertical hydraulic communication through boreholes was 43.75 Mm³/yr, as calculated based on the difference in the vertical flow transfer figures (according to the model) with and without boreholes. The transfers through the boreholes were 23.44 Mm³/yr between the Quaternary and Pliocene layers, 19.86 Mm³/yr between the Pliocene and Messinian layers, and 0.45 Mm³/yr between the Messinian and Tortonian layers (

Table 6. Vertical hydraulic communication through boreholes in transient state (2010–2015) (Mm³/yr).

Designation Transfer	Global Vertical Transfer (1)	Hydro-Geological Vertical Transfer (2)	Transfer in Areas With Boreholes (1-2)	Transfer in Areas Without Boreholes (3)	Transfer Through Boreholes (model) (1-2-3)	Modified Transfer Through Boreholes, IGME (1991) (Estimated)	Transfer Through Boreholes, IGME (1991) (Estimated)
Quaternary-Pliocene	44.53	10.28	34.25	10.50	23.75	15.77	23.65
Pliocene- Messinian	25.90	4.64	21.26	5.45	15.81	18.92	28.38
Messinian-Tortonian	2.00	1.45	0.55	0.10	0.45	1.38	0
∑		16.37			40.01	36.07	52.03

).

These results were compared with the estimated values from the IGME study that was carried out in 1991 [30], which were modified by reducing the vertical flows that circulated through the wells to 1.00 l/s unit for the 500 wells that connected the Quaternary to lower stratums, 2.00 l/s per unit for the 300 wells that connect the Pliocene to lower stratums, and 1.25 l/s per unit for the 35 wells that connected the Messinian to lower stratums.

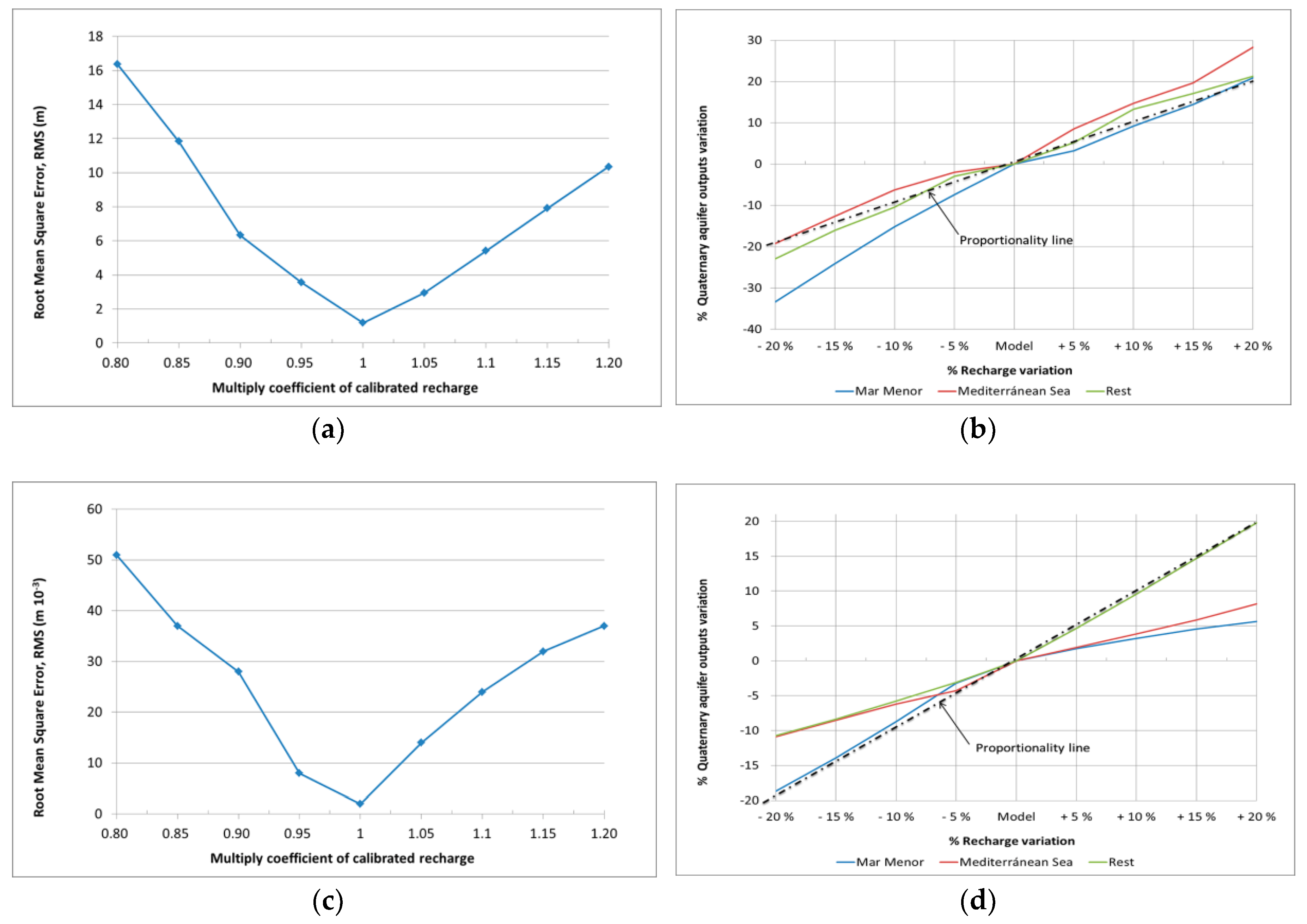
4.4. Sensitivity Analysis

Of the hydrogeological parameters that were used to carry out the model’s sensitivity analysis, recharge was chosen because it has long aroused scientific interest and has been the subject of studies on the Campo de Cartagena [7,11]. Therefore, recharge was studied in this work for both the steady state and the transient state. In the first case, the variations in the results due to slight variations in the inputs for natural recharge were studied, and the proportionality between these recharge inputs and results obtained were analyzed, all according to the methodology that Panagopulos used in 2012 [34]. Through this sensitivity analysis, it was possible to determine the degree of changes to the water system that would produce variations in annual rainfall due to climate change. In the second case, the analysis of the recharge variation (i.e., the sum of the natural recharge plus the returns for irrigation) in the transient state also is of scientific interest due to the uncertainty that persists with regard to irrigation returns. In both cases, the goals were to analyse how slight variations in these values affected the entire aquifer system, as well as to quantify the degree of influence these changes had on the results.

With these objectives, the model was executed for both regimes, using 9 values of natural recharge between 0.8 and 1.2 times the calibrated value of 47.00 Mm³/yr in the steady state for Figure 10a,b. For the transient state, the same interval was used for the calibrated value of 116.20 Mm³/yr, in Figure 10c,d. In each execution of the model as part of the sensitivity analysis, the RMSE error and the percentage variation in the output flow of the Quaternary aquifer layer were calculated.

In the analysis of each graph, with regard to the steady state and recharge values within the calibration (Figure 10a), the model was more sensitive to variations below the aforementioned calibration value and less sensitive to higher values. For values lower than the calibration value, the most sensitive water-flow output was towards the Mar Menor, and for values greater than the calibration, the most sensitive output was towards the Mediterranean Sea, with a clear proportionality (Figure 10b).

For the transient state, the variation of the RMSE was generally acceptable. Regarding the sensitivity of the model, the transient state was also somewhat more sensitive to decreasing values (Figure 10c) than to increasing ones. With respect to the outputs of the Quaternary layer, for decreasing values, the most sensitive output was again the Mar Menor, and for increasing values, the lateral outputs to the Mar Menor and the Mediterranean Sea were the most stable, with the vertical flow transfers being the most sensitive to increases in recharge.

In multilayered coastal aquifers in semi-arid zones, where contact with the sea is mainly carried out through the Quaternary upper aquifer and through under- or over-exploitation conditions, a decrease in recharge significantly affected the volumes of transfer from the aquifer to the sea. For the increasing recharge values, the volumes of transfer of the flow to the sea grew in a smaller proportion, thus, considerably increasing the vertical transfers between layers.

5. Discussion

The reconstruction of the aquifer’s temporal evolution in the transient regime was confirmed, and there was uncertainty associated with the estimation of the initial values due to the lack of official data, as well as the inversion of the hydraulic gradient due to a century of anthropization. The resulting evolution is similar to those proposed in similar studies [7]. The flow model accounted for the duality between the sub-basins of Torre-Pacheco and San Javier, where groundwater head respectively increased and decreased since the beginning of the TSWT. Quantifications of the dual effect of irrigation have been proposed. Changes have been shown to be particularly due to reduced piezometric levels in specific periods in the (mostly) confined aquifers. Recovery was variable depending on the stratum that was involved in the TSWT (and the sub-basin where it is located), and due to the high recovery in the unconfined aquifer causing agrochemical contamination. At present, there is a fragile water balance due to decreased net demand and increased contributions of surface and regenerated water.

It is necessary to consider that, during several periods of drought at the end of the 20th century, groundwater extractions were as high as 125 Mm³/yr, according to official data and other studies; this subjected the system to water stress. However, this study’s model revealed that, to reach the observed piezometry values, there must have been periods with extractions close to 220 Mm³/yr; however, there is still uncertainty regarding the real extraction values. For extraction values of 90–92 Mm³/yr, the highest levels of the aquifer are stable or have only slight declines, but the lowest levels are still subject to overexploitation. The results for water-mass balance in this study (

Table 7. Comparative transient-state water balance of the Campo de Cartagena for the models used in this study and in others (Mm³/yr).

Concepts		IGME [30]		CHS [25]	Jiménez-Martínez et al. (2016) [3]		This Study
		Quaternary	Others	Global	Quaternary	Global	Quaternary	Others
Inputs	Net infiltration	46	4	76	46	-	40	7
	Irrigation returns	23	0	18	66	-	73	0
	To other aquifers	-	-	-	-	-	3	57
	Total	69	4	94	112	112	116	64
Outputs	Pumps	2	19	88	-	77	23	68
	Lateral to sea (mainly Mar Menor)	5	0	6	68	68	40	0
	To other aquifers		0	0	46	0	44	1
	Losses	0	0	0	2	2	1	1
	Total	54	19	94	116	147	108	70
Balance		15	−15	0	−4	−35	8	−6
Observations		This positive balance translated into elevations in the Quaternary’s piezometric level, thus causing drainage problems in the lower areas.		This was balanced.	This was balanced on average. There was overexploitation of the lower aquifers. The Triassic of Victories was not incorporated.		A positive balance in the Quaternary caused a rise in piezometric levels. The rest of the system was in balance, with slight overexploitation in the Messinian.
Calculation procedures		Piezometry measured in 1998, with a gradient of 3 per thousand, 48 m2/day and 29 km of front.		Accepted the IGME value [30].	The 60–40 distribution of the recharge hydrological model was according to previous articles.		The procedures were according to the hydrogeological flow model of the entire aquifer system.

) are 47 Mm³/yr for rain recharge and 73 Mm³/yr for the recharge of irrigation return, and these values are similar to those provided in other recent studies (averages of 46 and 66 Mm³/yr, respectively); this study’s value of 44 Mm³/yr for vertical transfer is also similar to the average of 46 Mm³/yr value from other studies [3]. For both stationary and transient states, there is evidence of water transfer from the Quaternary layer to the Mar Menor lagoon (approximately 35 Mm³/yr) and to the Mediterranean Sea (approximately 5.5 Mm³/yr). These are stable values for all non-severe modifications to the aquifer’s hydraulic conductivity, specific storage and pumping. These values are somewhat higher than those calculated using another flow model, in Senent et al. (2009) [9], which were 25.9 Mm³/yr and 3.1 Mm³/yr, respectively, but somewhat lower than those calculated in Jiménez-Martínez et al. (2016) [3], which showed a volume of 68 Mm³/yr for both discharges.

For the stationary state, the existence of an internal hydrological communication between the layers of the aquifers was verified; it was estimated at approximately 16.37 Mm³/yr. This hydraulic communication was simulated by executing a model in which only the following traversed the aquitards: The Cabezo Gordo horst and the edge contacts in the Triassic of the Victories, to the north of the Sierra de Cartagena-La Unión and the outcrops of the Sierra of Carrascoy. This study’s results also revealed the water balances of the initial, non-anthropic stage. This hydraulic communication acted by exercising a slight control of internal pressures in the confined areas where artesianism was present.

This study’s results also included a first approximation of the quantification of the vertical flow transfer through abandoned or leaking boreholes (Table 6), as well as the hydraulic communication between aquifer layers and through their interrelations with the Mar Menor lagoon and the Mediterranean Sea (Table 7). The data for these measures were similar to those contained in other studies (such as [3,25]), except that this study required slightly higher extractions to calibrate the model and indicated slightly greater differences in the transfer flow to the Mar Menor from the Quaternary aquifer layer.

The values in this study were lower than those from a past study [30] with regard to the hydraulic communication between layers through wells, as the values of transmissivity used in this study after the model’s calibration recommended such an adjustment. The values obtained for the vertical hydraulic communication were around 55% of the total flow, which indicates that these values are worthy of some consideration. The scarcity of data related to this work, despite the progress that has been made with regard to real extractions from pumping, indicates continued uncertainty, so MODFLOW is an adequate tool in this study [42]. The levels of recharge and extractions by pumping require future, more in-depth studies, as the uncertainty of these parameters indicates that the obtained results should be treated with caution.

The resulting groundwater flow model allowed for the integration of the hydrogeological information obtained in this study, as well as for the generation of a tool that can advance the hydrogeological study of coastal multilayer aquifers that are subject to intensive exploitation and that are located in semi-arid environments. The Campo de Cartagena aquifer system was used in this study as a scientific laboratory to examine the hydrodynamic effects of a very anthropized system. It proved possible to reproduce the evolution during the last century by estimating values for the first 45 years using a mathematical function. An order of magnitude has also been achieved for the extractions that were carried out in periods with little or no data, thus, establishing extractive volume intervals that can be used for the sustainable management of the water system. Water balances were also generated for the barriers between the aquifer layers and for the layers’ discharges towards the Mar Menor and the Mediterranean Sea. Finally, the first quantitative approach for determining the hydraulic communication between these layers was generated.

6. Conclusions

Among the main conclusions of the present study, we can highlight the following:

• The water balances generated and analyzed in the present study indicate the importance of irrigation returns in the Campo de Cartagena’s multilayer aquifer system—and generally, in similar systems that are linked to intensive agriculture in semi-arid zones. Slight drops in recharge significantly unbalanced the system’s ability to meet the intended exploitation.
• There is hydraulic communication between aquifer layers, partly caused by intrusions in aquitards such as the Cabezo Gordo horst, by contact with the Triassic of Los Victorias or Sierra Cartagena-La Unión, and by the existence of more than 2000 wells and boreholes, 600 of which cross several aquifers and thus generate direct vertical hydraulic communication.
• The vertical hydraulic communication through the wells was calculated at 40.01 Mm³/yr. If the total flow transfer across the aquifer is 84.68 Mm³/yr, this implies that 47.23% of the total flow takes place through vertical communication. The remaining 52.77% takes place through discontinuities, contacts and infiltration between layers. The model considered the fact that the Pliocene and Messinian aquifer layers lie under the Mar Menor lagoon and the Mediterranean Sea, as well as the fact that there is no communication between those masses of water and the inferior confined aquifers in that zone.
• Total present withdrawal in the Campo de Cartagena multilayer aquifer system is evaluated to be 91 Mm³/yr. As groundwater was the only source of water before the beginning of the TSWT, withdrawal values introduced into the model for its calibration were higher. The water balance is clearly favorable to the recovery of water levels in the Quaternary aquifer layer, as there is both water balance in the Pliocene aquifer layer and overexploitation in the Messinian aquifer layer.
• The average value for the annual global recharge was established as approximately 123 Mm³/yr for the period studied. However, the study of recharge and pumping of Quaternary-layer water for private desalination plants deserves further investigation.
• In the Triassic areas of Los Victorias and Cabezo Gordo, heavy falls in the piezometric levels occurred, even after the drying of the cells caused by the strong hydraulic gradients where communication between aquifers occurred. Such zones constitute carbonate aquifers, whose interrelations with the multilayer aquifer are difficult to model.
• This historical study was carried out by fitting the entire aquifer system into a numerical model, and it provided valuable information to stakeholders for sustainable management of the aquifer in the future. The water-balance values that the model provided were similar to the figures from other studies, and the recovery of piezometric levels in the upper aquifer, as observed in recent decades, was corroborated.
• Two desirable studies to carry out in the future include an analysis of possible pumping using scavenger wells near the coast, which would reduce the discharge of the Quaternary layer to the Mar Menor, and a study regarding transferring flow from the Quaternary to the Messinian so as to recharge the latter and minimize discharge to the Mar Menor.