Abstract
Application of integrated hydrological models to manage a watershed’s water resources are increasingly finding their way into the decision-making processes. The Soil and Water Assessment Tool (SWAT) is a multi-process model integrating hydrology, ecology, agriculture, and water quality. SWAT is a continuation of nearly 40 years of modeling efforts conducted by the United States Department of Agriculture (USDA) Agricultural Research Service (ARS). A large number of SWAT-related papers have appeared in ISI journals, building a world-wide consensus around the model’s stability and usefulness. The current issue is a collection of the latest research using SWAT as the modeling tool. Most models must undergo calibration/validation and uncertainty analysis. Unfortunately, these sciences are not formal subjects of teaching in most universities and the students are often left to their own resources to calibrate their model. In this paper, we focus on calibration and uncertainty analysis highlighting some serious issues in the calibration of distributed models. A protocol for calibration is also highlighted to guide the users to obtain better modeling results. Finally, a summary of the papers published in this special issue is provided in the Appendix.
1. Introduction
This special issue on “Integrated Soil and Water Management” deals with the application of the Soil and Water Assessment Tools (SWAT) [1] to a range of issues in watershed management. A total of 27 papers attest to the importance of the subject and the high level of research being conducted all over the globe. A common factor in almost all the published papers is the calibration/validation and uncertainty analysis of the models. Of the 27 papers published in this issue, 20 are calibrated with SWAT-CUP [2,3,4]. As the credibility of a model’s performance is in the calibration/validation and uncertainty results, we devote this overview paper to the outstanding issues in model calibration and uncertainty analysis.
Steps for building a hydrologic model include: (i) creating the model with a hydrologic program, such as in our case, ArcSWAT; (ii) performing sensitivity analysis; (iii) performing calibration and uncertainty analysis; (iv) validating the model, and in some case; (v) performing risk analysis. Here we discuss these steps and highlight some outstanding issues in the calibration of large-scale watershed models. A protocol for calibrating a SWAT model with SWAT-CUP is also proposed. Finally, we briefly review all papers published in this special issue in the Appendix.
To avoid any confusion and for the sake of standardizing the SWAT model calibration terminology, we summarized the definition of some common terms in Table 1.

Table 1.
Definition of some terminologies.
Next to the terms in Table 1, the term sensitivity analysis refers to the identification of the most important influence factor in the model. Sensitivity analysis is important from two points of view: First, parameters represent processes, and sensitivity analysis provides information on the most important processes in the study region. Second, sensitivity analysis helps to decrease the number of parameters in the calibration procedure by eliminating the parameters identified as not sensitive. Two general types of sensitivity analysis are usually performed. These are one-at-a-time (OAT) or local sensitivity analysis, and all-at-a-time (AAT) or global sensitivity analysis. In OAT, all parameters are held constant while changing one to identify its effect on some model output or objective function. In this case, only a few (3–5) model runs are usually sufficient (Figure 1). In the AAT, however, all parameters are changing; hence, a larger number of runs (500–1000 or more, depending on the number of parameters and procedure) are needed in order to see the impact of each parameter on the objective function. Both procedures have limitations and advantages. Limitation of OAT is that sensitivity of one parameter is often dependent on the values of other parameters, which are all fixed to values whose accuracy is not known. The advantage of OAT is that it is simple and quick. The limitation of AAT is that parameter ranges and the number of runs affect the relative sensitivity of the parameters. The advantage is that AAT produces more reliable results. In SWAT-CUP, OAT is used to directly compare the impact of three to five parameter values on the output signal (Figure 1), whereas AAT uses a multiple regression approach to quantify sensitivity of each parameter:
where is the objective function value, α is the regression constant, and β is the coefficient of parameters. A t-test is then used to identify the relative significance of each parameter b. The sensitivities given above are estimates of the average changes in the objective function resulting from changes in each parameter, while all other parameters are changing. This gives relative sensitivities based on linear approximations and, hence, only provides partial information about the sensitivity of the objective function to model parameters. In this analysis, the larger in absolute value the value of t-stat, and the smaller the p-value, the more sensitive the parameter.
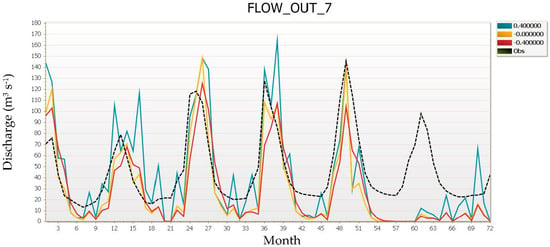
Figure 1.
Sensitivity of discharge to three different values of CN2 in one-at-a-time (OAT) analysis.
The term calibration refers to a procedure where the difference between model simulation and observation are minimized. Through this procedure, it is hoped that the regional model correctly simulates true processes in the physical system (Figure 2).
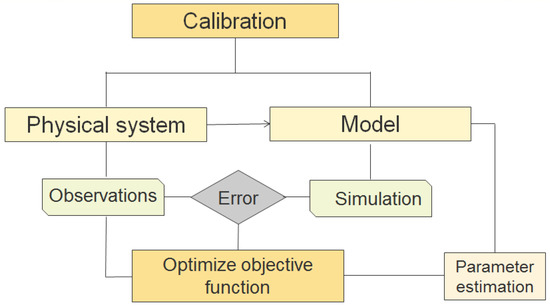
Figure 2.
Conceptualization of model calibration.
Mathematically, calibration boils down to optimization of an objective function, i.e.,
or,
where is the objective function, θ is a vector of model parameters, xo is an observed variable, xs is the corresponding simulated variable, v is the number of measured variables to be used to calibrate the model, wj is weight of the jth variable, and nj is the number of measured observations in the jth variable. The case for v > 1 if often referred to as multi-objective calibration containing, in our case, variables such as discharge, nitrate, sediment, etc. A large number of different objective function formulations exist in the literature, 11 of which are used in SWAT-CUP.
Calibration is inherently subjective and, therefore, intimately linked to model output uncertainty. Parameter estimation through calibration is concerned with the problem of making inferences about physical systems from measured output variables of the model (e.g., river discharge, sediment concentration, nitrate load, etc.). This is attractive because the direct measurement of parameters describing the physical system is time consuming, costly, tedious, and often has limited applicability. Uncertainty stems from the fact that nearly all measurements are subject to some error, models are simplifications of reality, and the inferences are usually statistical in nature. Furthermore, because one can only measure a limited number of (noisy) data and because physical systems are usually modeled by continuum equations, no calibration can lead to a single parameter set or a single output. In other words, if there is a single model that fits the measurements there will be many of them. This is an old concept known as the non-uniqueness problem in the optimization literature. Our goal in calibration is, then, to characterize the set of models, mainly through assigning distributions (uncertainties) to the parameters that fit the data to satisfy our assumptions as well as other prior information [3].
The term uncertainty analysis refers to the propagation of all model input uncertainties (mapped in the parameter distribution) to model outputs. Input uncertainties can stem from the lack of knowledge of physical model inputs such as climate, soil, and land-use, to model parameters and model structure. Identification of all acceptable model solutions in the face of all input uncertainties can, therefore, provide us with model uncertainty expressed in SWAT-CUP as 95% prediction uncertainty (95PPU) (Figure 3).
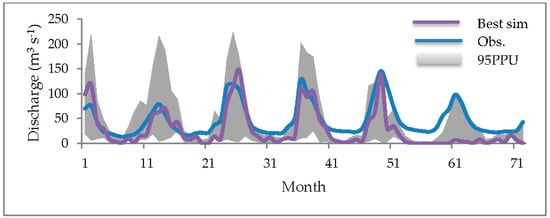
Figure 3.
Illustration of model output uncertainty expressed as 95% prediction uncertainty (95PPU) as well as measured and best simulated discharge variable.
To compare the 95PPU band with, for example, a discharge signal, we devised two statistics referred to as p-factor and r-factor [2,3]. p-factor is the percentage of measured data bracketed by the 95PPU band. These measurements are within the simulation uncertainty of our model; hence, they are simulated well and accounted for by the model. Subsequently, (1-p-factor) represent the measured data not simulated well by the model, in other words, (1-p-factor) is the model error. r-factor is a measure of the thickness of the 95PPU band and is calculated as the average 95PPU thickness divided by the standard deviation of the corresponding observed variable:
where and are the upper and lower boundary of the 95PPU at time-step t and simulation i, nj is the number of data points, and is the standard deviation of the jth observed variable.
Validation is used to build confidence in the calibrated parameters. For this purpose, the calibrated parameter ranges are applied to an independent measured dataset, without further changes. The analyst is required to do one iteration with the same number of simulations as in the last calibration iteration. Similar to calibration, validation results are also quantified by the p-factor, r-factor, and the objective function value. It is important that the data in validation period meets more or less the same physical criteria as the calibration period. For example, climate and land-use of the validation period should pertain to the same kind of climate and land-uses as the calibration period. Also, if for example, river discharge is used to calibrate the model, then the average and variance of discharges in the two periods should more or less be the same.
Risk analysis is a step usually ignored in most hydrological modeling. We often build a model, calibrate it and report the model uncertainty, but do not take the next step to analyze the problem. For example, we simulate nitrate concentration in the rivers or in the groundwater, or quantify soil erosion and soil losses, but do not go further to quantify their consequences in the environment or on human health. One impediment is usually the existence of uncertainty in the outputs. A large body of literature exists on decision-making under uncertainty, but there is still no standard and easy way of communicating the uncertainty to decision-makers. Environmental scientist researchers and engineers should pay more attention to this problem. One way forward would be to transform the uncertainty to risk. A monitory risk value is more tangible to a decision-maker than uncertainty. The risk can be calculated as the probability of failure (or loss) multiplied by the cost of failure (or loss):
To demonstrate, assume that we are interest in calculating the risk of soil loss due to erosion. To calculate the probability of soil loss, we propagate the parameter ranges that were obtained during calibration by performing an iteration of, for example, 1000 simulations. Using the “No_Observation” option for extraction, we extract the sediment loss from a sub-basin of interest (Table 2, column 1). Next, we can calculate the cost of soil loss in ways that could include loss of fertilizer, loss of crop yield, loss of organic matter, etc. [5,6,7]. Here, we assumed a cost of 10 $ tn−1 to replenish the loss of fertilizer (Table 2, column 2).

Table 2.
Statistics of cumulative distribution for soil loss resulting from model uncertainty.
In the “echo_95ppu_No_Obs.txt” file of SWAT-CUP, one can find the probability distribution of soil loss (Table 2, column 3). In this example, we have an uncertainty on soil loss in the range of (513 tn ha−1 to 1070 tn ha−1). It is important to realize that this range is the model solution. Most researchers here search for one number to carry their research forward. But the model, because of uncertainty, never just has one number as the solution. The risk can then be calculated by Equation (5) as the product of cost of soil loss by the probability of soil loss (Table 2, column 3).
To carry the example forward, assume that with the help of terracing we can cut down on soil loss. Implementing this management option in SWAT and running an iteration as before, we obtain the new loss soil and its probability distribution (Table 2). We can again calculate the risk of soil loss after terracing and calculate the Gain or profit of terracing as:
where b and a stand for before and after terracing. In the last row of Table 2, the expected values are reported, where the expected value of gain as a result of terracing is calculated to be 3735 $ ha−1. If the cost of terracing is less than this amount, then there is a profit in terracing. The same type of analysis can be done with different best-management options (BMP) in SWAT and the most profitable one selected.
Gain = Riskb − Riska
2. Outstanding Calibration and Uncertainty Analysis Issues
Calibration of watershed models suffers from a number of conceptual and technical issues, which we believe require a more careful consideration by the scientific community. These include: (1) inadequate definition of the base model; (2) parameterization; (3) objective function definition; (4) use of different optimization algorithms; (5) non-uniqueness; and (6) model conditionality on the face of the above issues. Two other issues having an adverse effect on calibration include: (7) time constraints; and (8) modeler’s inexperience and lack of sufficient understanding of model parameters. In the following, a short discussion of these issues is presented.
2.1. Inadequate Definition of the Base Model
An important setback in model calibration is to start the process with an inadequate model. Failure to correctly setup a hydrologic model may not allow proper calibration and uncertainty analyses, leading to inaccurate parameter estimates and wrong model prediction. To build a model with an accurate accounting of hydrological processes, a data-discrimination procedure is needed during model building. This includes: (i) identifying the best data set (e.g., climate, land-use, soil) from among, at times, many available data sources; (ii) accounting for important processes in accordance with the “correct neglect” principle where only ineffective processes are ignored in the model. Often important processes, which are usually ignored, include: springs, potholes, glacier/snow melts, wetlands, reservoirs, dams, water transfers, and irrigation. Accounting for these measures, if they exist, leads to a better physical accounting of hydrological processes, which significantly improves the overall model performance. This avoids unnecessary and arbitrary adjustment of parameters to compensate for the missing processes in the model structure.
In this special issue, Kamali et al. [8] address the issue of the existence of many datasets and their effects on the assessment of water resources. They combined 4 different climate data with 2 different land-use maps to build 8 different models that they calibrated and validated. These models led to different calibrated parameter sets, which consequently led to different quantification of water resources in the region of study (Figure 4).
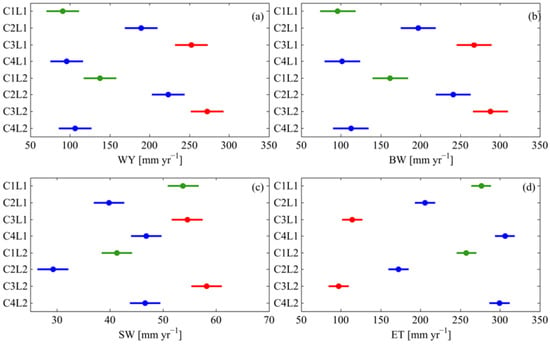
Figure 4.
Range of four water resources components. (a) WY = water yield; (b) BW = blue water; (c) SW = soil water; (d) ET = evapotranspiration obtained from eight calibrated models. C represents a climate data set, and L represents a land-use dataset. (Source: Kamali et al. [8]).
2.2. Parameterization
There are two issues in parameterization: (1) which parameters to use; and (2) how to regionalize the parameters. Not all SWAT parameters are relevant to all sub-basins, and not all should be used simultaneously to calibrate the model. For example, rainfall is a driving variable and should not be fitted with other parameters at the same time. Similarly, snow-melt parameters (SFTMP, SMTMP, SMFMX, SMFMN, TIMP) and canopy storage (CANMX), which introduce water into the system, should not be calibrated simultaneously with other parameters as they will cause identifiability problems. These parameters should be fitted first and fixed to their best values and then removed from further calibration.
The other issue deals with regionalization of the parameters. That is, how to distinguish between hydraulic conductivity of the same soil unit when it is under forest, as opposed to being under pasture or agriculture. For this purpose, a scheme is introduced in SWAT-CUP where a parameter can be regionalized to the HRU level using the following assignment:
where x is an identifier to indicate the type of change to be applied to the parameter (v is value change; a adds an increment to existing value; and r is for relative change of spatial parameters and it multiplies the existing parameter value by (1 + an increment)). <parname> is SWAT parameter name, <ext> is SWAT file extension code; <hydrogrp> is hydrologic group; <soltext> is soil texture; <landuse> is land-use type; <subbsn> is sub-basin number(s); and <slope> is the slope as it appears in the header line of SWAT input files. Any combination of the above factors can be used to calibrate a parameter. The analyst, however, must decide on the detail of regionalization as on the one hand, a large number of parameters could result, and on the other hand, by too much lumping, the spatial heterogeneity of the region may be lost. This balance is not easy to determine, and the choice of parameterization will affect the calibration results (see [9,10] for a discussion). Detailed information on spatial parameters is indispensable for building a correct watershed model. A combination of measured data and spatial analyses techniques using pedotransfer functions, geostatistical analysis, and remote sensing data would be the way forward.
x__<parname>.<ext>__<hydrogrp>__<soltext>__<landuse>__<subbsn>__<slope>
2.3. Use of Different Objective Functions
There are a large number of objective functions with different properties that could be used in model calibration [11,12]. The problem with the choice of objective functions is that they can produce statistically similar and good calibration and validation results, but with quite different parameter ranges. This adds a level of uncertainty to the calibration process, which could make the calibration exercise meaningless. In this special issue, Hooshmand et al. [13] used SUFI-2 with 7 different objective functions to calibrate discharge in Salman Dam and Karkhe Basins in Iran. They found that after calibration, each objective function found an acceptable solution, but at a different location in the parameter space (Figure 5).
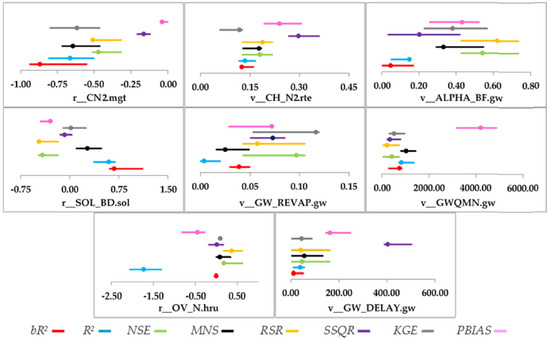
Figure 5.
Uncertainty ranges of calibrated parameters using different objective functions for a project in Karkheh River Basin, Iran. The points in each line show the best value of parameters, r_ refers to a relative change where the current values are multiplied by (one plus a factor from the given parameter range), and v_ refers to the substitution by a value from the given parameter range. (Source: Hooshmand et al. [13]).
2.4. Use of Different Optimization Algorithms
Yang et al. [14] showed that different calibration algorithms converge to different calibrated parameter ranges. They used SWAT-CUP to compare Generalized Likelihood Uncertainty Estimation (GLUE) [15], Parameter Solution (ParaSol) [16], Sequential Uncertainty Fitting (SUFI-2) [2,3,4], and Markov chain Monte Carlo (MCMC) [17,18,19] methods in an application to a watershed in China. They found that these different optimization algorithms each found a different solution at different locations in the parameter spaces with roughly the same discharge results. In this special issue, Hooshmand et al. [13] also showed that use of SUFI-2, GLUE, and ParaSol resulted in the identification of different parameters ranges, with similar calibration/validation results, which led to simulation of significantly different water-resources estimates (Figure 6).
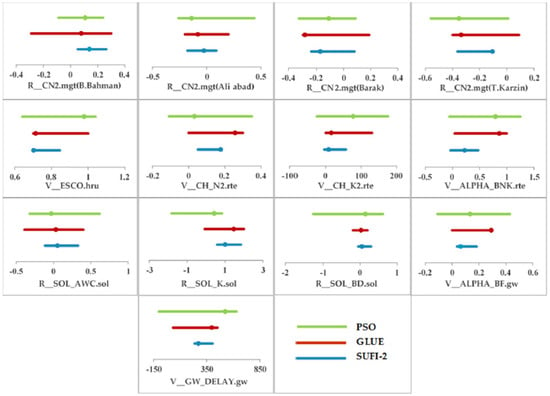
Figure 6.
Uncertainty ranges of the parameters based on all three methods applied in Salman Dam Basin, Iran. The points in each line show the best value of the parameters, r_ refers to a relative change where the current values are multiplied by one plus a factor from the given parameter range, and v_ refers to the substitution by a value from the given parameter range. (Source: Hooshmand et al. [13]).
2.5. Calibration Uncertainty or Model Non-Uniqueness
As mentioned before, a single parameter set results in a single model signal in a deterministic model application. In an inverse application (i.e., calibration), the measured variable could be reproduced with thousands of different parameter sets. This non-uniqueness is an inherent property of model calibration in distributed hydrological applications. An example is shown in Figure 7 where two very different parameter sets produce signals similar to the observed discharge.
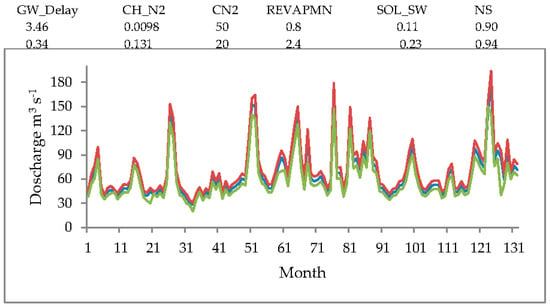
Figure 7.
Example of parameter non-uniqueness showing two similar discharge signals based on quite different parameter values.
We can visualize non-uniqueness by plotting the response surface of the objective function versus two calibrating parameters. As an example, Figure 8 shows the inverse of an objective function, based on the mean square error, plotted against CN2 and GW-REVAP in an example with 2400 simulations. In this example, CN2, GW-REVAP, ESCO, and GWQMN were changing simultaneously. Size and distribution of all the acceptable solutions (1/goal > 0.8) are shown in darker shade. This multi-modal attribute of the response surface is the reason why each algorithm or each objective function finds a different good solution.
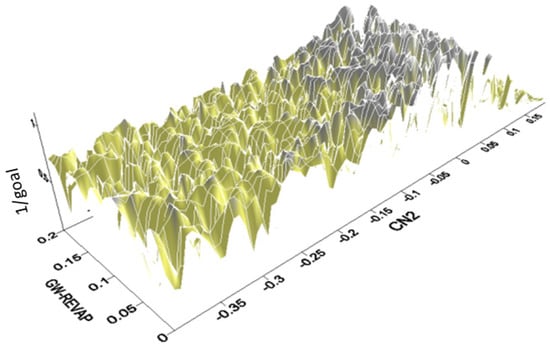
Figure 8.
The “multimodal” behavior of the objective function response surface. All red-colored peaks have statistically the same value of objective function, which occur at the different regions in the parameter space.
To limit the non-uniqueness problem, we should: (i) include more variables in the objective function (e.g., discharge, ET or crop yield, nutrient loads, etc.); (ii) use multiple outlets for calibration; and (iii) constrain the objective function with soft data (i.e., knowledge of local experts on nutrient and sediment loads from different land-uses, etc.). The downside of this is that a lot of data must be measured for calibration. The use of remote-sensing data, when it becomes practically available, could be extremely useful. In fact, the next big jump in watershed modeling will be made as a result of advances in remote-sensing data availability.
2.6. Calibrated Model Conditionality
A model calibrated for a discharge station at the outlet of a watershed should not be expected to provide good discharge results for outlets inside the watershed. The outlets inside should be “regionally” calibrated for the contributing sub-basins. Also, a model calibrated for discharge, should not be expected to simulate water quality. Calibrated parameters are always expressed as distributions to reflect the model uncertainty. In other words, they are always “conditioned” on the model assumptions and inputs, as well as the methods and data used for model calibration. Hence, a model calibrated, for example, for discharge, may not be adequate for prediction of sediment; or for application to another region; or for application to another time period.
A calibrated model is, therefore, always: (i) non-unique; (ii) subjective; (iii) conditional; and subsequently (iv) limited in the scope of its use. Hence, important questions arise as to: “When is a watershed model truly calibrated?” and “For what purpose can we use a calibrated watershed model?” For example: What are the requirements of a calibrated watershed model if we want to do land-use change analysis? Or, climate change analysis? Or, analysis of upstream/downstream relations in water allocation and distribution? Or, water quality analysis? Can any single calibrated watershed model address all these issues, or should there be a series of calibrated models each fitted to a certain purpose? We hope that these issues can be addressed more fully by research in this field.
Conditionality is, therefore, an important issue with calibrated models. Calibrated parameters (θ) are conditioned on the base model parameterization (p), variables used to calibrate the model (v), choice of objective function (g) and calibration algorithm (a), as well as weights used in a multi-objective calibration (w), the type and number of data points used for calibration (d), and calibration-validation dates (t), among other factors. Mathematically, we could express a calibrated model M as:
To obtain an unconditional calibrated model, the parameter set θ must be integrated over all factors. This may make model uncertainty too large for any practical application. Hence, a model must always be calibrated with respect to a certain objective, which makes a calibrated model only applicable to that objective.
2.7. Time Constraint
Time is often a major impediment in the calibration of large-scale and detailed hydrologic models. To overcome this, most projects are run with fewer simulations, resulting in less-than-optimum solutions. To deal with this problem, a parallel processing framework was created in the Windows platform [20] and linked to SUFI-2 in the SWAT-CUP software. In this methodology, calibration of SWAT is parallelized, where the total number of simulations is divided among the available processors. This offers a powerful alternative to the use of grid or cloud computing. The performance of parallel processing was judged by calculating speed-up, efficiency, and CPU usage (Figure 9).
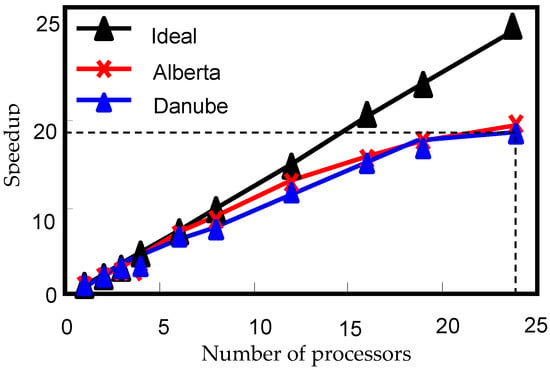
Figure 9.
The speed-up achieved for different Soil and Water Assessment Tools (SWAT) projects. The number of processors on the horizontal axis indicates the number of parallel jobs submitted. The figure shows that most projects could be run 10 times faster with about 6–8 processors. (Source: Rouholahnejad, et al. [20]).
2.8. Experience of the Modeler
The success of a calibration process depends on the accuracy of the mathematical model and the procedures chosen for the calibration as already noted. However, the experience of the modeler plays an important role, and in this sense, calibration can be described as an art as well as a science [21,22,23,24].
3. A Protocol for Calibration of Soil and Water Assessment Tools (SWAT) Models
Calibration of watershed models is a long and often tedious process of refining the model for processes and calibrating parameters. We should usually expect to spend as much time calibrating a model as we take to build the model. To calibrate the model we suggest using the following general approach (also see Abbaspour et al. [2]).
3.1. Pre-Calibration Input Data and Model Structure Improvement
Build the SWAT model in ArcSWAT or QSWAT using the best parameter estimates based on the available data, literature, and the analyst and local expertise. There is always more than one dataset (e.g., soil, land-use, climate, etc.) available for a region. Test each one and choose the best dataset to proceed. It should be noted that for calibration, the performance of the initial model should not be too drastically different from the measured data. If the initial simulation is too different, often calibration might be of little help. Therefore, one should include as much of the important processes in the model as possible. There may be processes not included in SWAT (e.g., wetland, glacier melt, micronutrients, impact of salinity on crop yield), or included in SWAT but with unavailable data (e.g., reservoir operation, water withdrawal, and water transfers); or with available data, but unknown to the modeler. This requires a good knowledge of the watershed, which may be gained from literature or local experts, or by using the “Maps” option in SWAT-CUP, which can recreate the sub-basins and rivers on the Microsoft’s Bing Maps (Figure 10).
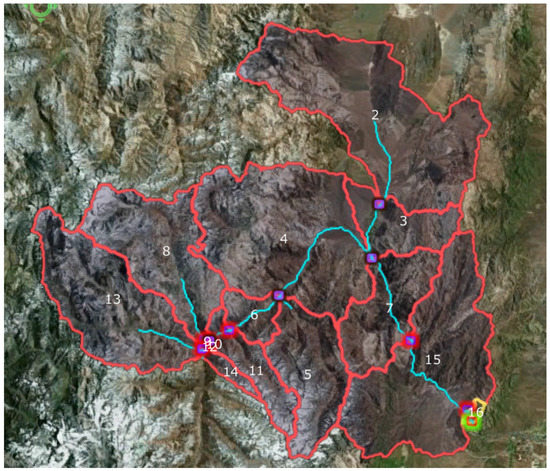
Figure 10.
The Maps option of SWAT-CUP can be used to see details of the watershed under investigation, such as dams, wrongly placed outlets, glaciers, high agricultural areas, etc.
At this stage, also check the contribution of rainfall, snow parameters, rainfall intercept, inputs from water treatment plants, and water transfers. A pre-calibration run of these parameters is necessary to identify their best values, and then to fix them in the model without further change.
3.2. Identify the Parameters to Optimize
Based on the performance of the initial model at each outlet station, relevant parameters in the upstream sub-basins are parameterized using the guidelines in Abbaspour et al. [2]. This procedure results in regionalization of the parameters.
3.3. Identify Other Sensitive Parameters
Next to parameters identified in step 2, use the one-at-a-time sensitivity analysis to check the sensitivity of other relevant parameters at each outlet. To set the initial ranges of parameters to be optimized, some experience and hydrological knowledge are required on the part of the analyst. In addition to the initial ranges, user-defined “absolute parameter ranges” should also be set if necessary. These are the upper and lower limits of what is physically a meaningful range for a parameter at a site.
3.4. Running the Model
After the model is parameterized and the ranges are assigned, the model is run some 300–1000 times, depending on the number of parameters, model’s execution time, and system’s capabilities. SUFI-2 is an iterative procedure and does not require too many runs in each iteration. Usually, 3–4 iterations should be enough to attain a reasonable result. Parallel processing can be used to greatly improve the runtime. PSO and GLUE need a larger number of iterations and simulations (100–5000).
3.5. Perform Post-Processing
After simulations in each iteration are completed; the post-processing option in SWAT-CUP calculates the objective function and the 95PPU for all observed variables in the objective function. New parameter ranges are suggested by the program for another iteration [2,3].
3.6. Modifying the Suggested New Parameters
The new parameters may contain values outside the desired or physically meaningful ranges. The suggested values should be modified by the user guiding the parameters in a certain desired direction, or to make sure that they are within the absolute parameter ranges. Use the new parameters to run another iteration until desired values of p-factor, r-factor, and the objective function is reached.
Author Contributions
All authors formulated the concept. Karim C. Abbaspour wrote the initial version, Saeid Ashraf Vaghefi and Raghvan Srinivasan contributed by editing and suggesting revisions.
Conflicts of Interest
There authors declare no conflict of interest.
Appendix A
Summary of the papers in the “Integrated Soil and Water Management” special issue (Table A1).
1,2—Chambers et al. [25,26] evaluated two different approaches for modeling historical and future streamflow and stream temperature in Rhode Island, USA. They found that between 1980–2009, the number of stressful events (i.e., high or low flows occurring simultaneously with stream temperatures exceeding 21 °C) increased by 55% and average streamflow increased by 60%. For future scenarios, however, the chance of stressful events increases on average by 6.5% under the low-emission scenario and by 14.2% under the high-emission scenario relative to historical periods.
3—Chen et al. [27] studied the effect of different fertilization and irrigation schemes on water and nitrate leaching from the root zone. They concluded that N-application based on soil testing helps to improve groundwater quality.
4—Cuceloglu et al. [28] simulated the water resources of Istanbul and quantified the spatial distribution of the region. Their results show that the annual blue-water potential of Istanbul is 3.5 billion m3, whereas the green-water flow and storage are 2.9 billion m3 and 0.7 billion m3, respectively.
5—Ding et al. [29] showed that total nitrogen load increased with increasing slope in a Yangtze River-cultivated Regosol soil.
6—Fabre et al. [30] studied the effect of permafrost degradation as a result of increasing temperature in the largest Arctic river system: the Yenisei River in central Siberia, Russia. Once the climate data and soil conditions were adapted to a permafrost watershed, the calibration results showed SWAT was able to estimate water fluxes at a daily time step, especially during unfrozen periods.
7—Fant et al. [31] evaluated the effect of climate change on water quality of the continental US. They report that under the business-as-usual emissions scenario, climate change is likely to cause economic impacts ranging from 1.2 to 2.3 (2005 billion) USD/year in 2050 and 2.7 to 4.8 (2005 billion) USD/year in 2090 across all climate and water-quality models.
8—Gharib et al. [32] investigated the combined effect of threshold selection and Generalized Pareto Distribution parameter estimation on the accuracy of flood quantiles. With their method, one third of the stations showed significant improvement.
9—Grusson et al. [33] studied the influence of spatial resolution of a gridded weather (16- and 32-km SAFRAN grids) dataset on SWAT output. They reported better performance of these data relative to measured station data.
10—Hooshmand et al. [13] investigated the impact of the choice of objective function and optimization algorithm on the calibrated parameters. They reported that different objective functions and algorithms produce acceptable calibration results, however, with significantly different parameters, which produce significantly different water-resources estimates. This adds another level of uncertainty on model prediction.
11—Kamali et al. [8] studied the impact of different databases on the water-resources estimates and concluded that while different databases may produce similar calibration results, the calibrated parameters are significantly different for different databases. They highlighted that “As the use of any one database among several produces questionable outputs, it is prudent for modelers to pay more attention to the selection of input data”.
12—Kamali et al. [34] analyzed characteristics and relationships among meteorological, agricultural, and hydrological droughts using the Drought Hazard Index derived from a SWAT application. They quantified characteristics such as severity, frequency, and duration of droughts using the Standardized Precipitation Index (SPI), Standardized Runoff Index (SRI), and Standardized Soil Water Index (SSWI) for historical (1980–2012) and near future (2020–2052) periods. They concluded that the duration and frequency of droughts will likely decrease in SPI. However, due to the impact of rising temperature, the duration and frequency of SRI and SSWI will intensify in the future.
13—Lee et al. [35] studied the impacts of the upstream Soyanggang and Chungju multi-purpose dams on the frequency of downstream floods in the Han River basin, Korea. They concluded that the two upstream dams reduce downstream floods by approximately 31%.
14—Li et al. [36] studied the effect of urban non-point source pollution on Baiyangdian Lake in China. They found that the pollutant loads for Pb, Zn, TN and TP accounted for about 30% of the total amount of pollutant load.
15—Ligaray et al. [37] studied the fate and transport of Malathion. They used a modified three-phase partitioning model in SWAT to classify the pesticide into dissolved, particle-bound, and dissolved organic carbon (DOC)-associated pesticide. They found that the modified model gave a slightly better performance than the original two-phase model.
16—Lutz at al. [38] evaluated the impact of a buffer zone on soil erosion. Their results indicated that between 0.2 to 1% less sediment could reach the Itumbiara reservoir with buffer strip provision, which would have an important effect on the life of the dam.
17—Marcinkowski et al. [39] studied the effect of climate change on the hydrology and water quality in Poland. They predicted an increase in TN losses.
18—Paul et al. [40] determined the response of SWAT to the addition of an onsite wastewater-treatment systems on nitrogen loading into the Hunt River in Rhode Island. They concluded that using the treatment systems data in the SWAT produced a better calibration and validation fit for total N.
19—Qi et al. [41] compared SWAT to a simpler Generalized Watershed Loading Function (GWLF) model. The performances of both models were assessed via comparison between simulated and measured monthly streamflow, sediment yield, and total nitrogen. The results showed that both models were generally able to simulate monthly streamflow, sediment, and total nitrogen loadings during the simulation period. However, SWAT produced more detailed information, while GWLF could produce better average values.
20—Rouholahnejad et al. [42] investigated the impact of climate and land-use change on the water resources of the Black Sea Basin. They concluded in general that the ensemble of the climate scenarios show a substantial part of the catchment will likely experience a decrease in freshwater resources by 30% to 50%.
21—Senent-Aparicio et al. [43] investigated the effect of climate change on water resources of the Segura River Basin and concluded that water resources were expected to experience a decrease of 2–54%.
22,23—Seo et al. [44,45] used SWAT to simulate hydrologic behavior of Low Impact Developments (LID) such as the installation of bioretention cells or permeable pavements. They report that application of LID practices decreases surface runoff and pollutant loadings for all land-uses. In addition, post-LID scenarios generally showed lower values of surface runoff, lower nitrate in high-density urban land-use, and lower total phosphorus in conventional medium-density urban areas.
24—Tan et al. [46] investigated the accuracy of three long-term gridded data records: APHRODITE, PERSIANN-CDR, and NCEP-CFSR. They concluded that the APHRODITE and PERSIANN-CDR data often underestimated extreme precipitation and streamflow, while the NCEP-CFSR data produced dramatic overestimations.
25—Vaghefi et al. [47] coupled SWAT to MODSIM, which is a program for optimization of water distribution. They concluded in their study that the coupled SWAT-MODSIM approach improved the accuracy of SWAT outputs by considering the water allocation derived from MODSIM.
26—Wangpimool et al. [48] studied the effect of Para Rubber Expansion of the water balance of Loei Province in Thailand. They found that displacement of original local field crops and disturbed forest land by Para rubber production resulted in an overall increase in evapotranspiration of roughly 3%.
27—White et al. [49] describe the development of a national (US) database of preprocessed climate data derived from monitoring stations applicable to USGS 12-digit watersheds. The authors conclude that the data described in this work are suitable for the intended SWAT and APEX application and also suitable for other modeling efforts, and are freely provided via the web.

Table A1.
Summary of the papers published in the special issue.
Table A1.
Summary of the papers published in the special issue.
| Important Processes | Location | Country | Calibration | Water Quality | Crop | Author | |
|---|---|---|---|---|---|---|---|
| 1 | Thermal stress | Rhode Island | USA | SWAT-CUP | Temp. | Chambers et al. | |
| 2 | Fish Habitat | Rhode Island | USA | SWAT-CUP | Temp. | Chambers et al. | |
| 3 | Leaching | North China Plain | China | NO3 | Maize | Chen et al. | |
| 4 | Water resources | Istanbul | Turkey | SWAT-CUP | Cuceloglu et al. | ||
| 5 | TN loss | Yangtze River | China | TN | Ding et al. | ||
| 6 | Permafrost | Central Siberia | Russia | SWAT-CUP | Fabre et al. | ||
| 7 | Climate change | Continental US | USA | WT, DO, TN, TP | Fant et al. | ||
| 8 | Flooding | Alberta | Canada | SWAT-CUP | Gharib et al. | ||
| 9 | Gridded rainfall | Garonne River watershed | France | SWAT-CUP | Grusson et al. | ||
| 10 | Uncertainty issues | Karkheh River Basin | Iran | SWAT-CUP | Houshmand et al. | ||
| 11 | Drought, Climate change | Karkheh River Basin | Iran | SWAT-CUP | Kamali et al. | ||
| 12 | Uncertainty | Karkheh River Basin | Iran | SWAT-CUP | Kamali et al. | ||
| 13 | Flooding | Paldang Dam | Korea | manual | Lee et al. | ||
| 14 | Non-point source pollution | Baoding City | China | manual | TN, TP | Li et al. | |
| 15 | Pesticide | Pagsanjan-Lumban Basin, | Philippines | SWAT-CUP | Ligaray et al. | ||
| 16 | Buffer strip | Itumbiara city | Braziil | manual | sediment | Lutz et al. | |
| 17 | Climate change | Upper Narew, Barycz | Poland | SWAT-CUP | Sediment, TN | Marcinkowski et al. | |
| 18 | Non-point source pollution | Hunt River Rhode Island | USA | SWAT-CUP | TN | Paul et al. | |
| 19 | SWAT, GWLF comparison | Tunxi and the Hanjiaying basins | China | SWAT-CUP | Sediment, TN | Qi et al. | |
| 20 | Climate–Land-use Change | Black Sea Basin | Europe | SWAT-CUP | Rouholahnejad et al. | ||
| 21 | Climate change | Segura River Basin | Spain | SWAT-CUP | Senent-Aparicio et al. | ||
| 22 | Optimal design | Clear Creek watershed (TX) | USA | SWAT-CUP | Seo et al. | ||
| 23 | Water quality | Clear Creek watershed (TX) | USA | SWAT-CUP | Seo et al. | ||
| 24 | Gridded rainfall | Kelantan River Basin | Malaysia | SWAT-CUP | Tan et al. | ||
| 25 | Coupling SWAT-MODSIM | Karkheh River Basin | Iran | SWAT-CUP | Wheat, maize | Vaghefi et al. | |
| 26 | Water balance | Loei Province | Thailand | SWAT-CUP | Para-rubber | Wangpimool et al. | |
| 27 | Climate data | USA | USA | White et al. |
References
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment. Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Klove, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, A.; van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Dechen, F.; Carmela, S.; Telles, T.S.; Guimaraes, M.D.; de Fatima, M.; De Maria, I.C. Losses and costs associated with water erosion according to soil cover rate. Bragantia 2015, 74, 224–233. [Google Scholar] [CrossRef]
- Gulati, A.; Rai, S.C. Cost estimation of soil erosion and nutrient loss from a watershed of the Chotanagpur Plateau, India. Curr. Sci. 2014, 107, 670–674. [Google Scholar]
- Mcqueen, A.D.; Shulstad, R.N.; Osborn, C.T. Controlling agricultural soil loss in Arkansas north lake Chicot watershed—A cost-analysis. J. Soil Water Conserv. 1982, 37, 182–185. [Google Scholar]
- Kamali, B.; Houshmand Kouchi, D.; Yang, H.; Abbaspour, K.C. Multilevel Drought Hazard Assessment under Climate Change Scenarios in Semi-Arid Regions—A Case Study of the Karkheh River Basin in Iran. Water 2017, 9, 241. [Google Scholar] [CrossRef]
- Pagliero, L.; Bouraoui, F.; Willems, P.; Diels, J. Large-Scale Hydrological Simulations Using the Soil Water Assessment Tool, Protocol Development, and Application in the Danube Basin. J. Environ. Qual. 2014, 4, 145–154. [Google Scholar] [CrossRef]
- Whittaker, G.; Confesor, R.; Di Luzio, M.; Arnold, J.G. Detection of overparameterization and overfitting in an automatic calibration of swat. Trans. ASABE 2010, 53, 1487–1499. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Houshmand Kouchi, D.; Esmaili, K.; Faridhosseini, A.; Sanaeinejad, S.H.; Khalili, D.; Abbaspour, K.C. Sensitivity of Calibrated Parameters and Water Resource Estimates on Different Objective Functions and Optimization Algorithms. Water 2017, 9, 384. [Google Scholar] [CrossRef]
- Yang, J.; Abbaspour, K.C.; Reichert, P.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T. Methods to quantify and identify the sources of uncertainty for river basin water quality models. Water Sci. Technol. 2006, 53, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Kuczera, G.; Parent, E. Monte Carlo assessment of parameter uncertainty in conceptual catchment models: The Metropolis algorithm. J. Hydrol. 1998, 211, 69–85. [Google Scholar] [CrossRef]
- Marshall, L.; Nott, D.; Sharma, A. A comparative study of Markov chain Monte Carlo methods for conceptual rainfall–runoff modeling. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Yang, H. Hydrological Modelling of the Chaohe Basin in China: Statistical Model Formulation and Bayesian Inference. J. Hydrol. 2007, 340, 167–182. [Google Scholar] [CrossRef]
- Rouholahnejad, E.; Abbaspour, K.C.; Vejdani, M.; Srinivasan, R; Schulin, R.; Lehmann, A. Parallelization framework for calibration of hydrological models. Environ. Model. Softw. 2012, 31, 28–36. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E.; Ormsbee, L.; Uber, J.; Bros, C.M.; Kalungi, P.; Burd, R.; Zazula-Coetzee, B.; Belrain, T.; Kang, D.; et al. Battle of the Water Calibration Networks. J. Water Resour. Plan. Manag. 2012, 138, 523–532. [Google Scholar] [CrossRef]
- Hollaender, H.M.; Bormann, H.; Blume, T.; Buytaert, W.; Chirico, G.B.; Exbrayat, J.F.; Gustafsson, D.; Hoelzel, H.; Krausse, T.; Kraft, P.; et al. Impact of modellers’ decisions on hydrological a priori predictions. Hydrol. Earth Syst. Sci. 2014, 18, 2065–2085. [Google Scholar] [CrossRef]
- Freni, G.; Mannina, G.; Viviani, G. Uncertainty in urban stormwater quality modelling: The effect of acceptability threshold in the GLUE methodology. Water Res. 2008, 42. [Google Scholar] [CrossRef] [PubMed]
- Whittemore, R. Is the time right for consensus on model calibration guidance? J. Environ. Eng. 2001, 127, 95–96. [Google Scholar] [CrossRef]
- Chambers, B.M.; Pradhanang, S.M.; Gold, A.J. Assessing Thermally Stressful Events in a Rhode Island Coldwater Fish Habitat Using the SWAT Model. Water 2017, 9, 667. [Google Scholar] [CrossRef]
- Chambers, B.M.; Pradhanang, S.M.; Gold, A.J. Simulating Climate Change Induced Thermal Stress in Coldwater Fish Habitat Using SWAT Model. Water 2017, 9, 732. [Google Scholar] [CrossRef]
- Chen, S.; Sun, C.; Wu, W.; Sun, C. Water Leakage and Nitrate Leaching Characteristics in the Winter Wheat–Summer Maize Rotation System in the North China Plain under Different Irrigation and Fertilization Management Practices. Water 2017, 9, 141. [Google Scholar] [CrossRef]
- Cuceloglu, G.; Abbaspour, K.C.; Ozturk, I. Assessing the Water-Resources Potential of Istanbul by Using a Soil and Water Assessment Tool (SWAT) Hydrological Model. Water 2017, 9, 814. [Google Scholar] [CrossRef]
- Ding, X.; Xue, Y.; Lin, M.; Jiang, G. Influence Mechanisms of Rainfall and Terrain Characteristics on Total Nitrogen Losses from Regosol. Water 2017, 9, 167. [Google Scholar] [CrossRef]
- Fabre, C.; Sauvage, S.; Tananaev, N.; Srinivasan, R.; Teisserenc, R.; Miguel Sánchez Pérez, J. Using Modeling Tools to Better Understand Permafrost Hydrology. Water 2017, 9, 418. [Google Scholar] [CrossRef]
- Fant, C.; Srinivasan, R.; Boehlert, B.; Rennels, L.; Chapra, S.C.; Strzepek, K.M.; Corona, J.; Allen, A.; Martinich, J. Climate Change Impacts on US Water Quality Using Two Models: HAWQS and US Basins. Water 2017, 9, 118. [Google Scholar] [CrossRef]
- Gharib, A.; Davies, E.G.R.; Goss, G.G.; Faramarzi, M. Assessment of the Combined Effects of Threshold Selection and Parameter Estimation of Generalized Pareto Distribution with Applications to Flood Frequency Analysis. Water 2017, 9, 692. [Google Scholar] [CrossRef]
- Grusson, Y.; Anctil, F.; Sauvage, S.; Miguel Sánchez Pérez, J. Testing the SWAT Model with GriddedWeather Data of Different Spatial Resolutions. Water 2017, 9, 54. [Google Scholar] [CrossRef]
- Kamali, B.; Abbaspour, K.C.; Yang, H. Assessing the Uncertainty of Multiple Input Datasets in the Prediction of Water Resource Components. Water 2017, 9, 709. [Google Scholar] [CrossRef]
- Lee, J.E.; Heo, J.H.; Lee, J.; Kim, N.W. Assessment of Flood Frequency Alteration by Dam Construction via SWAT Simulation. Water 2017, 9, 264. [Google Scholar] [CrossRef]
- Li, C.; Zheng, X.; Zhao, F.; Wang, X.; Cai, Y.; Zhang, N. Effects of Urban Non-Point Source Pollution from Baoding City on Baiyangdian Lake, China. Water 2017, 9, 249. [Google Scholar] [CrossRef]
- Ligaray, M.; Kim, M.; Baek, S.; Ra, J.S.; Chun, J.A.; Park, Y.; Boithias, L.; Ribolzi, O.; Chon, K.; Cho, K.H. Modeling the Fate and Transport of Malathion in the Pagsanjan-Lumban Basin, Philippines. Water 2017, 9, 451. [Google Scholar] [CrossRef]
- Luz, M.P.; Beevers, L.C.; Cuthbertson, A.J.S.; Medero, G.M.; Dias, V.S.; Nascimento, D.T.F. The Mitigation Potential of Buffer Strips for Reservoir Sediment Yields: The Itumbiara Hydroelectric Power Plant in Brazil. Water 2016, 8, 489. [Google Scholar] [CrossRef]
- Marcinkowski, P.; Piniewski, M.; Kardel, I.; Szcześniak, M.; Benestad, R.; Srinivasan, R.; Ignar, S.; Okruszko, T. Effect of Climate Change on Hydrology, Sediment and Nutrient Losses in Two Lowland Catchments in Poland. Water 2017, 9, 156. [Google Scholar] [CrossRef]
- Paul, S.; Cashman, M.A.; Szura, K.; Pradhanang, S.M. Assessment of Nitrogen Inputs into Hunt River by OnsiteWastewater Treatment Systems via SWAT Simulation. Water 2017, 9, 610. [Google Scholar] [CrossRef]
- Qi, Z.; Kang, G.; Chu, C.; Qiu, Y.; Xu, Z.; Wang, Y. Comparison of SWAT and GWLF Model Simulation Performance in Humid South and Semi-Arid North of China. Water 2017, 9, 567. [Google Scholar] [CrossRef]
- Rouholahnejad, E.; Abbaspour, K.C.; Lehmann, A. Water Resources of the Black Sea Catchment under Future Climate and Landuse Change Projections. Water 2017, 9, 598. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Pérez-Sánchez, J.; Carrillo-García, J.; Soto, J. Using SWAT and Fuzzy TOPSIS to Assess the Impact of Climate Change in the Headwaters of the Segura River Basin (SE Spain). Water 2017, 9, 149. [Google Scholar] [CrossRef]
- Seo, M.; Jaber, F.; Srinivasan, R.; Jeong, J. Evaluating the Impact of Low Impact Development (LID) Practices on Water Quantity and Quality under Different Development Designs Using SWAT. Water 2017, 9, 193. [Google Scholar] [CrossRef]
- Seo, M.; Jaber, F.; Srinivasan, R. Evaluating Various Low-Impact Development Scenarios for Optimal Design Criteria Development. Water 2017, 9, 270. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Cracknell, A.P. Assessment of Three Long-Term Gridded Climate Products for Hydro-Climatic Simulations in Tropical River Basins. Water 2017, 9, 229. [Google Scholar] [CrossRef]
- Vaghefi, S.A.; Abbaspour, K.C.; Faramarzi, M.; Srinivasan, R.; Arnold, J.G. Modeling Crop Water Productivity Using a Coupled SWAT–MODSIM Model. Water 2017, 9, 157. [Google Scholar] [CrossRef]
- Wangpimoo, W.; Pongput, K.; Tangtham, N.; Prachansri, S.; Gassman, P.W. The Impact of Para Rubber Expansion on Streamflow and OtherWater Balance Components of the Nam Loei River Basin, Thailand. Water 2017, 9, 1. [Google Scholar] [CrossRef]
- White, M.J.; Gambone, M.; Haney, E.; Arnold, J.; Gao, J. Development of a Station Based Climate Database for SWAT and APEX Assessments in the US. Water 2017, 9, 437. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).