Observed Response of the Raindrop Size Distribution to Changes in the Melting Layer
Abstract
1. Introduction
2. Datasets and Methods
2.1. Instrumentation and Datasets
2.2. Radar Identification of the Melting Layer
2.3. Retrieval of the Raindrop Size Distribution
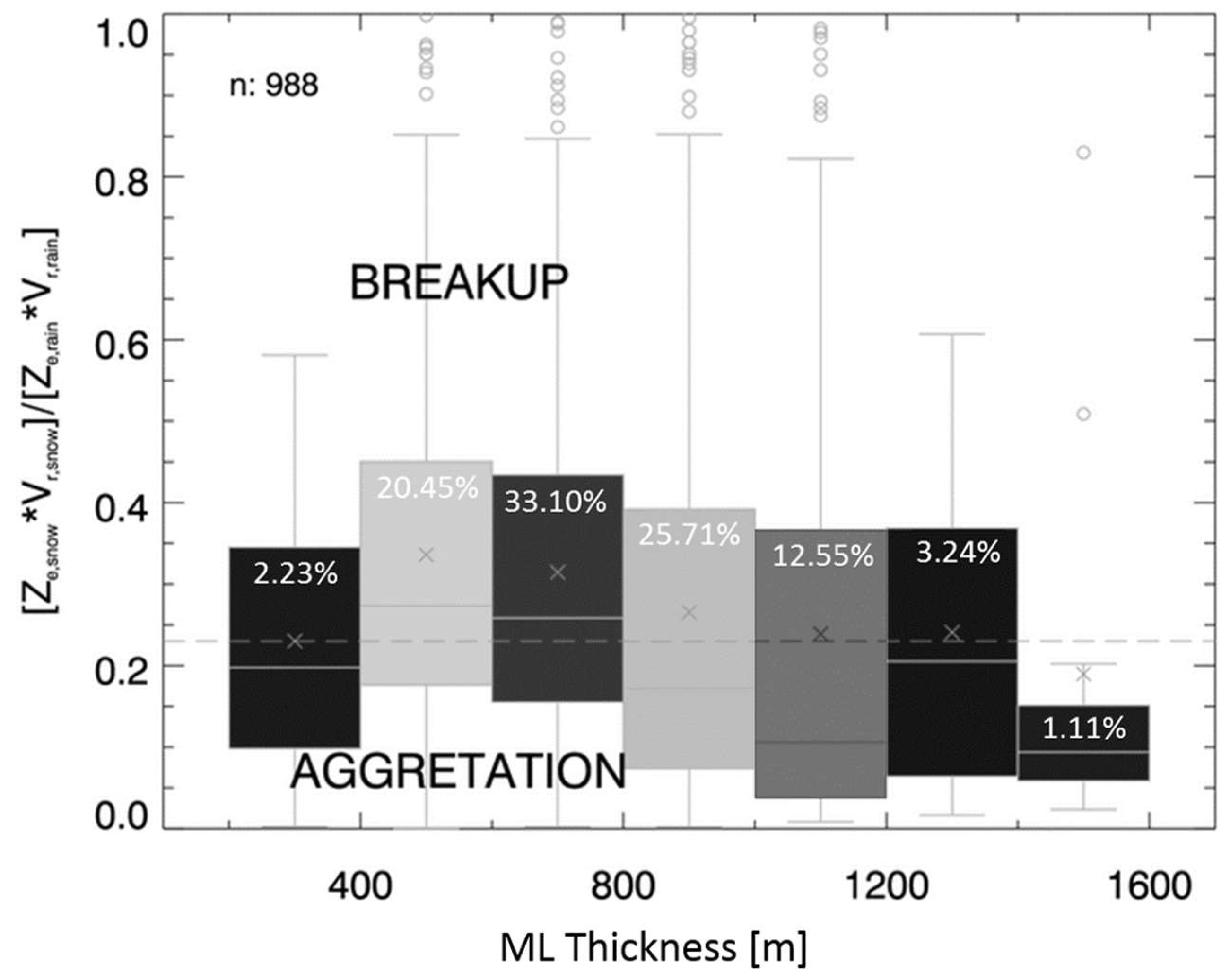
3. Results
3.1. Raindrop Sizes at the Ground
3.2. Evolution of the Raindrop Size Distribution in the Vertical Column
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Alabama (ARMOR):Dm = 0.5969 + 1.7953ZDR − 1.1111ZDR2 + 0.5171ZDR3 − 0.1360ZDR4 + 0.0142ZDR5, −0.2 ≤ ZDR ≤ 4.7 dB
- Iowa (NPOL):Dm = 0.5953 + 1.6092ZDR − 1.0567ZDR2 + 0.5762ZDR3 − 0.1696ZDR4 + 0.0219ZDR5, −0.3 < ZDR ≤ 3.7 dB
| Location | Observation Period (YYYY-MM-DD) | Number of Raindrops(n) (in Millions) | Total 1-min RSD Spectra (n ≥ 100) | Rainfall Rates (mm/h) | Total Rainfall (mm) |
|---|---|---|---|---|---|
| Huntsville, AL (number. of 2DVDs: 4) | 2007-07-07 to 2013-12-09 | 75.3 | 109,969 | 0.006–157.4 | 5903 |
| Eastern Iowa (IFloodS) (number of 2DVDs: 6) | 2013-04-09 to 2013-06-16 | 16.3 | 24,900 | 0.006–121.2 | 970.5 |
References
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001; ISBN 0-521-62384-7. [Google Scholar]
- Ryzhkov, A.V.; Schuur, T.J.; Burgess, D.W.; Heinselman, P.L.; Giangrande, S.E.; Zrnic, D.S. The Joint Polarization Experiment: Polarimetric rainfall measurements and hydrometeor classification. Bull. Am. Meteorol. Soc. 2005, 86, 809–824. [Google Scholar] [CrossRef]
- Boodoo, S.; Hudak, D.; Ryzhkov, A.; Zhang, P.; Donaldson, N.; Sills, D.; Reid, J.; Boodoo, S.; Hudak, D.; Ryzhkov, A.; et al. Quantitative precipitation estimation from a C-band dual-polarized radar for the 8 July 2013 flood in Toronto, Canada. J. Hydrometeorol. 2015, 16, 2027–2044. [Google Scholar] [CrossRef]
- Ryzhkov, A.V. The Impact of beam broadening on the quality of radar polarimetric data. J. Atmos. Ocean. Technol. 2007, 24, 729–744. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Review of the different sources of uncertainty in single polarization radar-based estimates of rainfall. Surv. Geophys. 2010, 31, 107–129. [Google Scholar] [CrossRef]
- Gorgucci, E.; Baldini, L. Influence of beam broadening on the accuracy of radar polarimetric rainfall estimation. J. Hydrometeorol. 2015, 16, 1356–1371. [Google Scholar] [CrossRef]
- Joss, J.; Lee, R. The application of radar-gauge comparisons to operational precipitation profile corrections. J. Appl. Meteorol. 1995, 34, 2612–2630. [Google Scholar] [CrossRef]
- Bellon, A.; Lee, G.W.; Zawadzki, I. Error statistics of VPR corrections in stratiform precipitation. J. Appl. Meteorol. 2005, 44, 998–1015. [Google Scholar] [CrossRef]
- Maahn, M.; Burgard, C.; Crewell, S.; Gorodetskaya, I.V.; Kneifel, S.; Lhermitte, S.; Van Tricht, K.; van Lipzig, N.P.M. How does the spaceborne radar blind zone affect derived surface snowfall statistics in polar regions? J. Geophys. Res. Atmos. 2014, 119, 13604–13620. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Meneghini, R.; Zawadzki, I. Global and local precipitation measurements by radar. Meteorol. Monogr. 2003, 30, 215. [Google Scholar] [CrossRef]
- Iguchi, T.; Kozu, T.; Kwiatkowski, J.; Meneghini, R.; Awaka, J.; Okamoto, K. Uncertainties in the rain profiling algorithm for the TRMM precipitation radar. J. Meteorol. Soc. Jpn. 2009, 87A, 1–30. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation; Mysak, L.A., Hamilton, K., Eds.; Atmospheric and Oceanographic Sciences Library; Springer: Dordrecht, The Netherlands, 2010; Volume 18, ISBN 978-0-7923-4211-3. [Google Scholar]
- Waldvogel, A. The N0 Jump of Raindrop Spectra. J. Atmos. Sci. 1974, 31, 1067–1078. [Google Scholar] [CrossRef]
- Huggel, A.; Schmid, W.; Waldvogel, A. Raindrop size distributions and the radar bright band. J. Appl. Meteorol. 1996, 35, 1688–1701. [Google Scholar] [CrossRef]
- Brandes, E.A.; Zhang, G.; Vivekanandan, J. Drop size distribution retrieval with polarimetric radar: Model and application. J. Appl. Meteorol. 2004, 43, 461–475. [Google Scholar] [CrossRef]
- Sharma, S.; Konwar, M.; Sarma, D.K.; Kalapureddy, M.C.R.; Jain, A.R. Characteristics of rain integral parameters during tropical convective, transition, and stratiform rain at Gadanki and its application in rain retrieval. J. Appl. Meteorol. Climatol. 2009, 48, 1245–1266. [Google Scholar] [CrossRef]
- Andrić, J.; Kumjian, M.R.; Zrnić, D.S.; Straka, J.M.; Melnikov, V.M. Polarimetric signatures above the melting layer in winter storms: An observational and modeling study. J. Appl. Meteorol. Climatol. 2013, 52, 682–700. [Google Scholar] [CrossRef]
- Yoshikawa, E.; Kida, S.; Yoshida, S.; Morimoto, T.; Ushio, T.; Kawasaki, Z. Vertical structure of raindrop size distribution in lower atmospheric boundary layer. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Oue, M.; Uyeda, H.; Shusse, Y. Two types of precipitation particle distribution in convective cells accompanying a Baiu frontal rainband around Okinawa Island, Japan. J. Geophys. Res. 2010, 115, D02201. [Google Scholar] [CrossRef]
- Kim, D.-K.; Kim, Y.-H.; Chang, D.-E. A study of microphysical properties within a precipitation system using wind profiler spectra. Asia Pac. J. Atmos. Sci. 2011, 47, 413–420. [Google Scholar] [CrossRef]
- Petersen, W.A.; Knupp, K.R. Coauthors The UAH-NSSTC/WHNT ARMOR C-band dual-polarimetric radar: A unique collaboration in research, education and technology transfer. In Proceedings of the 32nd Conference on Radar Meteorology, Albuquerque, NM, USA, 24–29 October 2005; American Meteor Society: Albuquerque, NM, USA, 2005; p. 12R.4. [Google Scholar]
- Gerlach, J.; Petersen, W.A. The NASA transportable S-band dual-polarimetric radar. Antenna system upgrades, performance and deployment during MC3E. In Proceedings of the 35th Conference on Radar Meteorology, Pittsburgh, PA, USA, 26–30 September 2011; American Meteorological Society: Pittsburgh, PA, USA, 2011; p. P192. [Google Scholar]
- Petersen, W.A.; Krajewski, W. Status update on the GPM Ground Validation Iowa Flood Studies (IFloodS) Field Experiement. In European Geosciences Union General Assembly; European Geosciences Union: Vienna, Austria, 2013. [Google Scholar]
- Doviak, R.J.; Bringi, V.; Ryzhkov, A.; Zahrai, A.; Zrnić, D. Considerations for polarimetric upgrades to operational WSR-88D radars. J. Atmos. Ocean. Technol. 2000, 17, 257–278. [Google Scholar] [CrossRef]
- Scott, R.D.; Krehbiel, P.R.; Rison, W. The use of simultaneous horizontal and vertical transmissions for dual-polarization radar meteorological observations. J. Atmos. Ocean. Technol. 2001, 18, 629–648. [Google Scholar] [CrossRef]
- Kruger, A.; Krajewski, W.F. Two-dimensional video disdrometer: A description. J. Atmos. Ocean. Technol. 2002, 19, 602–617. [Google Scholar] [CrossRef]
- Schönhuber, M.; Lammer, G.; Randeu, W.L. The 2D-Video-Distrometer. In Precipitation: Advances in Measurement, Estimation and Prediction; Michaelides, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–31. ISBN 978-3-540-77654-3. [Google Scholar]
- Matrosov, S.Y.; Clark, K.A.; Kingsmill, D.E. A polarimetric radar approach to identify rain, melting-layer, and snow regions for applying corrections to vertical profiles of reflectivity. J. Appl. Meteorol. Climatol. 2007, 46, 154–166. [Google Scholar] [CrossRef]
- Giangrande, S.E.; Krause, J.M.; Ryzhkov, A.V. Automatic designation of the melting layer with a polarimetric prototype of the WSR-88D radar. J. Appl. Meteorol. Climatol. 2008, 47, 1354–1364. [Google Scholar] [CrossRef]
- Shusse, Y.; Nakagawa, K.; Takahashi, N.; Satoh, S.; Iguchi, T. Characteristics of polarimetric radar variables in three types of rainfalls in a Baiu front event over the East China Sea. J. Meteorol. Soc. Jpn. 2009, 87, 865–875. [Google Scholar] [CrossRef]
- Boodoo, S.; Hudak, D.; Donaldson, N.; Leduc, M. Application of dual-polarization radar melting-layer detection algorithm. J. Appl. Meteorol. Climatol. 2010, 49, 1779–1793. [Google Scholar] [CrossRef]
- Wolfensberger, D.; Scipion, D.; Berne, A. Detection and characterization of the melting layer based on polarimetric radar scans. Q. J. R. Meteorol. Soc. 2016, 142, 108–124. [Google Scholar] [CrossRef]
- Caylor, I.J.; Illingworth, A.J. Identification of the bright band and hydrometeors using co-polar dual polarization radar. In Proceedings of the Preprints, 24th American Meteorological Socienty Conference on Radar Meteorology, Tallahassee, FL, USA, 27–31 March 1989; American Meteorological Society: Boston, MA, USA, 1989; pp. 9–12. [Google Scholar]
- Balakrishnan, N.; Zrnic, D.S. Use of polarization to characterize precipitation and discriminate large hail. J. Atmos. Sci. 1990, 47, 1525–1540. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Dévényi, D.; Weygandt, S.S.; Brundage, K.J.; Brown, J.M.; Grell, G.A.; Kim, D.; Schwartz, B.E.; Smirnova, T.G.; Smith, T.L.; et al. An Hourly Assimilation–Forecast Cycle: The RUC. Mon. Weather Rev. 2004, 132, 495–518. [Google Scholar] [CrossRef]
- Aydin, K.; Giridhar, V. C-band dual-polarization radar observables in rain. J. Atmos. Ocean. Technol. 1992, 9, 383–390. [Google Scholar] [CrossRef]
- Baldini, L.; Gorgucci, E.; Petersen, W. Implementations of CSU hydrometeor classification scheme for C-band polarimetric radars. In Proceedings of the 32nd Conference on Radar Meteorology, Albuquerque, NM, USA, 24–29 October 2005; American Meteor Society: Albuquerque, NM, USA, 2005; p. P11.4. [Google Scholar]
- Zrnić, D.S.; Raghavan, R.; Chandrasekar, V. Observations of copolar correlation coefficient through a bright band at vertical incidence. J. Appl. Meteorol. 1994, 33, 45–52. [Google Scholar] [CrossRef]
- Brandes, E.A.; Ikeda, K. Freezing-level estimation with polarimetric radar. J. Appl. Meteorol. 2004, 43, 1541–1553. [Google Scholar] [CrossRef]
- Marshall, J.S. Precipitation trajectories and patterns. J. Meteorol. 1953, 10, 25–29. [Google Scholar] [CrossRef]
- Gunn, R.E.S.; Marshall, J.S. The effect of wind shear on falling precipitation. J. Meteorol. 1955, 12, 339–349. [Google Scholar] [CrossRef]
- Yuter, S.E.; Houze, R.A. Measurements of raindrop size distributions over the Pacific warm pool and implications for Z-R relations. J. Appl. Meteorol. 1997, 36, 847–867. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V. The impact of size sorting on the polarimetric radar variables. J. Atmos. Sci. 2012, 69, 2042–2060. [Google Scholar] [CrossRef]
- Gatlin, P.N.; Thurai, M.; Bringi, V.N.; Petersen, W.A.; Wolff, D.B.; Tokay, A.; Carey, L.D.; Wingo, M.; Thurai, M.; Petersen, W.A.; et al. Searching for large raindrops: A global summary of two-dimensional video disdrometer observations. J. Appl. Meteorol. Climatol. 2014, 1069–1089. [Google Scholar] [CrossRef]
- Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X.; Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X. The concept of “normalized” distribution to describe raindrop spectra: A tool for cloud physics and cloud remote sensing. J. Appl. Meteorol. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M.; Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; et al. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Bringi, V.N.; Keenan, T.D.; Chandrasekar, V. Correcting C-band radar reflectivity and differential reflectivity data for rain attenuation: A self-consistent method with constraints. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1906–1915. [Google Scholar] [CrossRef]
- Bringi, V.N.; Rasmussen, R.M.; Vivekanandan, J. Multiparameter Radar Measurements in Colorado Convective Storms. Part I: Graupel Melting Studies. J. Atmos. Sci. 1986, 43, 2545–2563. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Adams, W.M.; Bringi, V.N. Rigorous Approach to Polarimetric Radar Modeling of Hydrometeor Orientation Distributions. J. Appl. Meteorol. 1991, 30, 1053–1063. [Google Scholar] [CrossRef]
- Zhang, G.; Vivekanandan, J.; Brandes, E. A method for estimating rain rate and drop size distribution from polarimetric radar measurements. IEEE Trans. Geosci. Remote Sens. 2001, 39, 830–841. [Google Scholar] [CrossRef]
- Thurai, M.; Huang, G.J.; Bringi, V.N.; Randeu, W.L.; Schönhuber, M.; Thurai, M.; Huang, G.J.; Bringi, V.N.; Randeu, W.L.; Schönhuber, M. Drop shapes, model comparisons, and calculations of polarimetric radar parameters in rain. J. Atmos. Ocean. Technol. 2007, 24, 1019–1032. [Google Scholar] [CrossRef]
- Barber, P.; Yeh, C. Scattering of electromagnetic waves by arbitrarily shaped dielectric bodies. Appl. Opt. 1975, 14, 2864. [Google Scholar] [CrossRef] [PubMed]
- Mishchenko, M.I.; Travis, L.D. Capabilities and limitations of a current FORTRAN implementation of the T-matrix method for randomly oriented, rotationally symmetric scatterers. J. Quant. Spectrosc. Radiat. Transf. 1998, 60, 309–324. [Google Scholar] [CrossRef]
- Petersen, W.; Carey, L.D.; Gatlin, P.N.; Wingo, M.T.; Wolff, D.B.; Bringi, V.N. Drop size distribution measurements supporting the NASA Global Precipitation Measurement Mission: Infrastructure and preliminary results. In Proceedings of the 35th Conference on Radar Meteorology, Pittsburgh, PA, USA, 26–30 September 2011; American Meteorological Society: Pittsburgh, PA, USA, 2011; p. P36. [Google Scholar]
- Carey, L.D.; Petersen, W.A. Sensitivity of C-band polarimetric radar–based drop size estimates to maximum diameter. J. Appl. Meteorol. Climatol. 2015, 54, 1352–1371. [Google Scholar] [CrossRef]
- Gorgucci, E.; Chandrasekar, V.; Bringi, V.N.; Scarchilli, G. Estimation of raindrop size distribution parameters from polarimetric radar measurements. J. Atmos. Sci. 2002, 59, 2373–2384. [Google Scholar] [CrossRef]
- Brandes, E.A.; Zhang, G.; Vivekanandan, J. An evaluation of a drop distribution–based polarimetric radar rainfall estimator. J. Appl. Meteorol. 2003, 42, 652–660. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N.; Carey, L.D.; Gatlin, P.; Schultz, E.; Petersen, W.A. Estimating the accuracy of polarimetric radar–based retrievals of drop-size distribution parameters and rain rate: An application of error variance separation using radar-derived spatial correlations. J. Hydrometeorol. 2012, 13, 1066–1079. [Google Scholar] [CrossRef]
- Bringi, V.N.; Thurai, M.; Nakagawa, K.; Huang, G.J.; Kobayahsi, T.; Adachi, A.; Hanando, H.; Seizawa, S. Rainfall Estimation from C-Band Polarimetric Radar in Okinawa, Japan: Comparisons with 2D-Video Disdrometer and 400 MHz Wind Profiler. J. Meteorol. Soc. Jpn. 2006, 84, 705–724. [Google Scholar] [CrossRef]
- Bringi, V.N.; Williams, C.R.; Thurai, M.; May, P.T. Using dual-polarized radar and dual-frequency profiler for DSD characterization: A case study from Darwin, Australia. J. Atmos. Ocean. Technol. 2009, 26, 2107–2122. [Google Scholar] [CrossRef]
- Lee, C.K.; Lee, G.W.; Zawadzki, I.; Kim, K.-E. A preliminary analysis of spatial variability of raindrop size distributions during stratiform rain events. J. Appl. Meteorol. Climatol. 2009, 48, 270–283. [Google Scholar] [CrossRef]
- Bringi, V.N.; Tolstoy, L.; Thurai, M.; Petersen, W.A. Estimation of spatial correlation of drop size distribution parameters and rain rate using NASA’s S-band polarimetric radar and 2D video disdrometer network: Two case studies from MC3E. J. Hydrometeorol. 2015, 16, 1207–1221. [Google Scholar] [CrossRef]
- Stewart, R.E.; Marwitz, J.D.; Pace, J.C.; Carbone, R.E. Characteristics through the melting layer of stratiform clouds. J. Atmos. Sci. 1984, 41, 3227–3237. [Google Scholar] [CrossRef]
- McFarquhar, G.M.; Timlin, M.S.; Rauber, R.M.; Jewett, B.F.; Grim, J.A.; Jorgensen, D.P. Vertical variability of cloud hydrometeors in the stratiform region of mesoscale convective systems and bow echoes. Mon. Weather Rev. 2007, 135, 3405–3428. [Google Scholar] [CrossRef]
- Fabry, F.; Zawadzki, I. Long-term radar observations of the melting layer of precipitation and their interpretation. J. Atmos. Sci. 1995, 52, 838–851. [Google Scholar] [CrossRef]
- Smith, P.L.; Liu, Z.; Joss, J. A study of sampling-variability effects in raindrop size observations. J. Appl. Meteorol. 1993, 32, 1259–1269. [Google Scholar] [CrossRef]
- Klaassen, W. Radar observations and simulation of the melting layer of precipitation. J. Atmos. Sci. 1988, 45, 3741–3753. [Google Scholar] [CrossRef]
- Gage, K.S.; Williams, C.R.; Clark, W.L.; Johnston, P.E.; Carter, D.A. Profiler contributions to Tropical Rainfall Measuring Mission (TRMM) ground validation field campaigns. J. Atmos. Ocean. Technol. 2002, 19, 843–863. [Google Scholar] [CrossRef]
- Kim, D.-K.; Knupp, K.R.; Williams, C.R. Airflow and precipitation properties within the stratiform region of Tropical Storm Gabrielle during landfall. Mon. Weather Rev. 2009, 137, 1954–1971. [Google Scholar] [CrossRef]
- Matsuo, T.; Sasyo, Y. Melting of snowflakes below freezing level in the atmosphere. J. Meteorol. Soc. Jpn. Ser. II 1981, 59, 10–25. [Google Scholar] [CrossRef]
- Willis, P.T.; Heymsfield, A.J. Structure of the melting layer in mesoscale convective system stratiform precipitation. J. Atmos. Sci. 1989, 46, 2008–2025. [Google Scholar] [CrossRef]
- Barthazy, E.; Henrich, W.; Waldvogel, A. Size distribution of hydrometeors through the melting layer. Atmos. Res. 1998, 47–48, 193–208. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Bansemer, A.; Poellot, M.R.; Wood, N.; Heymsfield, A.J.; Bansemer, A.; Poellot, M.R.; Wood, N. Observations of ice microphysics through the melting layer. J. Atmos. Sci. 2015, 72, 2902–2928. [Google Scholar] [CrossRef]
- Mitra, S.K.; Vohl, O.; Ahr, M.; Pruppacher, H.R. A wind tunnel and theoretical study of the melting behavior of atmospheric ice particles. IV: Experiment and theory for snow flakes. J. Atmos. Sci. 1990, 47, 584–591. [Google Scholar] [CrossRef]
- Drummond, F.J.; Rogers, R.R.; Cohn, S.A.; Ecklund, W.L.; Carter, D.A.; Wilson, J.S. A new look at the melting layer. J. Atmos. Sci. 1996, 53, 759–769. [Google Scholar] [CrossRef]
- Cifelli, R.; Williams, C.R.; Rajopadhyaya, D.K.; Avery, S.K.; Gage, K.S.; May, P.T. Drop-size distribution characteristics in tropical mesoscale convective systems. J. Appl. Meteorol. 2000, 39, 760–777. [Google Scholar] [CrossRef]
- Kirankumar, N.V.P.; Rao, T.N.; Radhakrishna, B.; Rao, D.N. Statistical characteristics of raindrop size distribution in southwest monsoon season. J. Appl. Meteorol. Climatol. 2008, 47, 576–590. [Google Scholar] [CrossRef]
- Ruan, Z.; Ming, H.; Ma, J.; Ge, R.; Bian, L. Analysis of the microphysical properties of a stratiform rain event using an L-Band profiler radar. J. Meteorol. Res. 2014, 28, 268–280. [Google Scholar] [CrossRef]
- Zipser, E.J. Mesoscale and convective-scale downdrafts as distinct components of squall-line structure. Mon. Weather Rev. 1977, 105, 1568–1589. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V. The impact of evaporation on polarimetric characteristics of rain: Theoretical model and practical implications. J. Appl. Meteorol. Climatol. 2010, 49, 1247–1267. [Google Scholar] [CrossRef]
- Thurai, M.; Gatlin, P.N.; Bringi, V.N.N.; Petersen, W.A.; Notaros, B.; Carey, L.D.; Kennedy, P.; Notaroš, B.; Carey, L.D. Towards completing the rain drop size spectrum: Case studies involving 2D-video disdrometer, droplet spectrometer, and polarimetric radar measurements. J. Appl. Meteorol. Climatol. 2017, 56. submitted. [Google Scholar] [CrossRef]
- Peters, G.; Fischer, B.; Andersson, T. Rain observations with a vertically looking Micro Rain Radar (MRR). Boreal Environ. Res. 2002, 353–362. [Google Scholar]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) Mission for science and society. Bull. Am. Meteorol. Soc. 2016, 1679–1696. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N. Drop axis ratios from a 2D video disdrometer. J. Atmos. Ocean. Technol. 2005, 22, 966–978. [Google Scholar] [CrossRef]
- Huang, G.-J.; Bringi, V.N.; Thurai, M. Orientation angle distributions of drops after an 80-m fall using a 2D video disdrometer. J. Atmos. Ocean. Technol. 2008, 25, 1717–1723. [Google Scholar] [CrossRef]
- Keenan, T.D.; Carey, L.D.; Zrnić, D.S.; May, P.T. Sensitivity of 5-cm wavelength polarimetric radar variables to raindrop axial ratio and drop size distribution. J. Appl. Meteorol. 2001, 40, 526–545. [Google Scholar] [CrossRef]
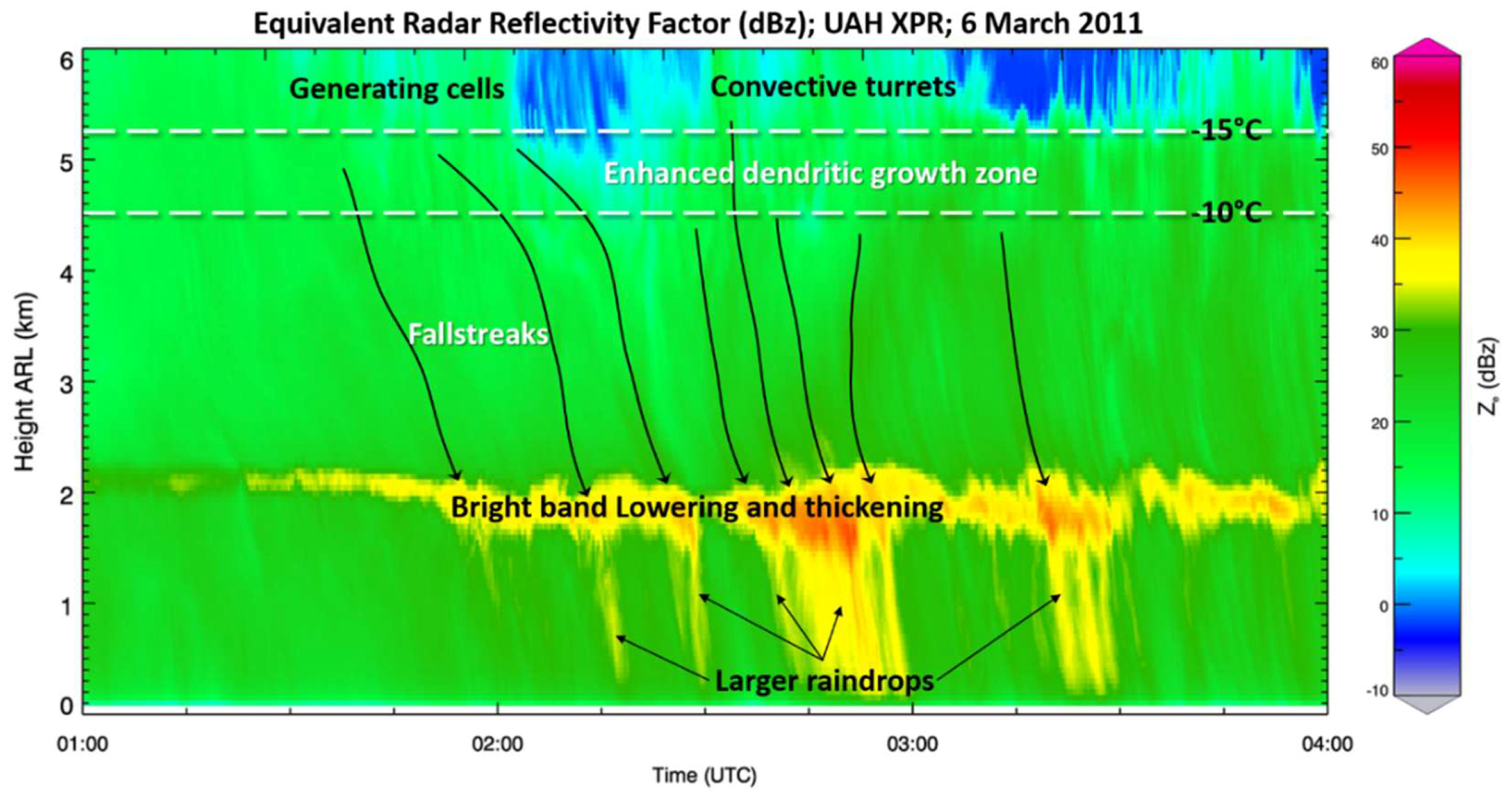
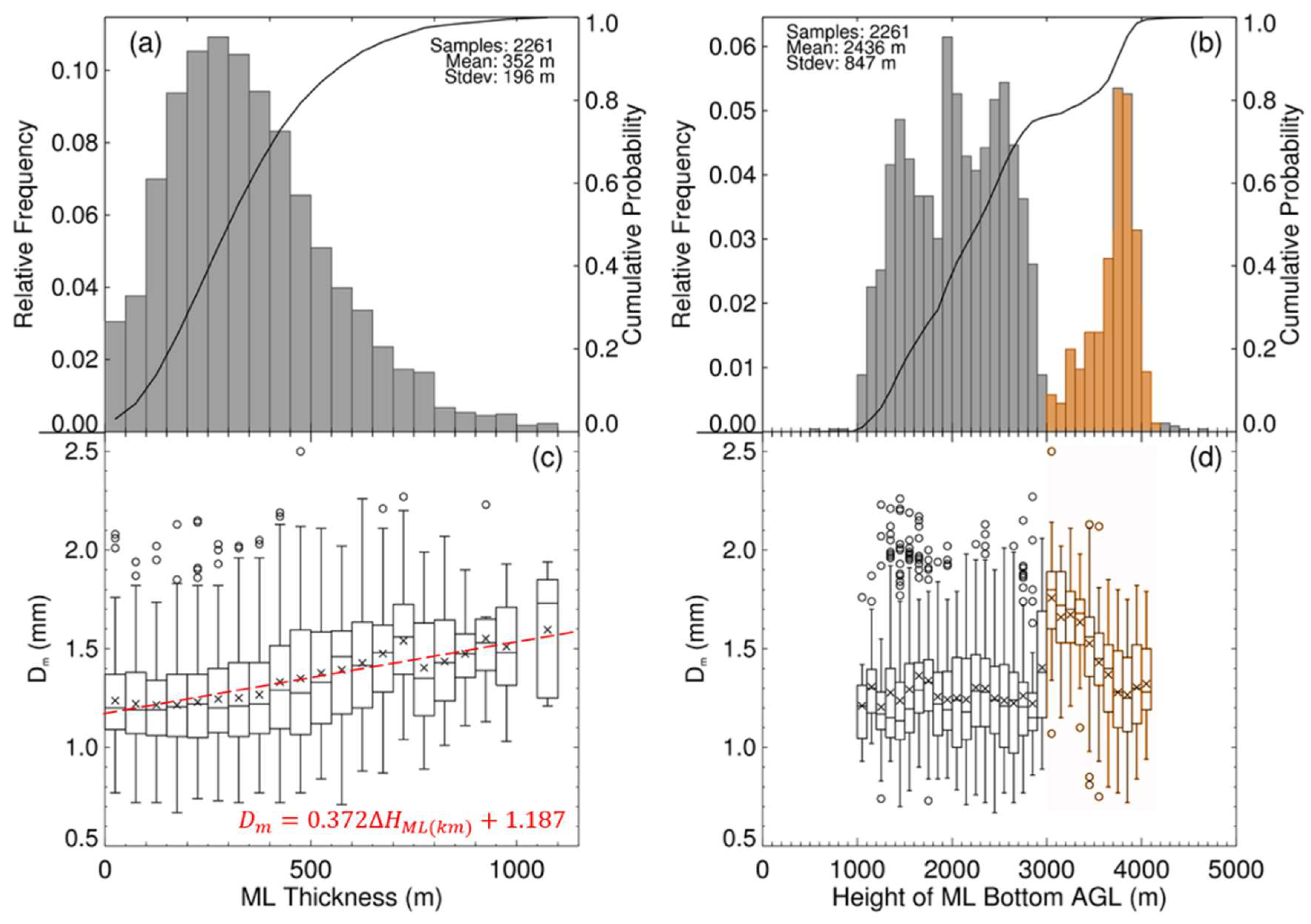
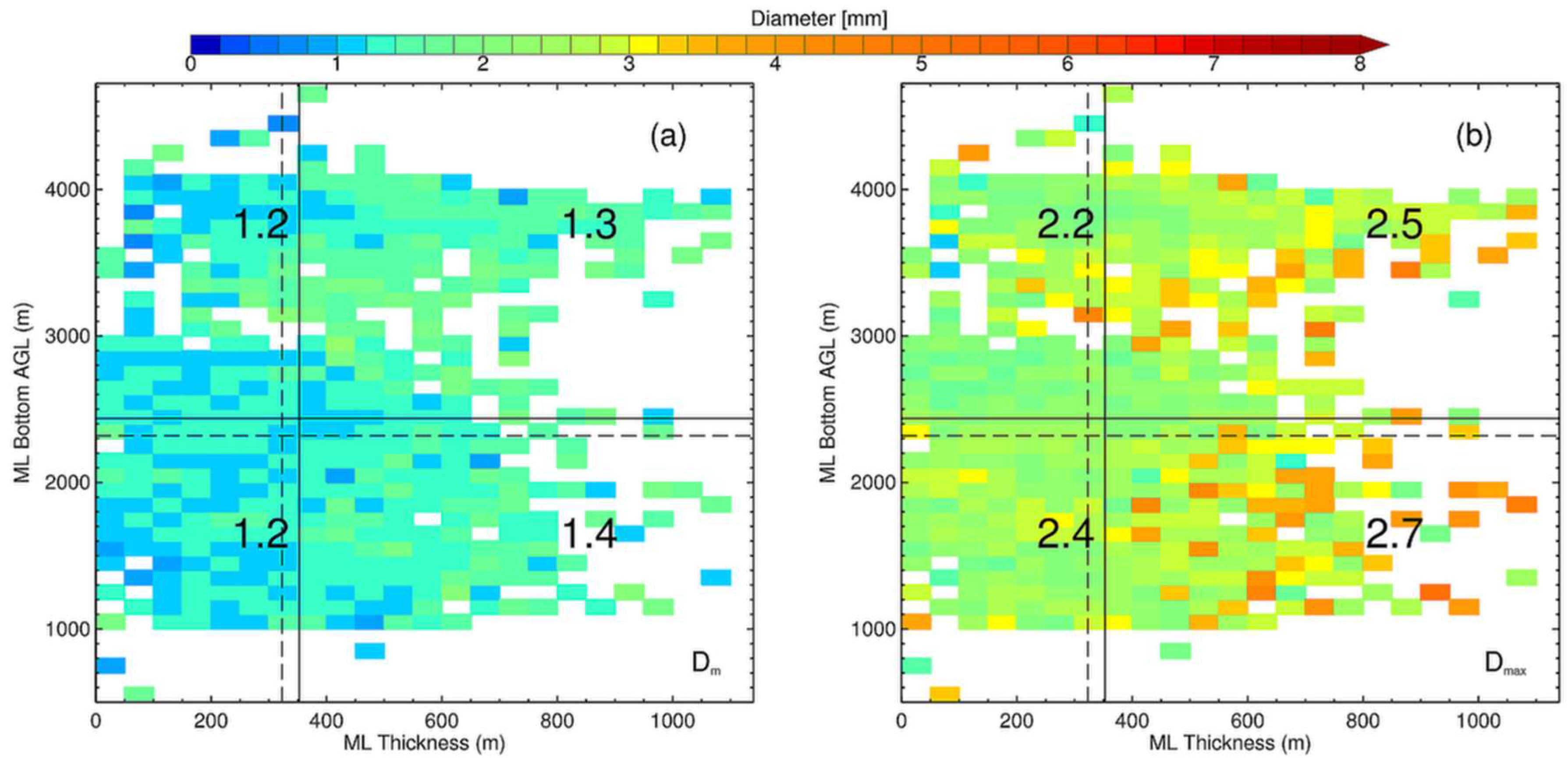
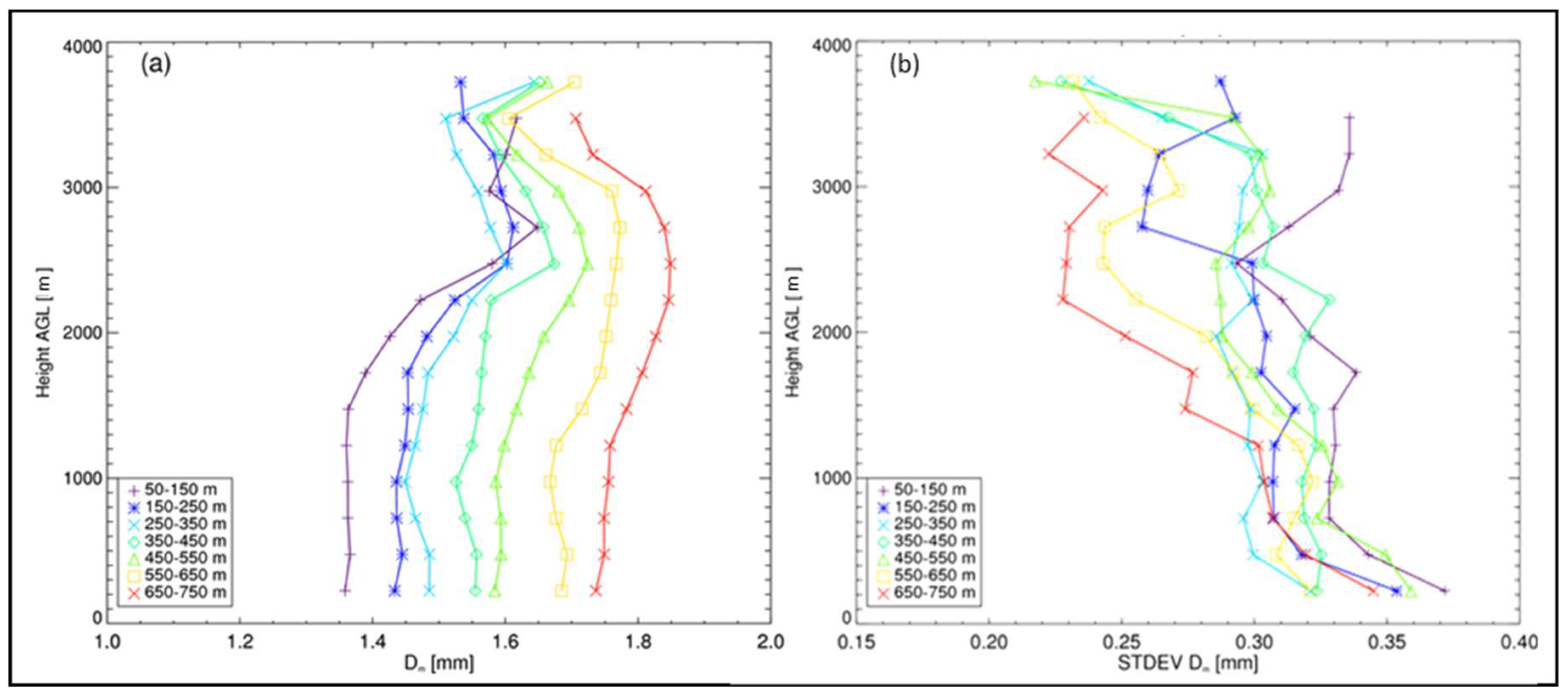
| ARMOR | Value/Description |
| Frequency | 5625 MHz |
| Peak transmitted power | 350 kW |
| Pulse duration | 0.8 µs |
| Pulse repetition frequency | 1200 Hz |
| Number of samples per bin | 128 |
| Beam width (3 dB) | 1.07° |
| Antenna | 3.7 m diameter; Center Feed Parabolic |
| Range resolution | 125 m |
| Polarization | Simultaneous Transmit/Receive of h and v |
| NPOL | Value/Description |
| Frequency | 2790–2810 MHz |
| Peak transmitted power | 850 kW |
| Pulse duration | 0.8 µs |
| Pulse repetition frequency | 1100 Hz |
| Number of samples per bin | 72 |
| Beam width (3 dB) | 0.95° |
| Antenna | 8.5 m diameter; Center Feed Parabolic |
| Range resolution | 150 m |
| Polarization | Simultaneous Transmit/Receive of h and v |
| Statistic | ML Top | ML Bottom |
|---|---|---|
| Number of days | 12 | 12 |
| Bias (m) | 221 | −241 |
| Root Mean Square Error (m) | 282 | 319 |
| Standard deviation (m) | 166 | 208 |
| Pearson correlation coefficient | 0.98 | 0.98 |
| ML Thickness (m) | Number of RHI Profiles | <Dm> ± σ(Dm) (mm) |
|---|---|---|
| 50 ≤ MLthick < 150 m | 384 | 1.40 ± 0.34 |
| 150 ≤ MLthick < 250 m | 665 | 1.47 ± 0.31 |
| 250 ≤ MLthick < 350 m | 697 | 1.49 ± 0.30 |
| 350 ≤ MLthick < 450 m | 601 | 1.57 ± 0.32 |
| 450 ≤ MLthick < 550 m | 423 | 1.62 ± 0.32 |
| 550 ≤ MLthick < 650 m | 295 | 1.71 ± 0.30 |
| 650 ≤ MLthick < 750 m | 172 | 1.78 ± 0.28 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gatlin, P.N.; Petersen, W.A.; Knupp, K.R.; Carey, L.D. Observed Response of the Raindrop Size Distribution to Changes in the Melting Layer. Atmosphere 2018, 9, 319. https://doi.org/10.3390/atmos9080319
Gatlin PN, Petersen WA, Knupp KR, Carey LD. Observed Response of the Raindrop Size Distribution to Changes in the Melting Layer. Atmosphere. 2018; 9(8):319. https://doi.org/10.3390/atmos9080319
Chicago/Turabian StyleGatlin, Patrick N., Walter A. Petersen, Kevin R. Knupp, and Lawrence D. Carey. 2018. "Observed Response of the Raindrop Size Distribution to Changes in the Melting Layer" Atmosphere 9, no. 8: 319. https://doi.org/10.3390/atmos9080319
APA StyleGatlin, P. N., Petersen, W. A., Knupp, K. R., & Carey, L. D. (2018). Observed Response of the Raindrop Size Distribution to Changes in the Melting Layer. Atmosphere, 9(8), 319. https://doi.org/10.3390/atmos9080319







