1. Introduction
Predicting when weather conditions will make a wildland fire difficult to manage is important but extremely difficult. Complex interactions at multiple scales between fire, fuels, topography, and weather (e.g., [
1]) combined with imperfect input data and insufficient model resolution make it practically impossible to produce perfect forecasts of fire conditions. Some researchers have tried to account for these interactions by using statistical analyses (e.g., [
2,
3,
4,
5]). The tools developed by these researchers have usefulness in certain situations, but often fail when tried at different locations or with different data because they are inherently dependent upon the input data and events used to define the tools [
6,
7].
For this study, we want to isolate the effects of weather on a wildland fire, so we define a fire weather index (FWI) as an index that includes only weather inputs and thus does not include explicit or implicit information about the state of wildland fuels or topography. Using this definition, the only FWIs in the literature are the Lower Atmospheric Severity Index (a.k.a. the Haines Index (HI) [
2,
8]), the Angström Index [
3], and a logistic-regression-based FWI recently developed for the Northeast United States [
4]. Of these FWIs, only the HI is widely used operationally to predict when weather conditions will make a wildland fire difficult to manage.
The new FWI defined in this article is based on a physical, non-statistical understanding of fire–atmosphere interactions. Ask any wildland fire expert about the weather components that lead to difficult fire conditions and the expert will reply with some combination of “hot, dry, and windy”. The key atmospheric variables underlying “hot, dry, and windy”—temperature, moisture, and wind—have direct physical effects on wildland fires. Our index is based on these variables, so we call our index the Hot-Dry-Windy Index (HDW). HDW, like any meteorological index, seeks to synthesize information about the state of the atmosphere into a quantity that can be used to assess the potential for certain types of atmospheric phenomena to occur. We want to establish and analyze this new FWI only in the context of meteorological factors—if HDW cannot adequately represent weather conditions, then the index’s validity would be in doubt.
A key challenge for defining an FWI is identifying temporal and spatial scales at which we can adequately quantify and test the index. At small scales, deterministic predictions of temperature, moisture, and wind variations that can affect a fire are practically impossible due to microscale (scales of motion <2 km, as defined in Ref. [
9]) non-linearities and imperfect input data. However, many of the weather conditions that affect the near-fire environment are driven by synoptic-scale and/or meso-alpha-scale processes (i.e., scales larger than about 200 km, as defined in Ref. [
9]) that are more spatially and temporally predictable, and conditions at these scales are often an adequate proxy for fire-scale variability. Thus, we chose to focus HDW on larger-scale atmospheric information. The ultimate goal of HDW is to quantify the potential for a wildland fire to become difficult to manage due to the influence of predictable, large-scale components of weather forecasts at multiple-day lead times, while leaving the assessment of less-certain, smaller-scale details to experts on the ground.
There are many other fire danger and fire behavior indices in the literature and in use that do not qualify as FWIs. The primary reason is because the most popular fire danger and fire behavior indices require not only weather inputs but also fuels and/or topography information. Some of these indices are even commonly referred to as FWIs (e.g., the “simple” index [
5], the Fosberg Fire Weather Index [
10,
11], and the McArthur Forest Fire Danger Index [
12,
13]), but these indices do not qualify as FWIs using our definition because they all either explicitly or implicitly include calculations based on fuels (e.g., flame length, fuel moisture, and rate of spread). One could conceivably hold fuel conditions constant in these non-weather-only indices and by doing so produce indices that vary only due to weather components. However, when a fire index is formulated using an explicit or implicit fuel relationship, the effects of the fuel-based parameters add variability due to the embedded non-linear computations. So, if a “true” FWI fails to identify a dangerous fire event, the index failed either because the weather was not adequately represented in the index or the weather did not have a significant impact on the fire. If a non-weather-only fire index fails to identify a fire event, it could be because of the aforementioned reasons but also could be due to the fuels and/or topography information in the calculation, which makes determining attribution, efficacy, and failure modes for the index more difficult. Furthermore, indices like those in Refs. [
5,
10,
11,
12,
13] include assumptions about fuels that make those indices more or less applicable to a given area based on the fuel types in that area; HDW and other “true” FWIs make no such assumptions. Thus, while research comparing HDW with existing fire indices at individual locations would be worthwhile to specific end users, a broad-scale comparison of HDW to fire indices formulated to include fuel information could unnecessarily restrict further exploration; we argue that this is undesirable in a paper that introduces a new index.
The rest of the paper is organized as follows:
Section 2 presents the science and formulation of HDW, and
Section 3 shows that HDW has predictive skill at identifying days when historical fires experienced significant fire behavior that made them difficult to manage. We close with a brief discussion and conclusions in
Section 4.
2. The Hot-Dry-Windy Index (HDW)
We begin our description of HDW by analyzing how the atmosphere physically affects a fire. The atmosphere generally affects a fire through three primary state variables—wind, temperature, and moisture (e.g., [
14]). At large scales, the effect of wind is straightforward—a stronger wind generally indicates that a wildland fire will spread more quickly and be more difficult to contain or control (e.g., [
15]). While wind shifts can also significantly affect fire behavior, they are inherently smaller scale and thus are not included in this formulation of HDW.
The effects of atmospheric heat and moisture on a fire are more difficult to quantify because these two variables do not have independent effects on a fire. Instead, as Ref. [
15] states, the primary effect of both atmospheric heat and moisture on a fire is to alter the rate at which moisture evaporates from fuels, which in turn affects fuel consumption, fire spread, and fire intensity. Thus, HDW uses a variable that combines atmospheric heat and moisture into one factor.
Historically, the fire community has used relative humidity (RH) as its preferred metric for combining temperature and humidity into one term (e.g., [
16,
17]). RH is defined as the ratio of the vapor pressure (e), a variable dependent solely on absolute moisture content (q), to the saturation vapor pressure (e
s), a variable dependent solely on temperature (T), times 100%:
However, RH can mask the total amount of evaporation that is possible at a given temperature. For example, 20% RH air at 0 °C can become saturated by increasing the vapor pressure by 4.9 hPa, while 20% RH air at 30 °C will only reach saturation when the vapor pressure is increased by 34.0 hPa. Although the RH is the same in both examples, the combined effect of T and q on the fire environment will be different. An essential element of our HDW formulation is that the key quantity for assessing the amount of possible evaporation is the difference—not the ratio—between e
s and e at a given temperature [
17]; larger differences between e
s and e are associated with larger evaporation rates in plant environments (e.g., [
18,
19]). A common variable for assessing the effect of the difference between e
s and e in a fire environment is the vapor pressure deficit (VPD; e.g., [
19,
20,
21,
22,
23,
24]):
VPD better accounts for the combined effect of temperature and moisture because a larger (smaller) VPD directly correlates to a faster (slower) evaporation rate, which is in turn associated with a greater (lesser) potential for the atmosphere to affect a fire.
To calculate HDW, we simply multiply the wind speed (U) by the VPD:
Using an index based on wind speed multiplied by the VPD ensures that HDW will be applicable everywhere because wind speed, temperature, and humidity can be observed or simulated at any point in the Earth’s atmosphere. Since both U and VPD are continuously varying quantities that are greater than or equal to zero, HDW values will always be greater than or equal to zero. This also means that HDW will be continuous, with none of the artificial break points or sign changes that occur in other indices (e.g., the HI, [
2], the Fosberg Fire Weather Index, [
10,
11], the National Fire Danger Rating System, [
25,
26]). We acknowledge that simply multiplying U and VPD is a limitation of HDW, but it appears to work at a basic level because our analyses have indicated that this simple formulation is able to discriminate the “worst” days on a given fire. Additional testing of other formulations could be undertaken to determine if more skillful combinations of U and VPD exist. For simplicity, HDW uses common meteorological units: m s
−1 for wind speed and hPa for VPD.
The depth of the atmosphere that will affect a fire can vary greatly from one fire to another, so we developed HDW to consider the weather conditions that are most likely to interact with the surface during the burning period on a given day. The daytime mixed layer is nearly always >500 m deep over land everywhere in the world (particularly on days when wildland fires are active), so we define HDW to use a 500-m layer just above the surface for its weather information. Choosing a deeper analysis layer (e.g., 1000 m or greater) would more often introduce weather conditions at some locations into HDW that would not affect a fire; the top of the deeper analysis layer will often be above the top of the observed mixed layer and air above the boundary layer is far less likely to affect the fire directly.
We also want HDW to identify the potential for the worst fire conditions due to large-scale weather effects, so, for a given instant in time, we compute the surface-adjusted VPD that would result from adiabatically lowering air from each level in the lowest 500 m to the surface. We then select the highest wind speed and the highest surface-adjusted VPD from any level in the lowest 500 m to calculate HDW. This means that the maximum VPD value and maximum wind speed might occur at different vertical levels, but near-surface mixing makes it possible that both the extracted VPD and wind speed maxima could affect the fire at some time on a given day.
Since we want to assess the influence of predictable, large-scale components of weather forecasts at multiple-day lead times, we also need to define a valid time scale to achieve this goal. Taking the maximum HDW value for each day will produce a fire weather forecast that indicates the potential for a fire to become difficult to manage in a multi-day comparative analysis. That day can then be analyzed further to focus on the atmospheric features that caused a given day’s HDW value to peak and assess how those features might affect a fire.
Finally, since HDW is not derived from a physical or dynamical formula that applies to fire activity, the units of HDW do not have an established physical significance for fire processes. To limit the potential for confusion among prospective users of the index, we recommend that units of hPa be used for the VPD and that units of m s−1 be used for U when calculating the value of HDW, but that the units of HDW (hPa m s−1) be ignored.
3. Evaluating HDW with Historical Fires
HDW needs to identify days when historical fires were difficult to manage if it is to have value as a forecast index. In this section, we demonstrate the application of HDW to four wildfires in the United States that represent a range of topographic and meteorological conditions in which fire behavior made a fire difficult to manage, since weather conditions, and in particular diurnal variations in near-surface weather, are strongly dependent upon topography. To do this, we need a meteorological dataset that is consistent over a long period of time with sufficient temporal and spatial resolution to assess the influence of predictable, synoptic-and meso-alpha-scale components of weather forecasts at multiple-day lead times. NCEP’s Climate Forecast System Reanalysis (CFSR; [
27]) was chosen as the best dataset for this analysis. The CFSR has 0.5-degree grid spacing, begins in 1979, covers the entire Earth, has a sufficiently small grid spacing that can resolve synoptic and meso-alpha processes, is being updated in near-real-time as the Climate Forecast System (CFSv2; [
28]), and is freely available. Because the vertical resolution of the CFSR is somewhat coarse (either 25 or 50 hPa intervals), we calculate HDW using the maximum wind speed and VPD from the surface and every pressure level up to and including the first level above 50 hPa above the surface. In most locations, 50 hPa above the surface is close to 500 m above the surface, which is the level we identified in the previous section as desirable for HDW. The choice of a 50 hPa-deep layer ensures that there are always at least three model levels used in the analysis: the surface, the first level above the surface, and the first level above 50 hPa. At CFSR grid points where the surface pressure is greater than 800 hPa, four levels are used. CFSR has 6-h output, so we take the maximum HDW value for each data point from 1200, 1800, and 0000 UTC (approximately the daytime period for most of the United States).
Table 1 lists the names and locations of the fires we selected and the day on each fire that exhibited the most significant fire behavior according to fire reports. For each fire, we present a 29-day time series of HDW using CFSR data at the land-based point closest to the starting location of the fire, centered on the day when the fire was most difficult to manage. Early HDW testers requested a comparison to the HI, which is the only fire weather index that is widely used operationally to predict when above-ground weather conditions will make a wildland fire difficult to manage. To compare HDW with the HI, we also present the Low, Mid, and High variants of the HI for the same time series using the same CFSR data used to calculate HDW. For calculating the HI, we follow the methodology recommended in Ref. [
2] and use 0000-UTC data to find the lapse rate and dewpoint depression required for each HI variant. Note that HI does not include any information about winds. We depart from the methodology recommended in Ref. [
2] by presenting all three variants at each location for comparison with HDW, rather than choosing a single variant based on the climatic divisions identified in the paper. For reference, we highlight the variant that should be used at each location based on the climatic divisions identified in that paper.
3.1. Pagami Creek Fire (MN, 2011)
We begin with the Pagami Creek Fire, a 37,507-ha fire that occurred in the Boundary Waters Canoe Area Wilderness of the Superior National Forest in northern Minnesota, USA. The Pagami Creek Fire started on 18 August 2011 and continued to burn into November. Sexton et al. [
29] identifies 12 September as the date on which the most “active fire behavior” was reported.
Figure 1a shows a time series of HDW from 29 August through 26 September for the CFSR grid point closest to the fire location. The time series indicates that HDW spiked on 12 September, so HDW identified the date on which the most active fire behavior occurred. This result suggests that the active fire behavior observed on 12 September was at least partially due to synoptic-and meso-alpha-scale weather features.
Figure 1b shows time series of the three HI variants for the same time period. None of the variants indicate a spike on 12 September, although the Low and Mid variants were a 5 on 11 September. However, the Mid variant reached a value of 6 on 8 September, and was a 5 on 9 September as well. Ref. [
29] identifies 11 September as a day on which active fire behavior occurred, but active fire behavior was not observed on the previous three days. Thus, HDW identifies the specific day on which the Pagami Creek Fire was most difficult to manage while the HI does not, although the HI may have had some value on other days for this event.
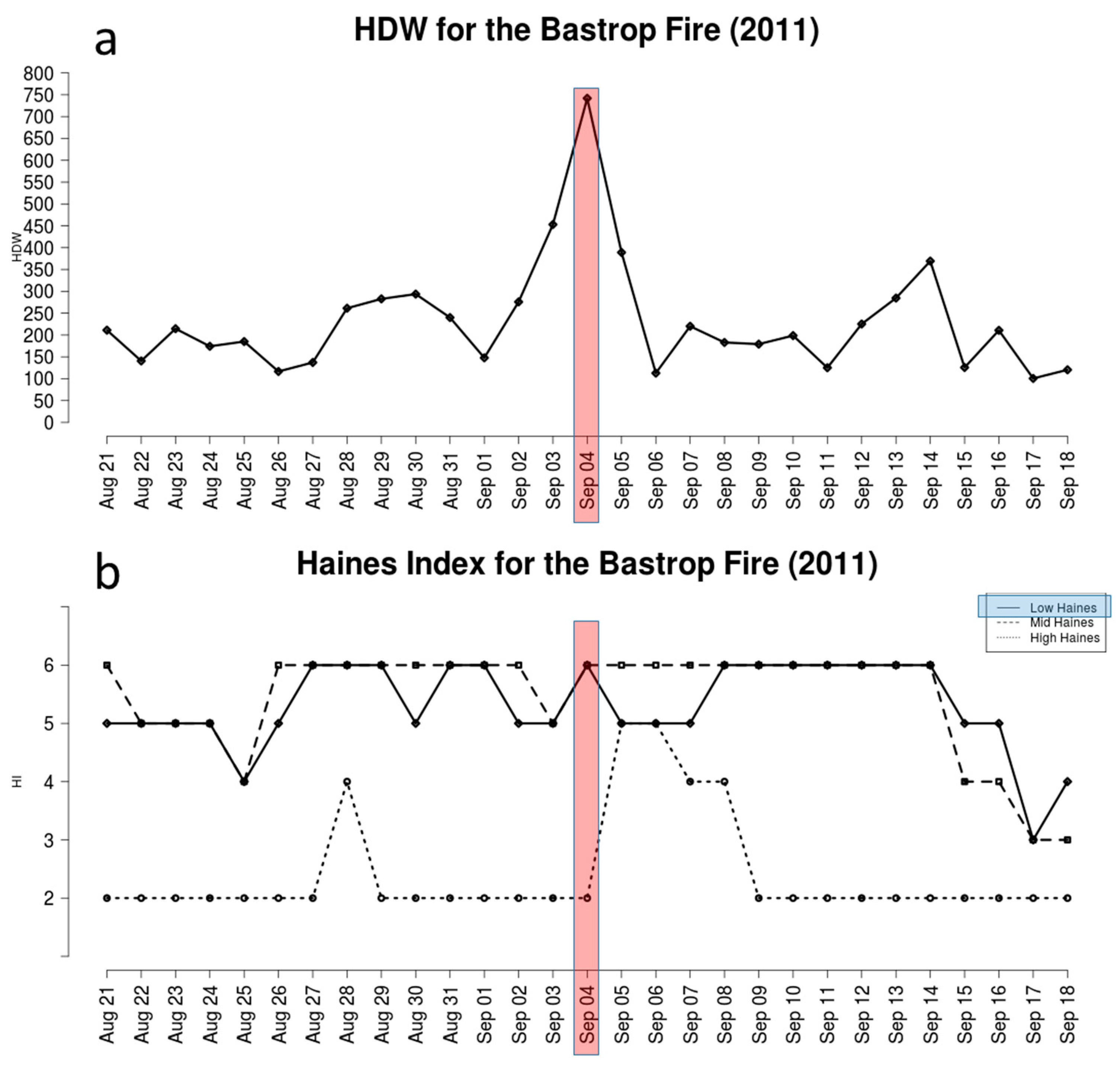
3.2. Bastrop County Complex (TX, 2011)
The Bastrop County Complex (2011) was a group of fires that occurred near Bastrop, TX, USA [
30,
31]. The fires burned 13,903 ha, destroyed 1799 structures, and caused two fatalities. The fires started on 4 September, which was also the day on which the most active fire behavior was reported, the largest area was burned, and the fires were most difficult to manage.
Figure 2 shows time series of HDW (
Figure 2a) and the three HI variants (
Figure 2b) from 21 August through 18 September. The HDW time series indicates a clear maximum on 4 September. The Low and Mid HI time series reach a value of 6 on 4 September, and the Low HI is higher on 4 September than on the days before and after. However, both the Low and Mid HI reach a value of 6 for multiple days earlier and later in the time series. This analysis shows that HDW can also identify days where an initiating fire may spread rapidly due to large-scale weather conditions, while the HI does not clearly differentiate the most difficult day from other days in the time series.
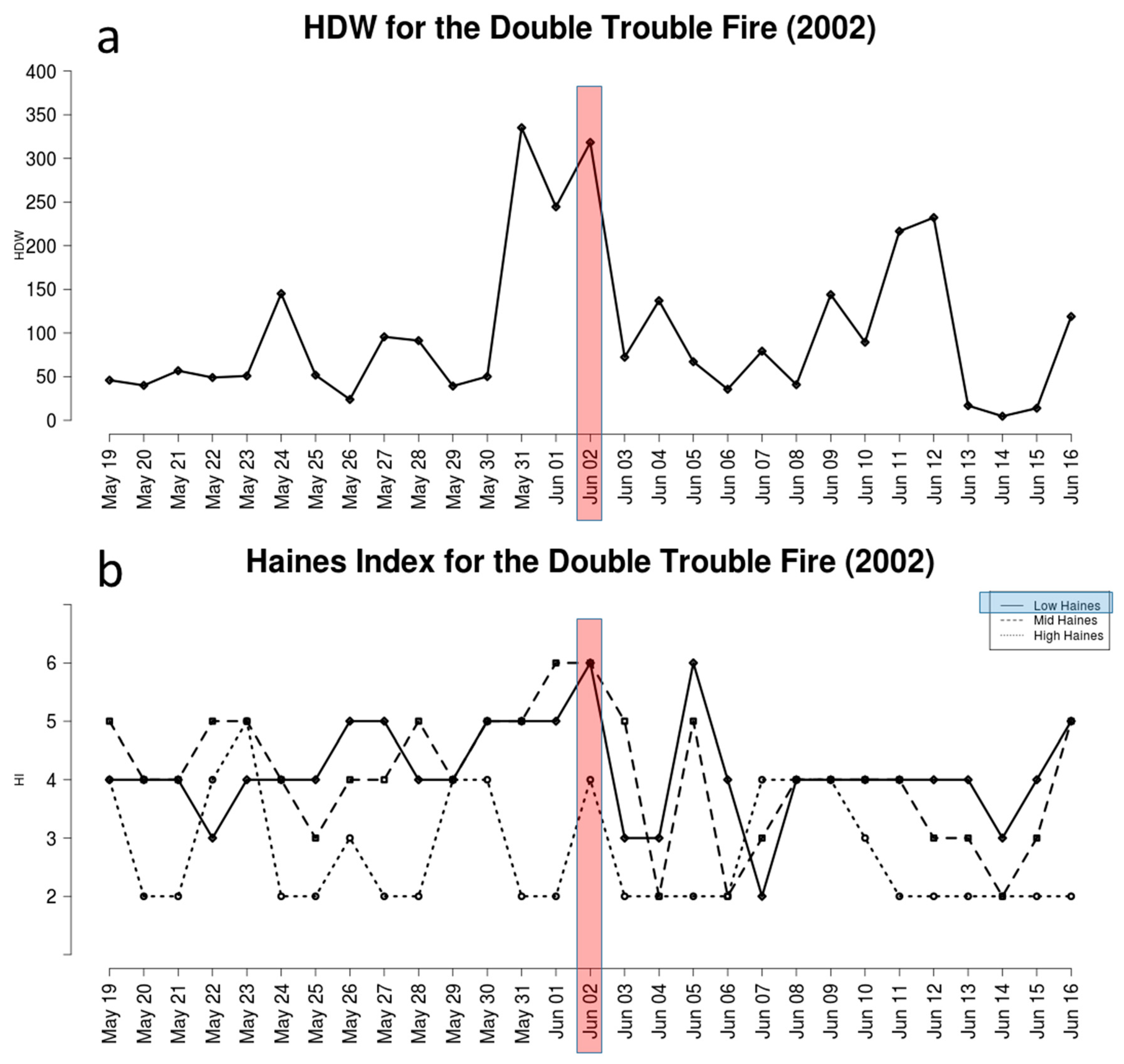
3.3. Double Trouble Fire (NJ, 2002)
Figure 3 presents time series of HDW and the HI variants for the Double Trouble Fire, which was a 526-ha, single-day event that occurred on 2 June near Beachwood, NJ, USA [
32,
33]. The HDW time series (
Figure 3a) shows that, for the period indicated in the figure, HDW was relatively high on 2 June. The analysis also shows that HDW was even higher on 31 May, two days earlier. Since there was no fire on that day at this location, it is not possible based on this analysis to state whether the higher HDW value on 31 May corresponded to a day on which active fire behavior would have occurred. This analysis suggests that HDW might have some value in identifying days where fires that were started (prescribed or otherwise) can become difficult to manage.
The time series of HI variants (
Figure 3b) show the Low and Mid HI reaching values of 5 and 6, respectively, on the day of the fire, but the HI exhibits similar values on days before and after the fire. It is also noteworthy that HI on 31 May is similar to several other days in the time series, while HDW reached its highest point in the time series on that date.
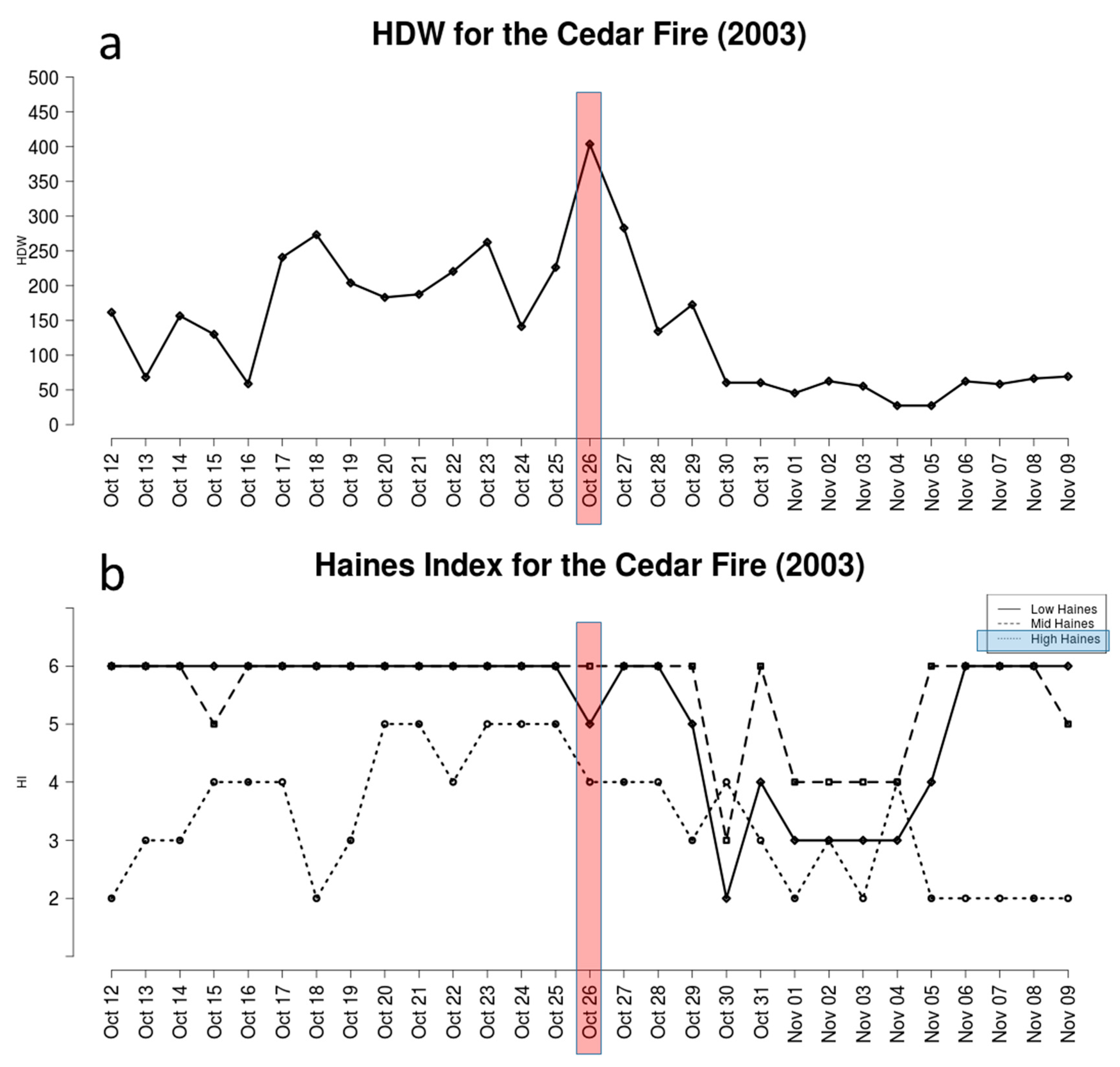
3.4. Cedar Fire (CA, 2003)
The 2003 Cedar Fire burned 113,424 ha near Julian, CA, USA, destroyed 355 structures, and destroyed 151 vehicles [
34]. The fire started on 23 October and spread rapidly toward the west, with the largest spread day occurring on 26 October as a Santa Ana wind event developed [
35]. Countryman et al. [
36] indicates that Santa Ana weather events often exacerbate wildfires that burn large areas in the autumn and winter in southern California, USA. Since Santa Ana events are characterized by strong winds, high temperatures, and low atmospheric moisture (large VPDs), HDW should generally be high during Santa Ana events. However, the spatial scale of the Santa Ana must be large enough to be resolved in the CFSR dataset for our analysis to be able to diagnose the resulting atmospheric effects.
Figure 4 shows time series of HDW (
Figure 4a) and the three HI variants (
Figure 4b). As with the three previous fires we analyzed, the HDW time series indicates a clear maximum on the day when the fire was most difficult to manage. Unlike most days when the maximum HDW comes from 1800 or 0000 UTC (driven largely by daytime heating), the maximum HDW for 26 October at this point occurred at 1200 UTC, when the Santa Ana event was strongest. None of the HI variants indicate that 26 October should significantly differ from other days in the time series, most likely because the HI does not consider wind, which was one of the most important weather parameters for the spread of the Cedar Fire.
4. Discussion and Conclusions
We have developed HDW and investigated its ability to assess the influence of predictable, synoptic- and meso-alpha-scale components of weather forecasts on wildland fires. HDW is calculated by multiplying the vapor pressure deficit by the wind speed, which accounts for whether a fire could become difficult to manage due to “hot and dry” and “windy” conditions, respectively. To account for vertical variations in heat, moisture, and wind speed and to help forecast the potential for the worst conditions that could affect a fire, HDW is defined as the product of the largest VPD and the highest wind speed in a 500-m layer just above the surface. HDW is compared with the HI using CFSR model output valid for four historical fires.
Our results indicate that HDW can identify days on which synoptic-and meso-alpha-scale weather processes can contribute to especially dangerous fire behavior. HDW is also shown to perform better than the HI when attempting to identify the day (or days) during each fire that has the potential to be the most difficult to manage. While one or more variants of the HI reach high values on the day of interest for some of the fires, HDW demonstrates superiority for this selection of fires that occurred in different regions and that span a range of environmental conditions.
Additionally, it should be noted that since HDW is based on the meteorological variables that govern the physics of fire processes, it is possible to speculate on why HDW would not be an effective index in some cases. The HI, in contrast, does not have a physical basis, which makes speculation on why it works or does not work difficult because the mechanisms are not clear.
By focusing on the multiple-day, predictable components of weather forecasts (i.e., synoptic-and meso-alpha-scale processes), HDW produces a forecast that fire weather forecasters and fire managers can use to anticipate when large-scale weather could make a wildland fire difficult to manage. Because of this formulation, it is necessary for the fire manager to be aware of the potential for fine-scale weather, topography, and fuel conditions to affect fire behavior and contribute to major management difficulties—HDW will, by definition, miss those effects. Furthermore, even when HDW does identify an anomalously high-risk day, it is always possible for local conditions to decrease or further increase the management difficulties.
The analysis presented here does not represent an exhaustive investigation of HDW across the full range of atmospheric phenomena that could affect whether a fire will become difficult to manage. For example, HDW as presented here should not be expected to detect frontal wind shifts or outflows from convective thunderstorms, which have a much shorter time scale than the CFSR input data. Additional analyses are necessary before HDW should be used as an operational, decision-informing forecast tool. These analyses include: (1) a statistical verification of the performance of the index against one or more fire metrics and comparisons of HDW with existing fire indices that include weather components; (2) climatological analyses to establish the significance of a particular value of HDW at a given location; (3) testing HDW with model forecast data to determine whether there are idiosyncrasies that develop from different sources of meteorological data with different model physics, temporal, and spatial resolutions; and (4) examinations of how alternative formulations of HDW (e.g., different analysis layers) vary on finer spatial and temporal scales (e.g., diurnal variations) to investigate its potential for anticipating the effect of wind shifts, thunderstorm outflows, firebrand transport and spotting, orographic circulations, and other complex phenomena during a wildland fire.